In-Situ X-ray Tomography Observation of Structure Evolution in 1,3,5-Triamino-2,4,6-Trinitrobenzene Based Polymer Bonded Explosive (TATB-PBX) under Thermo-Mechanical Loading
Abstract
:1. Introduction
2. Materials and Methods
3. Results
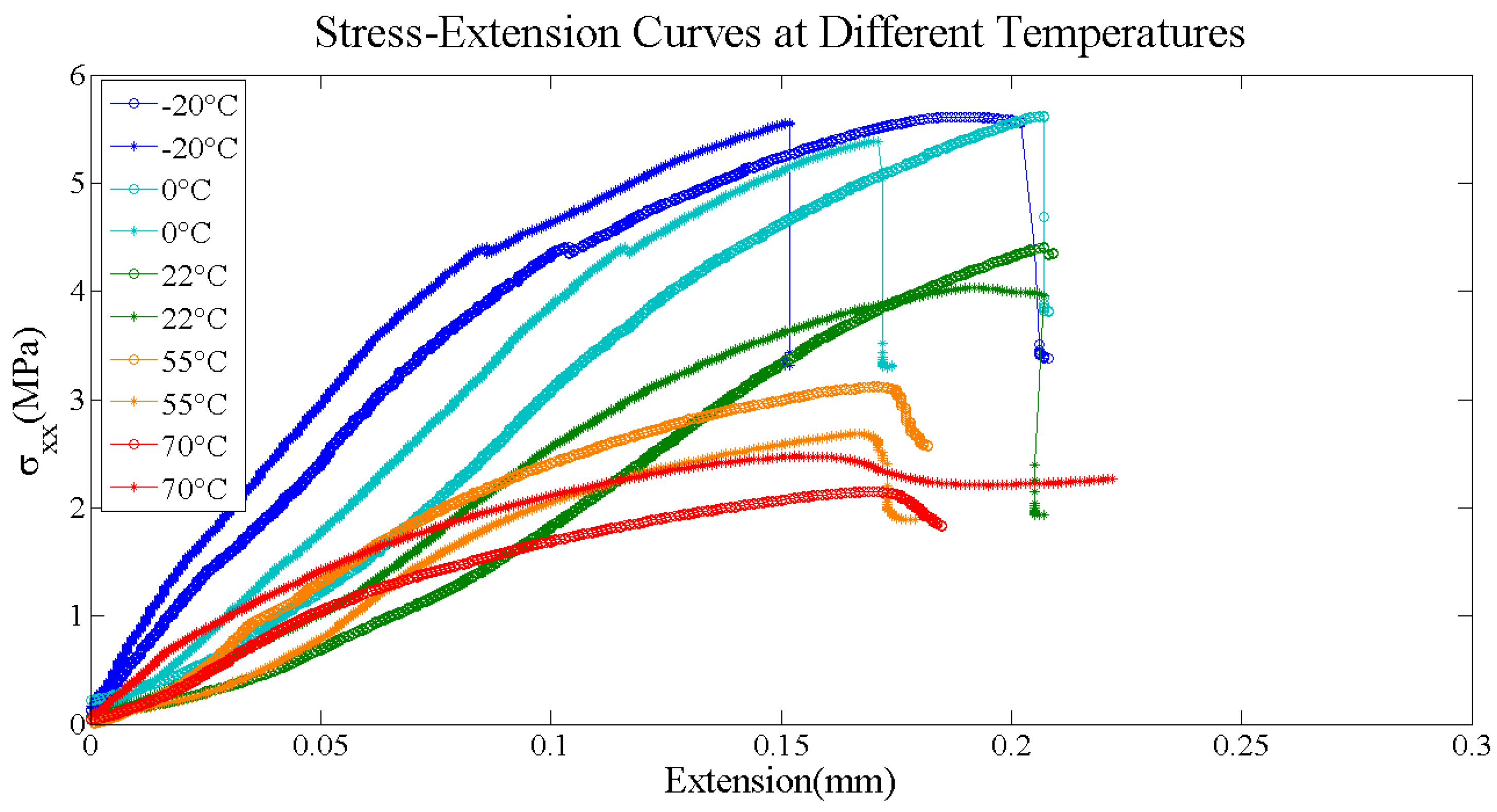
3.1. Stress-Extension Curves at Different Temperatures
3.2. CT Images and Digital Image Process
3.3. Fracture Mode Comparison
4. Discussion
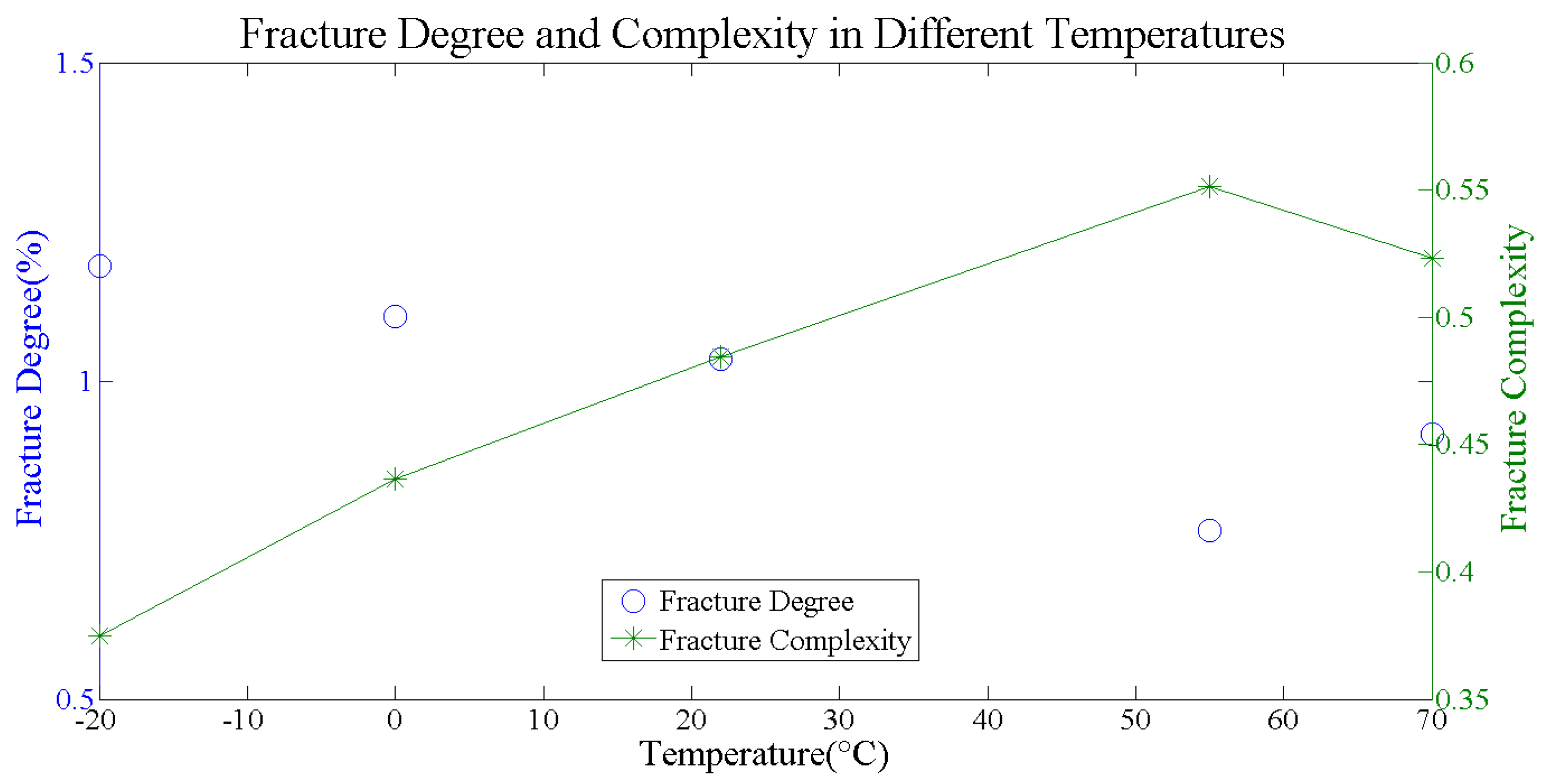
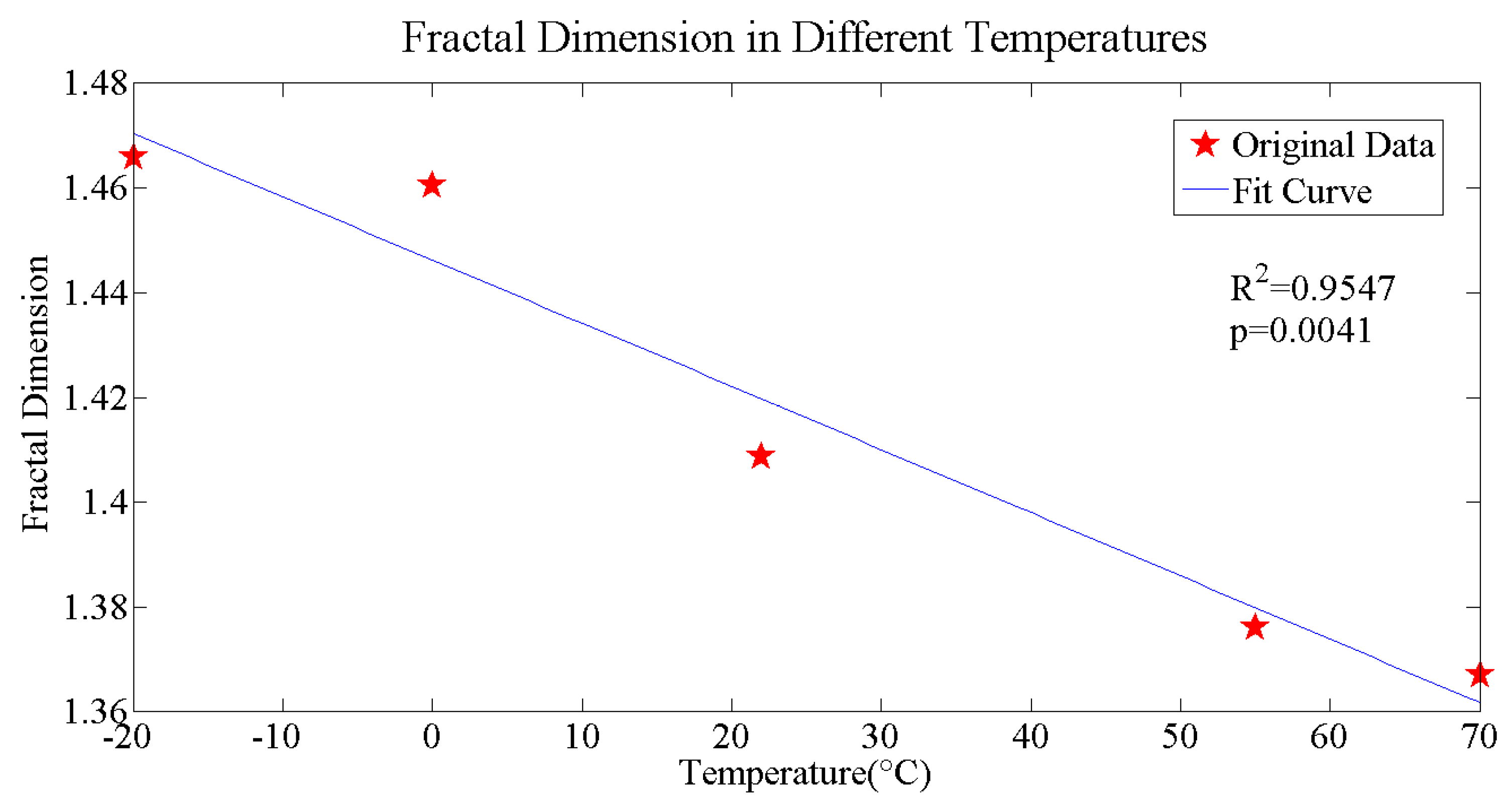
4.1. Degree, Complexity, and Fractal Dimension of Fracture
- choose a series of different sizes of cubes, ;
- use these cubes to fill the cracks, count the amount of cubes used, ; and,
- fit and .
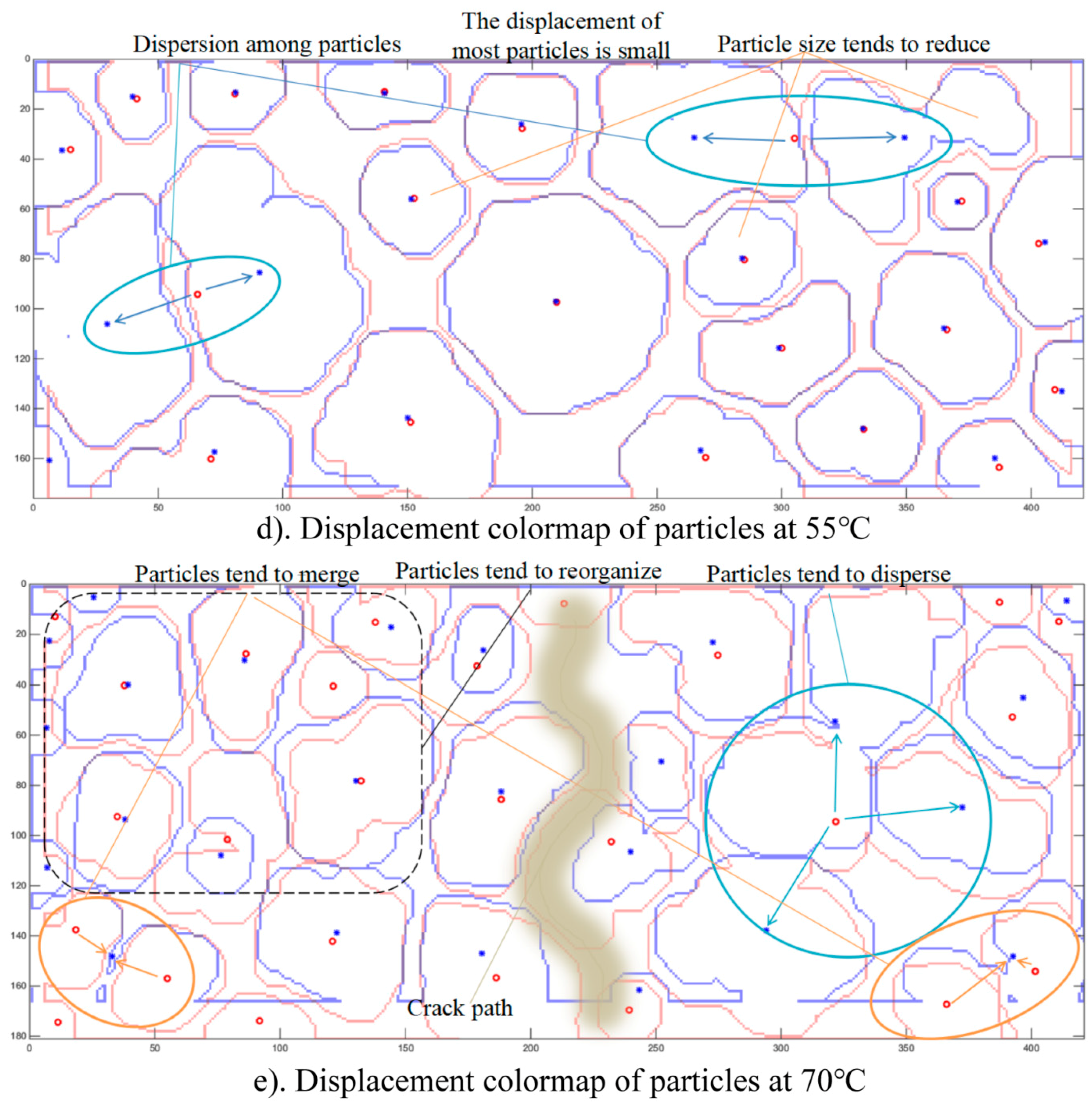
4.2. Interior Displacement Field of PBX
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Balzer, J.E.; Siviour, C.R.; Walley, S.M.; Proud, W.G.; Field, J.E. Behaviour of ammonium perchlorate-based propellants and a polymer-bonded explosive under impact loading. Proc. R. Soc. Lond. Ser. A 2004, 460, 781–806. [Google Scholar] [CrossRef]
- Barua, A.; Horie, Y.; Zhou, M. Energy localization in HMX-Estane polymer-bonded explosives during impact loading. J. Appl. Phys. 2012, 111, 399–586. [Google Scholar] [CrossRef]
- Tang, M.-F.; Li, M.; Lan, L.-G. Review on the mechanical properties of cast PBXs. Chin. J. Energ. Mater. 2013, 21, 812–817. [Google Scholar]
- Ellis, K.; Leppard, C.; Radesk, H. Mechanical properties and damage evaluation of a UK PBX. J. Mater. Sci. 2005, 40, 6241–6248. [Google Scholar] [CrossRef]
- Grantham, S.; Siviour, C.; Proud, W.; Field, J. High-strain rate Brazilian testing of an explosive simulant using speckle metrology. Meas. Sci. Technol. 2004, 15, 1867–1870. [Google Scholar] [CrossRef]
- Guo, B.-Q.; Xie, H.-M.; Chen, P.-W.; Zhang, Q.-M. Creep properties identification of PBX using digital image correlation. In Proceedings of the Fourth International Conference on Experimental Mechanics, Singapore, 18–20 November 2009. [Google Scholar]
- Tan, H.; Liu, C.; Huang, Y.; Geubelle, P. The cohesive law for the particle/matrix interfaces in high explosives. J. Mech. Phys. Solids 2005, 53, 1892–1917. [Google Scholar] [CrossRef]
- Zhou, Z.; Chen, P.-W.; Duan, Z.-P.; Huang, F.-L. Study on fracture behaviour of a polymer-bonded explosive simulant subjected to uniaxial compression using digital image correlation method. Strain 2012, 48, 326–332. [Google Scholar] [CrossRef]
- Chen, P.-W.; Huang, F.-L.; Ding, Y.-S. Microstructure, deformation and failure of polymer bonded explosives. J. Mater. Sci. 2007, 42, 5257–5280. [Google Scholar] [CrossRef]
- Rae, P.J.; Goldrein, H.T.; Palmer, S.J.P.; Field, J.E.; Lewis, A.L. Quasi-static studies of the deformation and failure of β-HMX based polymer bonded explosives. Proc. R. Soc. A 2002, 458, 743–762. [Google Scholar] [CrossRef]
- Palmer, S.J.P.; Field, J.E.; Huntley, J.M. Deformation, strengths and strains to failure of polymer bonded explosives. Proc. R. Soc. Lond. A 1993, 440, 399–419. [Google Scholar] [CrossRef]
- Hu, Z.; Luo, H.; Bardenhagen, S.G. Internal deformation measurement of polymer bonded sugar in compression by digital volume correlation of in-situ tomography. Exp. Mech. 2015, 55, 289–300. [Google Scholar] [CrossRef]
- Xue, C.; Sun, J.; Kang, B.; Liu, Y.; Liu, X.-F.; Song, G.-B.; Xue, Q.-B. The β−δ-phase transition and thermal expansion of octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine. Propellants Explos. Pyrotech. 2010, 35, 333–338. [Google Scholar] [CrossRef]
- Zhou, H.P.; Pang, H.Y.; Wen, M.P.; Li, J.-M.; Li, M. Comparative studies on the mechanical properties of three kinds of binders. Mater. Rev. 2009, 23, 34–36. [Google Scholar]
- Willey, T.M.; Lauderbach, L.; Gagliardi, F.; van Buuren, T.; Glascoe, E.A.; Tringe, J.W.; Lee, J.R.I.; Springer, H.K.; Ilavsky, J. Mesoscale evolution of voids and microstructural changes in HMX-based explosives during heating through the β-δ phase transition. J. Appl. Phys. 2015, 118, 055901. [Google Scholar] [CrossRef]
- Wang, X.-J.; Wu, Y.-Q.; Huang, F.-L.; Jiao, T.; Clifton, R.J. Mesoscale thermal-mechanical analysis of impacted granular and polymer-bonded explosives. Mech. Mater. 2016, 99, 68–78. [Google Scholar] [CrossRef]
- Wang, X.-J.; Wu, Y.-Q.; Huang, F.-L. Thermal–mechanical–chemical responses of polymer-bonded explosives using a mesoscopic reactive model under impact loading. J. Hazard. Mater. 2017, 321, 256–267. [Google Scholar] [CrossRef] [PubMed]
- Williamson, D.M.; Siviour, C.R.; Proud, W.G.; Palmer, S.J.P.; Govier, R.; Ellis, K.; Blackwell, P.; Leppard, C. Temperature–time response of a polymer bonded explosive in compression (EDC37). J. Phys. D Appl. Phys, 2008, 41, 085404. [Google Scholar] [CrossRef]
- Çolak, Ö.Ü. Mechanical behavior of PBXW-128 and PBXN-110 under uniaxial and multiaxial compression at different strain rates and temperatures. J. Test. Eval. 2004, 32, 390–395. [Google Scholar] [CrossRef]
- Thompson, D.G.; Deluca, R.; Brown, G.W. Time–temperature analysis, tension and compression in PBXs. J. Energ. Mater. 2012, 30, 299–323. [Google Scholar] [CrossRef]
- Tang, M.-F.; Wen, M.-P.; Tu, X.-Z.; Lan, L.-G.; Dai, X.-G. Influence and mechanism of high temperature and mechanical stress on the mechanical behaviors of PBXs. Chin. J. Energ. Mater. 2018, 26, 150–155. [Google Scholar]
- Liu, Z.-W.; Xie, H.-M.; Li, K.-X.; Chen, P.-W.; Huang, F.L. Fracture behavior of PBX simulation subject to combined thermal and mechanical loads. Polym. Test. 2009, 28, 627–635. [Google Scholar] [CrossRef]
- Awaji, H.; Sato, S. Diametral compressive testing method. J. Eng. Mater. Technol. 1979, 101, 139–147. [Google Scholar] [CrossRef]
- Pang, H.-Y.; Li, M.; Wen, M.-P.; Lan, L.-G.; Jing, S.-M. Comparison on the Brazilian test and tension test of the PBX. Chin. J. Energ. Mater. 2011, 34, 42–45. [Google Scholar]
- Pang, H.-Y.; Li, M.; Wen, M.-P.; Lan, L.-G.; Jing, S.-M. Different loading methods in Brazilian test for PBX. Chin. J. Energ. Mater. 2012, 20, 205–209. [Google Scholar]
- Epstein, N. On tortuosity and the tortuosity factor in flow and diffusion through porous media. Chem. Eng. Sci. 1989, 44, 777–779. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Wheeler, J.A. The fractal geometry of nature. Am. J. Phys. 1983, 51, 468. [Google Scholar] [CrossRef]
- Mecholsky, J.J.; Passoja, D.E.; Feinberg-Ringel, K.S. Quantitative analysis of brittle fracture surfaces using fractal geometry. J. Am. Ceram. Soc. 1989, 72, 60–65. [Google Scholar] [CrossRef]
- Horovistiz, A.L.; de Campos, K.A.; Shibata, S.; Prado, C.C.S.; de Oliveira Hein, L.R. Fractal characterization of brittle fracture in ceramics under mode I stress loading. Mater. Sci. Eng A 2010, 527, 4847–4850. [Google Scholar] [CrossRef]
- Khanbareh, H.; Wu, X.; Zwaag, S. Analysis of the fractal dimension of grain boundaries of AA7050 aluminum alloys and its relationship to fracture toughness. J. Mater. Sci. 2012, 47, 6246–6253. [Google Scholar] [CrossRef]
- Hilders, O.; Zambrano, N. The effect of aging on impact toughness and fracture surface fractal dimension in SAF 2507 super duplex stainless steel. J. Microsc. Ultrastruct. 2014, 2, 236–244. [Google Scholar] [CrossRef]
- Xie, H.-P.; Chen, Z.-D. Fractal geometry and fracture of rock. Acta Mech. Sinica 1988, 4, 255–264. [Google Scholar]
- Zheng, G.-M.; Zhao, J.; Li, L.; Cheng, X.; Wang, M. A fractal analysis of the crack extension paths in a Si3N4 ceramic tool composite. Int. J. Refract. Met. Hard Mater. 2015, 51, 160–168. [Google Scholar] [CrossRef]
- Cheng, K.-M.; Liu, X.-Y.; Guan, D.-B.; Xu, T.; Wei, Z. Fractal analysis of TATB-based explosive AFM morphology at different conditions. Propellants Explos. Pyrotech. 2007, 32, 301–306. [Google Scholar] [CrossRef]





© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, Z.-N.; Chen, H.; Li, J.-M.; Dai, B.; Zhang, W.-B. In-Situ X-ray Tomography Observation of Structure Evolution in 1,3,5-Triamino-2,4,6-Trinitrobenzene Based Polymer Bonded Explosive (TATB-PBX) under Thermo-Mechanical Loading. Materials 2018, 11, 732. https://doi.org/10.3390/ma11050732
Yuan Z-N, Chen H, Li J-M, Dai B, Zhang W-B. In-Situ X-ray Tomography Observation of Structure Evolution in 1,3,5-Triamino-2,4,6-Trinitrobenzene Based Polymer Bonded Explosive (TATB-PBX) under Thermo-Mechanical Loading. Materials. 2018; 11(5):732. https://doi.org/10.3390/ma11050732
Chicago/Turabian StyleYuan, Zeng-Nian, Hua Chen, Jing-Ming Li, Bin Dai, and Wei-Bin Zhang. 2018. "In-Situ X-ray Tomography Observation of Structure Evolution in 1,3,5-Triamino-2,4,6-Trinitrobenzene Based Polymer Bonded Explosive (TATB-PBX) under Thermo-Mechanical Loading" Materials 11, no. 5: 732. https://doi.org/10.3390/ma11050732
APA StyleYuan, Z.-N., Chen, H., Li, J.-M., Dai, B., & Zhang, W.-B. (2018). In-Situ X-ray Tomography Observation of Structure Evolution in 1,3,5-Triamino-2,4,6-Trinitrobenzene Based Polymer Bonded Explosive (TATB-PBX) under Thermo-Mechanical Loading. Materials, 11(5), 732. https://doi.org/10.3390/ma11050732




