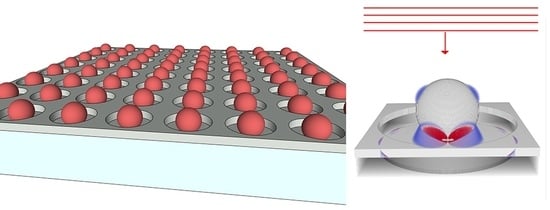
The Design and Optimization of Plasmonic Crystals for Surface Enhanced Raman Spectroscopy Using the Finite Difference Time Domain Method
Abstract
:1. Introduction
2. Results
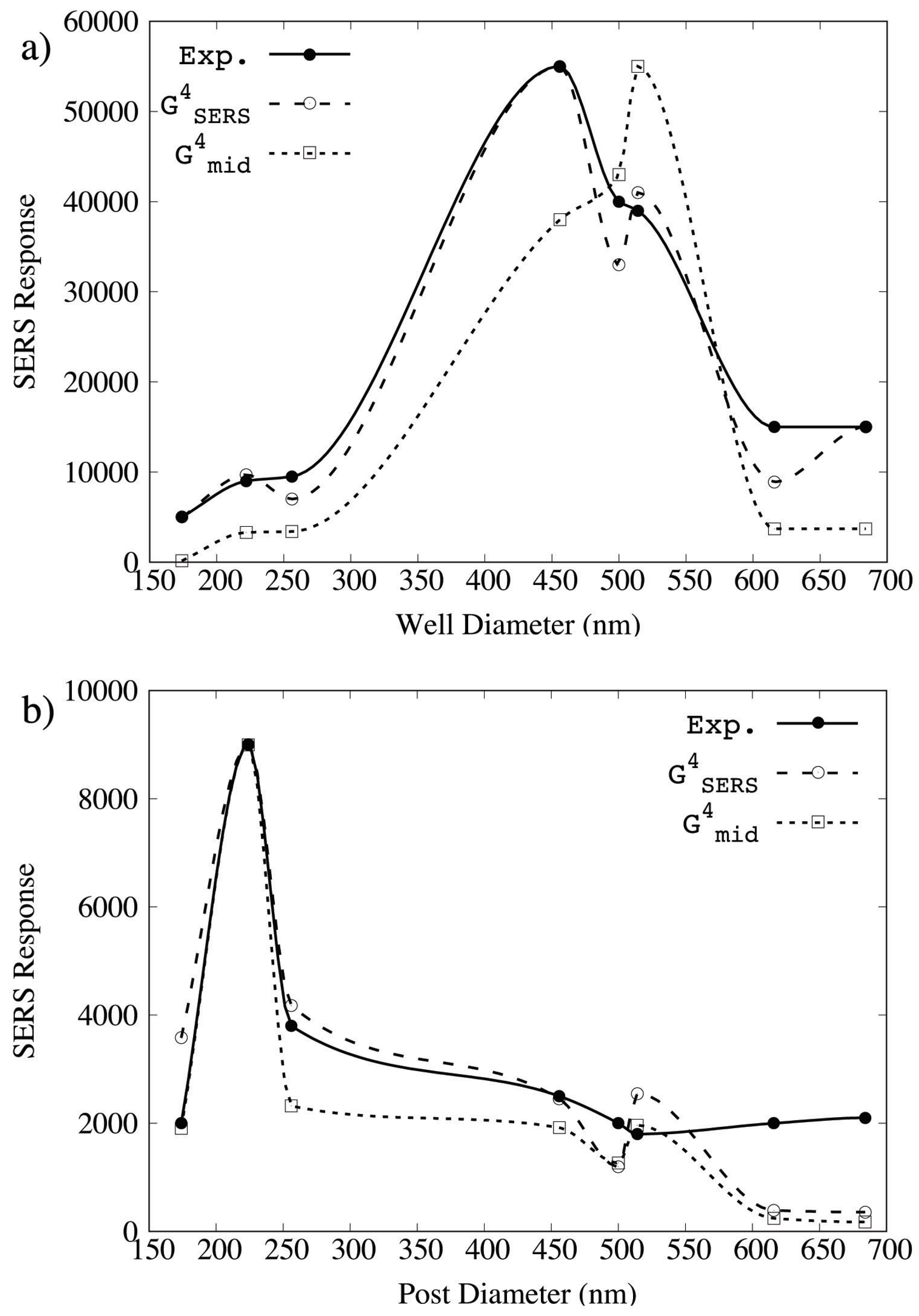
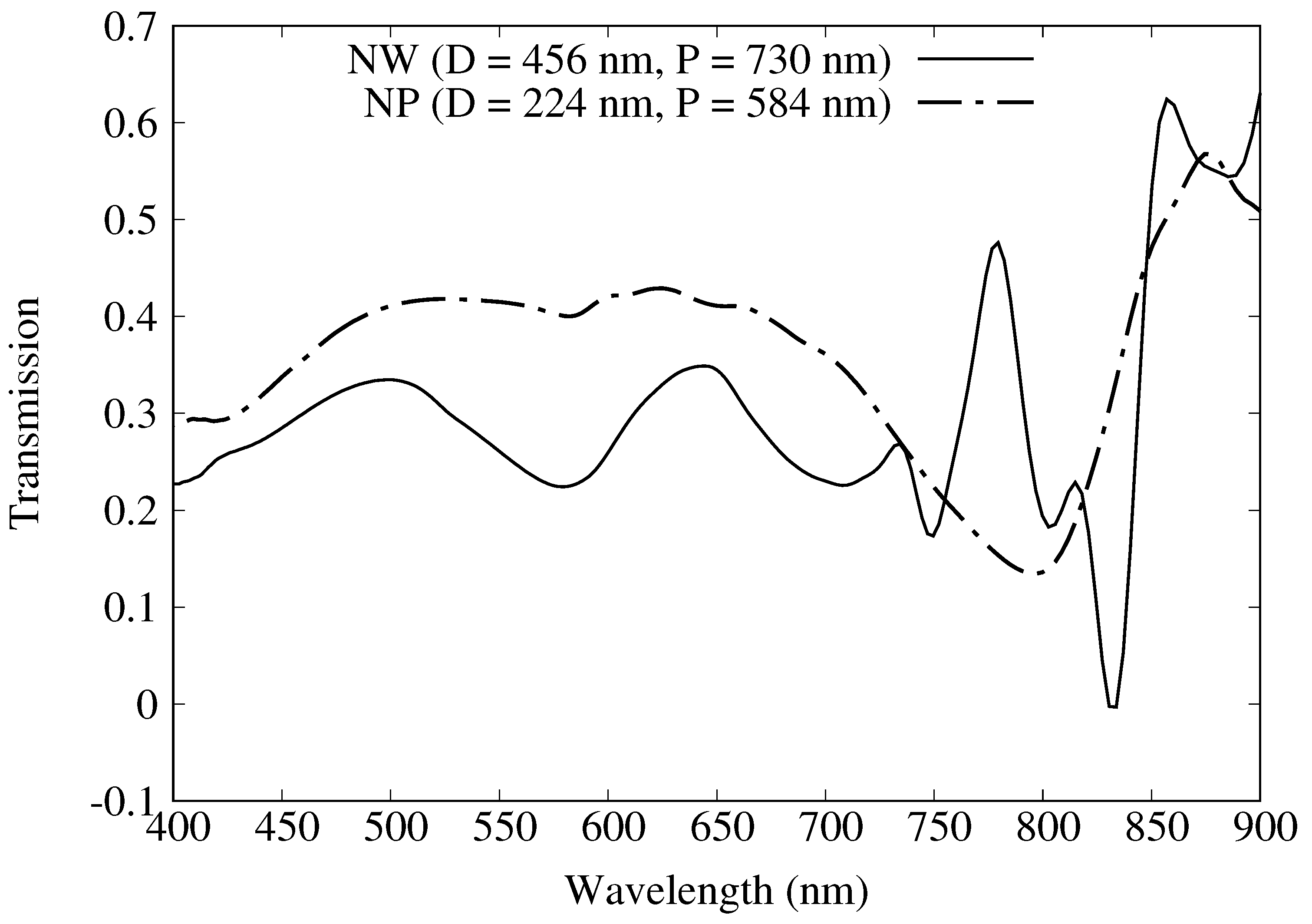
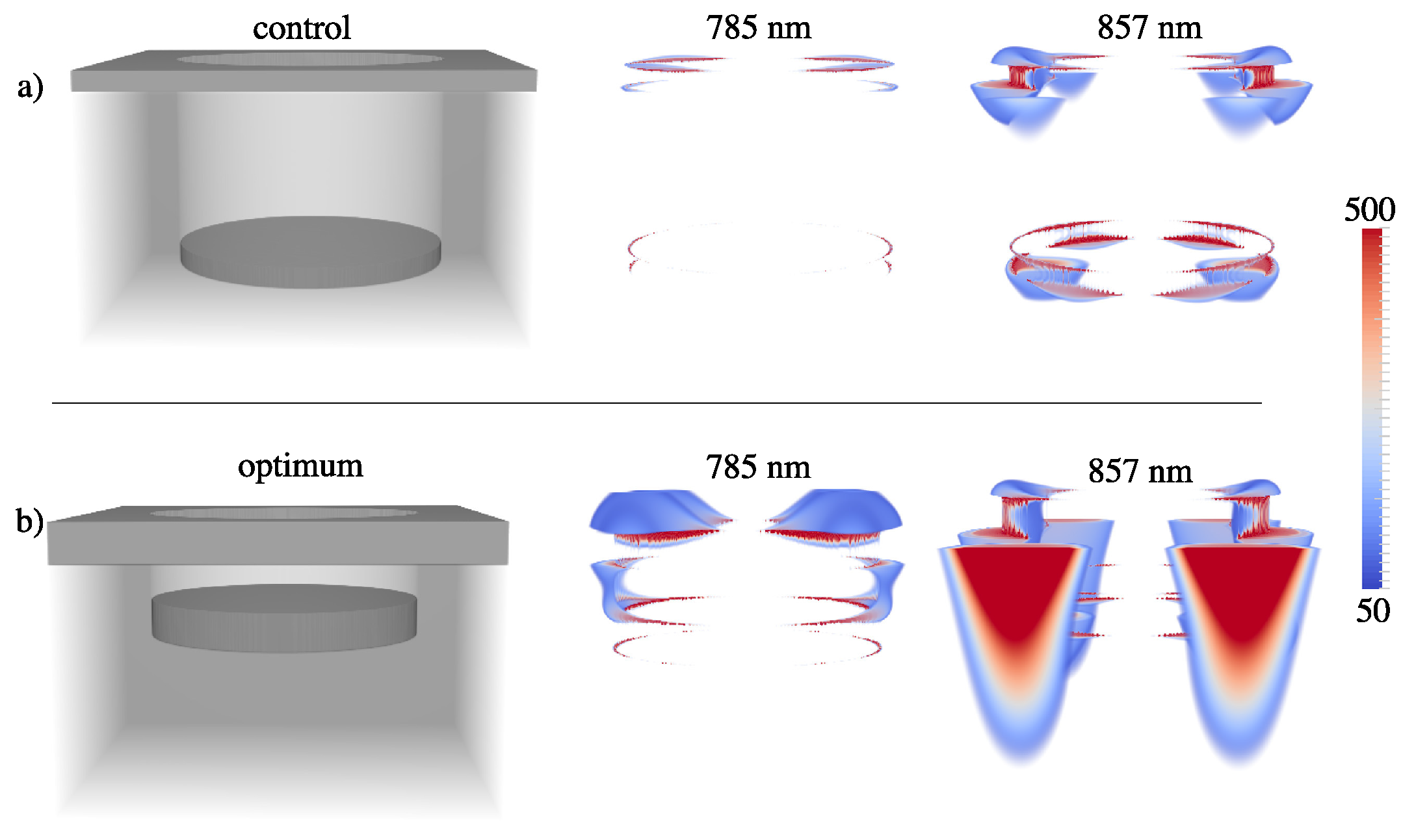
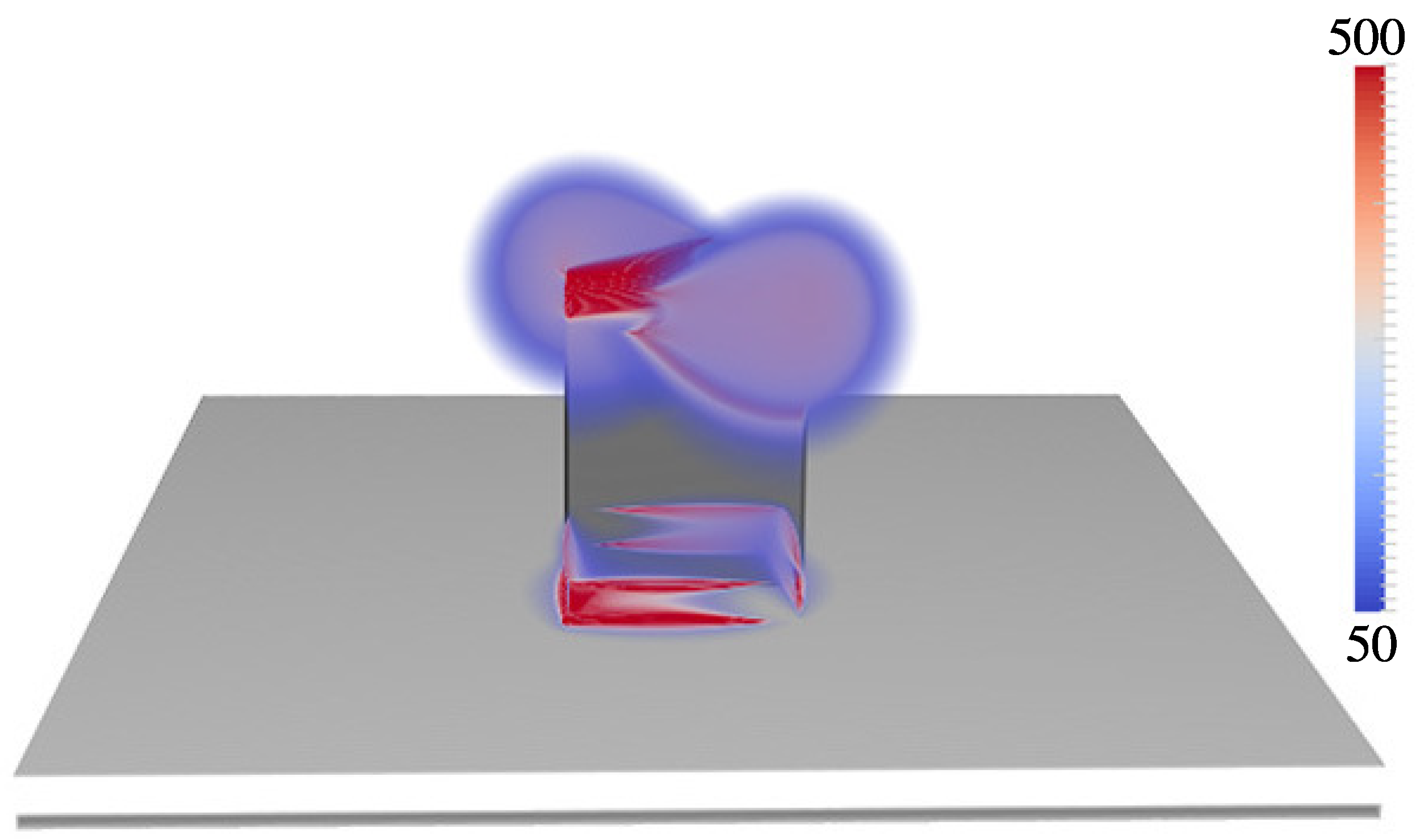
2.1. Comparison of FDTD Simulated SERS Responses for Nanowell and Nanopost Plasmonic Crystals
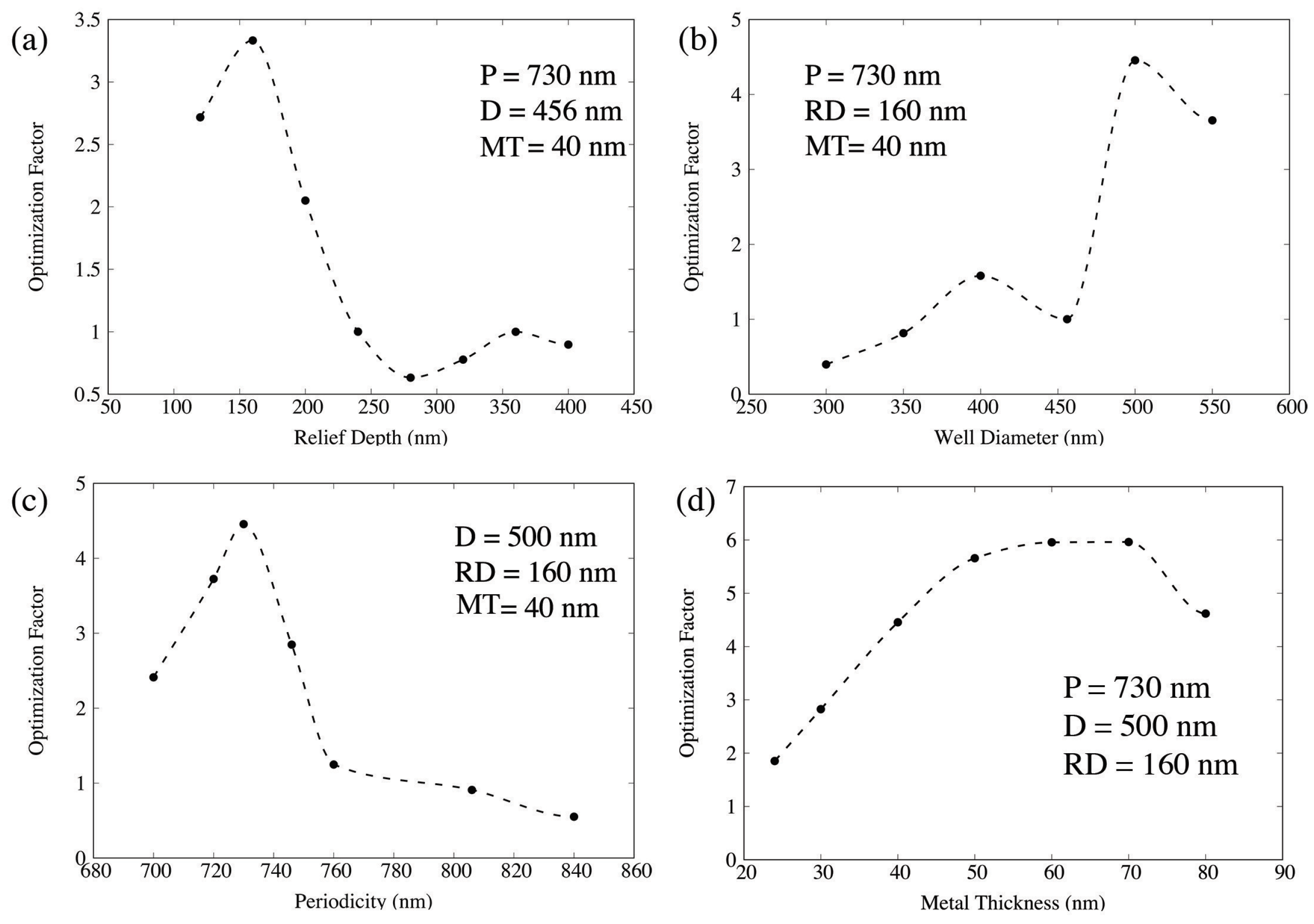
2.2. Optimization of FDTD Simulated SERS Responses for Nanowell and Nanopost Plasmonic Crystals
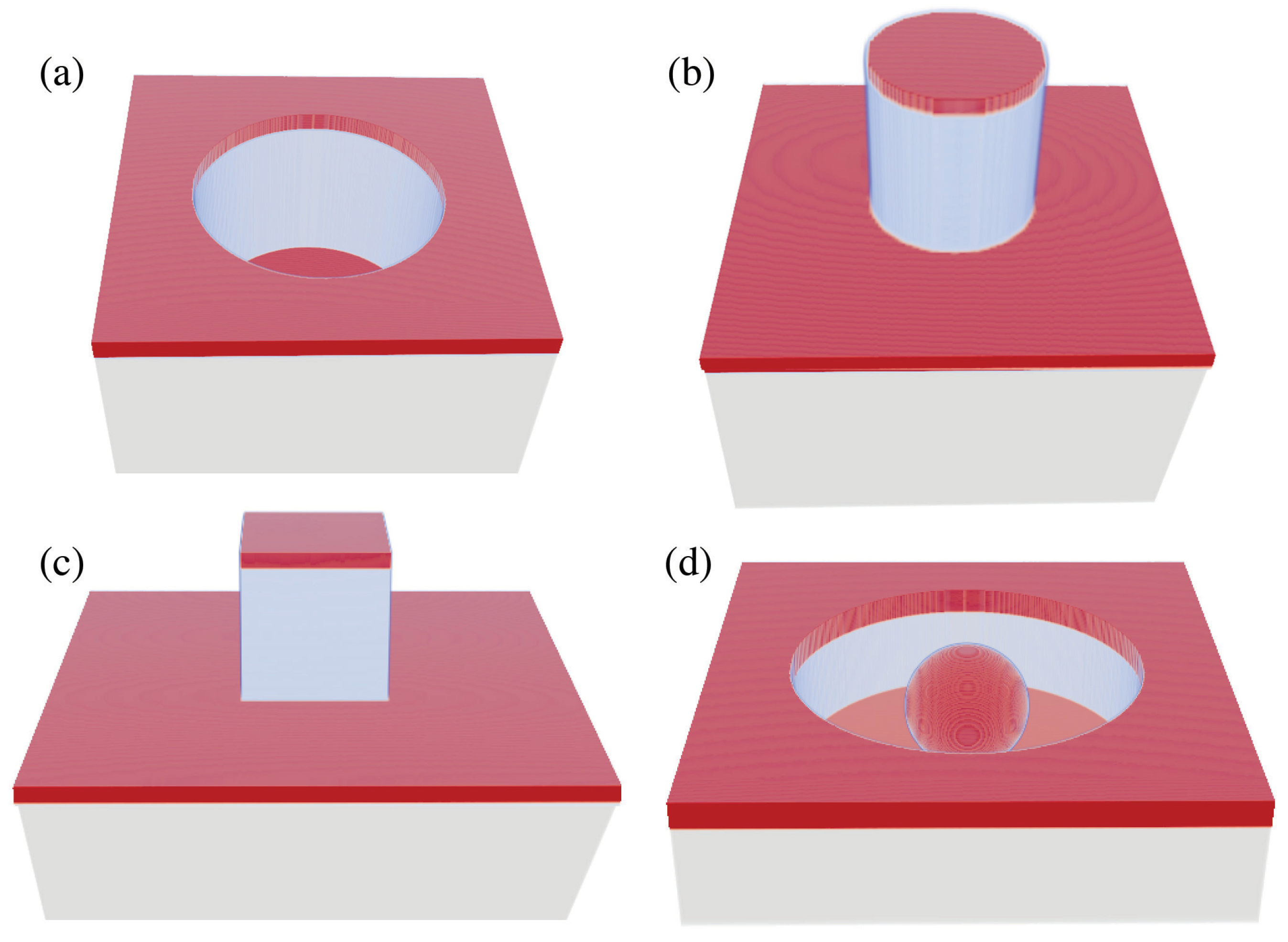
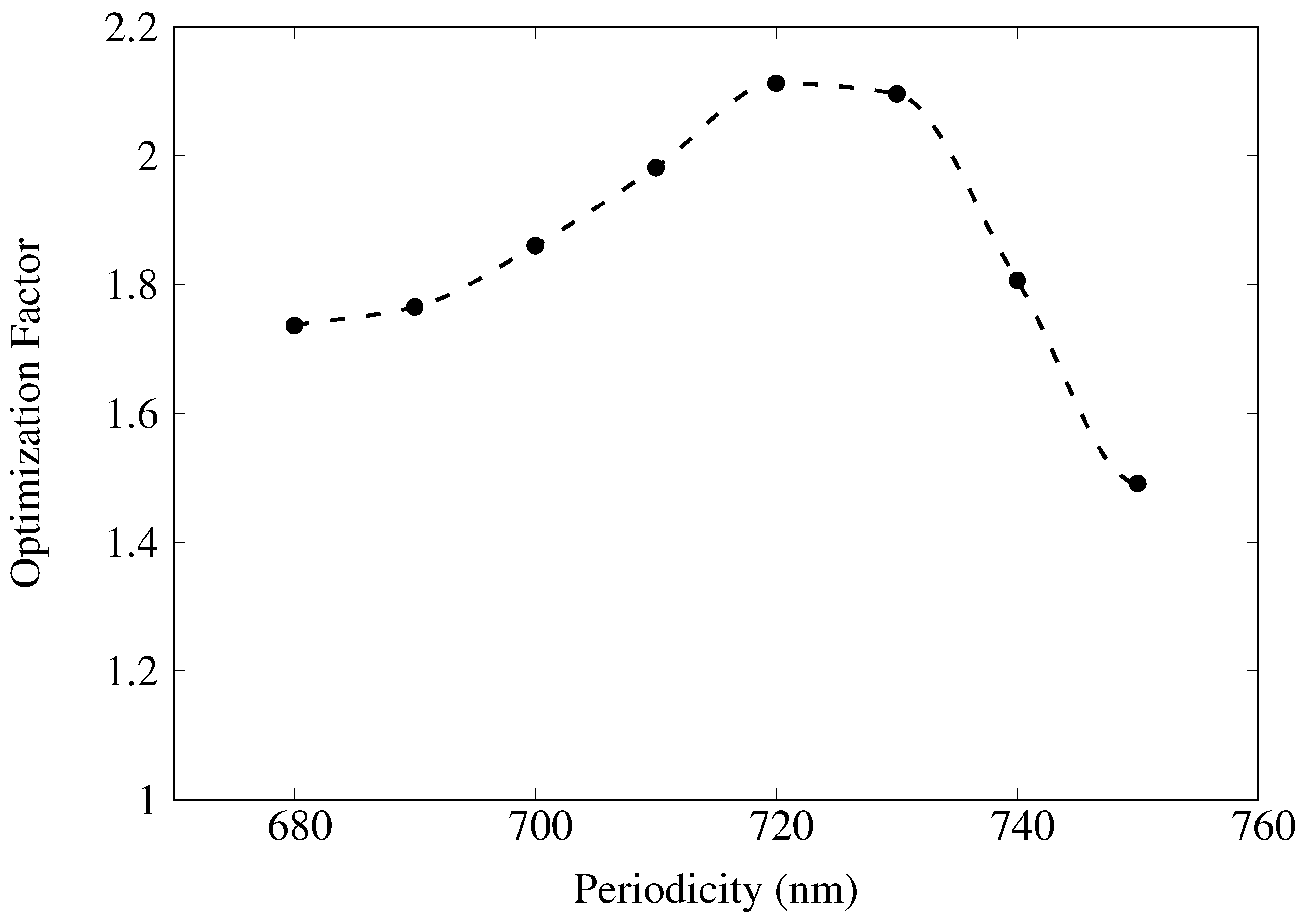
2.3. Optimization of FDTD Simulated SERS Responses for Novel Plasmonic Crystals
3. Discussion
4. Materials and Methods
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Fleischmann, M.; Hendra, P.J.; McQuillan, A.J. Raman spectra of pyridine adsorbed at a silver electrode. Chem. Phys. Lett. 1974, 26, 163–166. [Google Scholar] [CrossRef]
- Albrecht, M.G.; Creighton, J.A. Anomalously intense Raman spectra of pyridine at a silver electrode. J. Am. Chem. Soc. 1977, 99, 5215–5217. [Google Scholar] [CrossRef]
- Van Duyne, R.P.; Hulteen, J.C.; Treichel, D.A. Atomic force microscopy and surface-enhanced Raman spectroscopy. I. Silver island films and silver film over polymer nanosphere surfaces supported on glass. J. Chem. Phys. 1993, 99, 2101. [Google Scholar] [CrossRef]
- Raether, H. Surface Plasmons on Smooth and Rough Surfaces and on Gratings; Spring-Verlag: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; Wiley: New York, NY, USA, 1983. [Google Scholar]
- Kelly, K.L.; Coronado, E.; Zhao, L.L.; Schatz, G.C. The Optical Properties of Metal Nanoparticles: The Influence of Size, Shape, and Dielectric Environment. J. Phys. Chem. B 2003, 107, 668–677. [Google Scholar] [CrossRef]
- Eustis, S.; El-Sayed, M.A. Why gold nanoparticles are more precious than pretty gold: Noble metal surface plasmon resonance and its enhancement of the radiative and nonradiative properties of nanocrystals of different shapes. Chem. Soc. Rev. 2006, 305, 209–217. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.H.; Hulteen, J.; Schatz, G.C.; Van Duyne, R. A surface-enhanced hyper-Raman and surface-enhanced Raman scattering study of trans-1,2-bis(4-pyridyl)ethylene adsorbed onto silver film over nanosphere electrodes. Vibrational assignments: Experiment and theory. J. Chem. Phys. 1996, 104, 4313–4323. [Google Scholar] [CrossRef]
- Stewart, M.E.; Mack, N.H.; Malyarchuk, V.; Soares, J.A.N.T.; Lee, T.W.; Gray, S.K.; Nuzzo, R.G.; Rogers, J.A. Quantitative multispectral biosensing and 1D imaging using quasi-3D plasmonic crystals. Proc. Natl. Acad. Sci. USA 2006, 103, 17143–17148. [Google Scholar] [CrossRef] [PubMed]
- Stewart, M.E.; Anderton, C.R.; Thompson, L.B.; Maria, J.; Gray, S.K.; Rogers, J.A.; Nuzzo, R.G. Nanostructured Plasmonic Sensors. Chem. Rev. 2008, 108, 494–521. [Google Scholar] [CrossRef] [PubMed]
- Stewart, M.E.; Yao, J.; Maria, J.; Gray, S.K.; Rogers, J.A.; Nuzzo, R.G. Multispectral Thin Film Biosensing and Quantitative Imaging Using 3D Plasmonic Crystals. Anal. Chem. 2009, 81, 5980–5989. [Google Scholar] [CrossRef] [PubMed]
- Yao, J.; Le, A.P.; Schulmerich, M.V.; Maria, J.; Lee, T.W.; Gray, S.K.; Bhargava, R.; Rogers, J.A.; Nuzzo, R.G. Soft Embossing of Nanoscale Optical and Plasmonic Structures in Glass. ACS Nano 2011, 5, 5763–5774. [Google Scholar] [CrossRef] [PubMed]
- Baca, A.J.; Truong, T.T.; Cambrea, L.R.; Montgomery, J.M.; Gray, S.K.; Abdula, D.; Banks, T.R.; Yao, J.; Nuzzo, R.G.; Rogers, J.A. Molded plasmonic crystals for detecting and spatially imaging surface bound species by surface-enhanced Raman scattering. Appl. Phys. Lett. 2009, 94, 243109. [Google Scholar] [CrossRef]
- Baca, A.J.; Montgomery, J.M.; Cambrea, L.R.; Moran, M.; Johnson, L.; Yacoub, J.; Truong, T.T. Optimization of Nanopost Plasmonic Crystals for Surface Enhanced Raman Scattering. J. Phys. Chem. C 2011, 115, 7171–7178. [Google Scholar] [CrossRef]
- Taflove, A.; Hagness, S.C. Computational Electrodynamics: The Finite-Difference Time-Domain Method; Artech House: London, UK, 2000. [Google Scholar]
- Johnson, S.G.; Oskooi, A.; Taflove, A. (Eds.) Advances in FDTD Computational Electrodynamics: Photonics and Nanotechnology; Artech House: London, UK, 2013. [Google Scholar]
- Mayer, K.M.; Hafner, J.H. Localized Surface Plasmon Resonance Sensors. Chem. Rev. 2011, 111, 3828–3857. [Google Scholar] [CrossRef] [PubMed]
- Ungaro, C.; Gray, S.K.; Gupta, M.C. Graded-index structures for high-efficiency solar thermophotovoltaic emitting surfaces. Opt. Lett. 2014, 39, 5259–5262. [Google Scholar] [CrossRef] [PubMed]
- Ono, A.; Kato, J.i.; Kawata, S. Subwavelength Optical Imaging through a Metallic Nanorod Array. Phys. Rev. Lett. 2005, 95, 267407. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Dou, X.; Dai, Y.; Wang, X.; Min, C.; Yuan, X. All-optical manipulation of micrometer-sized metallic particles. Photon. Res. 2018, 6, 66–71. [Google Scholar] [CrossRef]
- Lu, H.; Gan, X.; Mao, D.; Jia, B.; Zhao, J. Flexibly tunable high-quality-factor induced transparency in plasmonic systems. Sci. Rep. 2018, 8, 1558. [Google Scholar] [CrossRef] [PubMed]
- Oubre, C.; Nordlander, P. Finite-difference Time-domain Studies of the Optical Properties of Nanoshell Dimers. J. Phys. Chem. B 2005, 109, 10042–10051. [Google Scholar] [CrossRef] [PubMed]
- Lal, S.; Grady, N.K.; Kundu, J.; Levin, C.S.; Lassiter, J.B.; Halas, N.J. Tailoring plasmonic substrates for surface enhanced spectroscopies. Chem. Soc. Rev. 2008, 37, 898–911. [Google Scholar] [CrossRef] [PubMed]
- Wang, A.X.; Kong, X. Review of Recent Progress of Plasmonic Materials and Nano-Structures for Surface- Enhanced Raman Scattering. Materials 2015, 8, 3024–3052. [Google Scholar] [CrossRef] [PubMed]
- Grimault, A.S.; Vial, A.; de la Chapelle, M.L. Modeling of regular gold nanostructures arrays for SERS applications using a 3D FDTD method. Appl. Phys. B 2006, 84, 111–115. [Google Scholar] [CrossRef]
- Baca, A.J.; Baca, J.; Montgomery, J.M.; Cambrea, L.R.; Funcheon, P.; Johnson, L.; Moran, M.; Connor, D. Mosaic-like Silver Nanobowl Plasmonic Crystals as Highly Active Surface-Enhanced Raman Scattering Substrates. J. Phys. Chem. 2015, 119, 17790–17799. [Google Scholar] [CrossRef]
- Dhawan, A.; Gerhold, M.; Vo-Dinh, T. Theoretical Simulation and Focused Ion Beam Fabrication of Gold Nanostructures for Surface-Enhanced Raman Scattering (SERS). Nanobiotechnol 2007, 3, 164–171. [Google Scholar] [CrossRef] [PubMed]
- Kang, S.; Lehman, S.E.; Schulmerich, M.V.; Le, A.P.; Lee, T.; Gray, S.K.; Bhargava, R.; Nuzzo, R.G. Refractive index sensing and surface-enhanced Raman spectroscopy using silver-gold layered bimetallic plasmonic crystals. Beilstein J. Nanotechnol. 2017, 8, 2492–2503. [Google Scholar] [CrossRef] [PubMed]
- Haynes, C.L.; Van Duyne, R.P. Plasmon-Sampled Surface-Enhanced Raman Excitation Spectroscopy. J. Phys. Chem. B 2003, 107, 7426–7433. [Google Scholar] [CrossRef]
- Ziegler, C.; Eychmüller, A. Seeded Growth Synthesis of Uniform Gold Nanoparticles with Diameters of 15–300 nm. J. Phys. Chem. C 2011, 115, 4502–4506. [Google Scholar] [CrossRef]
- Oskooi, A.; Roundy, D.; Ibanescu, M.; Bermel, P.; Joannopoulos, J.; Johnson, S. MEEP: A flexible free-software package for electromagnetic simulations by the FDTD method. Comp. Phys. Comm. 2010, 181, 687–702. [Google Scholar] [CrossRef]
- Johnston, B.; Christy, R. Optical constants of the noble metals. Phys. Rev. B 1972, 6, 4370. [Google Scholar] [CrossRef]
- Oskooi, A.; Johnson, S. Distinguishing correct from incorrect PML proposals and a corrected unsplit PML for anisotropic, dispersive media. J. Comp. Phys. 2011, 230, 2369–2377. [Google Scholar] [CrossRef]
- Mie, G. Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen. Ann. Phys. 1908, 25, 377–445. [Google Scholar] [CrossRef]
- Ahrens, J.; Geveci, B.; Law, C. ParaView: An End-User Tool for Large Data Visualization, Visualization Handbook; Elsevier: New York, NY, USA, 2005. [Google Scholar]
- Ayachit, U. The ParaView Guide: A Parallel Visualization Application; Kitware: New York, NY, USA, 2015. [Google Scholar]
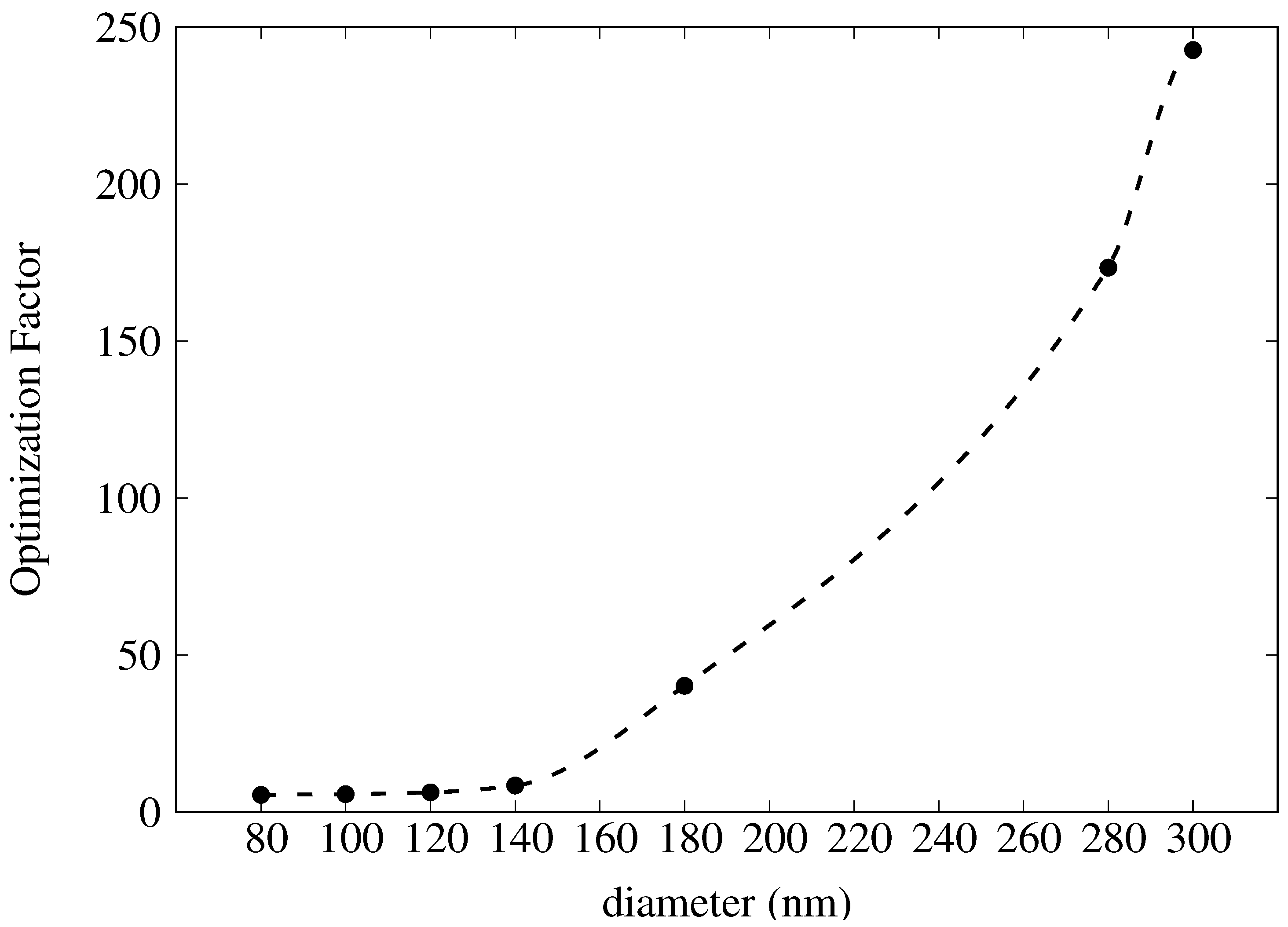
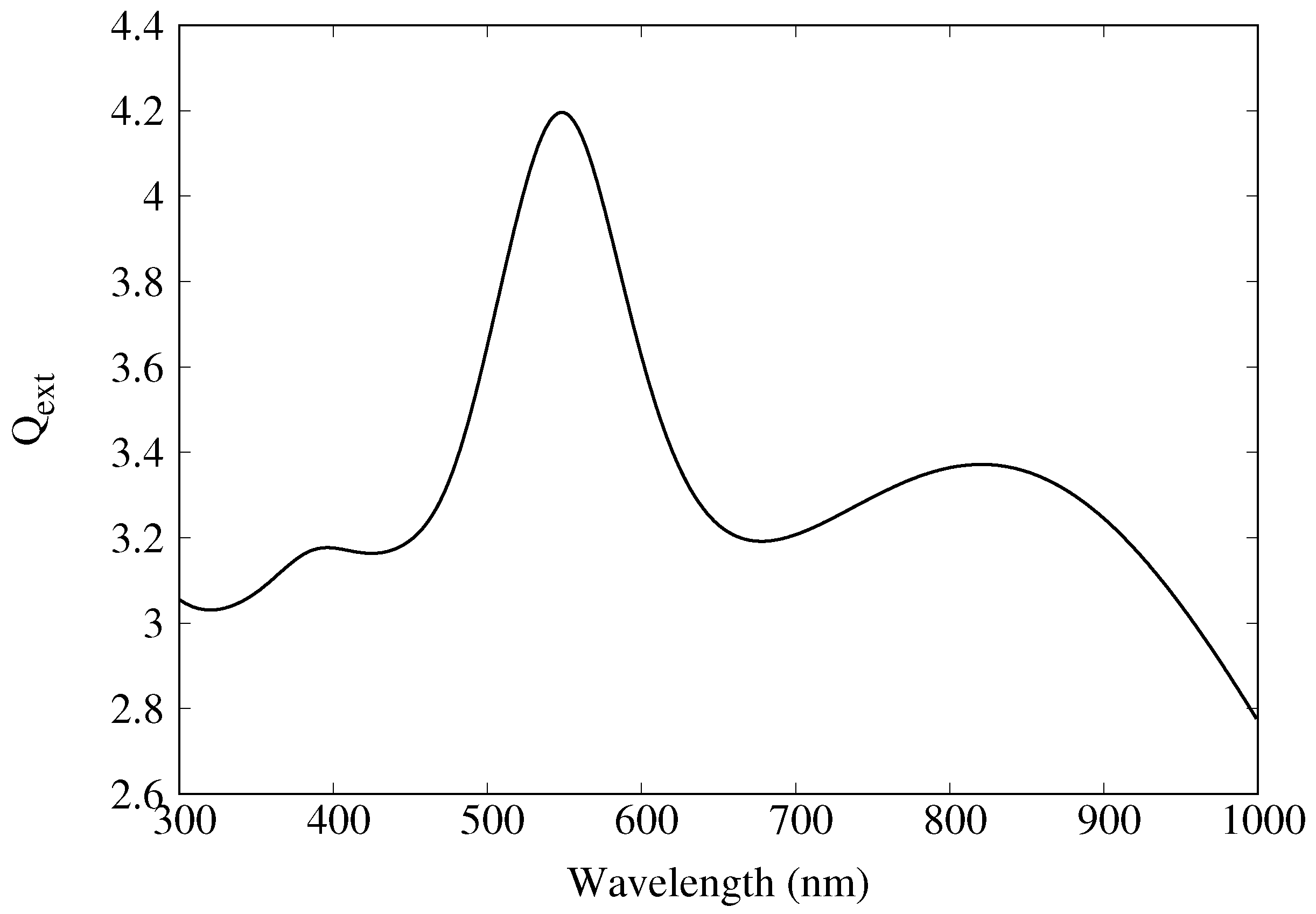
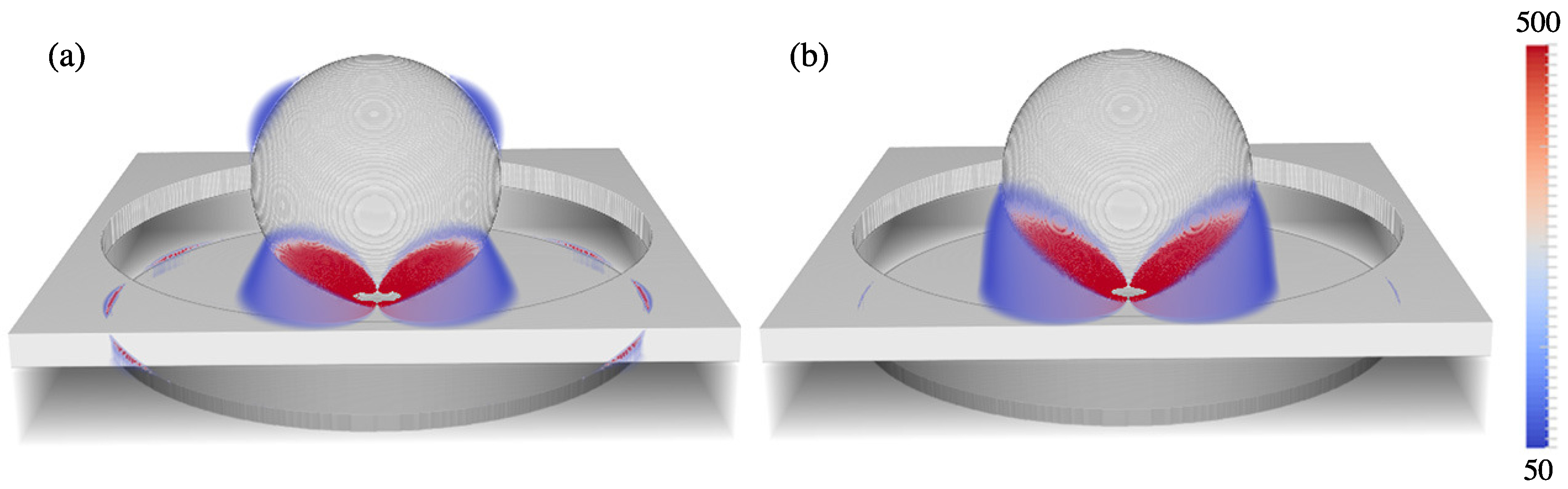
| Diameter (nm) | Periodicity (nm) |
|---|---|
| 174 | 490 |
| 224 | 584 |
| 256 | 658 |
| 456 | 730 |
| 500 | 800 |
| 514 | 760 |
| 616 | 1000 |
| 685 | 1100 |
| P (nm) | D (nm) | RD (nm) | O.F. | O.F. |
|---|---|---|---|---|
| ( nm) | ( nm) | |||
| 700 | 550 | 100 | 1163 | 917 |
| 700 | 550 | 140 | 401 | 366 |
| 700 | 550 | 180 | 320 | 213 |
| 700 | 600 | 100 | 1815 | 1171 |
| 700 | 600 | 140 | 619 | 751 |
| 700 | 600 | 180 | 452 | 460 |
| 700 | 650 | 100 | 2358 | 1405 |
| 700 | 650 | 140 | 887 | 966 |
| 700 | 650 | 180 | 627 | 616 |
| 730 | 550 | 100 | 870 | 600 |
| 730 | 550 | 140 | 223 | 307 |
| 730 | 550 | 180 | 147 | 181 |
| 730 | 600 | 100 | 1538 | 852 |
| 730 | 600 | 140 | 381 | 411 |
| 730 | 600 | 180 | 184 | 211 |
| 730 | 650 | 100 | 1920 | 1156 |
| 730 | 650 | 140 | 889 | 897 |
| 730 | 650 | 180 | 647 | 656 |
| 760 | 550 | 100 | 463 | 561 |
| 760 | 550 | 140 | 52 | 143 |
| 760 | 550 | 180 | 16 | 47 |
| 760 | 600 | 100 | 837 | 753 |
| 760 | 600 | 140 | 201 | 248 |
| 760 | 600 | 180 | 164 | 195 |
| 760 | 650 | 100 | 1050 | 880 |
| 760 | 650 | 140 | 347 | 437 |
| 760 | 650 | 180 | 292 | 351 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bigness, A.; Montgomery, J. The Design and Optimization of Plasmonic Crystals for Surface Enhanced Raman Spectroscopy Using the Finite Difference Time Domain Method. Materials 2018, 11, 672. https://doi.org/10.3390/ma11050672
Bigness A, Montgomery J. The Design and Optimization of Plasmonic Crystals for Surface Enhanced Raman Spectroscopy Using the Finite Difference Time Domain Method. Materials. 2018; 11(5):672. https://doi.org/10.3390/ma11050672
Chicago/Turabian StyleBigness, Alec, and Jason Montgomery. 2018. "The Design and Optimization of Plasmonic Crystals for Surface Enhanced Raman Spectroscopy Using the Finite Difference Time Domain Method" Materials 11, no. 5: 672. https://doi.org/10.3390/ma11050672
APA StyleBigness, A., & Montgomery, J. (2018). The Design and Optimization of Plasmonic Crystals for Surface Enhanced Raman Spectroscopy Using the Finite Difference Time Domain Method. Materials, 11(5), 672. https://doi.org/10.3390/ma11050672