Broadband Polarization Conversion Metasurface Based on Metal Cut-Wire Structure for Radar Cross Section Reduction
Abstract
1. Introduction
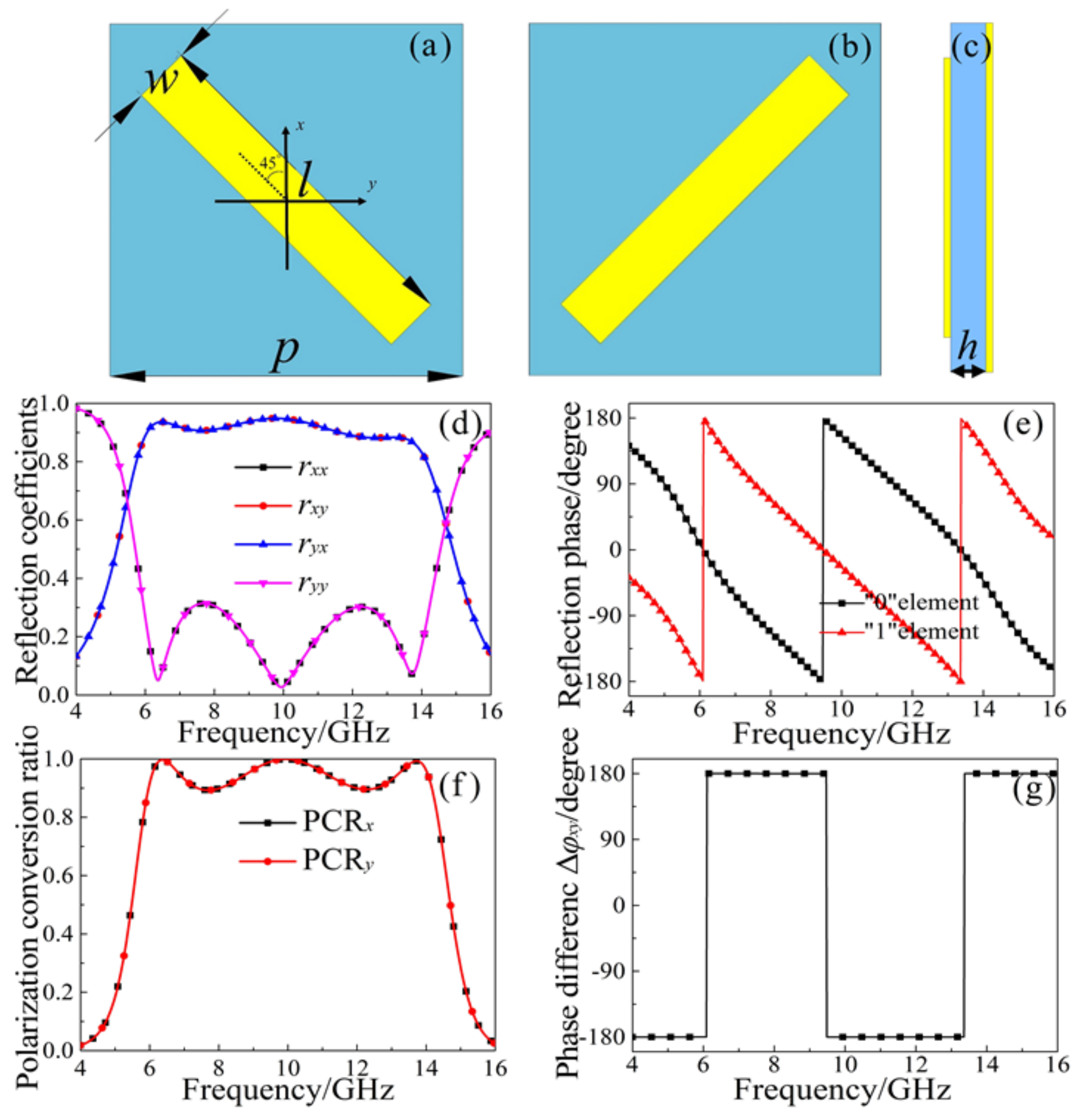
2. Design of Basic Unit and Theoretical Analysis
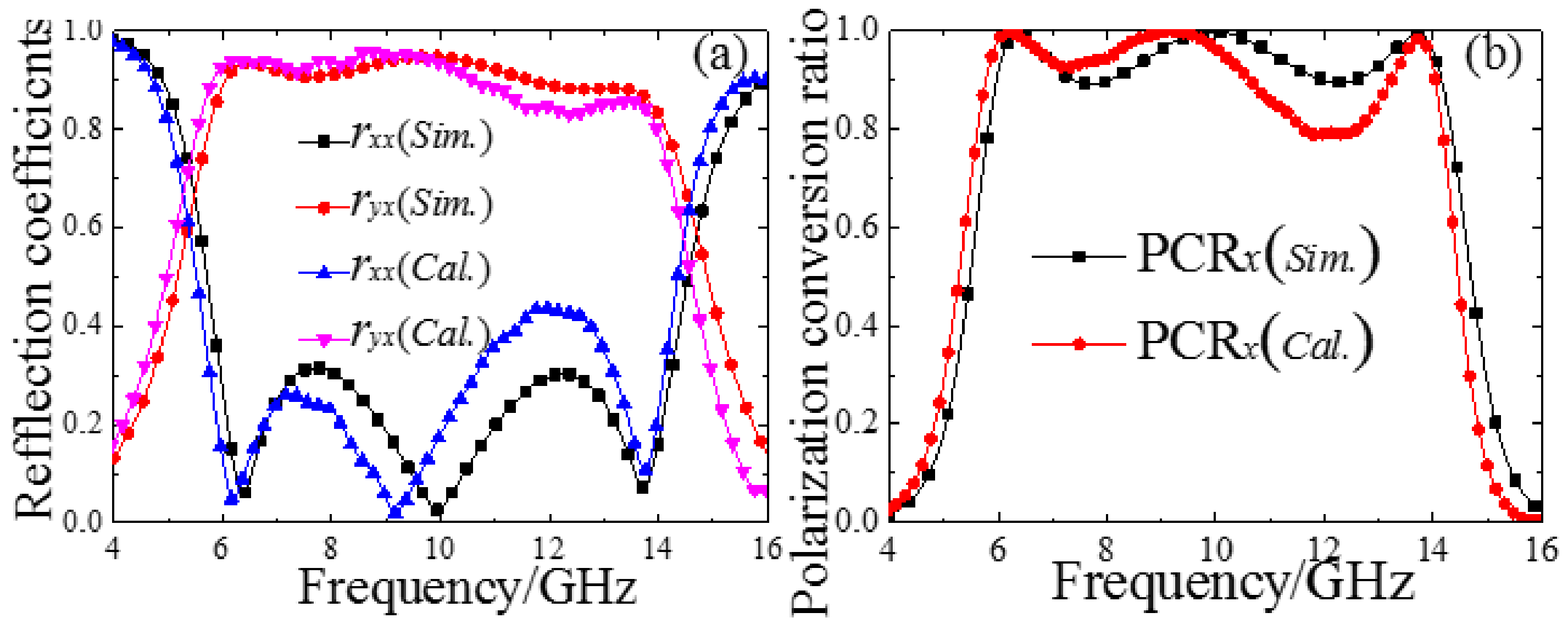
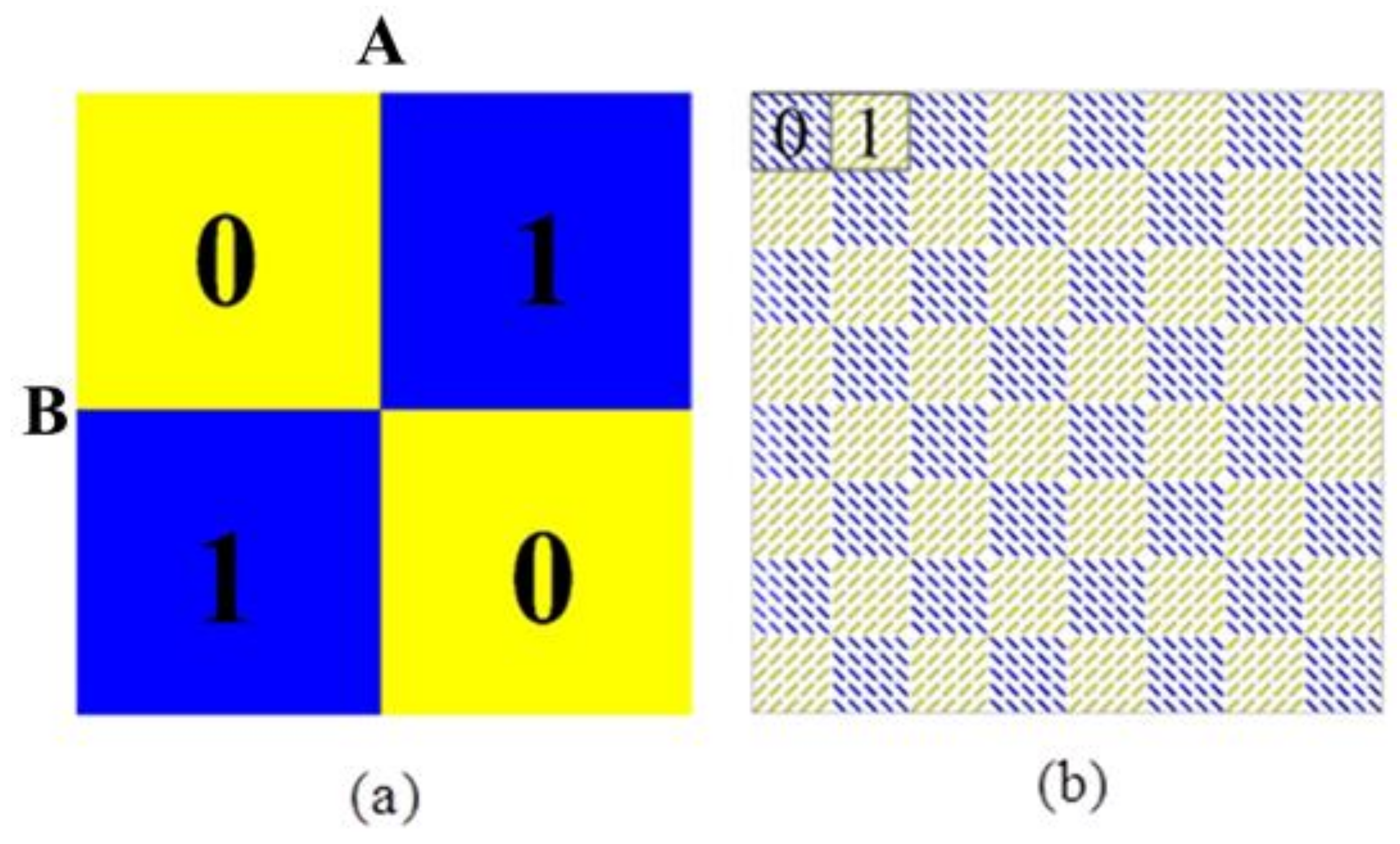
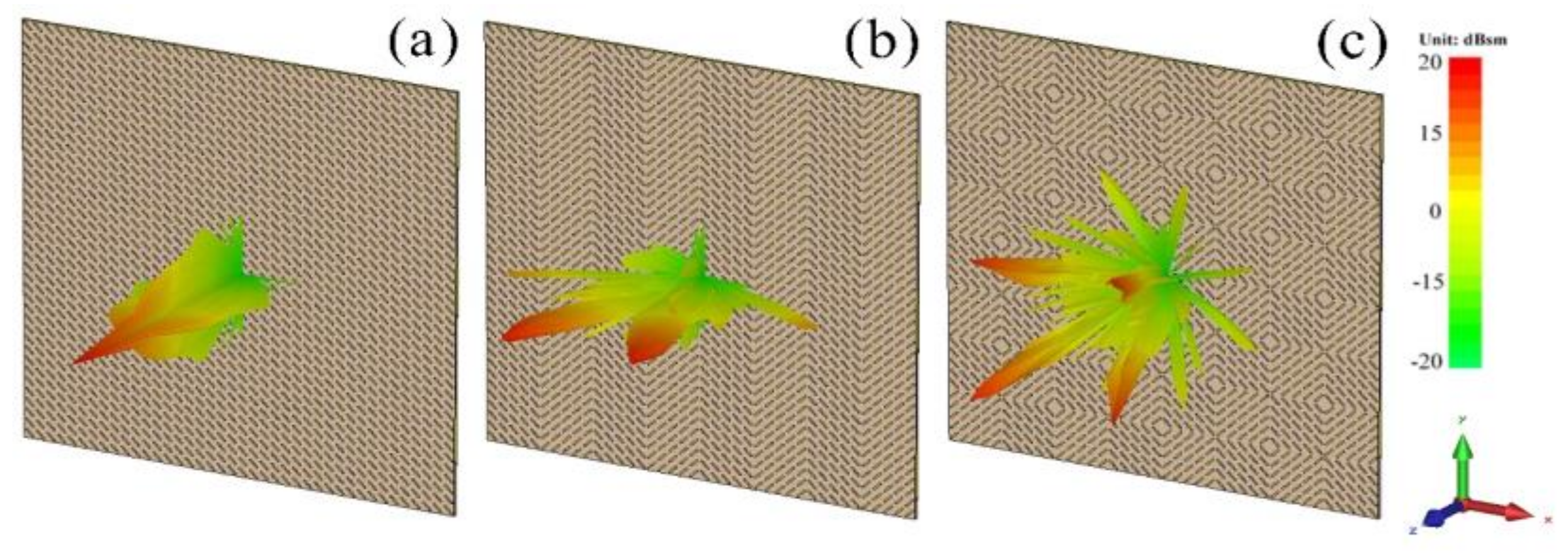
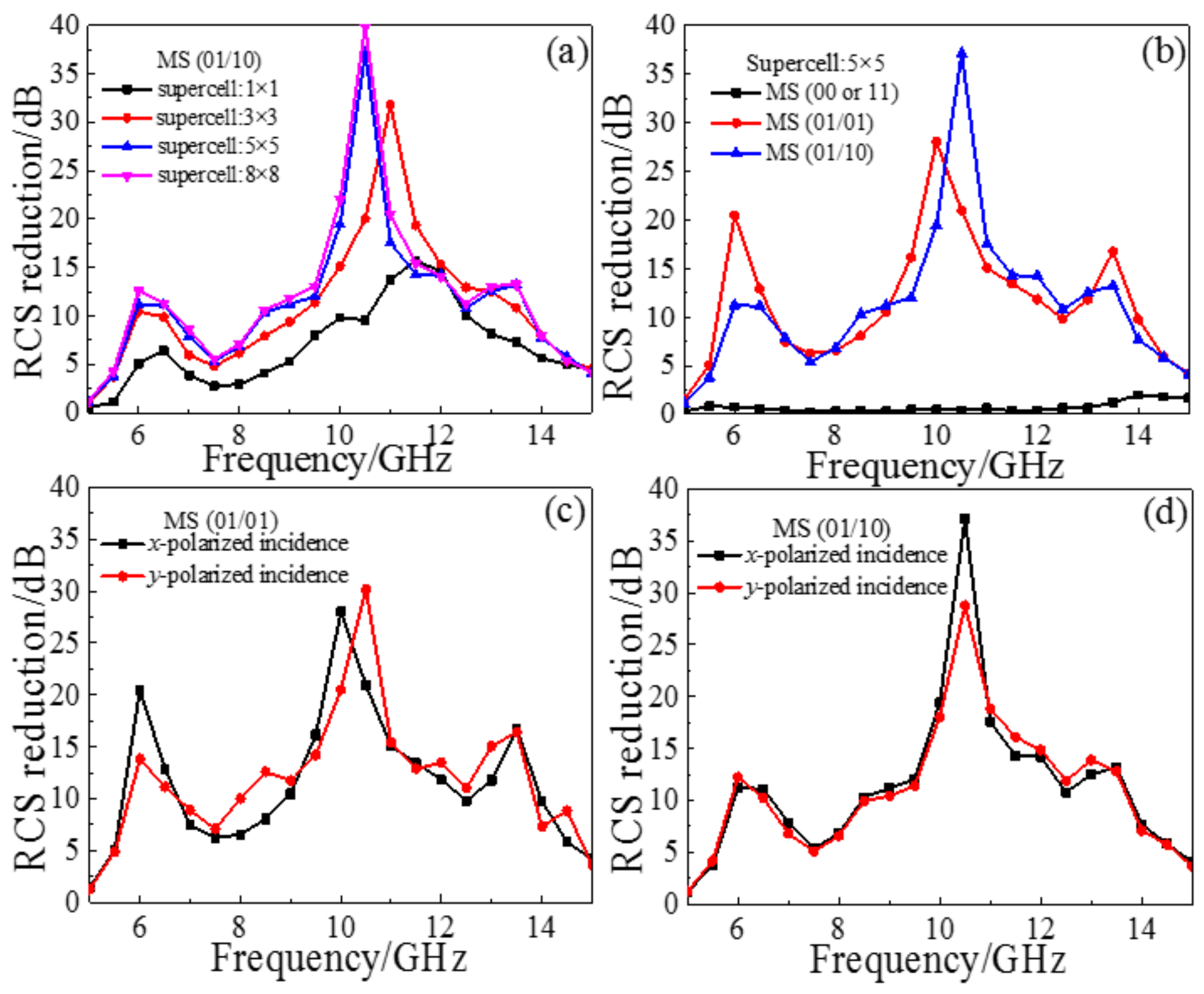
3. Simulation, Experiment and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Pendry, J.B.; Schurig, D.; Smith, D.R. Controlling electromagnetic fields. Science 2006, 312, 1780–1782. [Google Scholar] [CrossRef] [PubMed]
- Martin, F.; Falcone, F.; Bonache, J.; Marques, R. Miniaturized coplanar waveguide stop band filters based on multiple tuned split ring resonators. IEEE Microw. Wirel. Compon. Lett. 2003, 13, 511–513. [Google Scholar] [CrossRef]
- Smith, D.R.; Pendry, J.B.; Wiltshire, M.C.K. Metamaterials and negative refractive index. Science 2004, 305, 788–792. [Google Scholar] [CrossRef] [PubMed]
- Engheta, N. Circuits with light at nanoscales: Optical nanocircuits inspired by metamaterials. Science 2007, 317, 1698–1702. [Google Scholar] [CrossRef] [PubMed]
- Alù, A.; Engheta, N. Achieving transparency with plasmonic and metamaterial coatings. Phys. Rev. E 2005, 72, 016623. [Google Scholar] [CrossRef] [PubMed]
- Monticone, F.; Estakhri, N.M.; Alù, A. Full control of nanoscale optical transmission with a composite metascreen. Phys. Rev. Lett. 2013, 110, 203903. [Google Scholar] [CrossRef] [PubMed]
- Shelby, R.A.; Smith, D.R.; Schultz, S. Experimental verification of a negative index of refraction. Science 2001, 292, 77–79. [Google Scholar] [CrossRef] [PubMed]
- Pendry, J.B. Negative refraction makes a perfect lens. Phys. Rev. Lett. 2000, 85, 3966. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.X.; Tang, S.W.; Ling, X.H.; Luo, W.J.; Zhou, L. Flexible control of highly-directive emissions based on bifunctional metasurfaces with low polarization cross-talking. Ann. Phys. Berl. 2017, 529. [Google Scholar] [CrossRef]
- Alrasheed, S.; Fabrizio, E.D. Design and simulation of reflect-array metasurfaces in the visible regime. Appl. Opt. 2017, 56, 3213–3218. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.Z.; Cheng, Z.Z.; Mao, X.S.; Gong, R.Z. Ultra-thin multi-band polarization-insensitive microwave metamaterial absorber based on multiple-order responses using a single resonator structure. Materials 2017, 10, 1241. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.Z.; Wu, C.J.; Ge, C.C.; Yang, J.J.; Pei, X.J.; Jia, F.; Gong, R.Z. An ultra-thin dual-band phase-gradient metasurface using hybrid resonant structures for backward RCS reduction. Appl. Phys. B 2017, 123, 143. [Google Scholar] [CrossRef]
- Li, Y.F.; Wang, J.; Zhang, J.; Qu, S.B.; Pang, Y.Q.; Zheng, L.; Yan, M.B.; Xu, Z.; Zhang, A.X. Ultra-wide-band microwave composite absorbers based on phase gradient metasurfaces. Prog. Electromagn. Res. 2014, 40, 9–18. [Google Scholar] [CrossRef]
- Xu, H.X.; Ma, S.J.; Luo, W.J.; Cai, T.; Sun, S.L.; He, Q.; Zhou, L. Aberration-free and functionality-switchable meta-lenses based on tunable metasurfaces. Appl. Phys. Lett. 2016, 109, 193506. [Google Scholar] [CrossRef]
- Fan, Y.C.; Liu, Z.; Zhang, F.L.; Zhao, Q.; Wei, Z.Y.; Fu, Q.H.; Li, J.J.; Gu, C.Z.; Li, H.Q. Tunable mid-infrared coherent perfect absorption in a graphene meta-surface. Sci. Rep. 2015, 5, 13956. [Google Scholar] [CrossRef] [PubMed]
- Tian, S.; Liu, H.; Li, L. Design of 1-bit digital reconfigurable reflective metasurface for beam-scanning. Appl. Sci. Basel 2017, 7, 882. [Google Scholar] [CrossRef]
- Lee, S.H.; Choi, M.; Kim, T.T.; Lee, S.; Liu, M.; Yin, X.; Choi, H.K.; Lee, S.S.; Choi, C.G.; Choi, S.Y.; et al. Switching teraherz waves with gate-controlled active graphene metamaterials. Nat. Mater. 2012, 11, 936. [Google Scholar] [CrossRef] [PubMed]
- Politano, A.; Chiarello, G. Plasmon modes in graphene: Status and prospect. Nanoscale 2014, 6, 10927–10940. [Google Scholar] [CrossRef] [PubMed]
- Mitrofanov, O.; Viti, L.; Dardanis, E.; Giordano, M.C.; Ercolani, D.; Politano, A.; Sorba, L.; Vitiello, M.S. Near-field terahertz probes with room-temperature nanodetectors for subwavelength resolution imaging. Sci. Rep. 2017, 7, 44240. [Google Scholar] [CrossRef] [PubMed]
- Politano, A.; Viti, L.; Vitiello, M.S. Optoelectronic devices, plasmonics, and photonics with topological insulators. APL Mater. 2017, 5, 035504. [Google Scholar] [CrossRef]
- Yang, Q.; Gu, J.; Wang, D.; Zhang, X.; Tian, Z.; Ouyang, C.; Singh, R.; Han, J.; Zhang, W. Efficient flat metasurface lens for terahertz imaging. Opt. Express 2014, 22, 25931–25939. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.Z.; Fang, C.; Mao, X.S.; Gong, R.Z.; Wu, L. Design of an ultrabroadband and high-efficiency reflective linear polarization convertor at optical frequency. IEEE Photonics J. 2016, 8, 1–9. [Google Scholar] [CrossRef]
- Zhao, J.C.; Cheng, Y.Z. Ultra-broadband and high-efficiency reflective linear polarization convertor based on planar anisotropic metamaterial in microwave region. Optick 2017, 136, 52–57. [Google Scholar] [CrossRef]
- Jiang, W.; Xue, Y.; Gong, S.X. Polarization conversion metasurface for broadband radar cross section reduction. Prog. Electromagn. Res. Lett. 2016, 62, 9–15. [Google Scholar] [CrossRef]
- Li, H.P.; Wang, G.M.; Liang, J.G.; Gao, X.J. Wideband multifunctional metasurface for polarization conversion and gain enhancement. Prog. Electromagn. Res. 2016, 155, 115–125. [Google Scholar] [CrossRef]
- Song, Y.C.; Ding, J.; Guo, C.J.; Ren, Y.H.; Zhang, J.K. Ultra-broadband backscatter radar cross section reduction based on polarization-insensitive metasurface. IEEE Antennas Wirel. Propag. 2016, 15, 329–331. [Google Scholar] [CrossRef]
- Mo, W.C.; Wei, X.L.; Wang, K.J.; Li, Y.; Liu, J.S. Ultrathin flexible terahertz polarization converter based on metasurfaces. Opt. Express 2016, 24, 13621–13627. [Google Scholar] [CrossRef] [PubMed]
- Jiang, S.C.; Xiong, X.; Hu, Y.S.; Hu, Y.H.; Ma, G.B.; Peng, R.W.; Sun, C.; Wang, M. Controlling the polarization state of light with a dispersion-free metastructure. Phys. Rev. X 2014, 4, 021026. [Google Scholar] [CrossRef]
- Ding, F.; Wang, Z.; He, S.; Shalaev, V.M.; Kildishev, A.V. Broadband high-efficiency half-wave plate: A supercell-based plasmonic metasurface approach. ACS Nano 2015, 9, 4111–4119. [Google Scholar] [CrossRef] [PubMed]
- Burokur, S.N.; Daniel, J.P.; Ratajczak, P.; Lustrac, A.D. Tunable bilayered metasurface for frequency reconfigurable directive emissions. Appl. Phys. Lett. 2010, 97, 064101. [Google Scholar] [CrossRef]
- Burokur, S.N.; Ourir, A.; Daniel, J.P.; Ratajczak, P.; Lustrac, A.D. Highly directive ISM band cavity antenna using a bi-layered metasurface reflector. Microw. Opt. Technol. Lett. 2009, 51, 1393–1396. [Google Scholar] [CrossRef]
- Dong, G.X.; Shi, H.Y.; Li, W.; He, Y.C.; Zhang, A.X.; Xu, Z.; Wei, X.Y. A multi-band spoof surface plasmon polariton coupling metasurface based on dispersion engineering. J. Appl. Phys. 2016, 120, 084505. [Google Scholar] [CrossRef]
- Liang, L.J.; Qi, M.Q.; Yang, J.; Shen, X.P.; Zhai, J.Q.; Xu, W.Z.; Jin, B.B. Anomalous terahertz reflection and scattering by flexible and conformal coding metamaterials. Adv. Opt. Mater. 2015, 3, 1374–1380. [Google Scholar] [CrossRef]
- Liao, Z.; Luo, Y.; Fernandez-Dominguez, A.I.; Shen, X.P.; Maier, S.A.; Cui, T.J. High-order localized spoof surface plasmon resonances and experimental verifications. Sci. Rep. 2015, 5, 9590. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.Z.; Mao, X.S.; Wu, C.J.; Wu, L.; Gong, R.Z. Infrared non-planar plasmonic perfect absorber for enhanced sensitive refractive index sensing. Opt. Mater. 2016, 53, 195–200. [Google Scholar] [CrossRef]
- Wu, C.J.; Cheng, Y.Z.; Wang, W.Y.; He, B.; Gong, R.Z. Ultra-thin and polarization-independent phase gradient metasurface for high-efficiency spoof surface-plasmon-polariton coupling. Appl. Phys. Express 2015, 8, 122001. [Google Scholar] [CrossRef]
- Cheng, Y.Z.; Huang, M.L.; Chen, H.R.; Guo, Z.; Mao, X.S.; Gong, R.Z. Ultrathin six-band polarization-insensitive perfect metamaterial absorber based on a cross-cave patch resonator for terahertz waves. Materials 2017, 10, 591. [Google Scholar] [CrossRef] [PubMed]
- Pors, A.; Ding, F.; Chen, Y.; Radko, I.P.; Bozhevolnyi, S.I. Random-phase metasurfaces at optical wavelengths. Sci. Rep. 2016, 6, 28448. [Google Scholar] [CrossRef] [PubMed]
- Ding, F.; Pors, A.; Bozhevolnyi, S.I. Gradient metasurfaces: A review of fundamentals and applications. Rep. Prog. Phys. 2017, 81, 026401. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Pan, W.B.; Ma, X.L.; Luo, X.G. Wideband radar cross-section reduction of a stacked patch array antenna using metasurface. IEEE Antennas Wirel. Propag. 2015, 14, 1369–1372. [Google Scholar] [CrossRef]
- Liu, Y.; Hao, Y.W.; Li, K.; Gong, S.X. Wideband and polarization independent radar cross section reduction using holographic metasurface. IEEE Antennas Wirel. Propag. 2016, 15, 1028–1031. [Google Scholar] [CrossRef]
- Yuan, Y.; Jiang, C.; Liu, L.; Yu, S.; Cui, Z.; Chen, M.; Lin, S.; Wang, S.; Huang, L. Convenient, sensitive and high-throughput method for screening botanic origin. Sci. Rep. 2014, 4, 5395. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.J.; Cheng, Y.Z.; Wang, W.Y.; He, B.; Gong, R.Z. Design and radar cross section reduction experimental verification of phase gradient meta-surface based on cruciform structure. Acta Phys. Sin. 2015, 64, 164102. [Google Scholar]
- Cui, T.J.; Qi, M.Q.; Wan, X.; Zhao, J.; Cheng, Q. Coding metamaterials, digital metamaterials and programmable metamaterials. Light: Sci. Appl. 2014, 3, e218. [Google Scholar] [CrossRef]
- Su, P.; Zhao, Y.J.; Jia, S.L.; Shi, W.W.; Wang, H.L. An ultra-wideband and polarization-independent metasurface for RCS reduction. Sci. Rep. 2016, 6, 20387. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.Y.; Gu, C.Q.; Chen, X.L.; Li, Z.; Liu, L.L.; Xu, B.Z.; Zhou, Z.C. Broadband and broad-angle polarization-independent metasurface for radar cross section reduction. Sci. Rep. 2017, 7, 40782. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.; Cui, L.; Feng, Y.J.; Zhao, J.M.; Jiang, T.; Zhu, B. Coding metasurface for broadband microwave scattering reduction with optical transparency. Opt. Express 2017, 25, 5571–5579. [Google Scholar] [CrossRef] [PubMed]
- Sun, W.J.; He, Q.; Sun, S.L.; Zhou, L. High-efficiency surface plasmon meta-couplers: Concept and microwave-regime realizations. Light: Sci. Appl. 2016, 5, e16003. [Google Scholar] [CrossRef]
- Xu, H.X.; Tang, S.W.; Ma, S.J.; Luo, W.J.; Cai, T.; Sun, S.L.; He, Q.; Zhou, L. Tunable microwave metasurfaces for high-performance operations: Dispersion compensation and dynamical switch. Sci. Rep. 2016, 6, 38255. [Google Scholar] [CrossRef] [PubMed]
- Pan, W.B.; Huang, C.; Pu, M.B.; Ma, X.L.; Cui, J.H.; Zhao, B.; Luo, X.G. Combining the absorptive and radiative loss in metasurfaces for multi-spectral shaping of the electromagnetic scattering. Sci. Rep. 2016, 6, 21462. [Google Scholar] [CrossRef] [PubMed]
- Ma, H.F.; Liu, Y.Q.; Luan, K.; Cui, T.J. Multi-beam reflections with flexible control of polarizations by using anisotropic metasurfaces. Sci. Rep. 2016, 6, 39390. [Google Scholar] [CrossRef] [PubMed]
- Jia, Y.; Liu, Y.; Guo, Y.J.; Li, K.; Gong, S.X. Broadband polarization rotation reflective surfaces and their applications to RCS reduction. IEEE Trans. Antennas Propag. 2016, 64, 179–188. [Google Scholar] [CrossRef]
- Balanis, C.A. Antenna Theory: Analysis and Design; Wiley: New York, NY, USA, 2005. [Google Scholar]
- Zhao, Y.; Cao, X.Y.; Gao, J.; Sun, Y.; Yang, H.H.; Liu, X.; Zhou, Y.L.; Han, T.; Chen, W. Broadband diffusion metasurface based on a single anisotropic element and optimized by the simulated annealing algorithm. Sci. Rep. 2016, 6, 23896. [Google Scholar] [CrossRef] [PubMed]




© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.J.; Cheng, Y.Z.; Ge, C.C.; Gong, R.Z. Broadband Polarization Conversion Metasurface Based on Metal Cut-Wire Structure for Radar Cross Section Reduction. Materials 2018, 11, 626. https://doi.org/10.3390/ma11040626
Yang JJ, Cheng YZ, Ge CC, Gong RZ. Broadband Polarization Conversion Metasurface Based on Metal Cut-Wire Structure for Radar Cross Section Reduction. Materials. 2018; 11(4):626. https://doi.org/10.3390/ma11040626
Chicago/Turabian StyleYang, Jia Ji, Yong Zhi Cheng, Chen Chen Ge, and Rong Zhou Gong. 2018. "Broadband Polarization Conversion Metasurface Based on Metal Cut-Wire Structure for Radar Cross Section Reduction" Materials 11, no. 4: 626. https://doi.org/10.3390/ma11040626
APA StyleYang, J. J., Cheng, Y. Z., Ge, C. C., & Gong, R. Z. (2018). Broadband Polarization Conversion Metasurface Based on Metal Cut-Wire Structure for Radar Cross Section Reduction. Materials, 11(4), 626. https://doi.org/10.3390/ma11040626





