Effect of Weight on the Resonant Tuning of Energy Harvesting Devices Using Giant Magnetostrictive Materials
Abstract
:1. Introduction
2. Analysis
2.1. Basic Equation
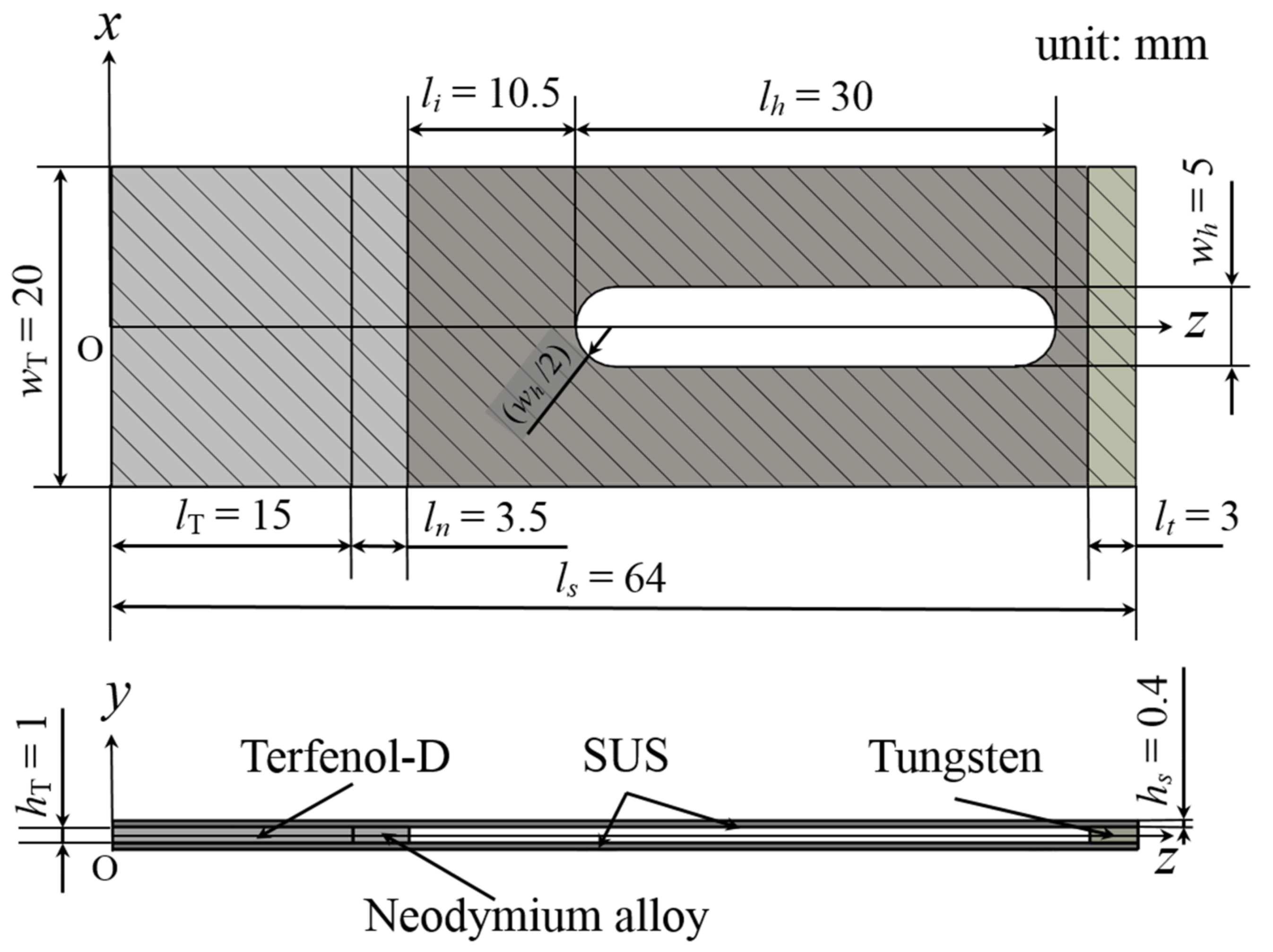
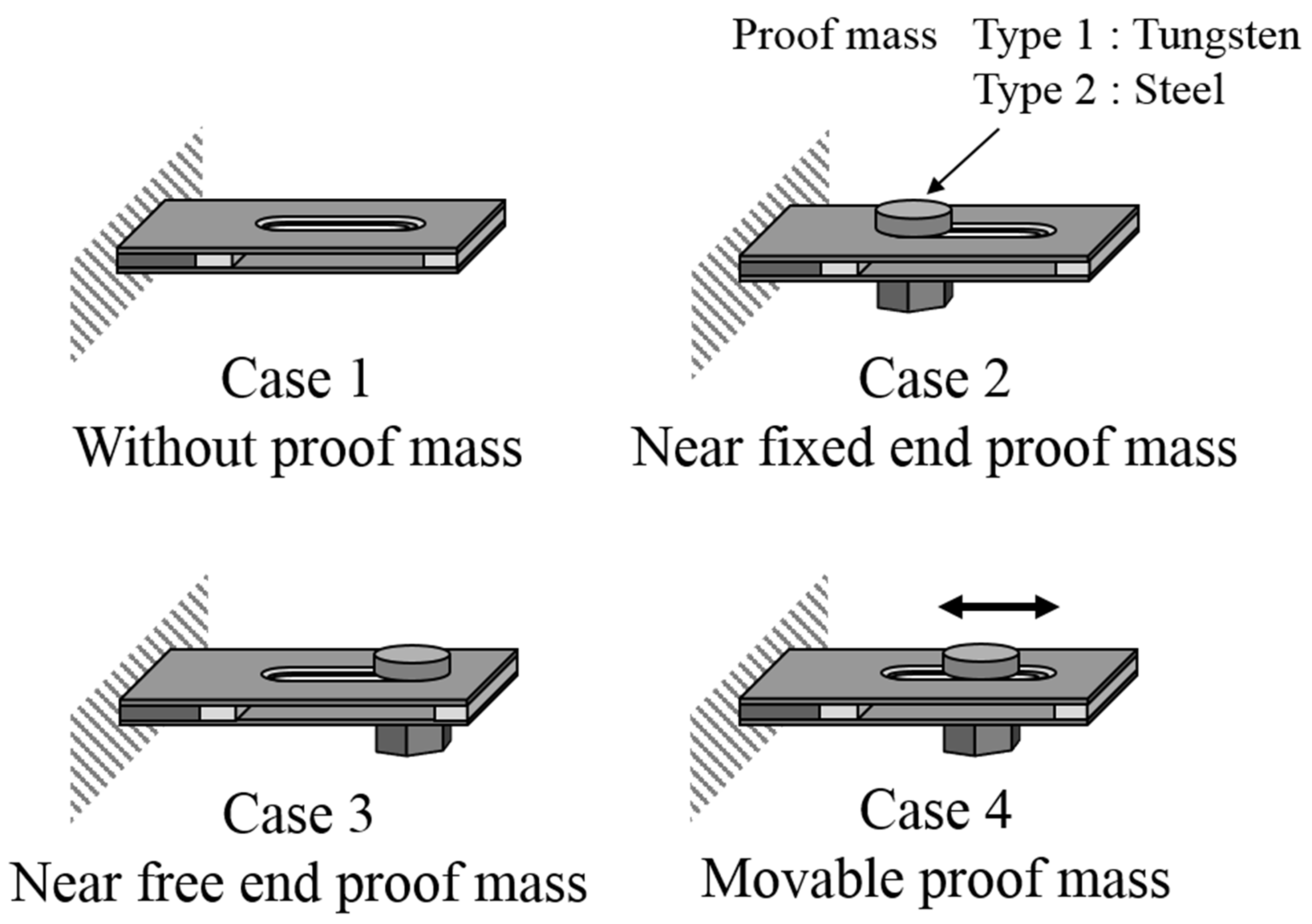
2.2. Model
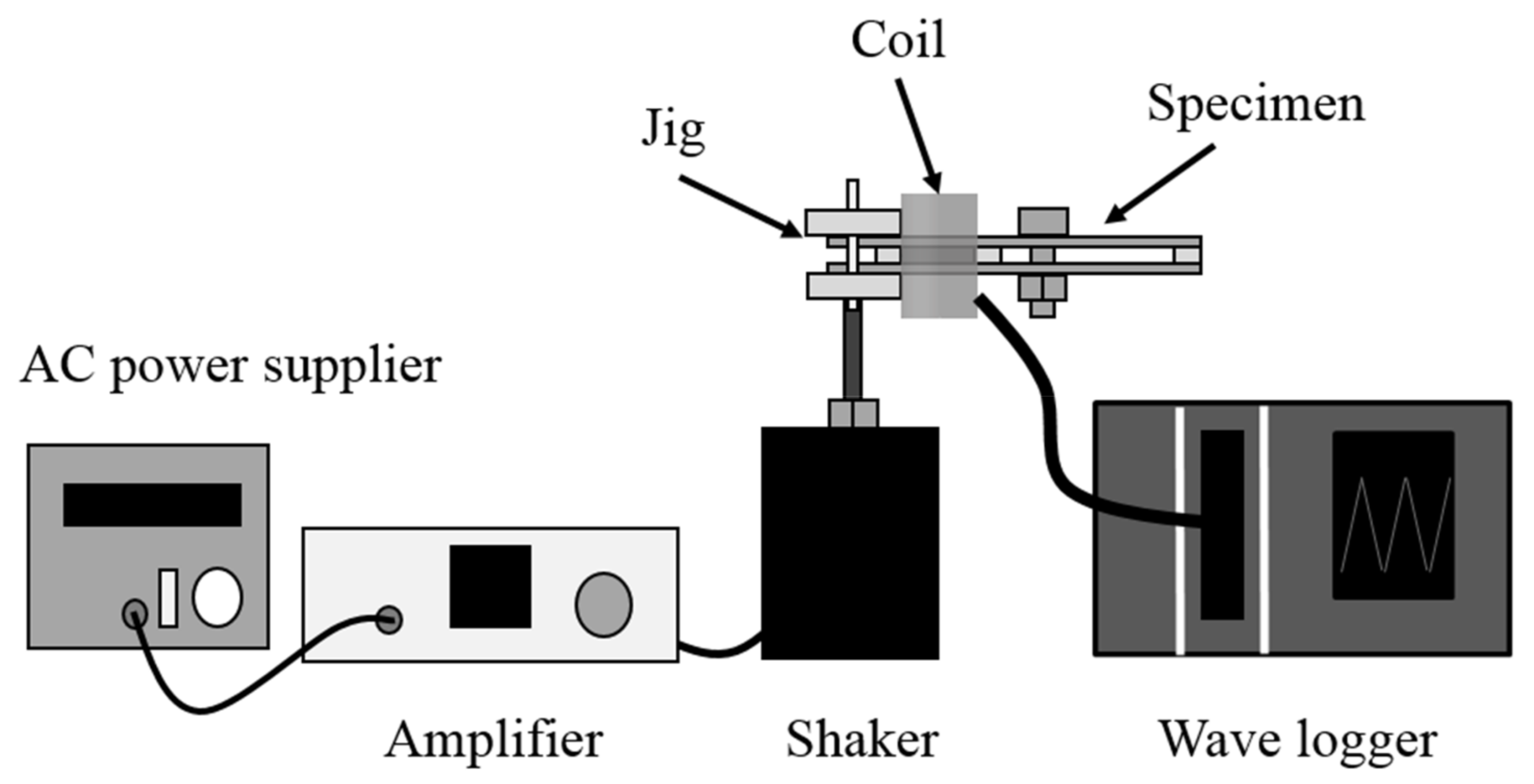
3. Experiments
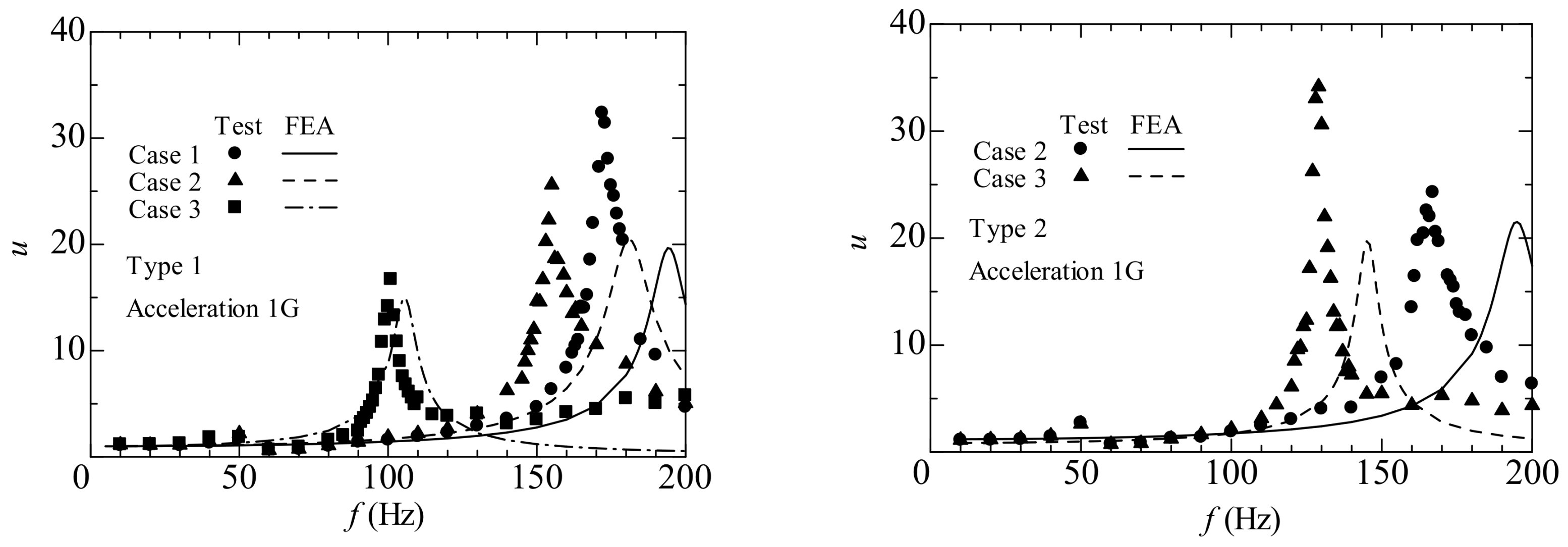
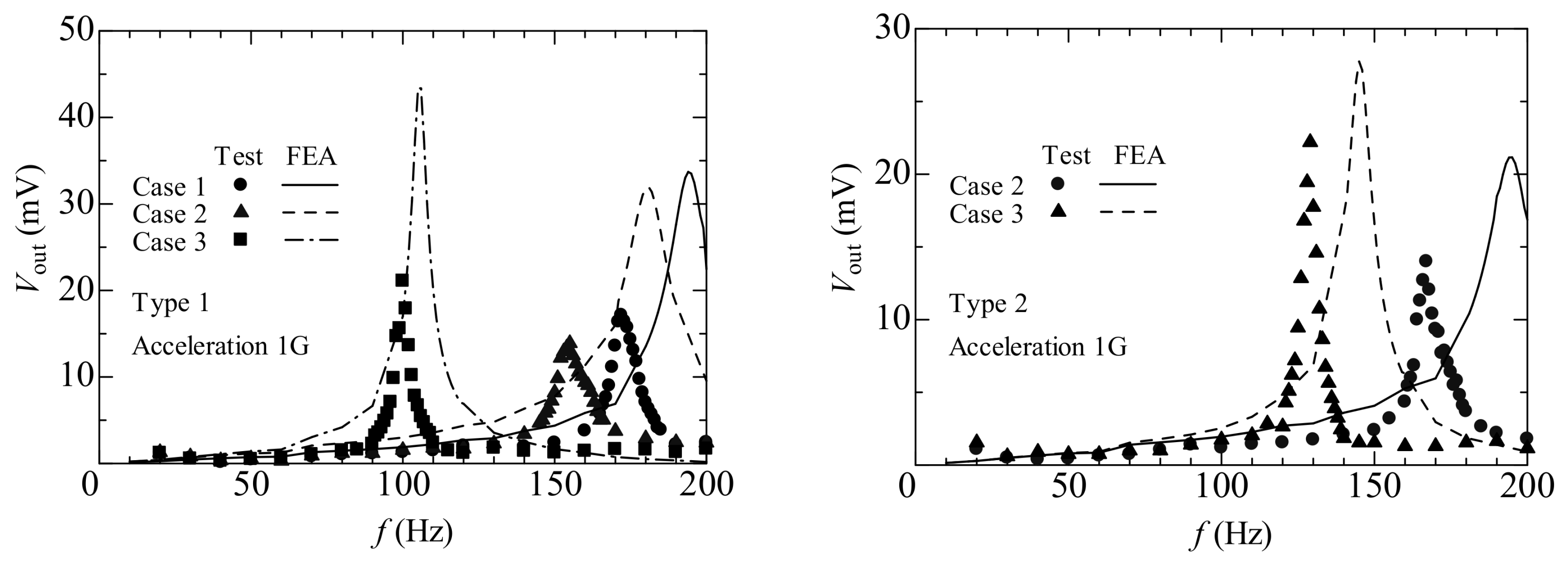
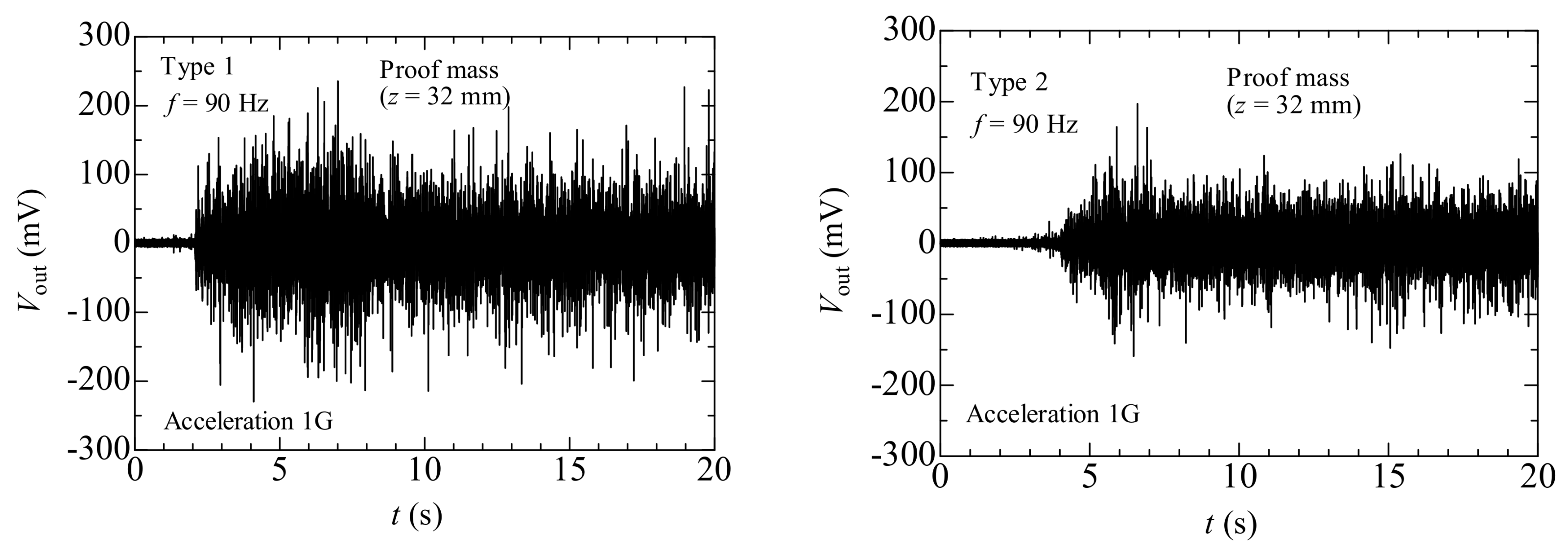
4. Results and Discussion
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Bozorth, R.M. Ferromagnetism; IEEE: New York, NY, USA, 1993. [Google Scholar]
- Engdahl, G. Handbook of Giant Magnetostrictive Materials; Academic: San Diego, CA, USA, 2000. [Google Scholar]
- Yang, Z.; Nakajima, K.; Onodera, R.; Tayama, T.; Chiba, D.; Narita, F. Magnetostrictive clad steel plates for high—Performance vibration energy harvesting. Appl. Phys. Lett. 2018, in press. [Google Scholar] [CrossRef]
- Narita, F.; Katabira, K. Stress-rate dependent output voltage for Fe29Co71 magnetostrictive fiber/polymer composites: fabrication, experimental observation and theoretical prediction. Mater. Trans. 2017, 58, 302–304. [Google Scholar] [CrossRef]
- Narita, F. Inverse magnetostrictive effect in Fe29Co71 wire/polymer composites. Adv. Eng. Mater. 2017, 19, 1600586. [Google Scholar] [CrossRef]
- Zhao, X.; Lord, D.G. Application of the Villari effect to electric power harvesting. J. Appl. Phys. 2006, 99, 08M703. [Google Scholar] [CrossRef]
- Hu, J.; Xu, F.; Huang, A.Q.; Yuan, F.G. Optimal design of a vibration-based energy harvester using magnetostrictive material (MsM). Smart Mater. Struct. 2011, 20, 015021. [Google Scholar] [CrossRef]
- Peigney, M.; Siegert, D. Piezoelectric energy harvesting from traffic-induced bridge vibrations. Smart Mater. Struct. 2013, 22, 095019. [Google Scholar] [CrossRef]
- Narita, F.; Fox, M. A review on piezoelectric, magnetostrictive, and magnetoelectric materials and device technologies for energy harvesting applications. Adv. Eng. Mater. 2018, 20, 1700743. [Google Scholar] [CrossRef]
- Holistic. Next Generation Energy-Harvesting Electronics. Available online: http://www.holistic.ecs.soton.ac.uk/ (accessed on 15 March 2018).
- Lallart, M.; Anton, S.R.; Inman, D.J. Frequency self-tuning scheme for broadband vibration energy harvesting. J. Intell. Mater. Syst. Struct. 2010, 21, 897–906. [Google Scholar] [CrossRef]
- Shindo, Y.; Narita, F. Dynamic bending/torsion and output power of S-shaped piezoelectric energy harvesters. Int. J. Mech. Mater. Des. 2014, 10, 305–311. [Google Scholar] [CrossRef]
- Firoozy, P.; Khadem, S.K.; Pourkiaee, S.M. Broadband energy harvesting using nonlinear vibrations of a magnetopiezoelastic cantilever beam. Int. J. Eng. Sci. 2017, 111, 113–133. [Google Scholar] [CrossRef]
- Miller, L.M.; Pillatsch, P.; Halvorsen, E.; Wright, P.K.; Yeatman, E.M.; Holmes, A.S. Experimental passive self-tuning behavior of a beam resonator with sliding proof mass. J. Sound Vibr. 2013, 332, 7142–7152. [Google Scholar] [CrossRef]
- Mori, K.; Horibe, T.; Ishikawa, S.; Shindo, Y.; Narita, F. Characteristics of vibration energy harvesting using giant magnetostrictive cantilevers with resonant tuning. Smart Mater. Struct. 2015, 24, 125032. [Google Scholar] [CrossRef]
- Alshits, V.I.; Darinskii, A.N.; Lothe, J. On the existence of surface waves in half-infinite anisotropic elastic media with piezoelectric and piezomagnetic properties. Wave Motion 1992, 16, 265–283. [Google Scholar] [CrossRef]
- Wang, L.; Yuan, F.G. Vibration energy harvesting by magnetostrictive material. Smart Mater. Struct. 2008, 17, 045009. [Google Scholar] [CrossRef]
- Nan, C.W.; Li, M.; Huang, J.H. Calculations of giant magnetoelectric effects in ferroic composites of rare-earth-iron alloys and ferroelectric polymers. Phys. Rev. B 2001, 63, 144415. [Google Scholar] [CrossRef]
| Elastic Compliance (×10−12 m2/N) | Piezo-Magnetic Constant (×10−9 m/A) | Magnetic Permittivity (×10−6 H/m) | Density (kg/m3) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| sH11 | sH33 | sH44 | sH12 | sH13 | dm31 | dm33 | dm15 | T11 | T33 | ||
| Terfenol-D | 17.9 | 17.9 | 26.3 | −5.88 | −5.88 | −5.3 | 11 | 28 | 36.1 | 13.7 | 9250 |
| Density (kg/m3) | Poisson’s Ratio (-) | Young’s Modulus (GPa) | |
|---|---|---|---|
| Stainless Steel | 7930 | 0.3 | 193 |
| Neodymium magnet | 7500 | 0.3 | 170 |
| Tungsten | 19,000 | 0.28 | 190 |
| Starting Position | ||||||
|---|---|---|---|---|---|---|
| Fixed-End Side (z = 32 mm) | Free-End Side (z = 32 mm) | Middle (z = 44 mm) | ||||
| f (Hz) | Type 1 | Type 2 | Type 1 | Type 2 | Type 1 | Type 2 |
| 10 | × | × | ○ | × | ○ | △ |
| 20 | × | × | ○ | ○ | ○ | ○ |
| 30 | × | × | ○ | ○ | ○ | ○ |
| 40 | × | × | ○ | ○ | ○ | ○ |
| 50 | × | × | ○ | × | ○ | × |
| 60 | ○ | ○ | × | × | ○ | ○ |
| 70 | ○ | ○ | × | × | ○ | ○ |
| 80 | ○ | ○ | × | × | ○ | ○ |
| 90 | ○ | ○ | × | × | ○ | ○ |
| 100 | ○ | × | × | × | ○ | △ |
| 110 | ○ | × | × | × | ○ | △ |
| 120 | ○ | × | × | △ | ○ | × |
| 130 | ○ | × | × | △ | △ | ○ |
| 140 | △ | × | × | ○ | △ | ○ |
| 150 | △ | × | × | ○ | △ | ○ |
| 160 | △ | × | × | ○ | △ | ○ |
| 170 | △ | × | × | × | △ | × |
| 180 | △ | × | × | × | × | × |
| 190 | × | × | × | × | △ | × |
| 200 | × | × | × | × | △ | × |
| Toward free-end side | ○: Move to the other side | |||||
| Toward fixed-end side | △: Stop before end side | |||||
| ×: No movement | ||||||
| (a) | (b) | ||||
|---|---|---|---|---|---|
| Case 2 | Case 3 | Starting Position | |||
| f (Hz) | utip (mm) | f (Hz) | Fixed-End Side (z = 32 mm) | Free-End Side (z = 56 mm) | |
| 10 | 2.745 | 2.782 | 10 | × | ○ |
| 20 | 0.645 | 0.684 | 20 | × | ○ |
| 30 | 0.330 | 0.368 | 30 | × | ○ |
| 40 | 0.233 | 0.301 | 40 | × | ○ |
| 50 | 0.222 | 0.188 | 50 | × | ○ |
| 60 | 0.039 | 0.041 | 60 | ○ | × |
| 70 | 0.047 | 0.059 | 70 | ○ | × |
| 80 | 0.048 | 0.072 | 80 | ○ | × |
| 90 | 0.048 | 0.086 | 90 | ○ | × |
| 100 | 0.050 | 0.378 | 100 | ○ | × |
| 110 | 0.049 | 0.124 | 110 | ○ | × |
| 120 | 0.051 | 0.074 | 120 | ○ | × |
| 130 | 0.061 | 0.061 | 130 | ○ | × |
| 140 | 0.085 | 0.043 | 140 | △ | × |
| 150 | 0.164 | 0.039 | 150 | △ | × |
| 160 | 0.156 | 0.042 | 160 | △ | × |
| 170 | 0.080 | 0.034 | 170 | △ | × |
| 180 | 0.058 | 0.037 | 180 | △ | × |
| 190 | 0.041 | 0.034 | 190 | × | × |
| 200 | 0.030 | 0.034 | 200 | × | × |
| 0.17 mm~ | ○: Move to the other side | ||||
| 0.045~0.17 mm | △: Stop before end side | ||||
| ~0.045 mm | ×: No movement | ||||
| Toward free-end side | |||||
| Toward fixed-end side | |||||
| (a) | (b) | ||||
|---|---|---|---|---|---|
| Case 2 | Case 3 | Starting Position | |||
| f (Hz) | utip (mm) | f (Hz) | Fixed-End Side (z = 32 mm) | Free-End Side (z = 56 mm) | |
| 10 | 2.697 | 2.690 | 10 | × | × |
| 20 | 0.658 | 0.678 | 20 | × | ○ |
| 30 | 0.349 | 0.363 | 30 | × | ○ |
| 40 | 0.240 | 0.250 | 40 | × | ○ |
| 50 | 0.277 | 0.266 | 50 | × | × |
| 60 | 0.047 | 0.045 | 60 | ○ | × |
| 70 | 0.054 | 0.051 | 70 | ○ | × |
| 80 | 0.059 | 0.056 | 80 | ○ | × |
| 90 | 0.048 | 0.056 | 90 | ○ | × |
| 100 | 0.051 | 0.058 | 100 | × | × |
| 110 | 0.055 | 0.070 | 110 | × | × |
| 120 | 0.059 | 0.118 | 120 | × | △ |
| 130 | 0.060 | 0.456 | 130 | × | △ |
| 140 | 0.057 | 0.099 | 140 | × | ○ |
| 150 | 0.078 | 0.061 | 150 | × | ○ |
| 160 | 0.137 | 0.044 | 160 | × | ○ |
| 170 | 0.166 | 0.040 | 170 | × | × |
| 180 | 0.058 | 0.032 | 180 | × | × |
| 190 | 0.047 | 0.026 | 190 | × | × |
| 200 | 0.038 | 0.026 | 200 | × | × |
| 0.06 mm~ | ○: Move to the other side | ||||
| 0.045~0.06 mm | △: Stop before end side | ||||
| ~0.045 mm | ×: No movement | ||||
| Toward free-end side | |||||
| Toward fixed-end side | |||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mori, K.; Horibe, T.; Ishikawa, S. Effect of Weight on the Resonant Tuning of Energy Harvesting Devices Using Giant Magnetostrictive Materials. Materials 2018, 11, 581. https://doi.org/10.3390/ma11040581
Mori K, Horibe T, Ishikawa S. Effect of Weight on the Resonant Tuning of Energy Harvesting Devices Using Giant Magnetostrictive Materials. Materials. 2018; 11(4):581. https://doi.org/10.3390/ma11040581
Chicago/Turabian StyleMori, Kotaro, Tadashi Horibe, and Shigekazu Ishikawa. 2018. "Effect of Weight on the Resonant Tuning of Energy Harvesting Devices Using Giant Magnetostrictive Materials" Materials 11, no. 4: 581. https://doi.org/10.3390/ma11040581
APA StyleMori, K., Horibe, T., & Ishikawa, S. (2018). Effect of Weight on the Resonant Tuning of Energy Harvesting Devices Using Giant Magnetostrictive Materials. Materials, 11(4), 581. https://doi.org/10.3390/ma11040581





