Thermomechanical Studies of Yielding and Strain Localization Phenomena of Gum Metal under Tension
Abstract
1. Introduction
2. Materials and Methods
2.1. Material and Specimens
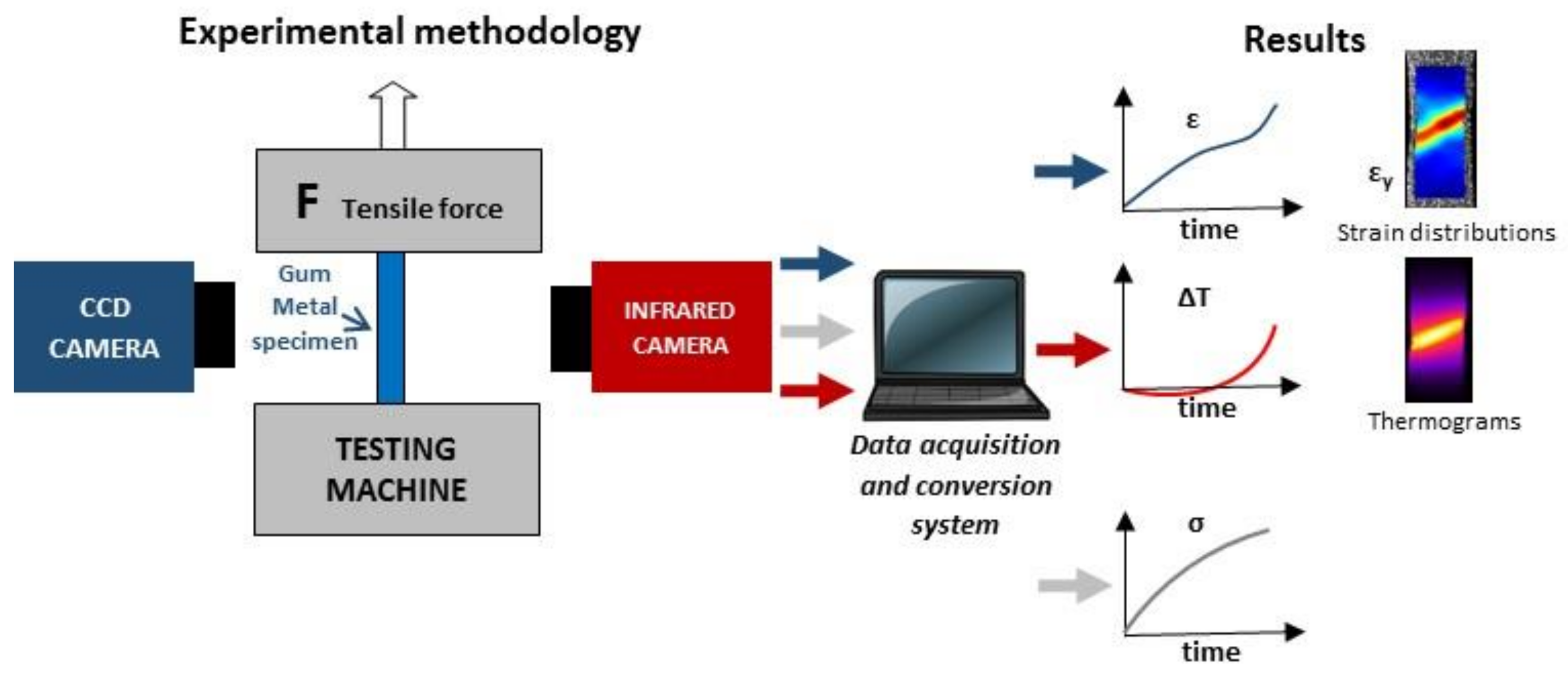
2.2. Determination of Mechanical and Thermal Fields Using DIC and IRT Techniques
3. Results
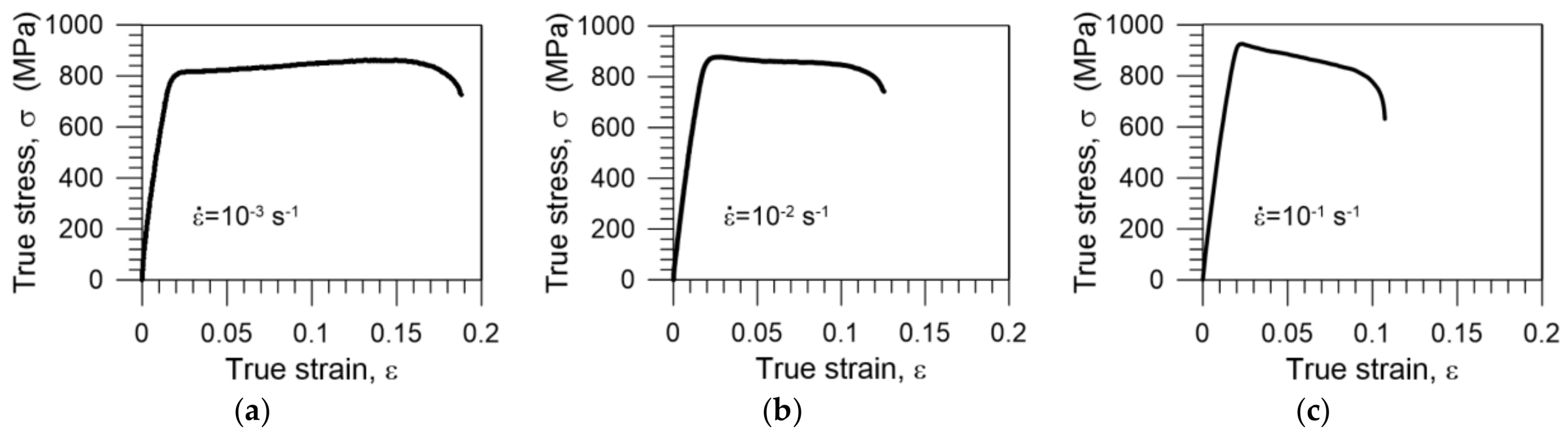
3.1. Macroscopic Mechanical Response of Gum Metal in Tension up to Rupture at Various Strain Rates
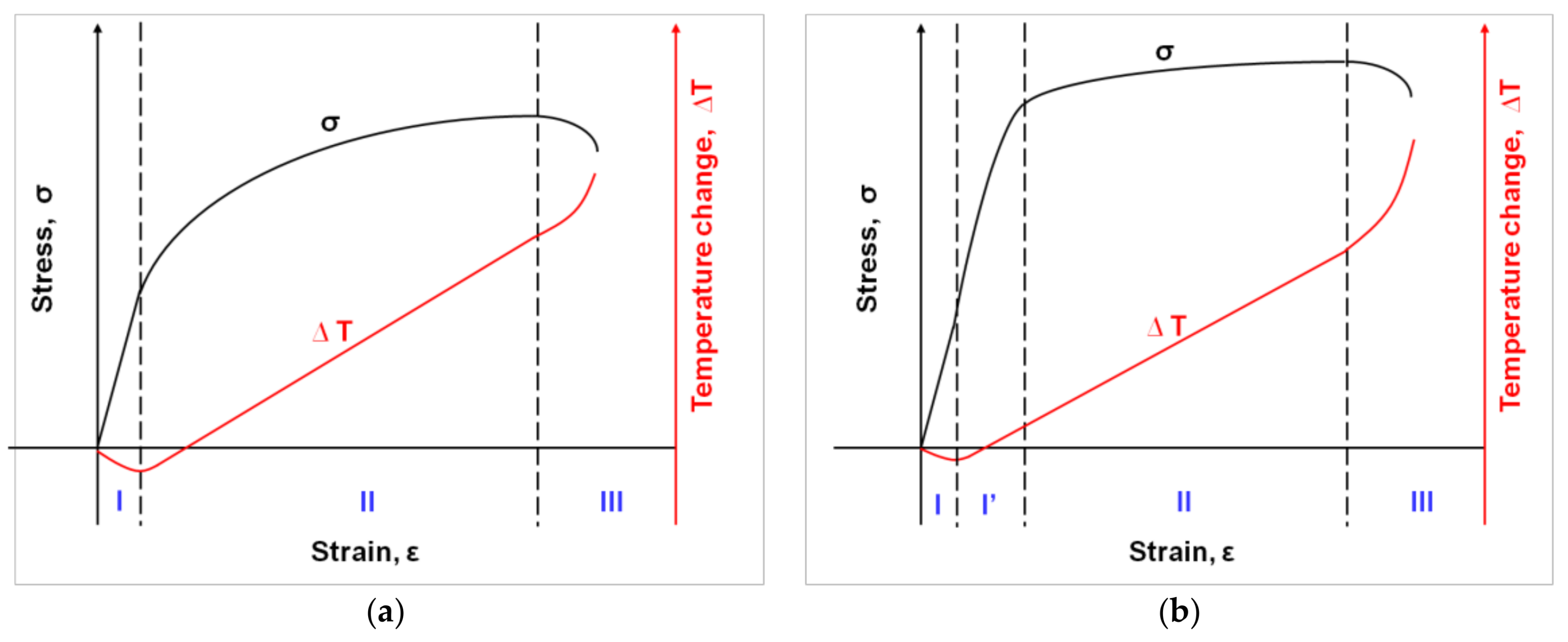
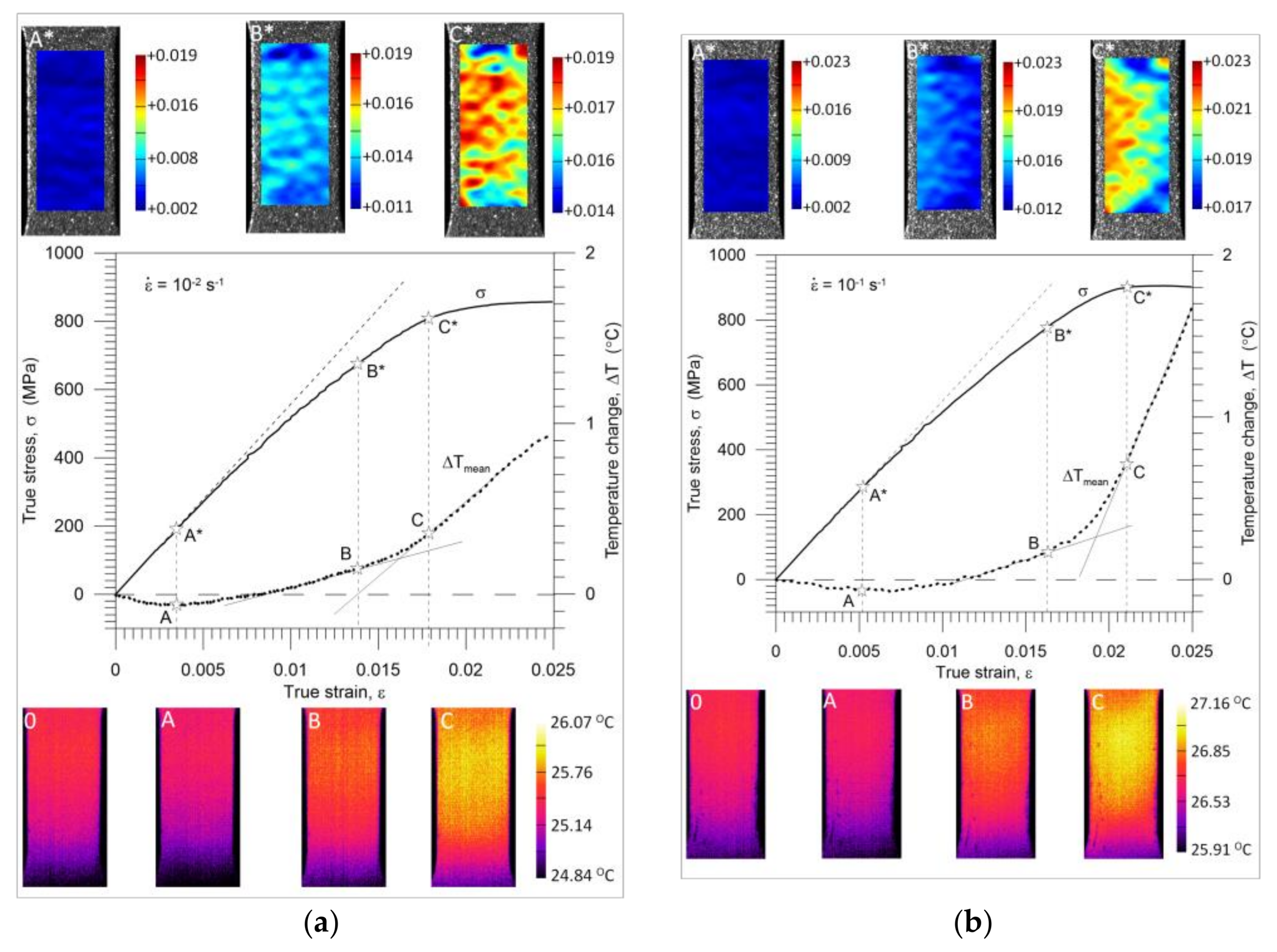
3.2. Gum Metal Thermomechanical Behavior during Elastic-Plastic Transition
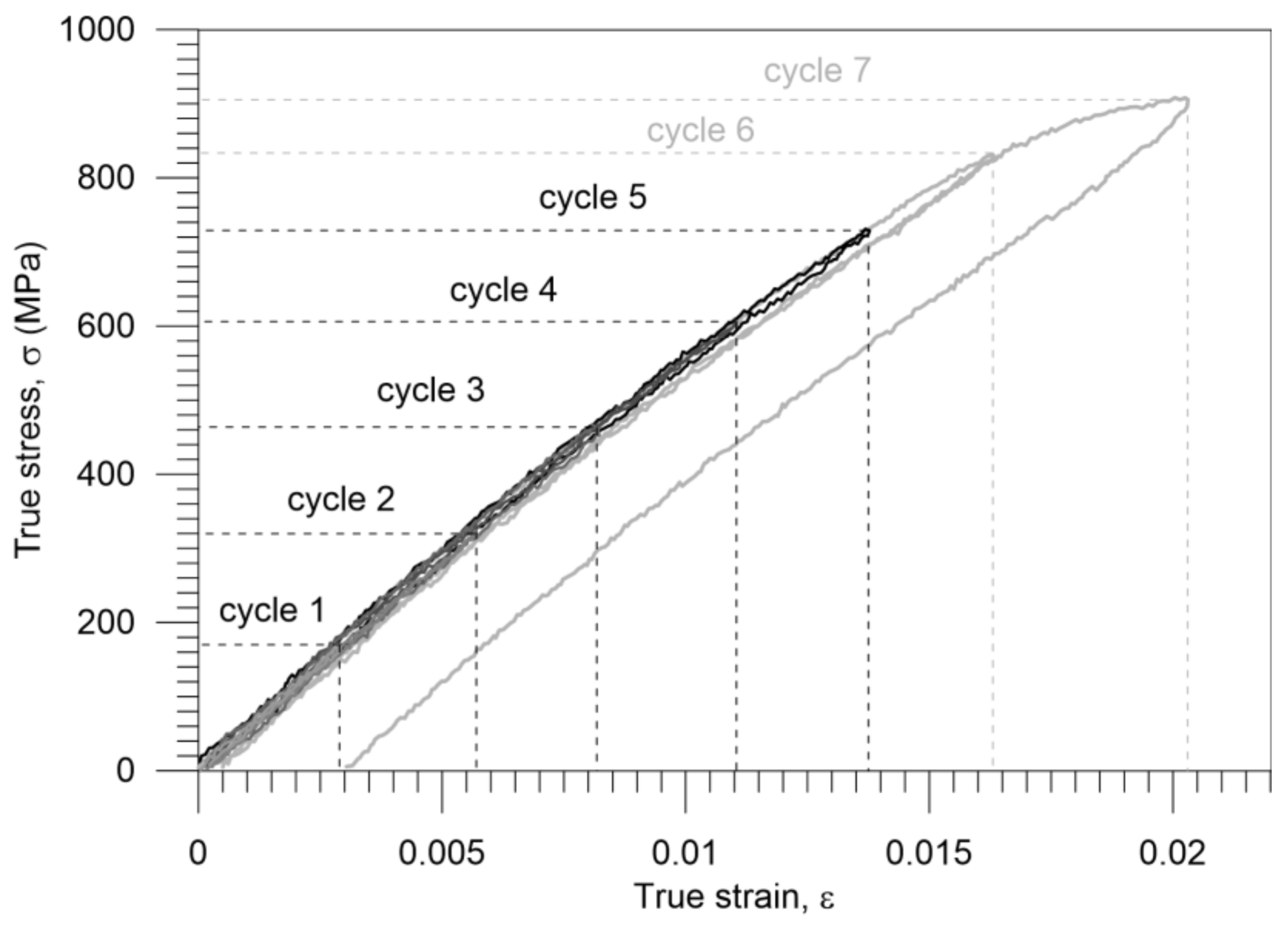
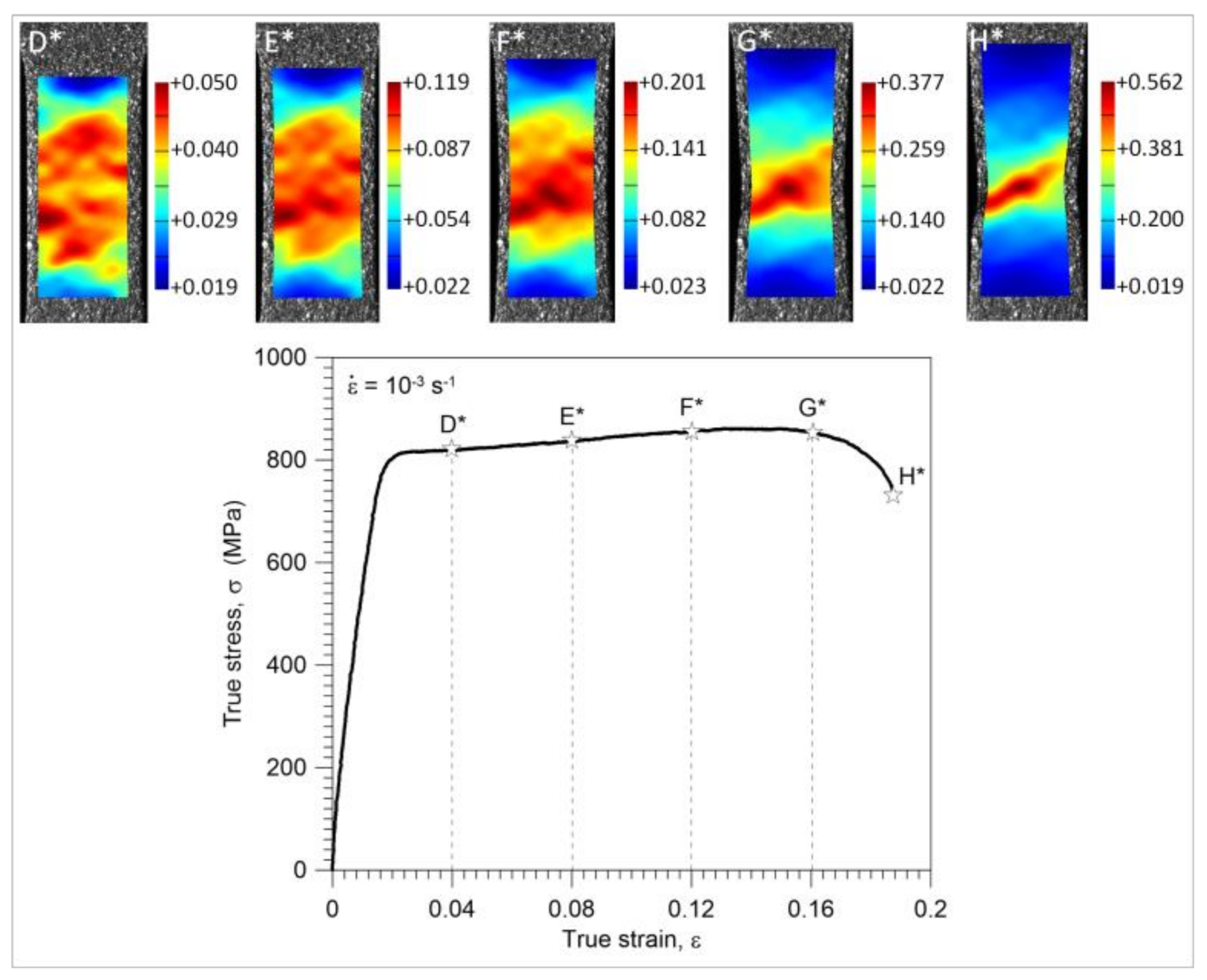
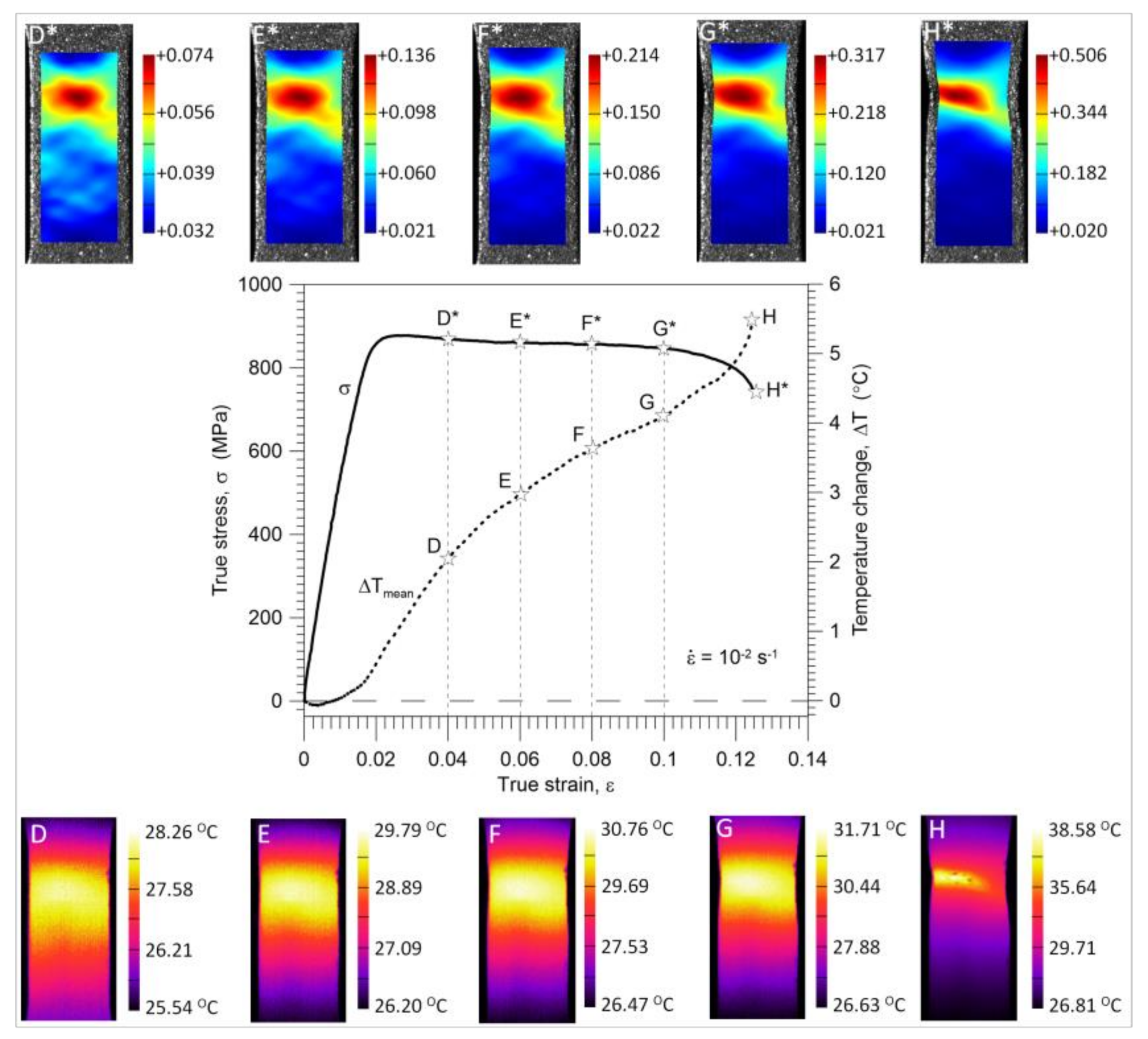
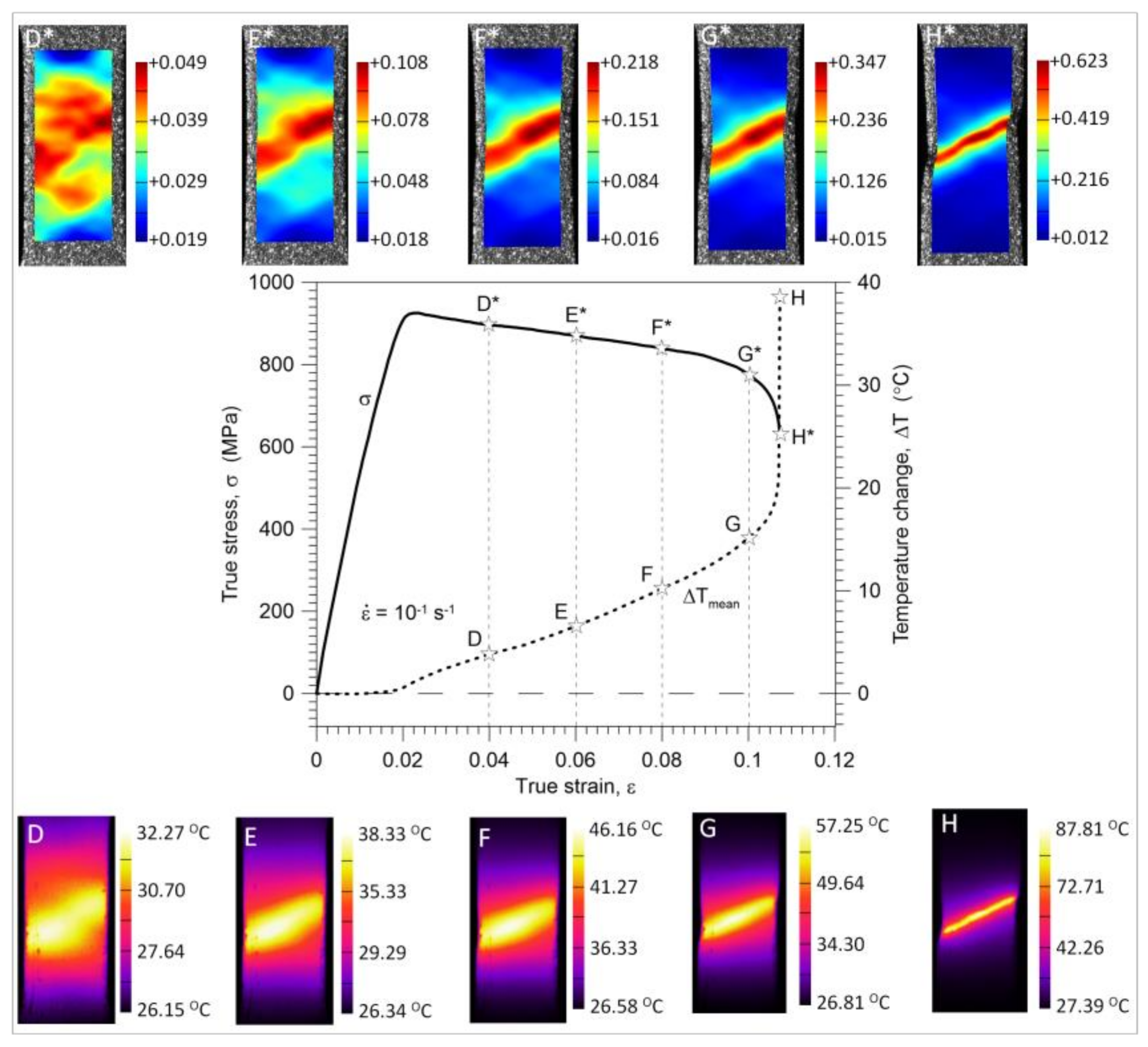
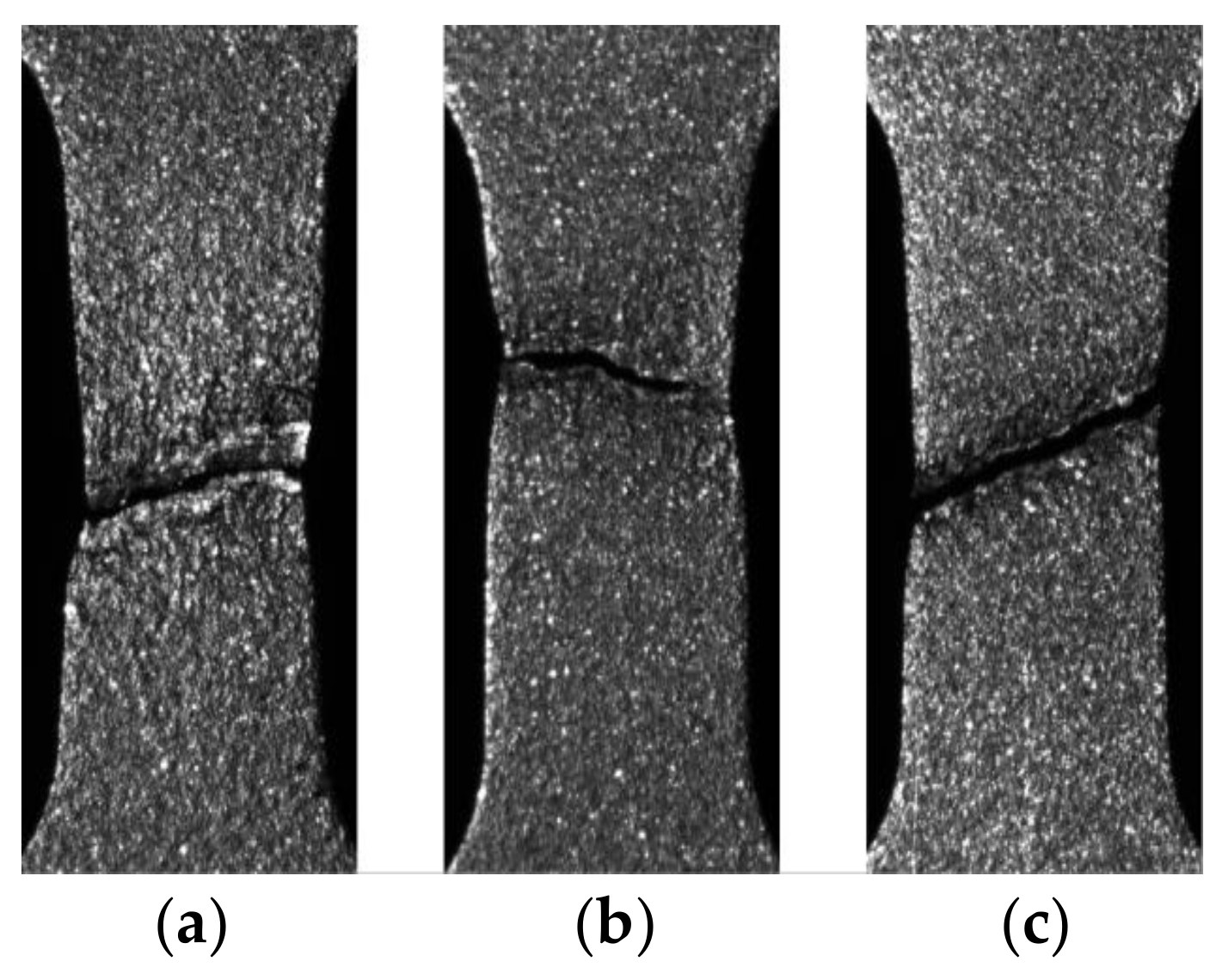
3.3. Nucleation and Development of the Strain Localization
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Saito, T.; Furuta, T.; Hwang, J.H.; Kuramoto, S.; Nishino, K.; Suzuki, N.; Chen, R.; Yamada, A.; Ito, K.; Seno, Y.; et al. Multifunctional Alloys obtained via a dislocation free plastic deformation mechanism. Science 2003, 300, 464–467. [Google Scholar] [CrossRef] [PubMed]
- Kuramoto, S.; Furuta, T.; Hwang, J.; Nishino, K.; Saito, T. Elastic properties of Gum Metal. Mater. Sci. Eng. A 2006, 442, 454–457. [Google Scholar] [CrossRef]
- Kuramoto, S.; Furuta, T.; Hwang, J.H.; Nishino, K.; Saito, T. Plastic deformation in a multifunctional Ti-Nb-Ta-Zr-O alloy. Metall. Mater. Trans. A 2006, 37, 657–662. [Google Scholar] [CrossRef]
- Talling, R.J.; Dashwood, R.J.; Jackson, M.; Dye, D. On the mechanism of superelasticity in Gum Metal. Acta Mater. 2009, 57, 1188–1198. [Google Scholar] [CrossRef]
- Guo, W.; Quadir, M.Z.; Moricca, S.; Eddows, T.; Ferry, M. Microstructural evolution and final properties of a cold-swaged multifunctional Ti–Nb–Ta–Zr–O alloy produced by a powder metallurgy route. Mater. Sci. Eng. A 2013, 575, 206–216. [Google Scholar] [CrossRef]
- Kamimura, Y.; Katakura, S.; Edagawa, K.; Takeuchi, S.; Kuramoto, S.; Furuta, T. Thermally Activated Deformation of Gum Metal: A Strong Evidence for the Peierls Mechanism of Deformation. Metall. Mater. Trans. A 2015, 56, 2084–2087. [Google Scholar] [CrossRef]
- Kuramoto, S.; Furuta, T.; Nagasako, N.; Morris, J.W. Localized Shear Deformation in Gum Metal at Ideal Strength. In The Minerals, Metals & Materials Society (TMS), Supplemental Proceedings: Materials Fabrication, Properties, Characterization, and Modeling; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011; Volume 2, pp. 567–574. [Google Scholar]
- Vorontsov, V.A.; Jones, N.G.; Rahman, K.M.; Dye, D. Superelastic load cycling of Gum Metal. Acta Mater. 2015, 88, 323–333. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, Y.; Wu, H.; Lan, X.; Qiu, J.; Hu, T.; Tang, H. Room temperature creep behavior of Ti-Nb-Ta-Zr-O alloy. Mater. Charact. 2016, 118, 29–36. [Google Scholar] [CrossRef]
- Furuta, T.; Kuramoto, S.; Morris, J.W.; Nagasako, N.; Withey, E.; Chrzan, D.C. The mechanism of strength and deformation in Gum Metal. Scr. Mater. 2013, 68, 767–772. [Google Scholar] [CrossRef]
- Tanaka, Y.; Kondo, M.; Miyazaki, N.; Ueji, R. Deformation behavior of pure titanium at a wide range of strain rates. J. Phys. Conf. Ser. 2010, 240, 012021. [Google Scholar] [CrossRef]
- Duan, H.; Xu, H.; Su, W.; Ke, Y.; Liu, Z.; Song, H. Effect of oxygen on the microstructure and mechanical properties of Ti-23Nb-0.7Ta-2Zr alloy. Int. J. Miner. Metall. Mater. 2012, 19, 1128–1133. [Google Scholar] [CrossRef]
- Nagasako, N.; Asahi, R.; Isheim, D.; Seidman, D.N.; Kuramoto, S.; Furuta, T. Microscopic study of gum-metal alloys: A role of trace oxygen for dislocation-free deformation. Acta Mater. 2016, 105, 347–354. [Google Scholar] [CrossRef]
- Wei, L.S.; Kim, H.Y.; Koyano, T.; Miyazaki, S. Effects of oxygen concentration and temperature on deformation behavior of Ti-Nb-Zr-Ta-O alloys. Scr. Mater. 2016, 12, 55–58. [Google Scholar] [CrossRef]
- Tane, M.; Nakano, T.; Kuramoto, S.; Niinomi, M.; Takesue, N.; Nakajima, H. ω Transformation in cold-worked Ti–Nb–Ta–Zr–O alloys with low body-centered cubic phase stability and its correlation with their elastic properties. Acta Mater. 2013, 61, 139–150. [Google Scholar] [CrossRef]
- Kim, H.Y.; Miyazaki, S. Several Issues in the Development of Ti–Nb-Based Shape Memory Alloys. Shap. Mem. Superelasticity 2016, 2, 380–390. [Google Scholar] [CrossRef]
- Lai, M.J.; Tasan, C.C.; Raabe, D. Deformation mechanism of ω-enriched Ti–Nb-based gum metal: Dislocation channeling and deformation induced ω–β transformation. Acta Mater. 2015, 100, 290–300. [Google Scholar] [CrossRef]
- Ghidelli, M.; Sebastiani, M.; Johanns, K.E.; Pharr, G.M. Effects of indenter angle on micro-scale fracture toughness measurement by pillar splitting. J. Am. Ceram. Soc. 2017, 100, 5731–5738. [Google Scholar] [CrossRef]
- Thomson, W. On the thermoelastic and thermomagnetic properties of matter. Trans. R. Soc. Edin. 1853, 20, 57–77. [Google Scholar]
- Chrysochoos, A. Infrared thermography applied to the analysis of material behaviour: A brief overview. QIRT J. 2012, 9, 193–208. [Google Scholar] [CrossRef]
- Pieczyska, E.A. Thermoelastic effect in austenitic steel referred to its hardening. J. Theor. App. Mech. 1999, 2, 349–368. [Google Scholar]
- Maj, M.; Oliferuk, W. Analysis of plastic strain localization on the basis of strain and temperature fields. Arch. Metall. Mater. 2012, 57, 1111–1116. [Google Scholar] [CrossRef]
- Pieczyska, E.A.; Maj, M.; Kowalczyk-Gajewska, K.; Staszczak, M.; Gradys, A.; Majewski, M.; Cristea, M.; Tobushi, H.; Hayashi, S. Thermomechanical properties of polyurethane shape memory polymer-experiment and modelling. Smart Mater. Struct. 2015, 24, 045043-1–16. [Google Scholar] [CrossRef]
- Pieczyska, E.A.; Maj, M.; Furuta, T.; Kuramoto, S. Gum Metal– unique properties and results of initial investigation of a new titanium alloy—extended paper. In Advances in Mechanics: Theoretical, Computational and Interdisciplinary; Kleiber, M., Burczyński, T., Wilde, K., Górski, J., Winkelmann, K., Smakosz, Ł., Eds.; CRC Press/Balkema, Taylor & Francis: London, UK, 2016; pp. 469–472. [Google Scholar]
- Oliferuk, W.; Maj, M.; Zembrzycki, K. Determination of the Energy Storage Rate Distribution in the Area of Strain Localization Using Infrared and Visible Imaging. Exp. Mech. 2015, 55, 753–760. [Google Scholar] [CrossRef]
- Pieczyska, E.A.; Gadaj, S.P.; Nowacki, W.K.; Tobushi, H. Phase-transformation fronts evolution for strain- and stress- controlled tension tests in TiNi Shape Memory Alloy. Exp. Mech. 2006, 46, 531–542. [Google Scholar] [CrossRef]
- Chrysochoos, A.; Wattrisse, B.; Muracciole, J.M.; El Kaïm, Y. Fields of stored energy associated with localized necking of steel. J. Mech. Mater. Struct. 2009, 4, 245–262. [Google Scholar] [CrossRef]
- Pottier, T.; Toussaint, F.; Louche, H.; Vacher, P. Inelastic heat fraction estimation from two successive mechanical and thermal analyses and full-field measurements. Eur. J. Mech. A/Solids 2013, 38, 1–11. [Google Scholar] [CrossRef]
- Li, L.; Muracciole, J.M.; Waltz, L.; Sabatier, L.; Barou, F.; Wattrisse, B. Local experimental investigations of the thermomechanical behavior of a coarse-grained aluminum multicrystal using combined DIC and IRT methods. Opt. Lasers Eng. 2016, 81, 1–10. [Google Scholar] [CrossRef]
- Nowak, M.; Maj, M. Determination of coupled mechanical and thermal fields using 2D digital image correlation and infrared thermography: Numerical procedures and results. Arch. Civ. Mech. Eng. 2018, 18, 630–644. [Google Scholar] [CrossRef]
- Farren, W.S.; Taylor, G.I. The heat developed during plastic extension of metals. Proc. Roy. Soc. 1925, 107, 422–451. [Google Scholar] [CrossRef]
- Taylor, G.I.; Quinney, M.A. The latent energy remaining in a metal after cold working. Proc. Roy. Soc. 1934, 143, 307–326. [Google Scholar] [CrossRef]
- Bever, M.B.; Holt, D.L.; Titchener, A.L. The Stored Energy of Cold Work. Prog. Mater. Sci. 1973, 17, 5–177. [Google Scholar] [CrossRef]
- Golasiński, K.M.; Pieczyska, E.A.; Staszczak, M.; Maj, M.; Furuta, T.; Kuramoto, S. Infrared thermography applied for experimental investigation of thermomechanical couplings in Gum Metal. QIRT J. 2017, 14, 226–233. [Google Scholar] [CrossRef]

| Cameras Properties | Manta G-125B | ThermaCam Phoenix |
|---|---|---|
| Resolution (pixel) | 1100 × 410 | 320 × 150 |
| Recording frequency (Hz) used for: | ||
| 10−3 s−1 | 2.93 | 5.86 |
| 10−2 s−1 | 14.57 | 116.6 |
| 10−1 s−1 | 58 | 583 |
| Exposure/integration time (ms) | 0.2 | 0.5 |
| Pixel size (μm) | 9.5 | 30 |
| Strain Rate | 10−3 s−1 | 10−2 s−1 | 10−1 s−1 |
|---|---|---|---|
| Toughness values (MJ ∙ m−3) | 152 | 97 | 81 |
| Strain Rate | Maximal Drop in Temperature (°C) | Strain at Minimal Temperature | Stress at Minimal Temperature (MPa) | Temperature at Reversible Deformation (°C) | Strain at Reversible Deformation | Stress at Reversible Deformation (MPa) |
|---|---|---|---|---|---|---|
| 10−2 s−1 | −0.062 | 0.0035 | 192 | +0.15 | 0.0138 | 674 |
| 10−1 s−1 | −0.071 | 0.0052 | 285 | +0.22 | 0.0163 | 780 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pieczyska, E.A.; Maj, M.; Golasiński, K.; Staszczak, M.; Furuta, T.; Kuramoto, S. Thermomechanical Studies of Yielding and Strain Localization Phenomena of Gum Metal under Tension. Materials 2018, 11, 567. https://doi.org/10.3390/ma11040567
Pieczyska EA, Maj M, Golasiński K, Staszczak M, Furuta T, Kuramoto S. Thermomechanical Studies of Yielding and Strain Localization Phenomena of Gum Metal under Tension. Materials. 2018; 11(4):567. https://doi.org/10.3390/ma11040567
Chicago/Turabian StylePieczyska, Elżbieta A., Michał Maj, Karol Golasiński, Maria Staszczak, Tadahiko Furuta, and Shigeru Kuramoto. 2018. "Thermomechanical Studies of Yielding and Strain Localization Phenomena of Gum Metal under Tension" Materials 11, no. 4: 567. https://doi.org/10.3390/ma11040567
APA StylePieczyska, E. A., Maj, M., Golasiński, K., Staszczak, M., Furuta, T., & Kuramoto, S. (2018). Thermomechanical Studies of Yielding and Strain Localization Phenomena of Gum Metal under Tension. Materials, 11(4), 567. https://doi.org/10.3390/ma11040567






