The Influence of Metakaolinite on the Development of Thermal Cracks in a Cement Matrix
Abstract
:1. Introduction
2. Materials and Methodology
2.1. Materials Used, Samples Maturation and Thermal Load
- C42—100% CEM I 42.5R and water,
- C42MT—90 CEM I 42.5R, 10% MT, and water,
- C52—100% CEM I 52.5R and water,
- C52MT—90 CEM I 52.5R, 10% MT, and water.
2.2. Examination of the Selected Physical and Mechanical Features
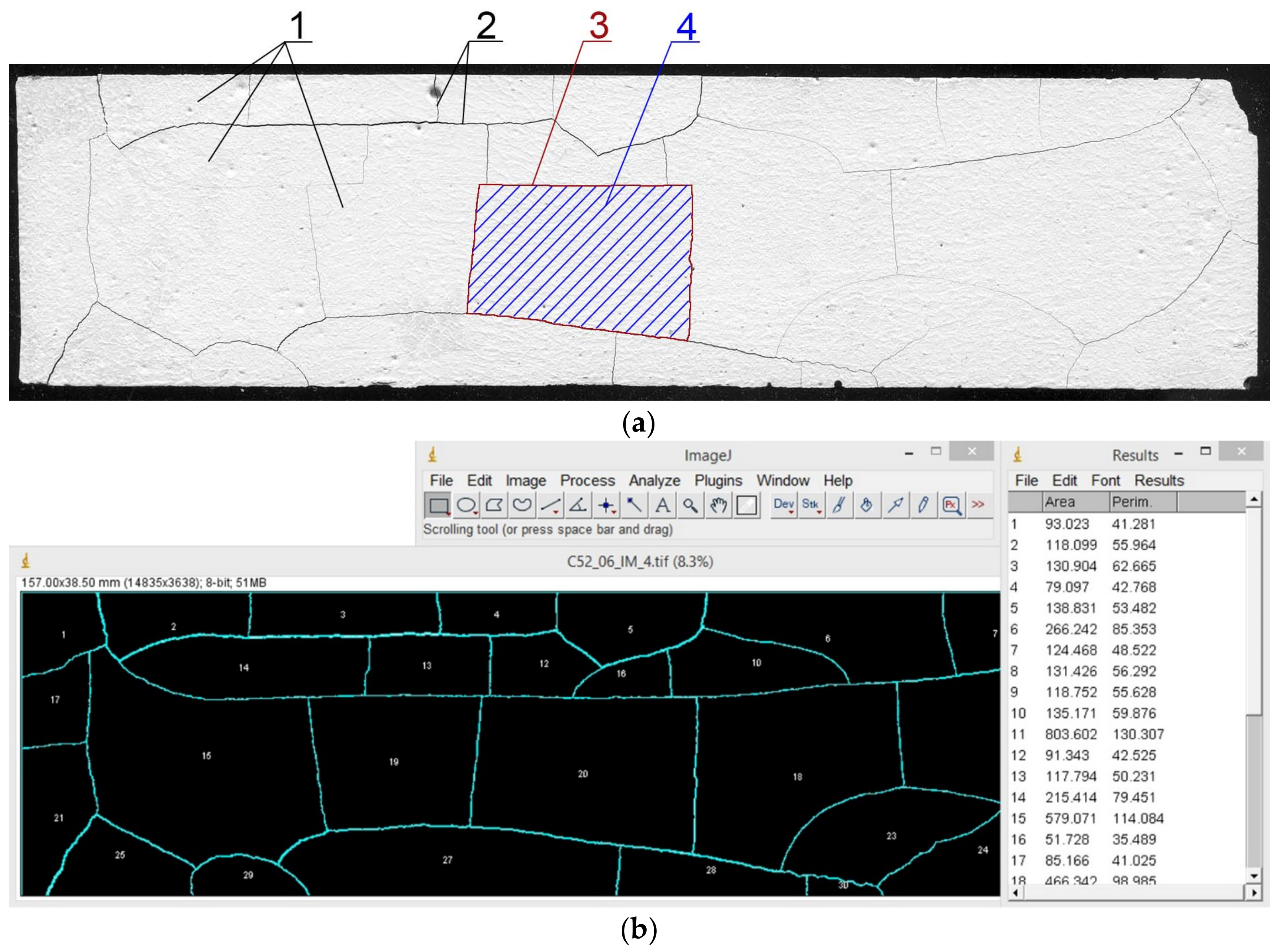
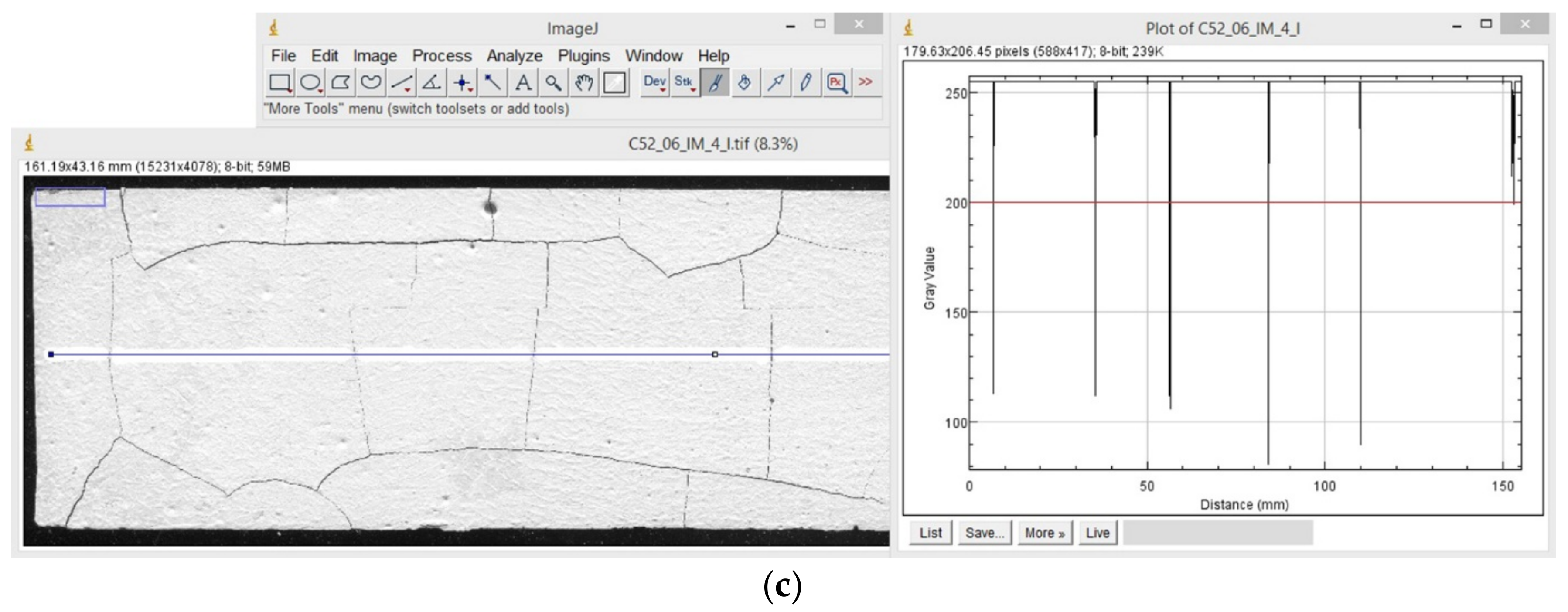
2.3. Image Analysis
- —the cluster average area—the parameter of R(2) space,
- —the cluster average perimeter—the parameter of R(2) space,
- —the crack average width—the parameter of R(1) space.
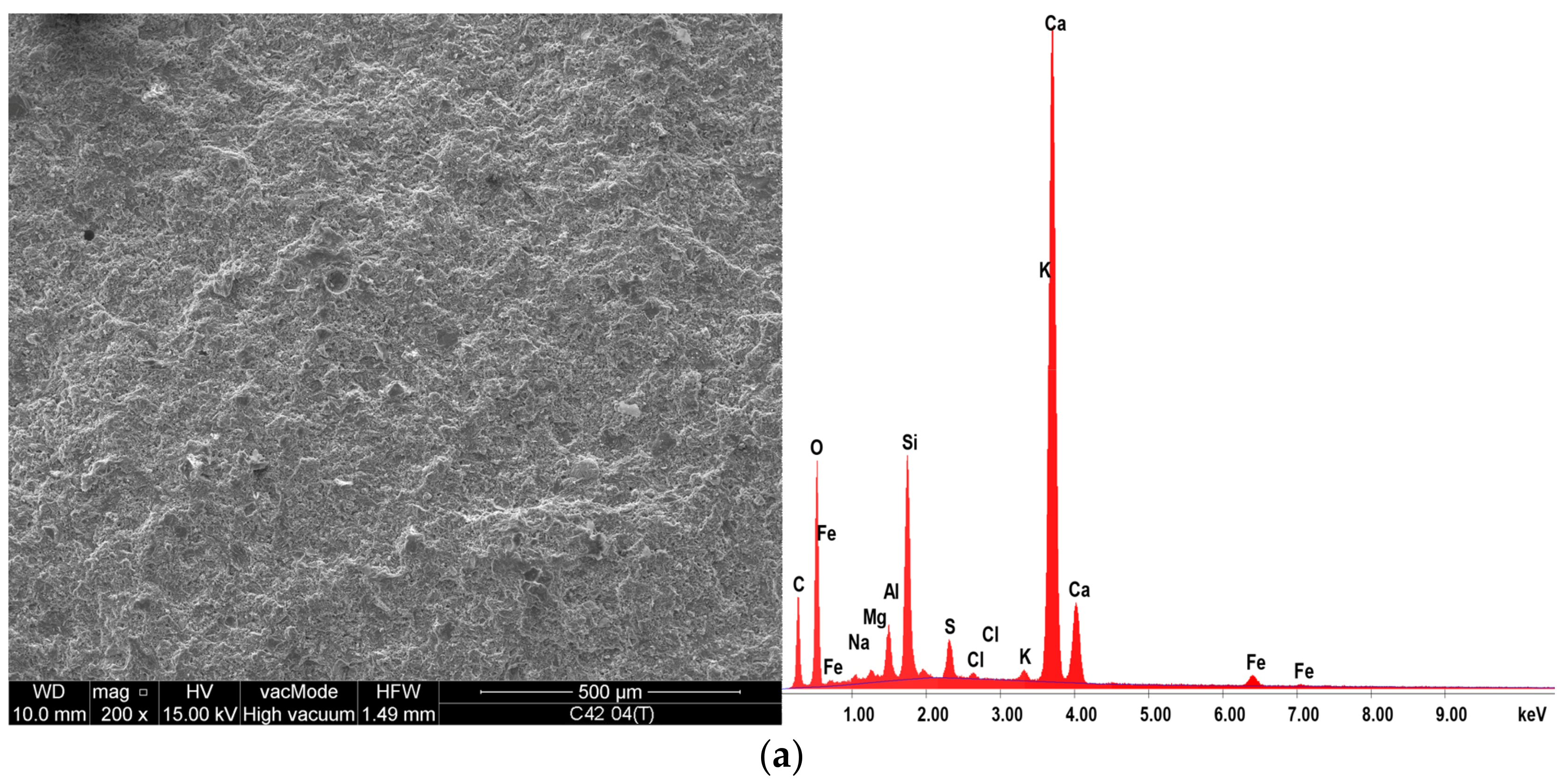
2.4. SEM and EDS
3. Results and Discussion
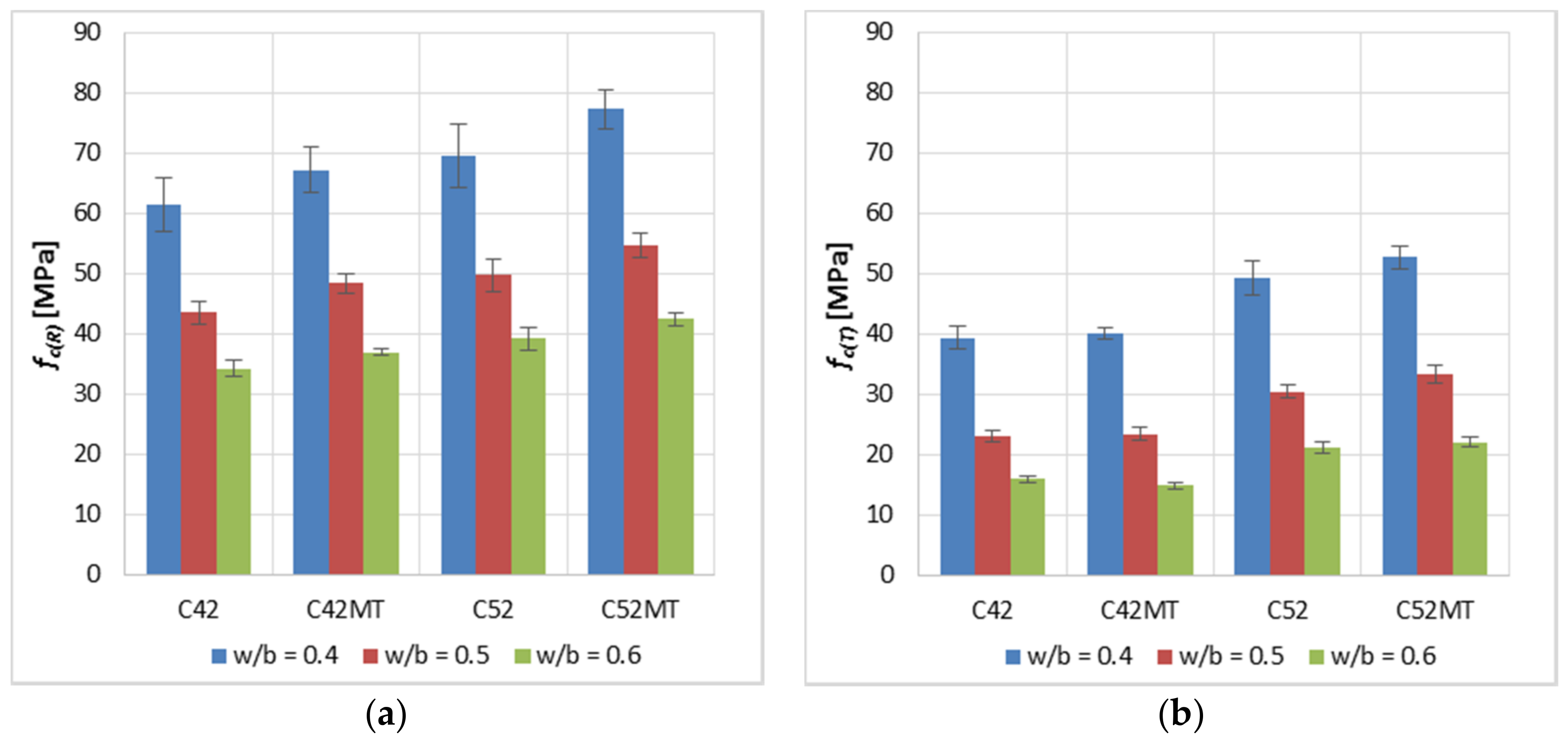
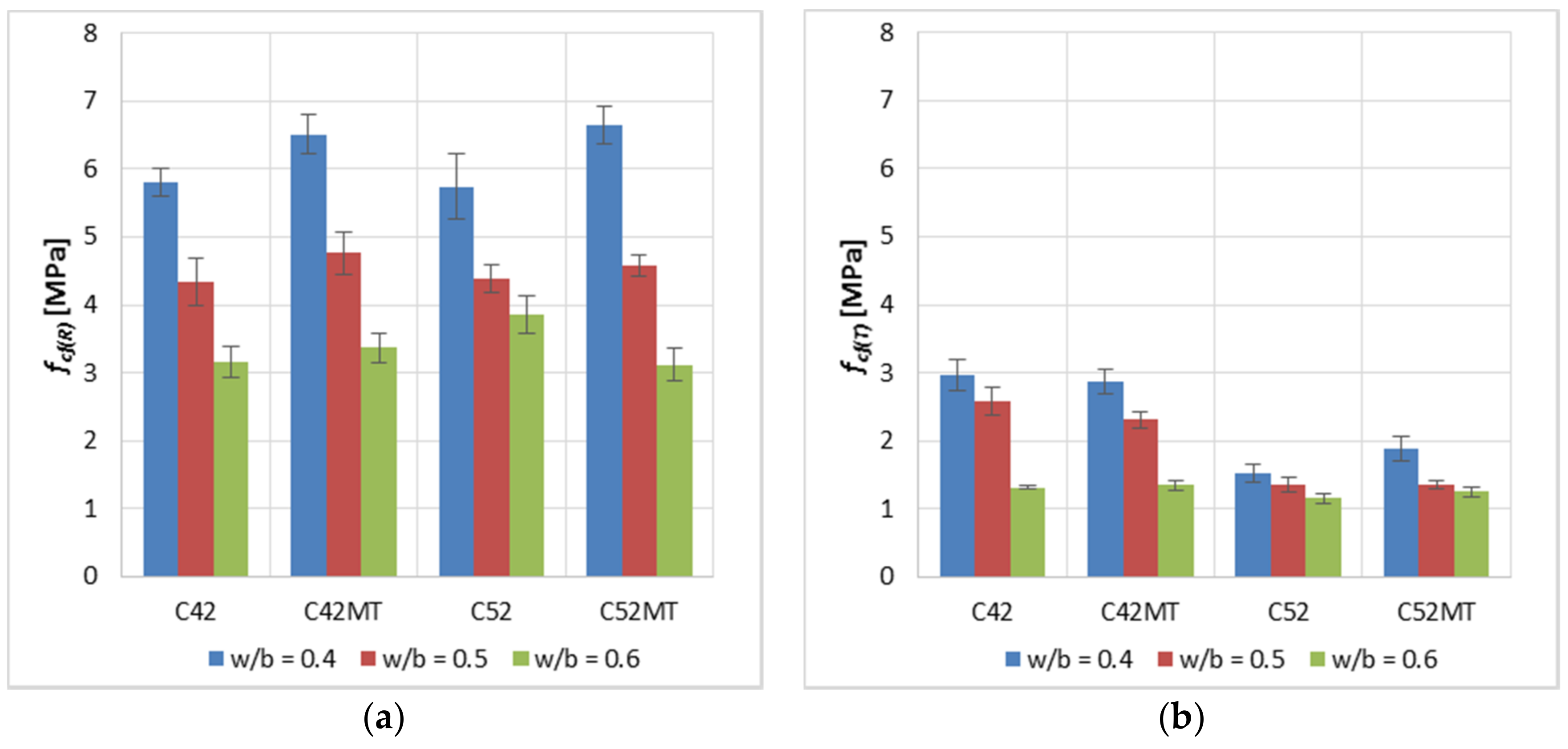
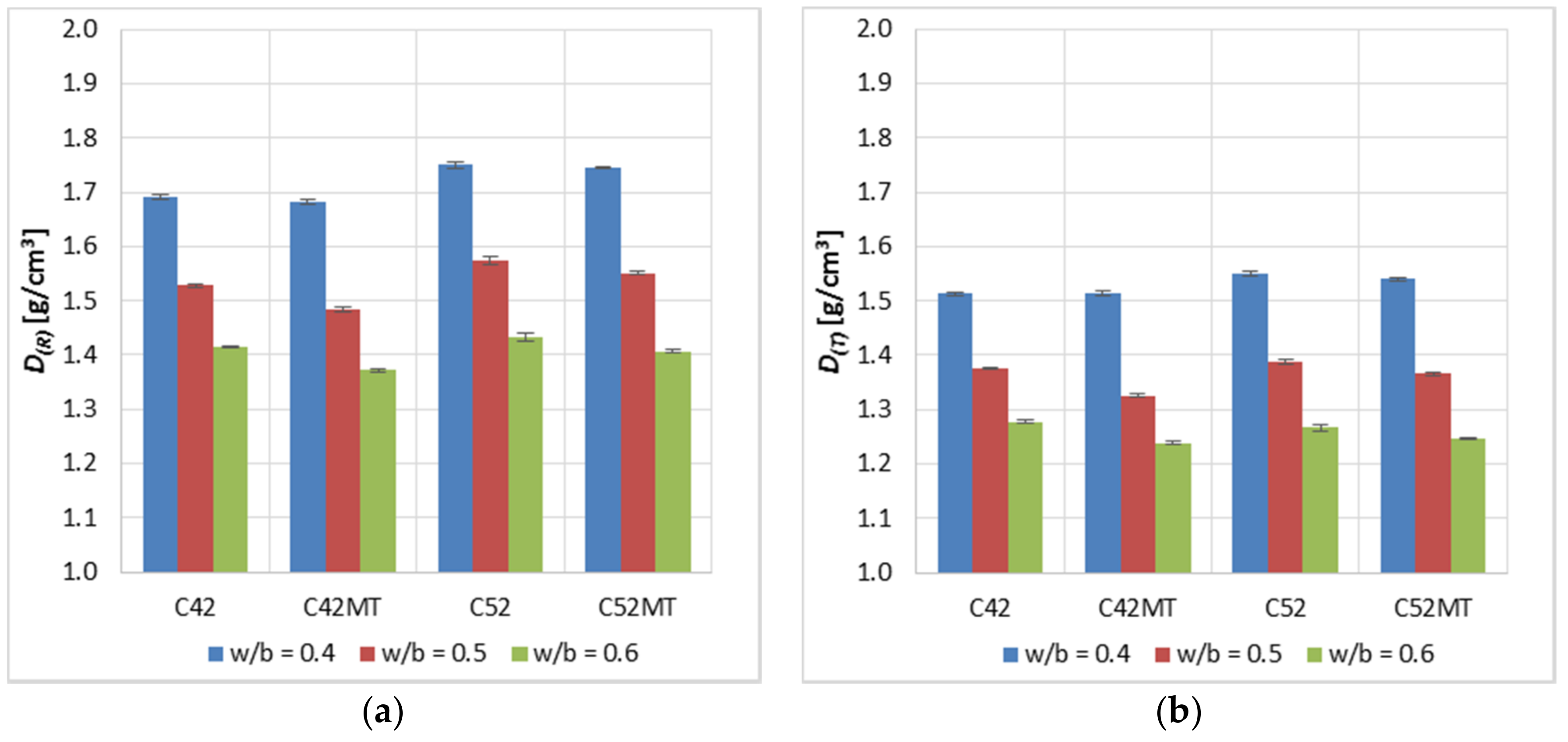
3.1. Mechano-Physical Properties of the Cement Pastes
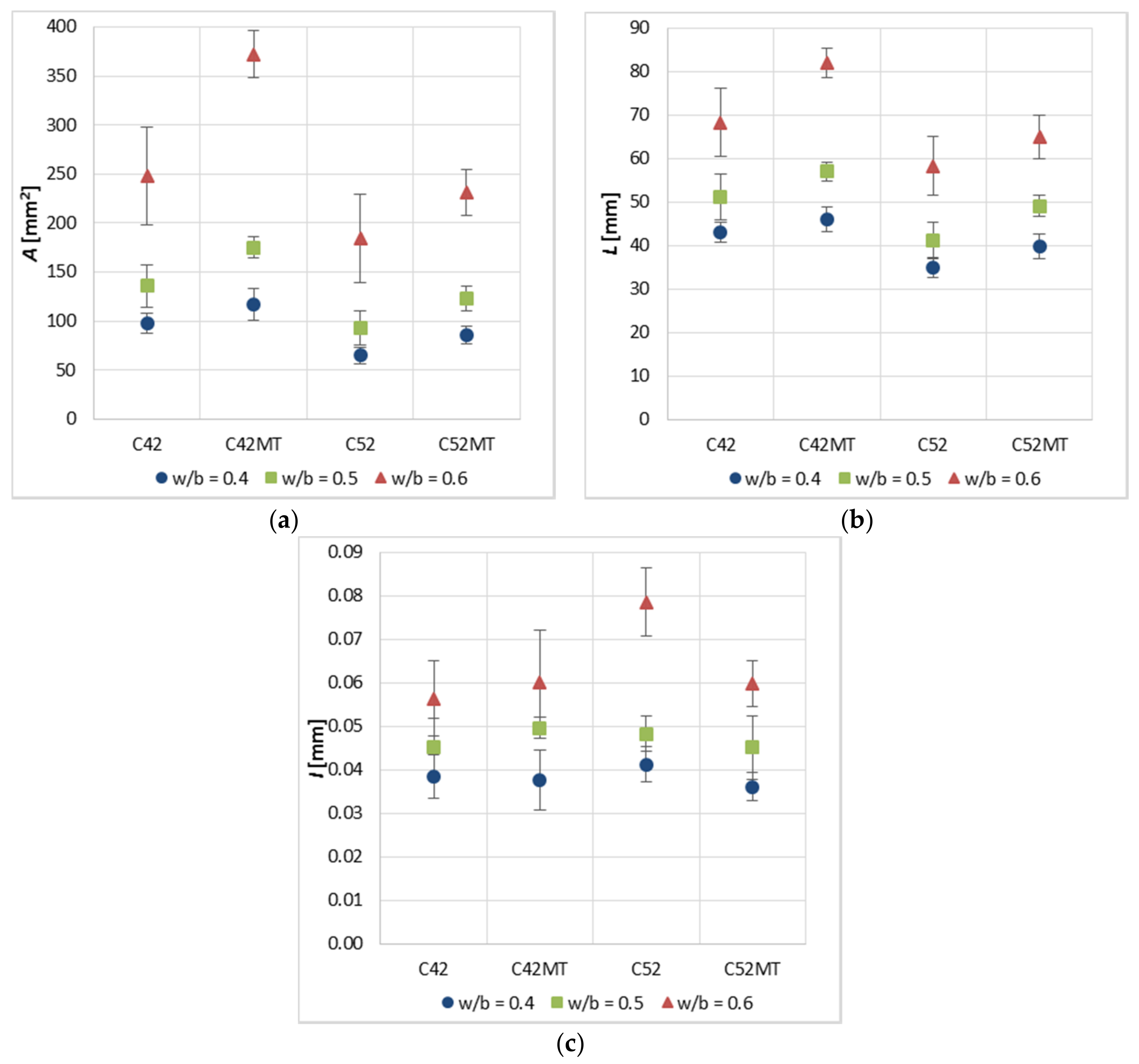
3.2. Geometric Characteristics of Cluster Cracks
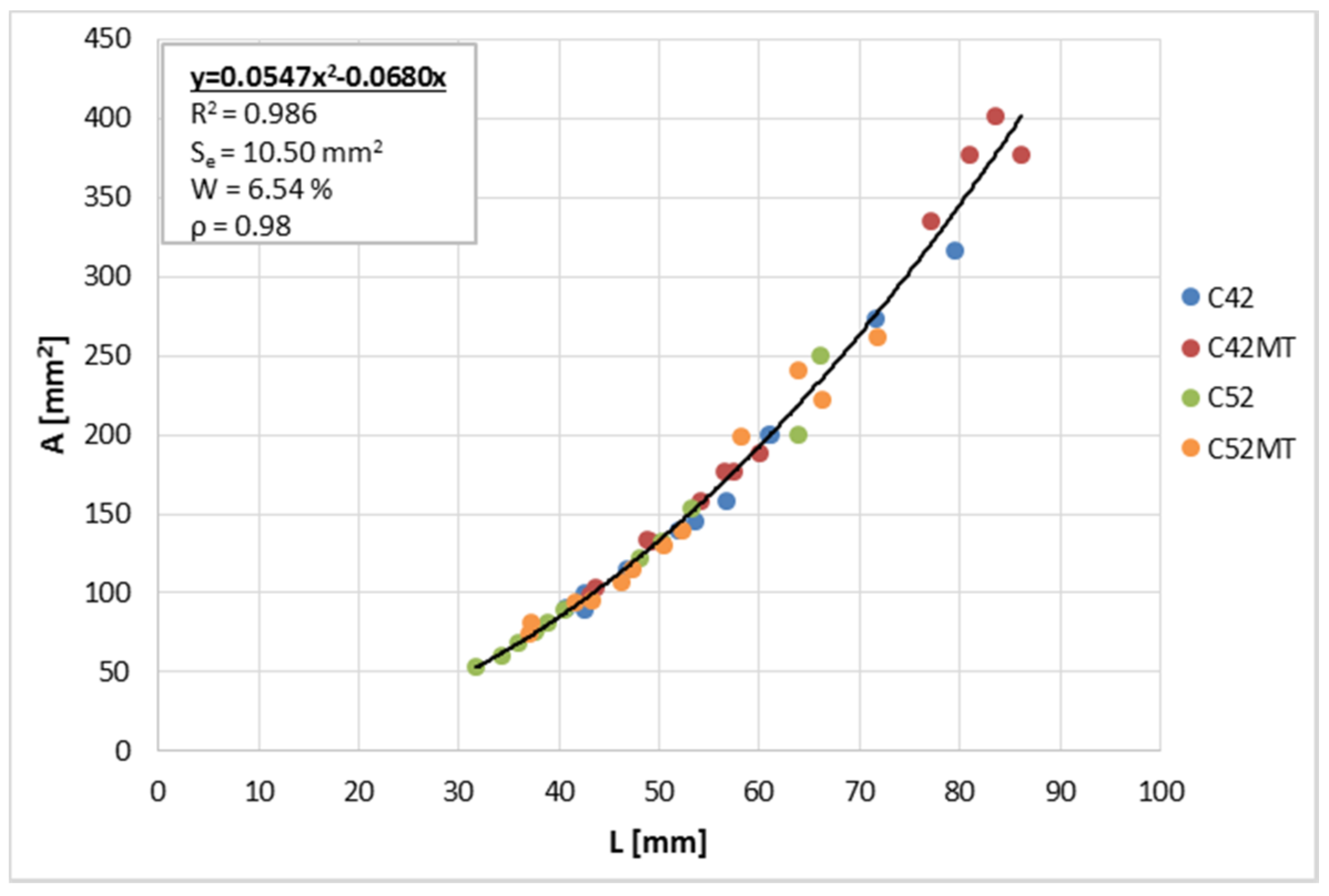
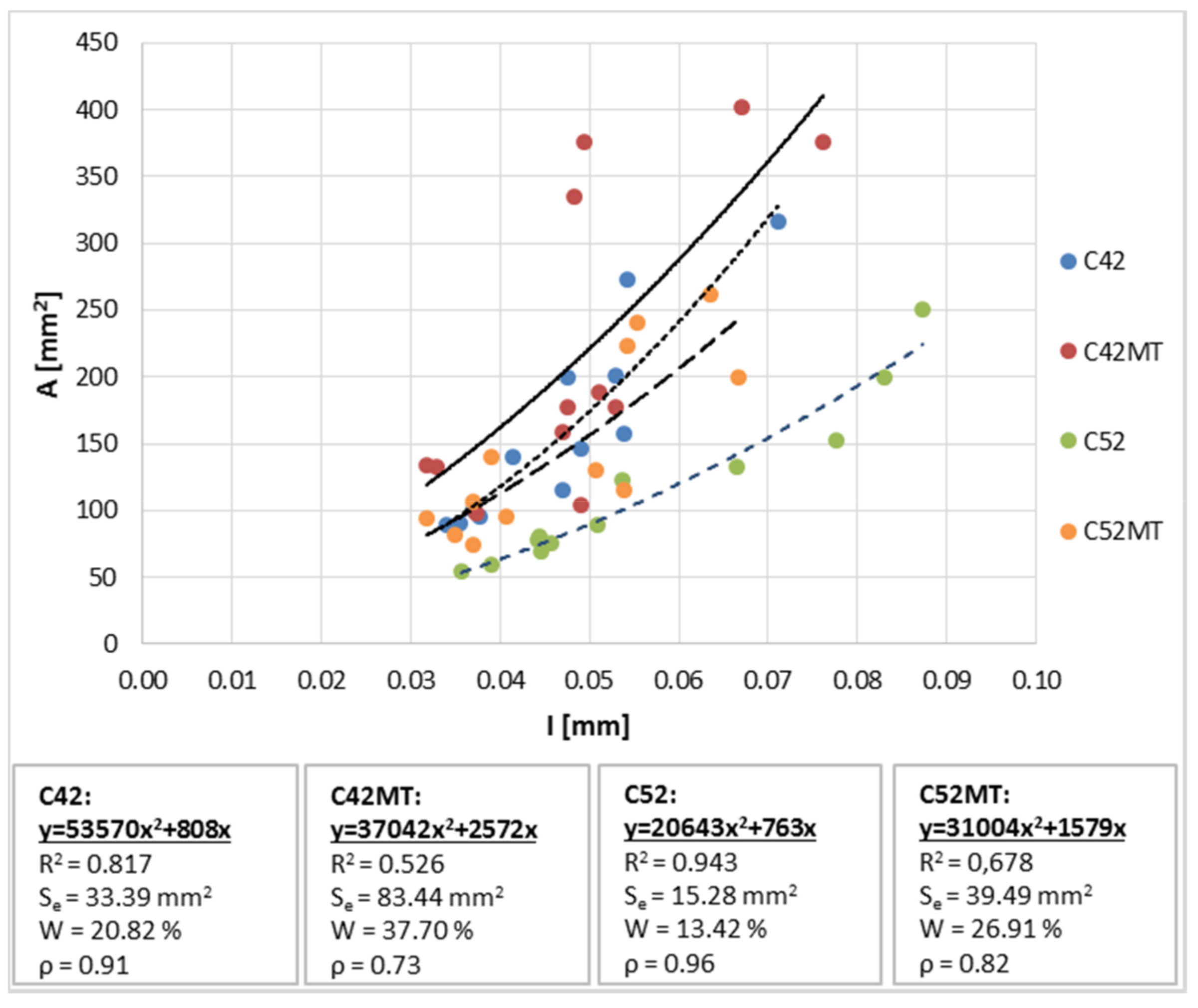
3.3. Correlations Between Parameters
3.4. Analysis of the Local Microstructure
4. Conclusions
- The use of MT as a substitute for 10% of the cement’s mass positively affects the strength parameters of the reference cement paste. After the thermal shock effect, the beneficial effect of MT was still observed; however, it was smaller compared to the reference samples.
- Computer image analysis can be successfully applied to the quantitative description of the surface structure of cluster cracks.
- Geometric characteristics of the thermal cracks depend on technological variables in the process of cement paste production, i.e., the cement’s class, the w/b ratio, the presence of a pozzolanic additive. The process of the structure self-assembly, which affects the cluster layout on the sample’s surface, is shaped by intermolecular interactions in the dispersion environment of cement paste, and by the physico-chemical changes of the system occurring as a result of the cement hydration process.
- The geometrical dependence of clusters (the relationship between and ) is constant, regardless of the technological variables of the cement paste.
- The relationship depends on the type of cement and the presence of MT, and for estimation purposes, the relationship should be considered with division into series. As the size of the cluster increases, the crack width also increases.
- In the aspect of the material’s durability and resistance to an aggressive environment, the best situation is when the material has a large surface area of clusters, with the smallest width of the cracks. Among the cement pastes tested, the best features in this aspect have obtained a cement paste made of cement with a larger grain size (CEM I 42.5R), in which MT was used.
- The products of the pozzolanic reaction after adding MT to the cement paste seal the contact zone between the clusters. This results in increased cohesion of the material, which translates into a higher mechanical strength.
- Analysis of the correlation indicated that the stereological parameters of the cracks are strongly correlated with the physical and mechanical properties of the cement pastes. Only in the case of fcf(T) dependencies with the cracks’ geometry are characterized by a weak correlation and the estimation attempt would be burdened with a large error.
- SEM analysis confirmed that cluster cracks have a fractal character and the structures visible in the macroscale are also found in the microscale.
Acknowledgments
Conflicts of Interest
References
- Fic, S.; Vyrovoy, V.N.; Dorofeev, V.S. Procesy Samoorganizacji Struktury Kompozytowych Materiałów Budowlanych; Politechnika Lubelska: Lublin, Poland, 2013. [Google Scholar]
- Sukhanov, V.; Vyrovoy, V.; Dorofeev, V. Crack’s role in structural development of the constructional composite materials. Mod. Ind. Civ. Constr. 2011, 7, 135–141. [Google Scholar]
- Czarnecki, L.; Emmons, P.H. Naprawa i Ochrona Konstrukcji Betonowych; Polski Cement: Kraków, Poland, 2002. [Google Scholar]
- Yang, Y.; Yang, C.; Huang, C. Thin crack observation in a reinforced concrete bridge pier test using image processing and analysis. Adv. Eng. Softw. 2015, 83, 99–108. [Google Scholar] [CrossRef]
- Li, L.; Wang, Q.; Zhang, G.; Shi, L.; Dong, J.; Jia, P. A method of detecting the cracks of concrete undergo high-temperature. Constr. Build. Mater. 2018, 162, 345–358. [Google Scholar] [CrossRef]
- Pacheco, J.; Savija, B.; Schlangen, E.; Polder, R. Assessment of cracks in reinforced concrete by means of electrical resistance and image analysis. Constr. Build. Mater. 2014, 65, 417–426. [Google Scholar] [CrossRef]
- Nemati, K.M.; Monteiro, P.J.; Scrivener, K.L. Analysis of compressive stress-induced cracks in concrete. ACI Mater. J. 1998, 95, 617–630. [Google Scholar]
- Ringot, E. Automatic quantification of microcracks network by stereological method of total projections in mortars and concretes. Cem. Concr. Res. 1988, 18, 35–43. [Google Scholar] [CrossRef]
- Ringot, E.; Bascoul, A. About the analysis of microcracking in concrete. Cem. Concr. Compos. 2001, 23, 261–266. [Google Scholar] [CrossRef]
- Sinha, S.K.; Fieguth, P.W. Segmentation of buries concrete pipe images. Autom. Constr. 2005, 15, 47–57. [Google Scholar] [CrossRef]
- Sinha, S.K.; Fieguth, P.W. Automated detection of cracks in buried concrete pipe images. Autom. Constr. 2006, 15, 58–72. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Nakamura, S.; Saegusa, R.; Hashimoto, S. Image-based crack detection for real concrete surfaces. IEEJ Trans. Electr. Electron. Eng. 2008, 3, 128–135. [Google Scholar] [CrossRef]
- Fic, S.; Szelag, M. Analysis of the development of cluster cracks caused by elevated temperatures in cement paste. Constr. Build. Mater. 2015, 83, 223–229. [Google Scholar] [CrossRef]
- Zhang, Y. Study on Microstructure and Rheological Properties of Cement-Chemical Admixtures-Water Dispersion System at Early Stage; Springer: Berlin, Germany, 2017. [Google Scholar]
- Zhang, Y.; Kong, X.; Gao, L.; Lu, Z.; Zhou, S.; Dong, B.; Xing, F. In-situ measurement of viscoelastic properties of fresh cement paste by a microrheology analyzer. Cem. Concr. Res. 2016, 79, 291–300. [Google Scholar] [CrossRef]
- Gierczycki, A.T. Procesy Agregacji i Rozpadu w Układach Dyspersyjnych Ciało Stałe-Ciecz; Wydawnictwo Politechniki Śląskiej: Gliwice, Poland, 2014. [Google Scholar]
- Lazzari, S.; Nicoud, L.; Jaquet, B.; Lattuada, M.; Morbidelli, M. Fractal-like structures in colloid science. Adv. Coll. Interface Sci. 2016, 235, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Hunter, R.J. Introduction to Modern Colloid Science; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Herega, A.N. Physical aspects of self-organization processes in composites. 1. Simulation of percolation clusters of phases and of inner boundaries. Nanomech. Sci. Technol. Int. J. 2013, 4. [Google Scholar] [CrossRef]
- Vyrovoy, V.N.; Dorofeev, V.S.; Sukhanov, V.G. Composite Building Materials and Constructions. In Structure, Self-Organization, Properties; Publishers TES: Odessa, Ukraine, 2010. [Google Scholar]
- Rebinder, P.A. Surface phenomena in disperse systems. In Physicochemical Mechanics; Nauka: Moscow, Russia, 1979. [Google Scholar]
- Solomatov, V.I.; Vyrovoy, V.N.; Bobryshev, A.N. Polystructural Theory of Composite Building Materials; Publishers FAN: Tashkent, Uzbekistan, 1991. [Google Scholar]
- Solomatov, V.I. Polystructural theory development of composite building materials. In The Success of Modern Materials Science: Proceedings of the Anniversary Conference; RAASN, MGPUS: Moscow, Russia, 2001; pp. 56–66. [Google Scholar]
- Korenkova, S.; Sidorenko, Y.; Jemiolo, S.; Gajewski, M.; Krzeminski, M. Improving durability of cement composite materials. Procedia Eng. 2015, 111, 420–424. [Google Scholar] [CrossRef]
- Szeląg, M. Wpływ Składu Kompozytów Cementowych na Geometrię ich Spękań Termicznych; Lublin University of Technology: Lublin, Poland, 2017. [Google Scholar]
- Bogue, R.H. The Chemistry of Portland Cement; Reinhold publishing corporation: New York, NY, USA, 1947. [Google Scholar]
- En 196-1. Methods of Testing Cement—Part 1: Determination of Strength; European Committee for Standarization: Brussels, Belgium, 2016. [Google Scholar]
- Fernandes, B.; Gil, A.M.; Bolina, F.L.; Tutikian, B.F. Microstructure of concrete subjected to elevated temperatures: Physico-chemical changes and analysis techniques. Rev. IBRACON Estrut. Mater. 2017, 10, 838–863. [Google Scholar] [CrossRef]
- Szeląg, M.; Fic, S. Analiza rozwoju spękań klastrowych w zaczynie cementowym modyfikowanym mikrokrzemionką. Budownictwo i Architektura 2015, 14, 117–127. [Google Scholar]
- Szeląg, M. The influence of microsilica on the cluster cracks’ geometry of cement paste. In Proceedings of the 18th International Conference on Civil Engineering and Building Materials, Rome, Italy, 2–3 May 2016. [Google Scholar]
- Szeląg, M.; Fic, S. The use of image analysis techniques to describe a cluster cracks in the cement paste with the addition of metakaolinite. In Proceedings of the 18th International Conference on Civil, Environmental and Structural Engineering, Kuala Lumpur, Malezja, 14–15 March 2016. [Google Scholar]
- Szelag, M. Mechano-physical properties and microstructure of carbon nanotube reinforced cement paste after thermal load. Nanomaterials 2017, 7, 22. [Google Scholar] [CrossRef] [PubMed]
- Szeląg, M. Application of multiwall carbon nanotubes with anionic surfactant to cement paste. In Proceedings of the 20th International Conference on Concrete Engineering and Technology, Zurich, Switzerland, 30–31 July 2018. [Google Scholar]
- En 12390-5. Testing Hardened Concrete—Part 5: Flexural Strength of Test Specimens; European Committee for Standarization: Brussels, Belgium, 2009. [Google Scholar]
- En 12390-3. Testing Hardened Concrete—Part 3: Compressive Strength of Test Specimens; European Committee for Standarization: Brussels, Belgium, 2009. [Google Scholar]
- En 12390-7. Testing Hardened Concrete—Part 7: Density of Hardened Concrete; European Committee for Standarization: Brussels, Belgium, 2009. [Google Scholar]
- Recho, N. Fracture Mechanics and Crack Growth; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Neville, A.M. Properties of Concrete, 4th ed.; Arkady: Warszawa, Poland, 2000. [Google Scholar]
- Soutsos, M.; Domone, P. Construction Materials, Their Nature and Behaviour, 5th ed.; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Zegardlo, B.; Szelag, M.; Ogrodnik, P. Ultra-high strength concrete made with recycled aggregate from sanitary ceramic wastes—The method of production and the interfacial transition zone. Constr. Build. Mater. 2016, 122, 736–742. [Google Scholar] [CrossRef]
- Sadowski, T.; Golewski, G. A failure analysis of concrete composites incorporating fly ash during torsional loading. Compos. Struct. 2018, 183, 527–535. [Google Scholar] [CrossRef]
- Esposito, R.; Anac, C.; Hendriks, M.; Copuroglu, O. Influence of the alkali-silica reaction on the mechanical degradation of concrete. J. Mater. Civ. Eng. 2016, 28. [Google Scholar] [CrossRef]
- Savija, B.; Zhang, H.; Schlangen, E. Influence of microencapsulated phase change material (PCM) addition on (micro) mechanical properties of cement paste. Materials 2017, 10, 863. [Google Scholar] [CrossRef]
- Mitsui, K.; Li, Z.; Lange, D.; Shah, S. Relationship between microstructure and mechanical-properties of the paste-aggregate interface. ACI Mater. J. 1994, 91, 30–39. [Google Scholar]
- Hlobil, M.; Smilauer, V.; Chanvillard, G. Micromechanical multiscale fracture model for compressive strength of blended cement pastes. Cem. Concr. Res. 2016, 83, 188–202. [Google Scholar] [CrossRef]
- Diamond, S. The microstructures of cement paste in concrete. In Proceedings of the 8th International Congress on the Chemistry of Cement, Rio de Janeiro, Brazil, 22–28 September 1986. [Google Scholar]
- Antoni, M.; Rossen, J.; Martirena, F.; Scrivener, K. Cement substitution by a combination of metakaolin and limestone. Cem. Concr. Res. 2012, 42, 1579–1589. [Google Scholar] [CrossRef]
- Poon, C.; Lam, L.; Kou, S.; Wong, Y.; Wong, R. Rate of pozzolanic reaction of metakaolin in high-performance cement pastes. Cem. Concr. Res. 2001, 31, 1301–1306. [Google Scholar] [CrossRef]
- Wild, S.; Khatib, J. Portlandite consumption in metakaolin cement pastes and mortars. Cem. Concr. Res. 1997, 27, 137–146. [Google Scholar] [CrossRef]



| Cement’s Class | Chemical Analysis [%] | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| SiO2 | Fe2O3 | Al2O3 | CaO | MgO | SO3 | Cl | Na2O | K2O | |
| CEM I 42.5R | 20.18 | 3.39 | 4.38 | 64.79 | 1.17 | 2.91 | 0.083 | 0.26 | 0.49 |
| CEM I 52.5R | 20.19 | 3.30 | 4.33 | 64.76 | 1.17 | 3.16 | 0.078 | 0.26 | 0.48 |
| Mineral Composition [%] | Blaine Specific Surface Area [cm2/g] | ||||||||
| Cement’s Class | C3S | C2S | C3A | C4AF | |||||
| CEM I 42.5R | 63.41 | 8.92 | 5.88 | 10.31 | 4010 | ||||
| CEM I 52.5R | 62.97 | 9.28 | 5.90 | 10.03 | 4596 | ||||
| Parameter | fc(R) | fc(T) | fcf(R) | fcf(T) | D(R) | D(T) | |||
|---|---|---|---|---|---|---|---|---|---|
| fc(R) | 1.00 | - | - | - | - | - | - | - | - |
| fc(T) | 0.98 | 1.00 | - | - | - | - | - | - | - |
| fcf(R) | 0.95 | 0.91 | 1.00 | - | - | - | - | - | - |
| fcf(T) | 0.43 | 0.33 | 0.63 | 1.00 | - | - | - | - | - |
| D(R) | 0.95 | 0.97 | 0.94 | 0.50 | 1.00 | - | - | - | - |
| D(T) | 0.94 | 0.94 | 0.94 | 0.56 | 0.99 | 1.00 | - | - | - |
| −0.76 | −0.81 | −0.75 | −0.39 | −0.85 | −0.82 | 1.00 | - | - | |
| −0.81 | −0.86 | −0.79 | −0.37 | −0.90 | −0.87 | 0.98 | 1.00 | - | |
| −0.79 | −0.75 | −0.78 | −0.63 | −0.82 | −0.84 | 0.61 | 0.68 | 1.00 |
| Oxide | Percentage of Oxides before/after Thermal Load [%] | |||||||
|---|---|---|---|---|---|---|---|---|
| C42 | C42MT | C52 | C52MT | |||||
| before | after | before | after | before | after | before | after | |
| Na2O | 1.17 | 0.98 | 0.78 | 0.62 | 1.00 | 0.79 | 0.65 | 0.59 |
| MgO | 1.13 | 1.18 | 1.09 | 1.07 | 1.03 | 1.06 | 0.97 | 0.98 |
| Al2O5 | 5.90 | 6.36 | 9.58 | 9.98 | 6.34 | 6.58 | 10.14 | 10.01 |
| SiO2 | 21.41 | 21.56 | 23.01 | 23.22 | 22.43 | 22.87 | 23.54 | 23.78 |
| SO3 | 3.91 | 4.45 | 4.23 | 4.35 | 3.44 | 3.78 | 4.00 | 4.22 |
| K2O | 1.02 | 0.69 | 1.01 | 0.88 | 0.95 | 0.52 | 0.94 | 0.74 |
| CaO | 62.55 | 61.68 | 57.31 | 56.86 | 61.80 | 61.30 | 56.90 | 56.68 |
| Fe2O3 | 2.91 | 3.10 | 2.99 | 3.02 | 3.01 | 3.10 | 2.86 | 3.00 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szeląg, M. The Influence of Metakaolinite on the Development of Thermal Cracks in a Cement Matrix. Materials 2018, 11, 520. https://doi.org/10.3390/ma11040520
Szeląg M. The Influence of Metakaolinite on the Development of Thermal Cracks in a Cement Matrix. Materials. 2018; 11(4):520. https://doi.org/10.3390/ma11040520
Chicago/Turabian StyleSzeląg, Maciej. 2018. "The Influence of Metakaolinite on the Development of Thermal Cracks in a Cement Matrix" Materials 11, no. 4: 520. https://doi.org/10.3390/ma11040520
APA StyleSzeląg, M. (2018). The Influence of Metakaolinite on the Development of Thermal Cracks in a Cement Matrix. Materials, 11(4), 520. https://doi.org/10.3390/ma11040520





