Microstructure Evolution and Flow Stress Model of a 20Mn5 Hollow Steel Ingot during Hot Compression
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Material
2.2. Experimental Procedure
3. Results and Discussion
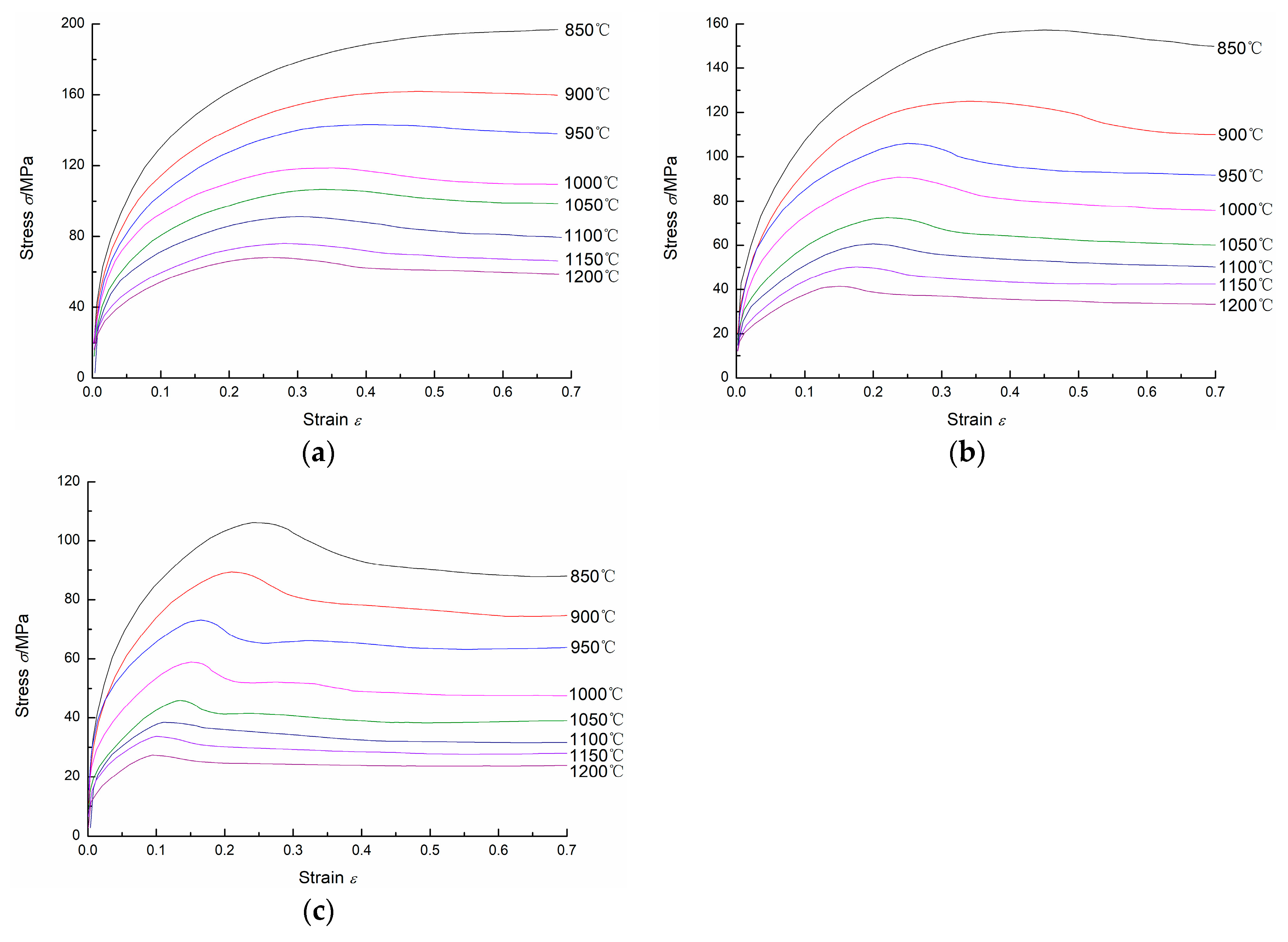
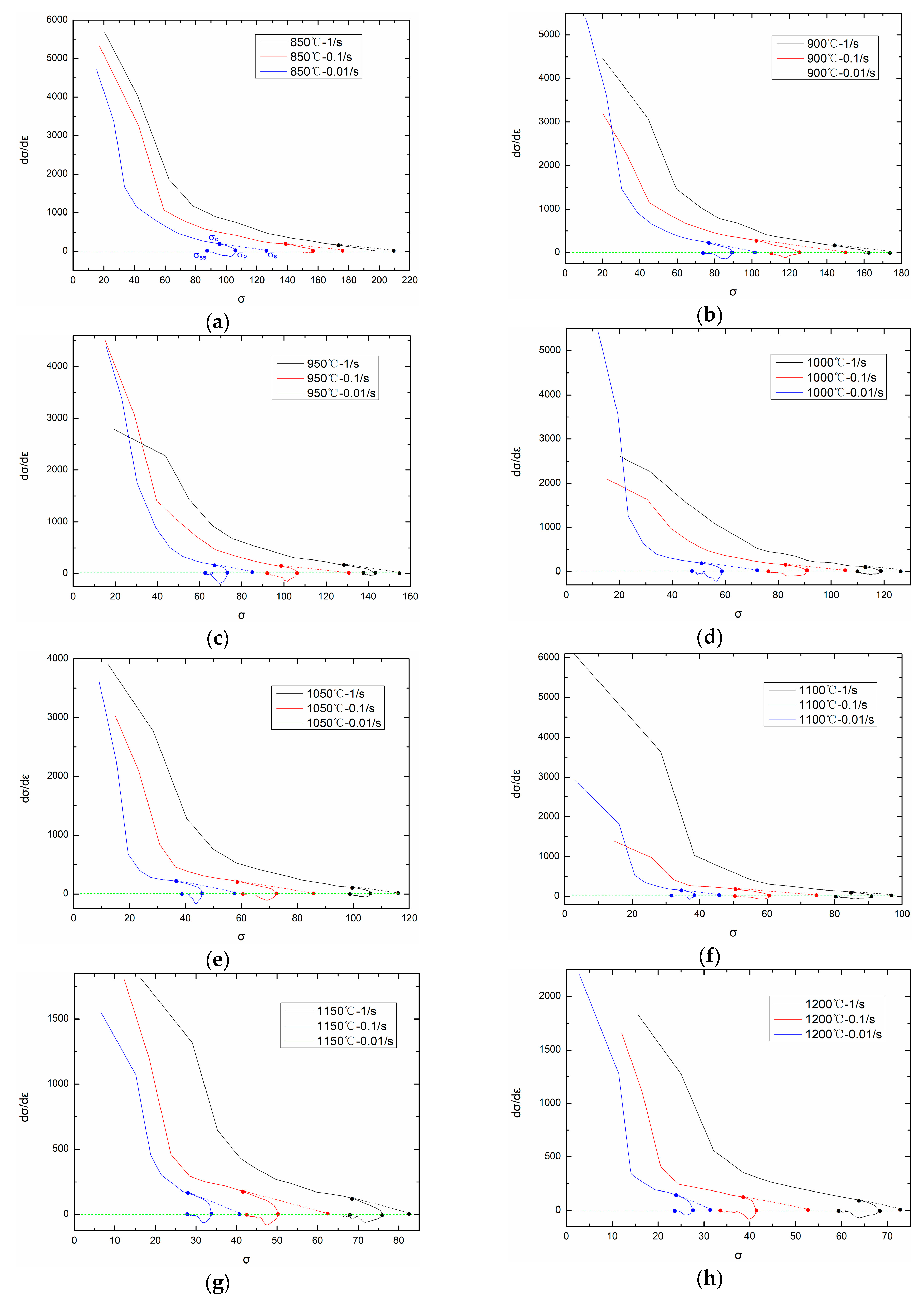
3.1. Flow Stress Curves
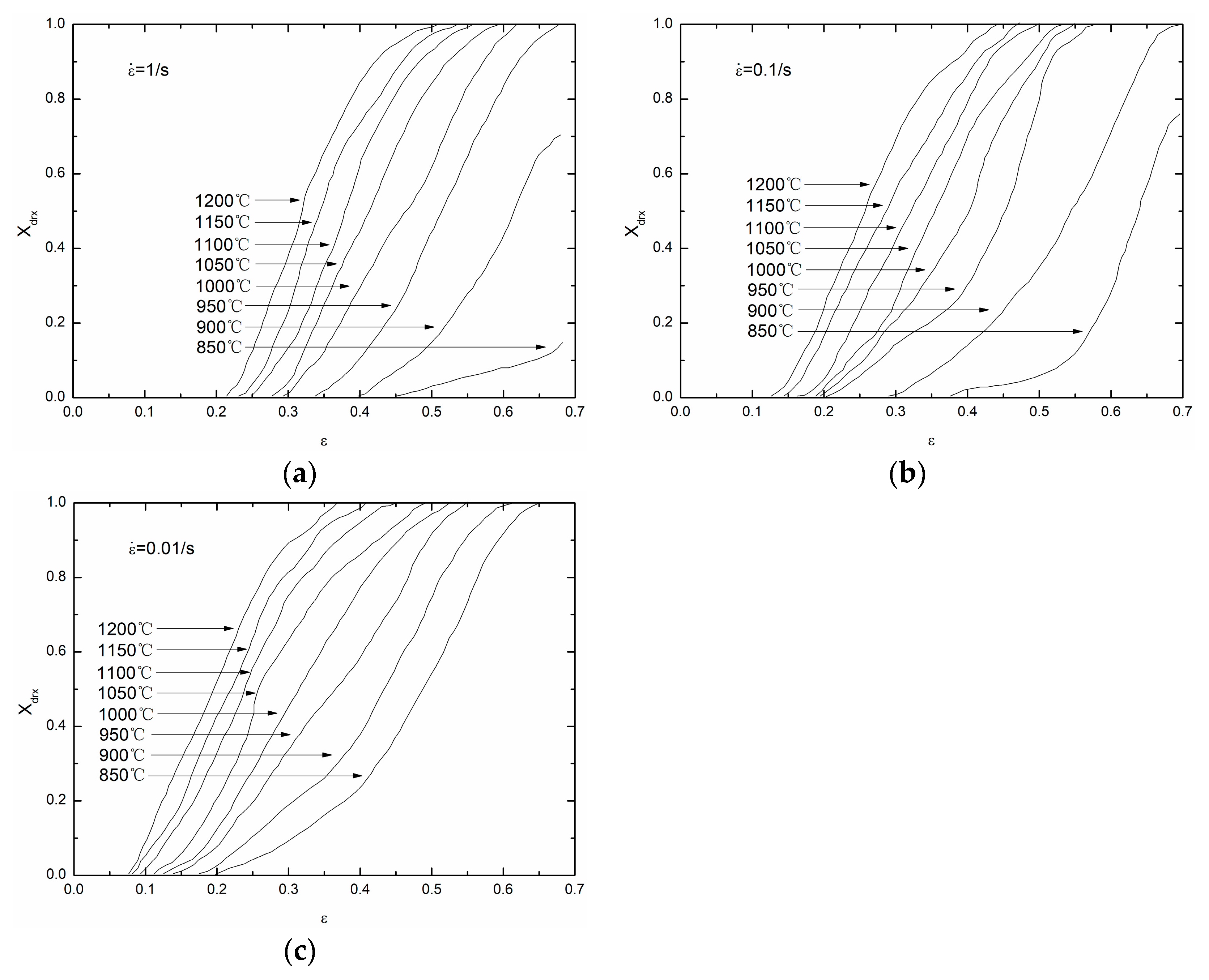
3.2. Effect of Temperature and Strain Rate on Microstructure after Hot Compression
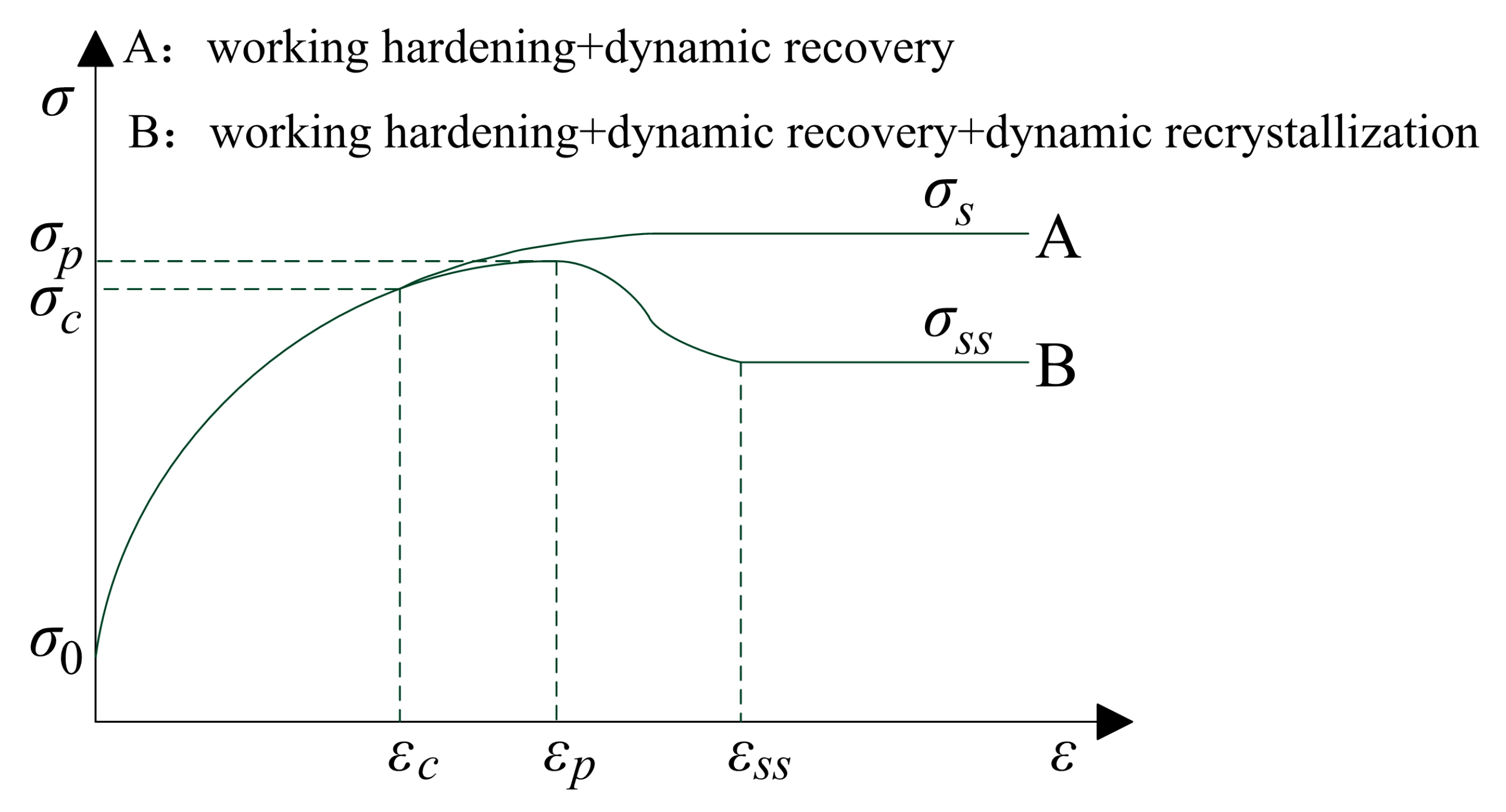
4. Establishment of A Two-Stage Constitutive Model and Its Verification
4.1. The Derivation of A Two-Stage Constitutive Model
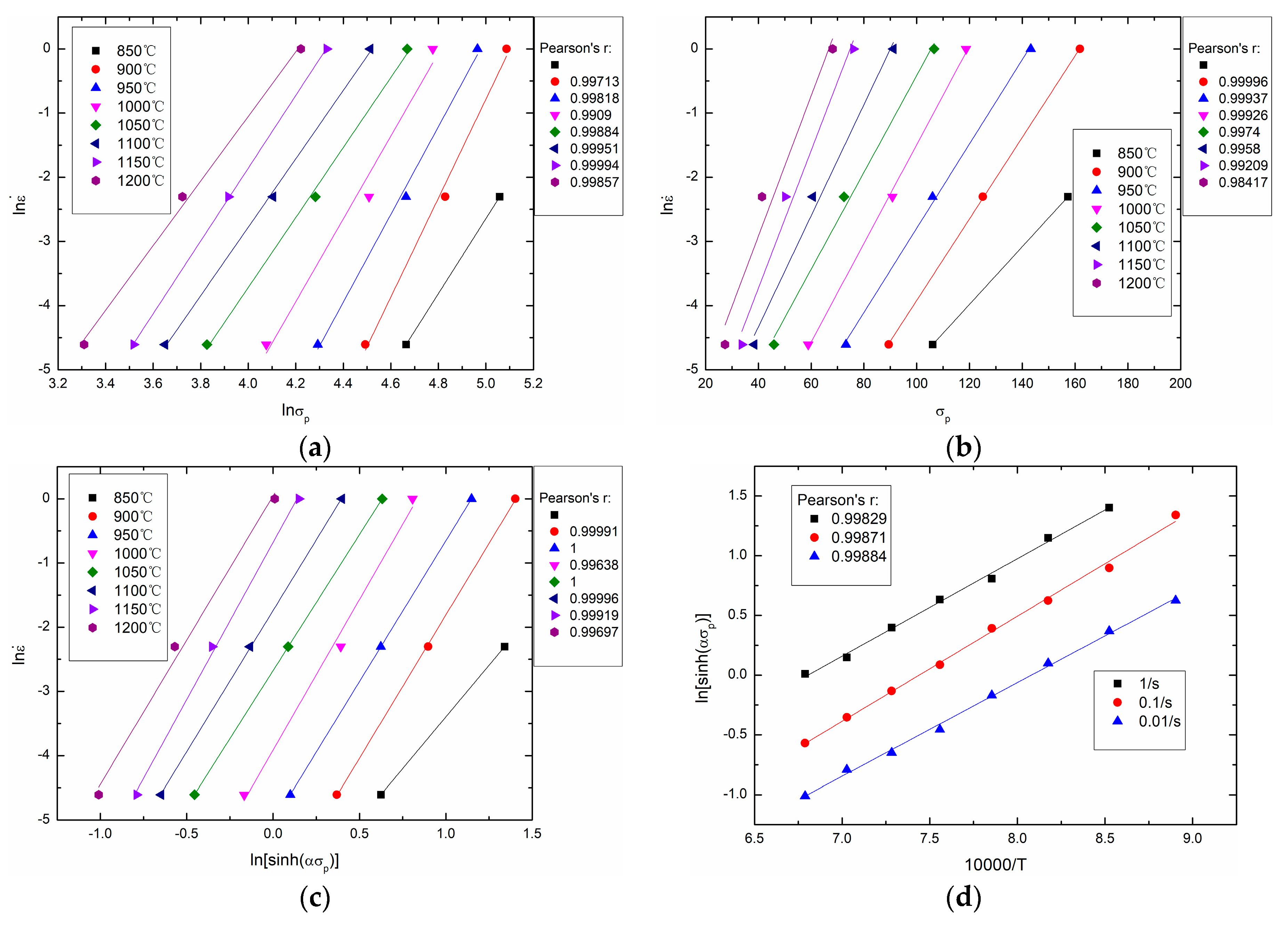
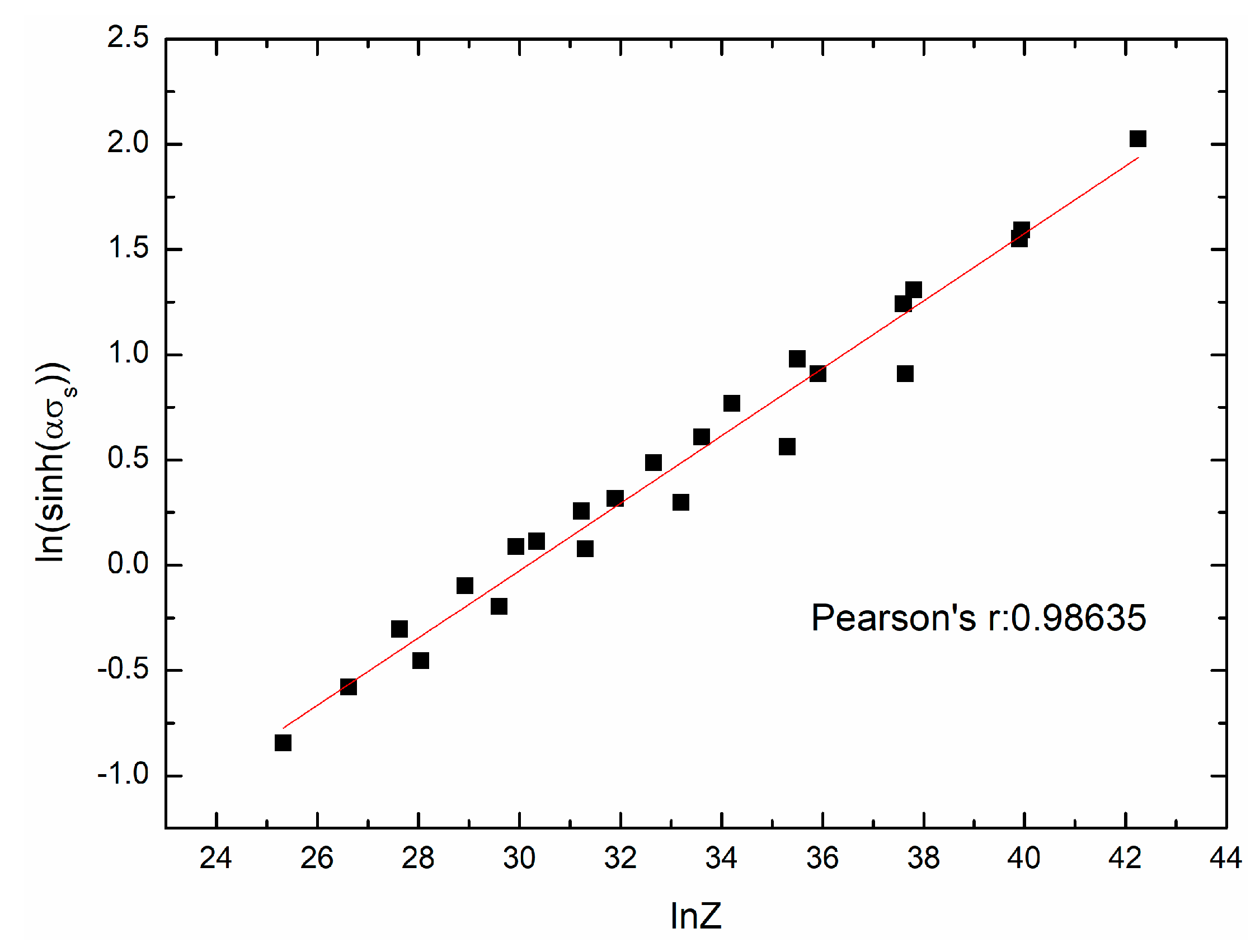
4.2. Determination of Material Constants(α, n, Q and A) Based on the Peak Stress
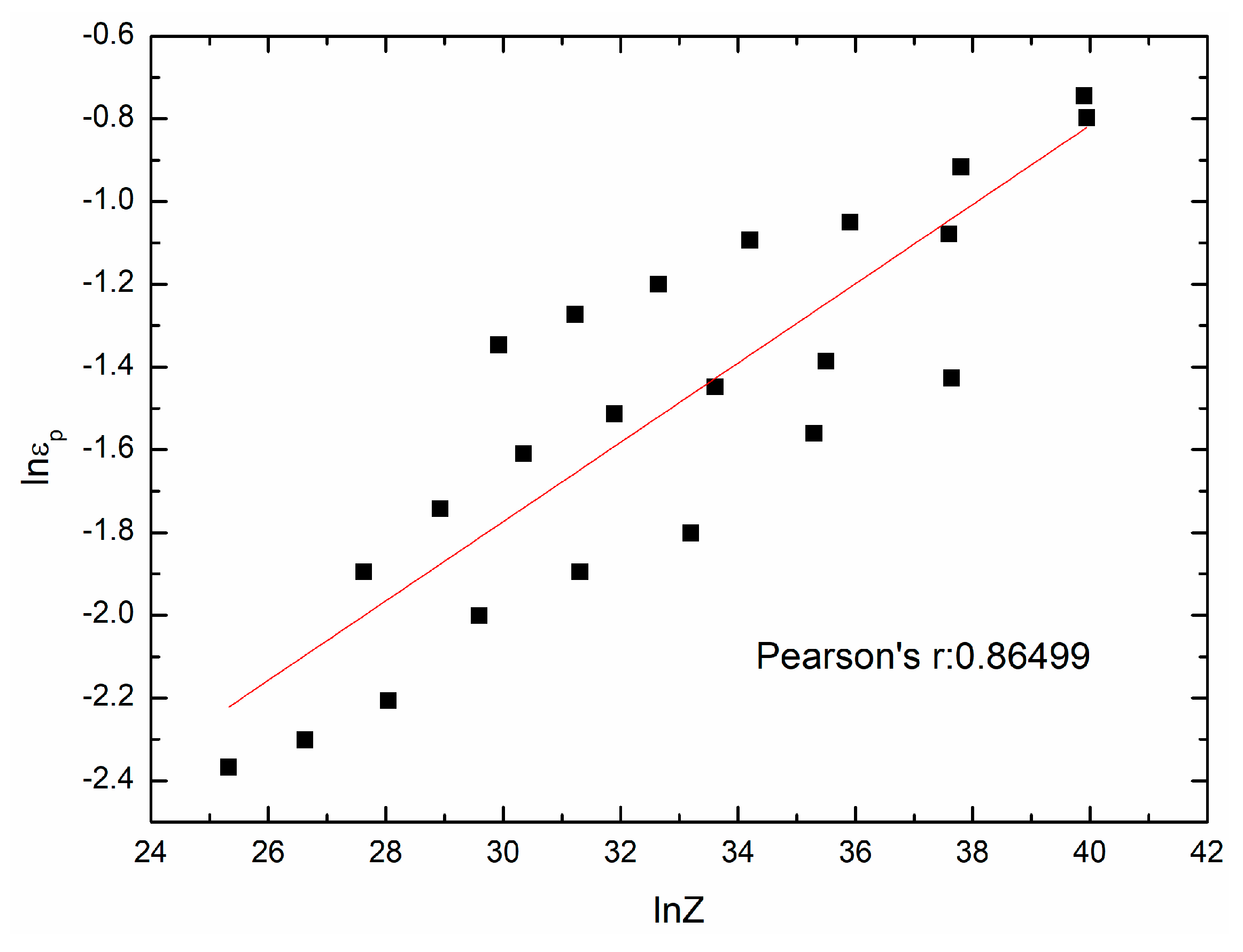
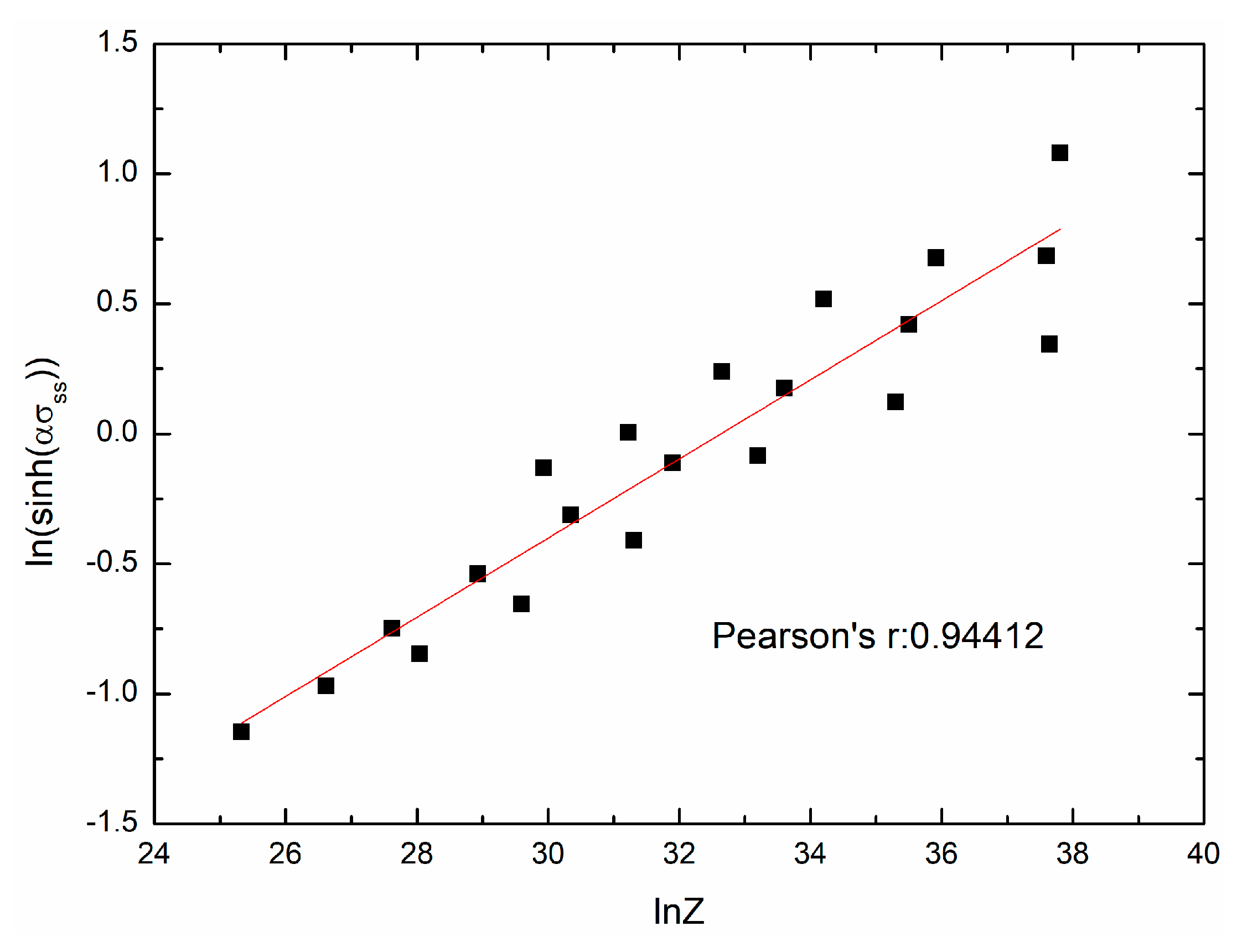
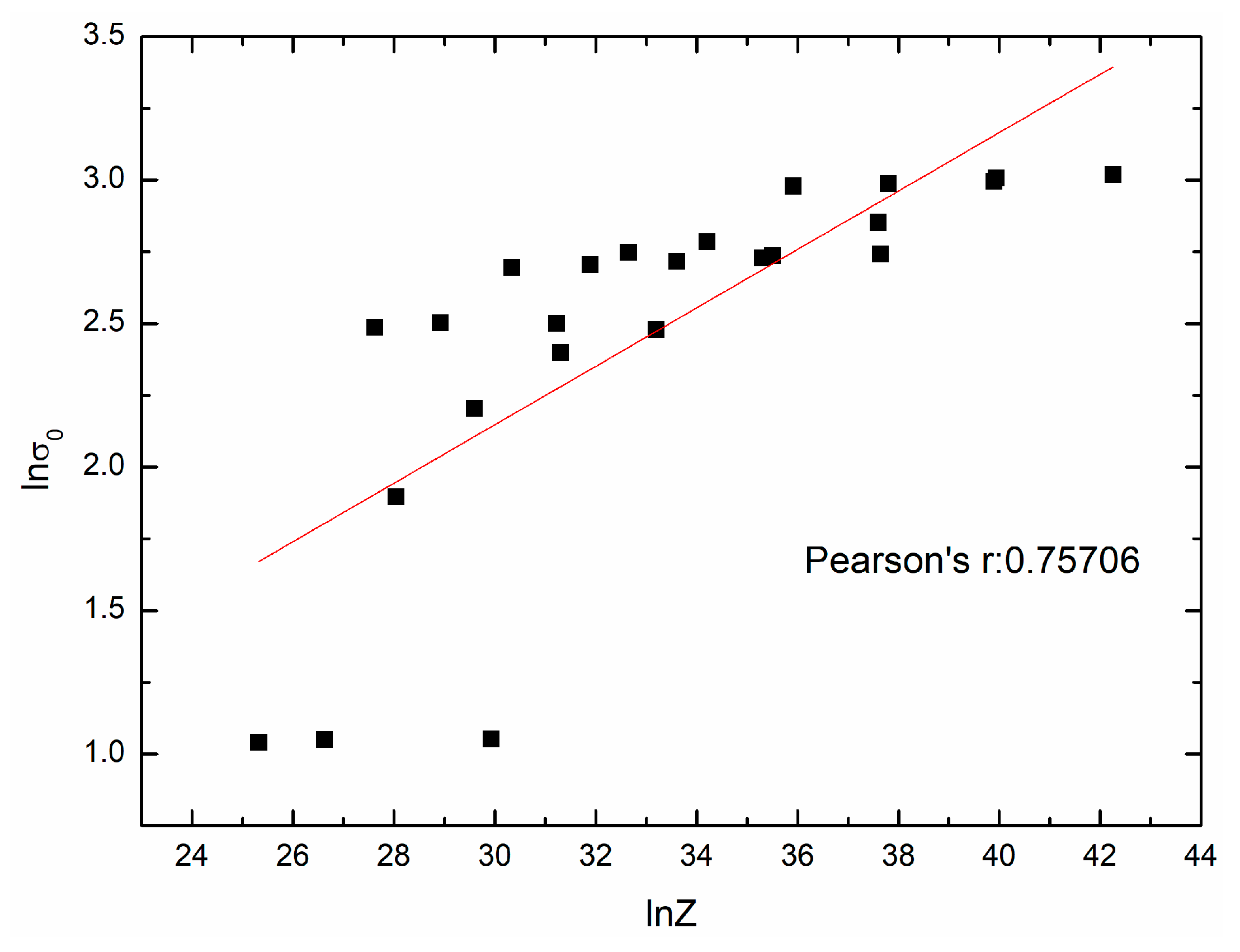
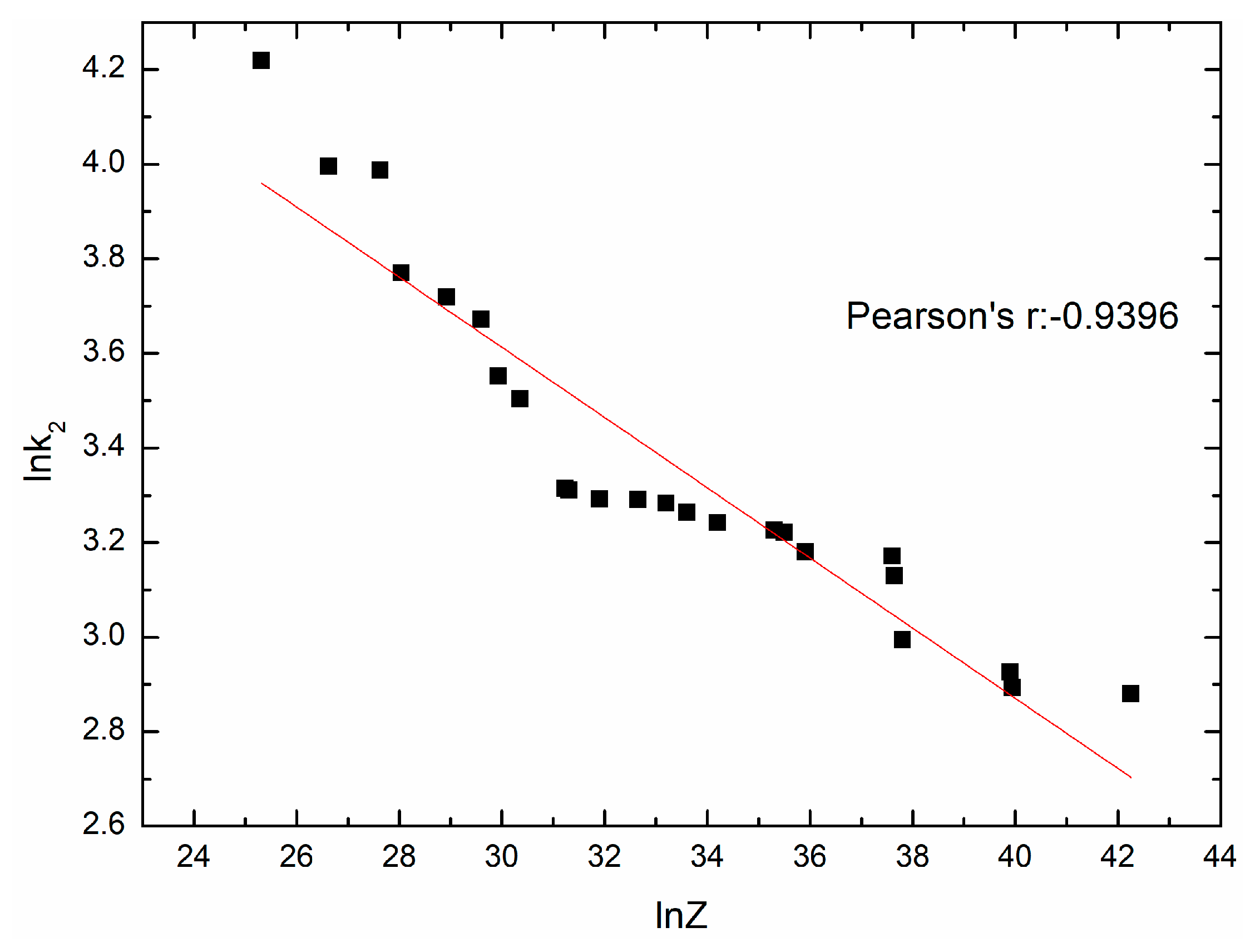
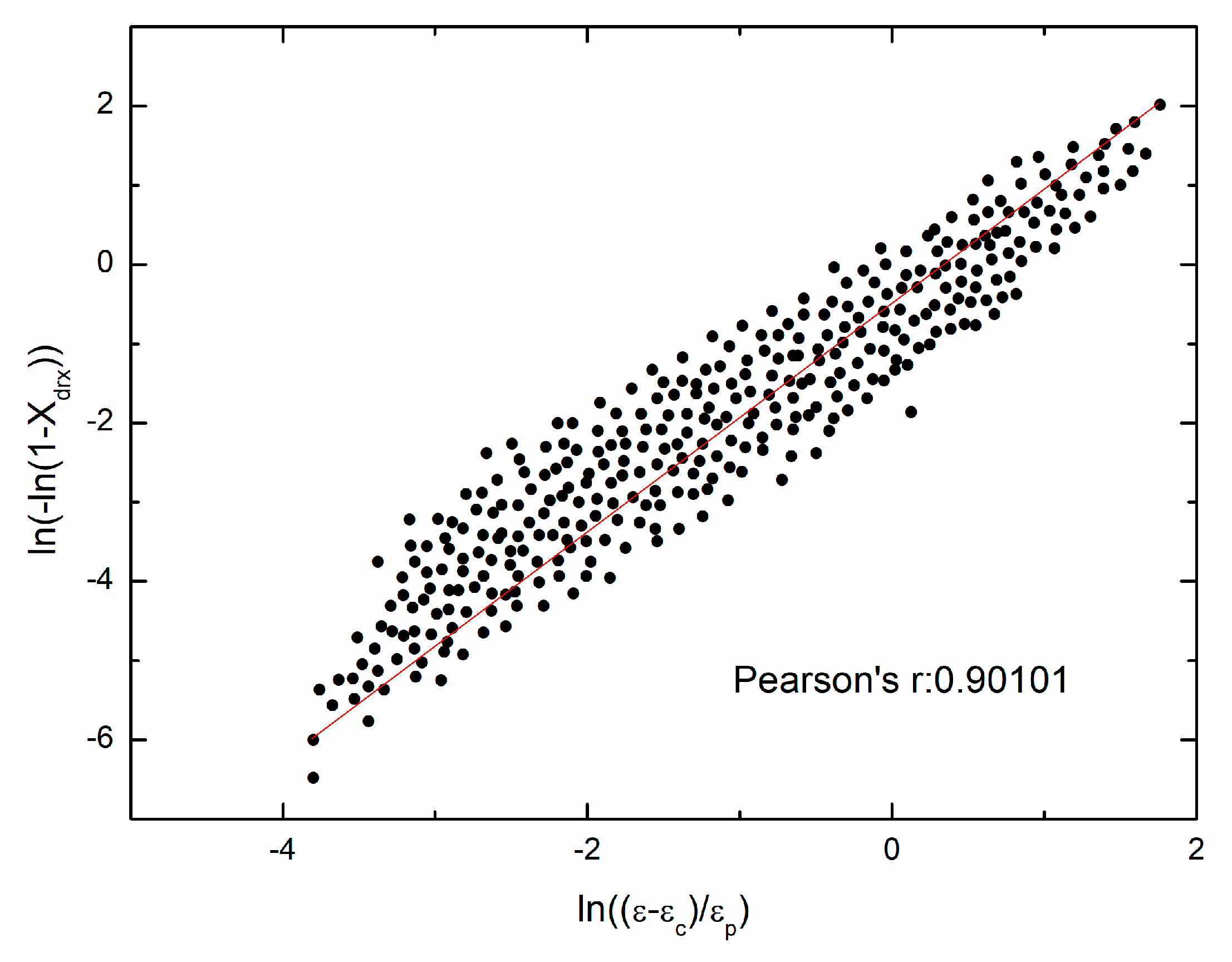
4.3. Determination of Material Parameters(εp, εc, σs, σss, σ0, k2, kd, nd) in the Two-Stage Constitutive Model
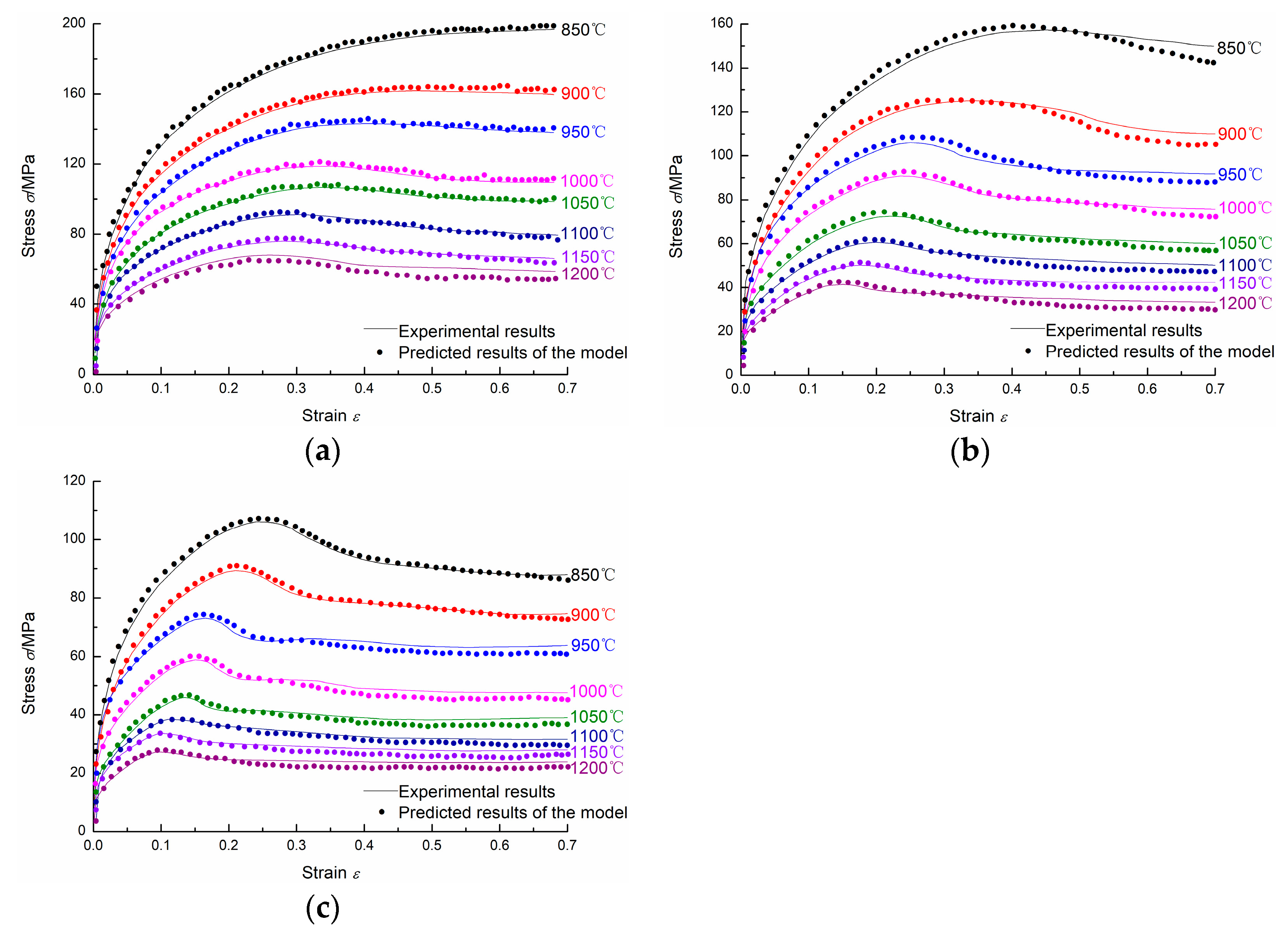
4.4. Verification of the Proposed Two-Stage Constitutive Model
5. Conclusions
- (1)
- During hot compression of 20Mn5 steel, firstly, the flow stress increases to a peak stress, and then the flow stress decreases gradually to a steady state stress with the increase of strain. Peak stress does not occur only at 850 °C and 1/s. At higher temperatures and lower strain rates, the peak strain, steady state strain, peak stress, and steady state stress are smaller.
- (2)
- The material constants (α, n, Q, and A) are calculated based on the peak stress.
- (3)
- A two-stage constitutive model of 20Mn5 steel is established. The related material parameters (εp, εc, σs, σss, σ0, k2, nd, and kd) are determined.
- (4)
- The proposed constitutive model can give a good prediction of the flow stress for different temperatures, strain rates, and strains, and can be used for numerical simulation of hot forging of 20Mn5 hollow steel ingots.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Liu, M.; Ma, Q.X. Research on rotatory deformation uniformity and compaction effect of super-heavy hollow steel ingot. J. Mech. Eng. 2016, 52, 90–96. [Google Scholar] [CrossRef]
- Liu, M.; Dong, X.L.; Ma, Q.X. Investigation on hollow steel ingot forging process of heavy cylinder forging. J. Plast. Eng. 2013, 20, 1–8. [Google Scholar] [CrossRef]
- Mao, W.M.; Zhao, X.B. Recrystallization and Grain Growth of Metal, 1st ed.; Metallurgical Industry Press: Beijing, China, 1994; pp. 218–241. [Google Scholar]
- Chen, F.; Feng, G.W.; Cui, Z.S. New constitutive model for hot working. Metall. Mater. Trans. A. 2016, 47, 1229–1239. [Google Scholar] [CrossRef]
- Dong, D.Q.; Chen, F.; Cui, Z.S. A physically-based constitutive model for SA508-III steel: modeling and experimental verification. Mater. Sci. Eng. A. 2015, 634, 103–115. [Google Scholar] [CrossRef]
- Chen, F.; Cui, Z.S.; Chen, S.J. Recrystallization of 30Cr2Ni4MoV ultra-super-critical rotor steel during hot deformation. Part I: dynamic recrystallization. Mater. Sci. Eng. A. 2011, 528, 5073–5080. [Google Scholar] [CrossRef]
- Chen, F.; Liu, J.; Ou, H.G.; Liu, B.; Cui, Z.S.; Long, H. Flow characteristics and intrinsic workability of IN718 superalloy. Mater. Sci. Eng. A. 2015, 642, 279–287. [Google Scholar] [CrossRef]
- Li, X.C.; Duan, L.L.; Li, J.W.; Wu, X.C. Experimental study and numerical simulation of dynamic recrystallization behavior of a micro-alloyed plastic mold steel. Mater. Des. 2015, 66, 309–320. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, G.Q.; Chen, L.; Li, J.L. A comparative study of several constitutive models for power metallurgy tungsten at elevated temperature. Mater. Des. 2016, 90, 91–100. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, X.M. A critical review of experimental results and constitutive descriptions for metals and alloys in hot working. Mater. Des. 2011, 32, 1733–1759. [Google Scholar] [CrossRef]
- Wang, J.; Yang, H.T.; Wang, X.G.; Xiao, H. A new mathematical model for predicting flow stress up to the critical strain during hot deformation. Mater. Des. 2015, 65, 637–643. [Google Scholar] [CrossRef]
- Solhjoo, S.; Vakis, A.I.; Pei, Y.T.T. Two phenomenological models to predict the single peak flow stress curves up to the peak during hot deformation. Mech. Mater. 2017, 105, 61–66. [Google Scholar] [CrossRef]
- Ji, G.L.; Li, Q.; Li, L. A physical-based constitutive relation to predict flow stress for Cu-0.4Mg alloy during hot working. Mater. Sci. Eng. A 2014, 615, 247–254. [Google Scholar] [CrossRef]
- Ji, G.L.; Li, Q.; Ding, K.Y.; Yang, L.; Li, L. A physical-based constitutive model for high temperature deformation of Cu-0.36Cr-0.03Zr alloy. J. Alloys Compd. 2015, 648, 397–407. [Google Scholar] [CrossRef]
- Ji, G.L.; Li, L.; Qin, F.L.; Zhu, L.Y.; Li, Q. Comparative study of phenomenological constitutive equations for an as-rolled M50NiL steel during hot deformation. J. Alloys Compd. 2017, 695, 2389–2399. [Google Scholar] [CrossRef]
- Ji, G.L.; Li, F.G.; Li, Q.H.; Li, H.Q.; Li, Z. Research on the dynamic recrystallization kinetics of Aermet100 steel. Mater. Sci. Eng. A. 2010, 527, 2350–2355. [Google Scholar] [CrossRef]
- Ji, G.L.; Li, Q.; Li, L. The kinetics of dynamic recrystallization of Cu-0.4Mg alloy. Mater. Sci. Eng. A 2013, 586, 197–203. [Google Scholar] [CrossRef]
- Busso, E.P. A continuum theory for dynamic recrystallization with microstructure-related length scales. Int. J. Plast. 1998, 14, 319–353. [Google Scholar] [CrossRef]
- McQueen, H.J.; Ryan, N.D. Constitutive analysis in hot working. Mater. Sci. Eng. A. 2002, 322, 43–63. [Google Scholar] [CrossRef]
- McQueen, H.J. Development of dynamic recrystallization theory. Mater. Sci. Eng. A. 2004, 387–389, 203–208. [Google Scholar] [CrossRef]
- McQueen, H.J.; Imbert, C.A.C. Dynamic recrystallization: plasticity enhancing structural development. J. Alloys Compd. 2004, 378, 35–43. [Google Scholar] [CrossRef]
- McQueen, H.J.; Yue, S.; Ryan, N.D.; Fry, E. Hot working characteristics of steels in austenitic state. J. Mater. Process. Technol. 1995, 53, 293–310. [Google Scholar] [CrossRef]
- Medina, S.F.; Hernandez, C.A. Modelling of the dynamic recrystallization of austenite in low alloy and microalloyed steels. Acta Mater. 1996, 44, 165–171. [Google Scholar] [CrossRef]
- Poliak, E.I.; Jonas, J.J. Initiation of dynamic recrystallization in constant strain rate hot deformation. ISIJ Int. 2007, 43, 684–691. [Google Scholar] [CrossRef]
- Stewart, G.R.; Jonas, J.J.; Montheillet, F. Kinetics and critical conditions for the initiation of dynamic recrystallization in 304 stainless steel. ISIJ Int. 2004, 44, 1581–1589. [Google Scholar] [CrossRef]
- Kim, S.I.; Yoo, Y.C. Dynamic recrystallization behavior of AISI 304 stainless steel. Mater. Sci. Eng. A. 2001, 311, 108–113. [Google Scholar] [CrossRef]
- Kim, S.I.; Lee, Y.; Lee, D.L.; Yoo, Y.C. Modeling of AGS and recrystallized fraction of microalloyed medium carbon steel during hot deformation. Mater. Sci. Eng. A. 2003, 355, 384–393. [Google Scholar] [CrossRef]




| C | Si | Mn | P | S | Cr | Ni | Mo | Al |
|---|---|---|---|---|---|---|---|---|
| 0.24 | 0.26 | 1.47 | 0.0084 | 0.0020 | 0.15 | 0.076 | 0.020 | 0.015 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Ma, Q.-X.; Luo, J.-B. Microstructure Evolution and Flow Stress Model of a 20Mn5 Hollow Steel Ingot during Hot Compression. Materials 2018, 11, 463. https://doi.org/10.3390/ma11040463
Liu M, Ma Q-X, Luo J-B. Microstructure Evolution and Flow Stress Model of a 20Mn5 Hollow Steel Ingot during Hot Compression. Materials. 2018; 11(4):463. https://doi.org/10.3390/ma11040463
Chicago/Turabian StyleLiu, Min, Qing-Xian Ma, and Jian-Bin Luo. 2018. "Microstructure Evolution and Flow Stress Model of a 20Mn5 Hollow Steel Ingot during Hot Compression" Materials 11, no. 4: 463. https://doi.org/10.3390/ma11040463
APA StyleLiu, M., Ma, Q.-X., & Luo, J.-B. (2018). Microstructure Evolution and Flow Stress Model of a 20Mn5 Hollow Steel Ingot during Hot Compression. Materials, 11(4), 463. https://doi.org/10.3390/ma11040463




