Light Trapping with Silicon Light Funnel Arrays
Abstract
1. Introduction
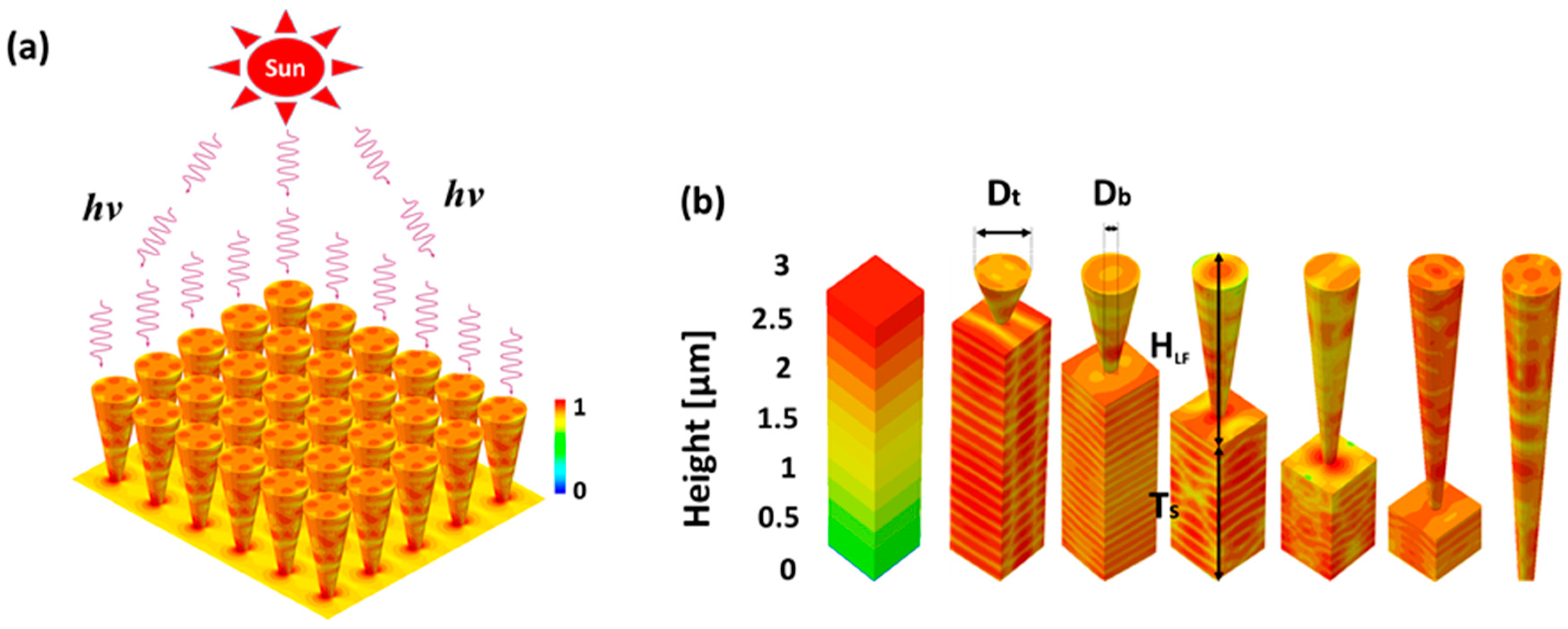
2. Materials and Methods
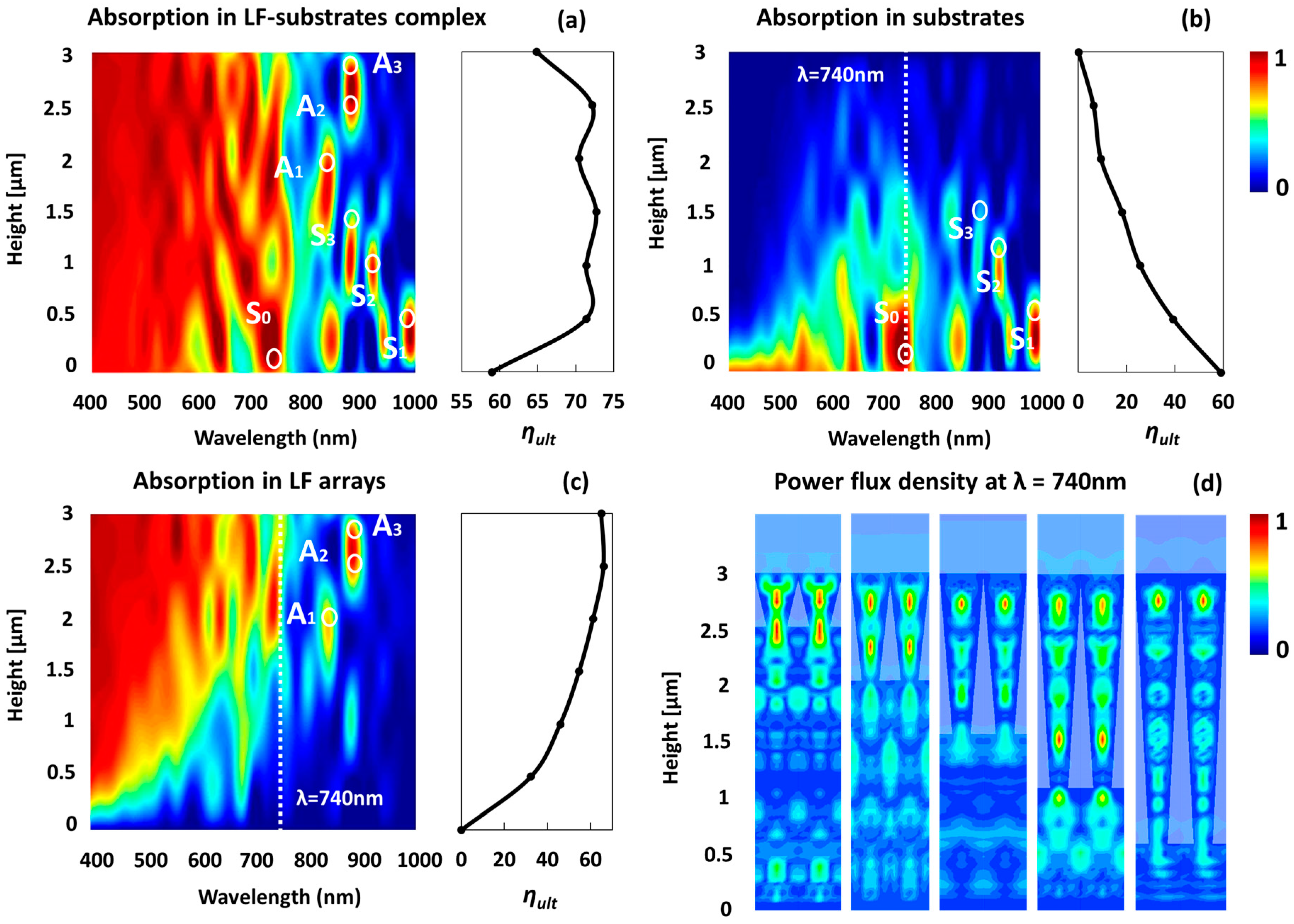
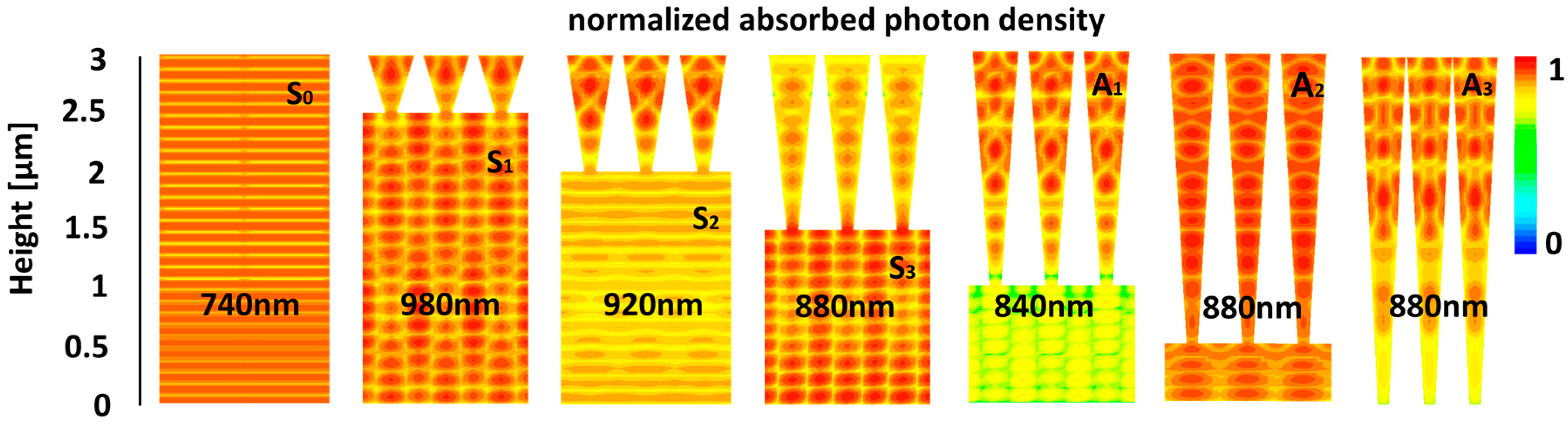
3. Results
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fonash, S.J. Introduction to Light Trapping in Solar Cell and Photo-Detector Devices; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Callahan, D.M.; Munday, J.N.; Atwater, H.A. Solar cell light trapping beyond the ray optic limit. Nano Lett. 2012, 12, 214–218. [Google Scholar] [CrossRef] [PubMed]
- Wallentin, J.; Anttu, N.; Asoli, D.; Huffman, M.; Åberg, I.; Magnusson, M.H.; Siefer, G.; Fuss-Kailuweit, P.; Dimroth, F.; Witzigmann, B.; et al. InP nanowire array solar cells achieving 13.8% efficiency by exceeding the ray optics limit. Science 2013, 339, 1057–1060. [Google Scholar] [CrossRef] [PubMed]
- Kosten, E.D.; Warren, E.L.; Atwater, H.A. Ray optical light trapping in silicon microwires: Exceeding the 2n2 intensity limit. Opt. Express 2011, 19, 3316–3331. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Yu, Z.; Raman, A.; Fan, S. Fundamental limit of nanophotonic light trapping in solar cells. Proc. Natl. Acad. Sci. USA 2010, 107, 17491–17496. [Google Scholar] [CrossRef] [PubMed]
- Taretto, K.; Rau, U. Modeling Extremely Thin Absorber Solar Cells for Optimized Design. Prog. Photovolt. Res. Appl. 2004, 12, 573–591. [Google Scholar] [CrossRef]
- Brongersma, M.L.; Cui, Y.; Fan, S. Light management for photovoltaics using high-index nanostructures. Nat. Mater. 2014, 13, 451–460. [Google Scholar] [CrossRef] [PubMed]
- Ferry, V.E.; Verschuuren, M.A.; Li, H.B.T.; Verhagen, E.; Walters, R.J.; Schropp, R.E.I.; Atwater, H.A.; Polman, A. Light Trapping in Thin Flim Plasmonic Solar Cells. In Proceedings of the 25th EU-PVSEC Conference, Valencia, Spain, 6–10 September 2010; pp. 4–8. [Google Scholar]
- Mann, S.A.; Grote, R.R.; Osgood, R.M.; Schuller, J.A. Dielectric particle and void resonators for thin film solar cell textures. Opt. Express 2011, 19, 25729–25740. [Google Scholar] [CrossRef] [PubMed]
- Mann, S.A.; Garnett, E.C. Extreme light absorption in thin semiconductor films wrapped around metal nanowires. Nano Lett. 2013, 13, 3173–3178. [Google Scholar] [CrossRef] [PubMed]
- Garnett, E.C.; Yang, P. Light trapping in silicon nanowire solar cells. Nano Lett. 2010, 10, 1082–1087. [Google Scholar] [CrossRef] [PubMed]
- Atwater, H.A.; Polman, A. Plasmonics for improved photovoltaic devices. Nat. Mater. 2010, 9, 205–213. [Google Scholar] [CrossRef] [PubMed]
- Pala, R.A.; Liu, J.S.; Barnard, E.S.; Askarov, D.; Garnett, E.C.; Fan, S.; Brongersma, M.L. Optimization of non-periodic plasmonic light-trapping layers for thin-film solar cells. Nat. Commun. 2013, 4, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Tan, H.; Santbergen, R.; Smets, A.H.; Zeman, M. Plasmonic light trapping in thin-film silicon solar cells with improved self-assembled silver nanoparticles. Nano Lett. 2012, 12, 4070–4076. [Google Scholar] [CrossRef] [PubMed]
- Beck, F.J.; Mokkapati, S.; Catchpole, K.R. Plasmonic light-trapping for Si solar cells using self-assembled, Ag nanoparticles. Prog. Photovolt. Res. Appl. 2010, 18, 500–504. [Google Scholar] [CrossRef]
- Martins, E.R.; Li, J.; Liu, Y.; Depauw, V.; Chen, Z.; Zhou, J.; Krauss, T.F. Deterministic quasi-random nanostructures for photon control. Nat. Commun. 2013, 4, 2665. [Google Scholar] [CrossRef] [PubMed]
- Fountaine, K.T.; Kendall, C.G.; Atwater, H.A. Near-unity broadband absorption designs for semiconducting nanowire arrays via localized radial mode excitation. Opt. Express 2014, 22, A930. [Google Scholar] [CrossRef] [PubMed]
- Van Lare, M.-C.; Polman, A. Optimized Scattering Power Spectral Density of Photovoltaic Light-Trapping Patterns. ACS Photonics 2015, 2, 822–831. [Google Scholar] [CrossRef]
- Gaucher, A.; Cattoni, A.; Dupuis, C.; Chen, W.; Cariou, R.; Foldyna, M.; Lalouat, L.; Drouard, E.; Seassal, C.; Roca i Cabarrocas, P.; et al. Ultrathin Epitaxial Silicon Solar Cells with Inverted Nanopyramid Arrays for Efficient Light Trapping. Nano Lett. 2016, 16, 5358–5364. [Google Scholar] [CrossRef] [PubMed]
- Liang, X.; Shu, L.; Lin, H.; Fang, M.; Zhang, H.; Dong, G.; Yip, S.; Xiu, F.; Ho, J.C. Inverted Silicon Nanopencil Array Solar Cells with Enhanced Contact Structures. Sci. Rep. 2016, 6, 34139. [Google Scholar] [CrossRef] [PubMed]
- Stuart, H.R.; Hall, D. Thermodynamic limit to light trapping in thin planar structures. J. Opt. Soc. Am. A 1997, 14, 3001–3008. [Google Scholar] [CrossRef]
- Rockstuhl, C.; Lederer, F. Photon management by metallic nanodiscs in thin film solar cells Photon management by metallic nanodiscs in thin film solar cells. Appl. Phys. Lett. 2009, 94, 213102. [Google Scholar] [CrossRef]
- Mokkapati, S.; Beck, F.J.; Polman, A.; Catchpole, K.R. Designing periodic arrays of metal nanoparticles for light-trapping applications in solar cells Designing periodic arrays of metal nanoparticles for light-trapping applications in solar cells. Appl. Phys. Lett. 2009, 95, 053115. [Google Scholar] [CrossRef]
- Pala, B.R.A.; White, J.; Barnard, E.; Liu, J.; Brongersma, M.L. Design of Plasmonic Thin-Film Solar Cells with Broadband Absorption Enhancements. Adv. Mater. 2009, 21, 3504–3509. [Google Scholar] [CrossRef]
- Mariani, G.; Scofield, A.C.; Hung, C.-H.; Huffaker, D.L. GaAs nanopillar-array solar cells employing in situ surface passivation. Nat. Commun. 2013, 4, 1497. [Google Scholar] [CrossRef] [PubMed]
- Alaeian, H.; Atre, A.C.; Dionne, J.A. Optimized light absorption in Si wire array solar cells. J. Opt. 2012, 14, 024006. [Google Scholar] [CrossRef]
- Hu, L.; Chen, G. Analysis of optical absorption in silicon nanowire arrays for photovoltaic applications. Nano Lett. 2007, 7, 3249–3252. [Google Scholar] [CrossRef] [PubMed]
- Kupec, J.; Witzigmann, B. Dispersion, wave propagation and efficiency analysis of nanowire solar cells. Opt. Express 2009, 17, 10399–10410. [Google Scholar] [CrossRef] [PubMed]
- Kupec, J.; Stoop, R.L.; Witzigmann, B. Light absorption and emission in nanowire array solar cells. Opt. Express 2010, 18, 4651–4656. [Google Scholar] [CrossRef] [PubMed]
- Spinelli, P.; Verschuuren, M.; Polman, A. Broadband omnidirectional antireflection coating based on subwavelength surface Mie resonators. Nat. Commun. 2012, 3, 692. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.K.; Zhang, X.; Hill, D.J.; Song, K.D.; Park, J.S.; Park, H.G.; Cahoon, J.F. Doubling absorption in nanowire solar cells with dielectric shell optical antennas. Nano Lett. 2015, 15, 753–758. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Yu, H.; Wong, S.M.; Zhang, G.; Sun, X.; Lo, P.G.Q.; Kwong, D.L. Si nanopillar array optimization on Si thin films for solar energy harvesting. Appl. Phys. Lett. 2009, 95, 033102. [Google Scholar] [CrossRef]
- Wong, S.M.; Yu, H.Y.; Li, J.S.; Zhang, G.; Lo, P.G.; Kwong, D.L. Design High-Efficiency Si Nanopillar-Array-Textured Thin-Film Solar Cell. IEEE Electron Device Lett. 2010, 31, 335–337. [Google Scholar] [CrossRef]
- Wang, H.-P.; Lai, K.-Y.; Lin, Y.-R.; Lin, C.-A.; He, J.-H. Periodic Si nanopillar arrays fabricated by colloidal lithography and catalytic etching for broadband and omnidirectional elimination of Fresnel reflection. Langmuir 2010, 26, 12855–12858. [Google Scholar] [CrossRef] [PubMed]
- Bezares, F.J.; Long, J.P.; Glembocki, O.J.; Guo, J.; Rendell, R.W.; Kasica, R.; Shirey, L.; Owrutsky, J.C.; Caldwell, J.D. Mie resonance-enhanced light absorption in periodic silicon nanopillar arrays. Opt. Express 2013, 21, 287–291. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Li, M.; Fu, P.; Li, R.; Song, D.; Shen, C.; Zhao, Y. A comparison of light-harvesting performance of silicon nanocones and nanowires for radial-junction solar cells. Sci. Rep. 2015, 5, 11532. [Google Scholar] [CrossRef] [PubMed]
- Fountaine, K.T.; Cheng, W.-H.; Bukowsky, C.R.; Atwater, H.A. Near-Unity Unselective Absorption in Sparse InP Nanowire Arrays. ACS Photonics 2016, 3, 1826–1832. [Google Scholar] [CrossRef]
- Wong, A.B.; Brittman, S.; Yu, Y.; Dasgupta, N.P.; Yang, P. Core-Shell CdS-Cu2S Nanorod Array Solar Cells. Nano Lett. 2015, 15, 4096–4101. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Pistol, M.-E.; Anttu, N. Design for strong absorption in a nanowire array tandem solar cell. Sci. Rep. 2016, 6, 32349. [Google Scholar] [CrossRef] [PubMed]
- Dorodnyy, A.; Alarcon-Lladó, E.; Shklover, V.; Hafner, C.; Fontcuberta i Morral, A.; Leuthold, J. Efficient Multiterminal Spectrum Splitting via a Nanowire Array Solar Cell. ACS Photonics 2015, 2, 1284–1288. [Google Scholar] [CrossRef] [PubMed]
- Nowzari, A.; Heurlin, M.; Jain, V.; Storm, K.; Hosseinnia, A.; Anttu, N.; Borgström, M.T.; Pettersson, H.; Samuelson, L. A comparative study of absorption in vertically and laterally oriented InP core-shell nanowire photovoltaic devices. Nano Lett. 2015, 15, 1809–1814. [Google Scholar] [CrossRef] [PubMed]
- Pudasaini, P.R.; Elam, D.; Ayon, A.A. Aluminum oxide passivated radial junction sub-micrometre pillar array textured silicon solar cells. J. Phys. D Appl. Phys. 2013, 46, 235104. [Google Scholar] [CrossRef]
- Vescovi, G.; Asoli, D.; Naseem, U.; Gilboy, J.P.; Sundvall, C.; Dahlgren, A.; Svensson, K.E.; Anttu, N.; Björk, M.T.; Samuelson, L.; et al. A GaAs nanowire array solar cell with 15.3% efficiency at 1 sun. IEEE J. Photovolt. 2016, 6, 185–190. [Google Scholar]
- Shalev, G.; Schmitt, S.; Brönstrup, G.; Christiansen, S. Maximizing the ultimate absorption efficiency of vertically-aligned semiconductor nanowire arrays with wires of a low absorption cross-section. Nano Energy 2015, 12, 801–809. [Google Scholar] [CrossRef]
- Shalev, G. Addressing carrier extraction from optically optimized nanopillar arrays for thin-film photovoltaics. Nanoscale 2017, 9, 15707–15716. [Google Scholar] [CrossRef] [PubMed]
- Schmitt, S.W.; Brönstrup, G.; Shalev, G.; Srivastava, S.K.; Bashouti, M.Y.; Döhler, G.H.; Christiansen, S.H. Probing photo-carrier collection efficiencies of individual silicon nanowire diodes on a wafer substrate. Nanoscale 2014, 6, 7897–7902. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Gao, P.; Liao, M.; Yang, X.; Ying, Z.; Zhou, S.; Ye, J.; Cui, Y. Realization of 13.6% Efficiency on 20 μm Thick Si/Organic Hybrid Heterojunction Solar Cells via Advanced Nanotexturing and Surface Recombination Suppression. ACS Nano 2015, 9, 6522–6531. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.Y.; Zhang, R.J.; Wang, S.Y.; Lu, M.; Chen, X.; Zheng, Y.X.; Chen, L.Y.; Ye, Z.; Wang, C.Z.; Ho, K.M. Broadband optical absorption by tunable Mie resonances in silicon nanocone arrays. Sci. Rep. 2015, 5, 7810. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.F.; Chattopadhyay, S.; Jen, Y.J.; Peng, C.Y.; Liu, T.A.; Hsu, Y.K.; Pan, C.L.; Lo, H.C.; Hsu, C.H.; Chang, Y.H.; et al. Improved broadband and quasi-omnidirectional anti-reflection properties with biomimetic silicon nanostructures. Nat. Nanotechnol. 2007, 2, 770–774. [Google Scholar] [CrossRef] [PubMed]
- Jeong, S.; McGehee, M.D.; Cui, Y. All-back-contact ultra-thin silicon nanocone solar cells with 13.7% power conversion efficiency. Nat. Commun. 2013, 4, 2950. [Google Scholar] [CrossRef] [PubMed]
- Savin, H.; Repo, P.; Von Gastrow, G.; Ortega, P.; Calle, E.; Garín, M.; Alcubilla, R. Black silicon solar cells with interdigitated back-contacts achieve 22.1% efficiency. Nat. Nanotechnol. 2015, 10, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Shalev, G.; Schmitt, S.W.; Embrechts, H.; Brönstrup, G.; Christiansen, S. Enhanced photovoltaics inspired by the fovea centralis. Sci. Rep. 2015, 5, 8570. [Google Scholar] [CrossRef] [PubMed]
- Spinelli, P.; Polman, A. Light Trapping in Thin Crystalline Si Solar Cells Using Surface Mie Scatterers. IEEE J. Photovolt. 2014, 4, 554–559. [Google Scholar] [CrossRef]
- Palik, E.D. Handbook of Optical Constants of Solids; Academic: Orlando, FL, USA, 1985. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prajapati, A.; Nissan, Y.; Gabay, T.; Shalev, G. Light Trapping with Silicon Light Funnel Arrays. Materials 2018, 11, 445. https://doi.org/10.3390/ma11030445
Prajapati A, Nissan Y, Gabay T, Shalev G. Light Trapping with Silicon Light Funnel Arrays. Materials. 2018; 11(3):445. https://doi.org/10.3390/ma11030445
Chicago/Turabian StylePrajapati, Ashish, Yuval Nissan, Tamir Gabay, and Gil Shalev. 2018. "Light Trapping with Silicon Light Funnel Arrays" Materials 11, no. 3: 445. https://doi.org/10.3390/ma11030445
APA StylePrajapati, A., Nissan, Y., Gabay, T., & Shalev, G. (2018). Light Trapping with Silicon Light Funnel Arrays. Materials, 11(3), 445. https://doi.org/10.3390/ma11030445






