Unusual Electrical Transport Driven by the Competition between Antiferromagnetism and Ferromagnetism in Antiperovskite Mn3Zn1−xCoxN
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sample Preparation
2.2. Characterization
3. Results and Discussion
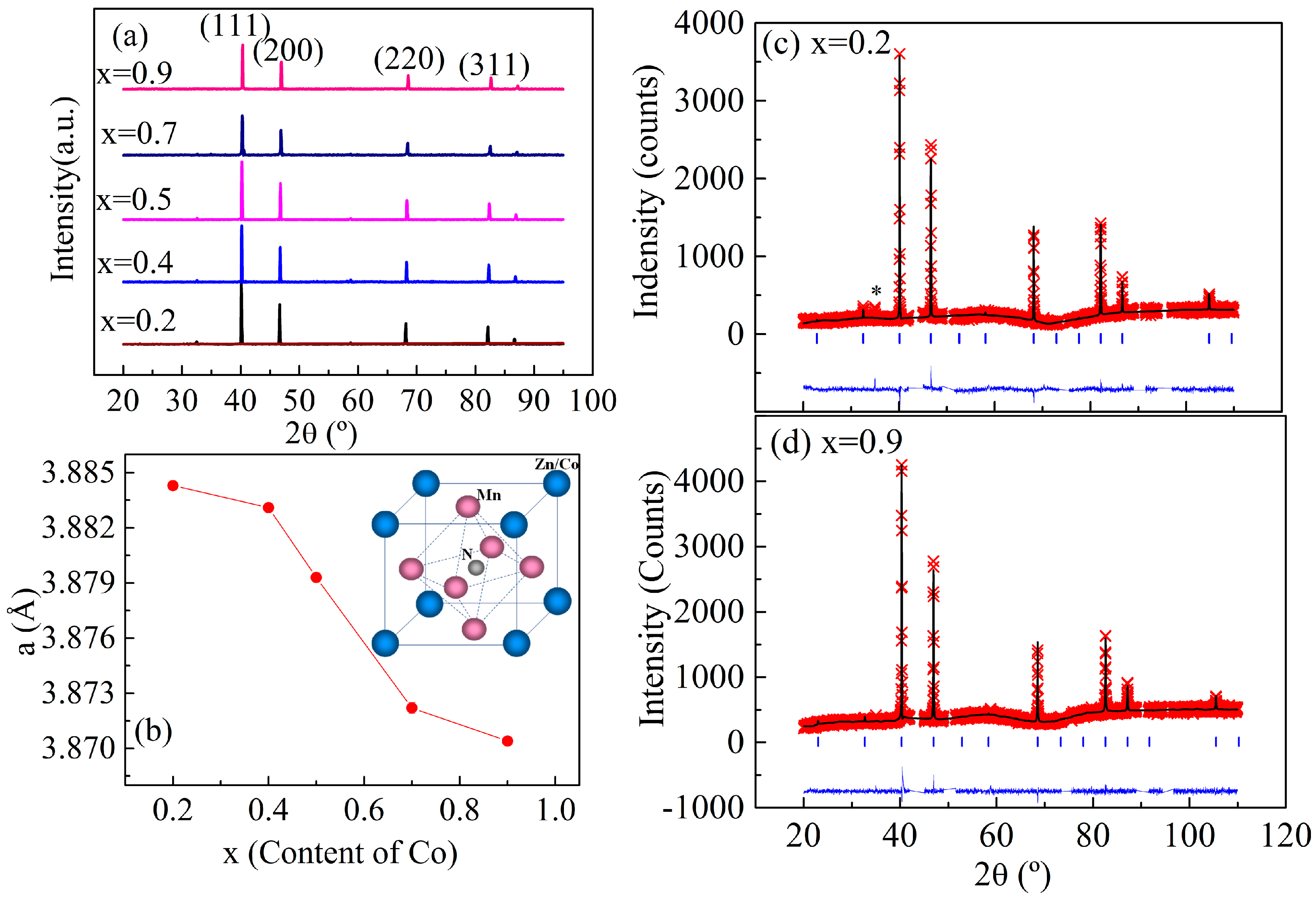
3.1. Crystal Structure
3.2. Magnetic Properties
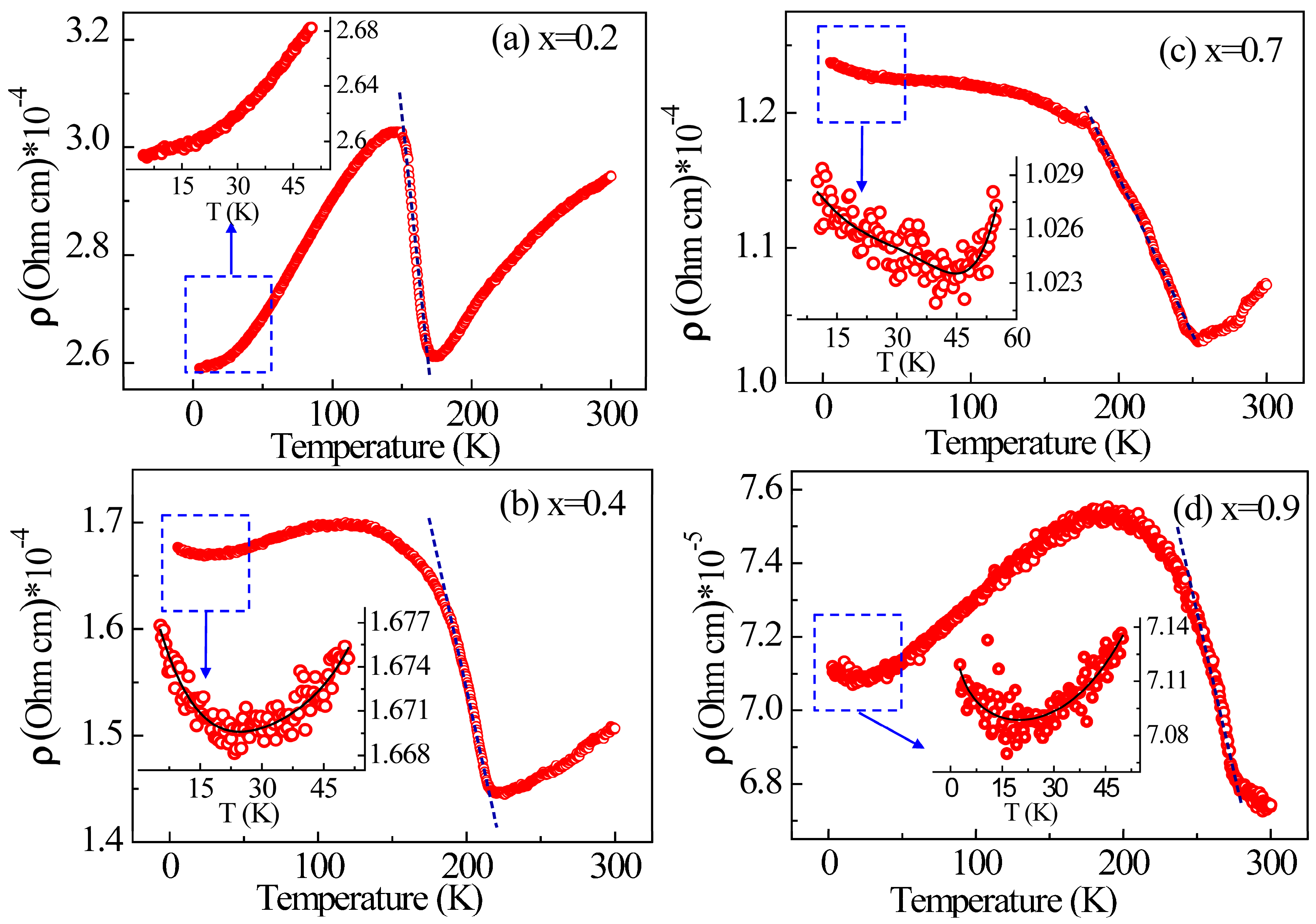
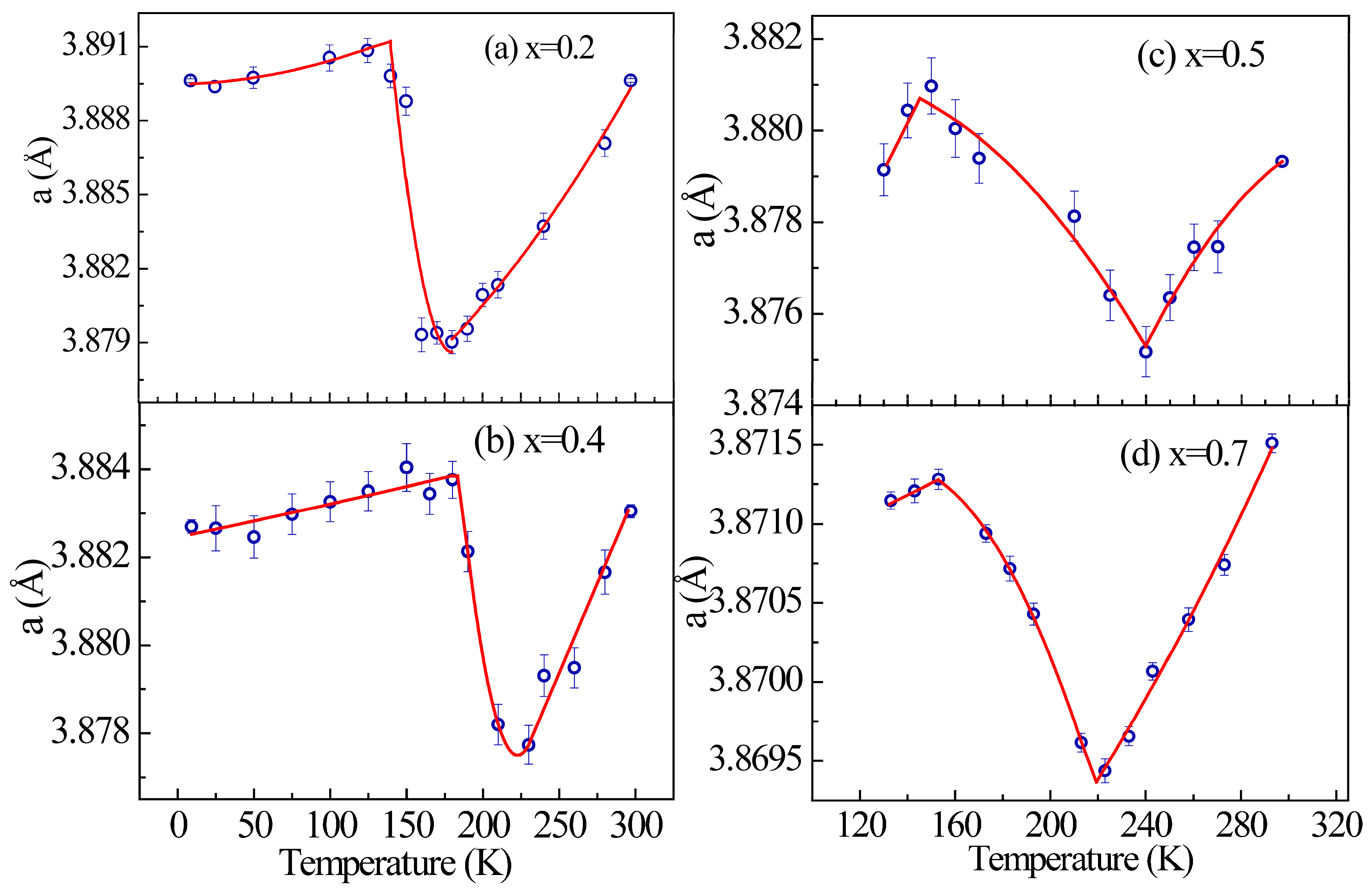
3.3. Electrical Transport Behavior and Negative Thermal Expansion
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wang, C.; Chu, L.H.; Yao, Q.R.; Sun, Y.; Wu, M.M.; Ding, L.; Yan, J.; Na, Y.Y.; Tang, W.H.; Li, G.; et al. Tuning the range, magnitude, and sign of the thermal expansion in intermetallic Mn3(Zn, M)xN(M= Ag, Ge). Phys. Rev. B 2012, 85, 220103(R). [Google Scholar] [CrossRef]
- Takenaka, K.; Takagi, H. Giant negative thermal expansion in Ge-doped anti-perovskite manganese nitrides. Appl. Phys. Lett. 2005, 87, 261902. [Google Scholar] [CrossRef]
- Song, X.Y.; Sun, Z.H.; Huang, Q.Z.; Rettenmayr, M.; Liu, X.; Seyring, M.; Li, G.; Rao, G.; Yin, F. Adjustable zero thermal expansion in antiperovskite manganese nitride. Adv. Mater. 2011, 23, 4690. [Google Scholar] [CrossRef] [PubMed]
- Chu, L.H.; Wang, C.; Yan, J.; Na, Y.Y.; Ding, L.; Sun, Y.; Wen, Y. Magnetic transition, lattice variation and electronic transport properties of Ag-doped Mn3Ni1−xAgxN antiperovskite compounds. Scr. Mater. 2012, 67, 173–176. [Google Scholar] [CrossRef]
- Lin, S.; Wang, B.S.; Lin, J.C.; Huang, Y.N.; Lu, W.J.; Zhao, B.C.; Tong, P.; Song, W.H.; Sun, Y.P. Tunable room-temperature zero temperature coefficient of resistivity in antiperovskite compounds Ga1−xCFe3 and Ga1−yAlyCFe3. Appl. Phys. Lett. 2012, 101, 011908. [Google Scholar] [CrossRef]
- Ding, L.; Wang, C.; Chu, L.H.; Yan, J.; Na, Y.Y.; Huang, Q.Z.; Chen, X. Near zero temperature coefficient of resistivity in antiperovskite Mn3Ni1‒xCuxN. Appl. Phys. Lett. 2011, 99, 251905. [Google Scholar] [CrossRef]
- Asano, K.; Koyama, K.; Takenaka, K. Magnetostriction in Mn3CuN. Appl. Phys. Lett. 2008, 92, 161909. [Google Scholar] [CrossRef]
- Huang, R.J.; Li, L.F.; Wu, Z.; Chu, X.; Xu, X.; Qian, L. Spin-glass behavior in the antiperovskite manganese nitride Mn3CuN codoped with Ge and Si. Solid State Commun. 2010, 150, 1617–1620. [Google Scholar] [CrossRef]
- Lin, S.; Shao, D.F.; Lin, J.C.; Zu, L.; Kan, X.C.; Wang, B.S.; Huang, Y.N.; Song, W.H.; Lu, W.J.; Tong, P.; et al. Spin-glass behavior and zero-field-cooled exchange bias in a Cr-based antiperovskite compound PdNCr3. J. Mater. Chem. C 2015, 3, 5683–5696. [Google Scholar] [CrossRef]
- Ding, L.; Wang, C.; Sun, Y.; Colin, C.V.; Chu, L.H. Spin-glass-like behavior and negative thermal expansion in antiperovskite Mn3Ni1‒xCuxN compounds. J. Appl. Phys. 2015, 117, 213915. [Google Scholar] [CrossRef]
- Yan, J.; Sun, Y.; Wu, H.; Huang, Q.Z.; Wang, C.; Shi, Z.; Deng, S.H.; Shi, K.W.; Lu, H.; Chu, L.H. Phase transitions and magnetocaloric effect in Mn3Cu0.89N0.96. Acta Mater. 2014, 74, 58–65. [Google Scholar] [CrossRef]
- Lin, S.; Wang, B.S.; Lin, J.C.; Zhang, L.; Hu, X.B.; Huang, Y.N.; Lu, W.J.; Zhao, B.C.; Tong, P.; Song, W.H.; et al. Composition dependent-magnetocaloric effect and low roomtemperature coefficient of resistivity study of iron-based antiperovskite compounds Sn1‒xGaxCFe3 (0 ≤ x ≤ 1.0). Appl. Phys. Lett. 2011, 99, 172503. [Google Scholar] [CrossRef]
- Jardin, J.P.; Labbe, J. Phase Transitions and Band Structure in Metallic Perovskites (Carbides and Nitrides). J. Solid State Chem. 1983, 46, 275–293. [Google Scholar] [CrossRef]
- Garcia, A.B.J.; Marcelli, A.; Davoli, I.; Bartolome, J. Local Electronic Structures at Selected Sites of Intermetallic perovskites Mn3MeX (Me=divalent metal, X = N, C). Il Nuovo Cim. D 1986, 7, 493–505. [Google Scholar] [CrossRef]
- Fruchart, D.; Bertaut, E.F.; Madar, R.; Fruchart, R. Diffraction neutronique de Mn3ZnN. J. Phys. Coll. 1971, 32, 876–877. [Google Scholar] [CrossRef]
- Deng, S.H.; Sun, Y.; Wang, L.; Shi, Z.; Wu, H.; Huang, Q.Z.; Yan, J.; Shi, K.W.; Hu, P.; Zaoui, A.; et al. Frustrated Triangular Magnetic Structures of Mn3ZnN: Applications in Thermal Expansion. J. Phys. Chem. C 2015, 119, 24983–24990. [Google Scholar] [CrossRef]
- Sun, Y.S.; Guo, Y.F.; Wang, X.X.; Tsujimoto, Y.; Matsushita, Y.; Shi, Y.G.; Wang, C.; Belik, A.A.; Yamaura, K. Resistive switching phenomenon driven by antiferromagnetic phase separation in an antiperovskite nitride Mn3ZnN. Appl. Phys. Lett. 2012, 100, 161907. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, C.; Huang, Q.; Guo, Y.; Chu, L.H.; Arai, M.; Yamaura, K. Neutron Diffraction Study of Unusual Phase Separation in the Antiperovskite Nitride Mn3ZnN. Inorg. Chem. 2012, 51, 7232–7236. [Google Scholar] [CrossRef] [PubMed]
- Chu, L.H.; Wang, C.; Bordet, P.; Colin, C.V.; Pairis, S.; Na, Y.; Yan, J.; Huang, Q. The effect of Zn vacancies on the physical properties of antiperovskite compounds Mn3ZnxN. Scr. Mater. 2013, 68, 968–971. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, C.; Wen, Y.; Zhu, K.; Zhao, J. Lattice contraction and magnetic and electronic transport properties of Mn3Zn1−xGexN. Appl. Phys. Lett. 2007, 91, 231913. [Google Scholar] [CrossRef]
- Qu, B.Y.; Pan, B.C. Nature of the negative thermal expansion in antiperovskite compound Mn3ZnN. J. Appl. Phys. 2010, 108, 113920. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, C.; Wen, Y.; Chu, L.H.; Pan, H.; Nie, M.; Tang, M. Negative Thermal Expansion and Magnetic Transition in Anti-Perovskite Structured Mn3Zn1‒xSnxN Compounds. J. Am. Ceram. Soc. 2010, 93, 2178–2181. [Google Scholar] [CrossRef]
- Tan, J.; Huang, R.; Li, W.; Han, Y.; Li, L. Broadened negative thermal expansion operation-temperature window in antiperovskite Mn3Zn0.6Ge0.4N prepared by spark plasma sintering. J. Alloys Compd. 2014, 593, 103–105. [Google Scholar] [CrossRef]
- Zhang, X.H.; Yin, Y.; Yuan, Q.; Han, J.C.; Zhang, Z.H.; Jian, J.K.; Zhao, J.G.; Song, B. Magnetoresistance reversal in antiperovskite compound Mn3Cu0.5Zn0.5N. J. Appl. Phys. 2014, 115, 123905. [Google Scholar] [CrossRef]
- Lin, J.C.; Wang, B.S.; Tong, P.; Lin, S.; Lu, W.J.; Zhu, X.B.; Yang, Z.R.; Song, W.H.; Dai, J.M.; Sun, Y.P. Tunable temperature coefficient of resistivity in C- and Co-doped CuNMn3. Scr. Mater. 2011, 65, 452–455. [Google Scholar] [CrossRef]
- Chu, L.H.; Wang, C.; Sun, Y.; Li, M.C.; Wan, Z.P.; Wang, Y.; Dou, S.Y.; Chu, Y. Doping Effect of Co at Ag Sites in Antiperovskite Mn3AgN Compounds. Chin. Phys. Lett. 2015, 32, 047501. [Google Scholar] [CrossRef]
- Roisnel, T.; Rodríguez-Carvajal, J. WinPLOTR: A Windows Tool for Powder Diffraction Pattern Analysis. Mater Sci. Forum 2001, 378, 118–123. [Google Scholar] [CrossRef]
- Motizuki, K.; Nagai, H. Electronic band structures and magnetism of the cubic perovskite-type manganese compounds Mn3MC (M = Zn, Ga, In, Sn). J. Phys. C Solid State Phys. 1988, 21, 5251–5258. [Google Scholar] [CrossRef]
- Li, B.Y.; Li, W.; Feng, W.; Zhang, Y.; Zhang, Z. Magnetic, transport and magnetotransport properties of Mn3+xSn1‒xC and Mn3ZnySn1‒yC compounds. Phys. Rev. B 2005, 72. [Google Scholar] [CrossRef]
- Abhay, N.P.; Radoslaw, C.B.; Jan, M.; Jacob, E.G.; Luke, A.K.D.; Paul, L.M.; Daniel, C.R. The Kondo Effect in the Presence of Ferromagnetism. Science 2004, 306, 86–89. [Google Scholar]
- Rana, D.S.; Markna, J.H.; Parmar, R.N.; Kuberkar, D.G.; Raychaudhuri, P.; John, J.; Malik, S.K. Low-temperature transport anomaly in the magnetoresistive compound (La0.5Pr0.2)Ba0.3MnO3. Phys. Rev. B 2005, 71, 212404. [Google Scholar] [CrossRef]
- Sun, Y.; Guo, Y.; Tsujimoto, Y.; Yang, J.; Shen, B.; Yi, W.; Matsushita, Y.; Wang, C.; Wang, X.; Li, J.; et al. Carbon-Induced Ferromagnetism in the Antiferromagnetic Metallic Host Material Mn3ZnN. Inorg. Chem. 2013, 52, 800–806. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Xu, Y.; Cao, S.; Cao, G.; Zhang, Y.; Jing, C. Kondo-like transport and its correlation with the spin-glass phase in perovskite manganites. Phys. Rev. B 2005, 72, 054410. [Google Scholar] [CrossRef]
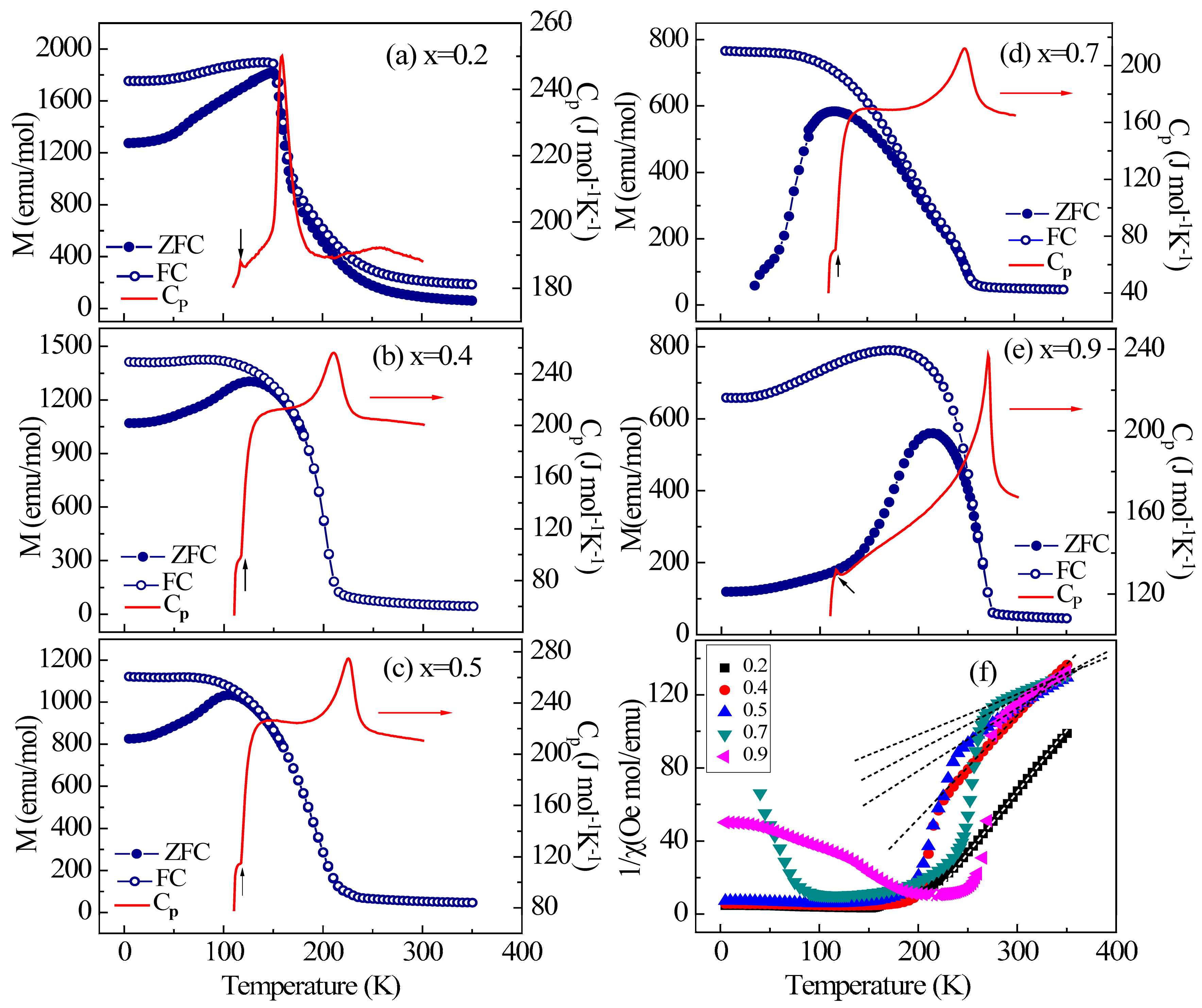

| Co (x) | Weiss Temperature (K) | Effective Moment μeff (μB) |
|---|---|---|
| 0.2 | 200 | 2.00 |
| 0.4 | 115 | 2.14 |
| 0.5 | −22 | 2.76 |
| 0.7 | −220 | 3.41 |
| 0.9 | −380 | 3.68 |
| x | A | B | C | D |
|---|---|---|---|---|
| 0.2 | - | - | - | - |
| 0.4 | 1.69 × 10−4 | 6.69 × 10−8 | 9.06 × 10−7 | 9.95 × 10−16 |
| 0.7 | 1.02 × 10−4 | 5.41 × 10−8 | 1.96 × 10−7 | 1.49 × 10−15 |
| 0.9 | 7.14 × 10−5 | 2.31 × 10−8 | 2.43 × 10−7 | 1.14 × 10−15 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, L.; Ding, L.; Wang, C.; Li, M.; Guo, Y.; Liu, Z. Unusual Electrical Transport Driven by the Competition between Antiferromagnetism and Ferromagnetism in Antiperovskite Mn3Zn1−xCoxN. Materials 2018, 11, 286. https://doi.org/10.3390/ma11020286
Chu L, Ding L, Wang C, Li M, Guo Y, Liu Z. Unusual Electrical Transport Driven by the Competition between Antiferromagnetism and Ferromagnetism in Antiperovskite Mn3Zn1−xCoxN. Materials. 2018; 11(2):286. https://doi.org/10.3390/ma11020286
Chicago/Turabian StyleChu, Lihua, Lei Ding, Cong Wang, Meicheng Li, Yanjiao Guo, and Zhuohai Liu. 2018. "Unusual Electrical Transport Driven by the Competition between Antiferromagnetism and Ferromagnetism in Antiperovskite Mn3Zn1−xCoxN" Materials 11, no. 2: 286. https://doi.org/10.3390/ma11020286
APA StyleChu, L., Ding, L., Wang, C., Li, M., Guo, Y., & Liu, Z. (2018). Unusual Electrical Transport Driven by the Competition between Antiferromagnetism and Ferromagnetism in Antiperovskite Mn3Zn1−xCoxN. Materials, 11(2), 286. https://doi.org/10.3390/ma11020286






