Abstract
While the rule of mixture is applicable for addressing the overall Poisson’s ratio of a concentrically aligned bi-layered rod under longitudinal loading, the same cannot be said for this rod under torsional loading due to the higher extent of deformation in the rod material further away from the torsional axis. In addition, the use of adhesives for attaching the solid inner rod to the hollow outer rod introduces an intermediate layer, thereby resulting in a tri-layered concentric rod if the adhesive layer is uniformly distributed. This paper investigates the effect of the adhesive properties on the overall auxeticity of a rod consisting of two concentrically aligned cylindrical isotropic foams with Poisson’s ratio of opposite signs under torsional loads. An indirect way for obtaining Poisson’s ratio of a concentrically tri-layered rod was obtained using a mechanics of materials approach. Results show that the auxeticity of such rods is influenced by the adhesive’s stiffness, Poisson’s ratio, thickness, and radius from the torsional axis.
1. Introduction
In the analysis of negative materials, the term “conventional materials” is typically adopted when referring to materials with properties that are normally taken for granted, such as positive Poisson’s ratio, positive thermal expansivity, and positive stiffness. For papers that deal with auxetic materials, “conventional” materials are those that exhibit a positive Poisson’s ratio. The problem of torsion of cylindrical rods made from conventional materials is well established and has been a subject of extensive research. The theory of generalized torsion was first worked out by Voigt and the rigorous theory of pure torsion was developed by Saint–Venant. There are many classical works on the theory of pure torsion (e.g., [1,2,3,4]). Tsukrov and Drach [5] gave explicit analytical expressions for displacement and stress fields in a multilayered composite cylinder with cylindrically orthotropic layers subjected to homogeneous boundary conditions. The solutions are derived under the assumption of perfect bonding between layers. Torsion of laminated cylindrical shells with adhesive interlayers was investigated by Maksymuk and Shcherbina [6]. Based on refined equations of the Timoshenko-type shell theory, the contact stresses in torsion of a two-layer cylindrical shell with an adhesive interlayer were numerically studied. The effect of the geometric and physical-mechanical parameters of the load-carrying layers and the adhesive interlayer of the shell on the distribution of the interlaminar tangential stress was analyzed as well. The magnetoelectric (ME) effect in a piezoelectric/piezomagnetic (PE/PM) composite cylinder, which is induced by a torsional deformation, was investigated by Huang and Zhang [7]. Both the PE and PM layers are circumferentially polarized. For a specific applied magnetic field, the displacement component in the PM layer was analytically presented. Levin et al. [8] considered a static problem of torsion of a cylinder composed of incompressible, nonlinear elastic materials at large deformations. The cylinder contained a central, round, cylindrical inclusion that was initially twisted and stretched (or compressed) along the axis and fastened to a strainless, external, hollow cylinder.
Since 1987, when negative Poisson’s ratio foams were developed by Lakes [9,10], it is known that materials and structures showing a negative Poisson’s ratio do exist in nature. Popereka and Balagurov [11] presented ferromagnetic films having a negative Poisson ratio; Milstein and Huang [12] confirmed the existence of a negative Poisson ratio in face-centered cubic (fcc) crystals. Simple mechanical [13,14,15] and thermodynamic [16] models, which show auxetic behavior, were found in the 80s of the 20th century; the latter was studied in the form of hexagonal molecules in two-dimensional (2D) lattice [17,18]. The counterintuitive nature of auxetic materials avails much potential as safer fasteners [19], improved arterial prostheses [20], artificial intervertebral discs [21], drug eluting stents [22] and other prostheses [23], more comfortable cushions [24,25], highly tunable molecular sieves [26,27,28,29], antivibration gloves [30], novel textiles [31], better material for diabetic shoes [32], safer pressure vessels [33] and other thin-walled structures [34], and a better performing crash/shock absorber [35,36]. It has also been found that novel properties, distinct from conventional or auxetic materials, arise when a composite structure is made from both conventional and auxetic materials. In addition to a recent comprehensive survey of auxetic materials and structures [37], the reader is also referred to a recent focus issue on “auxetics and other systems of anomalous characteristics” [38,39,40,41,42], as well as papers in this special issue [43,44,45,46,47,48].
Interlacing effects from the auxetic and conventional materials have been shown to give interesting properties in bi-layer [49,50], tri-layer [51,52], and multi-layered systems [53,54,55,56,57,58,59,60], and continuous unidirectional fiber composites [61]. One category of auxetic structural element is that of rods possessing circular or elliptical cross-sections with auxetic and conventional materials alternated in concentric [62,63], angular [64], and helical [65] directions. The earlier approach [62] assumes that (a) the interface between both the auxetic and conventional phases has no thickness and that (b) the bonding between both phases is perfect; due to finite element approximation used in the numerical model of the two-phase composites [63,64,65], an “interface layer” with thickness is present instead of the perfect bond between the material. In practice, adhesion is required between both phases such that the interface between both phases is replaced by an interphase and that the interphase has its own material properties and thickness. This paper attempts to model, by an analytical approach, a single tri-layered cylindrical rod consisting of a solid inner foam rod adhered to a hollow outer foam rod, with significant adhesive modulus as the interface of the two foam rods.
The overall auxeticity of a concentric rod whereby the core and shell possess Poisson’s ratio of opposite signs is influenced by the mode of loading [62]. It is obvious that during axial loading both the core and shell experience equal longitudinal strain but during torsional loading, the shell undergoes greater shear strain than the core. In this concentrically bi-layered rod system, the auxeticity during axial and torsional loading modes changes at different rates with respect to the ratio of the inner-to-outer diameters. This results in a range of inner-to-outer diameter ratios whereby the concentric rod exhibits overall Poisson’s ratio of different signs depending on the loading mode. However, the assumption of a bi-layered concentric foam system is no longer valid when a layer of high modulus adhesive exists between the two concentric rods. The adhesive layer can be thought of as an intermediate layer that fills the gap between the two concentric cylinders. Even in the case where the surfaces of the inner and outer cylinders are in contact with each other, the slight seepage of adhesive fluid into the foam before its solidification gives rise to a high modulus intermediate layer. The effect of the adhesive’s elastic properties under torsional load on the concentric foam rods of opposing Poisson’s ratio signs, but with comparable Young’s modulus, is investigated in this paper as a tri-layered concentric rod system.
2. Theory and Formulation
Unlike uniaxial loading whereby the diameter changes for non-zero Poisson’s ratio, there is no salient change in the rod diameter under torsional load. With reference to Figure 1, a component of radial increase due to one principal strain is canceled by a component of radial decrease due to another principal strain in the same plane. Hence, there is no change in the rod diameter under torsion. Nevertheless, it is obvious that the auxeticity of the rod must be related to that of the material that constitutes the rod.
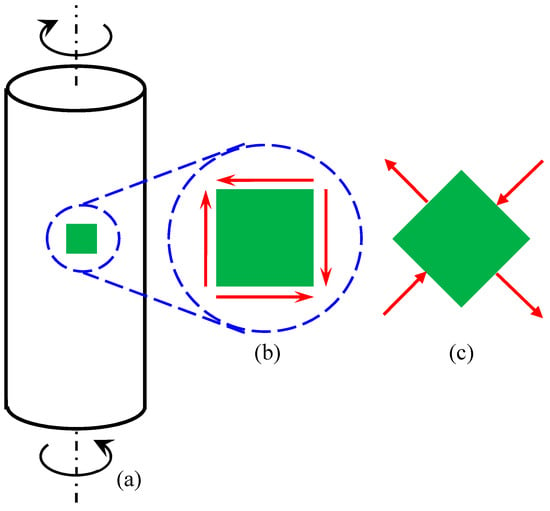
Figure 1.
Schematics for (a) a rod under torsion, (b) an elemental volume under pure shearing, and (c) an equivalent stress state at 45° showing in-plane principal stresses. Red arrows indicate stress directions.
2.1. Single Solid Rods
Since an observation on rod diameter yields no change regardless of the rod auxeticity, we herein consider the rod auxeticity—under torsional loading—in terms of the moduli ratio G/E (or E/G) using the elastic relation:
By virtue of Equation (1), the moduli ratio G/E→∞ (or E/G→0) as v→−1, and that G/E→1/3 (or E/G→3) as v→1/2. Hence, the auxeticity of a material can be inferred from the moduli ratio as an alternative to the usual way of measuring the change in dimension during axial loading. For a single solid rod of diameter D and length L undergoing torsion T, the angular twist φ is given as
whereby the polar moment area of the circular cross-section J is
Substituting Equations (1) and (3) into Equation (2), we have Poisson’s ratio of the rod:
or, for convenient comparison with subsequent sub-sections, we write
2.2. Bi-Layered Concentric Rods
As opposed to summative angular twist and common transmitted torsional load for two rods arranged in series, the case of two concentrically arranged rods is governed by a common angular twist with summative torsional loads as depicted in Figure 2a,b, respectively.
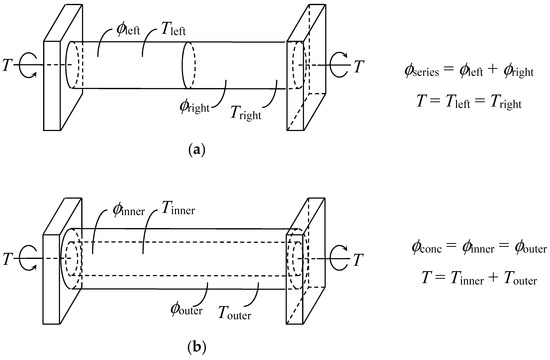
Figure 2.
Comparison between two rods in (a) series and (b) concentric arrangement.
Hence, the common angular twist for the inner and outer rods
and the summative torsional load
give
Substituting Equations (1) and (3) into Equation (8) leads to
It can be easily seen that Equation (9) can be reduced to Equation (5) under certain special cases; substituting Di = 0 (i.e., E = Eo for the entire rod) into Equation (9) leads to
or
while the substitution of Di = Do (i.e., E = Ei for the whole rod) into Equation (9) gives
or
Hence, by virtue of Equation (5) and neglecting the adhesive layer, the effective Poisson’s ratio for two perfectly bonded concentric cylinders under torsional loading mode is
where the term in parenthesis is given by Equation (9) in the case of a bi-layered concentric rod. However, to prevent unnecessary error, caution must be taken when using Equation (9) under some limiting conditions. For example, it is obvious that E = Ei and v = vi for the entire rod if we let Di = Do; however, substituting Di/Do = 1 and Ei/Eo→∞ into Equation (9) results in v = −1 instead of v = vi. The source of this error can be traced by considering the fact that the substitution of Di/Do = 1 into Equation (9) implies that Eo and the ratio Ei/Eo on the LHS and RHS of Equation (9), respectively, do not exist; the correct expression is indicated by Equation (12).
2.3. Tri-Layered Concentric Rods
Figure 3 shows the adhesive layer being the interlayer, thereby extending the bi-layered concentric rod into a more realistic tri-layered concentric rod with the thickness of the adhesive layer δ being
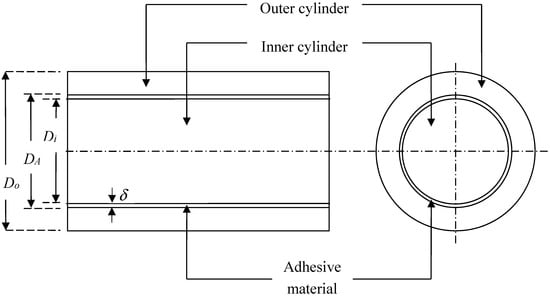
Figure 3.
Side (left) and axial (right) views of a rod made from two concentric foams with opposite Poisson’s ratio signs, in which the adhesive material is assumed to take on the shape of a thin cylindrical shell.
As in the case of a bi-layered concentric rod, the angular twist for a tri-layered rod is common
while the torsional load is carried by all three layers
Proceeding similarly as in the case of a bi-layered concentric rod, the effective Poisson’s ratio for a tri-layered concentric rod under torsional loading mode is
with
where
and
It can be seen from Equations (20) and (21) that as δ→0 or δ << Do, Equation (19) reduces to Equation (9). If the adhesive layer is very small in comparison to other radial dimensions and the adhesive modulus is in the same order as that of the foam material, then the following simplifications of
and
are valid for Equations (20) and (21), respectively. A direct consequence of this simplification is that Equation (19) resembles Equation (9); that is,
such that the influence from the adhesive material is confined to only one term, that is, on the second term on the RHS of Equation (24). Here, the relative modulus of the adhesive-to-outer foam material EA/Eo and the relative adhesive thickness δ/Do play equal importance. The simplification suggested in Equation (22), however, is no longer valid when the relative modulus of the adhesive material EA/Eo is several orders higher. Hence, the retention of Equation (20) with the use of Equation (23) provides balanced simplification and accuracy. Without diminishing the adhesive layer, the tri-layered concentric rods reduce to bi-layered ones under the following special cases: (a) Di = 0, in which the adhesive layer takes the place of the inner core in the form of a very slim reinforcement rod, and (b) Di ≈ Do with a very thin δ in which the adhesive layer takes the place of the outer shell in the form of a very thin tube. It can be shown that as Di→0, Equation (24) reduces to
Likewise, Equation (24) simplifies to
as Di→Do. It can be observed that the limiting conditions for the tri-layered rod as specified in Equations (25) and (26) closely resemble those of the bi-layered cases of Equations (10) and (12), respectively. In the results section, curves of the effective Poisson’s ratio for the tri-layered rods are plotted against Di/Do for the range 0 ≤ Di/Do ≤ 1 in which both extreme cases Di = 0 and Di = Do are valid under the earlier imposed condition that δ << Do.
3. Results and Discussion
The influence of the intermediate layer on the overall Poisson’s ratio of a rod made from foams of opposing Poisson’s ratio signs can be observed by considering the adhesive layer’s elastic and geometrical properties. Specifically, these properties are (a) the elastic properties in terms of the adhesive modulus relative to that of the foam EA/EFoam and the adhesive Poisson’s ratio vA, as well as the (b) geometrical properties in terms of the adhesive thickness relative to the rod diameter δ/Do and the adhesive diameter relative to that of the rod Di/Do.
In the plotted results of the effective Poisson’s ratio in Figure 4, Figure 5 and Figure 6, we adopt the concentrically tri-layered cylinder using Equations (18)–(20) and (23) for the case of an equal inner and outer foam modulus:
and equal Poisson’s ratio magnitudes for the inner and outer foams
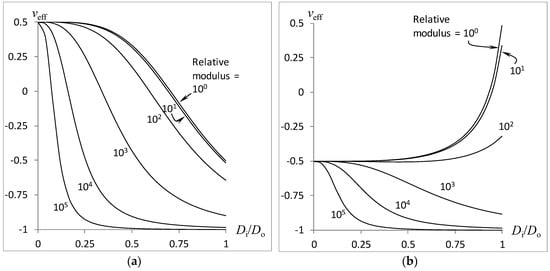
Figure 4.
Effect of relative adhesive modulus on the compound rod auxeticity: (a) Auxetic core; (b) Auxetic shell.
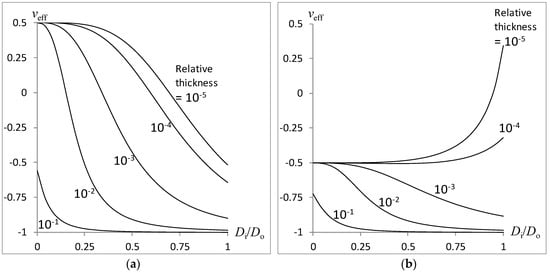
Figure 5.
Effect of relative adhesive thickness on the compound rod auxeticity: (a) Auxetic core; (b) Auxetic shell.
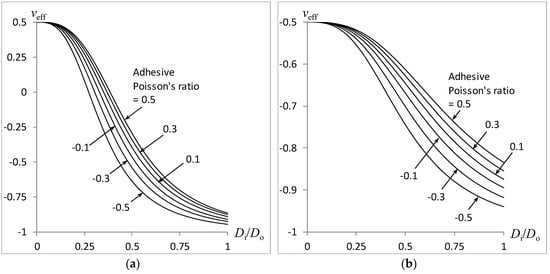
Figure 6.
Effect of adhesive Poisson’s ratio on the compound rod auxeticity: (a) Auxetic core; (b) Auxetic shell.
The effect of the relative moduli ratio EA/EFoam on the variation of the combined rod’s effective Poison’s ratio veff with the inner-to-outer cylinder diameters Di/Do is plotted in Figure 4 with relative adhesive thickness at δ/Do = 0.001, Poisson’s ratio of solidified adhesive at vA = 0, and relative adhesive modulus at EA/EFoam = 10n for n = 0, 1, 2, 3, 4, 5. Figure 4a and Figure 4b refer to the auxetic core (−vi = vo = 0.5) and auxetic shell (vi = −vo = 0.5), respectively. As expected, the rod auxeticity increases (or the overall Poisson’s ratio decreases) with the relative size of the auxetic core, as shown in Figure 4a. However, an unexpected trend is observed whereby the overall Poisson’s ratio approaches −1 as the inner-to-outer diameter approaches 1, although none of the material components possess a Poisson’s ratio lower than −0.5. Plotted results also reveal that the rod auxeticity increases with the use of a higher adhesive modulus. When the position of the auxetic and conventional parts are swopped, only the case of moderate relative adhesive modulus gives an intuitive trend, that is, increasing Poisson’s ratio with increasing conventional inner cylinder size. However, the trend reverses for an extremely large adhesive modulus. This may well be due to the high torsional stiffness that translates into a high ratio, which is associated with auxeticity.
The effect of relative moduli thickness (δ/Do) on the variation of the combined rod’s effective Poison’s ratio veff with the inner-to-outer cylinder diameters Di/Do is plotted in Figure 5 with relative adhesive modulus at EA/EFoam = 1000, Poisson’s ratio of solidified adhesive at vA = 0, and relative adhesive thickness at δ/Do = 10n for n = −1, −2, −3, −4, −5. Figure 5a,b correspond to the use of an auxetic core (−vi = vo = 0.5) and auxetic shell (vi = −vo = 0.5), respectively. The trends obtained in Figure 5 are somewhat similar to those of Figure 4, signifying an almost similar effect of adhesive thickness with adhesive modulus. The similarity is attributed to the increasing stiffness contributed by the intermediate layer’s increasing modulus and increasing thickness.
The effect of the adhesive’s Poisson’s ratio vA on the variation of the combined rod’s effective Poison’s ratio veff with the inner-to-outer cylinder diameters Di/Do is plotted in Figure 6 with a relative adhesive modulus at EA/EFoam = 1000, relative adhesive thickness at δ/Do = 0.001, and adhesive Poisson’s ratio at vA = ±0.1, ±0.3, ±0.5. Figure 6a,b correspond to the use of an auxetic core (−vi = vo = 0.5) and auxetic shell (vi = −vo = 0.5), respectively. As with Figure 4 and Figure 5, a drop in the overall Poisson’s ratio towards −1 is obtained with increasing adhesive ring diameter. As expected, the overall Poisson ratio is influenced by the Poisson’s ratio of the adhesive material, thereby causing an upward or downward shift in the overall Poisson’s ratio arising from the positive or negative sign of the adhesive material’s Poisson’s ratio.
The current findings complement the results of Maksymuk and Shcherbina [6], which conclude that at a constant total thickness of the adhesive block the value of the tangential contact stresses can be regulated (by changing the geometric and physical-mechanical parameters of the layers and adhesive interlayer) in order to increase the rigidity characteristics of composite multilayer cylindrical shells in torsion. While the usual or direct approach for obtaining the effective Poisson’s ratio attempts to apply an axial load on the concentric rod such that the arising interfacial surface gap mismatch is removed by means of geometrical compatibility, the absence of radial change in the torsion of concentric rods circumvents the need for bridging the gap. The advantage of this simplicity, however, renders the current model inaccurate when considering combinations of foam materials with significant differences in their Young’s modulus. Specifically, the imposition of Equations (6) and (16) for the bi-layered and tri-layered rods, respectively, implies that the inner and outer foams must rotate by equal amounts of angle but this is not the case when the torsional stiffness of the inner core and outer shell are significantly different; in addition to φi ≠ φo, an interfacial shear stress acting in the circumferential direction arises. Nevertheless, an accuracy of ±10% is achieved; that is, φi ≈ φo for the case of auxetic core (vi = −0.5) and auxetic shell (vo = −0.5) when 10/11 ≤ Ei/Eo ≤ 10/9 and 30/31 ≤ Ei/Eo ≤ 30/29, respectively.
So far the choice of Poisson’s ratio of foams has been limited to v = ±0.5. For other auxetic-conventional combinations within this range, one may expect the following combination of factors:
- (a)
- less pronounced effective Poisson’s ratio if the magnitudes are equal and less than 0.5,
- (b)
- the outer shell plays a larger role than the inner core in influencing the effective Poisson’s ratio under bending and especially torsion, but is directly proportional to the cross-sectional area for the axial load,
- (c)
- the foam with a larger Poisson’s ratio magnitude will exert a greater effect on the sign of the effective Poisson’s ratio.
4. Conclusions
The effect of adhesive properties on the overall auxeticity of a rod consisting of two concentrically aligned cylindrical isotropic foams with Poisson’s ratio of opposite signs—under torsional loading mode—has been investigated in this paper. Using the mechanics of materials approach, an indirect way for inferring the Poisson’s ratio of a concentrically multi-layered rod was obtained. Results show that the following factors increase the auxeticity of the rod under consideration: (a) adhesive modulus, (b) adhesive Poisson’s ratio, (c) adhesive thickness, and (d) adhesive radius. The plotted results also suggest that, even with each component possessing a Poisson’s ratio not lower than −0.5, the overall Poisson’s ratio within the framework of torsional loading approaches −1 as the outer shell thins. An understanding of the effect of adhesive elastic and geometrical properties of a rod made from concentrically aligned auxetic and conventional foams is useful for designing such rods whenever an adhesive with a large modulus is used for attaching both foams. Further refinements to the current model to cater for considerable differences in the inner and outer foams’ Young’s modulus is suggested for future work.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Ely, J.F.; Zienkiewicz, O.C. Torsion of compound bars—A relaxation solution. Int. J. Mech. Sci. 1960, 1, 356–365. [Google Scholar] [CrossRef]
- Lekhnitskii, S.G. Theory of Elasticity of an Anisotropic Body; Holden-Day: San Francisco, CA, USA, 1963; ISBN 978-071-471-657-2. [Google Scholar]
- Hashin, Z.; Rosen, B.W. The elastic moduli of fiber-reinforced materials. J. Appl. Mech. 1964, 31, 223–232. [Google Scholar] [CrossRef]
- Packham, B.A.; Shail, R. St. Venant torsion of composite cylinders. J. Elast. 1978, 8, 393–407. [Google Scholar] [CrossRef]
- Tsukrov, I.; Drach, B. Elastic deformation of composite cylinders with cylindrically orthotropic layers. Int. J. Solids Struct. 2010, 47, 25–33. [Google Scholar] [CrossRef]
- Maksymuk, A.V.; Shcherbina, N.N. Torsion of laminated cylindrical shells with adhesive interlayers. Mech. Compos. Mater. 1998, 34, 363–368. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, C.L. Magnetoelectric effect in a circumferentially polarized composite cylinder. Smart Mater. Struct. 2013, 22, 105018. [Google Scholar] [CrossRef]
- Levin, V.A.; Zubov, L.M.; Zingerman, K.M. The torsion of a composite, nonlinear-elastic cylinder with an inclusion having initial large strains. Int. J. Solids Struct. 2014, 51, 1403–1409. [Google Scholar] [CrossRef]
- Lakes, R. Foam structures with negative Poisson’s ratio. Science 1987, 235, 1038–1040. [Google Scholar] [CrossRef] [PubMed]
- Lakes, R. Negative Poisson’s ratio materials. Science 1987, 238, 551. [Google Scholar] [CrossRef] [PubMed]
- Popereka, M.Y.A.; Balagurov, V.G. Ferromagnetic films having a negative Poisson ratio. Fiz. Tverd. Tela 1969, 11, 3507–3513. [Google Scholar]
- Milstein, F.; Huang, K. Existence of a negative Poisson ratio in fcc crystals. Phys. Rev. B 1979, 19, 2030–2033. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F.; Schajer, G.S.; Robertson, C.I. The mechanics of two-dimensional cellular materials. Proc. R. Soc. Lond. A 1982, 382, 25–42. [Google Scholar] [CrossRef]
- Almgren, R.F. An isotropic three-dimensional structure with Poisson’s ratio = −1. J. Elast. 1985, 15, 427–430. [Google Scholar]
- Kolpakov, A.G. The determination of averaged characteristics for elastic skeletons. Prikl. Mat. Mekh. 1985, 49, 969–977. [Google Scholar]
- Wojciechowski, K.W. Constant thermodynamic tension Monte-Carlo studies of elastic properties of a two-dimensional system of hard cyclic hexamers. Mol. Phys. 1987, 61, 1247–1258. [Google Scholar] [CrossRef]
- Wojciechowski, K.W. Two-dimensional isotropic system with a negative Poisson ratio. Phys. Lett. A 1989, 137, 60–64. [Google Scholar] [CrossRef]
- Wojciechowski, K.W.; Branka, A.C. Negative Poisson ratio in a two-dimensional ‘‘isotropic’’ solid. Phys. Rev. A 1989, 40, 7222–7225. [Google Scholar] [CrossRef]
- Choi, J.B.; Lakes, R.S. Design of a fastener based on negative Poisson’s ratio foam. Cell. Polym. 1991, 10, 205–212. [Google Scholar]
- Caddock, B.D.; Evans, K.E. Negative Poisson ratios and strain-dependent mechanical properties in arterial prostheses. Biomaterials 1995, 16, 1109–1115. [Google Scholar] [CrossRef]
- Martz, E.O.; Lakes, R.S.; Goel, V.K.; Park, J.B. Design of an artificial intervertebral disc exhibiting a negative Poisson’s ratio. Cell. Polym. 2005, 24, 127–138. [Google Scholar]
- Dolla, W.J.S.; Fricke, B.A.; Becker, B.R. Structural and drug diffusion models of conventional and auxetic drug-eluting stents. J. Med. Dev. 2007, 1, 47–55. [Google Scholar] [CrossRef]
- Scarpa, F. Auxetic materials for bioprostheses. IEEE Signal Process. Mag. 2008, 25, 125–126. [Google Scholar] [CrossRef]
- Lakes, R.S.; Lowe, A. Negative Poisson’s ratio foam as seat cushion material. Cell. Polym. 2000, 19, 157–167. [Google Scholar]
- Wang, Y.C.; Lakes, R.S. Analytical parametric analysis of the contact problem of human buttocks and negative Poisson’s ratio foam cushions. Int. J. Solids Struct. 2002, 39, 4825–4838. [Google Scholar] [CrossRef]
- Alderson, A.; Rasburn, J.; Ameer-Bag, S.; Mullarkey, P.G.; Perrie, W.; Evans, K.E. An auxetic filter: A tuneable filter displaying enhanced size selectivity or defouling properties. Ind. Eng. Chem. Res. 2000, 39, 654–655. [Google Scholar] [CrossRef]
- Alderson, A.; Davies, P.J.; Evans, K.E.; Alderson, K.L.; Grima, J.N. Modelling of the mechanical and mass transport properties of auxetic molecular sieves: An idealised inorganic (zeolitic) host-guest system. Mol. Simul. 2005, 31, 889–896. [Google Scholar] [CrossRef]
- Alderson, A.; Davies, P.J.; Williams, M.R.; Evans, K.E.; Alderson, K.L.; Grima, J.N. Modelling of the mechanical and mass transport properties of auxetic molecular sieves: An idealised organic (polymeric honeycomb) host-guest system. Mol. Simul. 2005, 31, 897–905. [Google Scholar] [CrossRef]
- Lim, T.C.; Acharya, R.U. Performance Evaluation of Auxetic Molecular Sieves with Re-Entrant Structures. J. Biomed. Nanotechnol. 2010, 6, 718–724. [Google Scholar] [CrossRef] [PubMed]
- Scarpa, F.; Giacomin, J.; Zhang, Y.; Pastorino, P. Mechanical performance of auxetic polyurethane foam for antivibration glove applications. Cell. Polym. 2005, 24, 253–268. [Google Scholar]
- Alderson, A.; Alderson, K.L. Expanding materials and applications: Exploiting auxetic textiles. Tech. Text. Int. 2005, 14, 29–34. [Google Scholar]
- Park, K.O.; Choi, J.B.; Lee, S.J.; Choi, H.H.; Kim, J.K. Polyurethane foam with Negative Poisson’s ratio for diabetic shoe. Key Eng. Mater. 2005, 288–289, 677–680. [Google Scholar] [CrossRef]
- Ellul, B.; Muscat, M.; Grima, J.N. On the effect of the Poisson’s ratio (positive and negative) on the stability of pressure vessel heads. Phys. Status Solidi B 2009, 246, 2025–2032. [Google Scholar] [CrossRef]
- Salit, V.; Weller, T. On the feasibility of introducing auxetic behavior into thin-walled structures. Acta Mater. 2009, 57, 125–135. [Google Scholar] [CrossRef]
- Whitty, J.P.M.; Henderson, B.; Myler, P.; Chirwa, C. Crash performance of cellular foams with reduced relative density part 2: Rib deletion. Int. J. Crashworthiness 2007, 12, 689–698. [Google Scholar]
- Park, K.O.; Choi, J.B.; Park, J.C.; Park, D.J.; Kim, J.K. An improvement in shock absorbing behavior of polyurethane foam with a negative Poisson effect. Key Eng. Mater. 2007, 342–343, 845–848. [Google Scholar] [CrossRef]
- Lim, T.C. Auxetic Materials and Structures; Springer: Singapore, 2015; ISBN 978-981-287-274-6. [Google Scholar]
- Wojciechowski, K.W.; Scarpa, F.; Grima, J.N.; Alderson, A. Auxetics and other systems of anomalous characteristics. Phys. Status Solidi B 2017, 254, 1770266. [Google Scholar] [CrossRef]
- Lim, T.C. 2D structures exhibiting negative area compressibility. Phys. Status Solidi B 2017, 254, 1600682. [Google Scholar] [CrossRef]
- Lim, T.C. Auxetic and negative thermal expansion structure based on interconnected array of rings and sliding rods. Phys. Status Solidi B 2017, 254, 1600775. [Google Scholar] [CrossRef]
- Lim, T.C. An accurate design equation for the maximum deflection in a class of auxetic sectorial plates. Phys. Status Solidi B 2017, 254, 1600784. [Google Scholar] [CrossRef]
- Lim, T.C. Shear deformation in a class of thick hexagonal plates. Phys. Status Solidi B 2017, 254, 1700014. [Google Scholar] [CrossRef]
- Jiang, L.; Hu, H. Finite element modeling of multilayer orthogonal auxetic composites under low-velocity impact. Materials 2017, 10, 908. [Google Scholar] [CrossRef] [PubMed]
- Wormser, M.; Wein, F.; Stingl, M.; Körner, C. Design and additive manufacturing of 3D phononic band gap structures based on gradient based optimization. Materials 2017, 10, 1125. [Google Scholar] [CrossRef] [PubMed]
- Czarnecki, S.; Łukasiak, T.; Lewiński, T. The isotropic and cubic material designs. Recovery of the underlying microstructures appearing in the least compliant continuum bodies. Materials 2017, 10, 1137. [Google Scholar] [CrossRef] [PubMed]
- Pigłowski, P.M.; Narojczyk, J.W.; Poźniak, A.A.; Wojciechowski, K.W.; Tretiakov, K.V. Auxeticity of Yukawa systems with nanolayers in the (111) crystallographic plane. Materials 2017, 10, 1338. [Google Scholar] [CrossRef] [PubMed]
- Jopek, H. Finite element analysis of tunable composite tubes reinforced with auxetic structures. Materials 2017, 10, 1359. [Google Scholar] [CrossRef] [PubMed]
- Strek, T.; Jopek, H.; Idczak, E.; Wojciechowski, K.W. Computational modelling of structures with non-intuitive behavior. Materials 2017, 10, 1386. [Google Scholar] [CrossRef] [PubMed]
- Lim, T.C. Functionally graded beam for attaining Poisson-curving. J. Mater. Sci. Lett. 2002, 21, 1899–1901. [Google Scholar] [CrossRef]
- Gatt, R.; Attard, D.; Grima, J.N. On the behaviour of bi-material strips when subjected to changes in external hydrostatic pressure. Scr. Mater. 2009, 60, 65–67. [Google Scholar] [CrossRef]
- Lim, T.C. On simultaneous positive and negative Poisson’s ratio laminates. Phys. Status Solidi B 2007, 244, 910–918. [Google Scholar] [CrossRef]
- Lim, T.C. Mixed auxeticity of auxetic sandwich structures. Phys. Status Solidi B 2012, 249, 1366–1372. [Google Scholar] [CrossRef]
- Donescu, S.; Chiroiu, V.; Munteanu, L. On the Young’s modulus of a auxetic composite structure. Mech. Res. Commun. 2009, 36, 294–301. [Google Scholar] [CrossRef]
- Kocer, C.; McKenzie, D.R.; Bilek, M.M. Elastic properties of a material composed of alternating layers of negative and positive Poisson’s ratio. Mater. Sci. Eng. A 2009, 505, 111–115. [Google Scholar] [CrossRef]
- Lim, T.C. Out-of-plane modulus of semi-auxetic laminates. Eur. J. Mech. A Solids 2009, 28, 752–756. [Google Scholar] [CrossRef]
- Chirima, G.T.; Zied, K.M.; Ravirala, N.; Alderson, K.L.; Alderson, A. Numerical and analytical modelling of multi-layer adhesive–film interface systems. Phys. Status Solidi B 2009, 246, 2072–2082. [Google Scholar] [CrossRef]
- Lim, T.C. In-plane stiffness of semiauxetic laminates. J. Eng. Mech. 2010, 136, 1176–1180. [Google Scholar] [CrossRef]
- Lim, T.C.; Rajendra Acharya, U. Counterintuitive modulus from semi-auxetic laminates. Phys. Status Solidi B 2011, 248, 60–65. [Google Scholar] [CrossRef]
- Grima, J.N.; Oliveri, L.; Ellul, B.; Gatt, R.; Attard, D.; Cicala, G.; Recca, G. Adjustable and negative thermal expansion from multilayered systems. Phys. Status Solidi Rapid Res. Lett. 2010, 4, 133–135. [Google Scholar] [CrossRef]
- Lim, T.C. Coefficient of thermal expansion of stacked auxetic and negative thermal expansion laminates. Phys. Status Solidi B 2011, 248, 140–147. [Google Scholar] [CrossRef]
- Lim, T.C.; Acharya, U.R. Longitudinal modulus of semi-auxetic unidirectional fiber composites. J. Reinf. Plast. Compos. 2010, 29, 1441–1445. [Google Scholar] [CrossRef]
- Lim, T.C. Torsion of semi-auxetic rods. J. Mater. Sci. 2011, 46, 6904–6909. [Google Scholar] [CrossRef]
- Strek, T.; Jopek, H. Effective mechanical properties of concentric cylindrical composites with auxetic phase. Phys. Status Solidi B 2012, 249, 1359–1365. [Google Scholar] [CrossRef]
- Strek, T.; Jopek, H.; Fraska, A. Torsion of elliptical composite beams with auxetic phase. Phys. Status Solidi B 2016, 253, 1359–1368. [Google Scholar] [CrossRef]
- Jopek, H.; Strek, T. Torsion of a two-phased composite bar with helical distribution of constituents. Phys. Status Solidi B 2017, 254, 1700050. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).