An Improved Multi-Relaxation Time Lattice Boltzmann Method for the Non-Newtonian Influence of the Yielding Fluid Flow in Cement-3D Printing
Abstract
:1. Introduction
2. Improved MRT-LBM for Yielding Fluids
2.1. Rheological Equation of Yielding Fluids
2.2. Improved MRT-LBM
- (1)
- Conduct the physical transformation according to the dimension theory. The Reynolds number is taken as the key criteria, and then the other parameters used in simulation can be obtained.
- (2)
- Set the simulation domain and initial conditions, especially the initial value of the factor s8.
- (3)
- Calculate the equilibrium distribution function according to Equation (5).
- (4)
- Conduct the collision step, where the specific function is shown as:where ϱ(r,t) = Mf(r,t), ϱeq(r,t) = Mfeq(r,t), and the force term is mainly used to explain the non-Newtonian effect of yielding fluids. The calculations can be seen in Equations (15), (16), and (19).
- (5)
- Calculate the strain rate tensor and shearing rate by using Equations (11)–(13), then the kinetic viscosity can be obtained using Equation (3) and the relaxation factor s8 will be updated.
- (6)
- Conduct the streaming step, where the streaming function is shown as:
- (7)
- Process the boundary condition, where the non-equilibrium bounce-back scheme is taken as the boundary method.
- (8)
- Conduct the next calculation from Step (3).
- (9)
- Calculate the density and velocity, where the corresponding equations are:
3. Flow Analysis for the Mixture Fluids in Cement-3D Printing
3.1. Rheological Equation of Fluids
3.2. Structure of Extruding Head
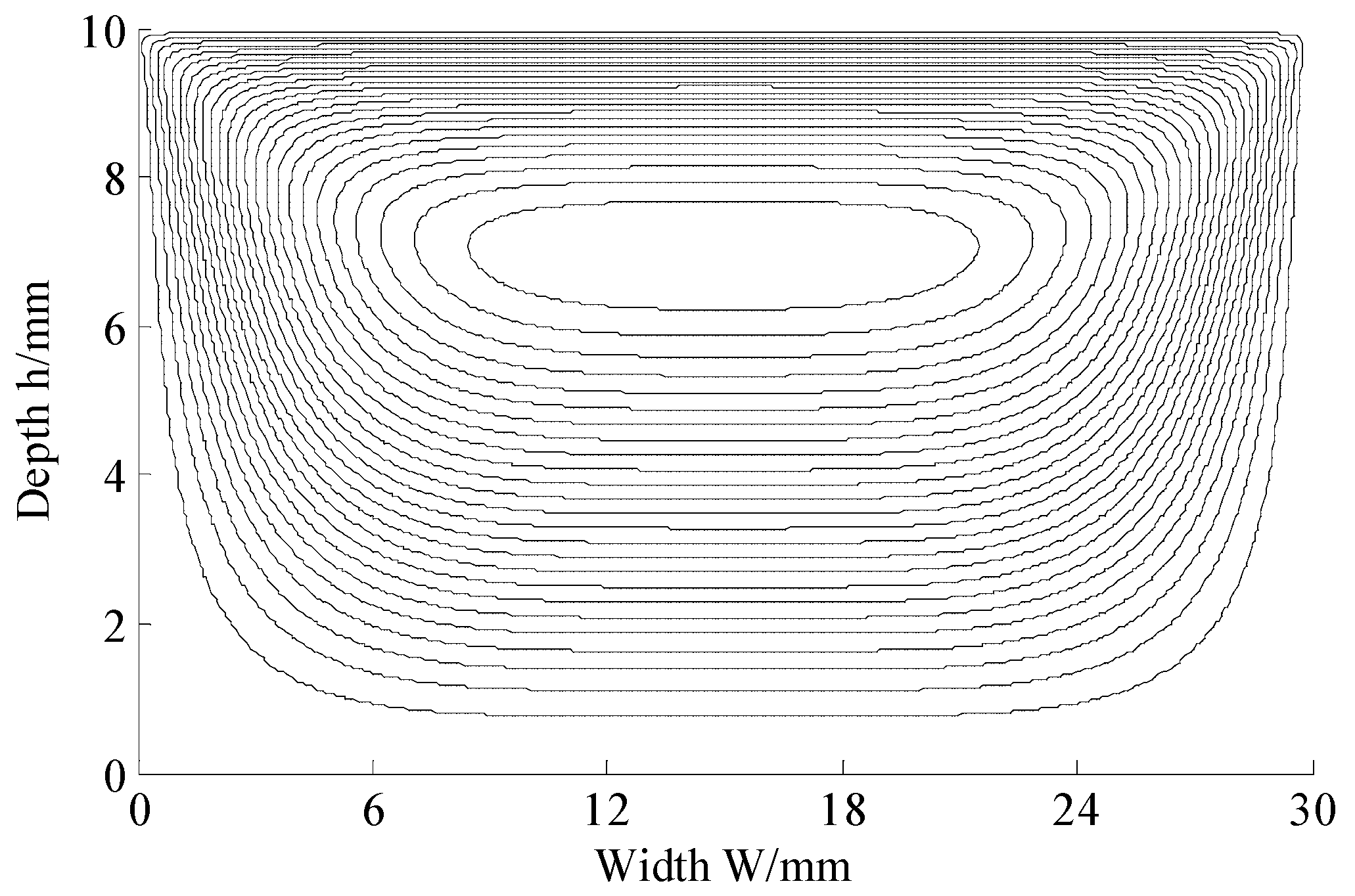
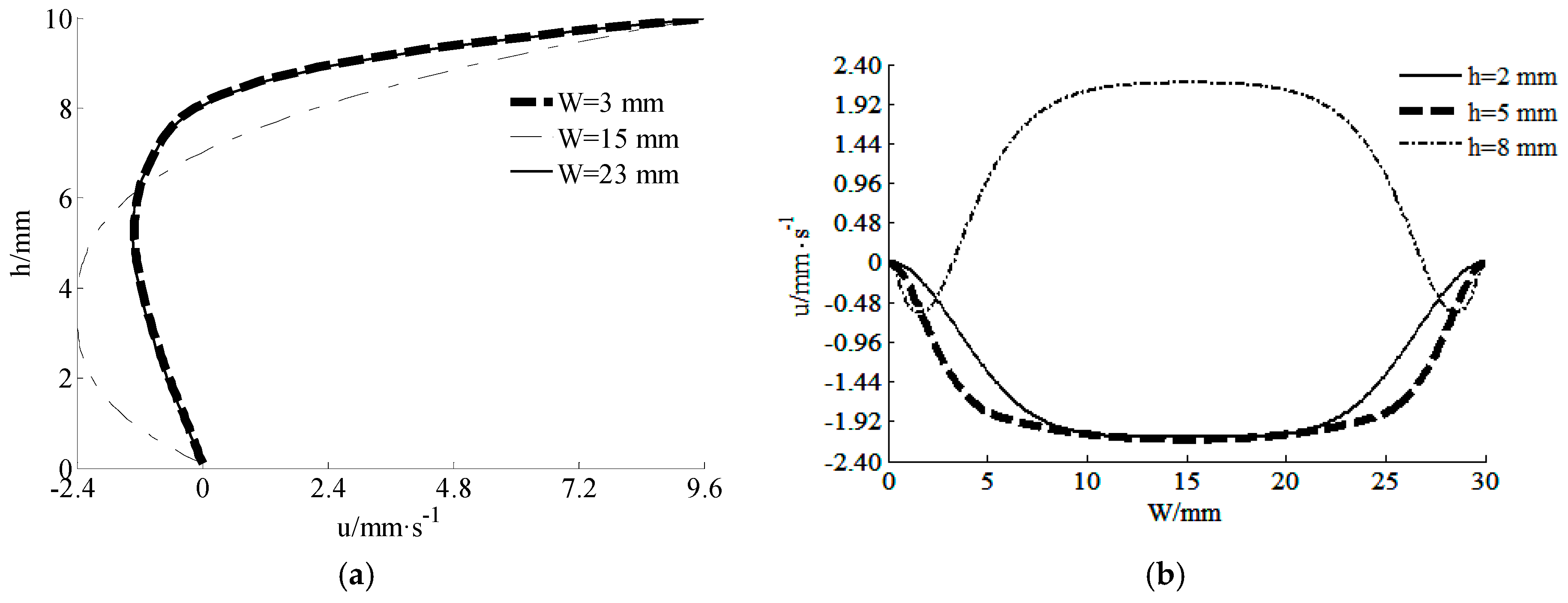
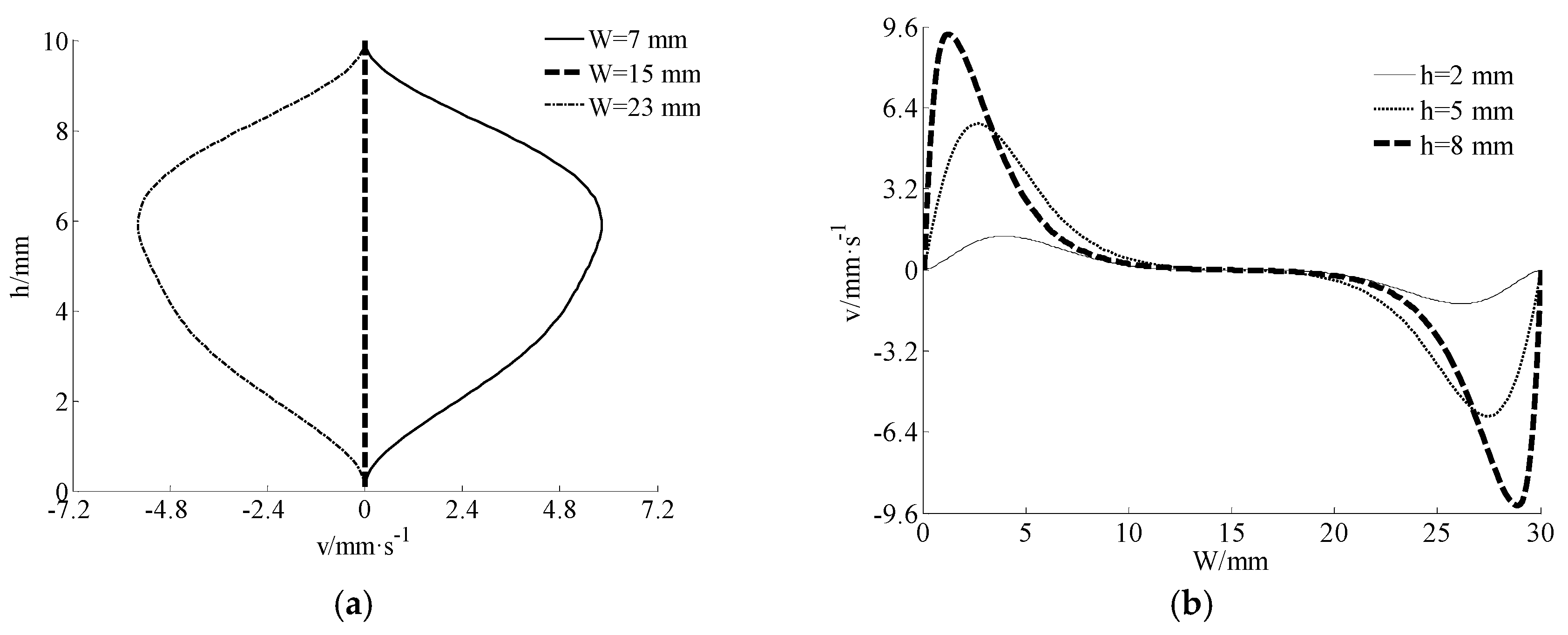
3.3. Flow Simulation using Improved MRT-LBM
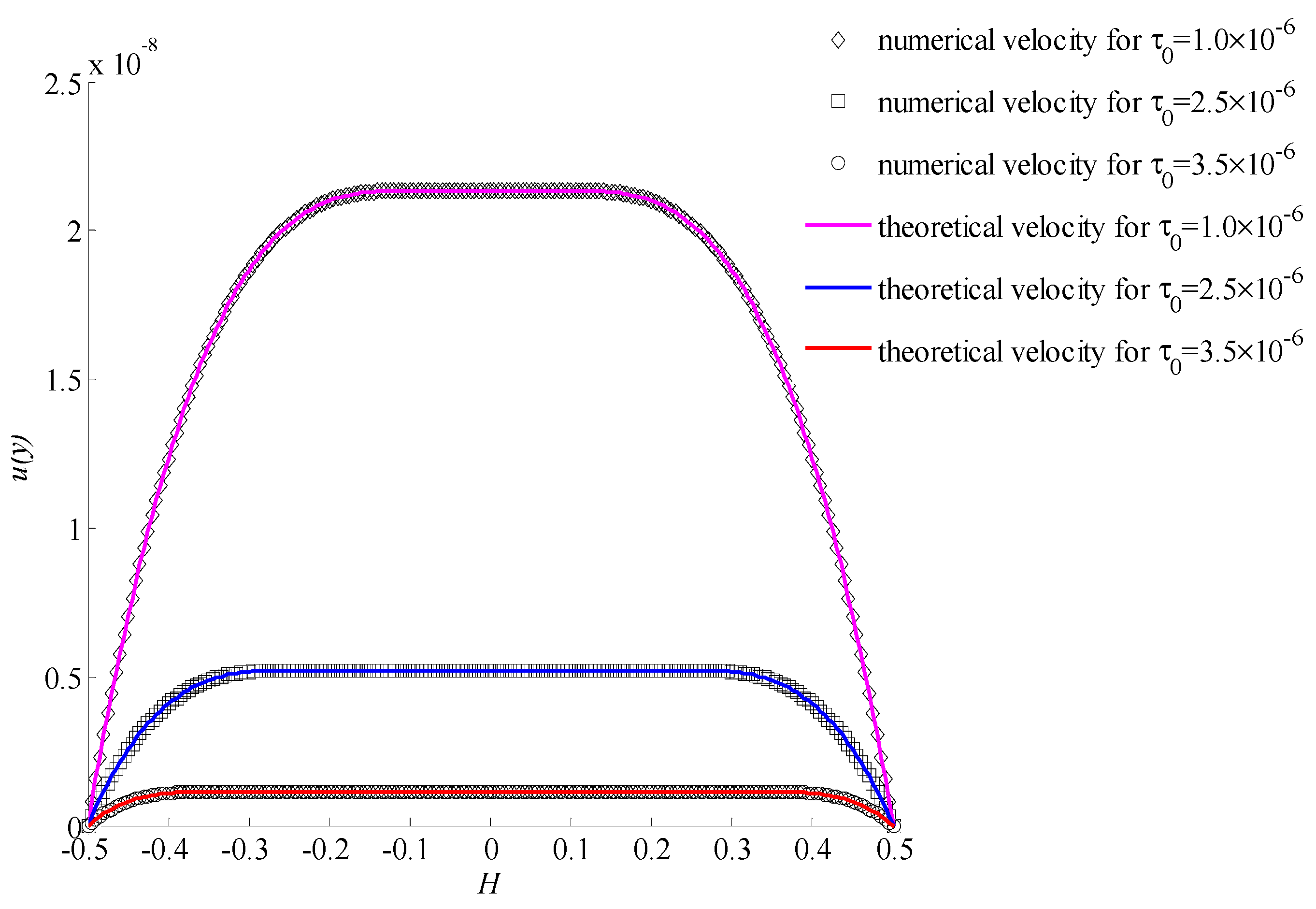
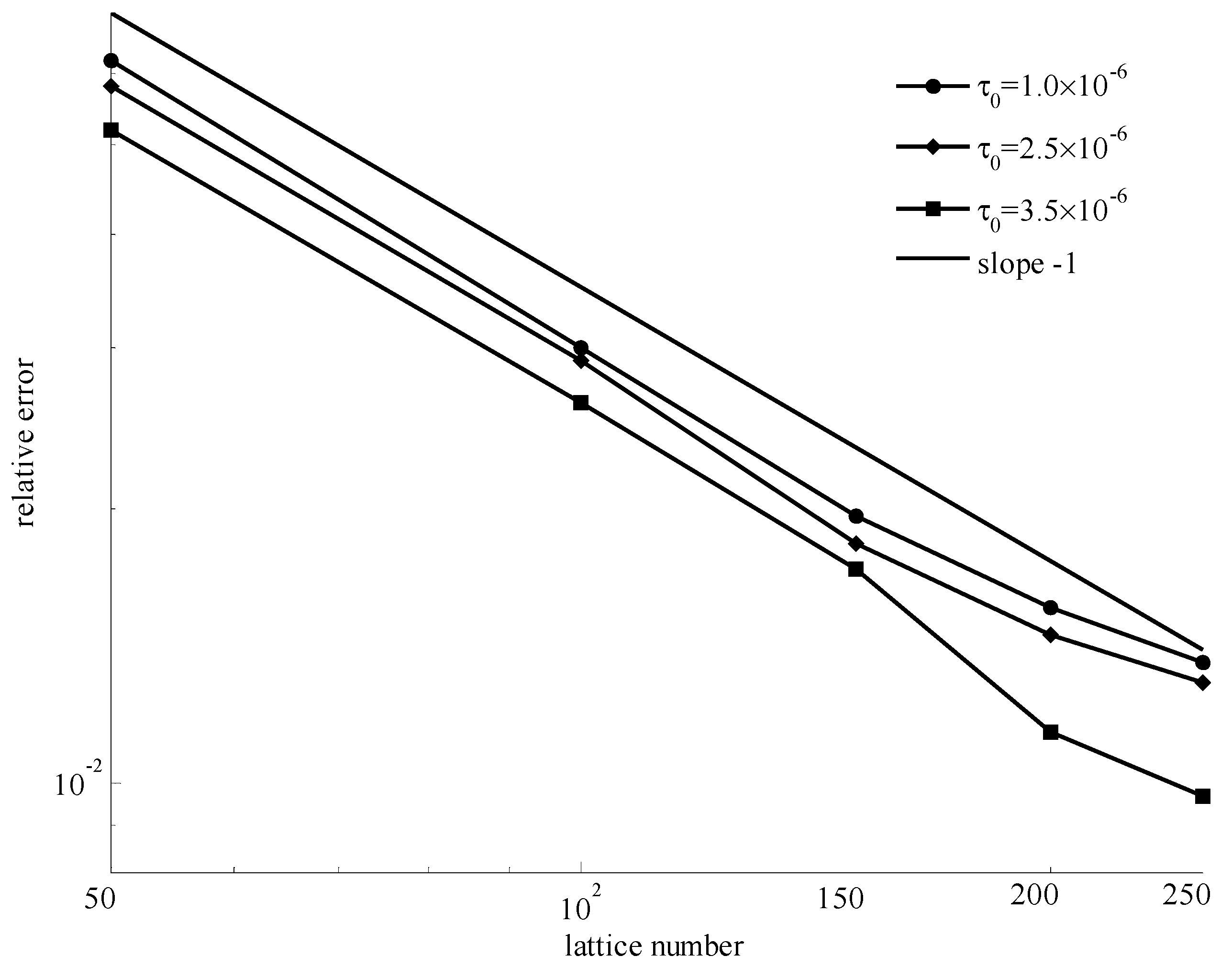
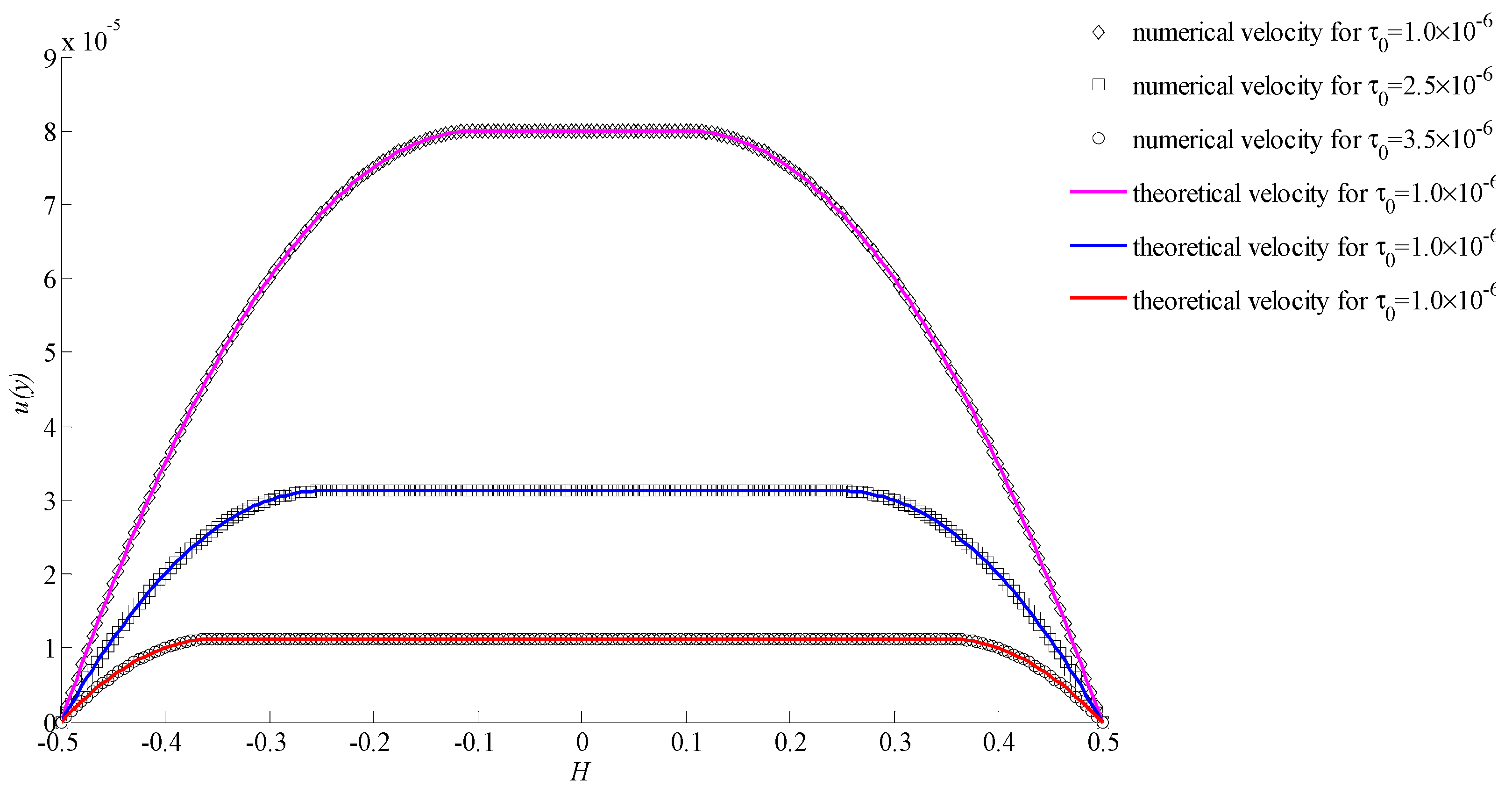
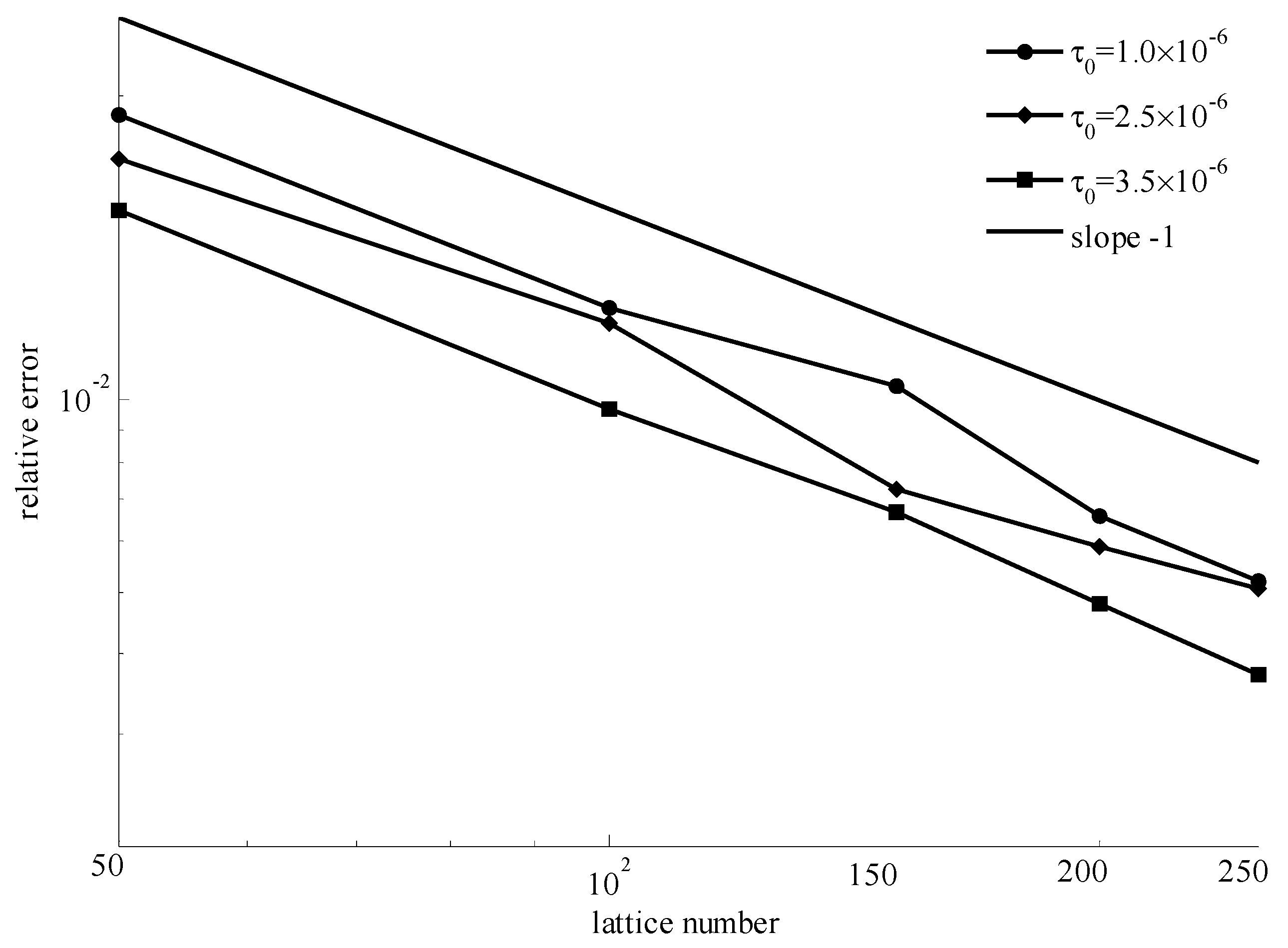
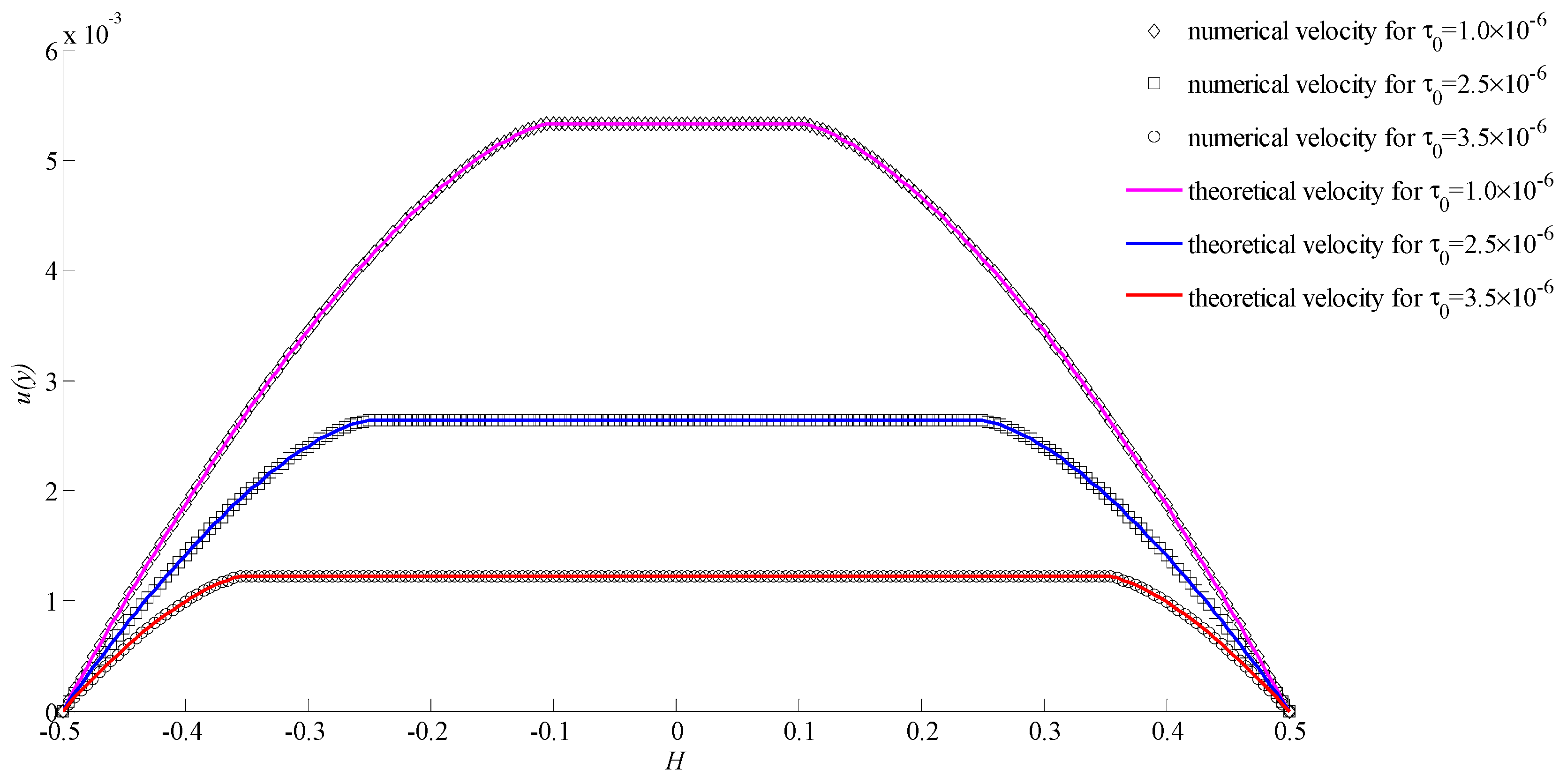
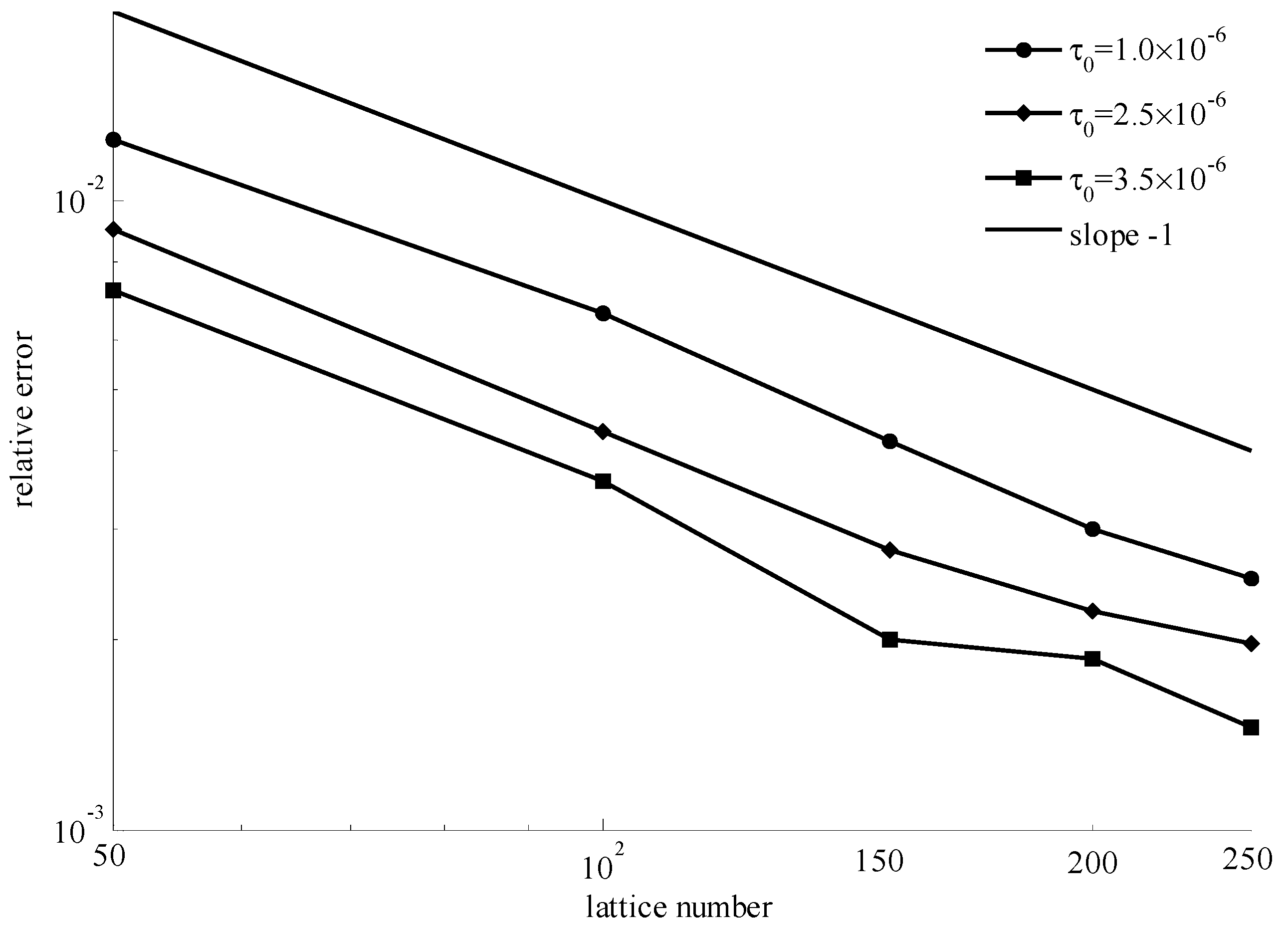
4. Validation and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bassoli, E.; Gatto, A.; Iuliano, L.; Grazia Violante, M. 3D printing technique applied to rapid casting. Rapid Prototyp. J. 2007, 13, 148–155. [Google Scholar] [CrossRef]
- Zhu, W.; Ma, X.; Gou, M.; Mei, D.; Zhang, K.; Chen, S. 3D printing of functional biomaterials for tissue engineering. Curr. Opin. Biotechnol. 2016, 40, 103–112. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Michalski, M.H.; Ross, J.S. The shape of things to come: 3D printing in medicine. JAMA 2014, 312, 2213–2214. [Google Scholar] [CrossRef] [PubMed]
- Ladd, C.; So, J.H.; Muth, J.; Dickey, M.D. 3D Printing of Free Standing Liquid Metal Microstructures. Adv. Mater. 2013, 25, 5081–5085. [Google Scholar] [CrossRef] [PubMed]
- Zeng, G.; Han, Z.; Liang, S. The applications and progress of manufacturing of metal parts by 3D printing technology. Mater. China 2014, 33, 376–382. [Google Scholar]
- Tay, Y.W.D.; Panda, B.; Paul, S.C.; Noor Mohamed, N.A.; Tan, M.J.; Leong, K.F. 3D printing trends in building and construction industry: A review. Virtual Phys. Prototyp. 2017, 12, 1–16. [Google Scholar] [CrossRef]
- Bos, F.; Wolfs, R.; Ahmed, Z.; Salet, T. Additive manufacturing of concrete in construction: potentials and challenges of 3D concrete printing. Virtual Phys. Prototyp 2016, 11, 209–225. [Google Scholar] [CrossRef]
- Xia, M.; Sanjayan, J. Method of formulating geopolymer for 3D printing for construction applications. Mater. Des. 2016, 110, 382–390. [Google Scholar] [CrossRef]
- Tay, Y.W.; Panda, B.; Paul, S.C.; Tan, M.J.; Qian, S.Z.; Leong, K.F.; Chua, C.K. Processing and properties of construction materials for 3D printing. Mater. Sci. Forum 2016, 861, 177–181. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Gorji-Bandpy, M.; Seyyedi, S.M.; Ganji, D.D.; Rokni, H.B.; Soleimani, S. Application of LBM in simulation of natural convection in a nanofluid filled square cavity with curve boundaries. Powder Technol. 2013, 247, 87–94. [Google Scholar] [CrossRef]
- Hou, S.; Zou, Q.; Chen, S.; Doolen, G.; Cogley, A.C. Simulation of cavity flow by the lattice Boltzmann method. J. Comput. Phys. 1995, 118, 329–347. [Google Scholar] [CrossRef]
- He, X.; Doolen, G. Lattice Boltzmann method on curvilinear coordinates system: Flow around a circular cylinder. J. Comput. Phys. 1997, 134, 306–315. [Google Scholar] [CrossRef]
- Gao, W.; Wang, J. Similarity solutions to the power-law generalized Newtonian fluid. J. Comput. Appl. Math. 2008, 222, 381–391. [Google Scholar] [CrossRef]
- Keslerová, R.; Kozel, K. Numerical study of steady and unsteady flow for power-law type generalized Newtonian fluids. Computing 2013, 95, 409–424. [Google Scholar] [CrossRef]
- Bulíček, M.; Pustějovská, P. On existence analysis of steady flows of generalized Newtonian fluids with concentration dependent power-law index. J. Math. Anal. Appl. 2013, 402, 157–166. [Google Scholar] [CrossRef]
- Sochi, T. Further validation to the variational method to obtain flow relations for generalized Newtonian fluids. Korea Aust. Rheol. J. 2015, 27, 113–124. [Google Scholar] [CrossRef] [Green Version]
- Niu, X.D.; Shu, C.; Chew, Y.T. Investigation of stability and hydrodynamics of different lattice Boltzmann models. J. Stat. Phys. 2004, 117, 665–680. [Google Scholar] [CrossRef]
- Gabbanelli, S.; Drazer, G.; Koplik, J. Lattice Boltzmann method for non-Newtonian (power-law) fluids. Phys. Rev. E 2005, 72, 046312. [Google Scholar] [CrossRef] [PubMed]
- Boyd, J.; Buick, J.; Green, S. A second-order accurate lattice Boltzmann non-Newtonian flow model. J. Phys. A Math. Gen. 2006, 39, 14241–14247. [Google Scholar] [CrossRef] [Green Version]
- Nejat, A.; Abdollahi, V.; Vahidkhah, K. Lattice Boltzmann simulation of non-Newtonian flows past confined cylinders. J. Nonnewton. Fluid Mech. 2011, 166, 689–697. [Google Scholar] [CrossRef]
- Orestis, M.; Guy, C.; Michel, D. Simulation of generalized Newtonian fluids with the lattice Boltzmann method. Int. J. Mod. Phys. C 2007, 18, 1939–1949. [Google Scholar]
- Tang, G.H.; Wang, S.B.; Ye, P.X.; Tao, W.Q. Bingham fluid simulation with the incompressible lattice Boltzmann model. J. Nonnewton. Fluid Mech. 2011, 166, 145–151. [Google Scholar] [CrossRef]
- Chen, S.; Sun, Q.; Jin, F.; Liu, J. Simulations of Bingham plastic flows with the multiple-relaxation-time lattice Boltzmann model. Sci. China Phys. Mech. Astron. 2014, 57, 532–540. [Google Scholar] [CrossRef]
- Wu, W.; Huang, X.; Yuan, H.; Xu, F.; Ma, J. A modified lattice boltzmann method for herschel-bulkley fluids. Rheol. Acta 2017, 56, 369–376. [Google Scholar] [CrossRef]
- Wu, W.; Huang, X.; Fang, C.; Gao, Y. An improved MRT-LBM for Herschel–Bulkley fluids with high Reynolds number. Numer. Heat Transfer 2017, 72, 409–420. [Google Scholar] [CrossRef]
- Papanastasiou, T.C.; Boudouvis, A.G. Flows of viscoplastic materials: models and computations. Comput. Struct. 1997, 64, 677–694. [Google Scholar] [CrossRef]
- Chai, Z.; Zhao, T.S. Effect of the forcing term in the multiple-relaxation-time lattice Boltzmann equation on the shear stress or the strain rate tensor. Phys. Rev. E 2012, 86, 016705. [Google Scholar] [CrossRef] [PubMed]
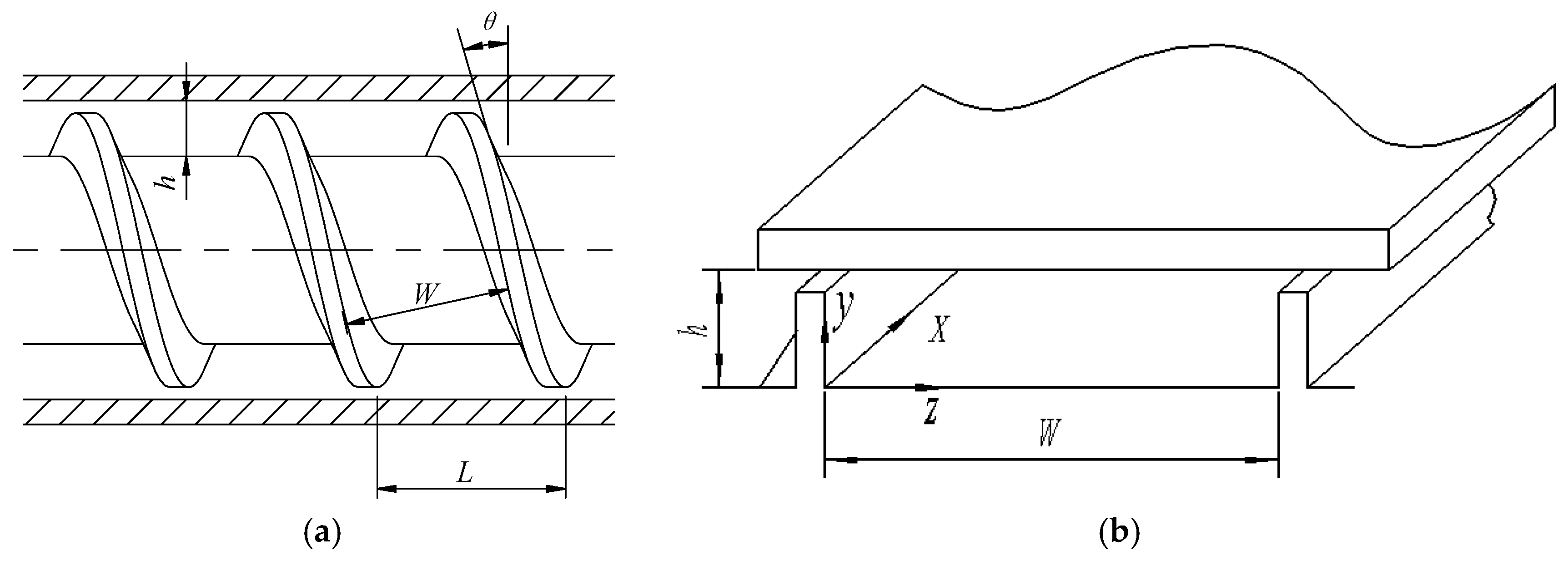
| Factor | Meaning | Value |
|---|---|---|
| W | the width of the channel | 30 mm |
| h | the depth of the channel | 10 mm |
| θ | angle of lead | 20° |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, T.; Gu, H.; Zhang, J.; Li, B.; Sun, J.; Wu, W. An Improved Multi-Relaxation Time Lattice Boltzmann Method for the Non-Newtonian Influence of the Yielding Fluid Flow in Cement-3D Printing. Materials 2018, 11, 2342. https://doi.org/10.3390/ma11112342
Huang T, Gu H, Zhang J, Li B, Sun J, Wu W. An Improved Multi-Relaxation Time Lattice Boltzmann Method for the Non-Newtonian Influence of the Yielding Fluid Flow in Cement-3D Printing. Materials. 2018; 11(11):2342. https://doi.org/10.3390/ma11112342
Chicago/Turabian StyleHuang, Tiancheng, Hai Gu, Jie Zhang, Bin Li, Jianhua Sun, and Weiwei Wu. 2018. "An Improved Multi-Relaxation Time Lattice Boltzmann Method for the Non-Newtonian Influence of the Yielding Fluid Flow in Cement-3D Printing" Materials 11, no. 11: 2342. https://doi.org/10.3390/ma11112342
APA StyleHuang, T., Gu, H., Zhang, J., Li, B., Sun, J., & Wu, W. (2018). An Improved Multi-Relaxation Time Lattice Boltzmann Method for the Non-Newtonian Influence of the Yielding Fluid Flow in Cement-3D Printing. Materials, 11(11), 2342. https://doi.org/10.3390/ma11112342




