Deformation and Failure Behavior of Wooden Sandwich Composites with Taiji Honeycomb Core under a Three-Point Bending Test
Abstract
:1. Introduction
2. Experiments
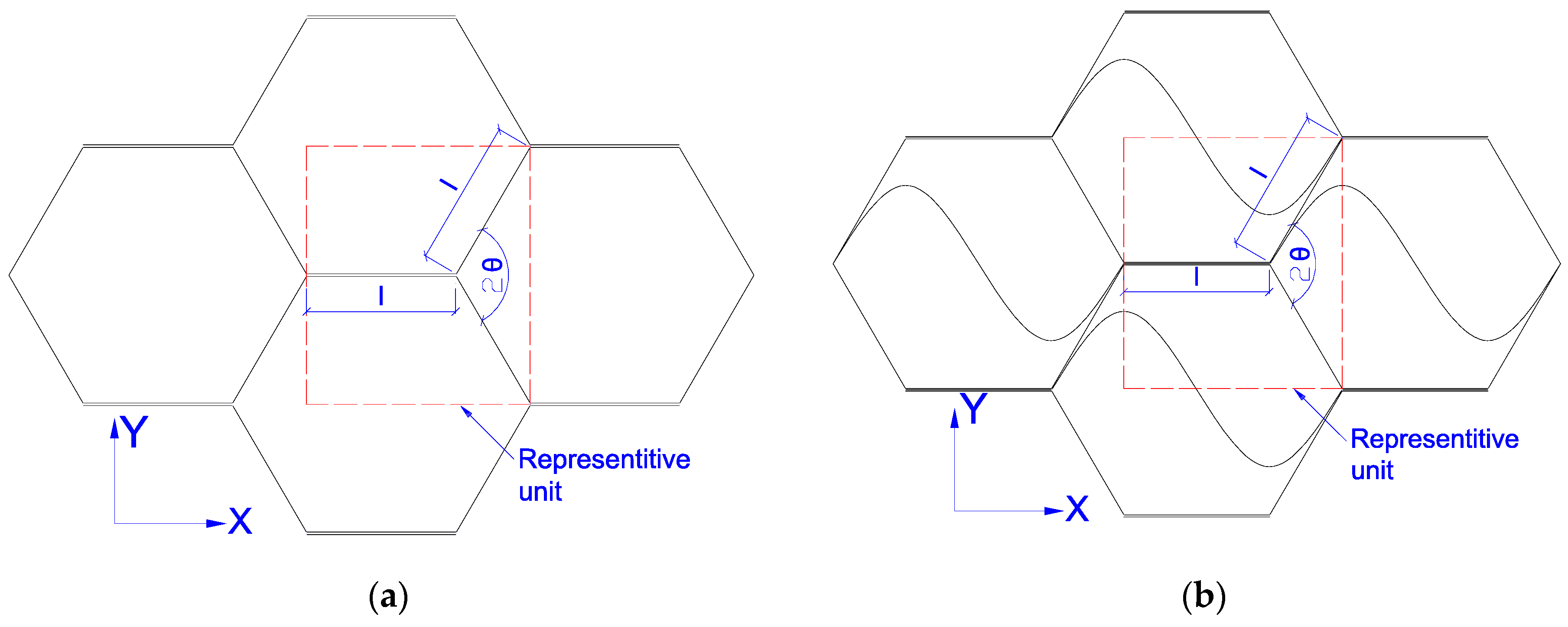
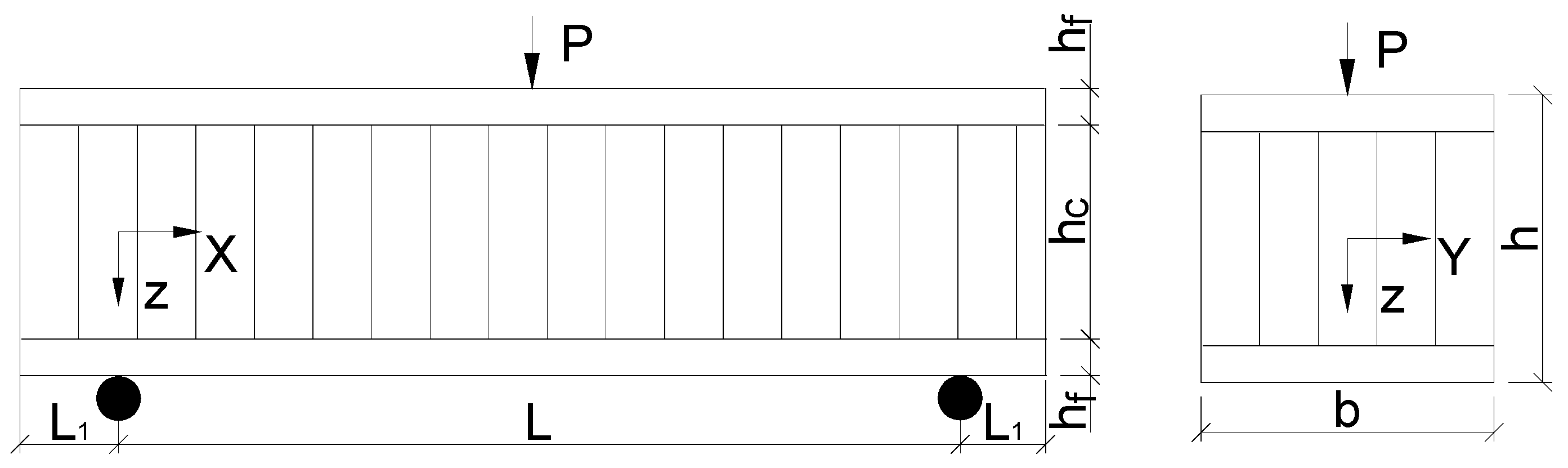
2.1. Composite Design
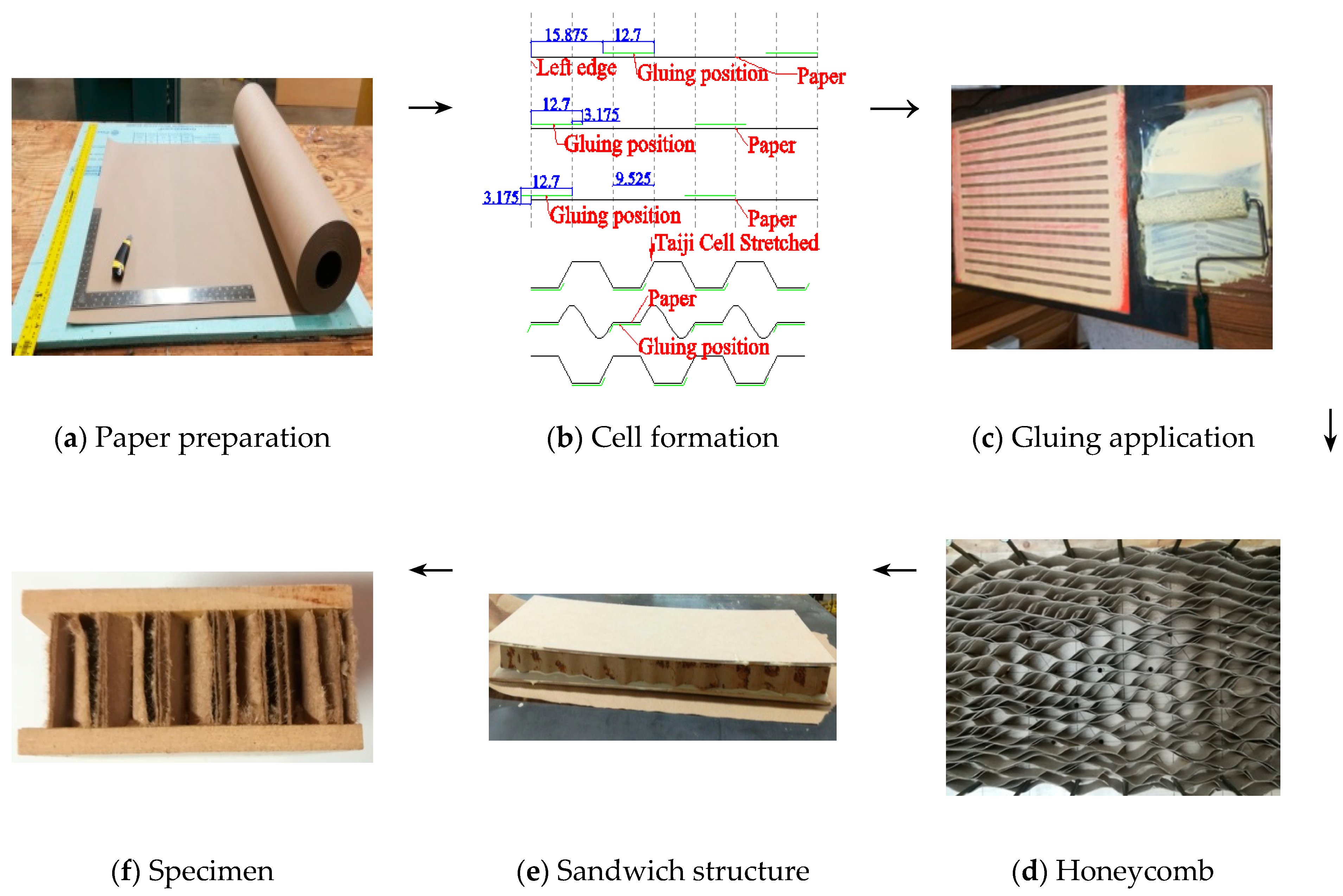
2.2. Specimen Fabrication
2.3. Test Methods
3. Result and Discuss
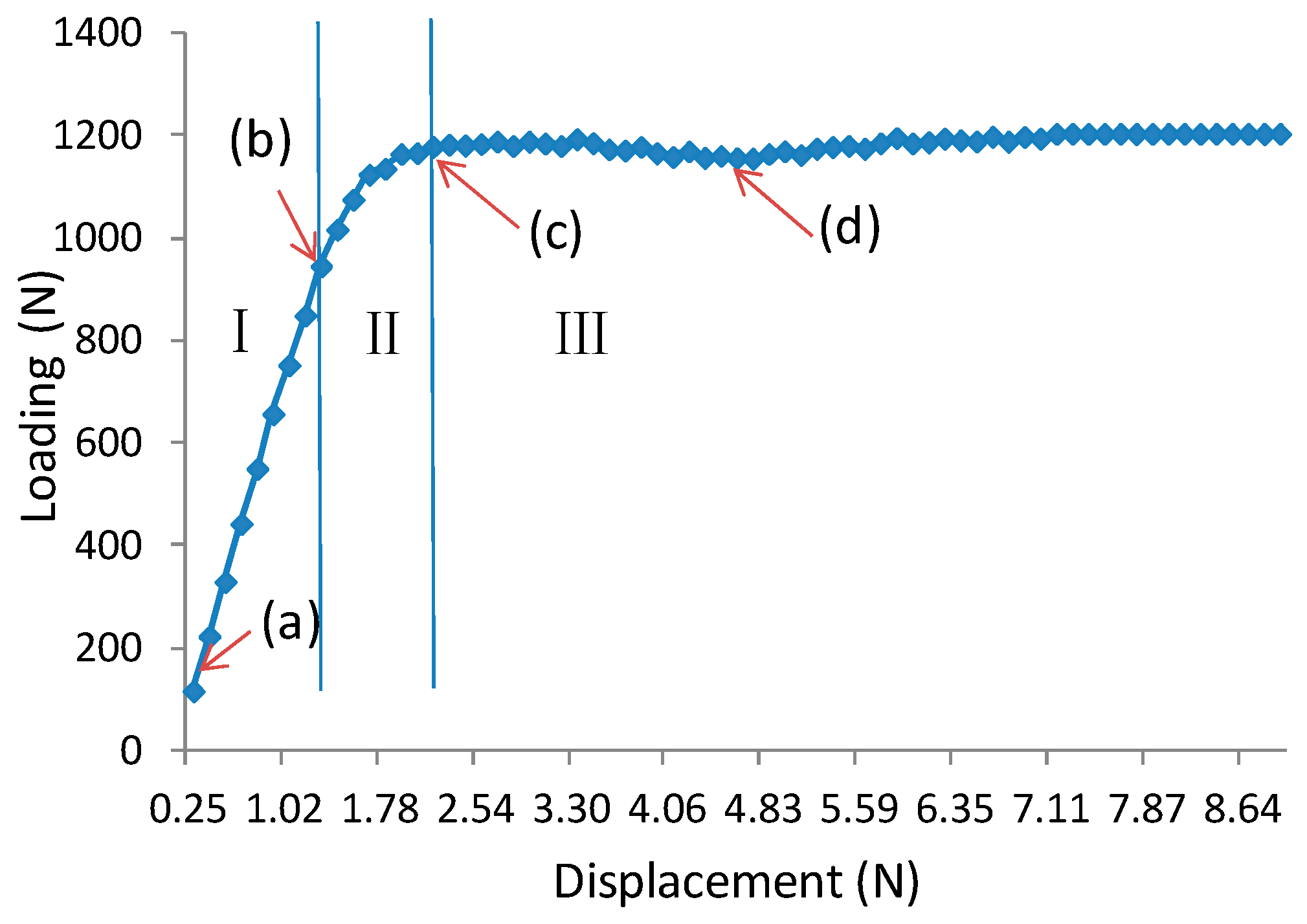
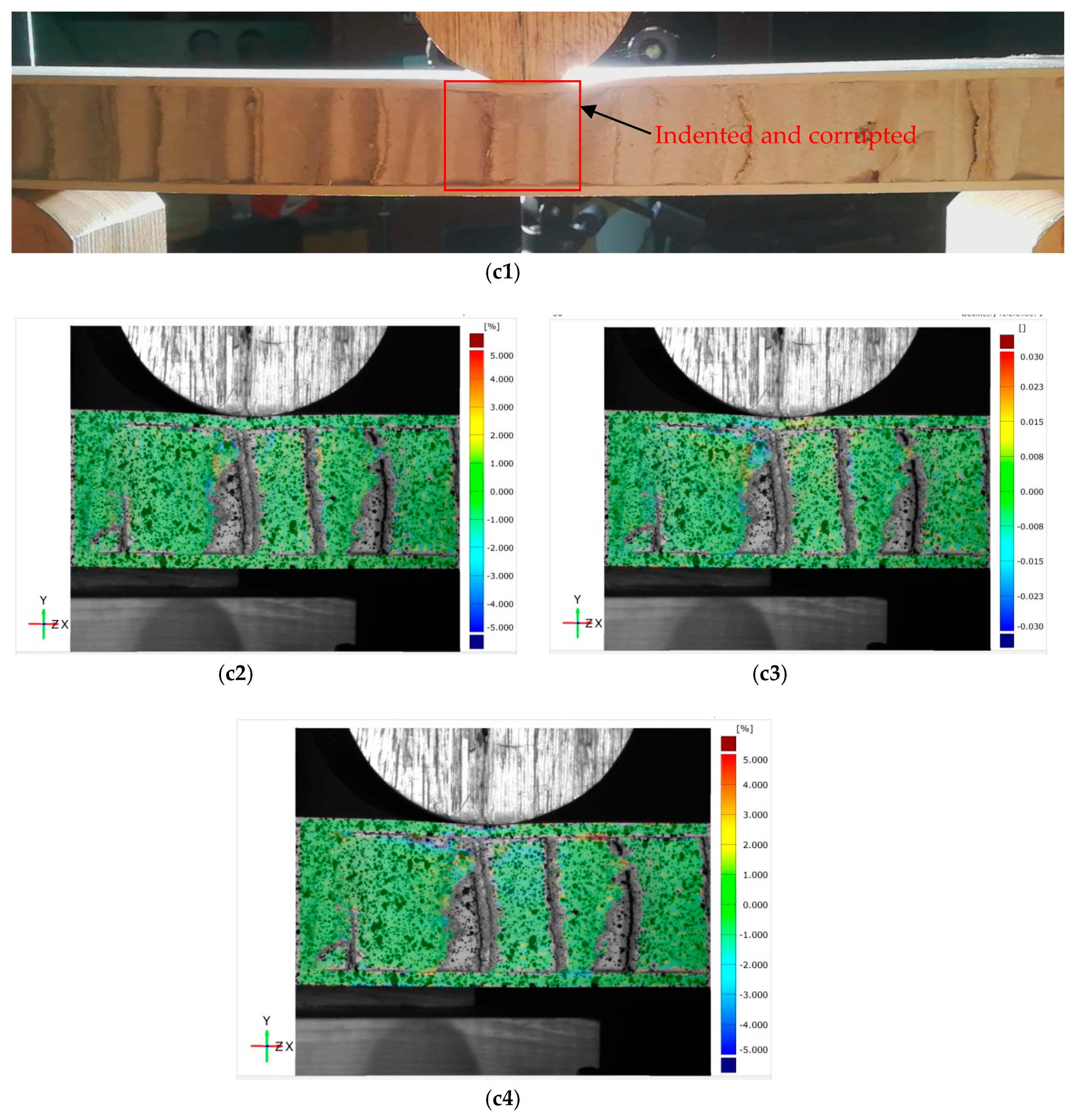
3.1. Failure Process of Sandwich Beam (Experimental Results)
3.2. Failure Load Prediction of Sandwich Beam
3.2.1. Shear Failure
3.2.2. Indentation
3.2.3. Face Yield
3.3. Mechanical Prediction of Taiji Honeycomb Core
3.3.1. Compression Buckling Stress
3.3.2. Shear Buckling Stress
3.3.3. Compression Modulus
3.4. Analytical Comparison between Taiji Honeycomb and Traditional Hexagonal One
3.5. Comparison between Experiment and Analytical Solution
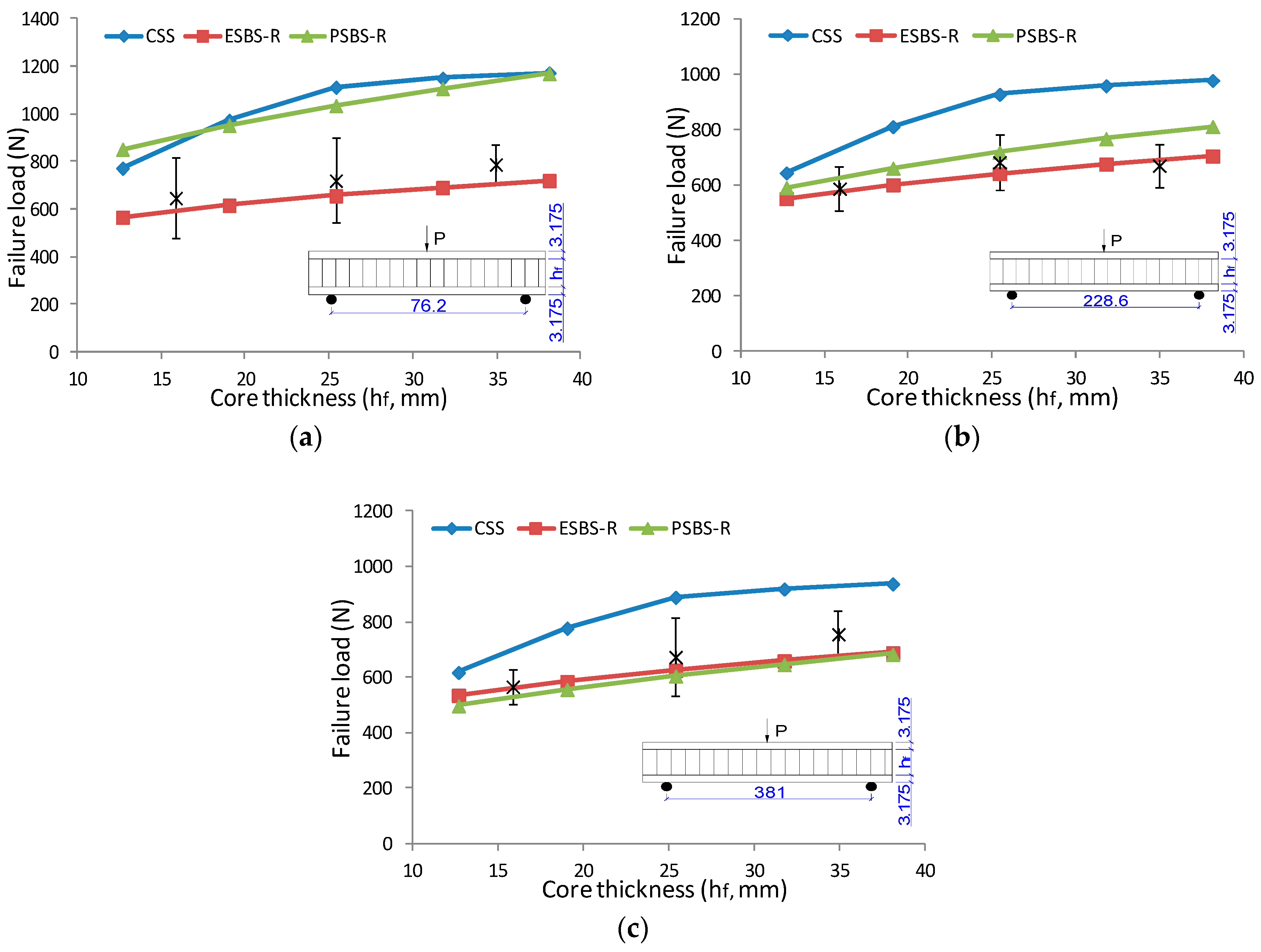
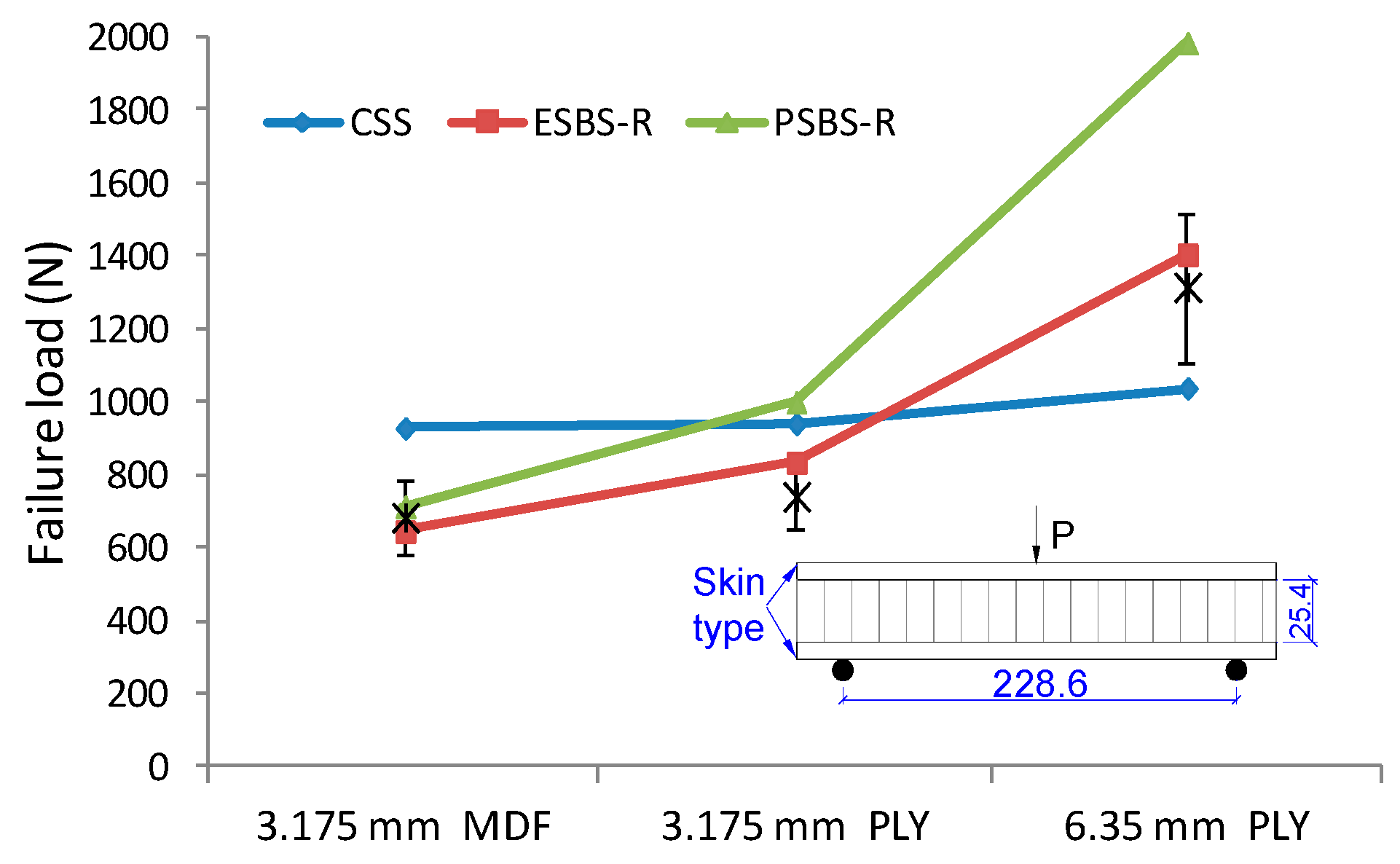
3.6. The Parametric Effect on Failure Load
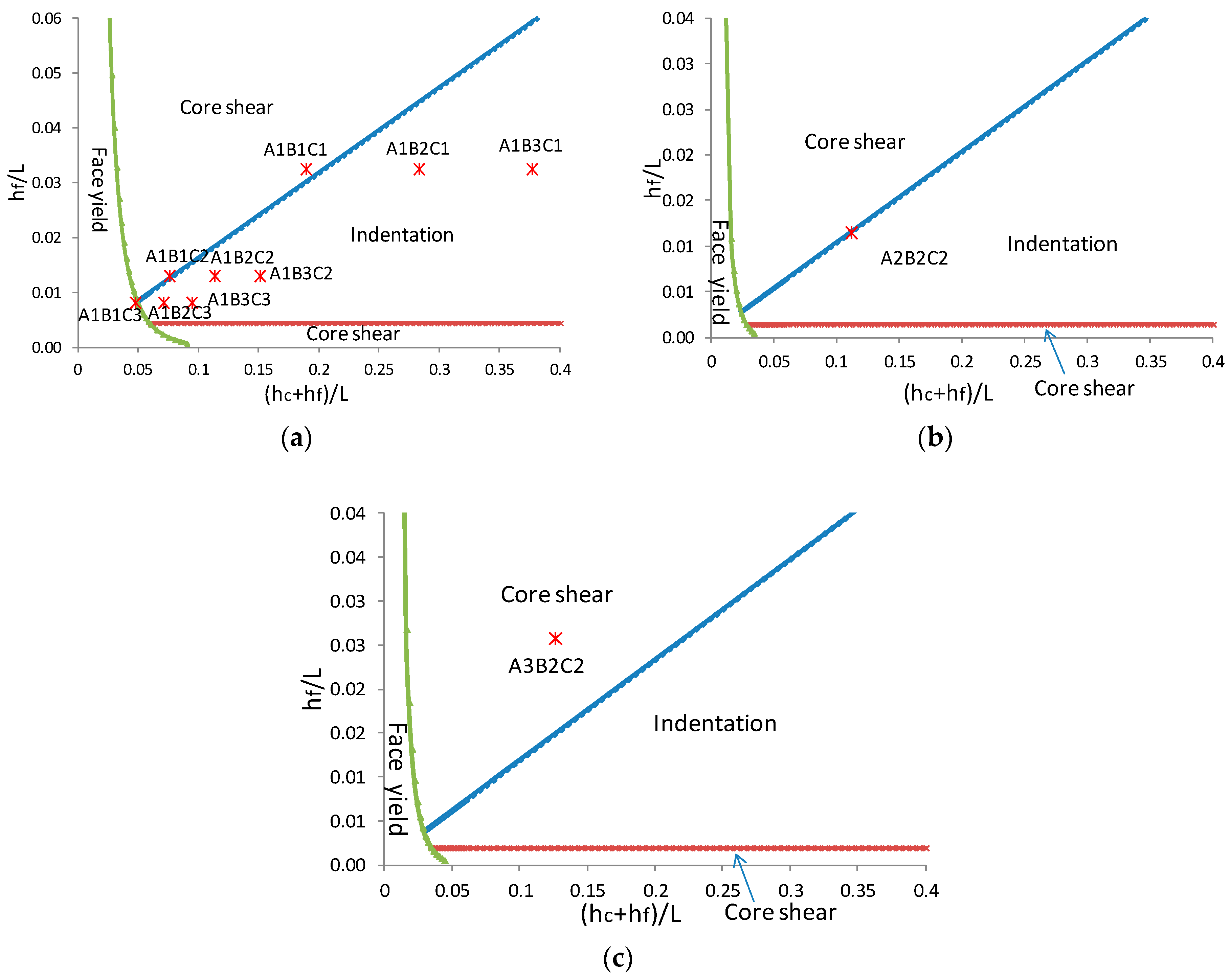
3.7. Failure Map of Sandwich Beam with Taiji Honeycomb Core
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Meng, F.C.; Chen, C.; Hu, D.Y.; Sun, S. Deformation behaviors of three-dimensional graphene honeycombs under out-of-plane compression: Atomistic simulations and predictive modeling. J. Mech. Phys. Solids 2017, 109, 241–251. [Google Scholar] [CrossRef]
- Carlsson, L.A.; Kardomateas, G.A. Structural and Failure Mechanics of Sandwich Composites; Springer Science and Business Media: New York, NY, USA, 2011. [Google Scholar]
- Hao, J.X.; Wu, X.F.; Liu, W.J. Modeling and verification of sandwich beam with wooden skin and honeycomb core subjected to transverse loading. Sci. Silv. Sin. 2014, 50, 128–137. [Google Scholar]
- Wu, X.F.; Xu, J.Y.; Hao, J.X. Calculating elastic constants of binderless bamboo-wood sandwich composite. BioResources 2015, 10, 4473–4484. [Google Scholar] [CrossRef]
- Reissner, E. Finite deflections of sandwich plates. J. Aeronaut. Sci. 1948, 15, 430–448. [Google Scholar] [CrossRef]
- Heath, W.G. Sandwich construction, Part 2: The optimum design of flat sandwich panesl. Aircr. Eng. 1969, 32, 230–235. [Google Scholar] [CrossRef]
- Daniel, I.M.; Abot, J.L. Fabrication, testing and analysis of composite sandwich beams. Composite Sci. Technol. 2000, 60, 2455–2463. [Google Scholar] [CrossRef]
- Duarte, I.; Teixeira-Dias, F.; Graca, A.; Ferreira, A.J. Failure modes and influence of the quasi-static deformation rate on the mechanical behavior of sandwich panels with Aluminum foam cores. Mech. Adv. Mater. Struct. 2010, 17, 335–342. [Google Scholar] [CrossRef]
- Valenza, A.; Fiore, V.; Calabrese, L. Three-point flexural behavior of GFRP sandwich composites: A failure map. Adv. Composite Mater. 2010, 19, 79–90. [Google Scholar] [CrossRef]
- Li, Z.B.; Chen, X.G.; Jiang, B.H.; Lu, F.Y. Local indentation of aluminum foam core sandwich beams at elevated temperatures. Composite Struct. 2016, 145, 142–148. [Google Scholar] [CrossRef]
- Ashby, M.F.; Evans, A.G.; Fleck, N.A.; Gibson, L.J.; Hutchinson, J.W.; Wadley, H.N.G. Metal Foams: A Design Guide; Butter Worth-Heinemann: London, UK, 2000. [Google Scholar]
- Minakuchi, S.; Okabe, Y.; Takeda, N. Segment-wise model for theoretical simulation of barely visible indentation damage in composite sandwich beams: Part1-Fourmulation. Compos. Part A Appl. Sci. Manuf. 2008, 39, 133–144. [Google Scholar] [CrossRef]
- Caprino, G.; Durante, M.; Leone, C.; Lopresto, V. The effect of shear on the local indentation and failure of sandwich beams with polymeric foam core loaded in flexure. Compos. Part B Eng. 2015, 71, 45–51. [Google Scholar] [CrossRef]
- Lim, T.S.; Lee, C.S.; Lee, D.G. Failure modes of foam core sandwich beams under static and impact loads. J. Compos. Mater. 2004, 38, 1639–1662. [Google Scholar] [CrossRef]
- Navarro, P.; Abrate, S.; Aubry, J.; Maguet, S.; Ferrero, J.F. Analytical modeling of indentation of composite sandwich beam. Compos. Struct. 2013, 100, 79–88. [Google Scholar] [CrossRef]
- Frostig, Y.; Baruch, M. Localized load effects in high-order bending of sandwich panels with flexible core. J. Eng. Mech. 1996, 122, 1069–1076. [Google Scholar] [CrossRef]
- Berggreen, C.; Simonsen, B.C.; Borum, K.K. Experimental and numerical study of interface crack propagation in foam-cored sandwich beams. J. Comp. Mater. 2007, 41, 493–520. [Google Scholar] [CrossRef]
- Gdoutos, E.E.; Balopoulos, V. Kinking of interfacial cracks in sandwich beams, Proceedings of the SEM 2007 Annual Conference and Exposition. In Proceedings of the Society for Experimental Mechanics, Springfield, MA, USA, 4–6 June 2007. [Google Scholar]
- Chen, Z.; Yan, N. Investigation of elastic moduli of kraft paper honeycomb core sandwich panels. Compos. Part B Eng. 2012, 43, 2107–2114. [Google Scholar] [CrossRef]
- Hao, J.X.; Wu, X.F.; Liu, W.J. Bending property of sandwich beam based on layer-wise first-order theory. J. Build. Mater. 2014, 17, 1049–1053. [Google Scholar]
- Wang, D.M.; Bai, Z.Y. Mechnical property of paper honeycomb structure under dynamic compression. Mater. Des. 2015, 77, 59–64. [Google Scholar] [CrossRef]
- Si, L.L. Study on the mechanical properties of wood material enhanced paper honeycomb core composite boards. Forest. Mach. Woodwork. Equip. 2012, 40, 25–28. [Google Scholar]
- ASTM D1037-06a. Standard Test Methods for Evaluating Properties of Wood-Base Fiber and Particle Panel Materials; ASTM International: West Conshohocken, PA, USA, 2011. [Google Scholar]
- Xavier, J.; De Jesus, A.M.P.; Morais, J.J.L.; Pinto, J.M.T. Stereovision measurements on evaluating the modulus of elasticity of wood by compression tests parallel to the grain. Constr. Build. Mater. 2012, 26, 207–215. [Google Scholar] [CrossRef]
- Jeong, G.Y.; Park, M.J. Evaluate orthotropic properties of wood using digital image correlation. Constr. Build. Mater. 2016, 113, 864–869. [Google Scholar] [CrossRef]
- Pereira, J.L.; Xavier, J.; Ghiassi, B.; Lousada, J.; Morasi, J. On the identification of earlywood and latewood radial elastic modulus of Pinus pinaster by digital image. J. Strain Anal. Eng. 2018. [Google Scholar] [CrossRef]
- Gdoutos, E.E.; Konsta-Gdoutos, M.S. The effect of load and geometry on the failure modes of sandwich beams. Appl. Compos. Mater. 2005, 12, 165–176. [Google Scholar] [CrossRef]
- Hao, J.X.; Wu, X.F.; Oporto, G.; Liu, W.J.; Wang, J.X. Three-point Flexural Failure Mechanism of Wooden Sandwich Composite with a Paper Honeycomb Core. Adv. Compos. Mater. 2018, 19, 79–90. [Google Scholar]
- Qin, Q.H.; Zhang, J.X.; Wang, Z.J.; Li, H.M.; Guo, D. Indentation of sandwich beams with metal foam core. Trans. Nonferrous met. Soc. 2014, 24, 2440–2446. [Google Scholar] [CrossRef]
- Pan, S.D.; Wu, L.Z.; Sun, Y.G.; Zhou, Z.G.; Qu, J.L. Longitudinal shear strength and failure process of honeycomb cores. Compos. Struct. 2006, 72, 42–46. [Google Scholar] [CrossRef]
- Zenkert, D.; Shipsha, A.; Persson, K. Static indentation and unloading response of sandwich beams. Compos. Part B Eng. 2004, 35, 511–522. [Google Scholar] [CrossRef]
- Steeves, C.A.; Fleck, N.A. Collapse mechanisms of sandwich beams with composite faces and a foam core, loaded in three-point bending. Part 1: Analytical models and minimum weight design. Int. J. Mech. Sci. 2004, 46, 561–583. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Gere, J.M. Theory of Elastic Instability, 2nd ed.; McGraw-Hill: New York, NY, USA, 1961. [Google Scholar]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Chen, C.; Harte, A.M.; Fleck, N.A. The plastic collapse of sandwich beams with a metallic foam core. Int. J. Mech. Sci. 2001, 43, 1483–1506. [Google Scholar] [CrossRef]








| Material | Thickness (mm) | Density (Kg/m3) | Moisture Content (%) | Bending Strength (MPa) | Bending Modulus (MPa) |
|---|---|---|---|---|---|
| MDF | 3.175 | 869.0 | 5.4 | 28.9 | 5399.9 |
| PLY | 3.175 | 683.6 | 5.6 | 88.2 | 20,578.0 |
| PLY | 6.35 | 672.5 | 5.4 | 64.2 | 13,598.7 |
| Material | Thickness (mm) | Moisture Content (%) | Tensile Strength (MPa) | Tensile Modulus (MPa) |
|---|---|---|---|---|
| Kraft paper | 0.1778 | 5.4 | 13.2 | 453.0 |
| Group | Code | Surface Sheet (A) | Core Thickness (B, mm) | Span Distance (D, mm) |
|---|---|---|---|---|
| 1 | A1B1C1 | 3.175 mm MDF | 15.875 | 76.2 |
| 2 | A1B2C1 | 3.175 mm MDF | 25.4 | 76.2 |
| 3 | A1B3C1 | 3.175 mm MDF | 34.925 | 76.2 |
| 4 | A1B1C2 | 3.175 mm MDF | 15.875 | 228.6 |
| 5 | A1B2C2 | 3.175 mm MDF | 25.4 | 228.6 |
| 6 | A1B3C2 | 3.175 mm MDF | 34.925 | 228.6 |
| 7 | A2B2C2 | 3.175 mm PLY | 25.4 | 228.6 |
| 8 | A3B2C2 | 6.35 mm PLY | 25.4 | 228.6 |
| 9 | A1B1C3 | 3.175 mm MDF | 15.875 | 381 |
| 10 | A1B2C3 | 3.175 mm MDF | 25.4 | 381 |
| 11 | A1B3C3 | 3.175 mm MDF | 34.925 | 381 |
| Group | Code | Surface Sheet (A) | Core Thickness (B, mm) | Span Distance (D, mm) | Fail Mode | Test Results (N) | Standard Deviation | CSS (N) | ES (N) | PSBS (N) | PSBS-R (N) | ESBS (N) | ESBS-R (N) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | A1B1C1 | 3.175 mm MDF | 15.875 | 76.2 | Indentation | 647.9 | 170.1 | ﹨ | 409.4 | 1125.4 | 893.1 | 420.1 | 629.7 |
| 2 | A1B2C1 | 3.175 mm MDF | 25.4 | 76.2 | Indentation | 721.2 | 178.3 | ﹨ | 541.1 | 1186.4 | 941.6 | 438.3 | 657.3 |
| 3 | A1B3C1 | 3.175 mm MDF | 34.925 | 76.2 | Indentation | 789.0 | 83.4 | ﹨ | 591.0 | 1344.8 | 1067.1 | 482.8 | 724.5 |
| 4 | A1B1C2 | 3.175 mm MDF | 15.875 | 228.6 | Indentation | 587.8 | 77.7 | ﹨ | 473.5 | 762.3 | 605.2 | 384.0 | 576.3 |
| 5 | A1B2C2 | 3.175 mm MDF | 25.4 | 228.6 | Indentation | 682.9 | 101.8 | ﹨ | 522.9 | 880.2 | 712.0 | 429.9 | 644.8 |
| 6 | A1B3C2 | 3.175 mm MDF | 34.925 | 228.6 | Indentation | 670.7 | 78.5 | ﹨ | 588.3 | 1007.9 | 801.0 | 468.1 | 702.2 |
| 7 | A2B2C2 | 3.175 mm PLY | 25.4 | 228.6 | Indentation/Core shear | 739.6 | 90.3 | 939.8 | 687.5 | 1258.0 | 998.6 | 555.8 | 833.5 |
| 8 | A3B2C2 | 6.35 mm PLY | 25.4 | 228.6 | Core shear | 1314.1 | 206.4 | 1037.3 | ﹨ | ﹨ | ﹨ | ﹨ | ﹨ |
| 9 | A1B1C3 | 3.175 mm MDF | 15.875 | 381 | Indentation with face yield | 567.5 | 63.0 | ﹨ | 482.4 | 705.8 | 560.3 | 392.0 | 587.8 |
| 10 | A1B2C3 | 3.175 mm MDF | 25.4 | 381 | Indentation | 674.6 | 141.7 | ﹨ | 553.1 | 815.2 | 647.0 | 439.7 | 659.5 |
| 11 | A1B3C3 | 3.175 mm MDF | 34.925 | 381 | Indentation | 756.9 | 81.7 | ﹨ | 585.6 | 870.9 | 691.1 | 463.2 | 694.6 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, J.; Wu, X.; Oporto, G.; Wang, J.; Dahle, G.; Nan, N. Deformation and Failure Behavior of Wooden Sandwich Composites with Taiji Honeycomb Core under a Three-Point Bending Test. Materials 2018, 11, 2325. https://doi.org/10.3390/ma11112325
Hao J, Wu X, Oporto G, Wang J, Dahle G, Nan N. Deformation and Failure Behavior of Wooden Sandwich Composites with Taiji Honeycomb Core under a Three-Point Bending Test. Materials. 2018; 11(11):2325. https://doi.org/10.3390/ma11112325
Chicago/Turabian StyleHao, Jingxin, Xinfeng Wu, Gloria Oporto, Jingxin Wang, Gregory Dahle, and Nan Nan. 2018. "Deformation and Failure Behavior of Wooden Sandwich Composites with Taiji Honeycomb Core under a Three-Point Bending Test" Materials 11, no. 11: 2325. https://doi.org/10.3390/ma11112325
APA StyleHao, J., Wu, X., Oporto, G., Wang, J., Dahle, G., & Nan, N. (2018). Deformation and Failure Behavior of Wooden Sandwich Composites with Taiji Honeycomb Core under a Three-Point Bending Test. Materials, 11(11), 2325. https://doi.org/10.3390/ma11112325







