Characterization and Analysis of Strain Heterogeneity at Grain-Scale of Titanium Alloy with Tri-Modal Microstructure during Tensile Deformation
Abstract
:1. Introduction
2. Experimental Procedure
2.1. Material and Initial Microstructure
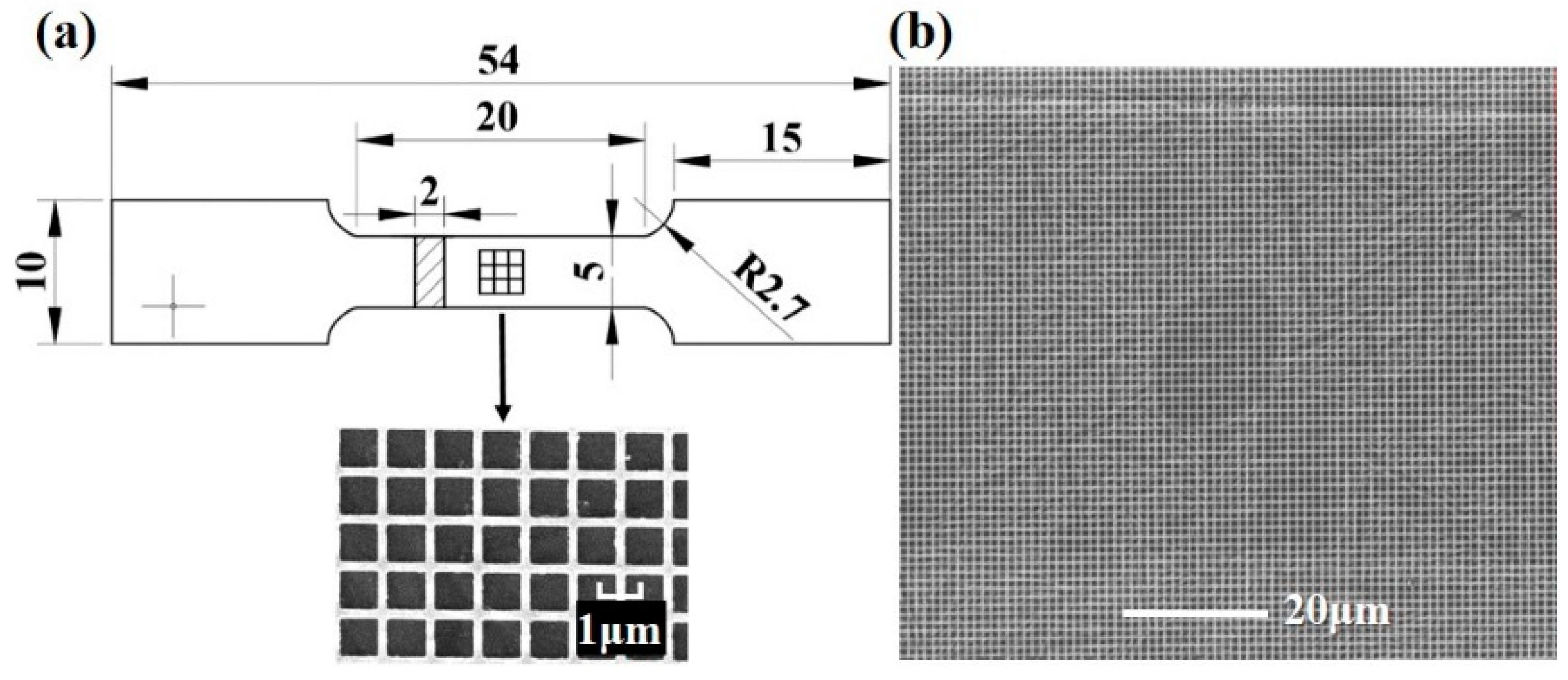
2.2. Tensile Testing and Mapping of Strain Field
3. Results and Discussion
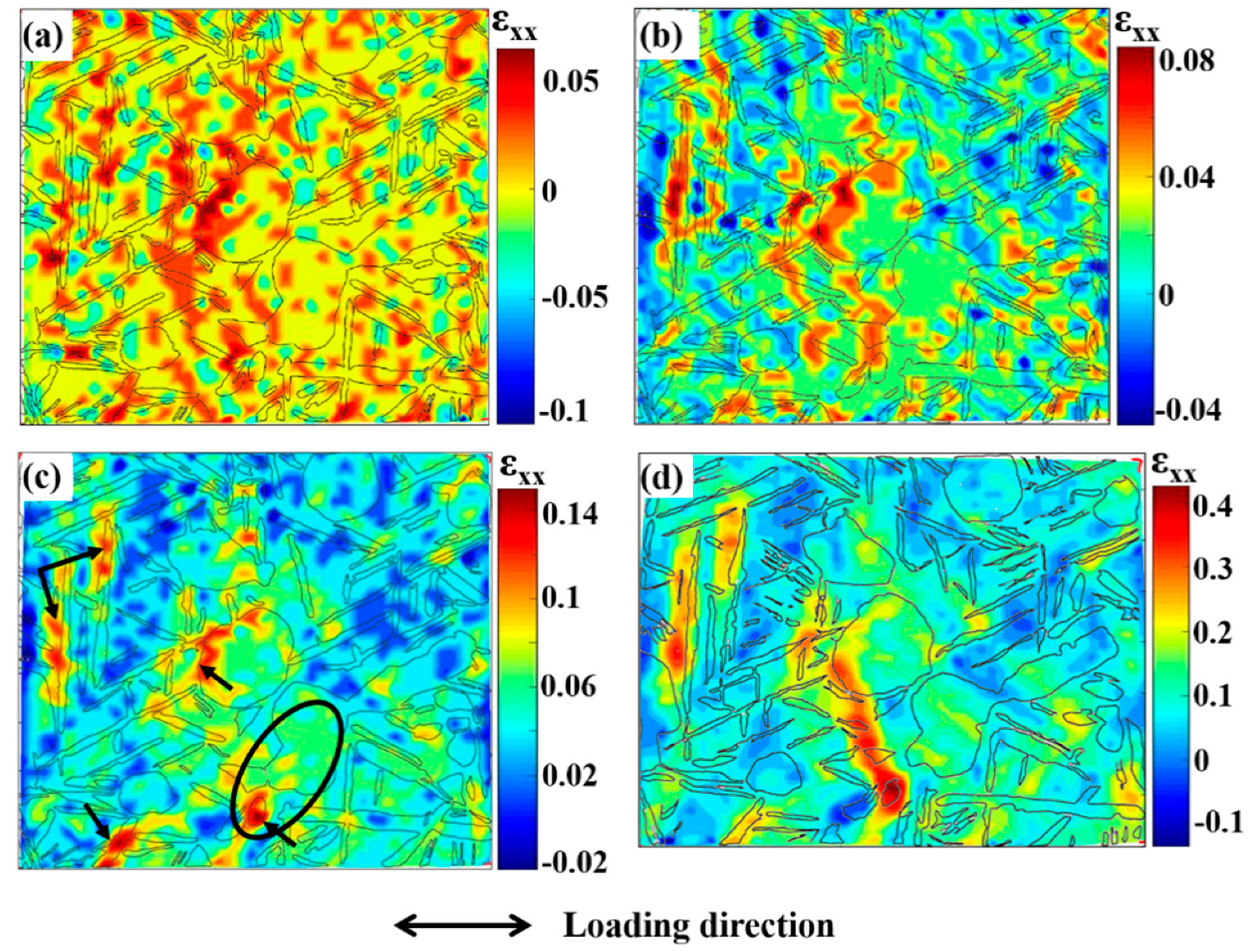
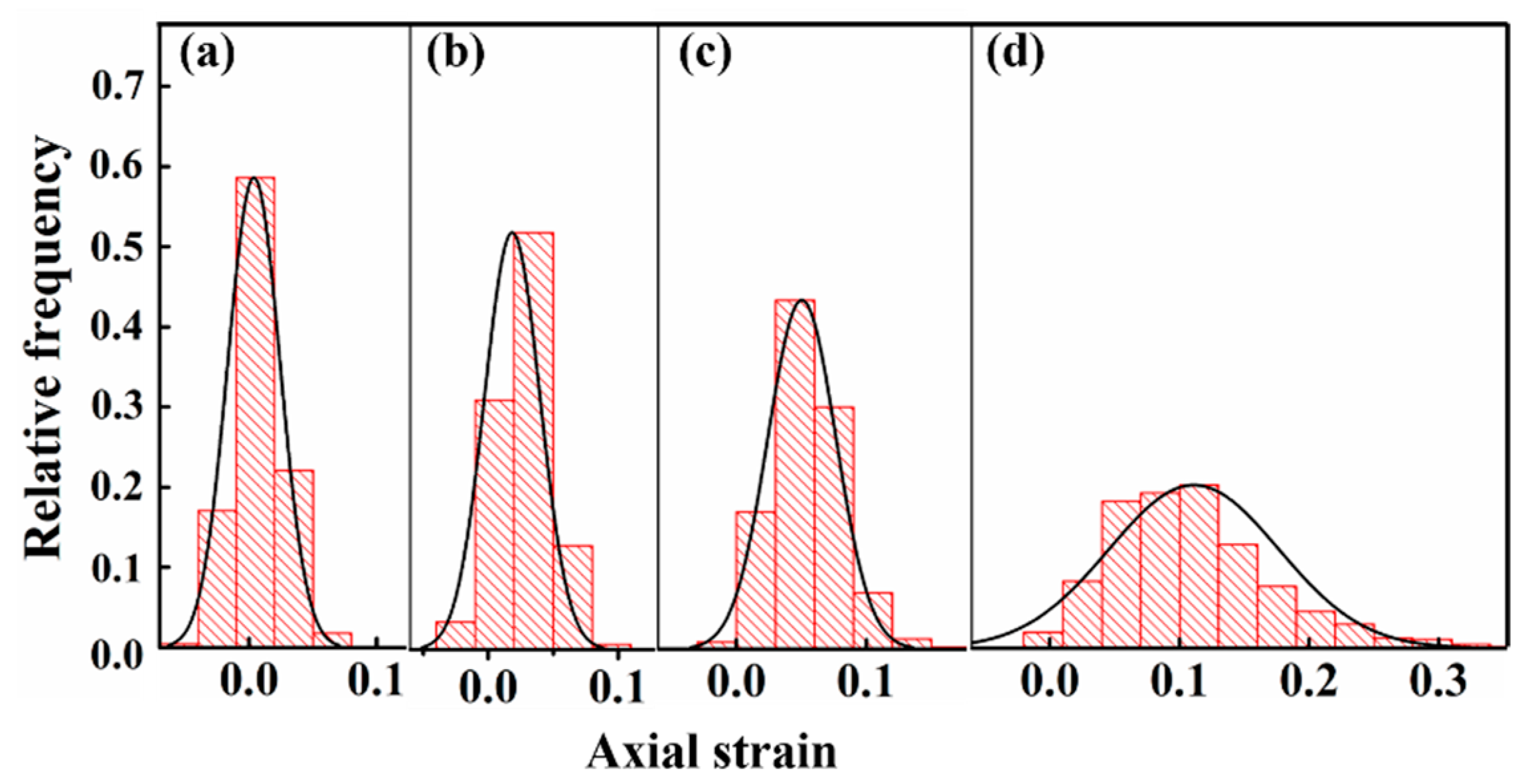
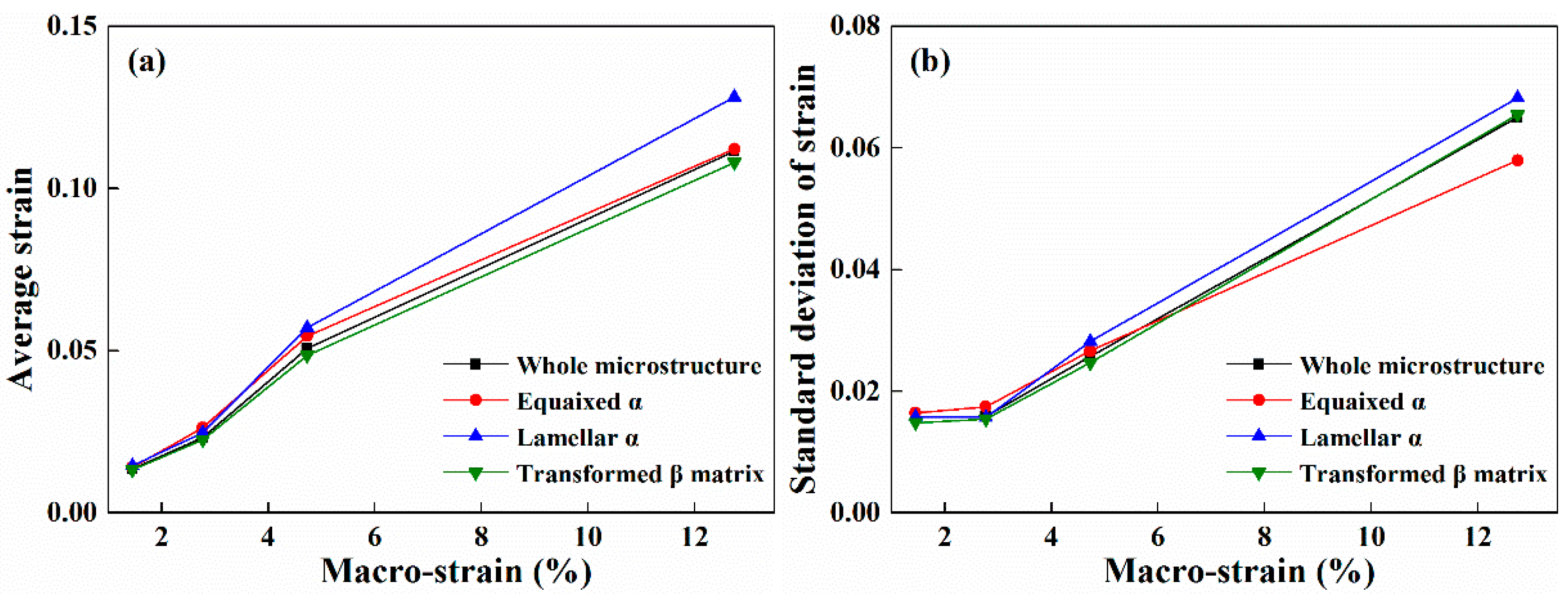
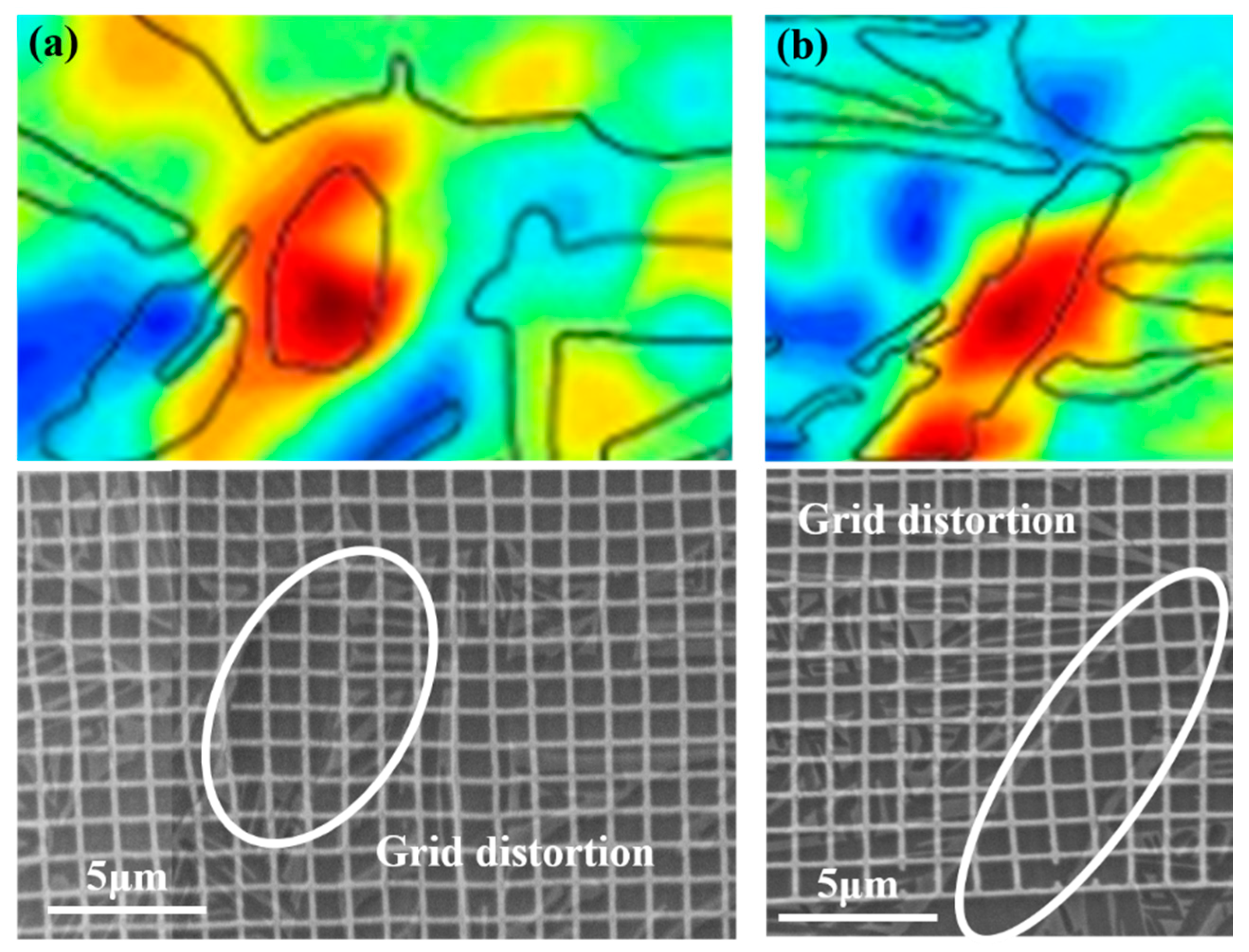
3.1. Characteristics of Strain Heterogeneity
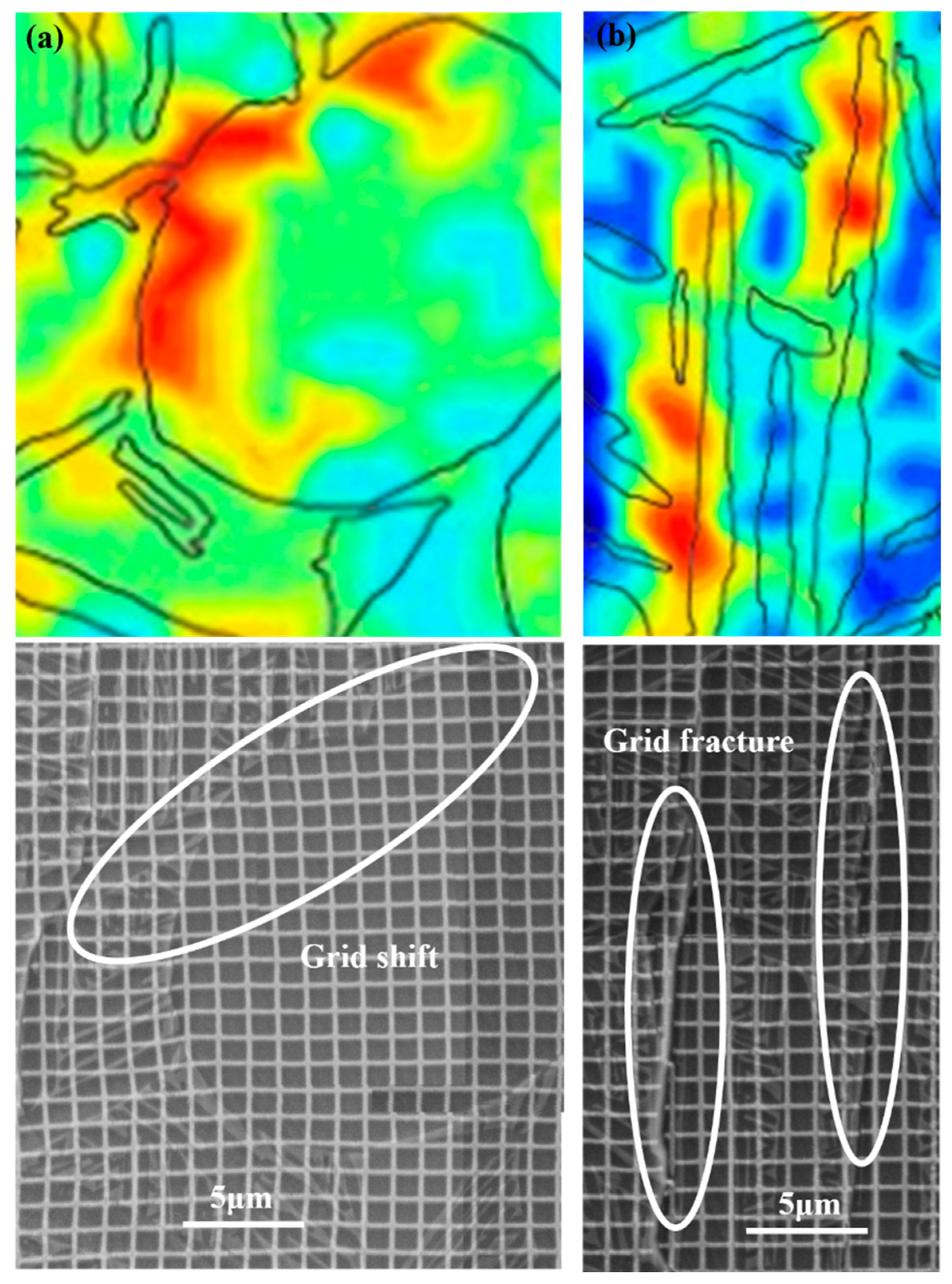
3.2. Strain Localization and Micro-Damage
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Banerjee, D.; Williams, J.C. Perspectives on titanium science and technology. Acta Mater. 2013, 61, 844–879. [Google Scholar] [CrossRef]
- Lütjering, G.; Williams, J.C. Titanium, 2nd ed.; Springer: Berlin, Germany, 2007; p. 203. ISBN 9783540713975. [Google Scholar]
- Li, H.W.; Sun, X.X.; Yang, H. A three-dimensional cellular automata-crystal plasticity finite element model for predicting the multiscale interaction among heterogeneous deformation, DRX microstructural evolution and mechanical responses in titanium alloys. Int. J. Plast. 2016, 87, 154–180. [Google Scholar] [CrossRef]
- Gao, P.F.; Lei, Z.N.; Li, Y.K.; Zhan, M. Low-cycle fatigue behavior and property of TA15 titanium alloy with tri-modal microstructure. Mater. Sci. Eng. A 2018, 736, 1–11. [Google Scholar] [CrossRef]
- Gao, P.F.; Cai, Y.; Zhan, M.; Fan, X.G.; Lei, Z.N. Crystallographic orientation evolution during the development of tri-modal microstructure in the hot working of TA15 titanium alloy. J. Alloys Compd. 2018, 741, 734–745. [Google Scholar] [CrossRef]
- Gao, P.F.; Zhan, M.; Fan, X.G.; Lei, Z.N.; Cai, Y. Hot deformation behavior and microstructure evolution of TA15 titanium alloy with nonuniform microstructure. Mater. Sci. Eng. A 2017, 689, 243–251. [Google Scholar] [CrossRef]
- Lei, Z.N.; Gao, P.F.; Li, H.W.; Fan, X.G.; Cai, Y.; Zhan, M. Microstructure characterization and nano & micro hardness of tri-modal microstructure of titanium alloy under different hot working conditions. Mater. Charact. 2017, 134, 236–245. [Google Scholar]
- Bieler, T.R.; Semiatin, S.L. The origins of heterogeneous deformation during primary hot working of Ti-6Al-4V. Int. J. Plast. 2002, 18, 1165–1189. [Google Scholar] [CrossRef]
- Matsuno, T.; Teodosiu, C.; Maeda, D.; Uenishi, A. Mesoscale simulation of the early evolution of ductile fracture in dual-phase steels. Int. J. Plast. 2015, 74, 17–34. [Google Scholar] [CrossRef]
- Tasan, C.C.; Hoefnagels, J.P.M.; Diehl, M.; Yan, D.; Roters, F.; Raabe, D. Strain localization and damage in dual phase steels investigated by coupled in-situ deformation experiments and crystal plasticity simulations. Int. J. Plast. 2014, 63, 198–210. [Google Scholar] [CrossRef] [Green Version]
- Sirinakorn, T.; Wongwises, S.; Uthaisangsuk, V. A study of local deformation and damage of dual phase steel. Mater. Des. 2014, 64, 729–742. [Google Scholar] [CrossRef]
- Ghadbeigi, H.; Pinna, C.; Celotto, S. Failure mechanisms in DP600 steel: Initiation, evolution and fracture. Mater. Sci. Eng. A 2013, 588, 420–431. [Google Scholar] [CrossRef] [Green Version]
- Laia, Q.; Bouaziz, O.; Gouné, M.; Brassart, L.; Verdier, M.; Parry, G.; Perlade, A.; Bréchet, Y.; Pardoen, T. Damage and fracture of dual-phase steels: Influence of martensite volume fraction. Mater. Sci. Eng. A 2015, 646, 322–331. [Google Scholar] [CrossRef]
- Jafari, M.; Ziaei-Rad, S.; Saeidi, N.; Jamshidian, M. Micromechanical analysis of martensite distribution on strain localization in dual phase steels by scanning electron microscopy and crystal plasticity simulation. Mater. Sci. Eng. A 2016, 670, 57–67. [Google Scholar] [CrossRef]
- Barkia, B.; Doquet, V.; Héripré, E.; Guillot, I. Characterization and analysis of deformation heterogeneities in commercial purity titanium. Mater. Charact. 2015, 108, 94–101. [Google Scholar] [CrossRef]
- Lunt, D.; Busolo, T.; Xu, X.; da Fonseca, J.Q.; Preuss, M. Effect of nanoscale α2 precipitation on strain localisation in a two-phase Ti-alloy. Acta Mater. 2017, 129, 72–82. [Google Scholar] [CrossRef]
- Ji, Z.; Yang, H. Microstructural design of two-phase titanium alloys by micro-scale strain distribution. Mater. Lett. 2016, 184, 157–161. [Google Scholar] [CrossRef]
- Zhang, X.C.; Zhong, F.; Shao, J.B.; Zhang, C.C.; Hou, N.X.; Yuan, G.J.; Tu, S.T. Failure mechanism and mode of Ti-6Al-4V alloy under uniaxial tensile loading: Experiments and micromechanical modeling. Mater. Sci. Eng. A 2016, 676, 536–545. [Google Scholar] [CrossRef]
- Katani, S.; Madadi, F.; Atapour, M.; Rad, S.Z. Micromechanical modelling of damage behaviour of Ti-6Al-4V. Mater. Des. 2013, 49, 1016–1021. [Google Scholar] [CrossRef]
- Zhou, Y.G.; Zeng, W.D.; Yu, H.Q. An investigation of a new near-beta forging process for titanium alloys and its application in aviation components. Mater. Sci. Eng. A 2005, 393, 204–212. [Google Scholar] [CrossRef]
- Gao, P.F.; Fan, X.G.; Yang, H. Role of processing parameters in the development of tri-modal microstructure during isothermal local loading forming of TA15 titanium alloy. J. Mater. Process. Technol. 2017, 239, 160–171. [Google Scholar] [CrossRef]
- Martin, G.; Sinclair, C.W.; Lebensohn, R.A. Microscale plastic strain heterogeneity in slip dominated deformation of magnesium alloy containing rare earth. Mater. Sci. Eng. A 2014, 603, 37–51. [Google Scholar] [CrossRef]
- Masaki, T.; Yoshimi, Y.; Higashida, K.; Shimokawa, T. A multiscale approach for the deformation mechanism in pearlite microstructure: Experimental measurements of strain distribution using a novel technique of precision markers. Mater. Sci. Eng. A 2014, 590, 37–43. [Google Scholar] [Green Version]




© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, P.; Li, Y.; Wu, R.; Lei, Z.; Cai, Y.; Zhan, M. Characterization and Analysis of Strain Heterogeneity at Grain-Scale of Titanium Alloy with Tri-Modal Microstructure during Tensile Deformation. Materials 2018, 11, 2194. https://doi.org/10.3390/ma11112194
Gao P, Li Y, Wu R, Lei Z, Cai Y, Zhan M. Characterization and Analysis of Strain Heterogeneity at Grain-Scale of Titanium Alloy with Tri-Modal Microstructure during Tensile Deformation. Materials. 2018; 11(11):2194. https://doi.org/10.3390/ma11112194
Chicago/Turabian StyleGao, Pengfei, Yanxi Li, Ronghai Wu, Zhenni Lei, Yang Cai, and Mei Zhan. 2018. "Characterization and Analysis of Strain Heterogeneity at Grain-Scale of Titanium Alloy with Tri-Modal Microstructure during Tensile Deformation" Materials 11, no. 11: 2194. https://doi.org/10.3390/ma11112194
APA StyleGao, P., Li, Y., Wu, R., Lei, Z., Cai, Y., & Zhan, M. (2018). Characterization and Analysis of Strain Heterogeneity at Grain-Scale of Titanium Alloy with Tri-Modal Microstructure during Tensile Deformation. Materials, 11(11), 2194. https://doi.org/10.3390/ma11112194




