Magneto-Electric Effect on Guided Waves in Functionally Graded Piezoelectric–Piezomagnetic Fan-Shaped Cylindrical Structures
Abstract
:1. Introduction
2. Mathematics and Formulation
3. Numerical Results
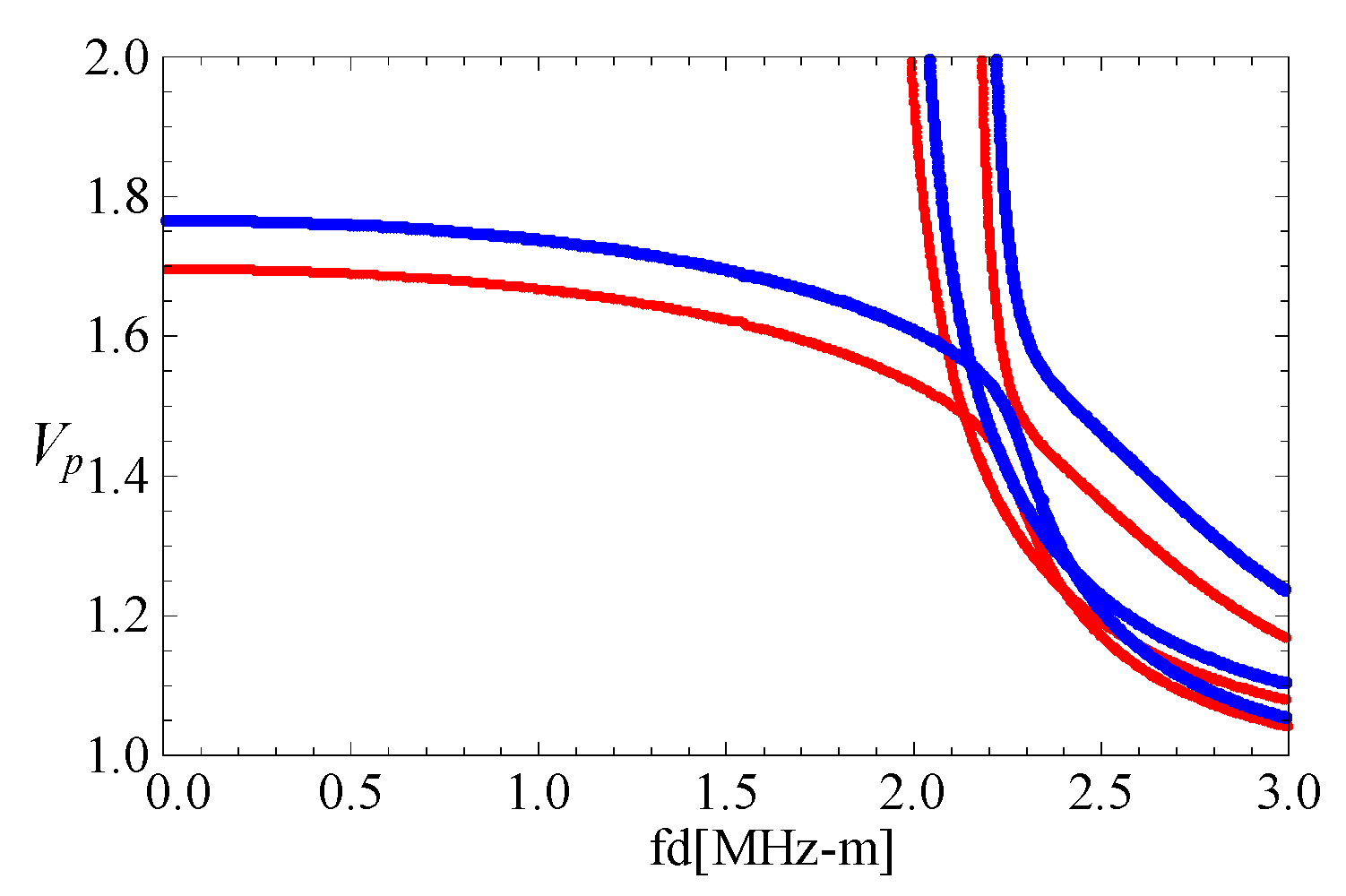
3.1. Comparison with Rectangular Bar
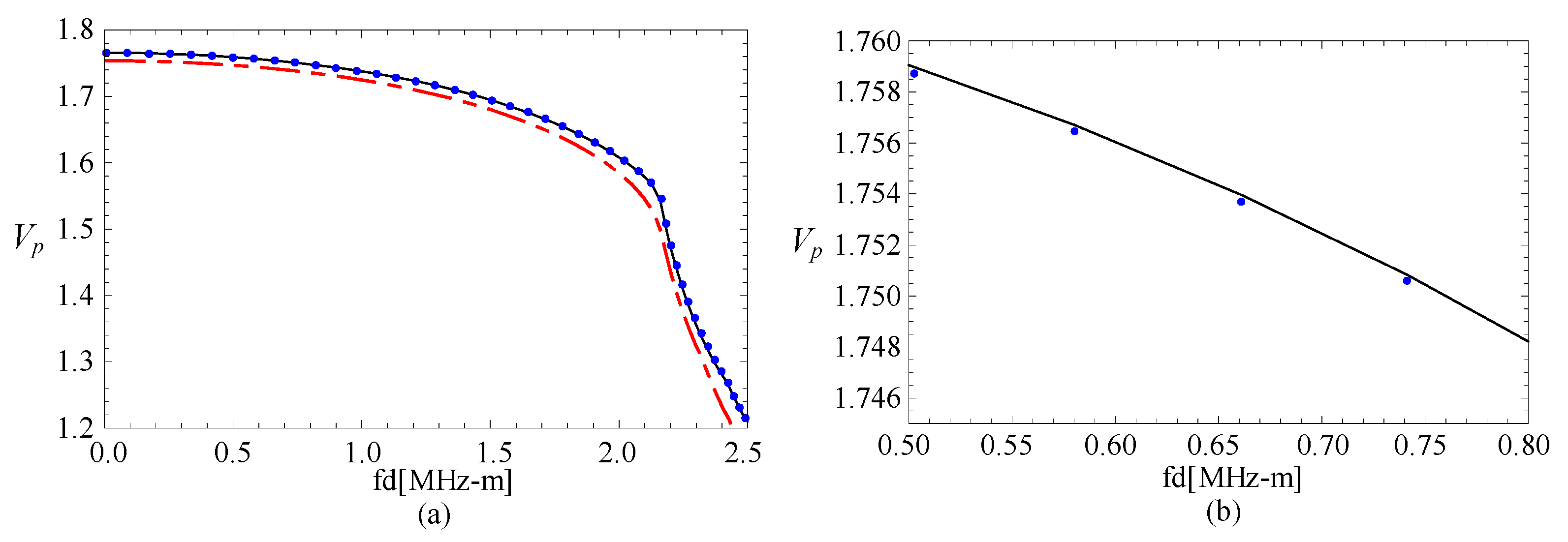
3.2. Convergence Confirmation
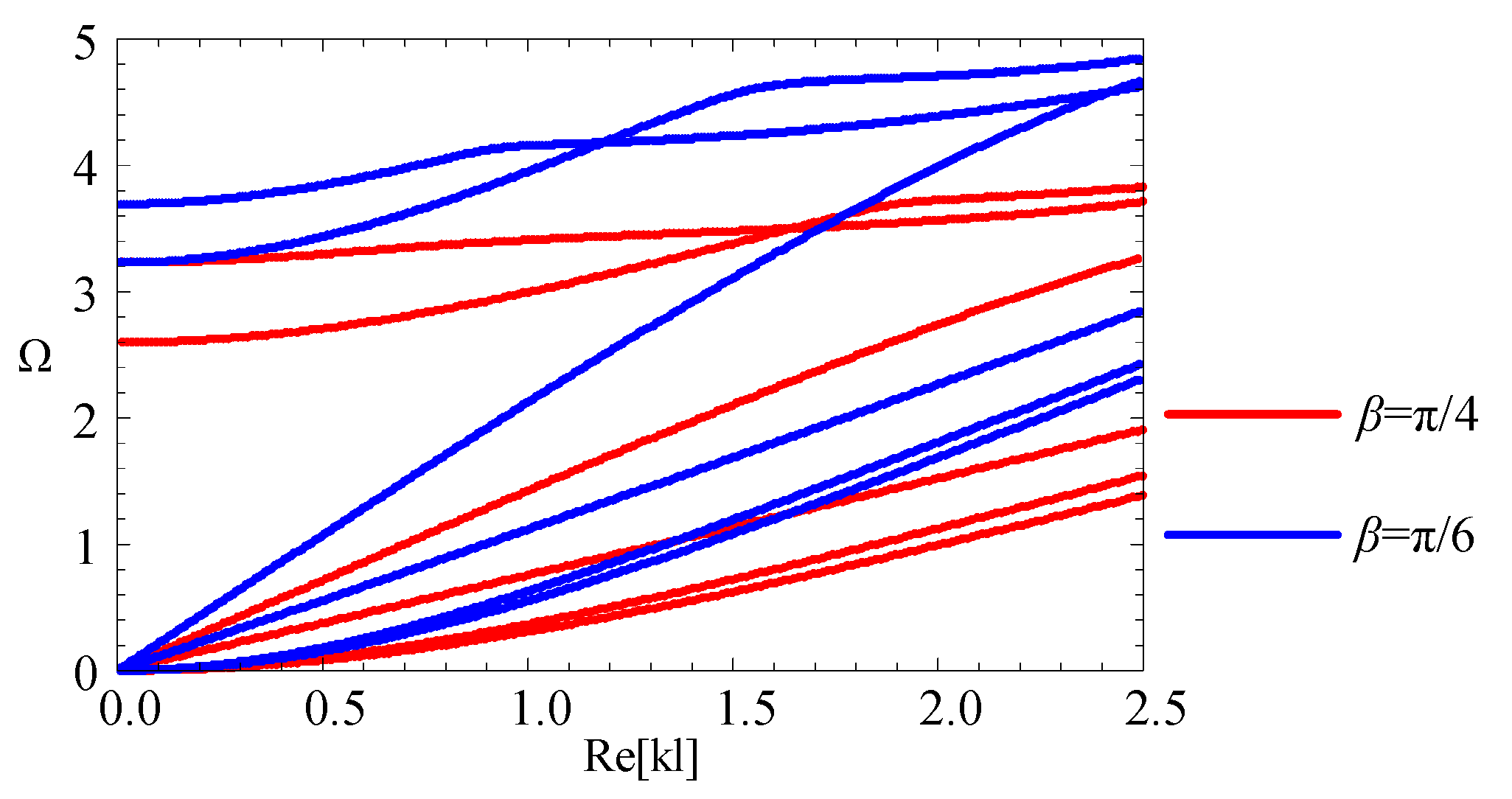
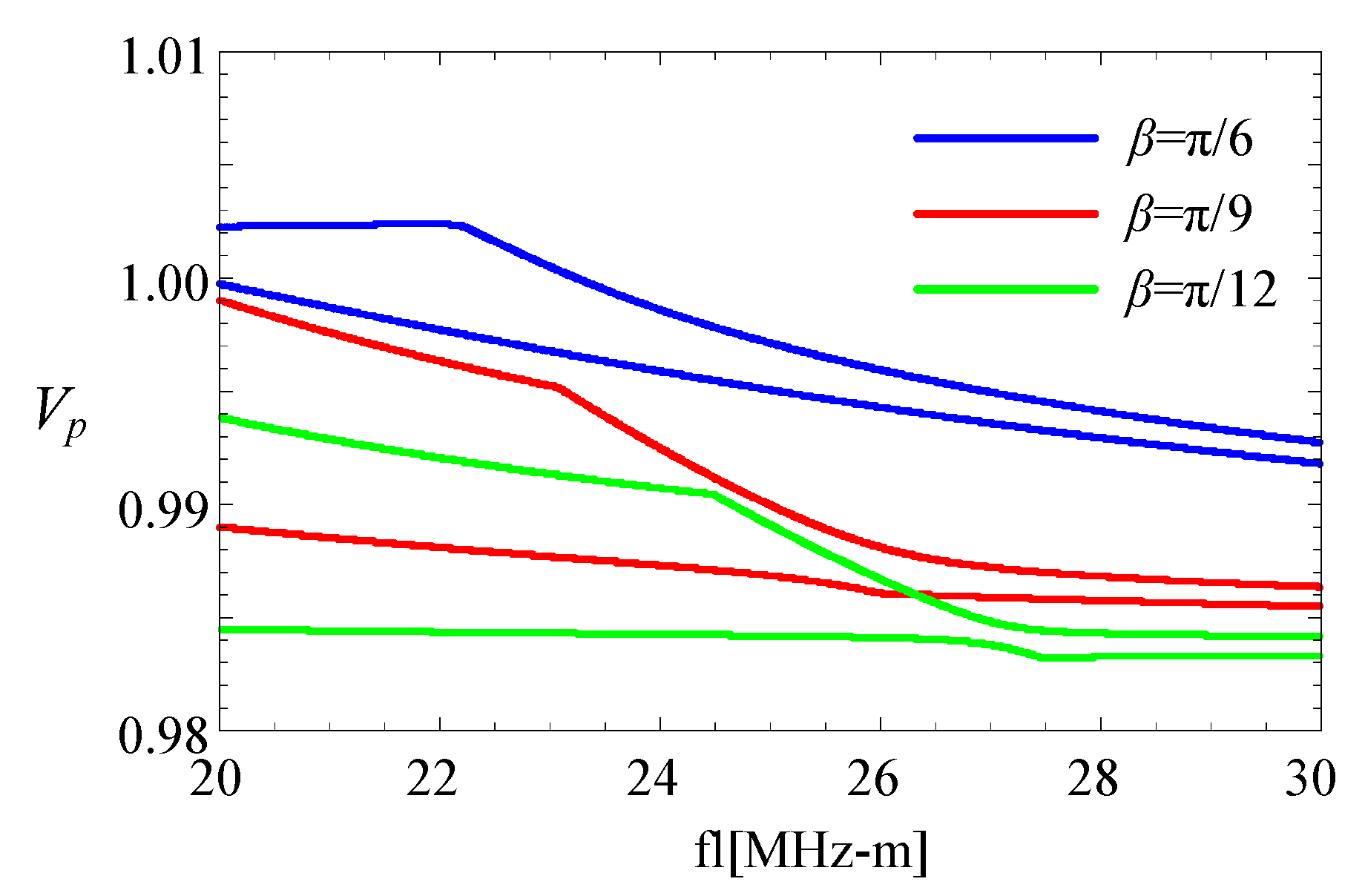
3.3. The Magneto-Electric Effect
3.4. The Influence of the Graded Functions
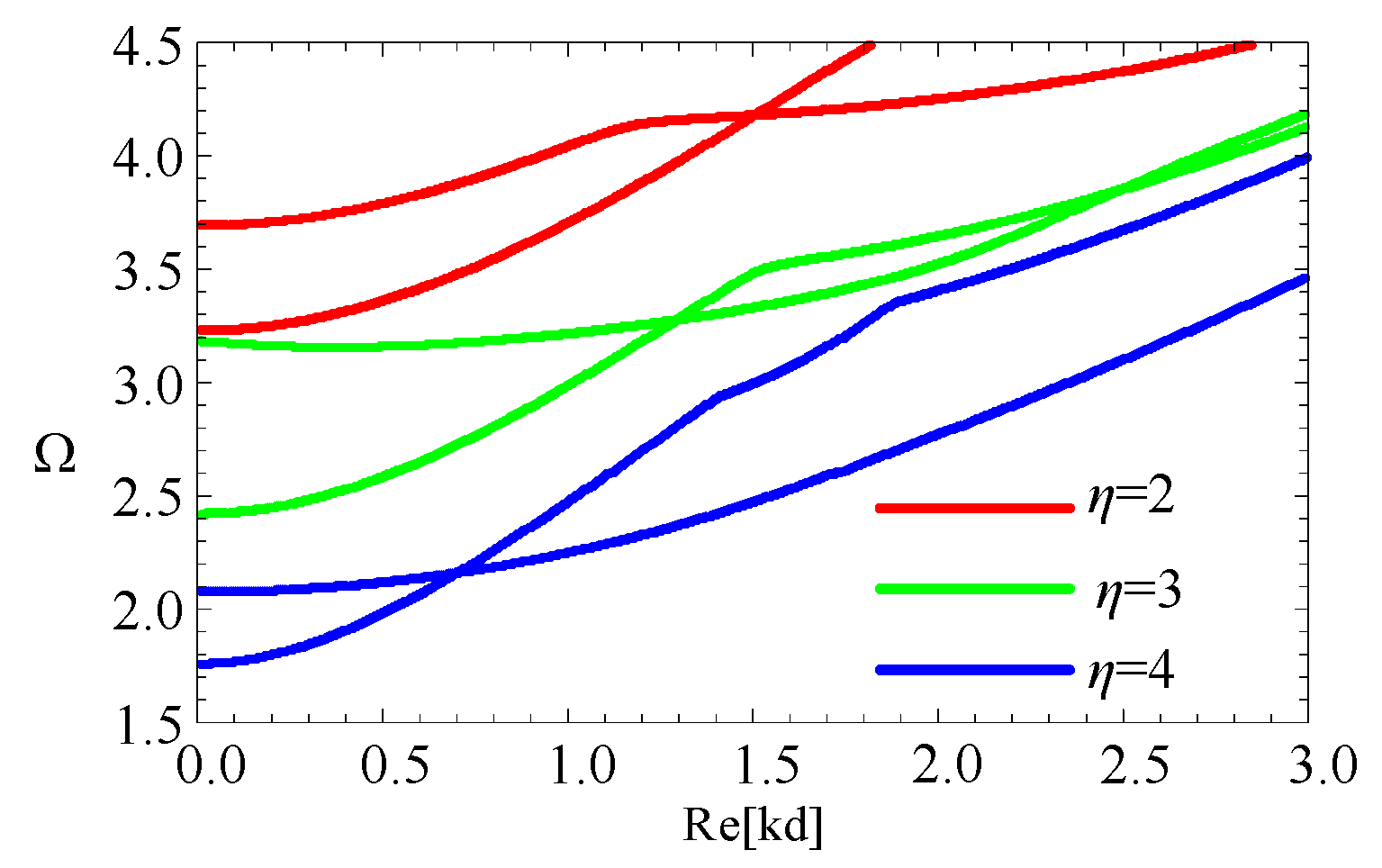
3.5. The Influence of the Geometric Size
3.6. Waves at High Frequencies
3.7. The Stress, Electric, and Magnetic Displacement Distribution
3.8. The Poynting Vector
4. Conclusions
- (1)
- If the radius-thickness ratio is bigger than 1000, fan-shaped cylindrical structures could be treated as a rectangular bar.
- (2)
- The variation in geometric size of the cross-section has remarkable influence on wave characteristics. The cut-off frequencies have a negative relationship with the cross-section area of the fan-shaped cylindrical structures.
- (3)
- For the FGPP fan-shaped cylindrical structures, the magneto-electric effect could be adjusted via altering the geometric size.
- (4)
- The phase velocities for higher modes at high frequencies approximatively approach a value which is below the shear velocity, and they also increase with the increase of β.
- (5)
- For the big wavenumber case, the Poynting vector distributions are concentrated in the region with more material of smaller elasticity modulus, and the Poynting vector distributions are also concentrated near the boundaries, especially near the corner.
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Qin, G.; Lu, C.; Zhang, X. Electric Current Dependent Fracture in GaN Piezoelectric Semiconductor Ceramics. Materials 2018, 11, 2000. [Google Scholar] [CrossRef] [PubMed]
- Ishaq, S.; Kanwal, F.; Atiq, S.; Moussa, M.; Azhar, U.; Imran, M.; Losic, D. Advancing Dielectric and Ferroelectric Properties of Piezoelectric Polymers by Combining Graphene and Ferroelectric Ceramic Additives for Energy Storage Applications. Materials 2018, 11, 1553. [Google Scholar] [CrossRef] [PubMed]
- Drahus, M.D.; Jakes, P.; Erdem, E. Manganese-doped (1 − x) BiScO3 − x PbTiO3, high-temperature ferroelectrics: Defect structure and mechanism of enhanced electric resistivity. Phys. Rev. B 2011, 84, 064113. [Google Scholar] [CrossRef]
- Kostsov, E.G. Ferroelectric-based electrostatic micromotors with nanometer gaps. IEEE Trans. Ultrason. Ferroelectr. 2006, 53, 2294–2298. [Google Scholar] [CrossRef]
- Jones, K.A.; Chow, T.P.; Wraback, M.; Sitar, Z.; Shahedipour, F.; Udwary, K.G.; Tompa, S. AlGaN devices and growth of device structures. J. Mater. Sci. 2015, 50, 3267–3307. [Google Scholar] [CrossRef]
- Erdem, E.; Eichel, R.A.; Kungl, H.; Hoffmann, M.J.; Ozarowski, A.; Tol, H.; Brunel, L.C. Local symmetry-reduction in tetragonal (La,Fe)-codoped Pb[Zr0.4Ti0.6]O3 piezoelectric ceramics. Phys. Scr. 2007, 2007, 12–16. [Google Scholar] [CrossRef]
- Bishay, P.L.; Sladek, J.; Sladek, V.; Atluri, S.N. Analysis of Functionally Graded Piezoelectric-piezomagnetic Composites Using Hybrid/Mixed Finite Elements and Node-Wise Material Properties. CMC-Comput. Mater. Contin. 2012, 29, 213–261. [Google Scholar]
- Afonin, S.M. Static and dynamic characteristics of multilayered electromagnetoelastic transducer of nano- and micrometric movements. Sov. J. Comput. Syst. Sci. 2010, 49, 73–85. [Google Scholar] [CrossRef]
- Chen, L.; Li, P.; Wen, Y. The magnetostrictive material effects on magnetic field sensitivity for magnetoelectric sensor. J. Appl. Phys. 2012, 111, 07E503. [Google Scholar] [CrossRef]
- Cao, X.; Shi, J.; Jin, F. Lamb wave propagation in the functionally graded piezoelectric–piezomagnetic material plate. Acta Mech. 2012, 223, 1081–1091. [Google Scholar] [CrossRef]
- Singh, B.M.; Rokne, J. Propagation of SH waves in layered functionally gradient piezoelectric–piezomagnetic structures. Philos. Mag. 2013, 93, 1690–1700. [Google Scholar] [CrossRef]
- Yu, J.; Wu, B. Circumferential wave in piezoelectric-piezomagnetic functionally graded cylindrical curved plates. Eur. J. Mech. 2009, 28, 560–568. [Google Scholar] [CrossRef]
- Li, P.; Jin, F.; Qian, Z. Propagation of the Bleustein–Gulyaev waves in a functionally graded transversely isotropic electro-magneto-elastic half-space. Eur. J. Mech. A Solids 2013, 37, 17–23. [Google Scholar] [CrossRef]
- Li, L.; Wei, P.J. Surface Wave Speed of Functionally Graded Magneto-Electro-Elastic Materials with Initial Stresses. J. Theor. Appl. Mech. 2014, 44, 49–64. [Google Scholar] [CrossRef] [Green Version]
- Xue, C.X.; Pan, E. On the longitudinal wave along a functionally graded piezoelectric-piezomagnetic rod. Int. J. Eng. Sci. 2013, 62, 48–55. [Google Scholar] [CrossRef]
- Arefi, M. Analysis of wave in a functionally graded piezoelectric-piezomagnetic nano-rod using nonlocal elasticity model subjected to electric and magnetic potentials. Acta Mech. 2016, 227, 2529–2542. [Google Scholar] [CrossRef]
- Narendar, S. Wave dispersion in functionally graded piezoelectric-piezomagnetic nonlocal rod. Aerosp. Sci. Technol. 2016, 51, 42–51. [Google Scholar] [CrossRef]
- Shen, X.; Ren, D.; Cao, X. Cut-off frequencies of circumferential horizontal shear waves in various functionally graded cylinder shells. Ultrasonics 2018, 84, 180–186. [Google Scholar] [CrossRef] [PubMed]
- Shodja, H.M.; Eskandari, S.; Eskandari, M. Shear horizontal surface acoustic waves in functionally graded magneto-electro-elastic half-space. J. Eng. Math. 2016, 97, 83–100. [Google Scholar] [CrossRef]
- Ezzin, H.; Ben, A.M.; Ghozlen, M.H. Love waves propagation in a transversely isotropic piezoelectric layer on a piezomagnetic half-space. Ultrasonics 2016, 69, 83–89. [Google Scholar] [CrossRef] [PubMed]
- Ezzin, H.; Mkaoir, M.; Amor, M.B. Rayleigh wave behavior in functionally graded magneto-electro-elastic material. Superlattices Microstruct. 2017, 112, 455–469. [Google Scholar] [CrossRef]
- Ezzin, H.; Ben, A.M.; Ghozlen, M.H. Lamb waves propagation in layered piezoelectric/piezomagnetic plates. Ultrasonics 2017, 76, 63–69. [Google Scholar] [CrossRef] [PubMed]
- Singhal, A.; Sahu, S.A. Chaudhary, S. Approximation of surface wave frequency in piezo-composite structure. Compos. Part B Eng. 2018, 144, 19–28. [Google Scholar] [CrossRef]
- Zhang, B.; Yu, J.; Shah, A.A.; Yang, X. Wave propagation in functionally graded piezoelectric-piezomagnetic rectangular bars. Sci. Eng. Compos. Mater. 2017, 24, 317–326. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, W.; Lü, C. Elastic waves in multiferroic cylinders of sectorial cross-section. Compos. Part B 2012, 43, 3001–3008. [Google Scholar] [CrossRef]
- Puzyrev, V. Elastic waves in piezoceramic cylinders of sector cross-section. Int. J. Solids Struct. 2010, 47, 2115–2122. [Google Scholar] [CrossRef]
- Puzyrev, V.; Storozhev, V. Wave propagation in axially polarized piezoelectric hollow cylinders of sector cross section. J. Sound Vib. 2011, 330, 4508–4518. [Google Scholar] [CrossRef]
- Storozhev, V.I. Propagation of Electroelastic Waves in Multilayer Piezoelectric Cylinders with a Sector Notch. Int. Appl. Mech. 2013, 49, 194–202. [Google Scholar] [CrossRef]
- Zhang, B.; Yu, J.G.; Zhang, X.M.; Ming, P.M. Complex guided waves in functionally graded piezoelectric cylindrical structures with sectorial cross-section. Appl. Math. Model. 2018, 63, 288–302. [Google Scholar] [CrossRef]
- Zuo, P.; Zhou, Y.; Fan, Z. Numerical studies of nonlinearly ultrasonic guided waves in uniform waveguides with arbitrary cross sections. Aip Adv. 2016, 6, 927–1010. [Google Scholar] [CrossRef]
- Fan, Z.; Lowe, M.J.; Castaings, M. Torsional waves propagation along a waveguide of arbitrary cross section immersed in a perfect fluid. J. Acoust. Soc. Am. 2008, 124, 2002–2010. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Yu, J.G.; Zhang, X.M. Guided wave propagation in cylindrical structures with sector cross-sections. Arch. Appl. Mech. 2017, 87, 1–12. [Google Scholar] [CrossRef]
- Yu, J.; Ma, Q.; Su, S. Wave propagation in non-homogeneous magneto-electro-elastic hollow cylinders. Ultrasonics 2008, 48, 664–677. [Google Scholar] [CrossRef] [PubMed]
- Srinivas, S.; Li, J.Y. The effective magneto-electro-elastic moduli of matrix-based multiferroic composites. J. Appl. Phys. 2006, 99, 043905. [Google Scholar] [CrossRef]
- Liu, Y.; Han, Q.; Huang, H.; Li, C.; Liu, X.; Wu, B. Computation of dispersion relations of functionally graded rectangular bars. Compos. Struct. 2015, 133, 31–38. [Google Scholar] [CrossRef]
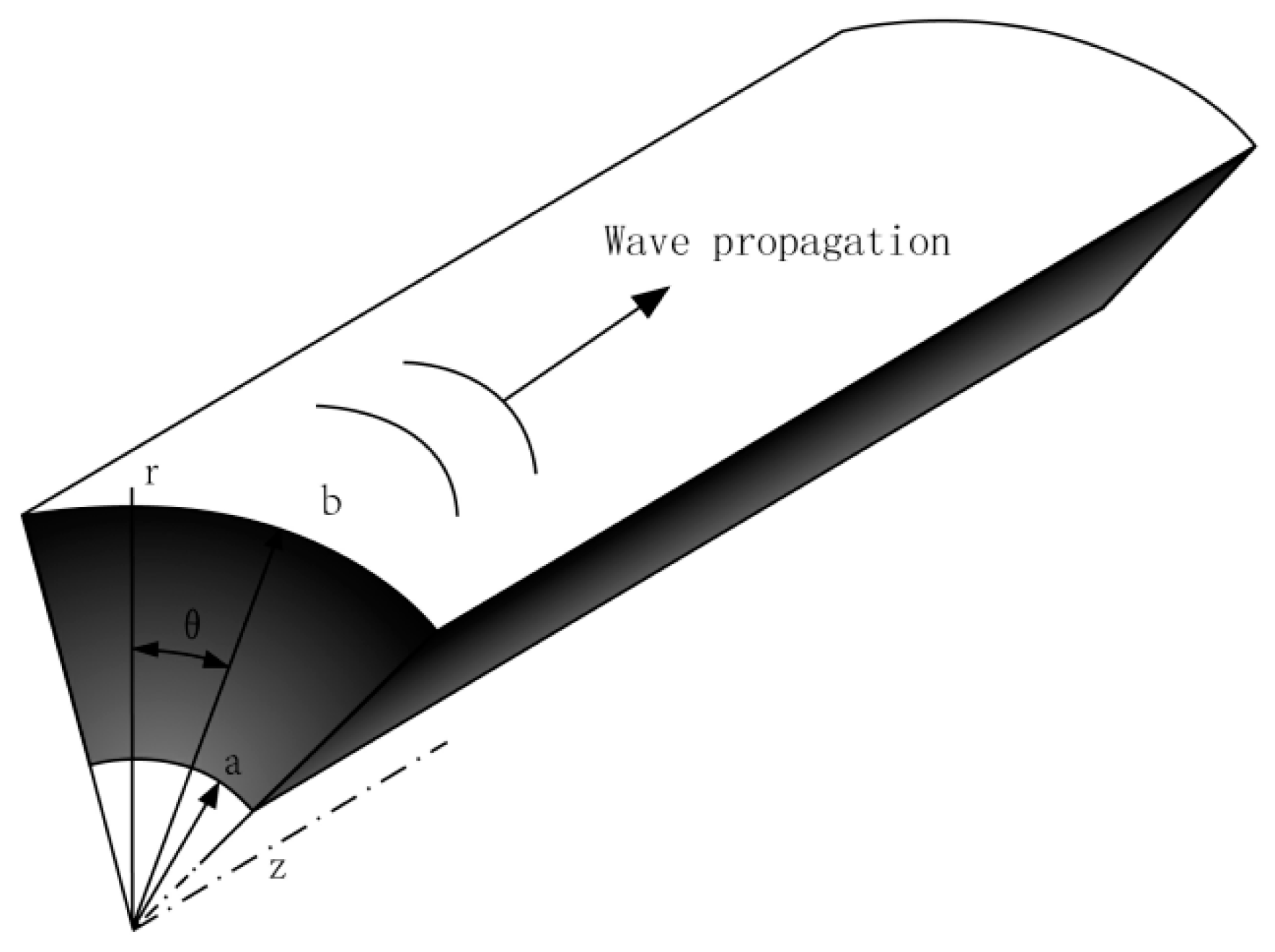
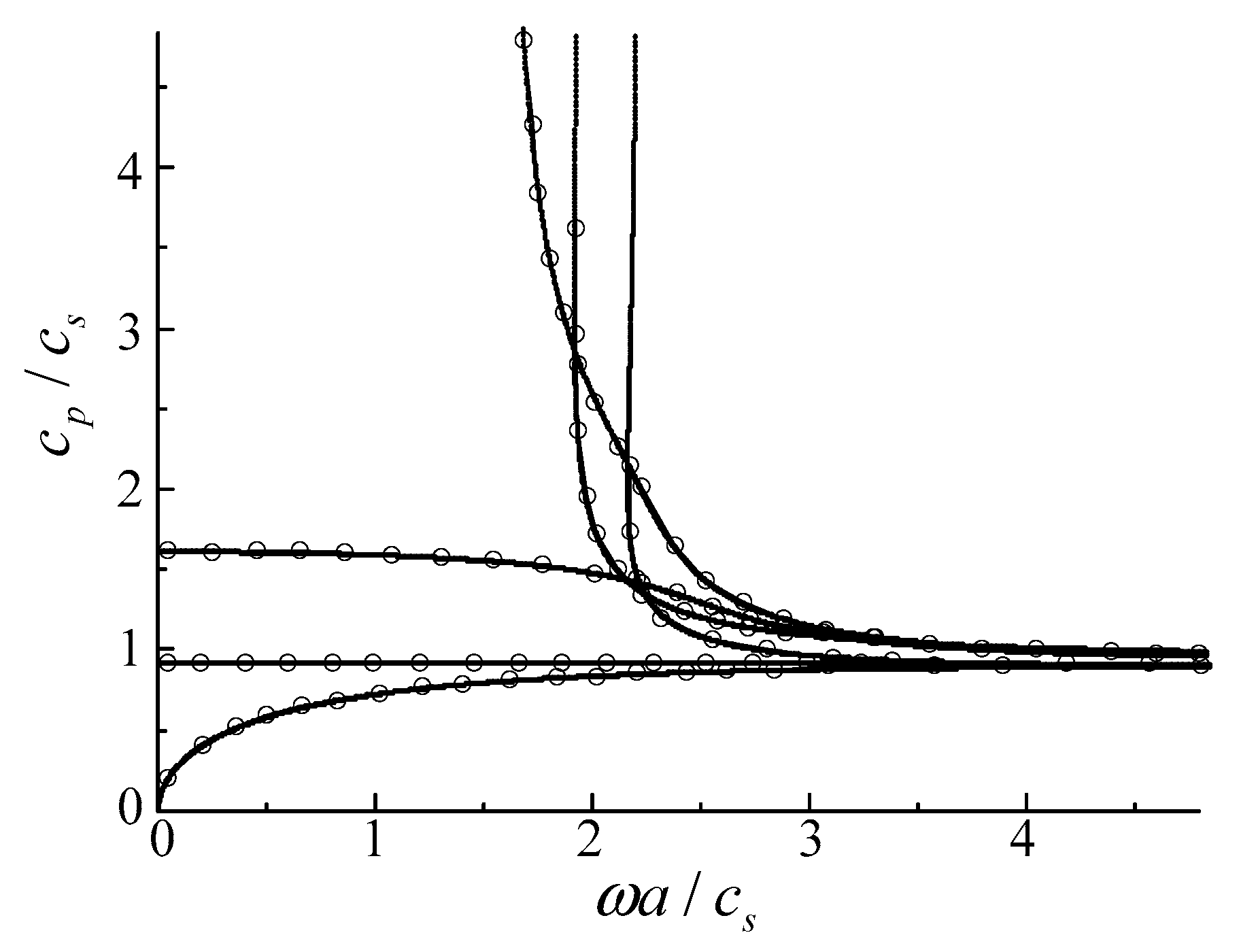
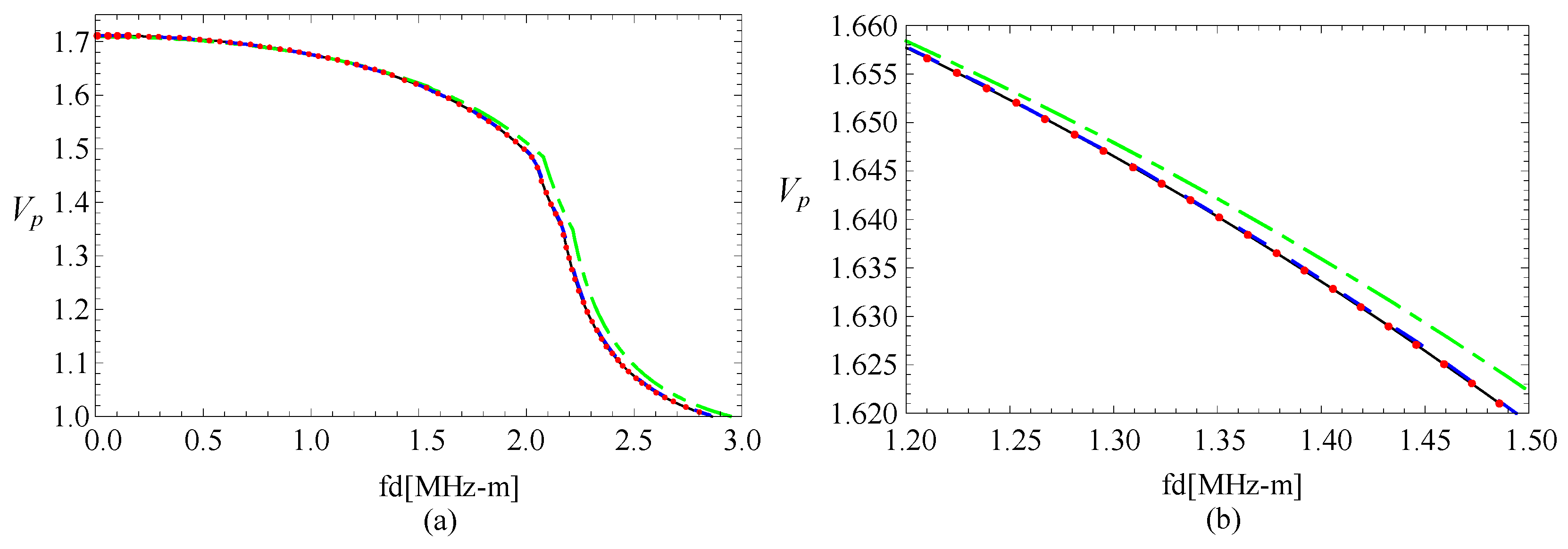
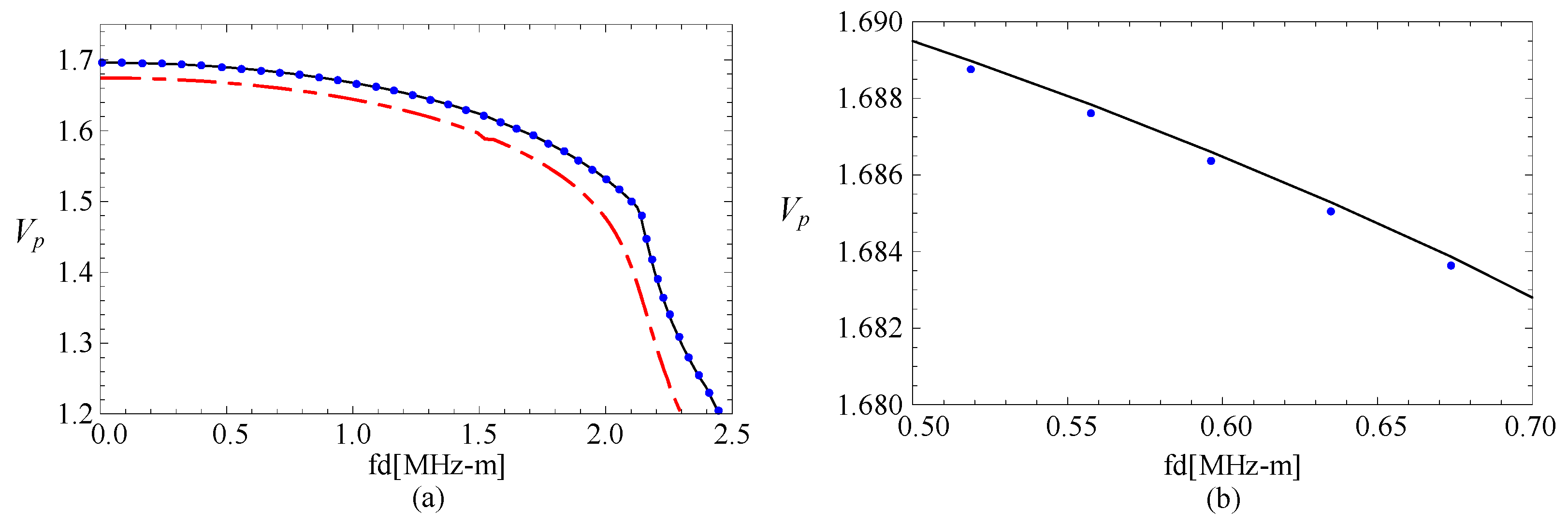
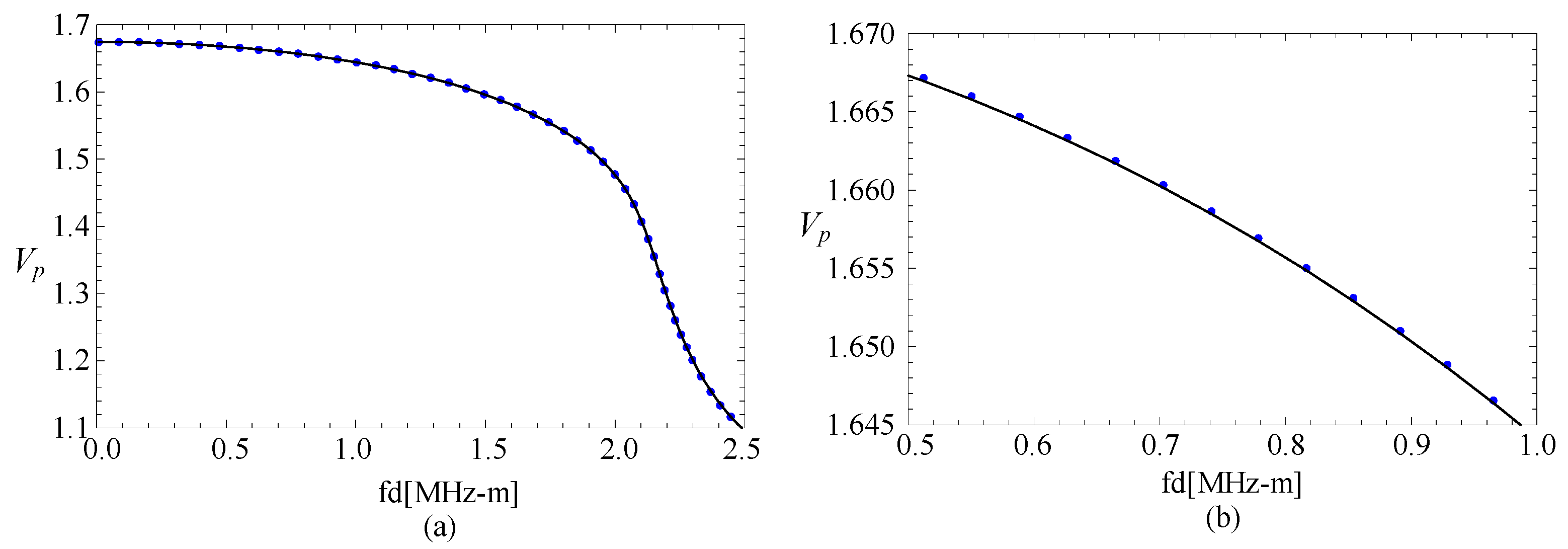
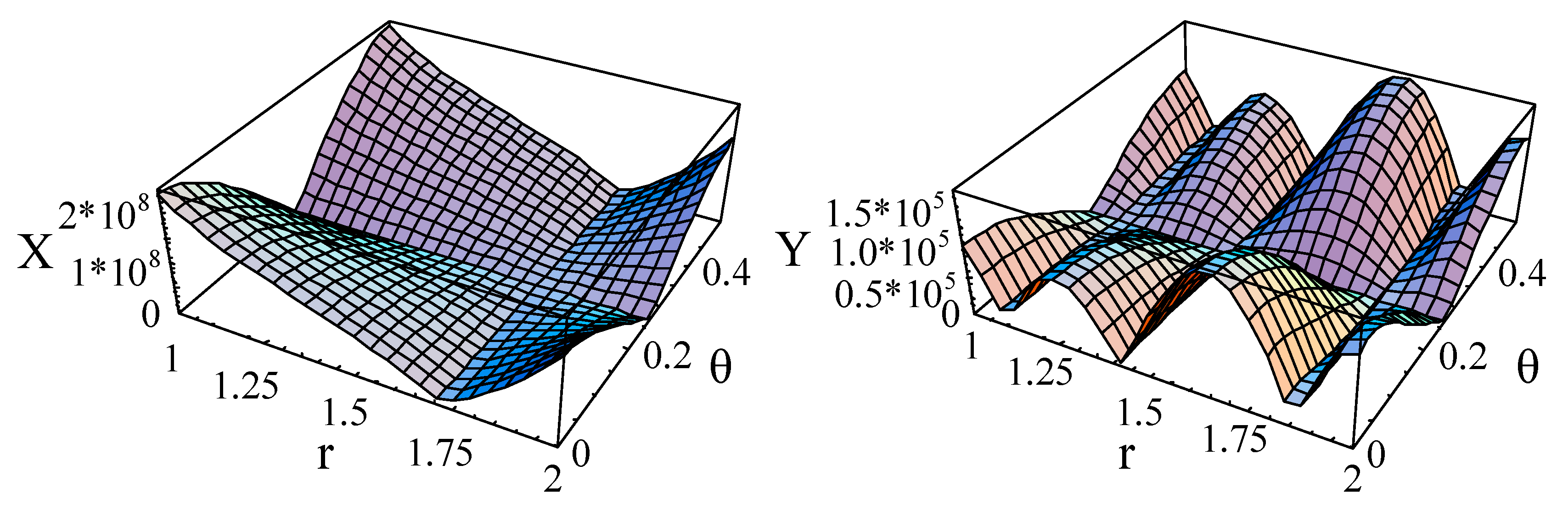
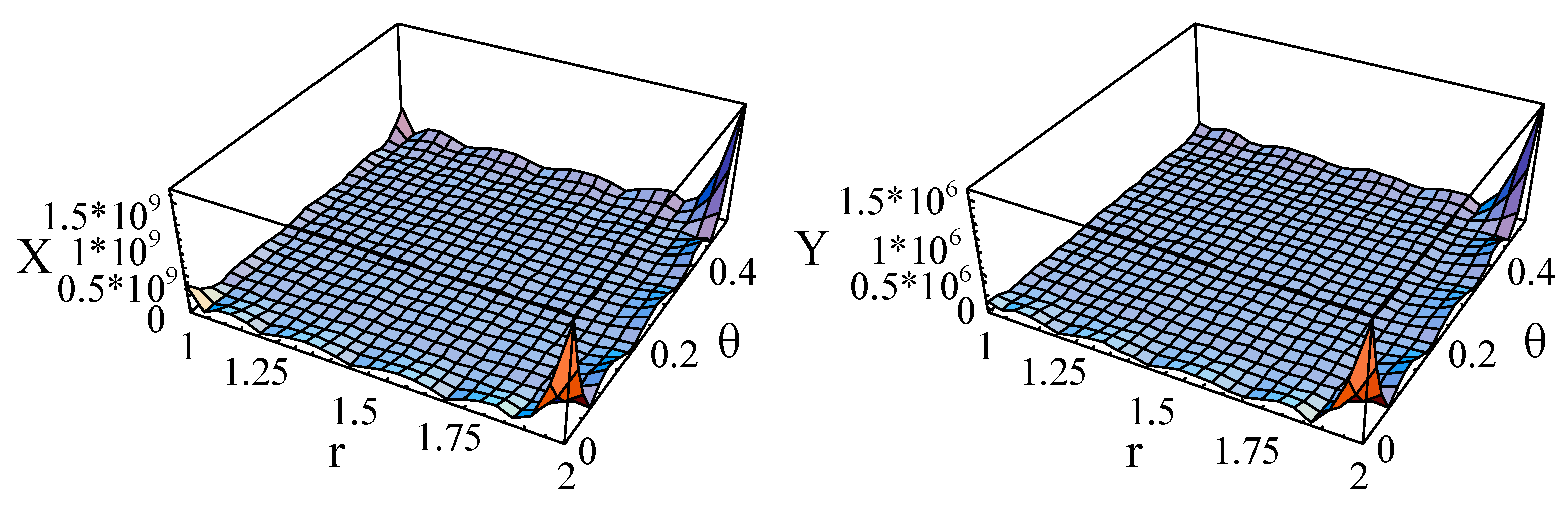
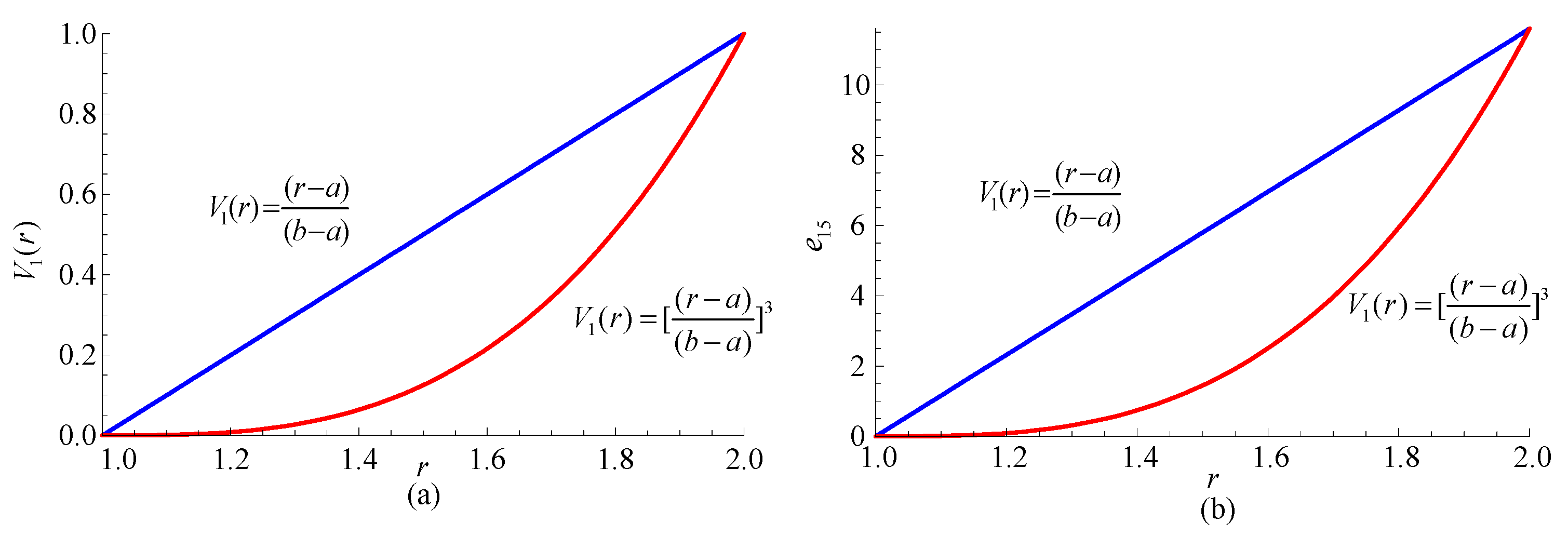
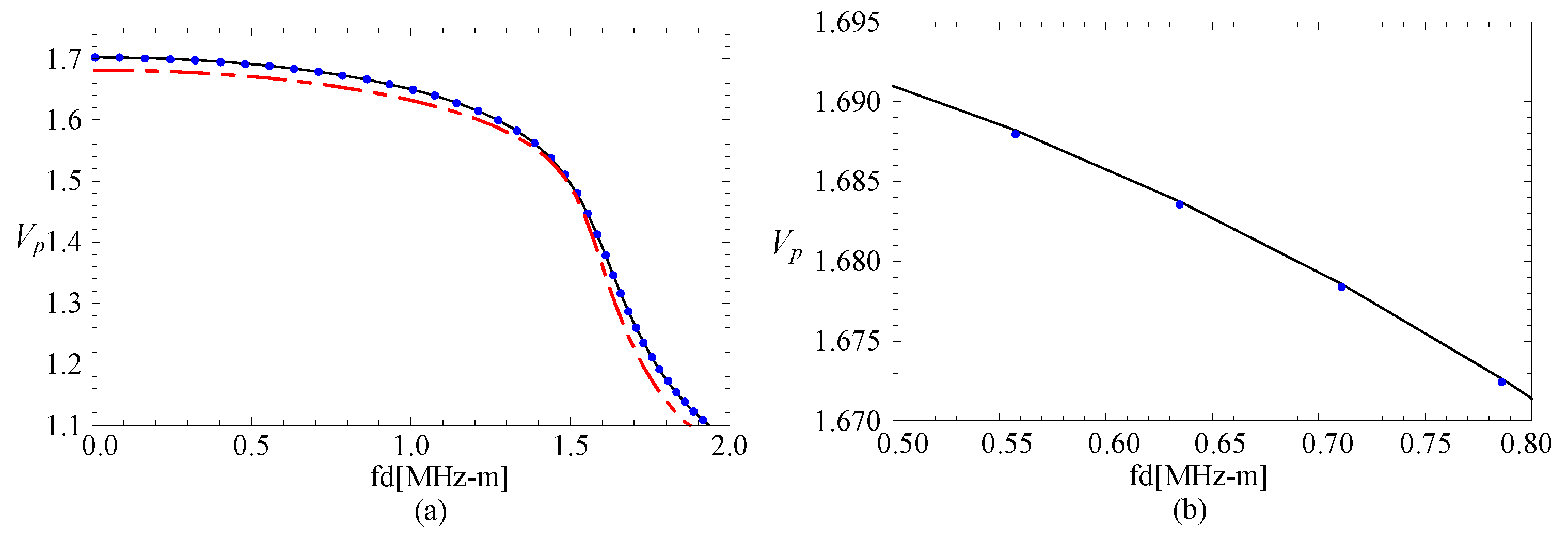
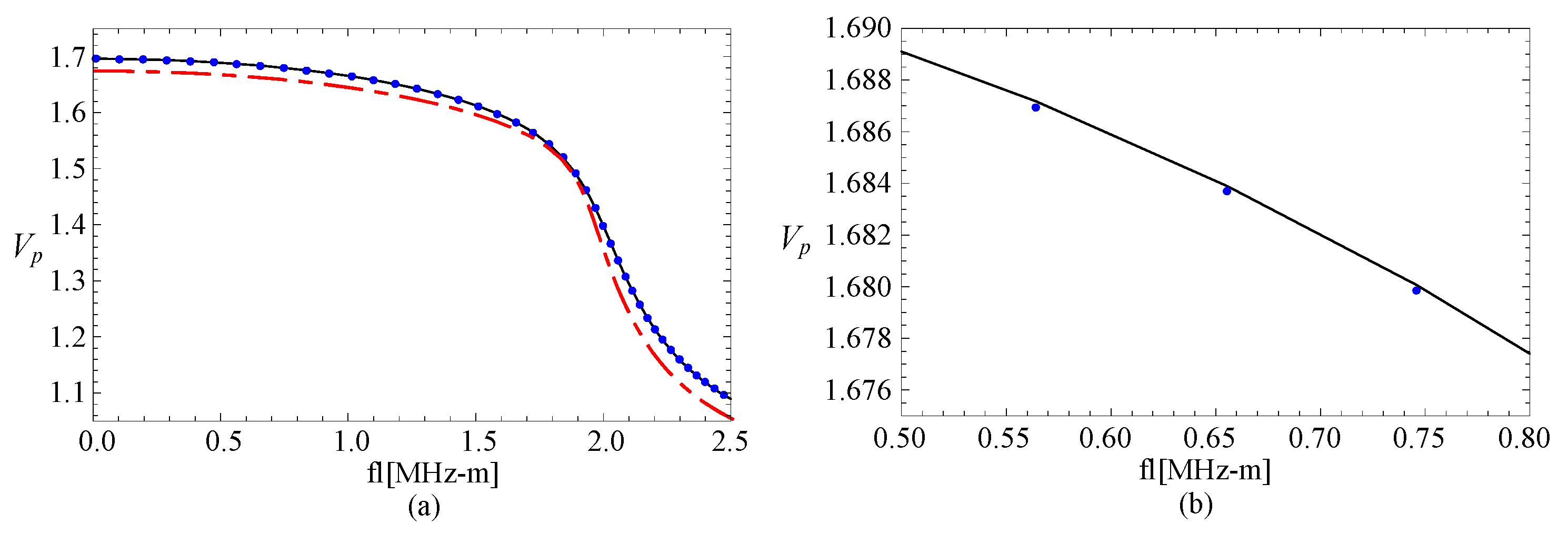
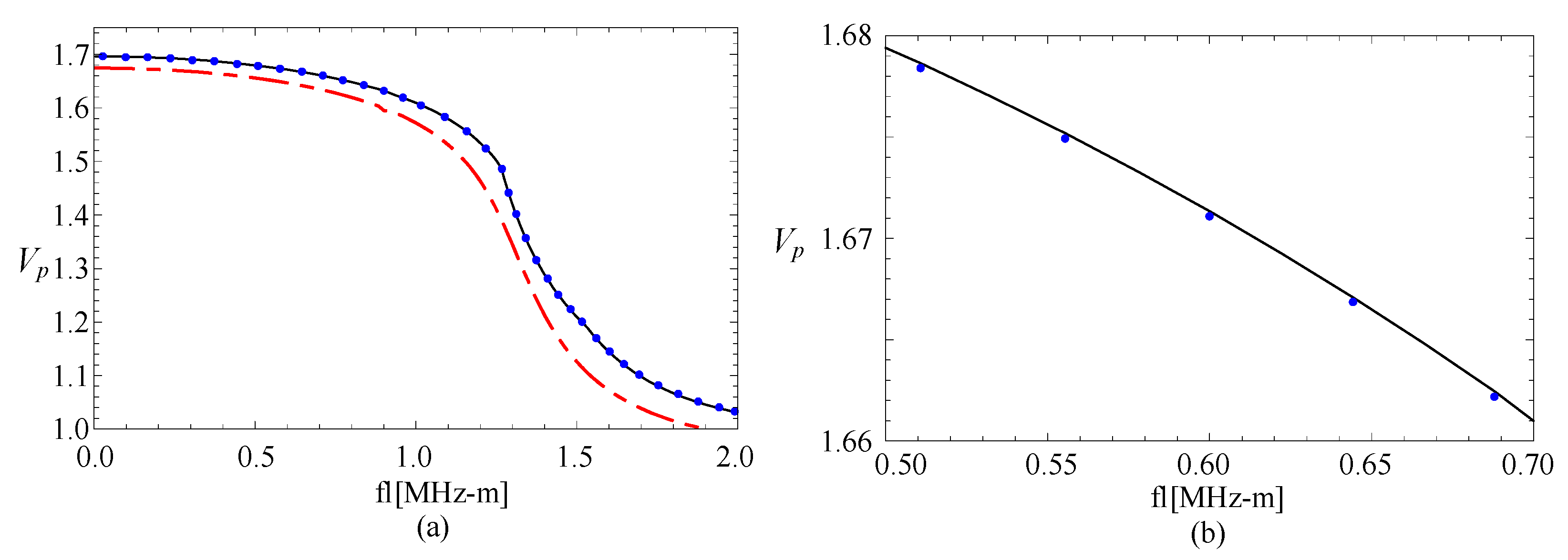

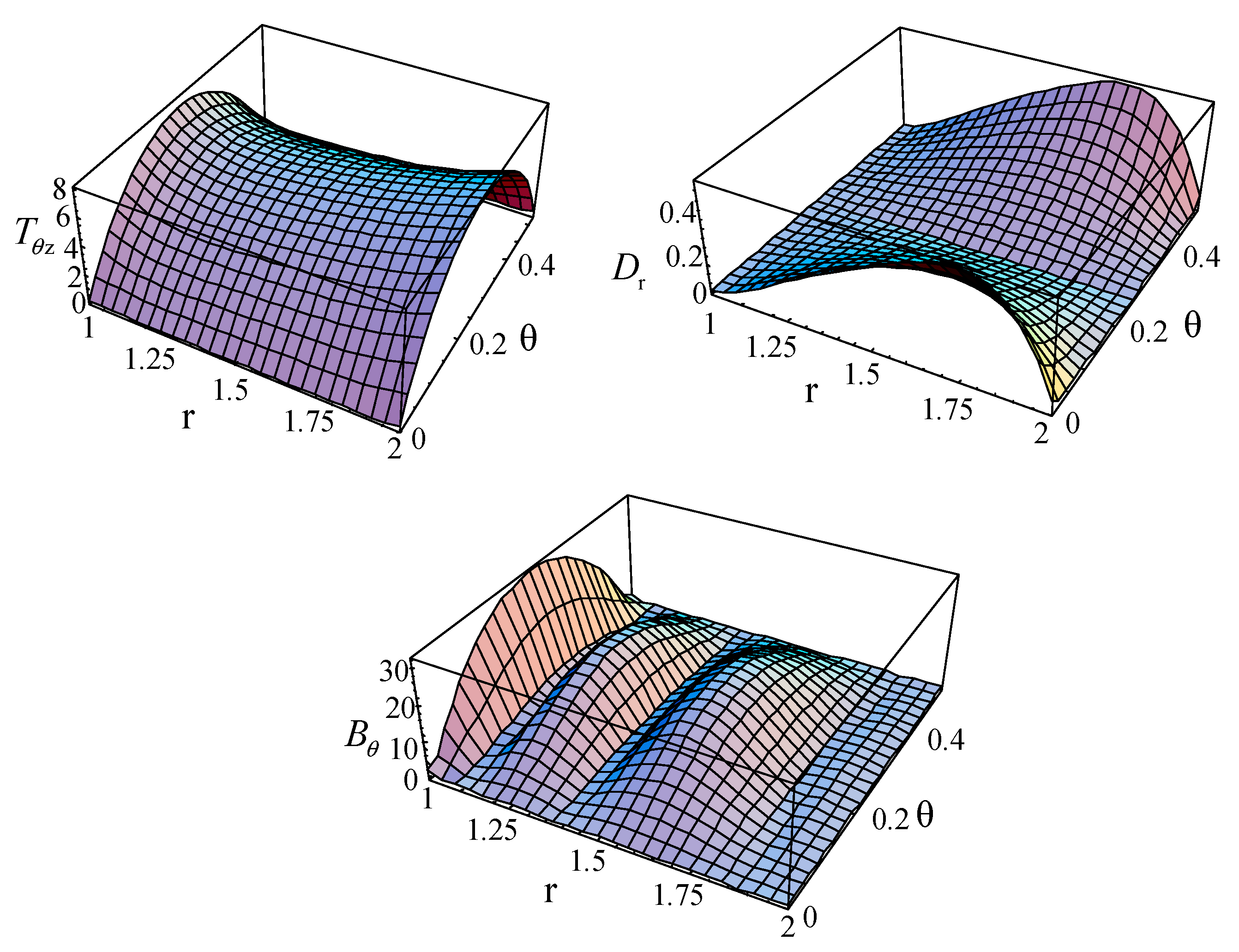
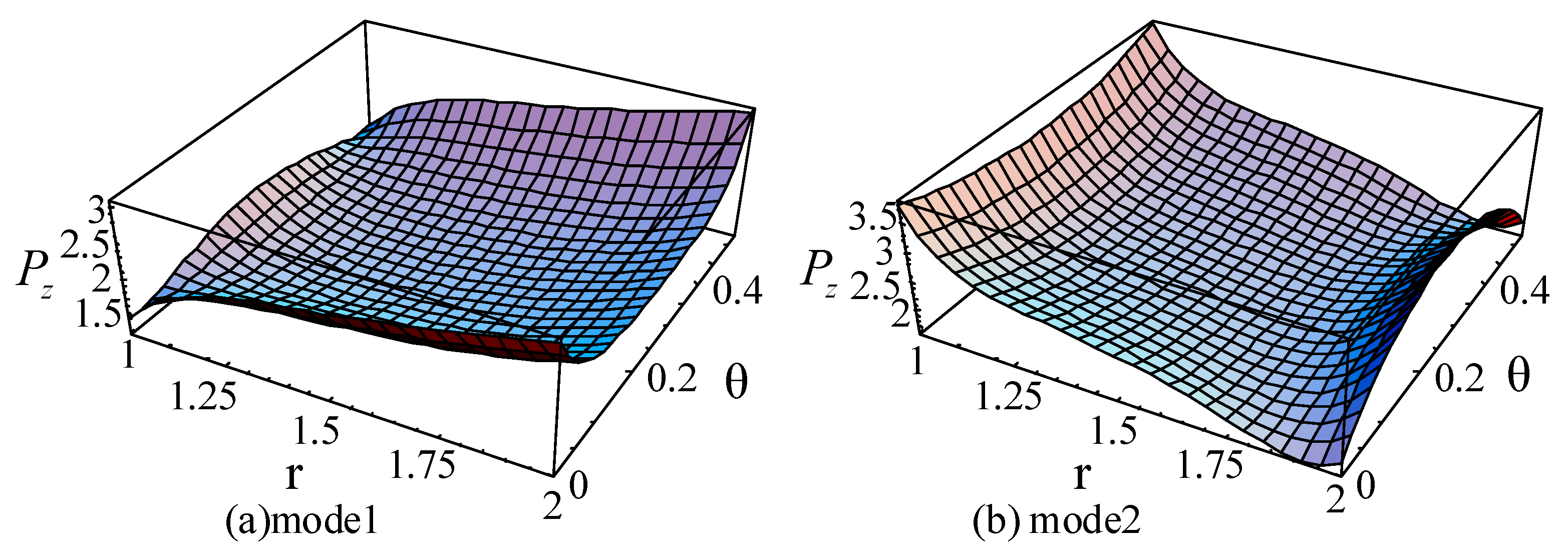
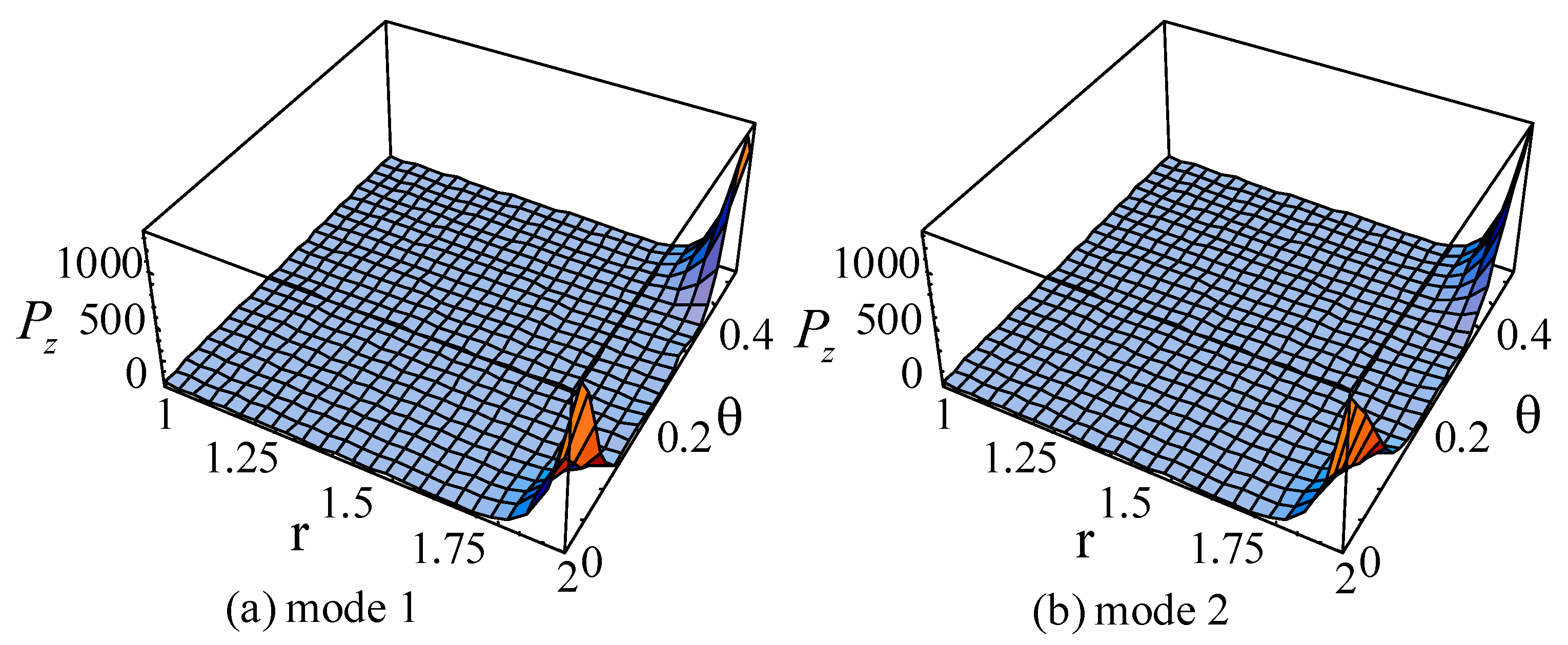
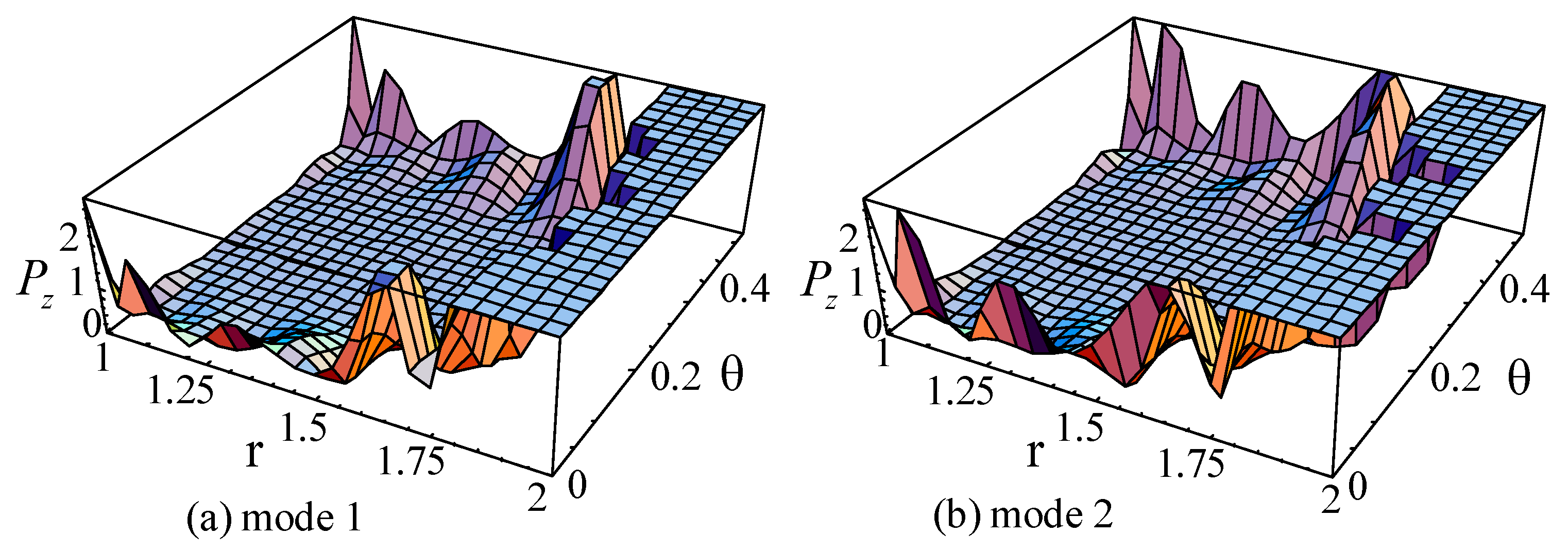
| M,J | Mode1 | Mode2 | Mode3 |
|---|---|---|---|
| 4,4 | 1054.86 | 1221.42 | 2564.77 |
| 4,5 | 1054.80 | 1221.34 | 2563.99 |
| 4,6 | 1054.79 | 1221.34 | 2563.12 |
| 5,4 | 1054.24 | 1220.87 | 2562.70 |
| 5,5 | 1054.19 | 1220.79 | 2561.84 |
| 5,6 | 1054.19 | 1220.79 | 2561.10 |
| 6,4 | 1054.27 | 1220.83 | 2560.59 |
| 6,5 | 1054.23 | 1220.75 | 2559.78 |
| 6,6 | 1054.22 | 1220.75 | 2559.17 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Yu, J.; Elmaimouni, L.; Zhang, X. Magneto-Electric Effect on Guided Waves in Functionally Graded Piezoelectric–Piezomagnetic Fan-Shaped Cylindrical Structures. Materials 2018, 11, 2174. https://doi.org/10.3390/ma11112174
Zhang B, Yu J, Elmaimouni L, Zhang X. Magneto-Electric Effect on Guided Waves in Functionally Graded Piezoelectric–Piezomagnetic Fan-Shaped Cylindrical Structures. Materials. 2018; 11(11):2174. https://doi.org/10.3390/ma11112174
Chicago/Turabian StyleZhang, Bo, Jiangong Yu, Lahoucine Elmaimouni, and Xiaoming Zhang. 2018. "Magneto-Electric Effect on Guided Waves in Functionally Graded Piezoelectric–Piezomagnetic Fan-Shaped Cylindrical Structures" Materials 11, no. 11: 2174. https://doi.org/10.3390/ma11112174
APA StyleZhang, B., Yu, J., Elmaimouni, L., & Zhang, X. (2018). Magneto-Electric Effect on Guided Waves in Functionally Graded Piezoelectric–Piezomagnetic Fan-Shaped Cylindrical Structures. Materials, 11(11), 2174. https://doi.org/10.3390/ma11112174





