Dynamic Loading of Lattice Structure Made by Selective Laser Melting-Numerical Model with Substitution of Geometrical Imperfections
Abstract
:1. Introduction
2. Materials and Methods
2.1. Speciments Fabrication Using SLM
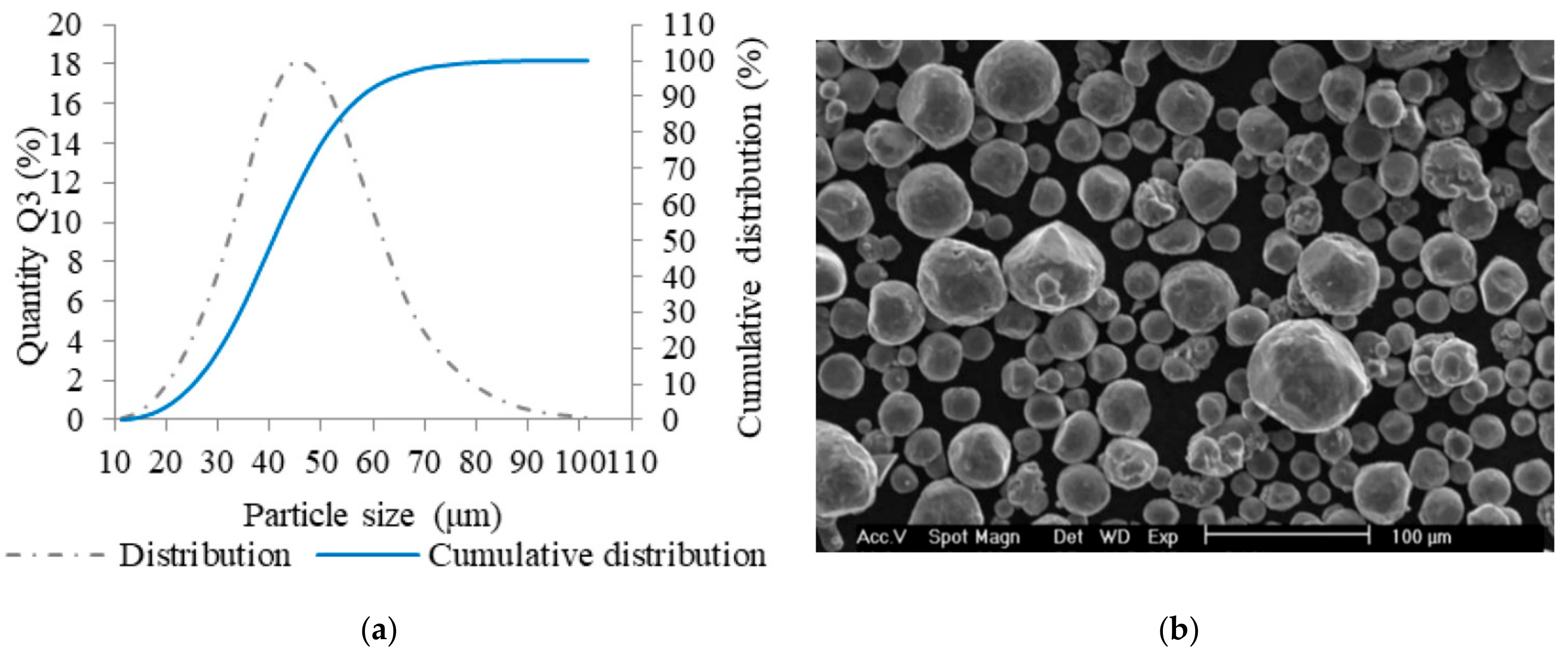
2.2. Metal Powder Analysis
2.3. Specimens for Mechanical Testing
2.3.1. Tensile Specimens
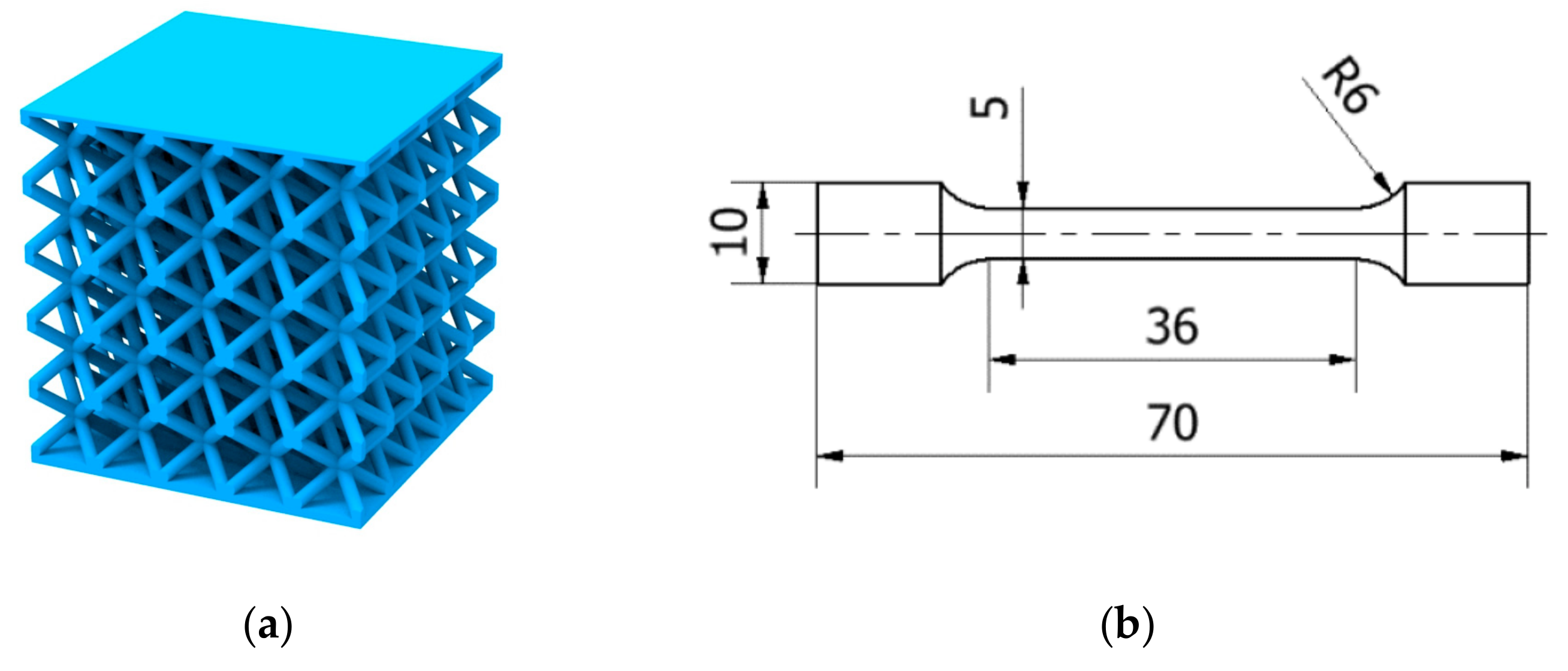
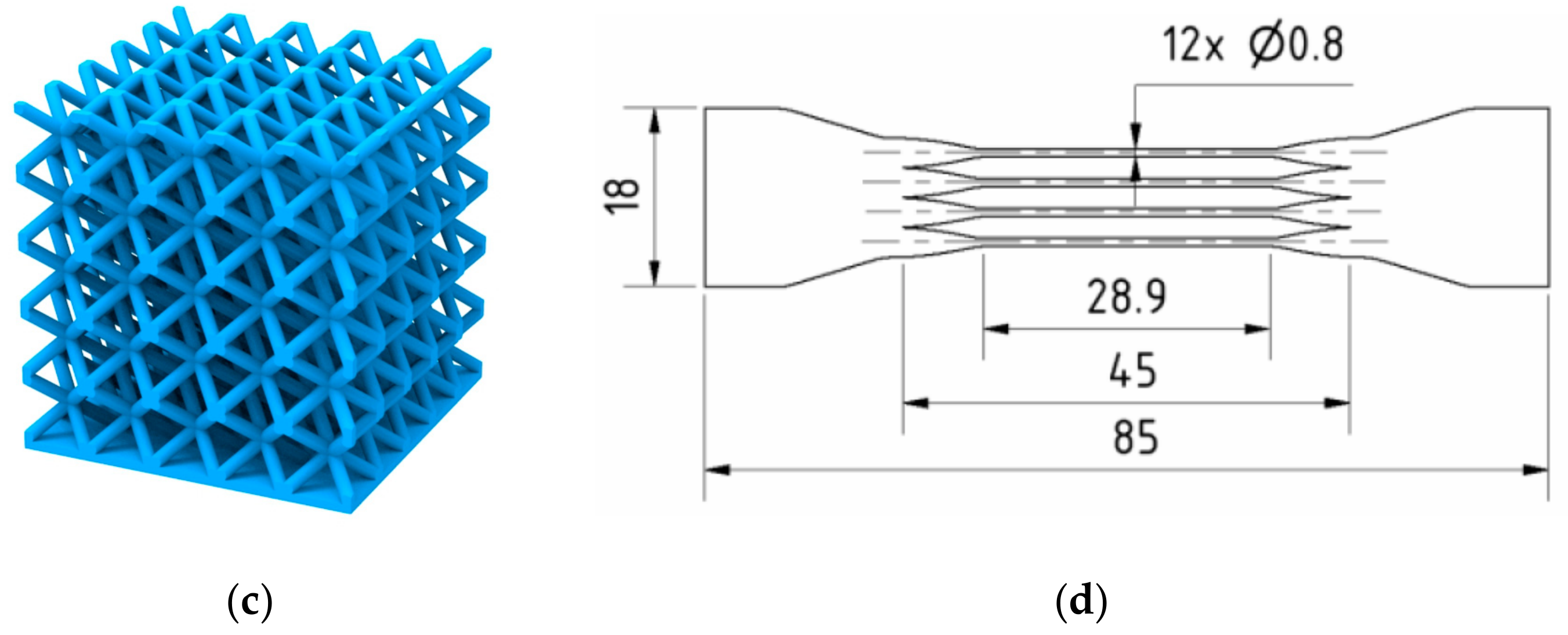
2.3.2. Lattice Structure Specimens
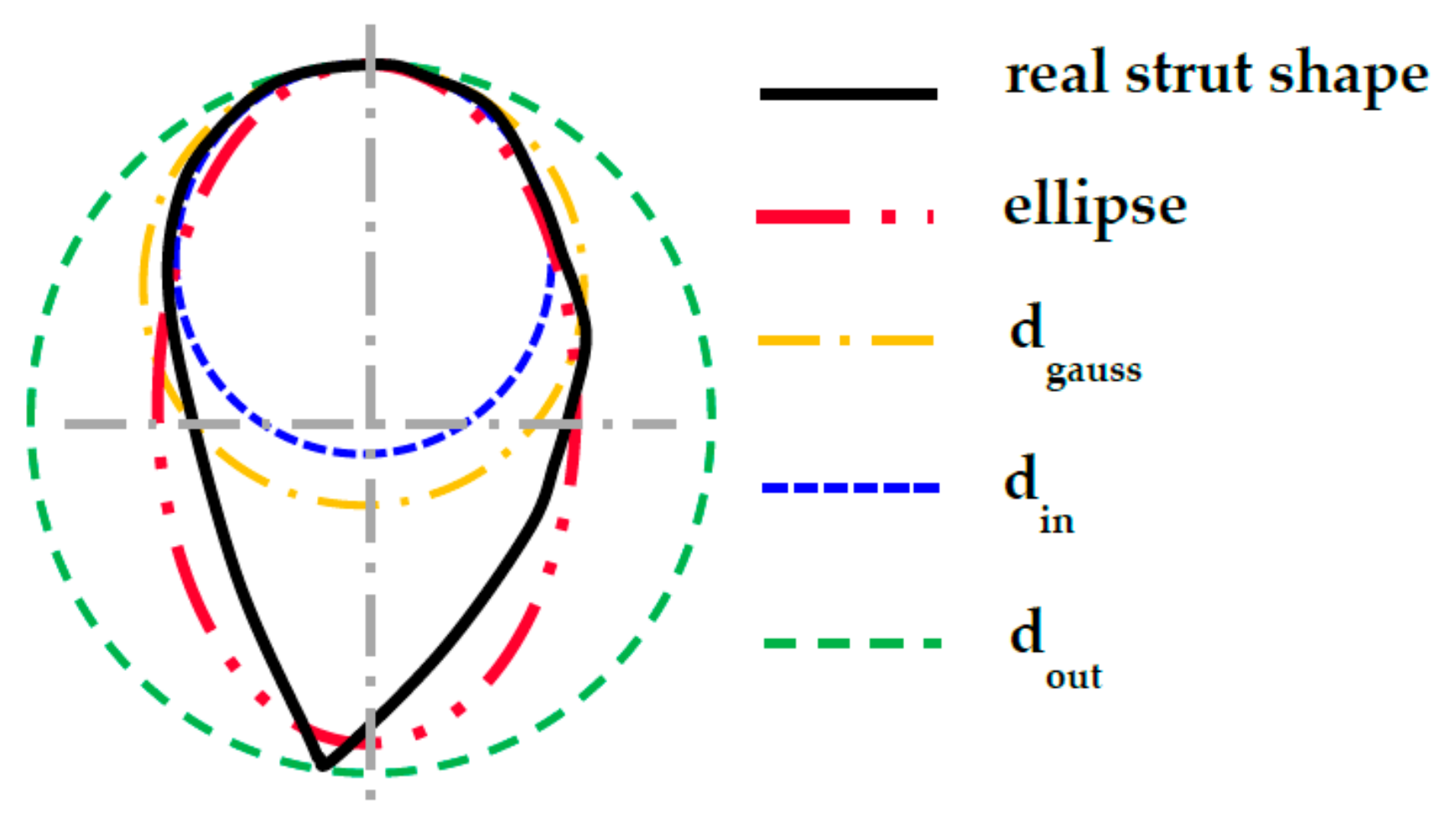
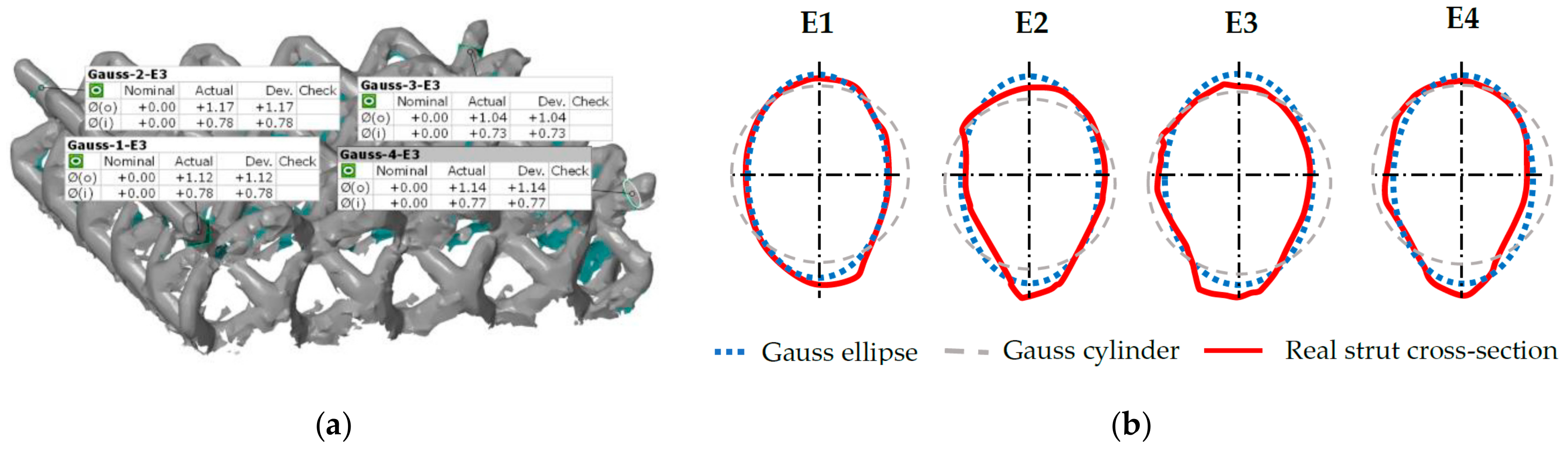
2.4. Shape of the Struts Analysis
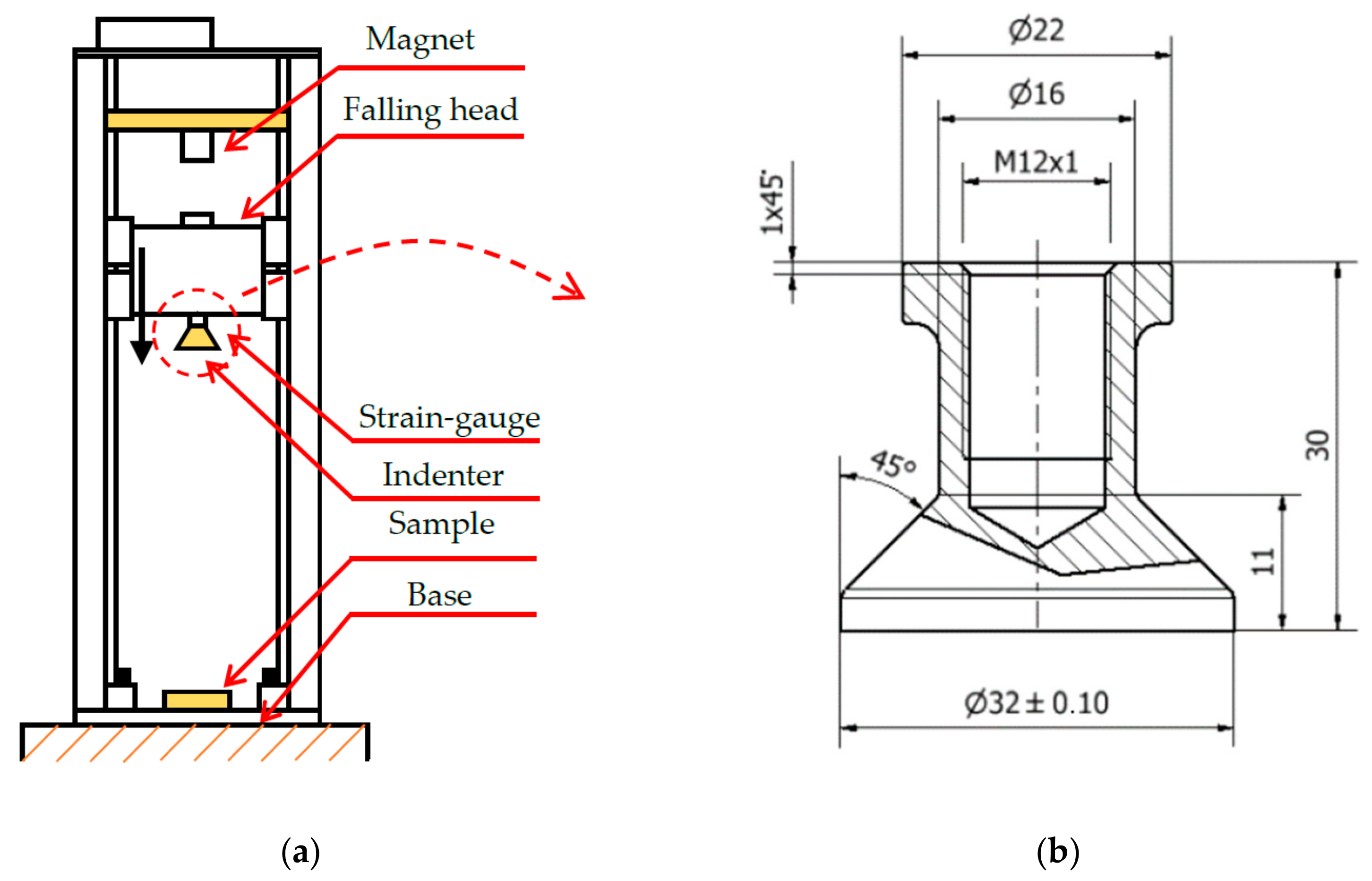
2.5. Mechanical Testing
2.5.1. Quasi-Static Mechanical Testing
2.5.2. Low-Velocity Impact Test
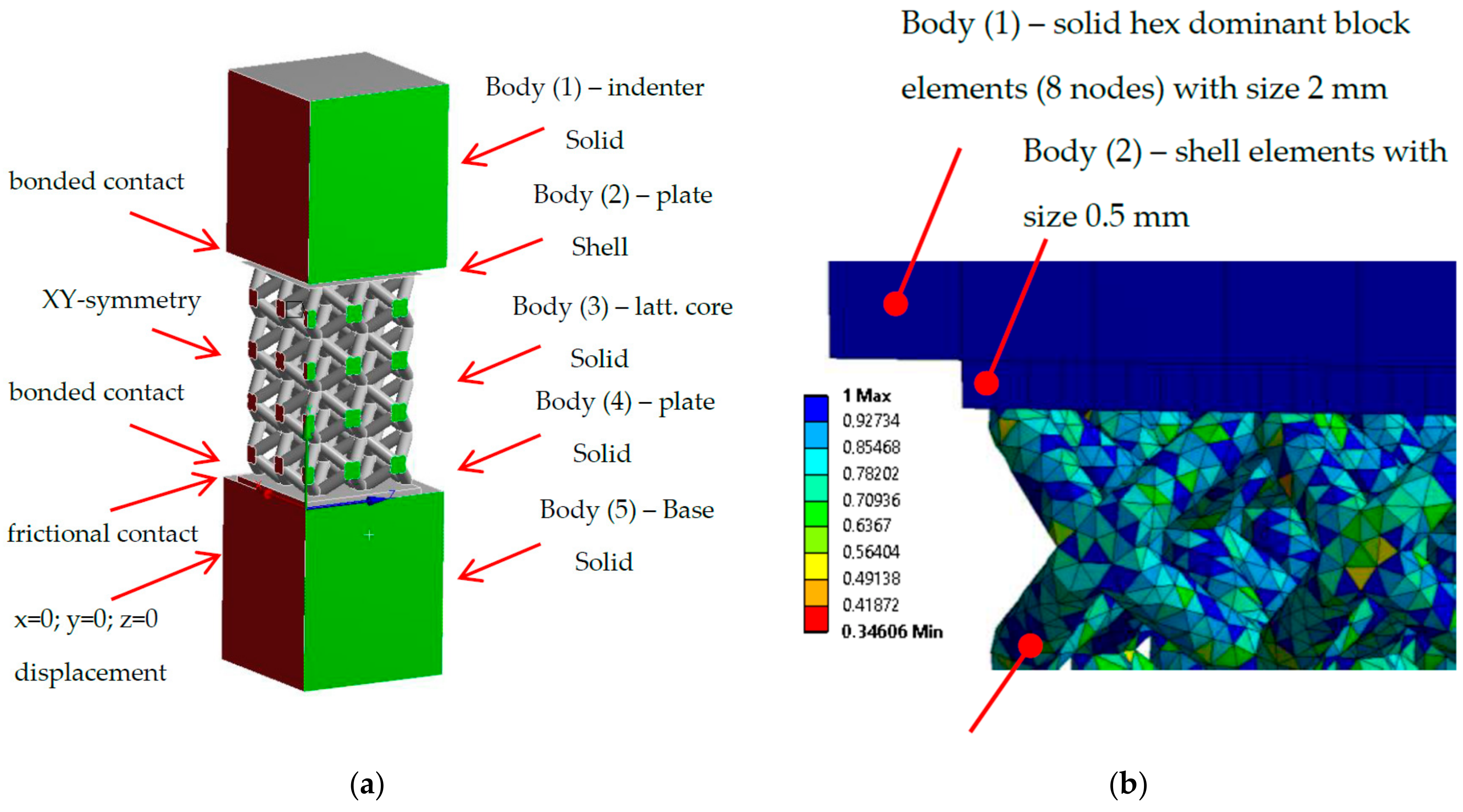
2.6. FEM Numerical Model
3. Results
3.1. The Analysis of Initial Weight and Height
3.2. Optical Measurement of the Lattice Structure
3.3. Mechanical Properties
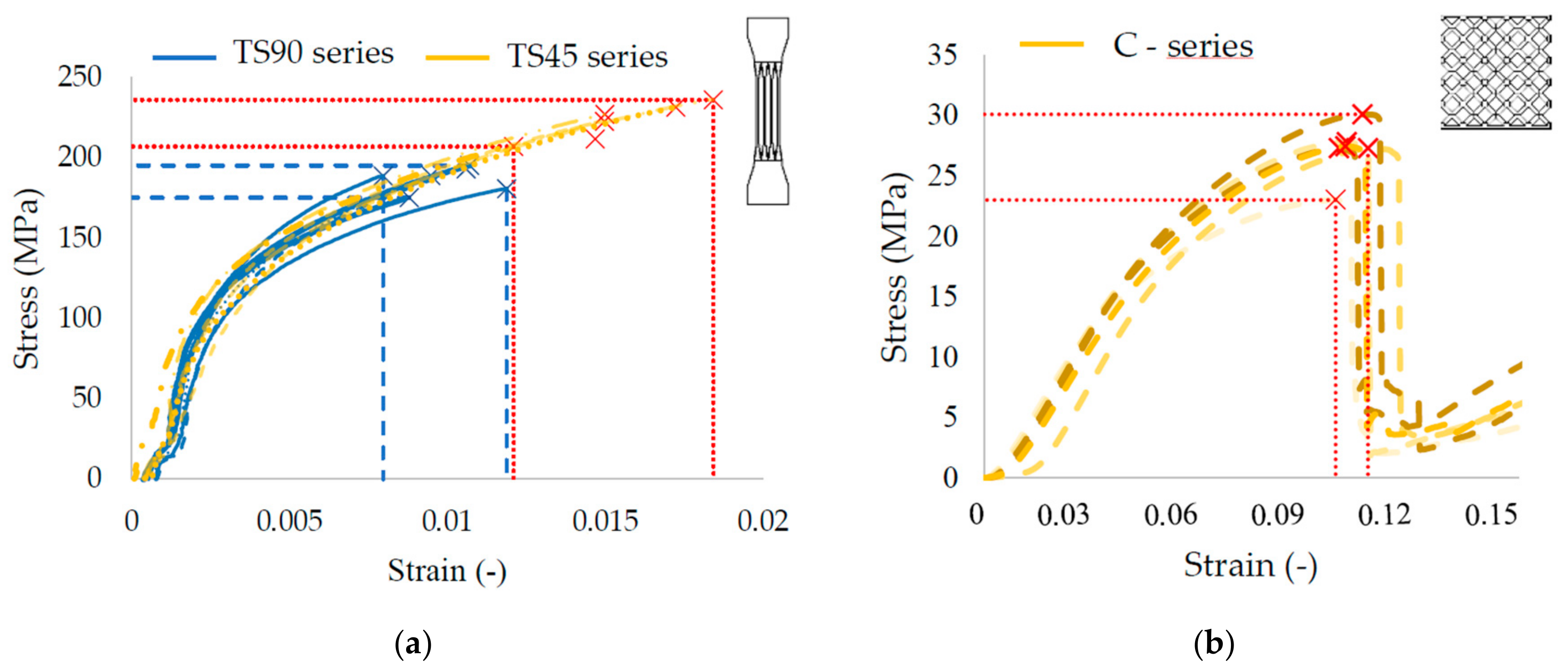
3.3.1. Quasi-Static Mechanical Testing
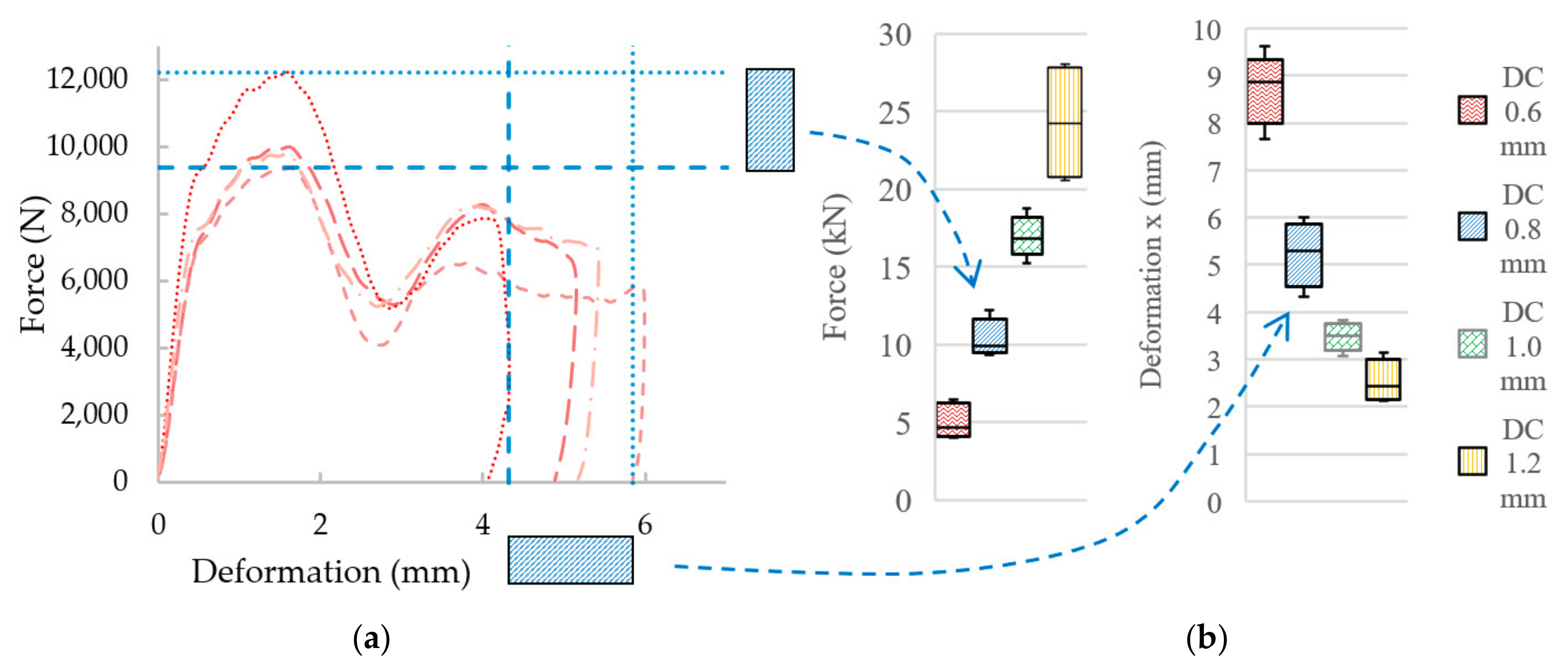
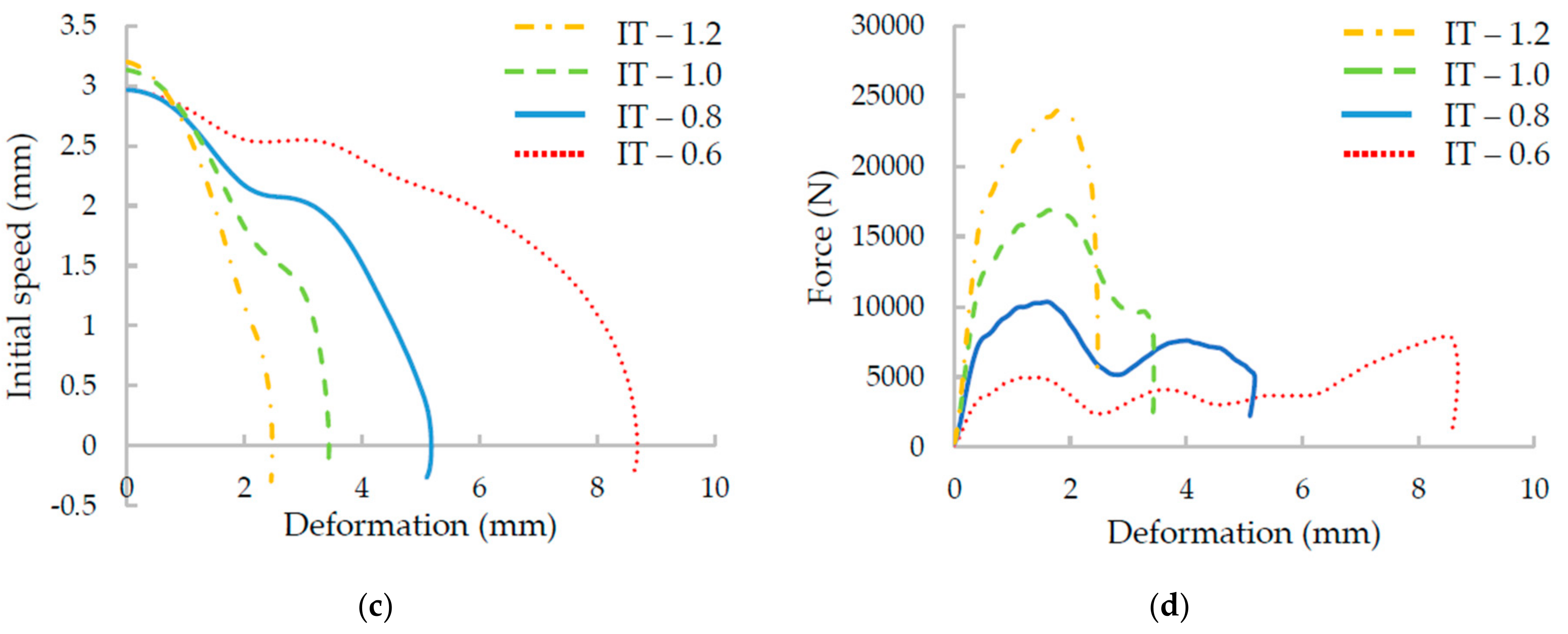
3.3.2. Low-Velocity Impact Test Results
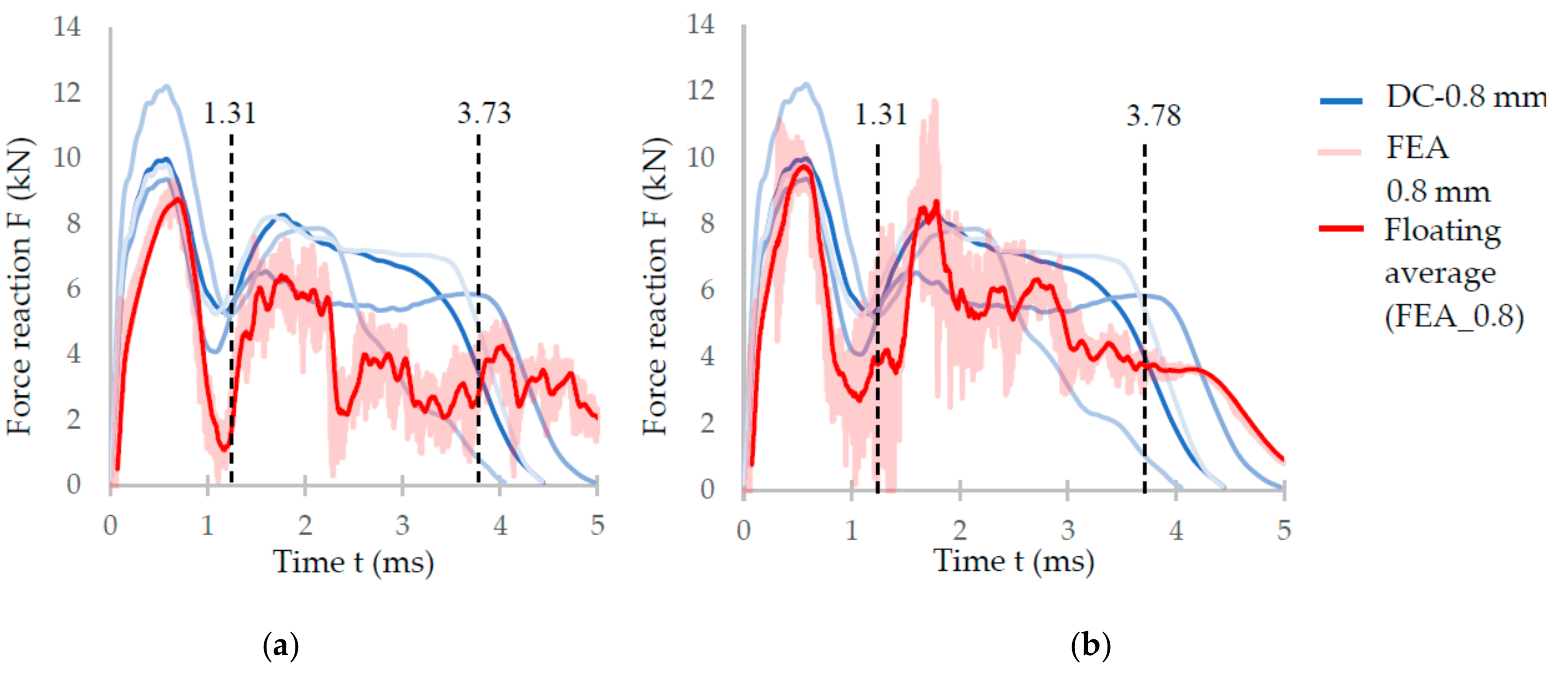
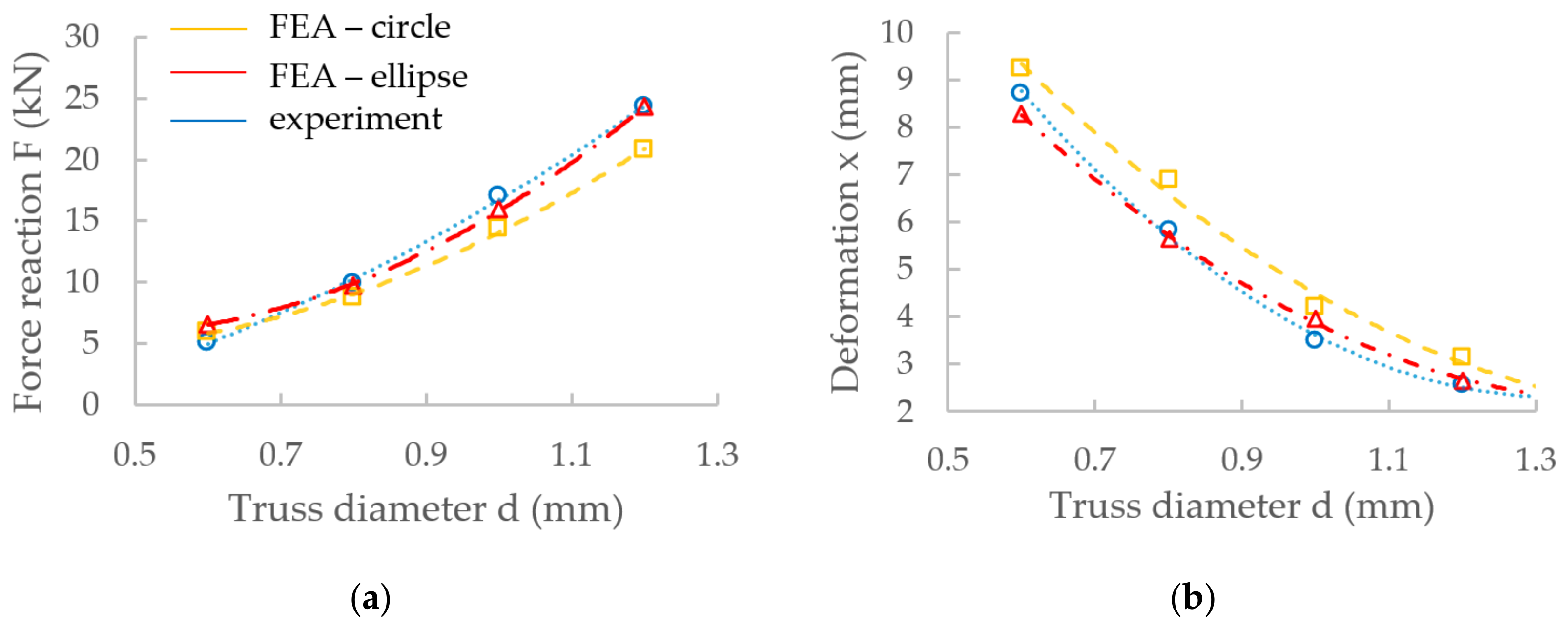
3.4. Finite Element Analysis (FEA)
3.4.1. FEA Material Models
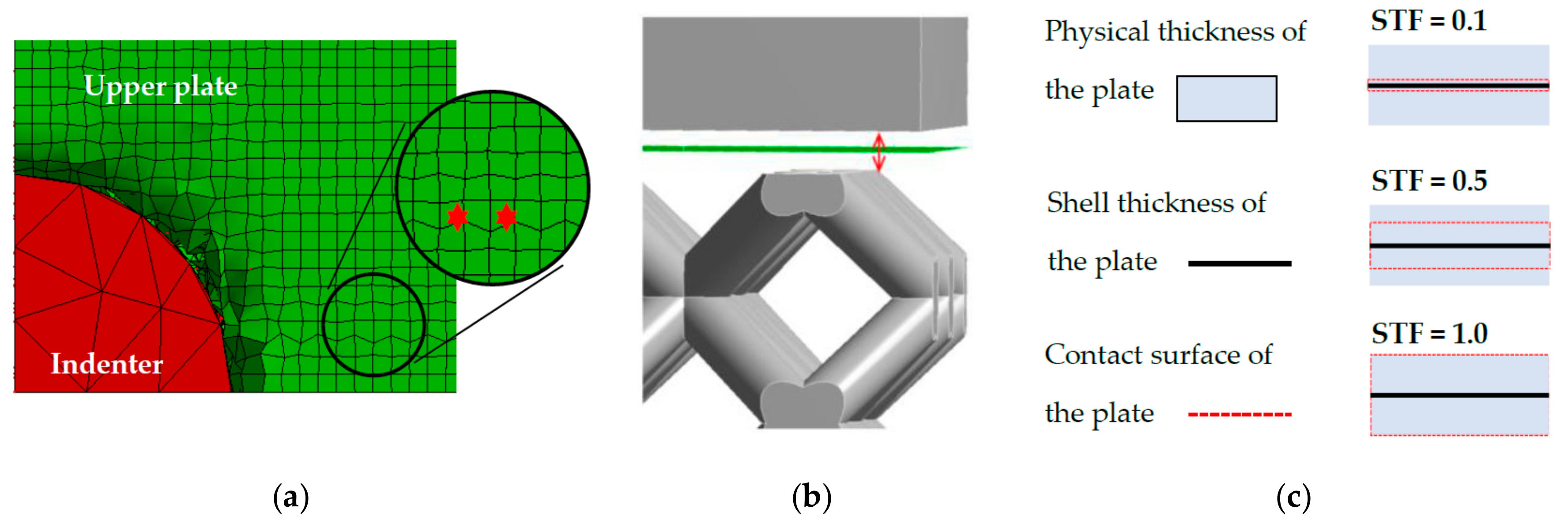
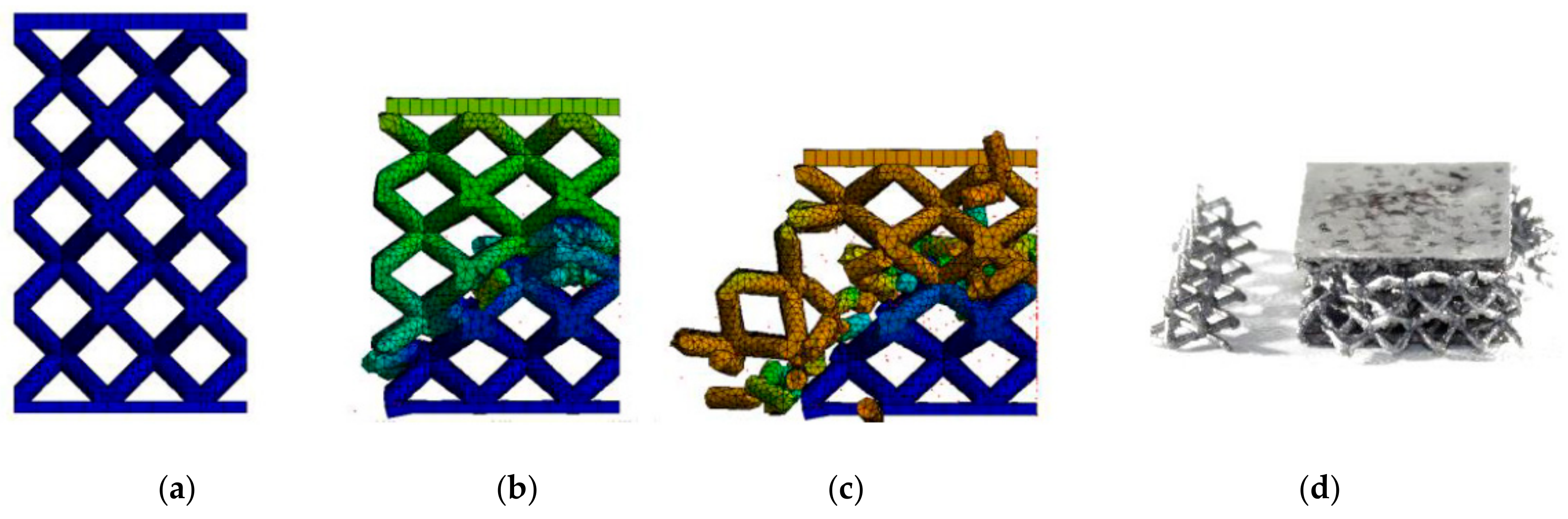
3.4.2. FEM Model
4. Discussion
4.1. Substitution of the Strut’s Real Cross-Section with the Ideal Cross-Section
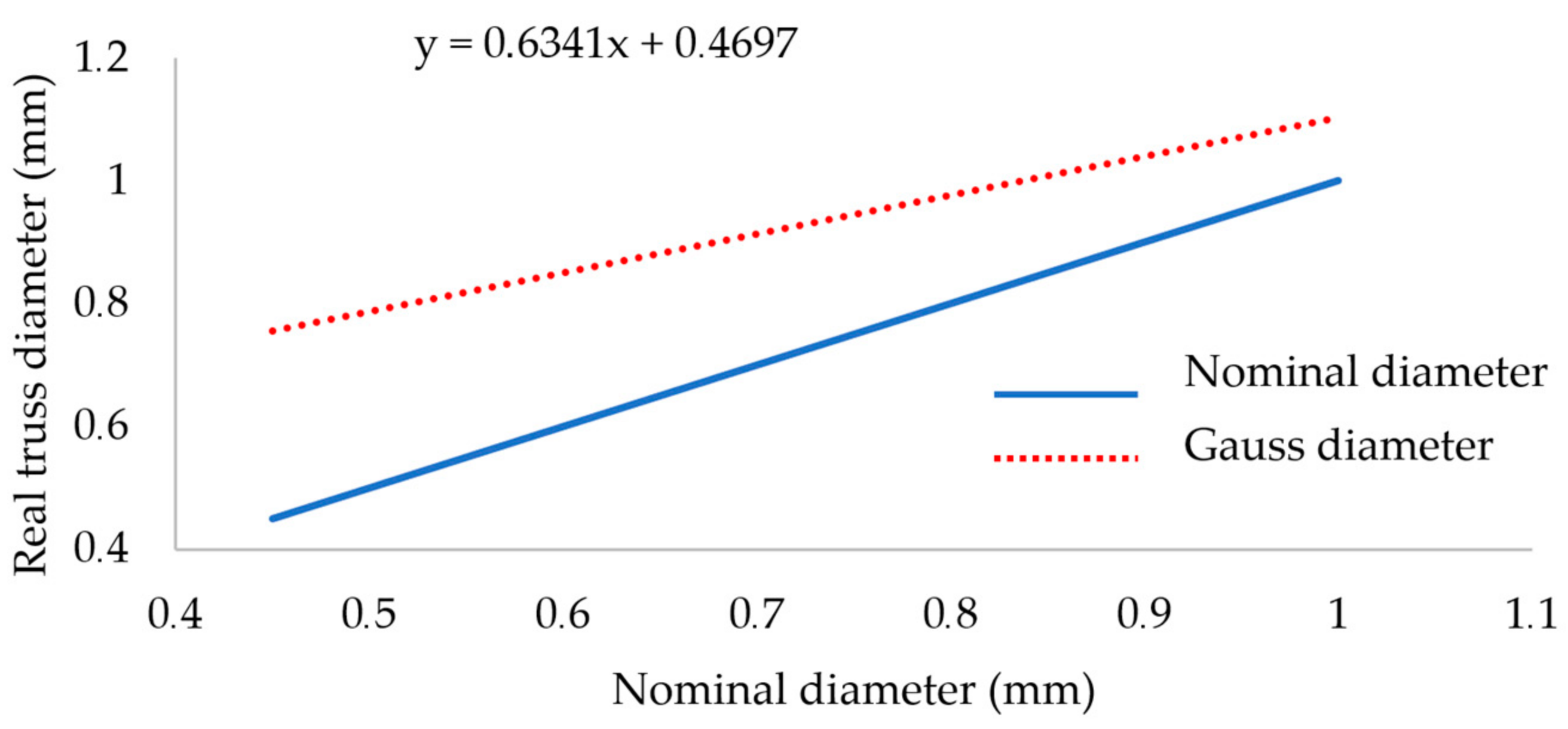
4.2. Application of Numerical Model to BCC Lattice Structures with Struts Diameter between 0.6–1.2 mm
4.3. Mechanical Testing
4.4. Criterion of Damage
5. Conclusions
- The numerical model of BCC micro-lattice structure under dynamic loading with the elliptic strut shape was developed. The results show that the elliptic shape of the lattice structure significantly decreases a deviation between FEA and the measured results compared to the circular cross-section (10%, measured in the first force peak).
- To find the correct mechanical properties for FEA material model, it is necessary to use the struts specimens with appropriate orientation during production due to the influence of internal porosity and surface roughness.
- The orientation during SLM production significantly influences the mechanical properties.
- The shape of the BCC lattice structure was analyzed using optical methods. A distinct “water drop” shape was found in the case of AlSi10Mg alloy.
- A weight comparison of the CAD design and the produced lattice structure shows that for simplification of the “water drop” shape of the strut, the Gaussian strut diameter should be used.
- The results of quasi-static mechanical testing show that the differences between mechanical properties of the 90° and 45° orientation are mainly in the plastic area of deformation and may by caused by the significant surface roughness.
Author Contributions
Funding
Conflicts of Interest
References
- Karagiozova, D. Dynamic buckling of elastic-plastic square tubes under axial impact—I: Stress wave propagation phenomenon. Int. J. Impact Eng. 2004, 30, 143–166. [Google Scholar] [CrossRef]
- Li, X.; Zhang, P.; Wang, Z.; Wu, G.; Zhao, L. Dynamic behavior of aluminum honeycomb sandwich panels under air blast: Experiment and numerical analysis. Compos. Struct. 2014, 108, 1001–1008. [Google Scholar] [CrossRef]
- Olabi, A.G.; Morris, E.; Hashmi, M.S.J. Metallic tube type energy absorbers: A synopsis. Thin Walled Struct. 2007, 45, 706–726. [Google Scholar] [CrossRef] [Green Version]
- Dharmasena, K.P.; Wadley, N.G.; Xue, Z.; Hutchinson, J.W. Mechanical response of metallic honeycomb sandwich panel structures to high-intensity dynamic loading. Int. J. Impact Eng. 2008, 35, 1063–1074. [Google Scholar] [CrossRef]
- Kopanidis, A.; Theodorakakos, A.; Gavaises, E.; Bouris, D. 3D numerical simulation of flow and conjugate heat transfer through a pore scale model of high porosity open cell metal foam. Int. J. Heat Mass Transf. 2010, 53, 2539–2550. [Google Scholar] [CrossRef]
- Shimizu, T.; Matsuzaki, K.; Nagai, H.; Kanetake, N. Production of high porosity metal foams using EPS beads as space holders. Mater. Sci. Eng. A 2012, 558, 343–348. [Google Scholar] [CrossRef]
- Zhu, L.; Guo, K.; Li, Y.; Yu, T.X.; Zhou, Q. Experimental study on the dynamic behaviour of aluminium foam sandwich plates under single and repeated impacts at low temperature. Int. J. Impact Eng. 2018, 114, 123–132. [Google Scholar] [CrossRef]
- Sun, B.; Zhang, R.; Zhang, Q.; Gideon, R.; Gu, B. Drop-weight impact damage of three-dimensional angle-interlock woven composites. J. Compos. Mater. 2013, 47, 2193–2209. [Google Scholar] [CrossRef]
- Vrana, R.; Koutny, D.; Paloušek, D. Impact Resistance of Different Types of Lattice Structures Manufactured by SLM. MM Sci. J. 2016, 2016, 1579–1585. [Google Scholar] [CrossRef]
- Mines, R.A.W.; Tsopanos, S.; Shen, Y.; Hasan, R.; McKown, S.T. Drop weight impact behaviour of sandwich panels with metallic micro lattice cores. Int. J. Impact Eng. 2013, 60, 120–132. [Google Scholar] [CrossRef]
- Harris, J.A.; Winter, R.E.; McShane, G.J. Impact response of additively manufactured metallic hybrid lattice materials. Int. J. Impact Eng. 2017, 104, 177–191. [Google Scholar] [CrossRef]
- Yadroitsev, I. Selective Laser Melting: Direct Manufacturing of 3D-Objects by Selective Laser Melting of Metal Powders; LAP Lambert: Saarbrücken, Germany, 2009. [Google Scholar]
- Thijs, L.; Kempen, K.; Kruth, J.-P.; van Humbeeck, J. Fine-structured aluminium products with controllable texture by selective laser melting of pre-alloyed AlSi10Mg powder. Acta Mater. 2013, 61, 1809–1819. [Google Scholar] [CrossRef] [Green Version]
- Qiu, C.; Yue, S.; Adkins, N.J.E.; Ward, M.; Hassanin, H.; Lee, P.D.; Withers, P.J.; Attallah, M.M. Influence of processing conditions on strut structure and compressive properties of cellular lattice structures fabricated by selective laser melting. Mater. Sci. Eng. A 2015, 628, 188–197. [Google Scholar] [CrossRef]
- Koutny, D.; Palousek, D.; Pantelejev, L.; Hoeller, C.; Pichler, R.; Tesicky, L.; Kaiser, J. Influence of scanning strategies on processing of aluminum alloy EN AW 2618 using selective laser melting. Materials 2018, 11, 298. [Google Scholar] [CrossRef] [PubMed]
- Han, X.; Zhu, H.; Nie, X.; Wang, G.; Zeng, X. Investigation on Selective Laser Melting AlSi10Mg Cellular Lattice Strut: Molten Pool Morphology, Surface Roughness and Dimensional Accuracy. Materials 2018, 11, 392. [Google Scholar] [CrossRef] [PubMed]
- Ilcik, J.; Koutny, D.; Palousek, D. Geometrical accuracy of the metal parts produced by selective laser melting: Initial tests. In Proceedings of the 54th International Conference of Machine-Design-Departments (ICMD), Hejnice, Czech Republic, 10–12 September 2013; pp. 573–582. [Google Scholar]
- Skalicky, P.; Koutny, D.; Pantelejev, L.; Palousek, D. Processing of aluminum alloy EN AW 7075 using selective laser melting: Initial study. In Proceedings of the 58th International Conference of Machine-Design-Departments (ICMD2017), Prague, Czech Republic, 6–8 September 2017; pp. 330–335. [Google Scholar]
- Vrana, R.; Koutny, D.; Palousek, D.; Pantelejev, L.; Jaros, J.; Zikmund, T.; Kaiser, J. Selective laser melting strategy for fabrication of thin struts usable in lattice structures. Materials 2018, 11, 1763. [Google Scholar] [CrossRef] [PubMed]
- Koutny, D.; Vrana, R.; Paloušek, D. Dimensional accuracy of single beams of AlSi10Mg alloy and 316L stainless steel manufactured by SLM. In Proceedings of the 5th International Conference on Additive Technologies (iCAT2014), Vienna, Austria, 16–17 October 2014; pp. 142–147. [Google Scholar]
- Suard, M.; Lhuissier, P.; Dendievel, R.; Vignat, F.; Blandin, J.J.; Villeneuve, F. Impact of EBM fabrication strategies on geometry and mechanical properties of titanium cellular structures. In Proceedings of the Fraunhofer Direct Digital Manufacturing Conference (DDMC 2014), Berlin, Germany, 12–13 March 2014. [Google Scholar]
- Vrana, R.; Koutny, D.; Paloušek, D.; Zikmund, T. Influence of selective laser melting process parameters on impact resistance of lattice structure made from AlSi10Mg. In Proceedings of the World PM 2016 Congress and Exhibition, Hamburg, Germany, 9–13 October 2016. [Google Scholar]
- Grytten, F.; Børvik, T.; Hopperstad, O.S.; Langseth, M. Low velocity perforation of AA5083-H116 aluminium plates. Int. J. Impact Eng. 2009, 36, 597–610. [Google Scholar] [CrossRef]
- Grytten, F.; Holmedal, B.; Hopperstad, O.S.; Børvik, T. Evaluation of identification methods for YLD2004-18p. Int. J. Plast. 2008, 24, 2248–2277. [Google Scholar] [CrossRef]
- Mohmmed, R.; Ahmed, A.; Elgalib, M.A.; Ali, H. Low Velocity Impact Properties of Foam Sandwich Composites: A Brief Review. Int. J. Eng. Sci. Innov. Technol. 2014, 3, 579–591. [Google Scholar]
- Mohmmed, R.; Zhang, F.; Sun, B.; Gu, B. Finite element analyses of low-velocity impact damage of foam sandwiched composites with different ply angles face sheets. Mater. Des. 2013, 47, 189–199. [Google Scholar] [CrossRef]
- Labeas, G.; Ptochos, E. Investigation of sandwich structures with innovative cellular metallic cores under low velocity impact loading. Plast. Rubber Compos. 2013, 42, 194–202. [Google Scholar] [CrossRef]
- Ozdemir, Z.; Tyas, A.; Goodall, R.; Askes, H. Energy absorption in lattice structures in dynamics: Nonlinear FE simulations. Int. J. Impact Eng. 2017, 102, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, A.; Dhar, S.; Acharyya, S.; Datta, D.; Nayak, N. Determination of Johnson cook material and failure model constants and numerical modelling of Charpy impact test of armour steel. Mater. Sci. Eng. A 2015, 640, 200–209. [Google Scholar] [CrossRef]
- Milani, A.S.; Dabboussi, W.; Nemes, J.A.; Abeyaratne, R.C. An improved multi-objective identification of Johnson-Cook material parameters. Int. J. Impact Eng. 2009, 36, 294–302. [Google Scholar] [CrossRef]
- Brandl, E.; Heckenberger, U.; Holzinger, V.; Buchbinder, D. Additive manufactured AlSi10Mg samples using Selective Laser Melting (SLM): Microstructure, high cycle fatigue, and fracture behavior. J. Mater. Des. 2012, 34, 159–169. [Google Scholar] [CrossRef]
- Vaverka, O.; Koutný, D.; Vrána, R.; Pantělejev, L.; Paloušek, D. Effect of heat treatment on mechanical properties and residual stresses in additively manufactured parts. In Proceedings of the Engineering Mechanics 2018 24th International Conference, Svratka, Czech Republic, 14–17 May 2018. [Google Scholar]
- Kempen, K.; Thijs, L.; van Humbeeck, J.; Kruth, J.-P. Mechanical properties of AlSi10Mg produced by selective laser melting. Phys. Procedia 2012, 39, 439–446. [Google Scholar] [CrossRef]
- Tsopanos, S.; Mines, R.A.W.; Mckown, S.; Shen, Y.; Cantwell, W.J.; Brooks, W.; Sutcliffe, C.J. The influence of processing parameters on the mechanical properties of selectively laser melted stainless steel microlattice structures. J. Manuf. Sci. Eng. 2010, 132, 1–12. [Google Scholar] [CrossRef]
- Xiao, L.; Song, W. Additively-manufactured functionally graded Ti-6Al-4V lattice structures with high strength under static and dynamic loading: Experiments. Int. J. Impact Eng. 2018, 111, 255–272. [Google Scholar] [CrossRef]
- Palousek, D.; Omasta, M.; Koutny, D.; Bednar, J.; Koutecky, T.; Dokoupil, F. Effect of matte coating on 3D optical measurement accuracy. Opt. Mater. 2015, 40, 1–9. [Google Scholar] [CrossRef]
- Ravari, M.R.K.; Kadkhodaei, M.; Ghaei, A. Effects of asymmetric material response on the mechanical behavior of porous shape memory alloys. J. Intell. Mater. Syst. Struct. 2016, 27, 1687–1701. [Google Scholar] [CrossRef]




| Shortcut | Description | Shortcut | Description |
|---|---|---|---|
| SLM | Selective laser melting technology | din | Maximum inscribed cylinder into the strut |
| FEA | Finite element analysis | dout | Minimum circumscribed cylinder on the strut surface |
| FEM | Finite element method | Ar | Cross-section area of real strut |
| YLR | Ytterbium fiber laser | ADin | Cross-section area of maximum inscribed cylinder into a strut |
| BCC | Body centered cubic | ADgauss | Cross-section area of Gauss strut cylinder |
| NM | Numerical model | ADout | Cross-section area of minimum circumscribed cylinder fitted on a strut surface |
| STF | Shell thickness factor | Aellipse | Cross-section area of an ellipse fitted to the strut surface |
| CAD | Computer aided design | a | Ellipse minor axes |
| EPS | Equivalent Plastic Strain | b | Ellipse major axes |
| BL-I | Bilinear isotropic hardening model of lattice core | e | Ellipse ratio |
| BL-II | Bilinear isotropic hardening model of bottom and upper plates | Fmax | Maximum force |
| EBM | Electron beam melting | xFmax | Deformation of the specimen at maximum force |
| CT | Computed tomography | σmax | Maximum engineering stress |
| aBCC | Length of BCC cell edge | εσmax | Strain at the maximum engineering stress |
| l | Length of the struts in the multi-strut tensile specimen | E | Young’s Modulus |
| d | Nominal lattice structure strut diameter | ET | Tangent Modulus |
| t | Specimen’s upper plate thickness | YTS0.2% | Offset yield strength at strain 0.2% |
| h | Height of the C-series specimens | UTS | Ultimate tensile strength |
| hCAD | Nominal CAD height of the specimen | EIn | Initiating impact energy, energy just before impact |
| tUpP | Thickness of the upper plate | vIn | Initiating speed, speed just before impact |
| mC | Weight of the C-series specimens | m | Weight of the falling head |
| mCAD_0.8 | CAD weight of the C-series specimen with nominal struts dimeter | tdef | Duration of deformation |
| mCAD_0.95 | CAD weight of the C-series specimen with Gauss stuts diameter and real upper plate thickness | xDyn | Deformation of the specimens under dynamic loading |
| Measured relative density of C-series | EAbs | Absorbed energy | |
| CAD_0.8 | Calculated relative density of the CAD model with nominal diameter d = 0.8 mm | vUp | Speed of the rebound |
| CAD_0.95 | Calculated relative density of the CAD model with measured Gaussian diameter d = 0.8 mm | kDyn | Average stiffness of the specimens under dynamic loading |
| dgauss | Ideal struts Gauss cylinder | PAbs | Absorption power of the specimens under dynamic loading |
| n | Number of the struts in the multi-strut specimen | hef | Effective length of the tensile specimen |
| ρInd | deliberately increased density of the indenter to represent the weight of the whole falling head | Einp | Input energy to the current layer of the lattice structure |
| SEM | Scanning electron microscopy | Elin | Linear energy—(laser power/laser speed) |
| (Avg. Values) | Measured | CAD | |||||||
|---|---|---|---|---|---|---|---|---|---|
| h | tUpP | m | hCAD | mCAD_0.8 | mCAD_0.95 | CAD_0.8 | CAD_0.95 | ||
| (mm) | (mm) | (g) | (%) | (mm) | (g) | (g) | (%) | (%) | |
| 21.04 | 0.75 | 6.97 | 31 | 20.80 | 4.72 | 6.94 | 21 | 31 | |
| (mm) | Corner Strut | dgauss | din | dout | Ellipse | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Minor Axis | Major Axis | ||||||||||
| S1 | 1 | 0.94 | 0.95 | 0.74 | 0.73 | 1.26 | 1.21 | 0.79 | 0.79 | 1.1 | 1.12 |
| 2 | 0.99 | 0.75 | 1.19 | 0.81 | 1.17 | ||||||
| 3 | 0.93 | 0.7 | 1.24 | 0.79 | 1.14 | ||||||
| 4 | 0.93 | 0.72 | 1.16 | 0.78 | 1.09 | ||||||
| S2 | 1 | 0.96 | 0.96 | 0.76 | 0.74 | 1.18 | 1.22 | 0.8 | 0.79 | 1.2 | 1.12 |
| 2 | 0.92 | 0.75 | 1.09 | 0.79 | 1.03 | ||||||
| 3 | 1.02 | 0.73 | 1.36 | 0.8 | 1.06 | ||||||
| 4 | 0.94 | 0.72 | 1.23 | 0.77 | 1.17 | ||||||
| S3 | 1 | 0.86 | 0.91 | 0.69 | 0.71 | 1.08 | 1.18 | 0.78 | 0.76 | 1.08 | 1.06 |
| 2 | 0.91 | 0.69 | 1.26 | 0.77 | 1.05 | ||||||
| 3 | 0.94 | 0.76 | 1.2 | 0.76 | 1.13 | ||||||
| 4 | 0.91 | 0.7 | 1.17 | 0.73 | 0.97 | ||||||
| S4 | 1 | 0.97 | 0.97 | 0.82 | 0.74 | 1.27 | 1.31 | 0.86 | 0.84 | 1.27 | 1.16 |
| 2 | 0.96 | 0.73 | 1.31 | 0.89 | 1.15 | ||||||
| 3 | 1.01 | 0.74 | 1.43 | 0.83 | 1.04 | ||||||
| 4 | 0.93 | 0.67 | 1.23 | 0.77 | 1.18 | ||||||
| 0.945 | 0.729 | 1.229 | 0.795 | 1.114 | |||||||
| (mm) | TS45 | TS90 | TB45 | TB90 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| dgauss | din | dout | dgauss | din | dout | dgauss | din | dout | dgauss | din | dout | |
| 1 | 0.88 | 0.66 | 1.07 | 0.78 | 0.61 | 1.09 | 5.05 | 4.91 | 5.49 | 5.03 | 4.94 | 5.36 |
| 2 | 0.88 | 0.69 | 1.14 | 79 | 0.68 | 1.03 | 5.04 | 4.89 | 5.66 | 5.02 | 4.9 | 5.45 |
| 3 | 0.89 | 0.72 | 1.15 | - | - | - | 5.03 | 4.85 | 5.6 | 5.01 | 4.93 | 5.57 |
| 4 | 0.9 | 0.74 | 1.19 | 0.79 | 0.71 | 0.88 | - | - | - | - | - | - |
| 5 | 0.9 | 0.7 | 1.34 | 0.8 | 0.69 | 1.06 | - | - | - | - | - | - |
| 6 | 0.91 | 0.71 | 1.29 | 0.78 | 0.69 | 0.87 | - | - | - | - | - | - |
| 0.89 | 0.70 | 1.20 | 0.79 | 0.68 | 0.99 | 5.04 | 4.88 | 5.58 | 5.02 | 4.92 | 5.46 | |
| Spec. | Fmax (N) | xFmax (mm) | σmax (MPa) | εσmax | E (GPa) | YTS0.2% (MPa) | UTS (MPa) | ET (MPa) |
|---|---|---|---|---|---|---|---|---|
| TS45 | 2270 | 0.462 | - | 0.015 | 71.6 | 131.6 | 224.2 | 6649 |
| TS90 | 1934 | 0.297 | - | 0.010 | 103.7 | 116.6 | 186.8 | 8701 |
| TB45 | 7625 | 1.030 | - | 0.026 | 96.1 | 227.0 | 382.2 | 4858 |
| TB90 | 6453 | 0.809 | - | 0.020 | 147.5 | 187.4 | 326 | 5753.3 |
| C | 10,860 | 2.133 | 27.2 | 0.103 | 483.5 | - | - | - |
| # | Fmax (N) | tdef (ms) | xDyn (mm) | vIn (m·s−1) | EIn (J) | EAbs (J) | vUp (m·s−1) | kDyn (N·mm−1) | PAbs (J·s−1) | |
|---|---|---|---|---|---|---|---|---|---|---|
| IT 0.6 | 4252 | 4.94 | 9.07 | 3.02 | 33.10 | 32.47 | 0.42 | 9005 | 6.58 | |
| 6479 | 4.64 | 7.67 | 2.95 | 31.51 | 31.19 | 0.30 | 6.73 | |||
| 4005 | 5.29 | 9.61 | 2.93 | 31.19 | 30.87 | 0.30 | 5.83 | |||
| 4660 | 5.04 | 8.86 | 2.95 | 31.48 | 31.20 | 0.28 | 6.19 | |||
| 6047 | 4.71 | 8.31 | 2.97 | 32.08 | 31.68 | 0.33 | 6.73 | |||
| 5089 | 4.92 | 8.70 | 2.96 | 31.87 | 31.48 | 0.32 | - | 6.41 | ||
| IT 0.8 | - | - | - | - | - | - | - | - | - | |
| 9989 | 3.41 | 5.15 | 2.97 | 32.03 | 31.58 | 0.35 | 19,417 | 9.27 | ||
| 9368 | 4.05 | 6.00 | 2.93 | 31.91 | 31.71 | 0.24 | 7.82 | |||
| 12,218 | 2.94 | 4.32 | >2.96 | 31.87 | 31.31 | 0.39 | 10.66 | |||
| 9795 | 3.52 | 5.43 | 2.96 | 31.72 | 31.08 | 0.42 | 8.83 | |||
| 10,343 | 3.48 | 5.22 | 2.96 | 31.88 | 31.42 | 0.35 | - | 9.15 | ||
| IT 1.0 | 15,223 | 2.79 | 3.83 | 3.07 | 34.22 | 33.89 | 0.30 | 29,371 | 12.14 | |
| 17,625 | 2.03 | 3.30 | 3.13 | 35.45 | 35.28 | 0.22 | 17.37 | |||
| 16,437 | 2.16 | 3.66 | 3.15 | 36.09 | 35.56 | 0.38 | 16.49 | |||
| 18,796 | 1.80 | 3.08 | 3.16 | 36.09 | 35.29 | 0.47 | 19.58 | |||
| 16,859 | 2.18 | 3.50 | 3.15 | 35.98 | 35.83 | 0.20 | 16.46 | |||
| 16,988 | 2.19 | 3.47 | 3.13 | 35.57 | 35.17 | 0.31 | - | 16.41 | ||
| IT 1.2 | 24,205 | 1.49 | 2.43 | 3.19 | 36.93 | 34.87 | 0.75 | 39,006 | 23.41 | |
| 28,067 | 1.31 | 2.17 | 3.22 | 37.61 | 35.22 | 0.81 | 26.84 | |||
| 20,597 | 1.89 | 3.14 | 3.21 | 37.30 | 36.44 | 0.48 | 19.33 | |||
| 27,627 | 1.31 | 2.13 | 3.21 | 37.28 | 34.92 | 0.81 | 26.61 | |||
| 20,990 | 1.80 | 2.87 | 3.17 | 36.54 | 35.41 | 0.56 | 19.65 | |||
| 24,297 | 1.56 | 2.55 | 3.20 | 37.13 | 35.38 | 0.68 | - | 23.17 | ||
| Parameters | BL-I (BCC) | BL-II (Plate) | Unit |
|---|---|---|---|
| Density | 2680 | 2680 | kg·m−3 |
| Isotropic Elasticity | - | - | - |
| Young’s Modulus | 70,723 | 96,100 | MPa |
| Poisson’s Ratio | 0.334 | 0.334 | - |
| Bulk Modulus | 7.1 × 1010 | 9.6 × 1010 | Pa |
| Shear Modulus | 2.7 × 1010 | 3.6 × 1010 | Pa |
| Bilinear Isotropic Hardening | - | - | - |
| Yield Strength | 135 | 227 | MPa |
| Tangent Modulus | 6586 | 4858 | MPa |
| Plastic Strain Failure | - | - | - |
| Max. Equivalent Plastic Strain EPS | 0.1025 | 0.1025 | - |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vrána, R.; Červinek, O.; Maňas, P.; Koutný, D.; Paloušek, D. Dynamic Loading of Lattice Structure Made by Selective Laser Melting-Numerical Model with Substitution of Geometrical Imperfections. Materials 2018, 11, 2129. https://doi.org/10.3390/ma11112129
Vrána R, Červinek O, Maňas P, Koutný D, Paloušek D. Dynamic Loading of Lattice Structure Made by Selective Laser Melting-Numerical Model with Substitution of Geometrical Imperfections. Materials. 2018; 11(11):2129. https://doi.org/10.3390/ma11112129
Chicago/Turabian StyleVrána, Radek, Ondřej Červinek, Pavel Maňas, Daniel Koutný, and David Paloušek. 2018. "Dynamic Loading of Lattice Structure Made by Selective Laser Melting-Numerical Model with Substitution of Geometrical Imperfections" Materials 11, no. 11: 2129. https://doi.org/10.3390/ma11112129





