Pressure Effect on Elastic Constants and Related Properties of Ti3Al Intermetallic Compound: A First-Principles Study
Abstract
1. Introduction
2. Theoretical Methods
2.1. Computational Details
2.2. Calculations of Elastic Constants
3. Results and Discussion
3.1. Bulk Properties at Zero Pressure
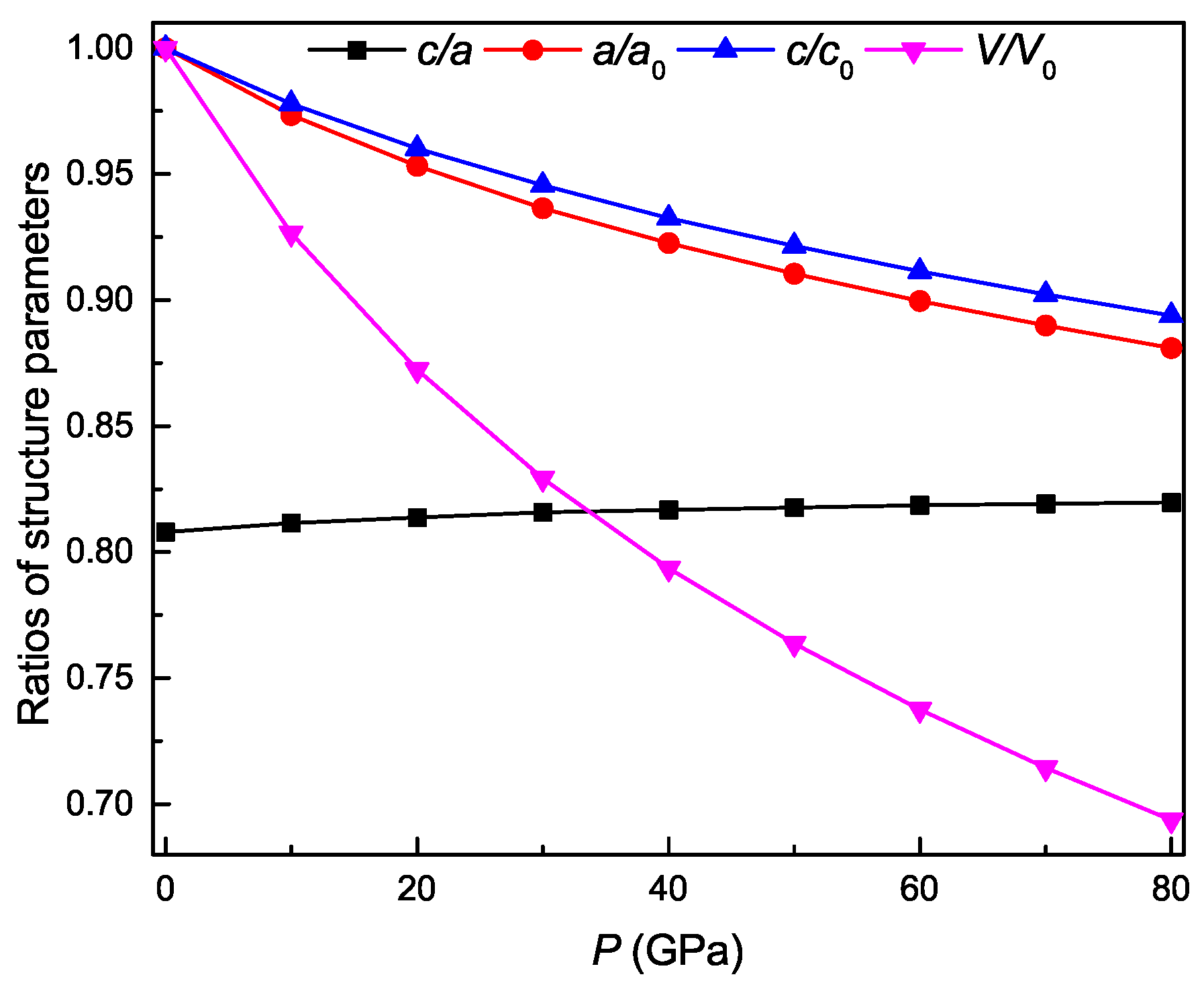
3.2. Pressure-Dependent Structure Parameters
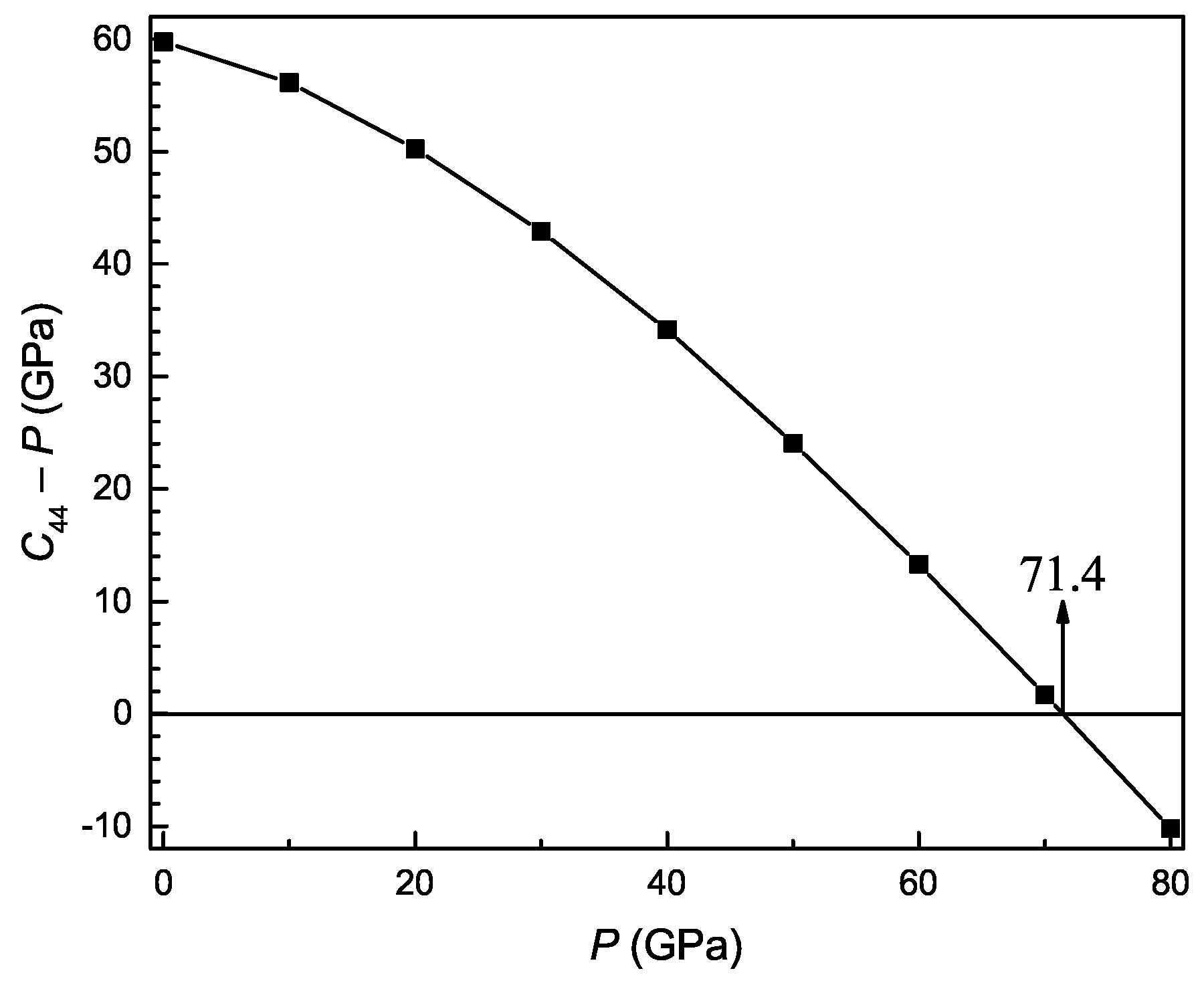
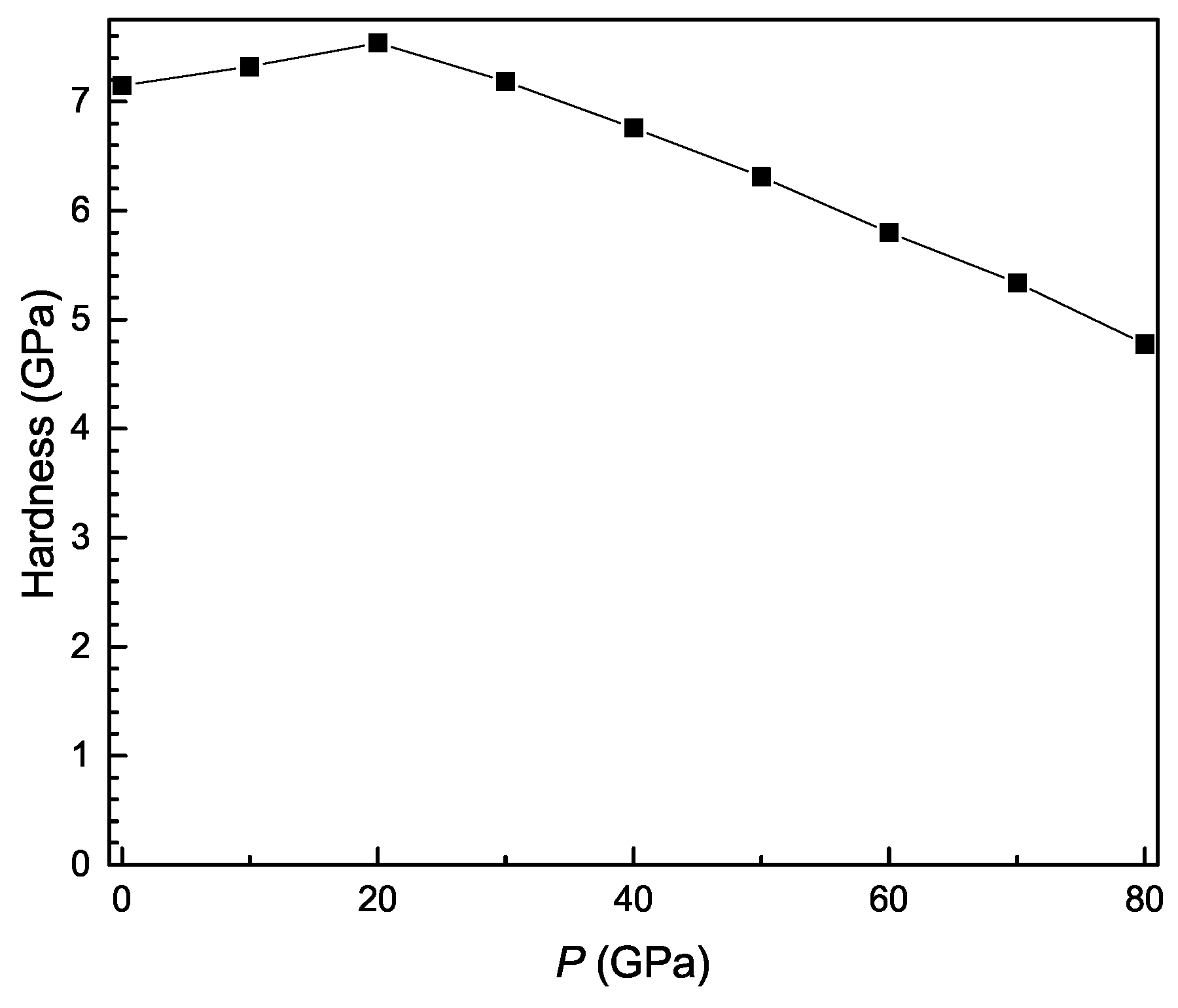
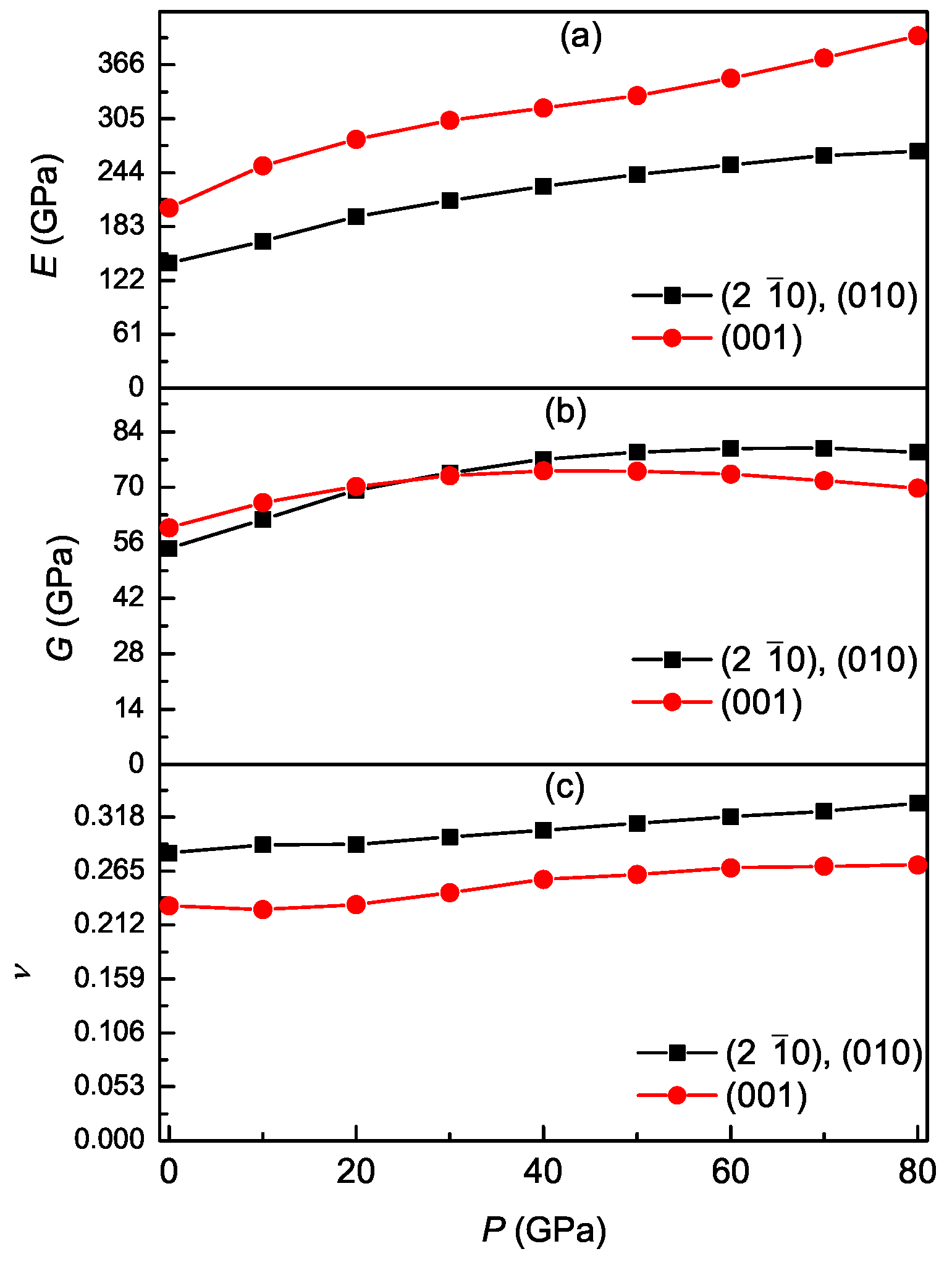
3.3. Pressure-Dependent Elastic Constants and Mechanical Properties
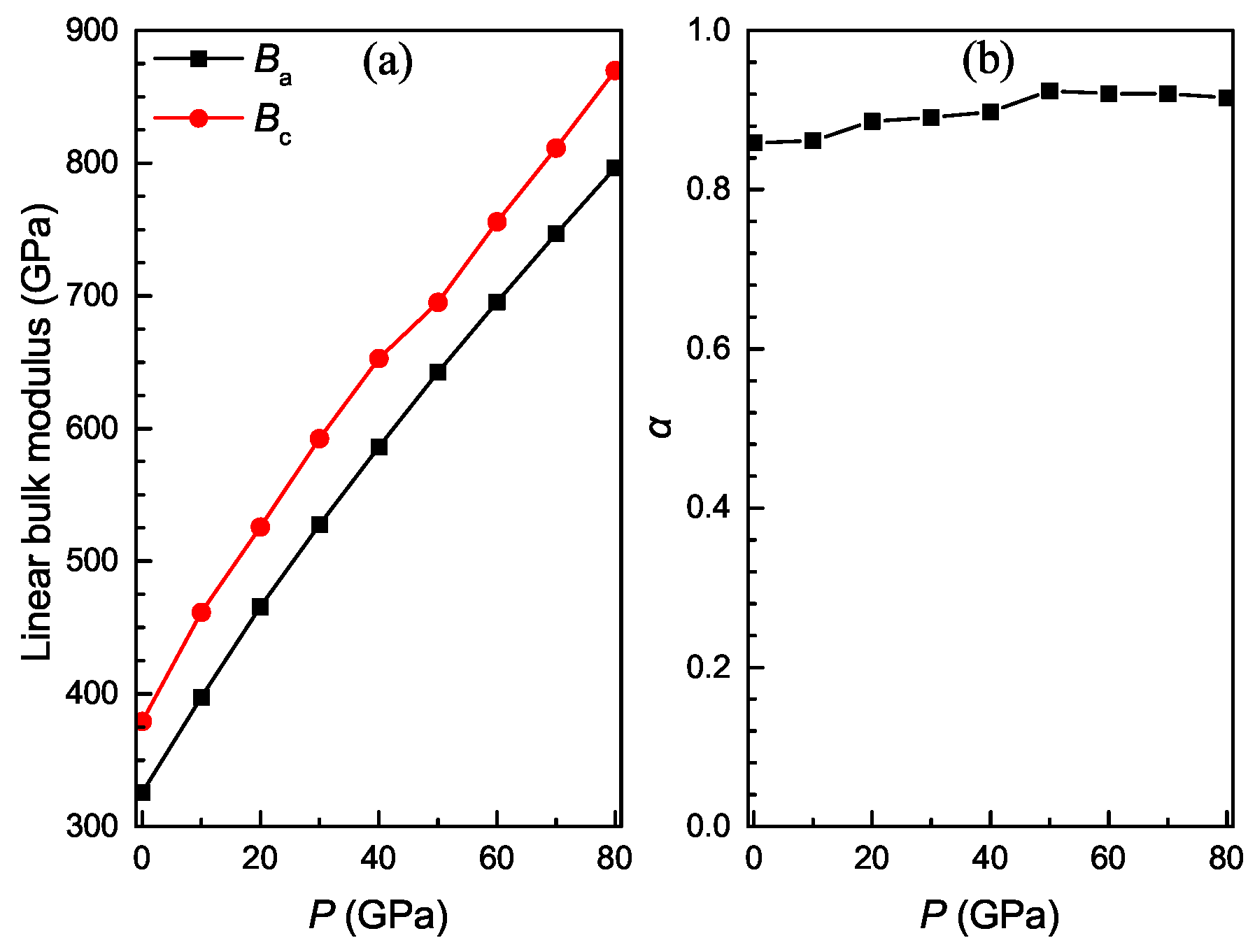
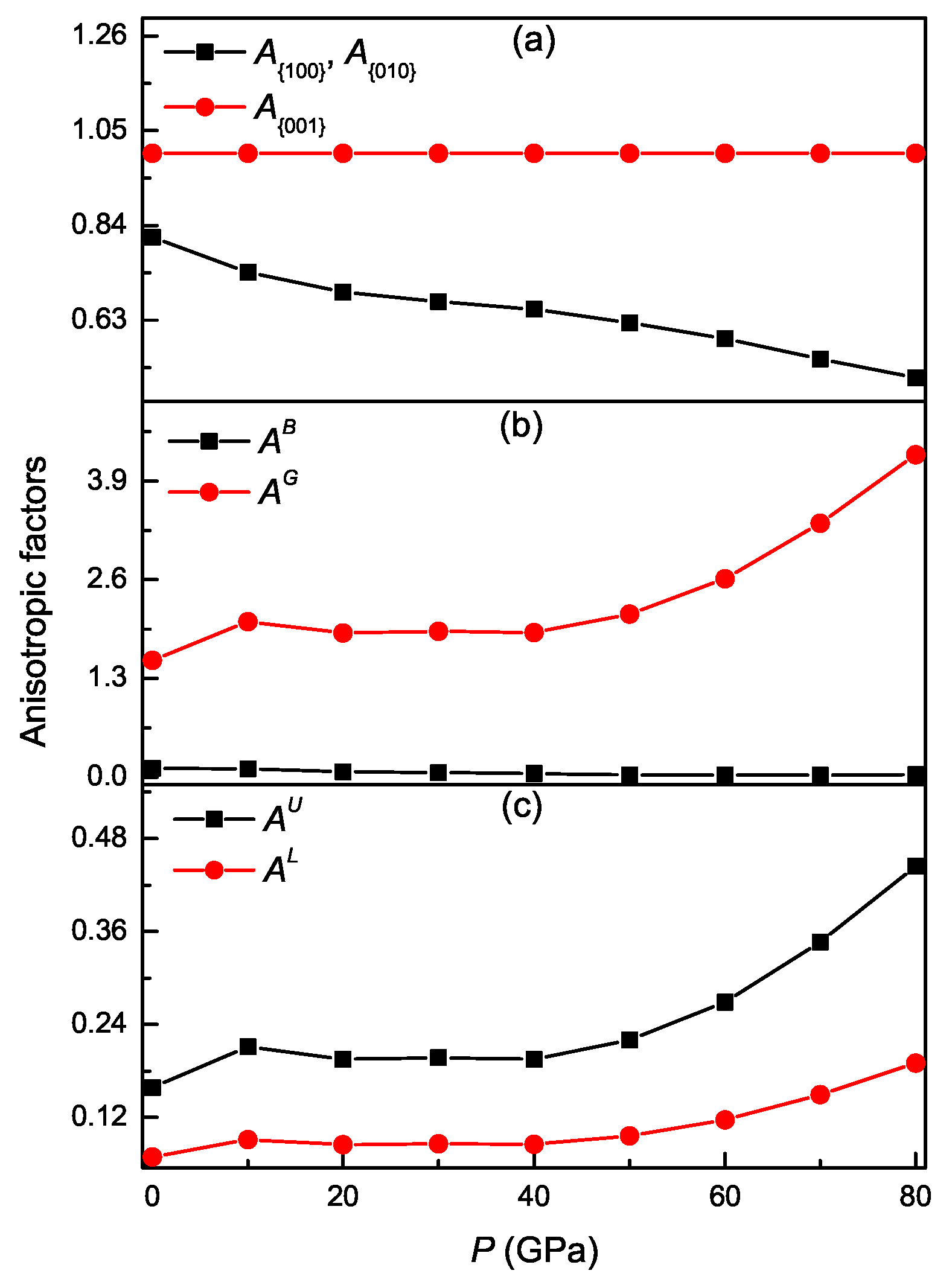
3.4. Pressure-Dependent Elastic Anisotropy
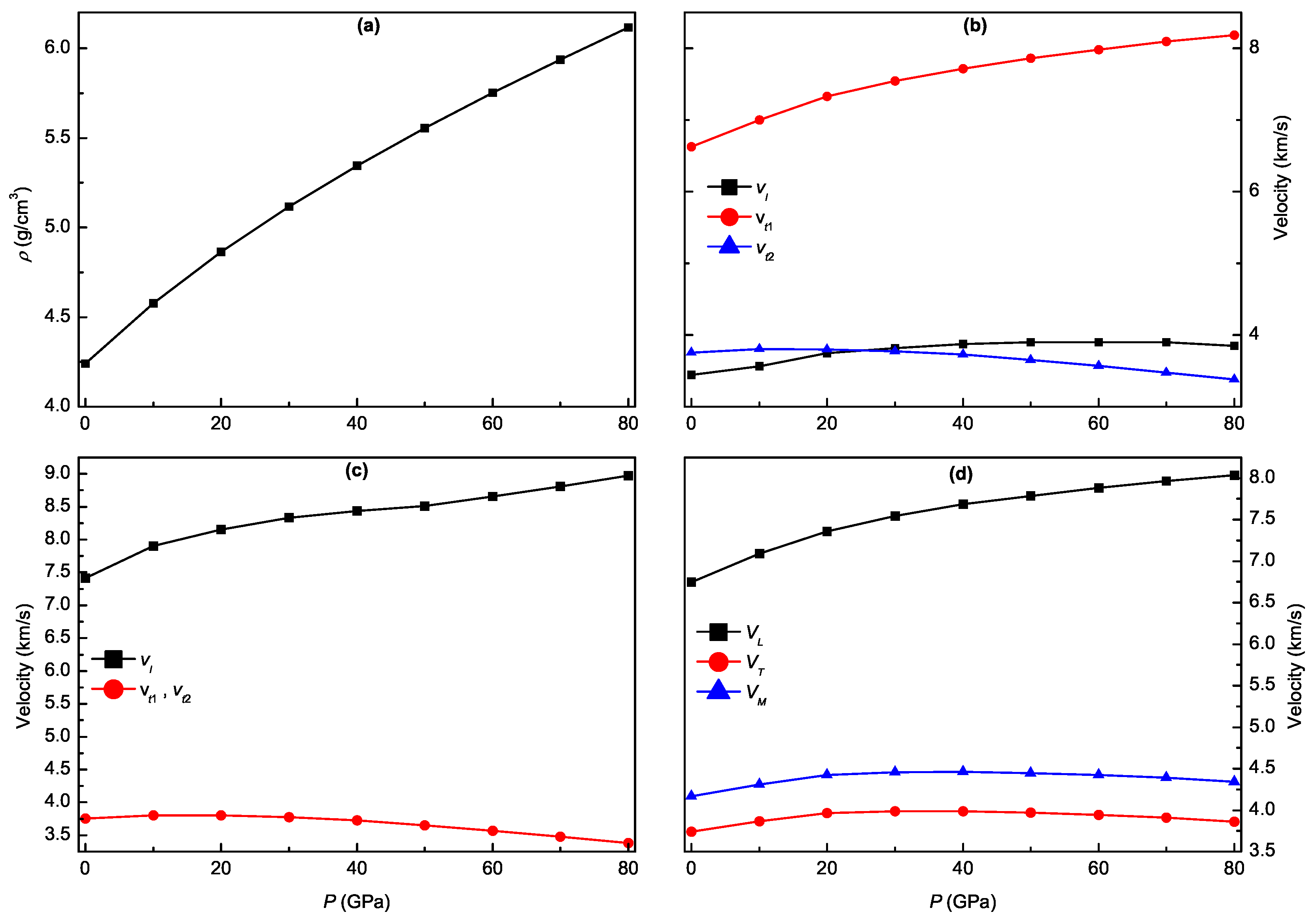
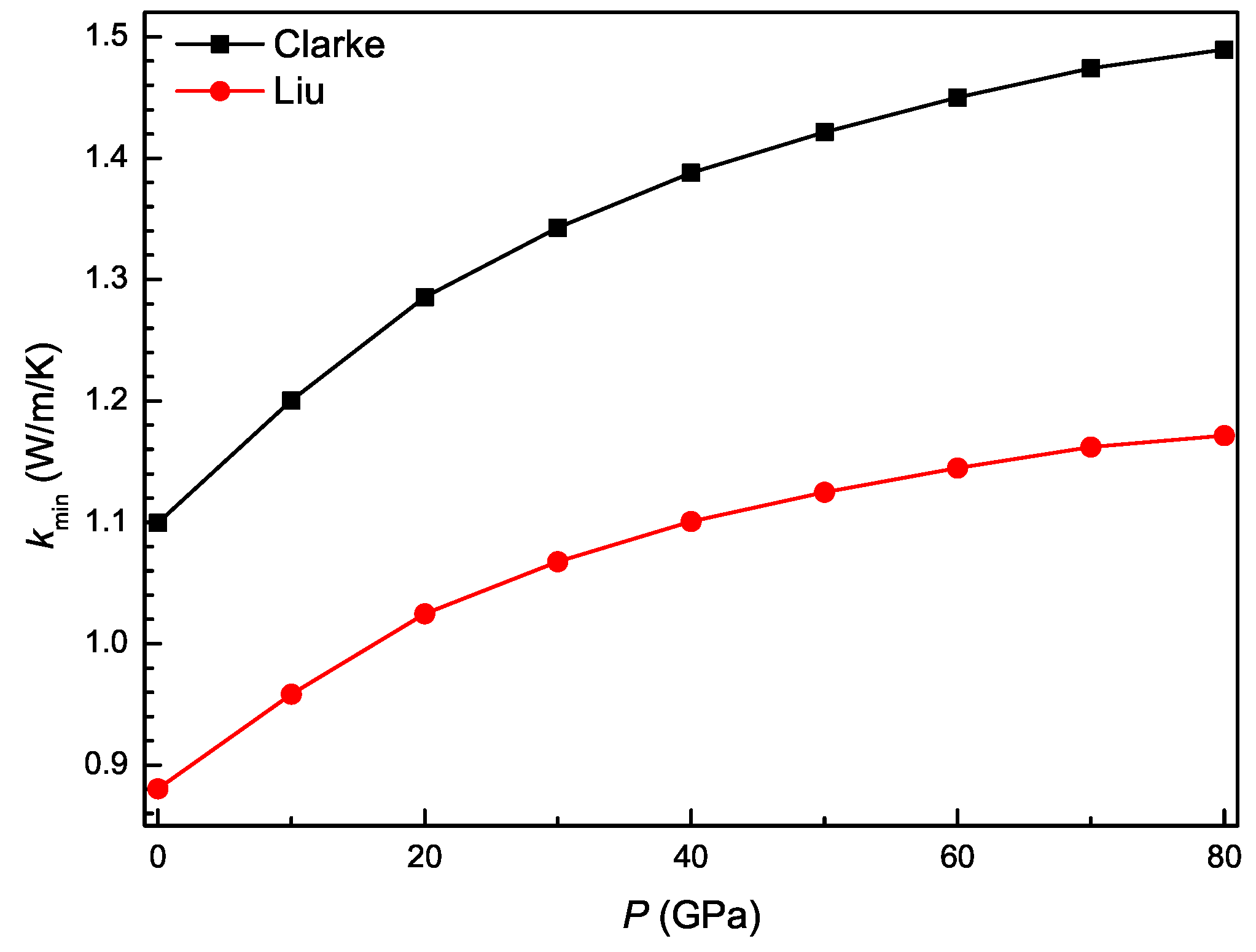
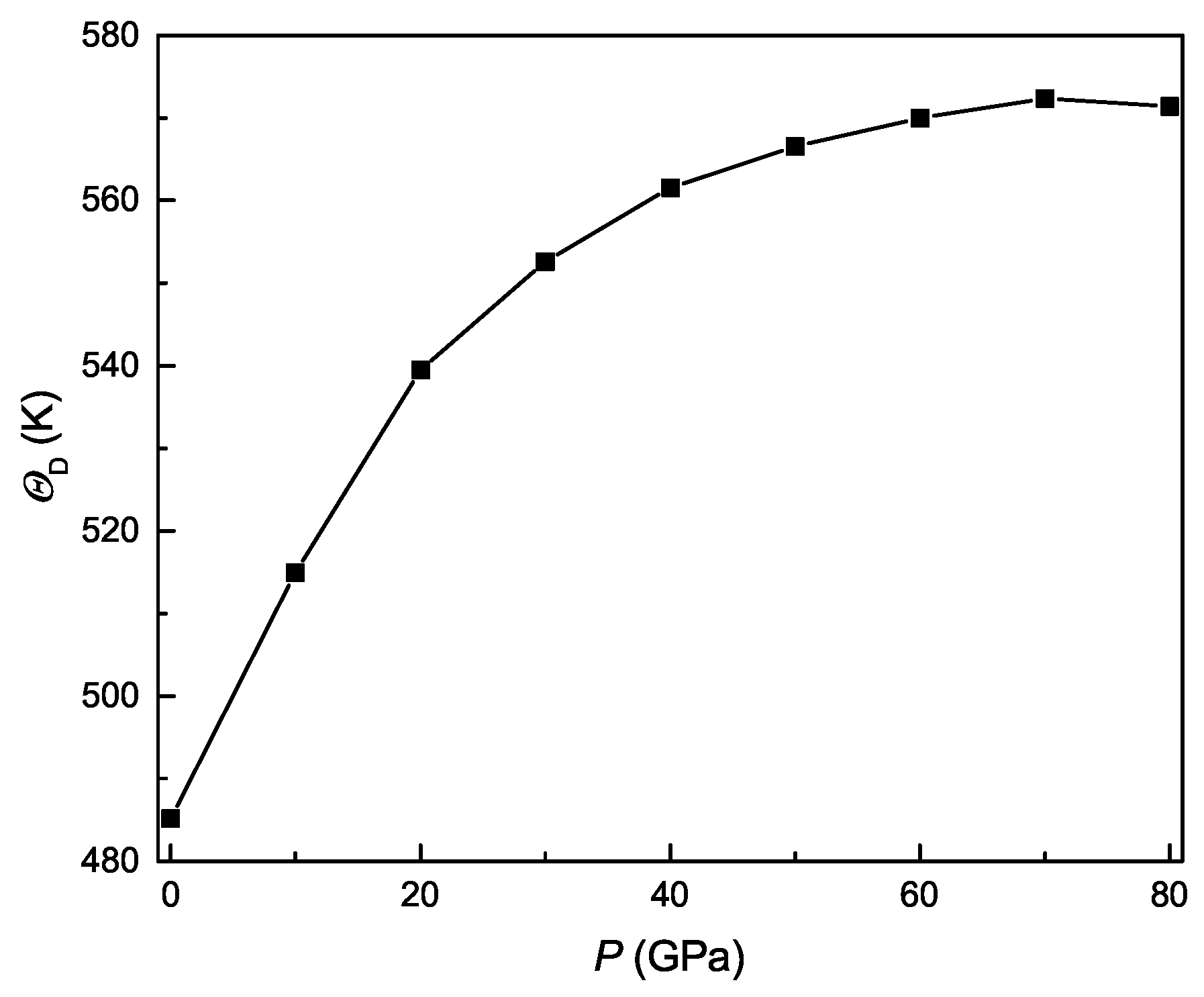
3.5. Pressure-Dependent Acoustic and Related Properties
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ravindran, P.; Fast, L.; Korzhavyi, P.A.; Johansson, B.; Wills, J.; Eriksson, O. Density functional theory for calculation of elastic properties of orthorhombic crystals: Application to TiSi2. J. Appl. Phys. 1998, 84, 4891–4904. [Google Scholar] [CrossRef]
- Djanarthany, S.; Viala, J.C.; Bouix, J. An overview of monolithic titanium aluminides based on Ti3Al and TiAl. Mater. Chem. Phys. 2001, 72, 301–319. [Google Scholar] [CrossRef]
- Court, S.A.; Löfvander, J.P.A.; Loretto, M.H.; Fraser, H.L. The influence of temperature and alloying additions on the mechanisms of plastic deformation of Ti3Al. Philos. Mag. A 1990, 61, 109–139. [Google Scholar] [CrossRef]
- Lipsitt, H.A.; Shechtman, D.; Schafrik, R. The deformation and fracture of TiAl at elevated temperatures. Metall. Trans. A 1975, 6, 1991–1996. [Google Scholar] [CrossRef]
- Umakoshi, Y.; Nakano, T.; Sumimoto, K.; Maeda, Y. Plastic anisotropy of Ti3Al single crystals. Mater. Res. Soc. Symp. Proc. 1993, 288, 441–446. [Google Scholar] [CrossRef]
- Sahu, P.C.; Chandra, N.V.; Shekar, C.; Yousuf, M.; Rajan, K.G. Implications of a pressure indcued phase transition in the search for cubic Ti3Al. Phys. Rev. Lett. 1997, 78, 1054–1057. [Google Scholar] [CrossRef]
- Rajagopalan, M.; Sahu, P.C.; Shekar, C.; Yousuf, M.; Rajan, K.G. Structural phase stability of Ti3Al under high pressure. Int. J. Mod. Phys. B 1999, 13, 841–845. [Google Scholar] [CrossRef]
- Dubrovinskaia, N.A.; Vennström, M.; Abrikosov, I.A.; Ahuja, R.; Ravindran, P.; Andersson, Y.; Eriksson, O.; Dmitriev, V.; Dubrovinsky, L.S. Absence of a pressure-induced structural phase transition in Ti3Al up to 25 GPa. Phys. Rev. B 2000, 63, 024106. [Google Scholar] [CrossRef]
- Zhang, C.; Hou, H.; Zhao, Y.; Yang, X.; Guo, Y. First-principles study on structural, ealstic thermal properties of γ-TiAl and α2-Ti3Al phases in TiAl-based alloy under high pressure. Int. J. Mod. Phys. B 2017, 31, 1750079. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B 1993, 48, 13115–13118. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple [Phys. Rev. Lett. 77, 3865 (1996)]. Phys. Rev. Lett. 1997, 78, 1396. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Hafne, R.J. Materials simulations using VASP—A quantum perspective to materials science. Comput. Phys. Commun. 2007, 177, 6–13. [Google Scholar] [CrossRef]
- Le Page, Y.; Saxe, P. Symmetry-general least-squares extraction of elastic data for strained materials from ab initio calculations of stress. Phys. Rev. B 2002, 65, 104104. [Google Scholar] [CrossRef]
- Wu, X.; Vanderbilt, D.; Hamann, D.R. Systematic treatment of displacements, and electric fields in density-functional perturbation theory. Phys. Rev. B 2005, 72, 035105. [Google Scholar] [CrossRef]
- Tanaka, K.; Koiwa, M. Single-crystal elastic constants of intermetallic compounds. Intermetallics 1996, 4, S29–S39. [Google Scholar] [CrossRef]
- Wei, Y.; Zhang, Y.; Lu, G.H.; Xu, B. Site preference and elastic properties of α2-Ti3Al with oxygen impurity: A first-principles study. Int. J. Mod. Phys. B 2010, 24, 2749–2755. [Google Scholar] [CrossRef]
- Liu, Y.L.; Liu, L.M.; Wang, S.Q.; Ye, H.Q. First-principles study of shear deformation in TiAl and Ti3Al. Intermetallics 2007, 15, 428–435. [Google Scholar] [CrossRef]
- Music, D.; Schneider, J.M. Effect of transition metal additives on electronic structure and elastic properties of TiAl and Ti3Al. Phys. Rev. B 2006, 74, 174110–174114. [Google Scholar] [CrossRef]
- Fu, C.L.; Zou, J.; Yoo, M.H. Elastic constants and planar fault energies of Ti3Al, and interfacial energies at the Ti3Al/TiAl interface by first-principles calculations. Scr. Metall. Mater. 1995, 33, 885–891. [Google Scholar] [CrossRef]
- Pearson, W.B. A Handbook of Lattice Spacing and Structure of Metals and Alloys; Pergamon: Oxford, UK, 1987; pp. 1–2. [Google Scholar]
- Mouhat, F.; Coudert, F.X. Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B 2014, 90, 224104. [Google Scholar] [CrossRef]
- Sinko, G.V.; Smirnow, N.A. Ab initio calculations of elastic constants and thermodynamic properties of bcc, fcc, and hcp Al crystals under pressure. J. Phys. Condens. Matter 2002, 14, 6989–7005. [Google Scholar]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. A 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Tao, X.; Yang, J.; Xi, L.; Ouyang, Y. First-principles investigation of the thermo-physical properties of Ca3Si4. J. Solid State Chem. 2012, 194, 179–187. [Google Scholar] [CrossRef]
- Mao, P.; Yu, B.; Liu, Z.; Wang, F.; Ju, Y. First-principles investigation on mechanical, electronic, and thermodynamic properties of Mg2Sr under high pressure. J. Appl. Phys. 2015, 117, 115903. [Google Scholar] [CrossRef]
- Voigt, W. Lehrbuch der Kristallphysik; Taubner: Leipzig, Germany, 1928. [Google Scholar]
- Reuss, A. Calculation of the flow limits of mixed crystals on the basis of the plasticity of monocrystals. Z. Angew. Math. Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Pugh, S.F. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Philos. Mag. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Frantsevich, I.N.; Voronov, F.F.; Bokuta, S.A. Elastic Constants and Elastic Moduli of Metals and Insulators Handbook; Frantsevich, I.N., Ed.; Naukova Dumka: Kiev, Ukraine, 1983; pp. 60–180. [Google Scholar]
- Pettifor, D.G. Theoretical predictions of structure and related properties of intermetallics. Mater. Sci. Technol. 1992, 8, 345–349. [Google Scholar] [CrossRef]
- Chen, X.Q.; Niu, H.; Li, D.; Li, Y. Intrinsic correlation between hardness and elasticity in polycrystalline materials and bulk metallic glasses. Intermetallics 2011, 19, 1275–1281. [Google Scholar] [CrossRef]
- Ravindran, P.; Vajeeston, P.; Vidya, R.; Kjekshus, A.; Fjellvåg, H. Detailed electronic structure studies on superconducting MgB2 and related compounds. Phys. Rev. B 2001, 64, 224509. [Google Scholar] [CrossRef]
- Pabst, W.; Gregorova, E. Effective elastic properties of alumina-zirconia composite ceramics—Part 2. Micromechanical modeling. Ceram. Silik. 2004, 48, 14–23. [Google Scholar]
- Chung, D.H.; Buessem, W.R. The elastic anisotropy of crystals. J. Appl. Phys. 1967, 38, 2010–2012. [Google Scholar] [CrossRef]
- Ranganathan, S.I.; Ostoja-Starzewski, M. Universal elastic anisotropy index. Phys. Rev. Lett. 2008, 101, 055504. [Google Scholar] [CrossRef] [PubMed]
- Kube, C.M. Elastic anisotropy of crystals. AIP Adv. 2016, 6, 095209. [Google Scholar] [CrossRef]
- Brugger, K. Determination of third-order elastic coefficients in crystals. J. Appl. Phys. 1965, 36, 768–773. [Google Scholar] [CrossRef]
- Duan, Y.H.; Sun, Y.; Peng, M.J.; Zhou, S.G. Anisotropic elastic properties of the Ca–Pb compounds. J. Alloys Compd. 2014, 595, 14–21. [Google Scholar] [CrossRef]
- Sun, L.; Gal, Y.; Xiao, B.; Li, Y.; Wang, G. Anisotropic elastic and thermal properties of titanium borides by first-principles calculations. J. Alloys Compd. 2013, 579, 457–467. [Google Scholar] [CrossRef]
- Schreiber, E.; Anderson, O.L.; Soga, N. Elastic Constants and Their Measurements; McGraw: New York, NY, USA, 1973. [Google Scholar]
- Anderson, O.L. A simplified method for calculating the debye temperature from elastic constants. J. Phys. Chem. Solids 1963, 24, 909–917. [Google Scholar] [CrossRef]
- Clarke, D.R. Materials selection guidelines for low thermal conductivity thermal barrier coatings. Surf. Coat. Technol. 2003, 163–164, 67–74. [Google Scholar] [CrossRef]
- Liu, B.; Wang, J.Y.; Li, F.Z.; Zhou, Y.C. Theoretical elastic stiffness, structural stability and thermal conductivity of La2T2O7 (T = Ge, Ti, Sn, Zr, Hf) pyrochlore. Acta Mater. 2010, 58, 4369–4377. [Google Scholar] [CrossRef]
- Callaway, J. Model for lattice thermal conductivity at low temperatures. Phys. Rev. 1959, 113, 1046–1051. [Google Scholar] [CrossRef]
- Collings, E.W.; Ho, J.C. Science, Technology and Application of Titanium; Jaffee, R.I., Promisel, N.E., Eds.; Pergamon: London, UK, 1970; pp. 331–347. [Google Scholar]
- Gehlen, P.C. Science, Technology and Application of Titanium; Jaffee, R.I., Promisel, N.E., Eds.; Pergamon: London, UK, 1970; pp. 349–357. [Google Scholar]



| a | |||||||
|---|---|---|---|---|---|---|---|
| Present | 5.758 | 0.808 | 186.18 | 85.57 | 62.76 | 233.03 | 59.75 |
| Exp. [21,26] | 5.77 | 0.80 | 183.2 | 89.0 | 62.6 | 225.1 | 64.1 |
| Theo. [22] | 5.74 | 0.81 | 184.67 | 82.37 | 63.41 | 225.08 | 53.97 |
| Theo. [24] | 5.772 | 0.803 | 72 | ||||
| Theo. [9] | 5.76 | 0.809 | 192.2 | 80.5 | 62.5 | 232.9 | 61.6 |
| Theo. [23] | 5.72 | 0.81 | 185 | 83 | 63 | 231 | 57 |
| Theo. [25] | 5.64 | 0.81 | 221 | 71 | 85 | 238 | 69 |
| P | |||||
|---|---|---|---|---|---|
| 0 | 186.18 | 85.57 | 62.76 | 233.03 | 59.75 |
| 10 | 224.30 | 108.15 | 75.51 | 286.13 | 66.15 |
| 20 | 261.44 | 124.83 | 89.61 | 323.41 | 70.22 |
| 30 | 291.09 | 142.23 | 105.72 | 354.83 | 72.90 |
| 40 | 318.32 | 157.86 | 122.34 | 380.17 | 74.16 |
| 50 | 343.06 | 174.27 | 135.46 | 402.06 | 74.06 |
| 60 | 366.48 | 191.39 | 149.52 | 430.75 | 73.29 |
| 70 | 389.37 | 208.75 | 161.36 | 460.66 | 71.69 |
| 80 | 409.54 | 228.60 | 172.83 | 492.29 | 69.81 |
| P | |||||
|---|---|---|---|---|---|
| 0 | 7.07 | −2.87 | −1.13 | 4.9 | 16.74 |
| 10 | 6.01 | −2.6 | −0.901945 | 3.97 | 15.12 |
| 20 | 5.15 | −2.17 | −0.823186 | 3.55 | 14.24 |
| 30 | 4.71 | −2.01 | −0.804515 | 3.3 | 13.72 |
| 40 | 4.37 | −1.86 | −0.809706 | 3.15 | 13.48 |
| 50 | 4.14 | −1.79 | −0.790763 | 3.02 | 13.5 |
| 60 | 3.96 | −1.75 | −0.764448 | 2.85 | 13.64 |
| 70 | 3.80 | −1.74 | −0.722140 | 2.68 | 13.95 |
| 80 | 3.73 | −1.8 | −0.679304 | 2.51 | 14.33 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, X.; Peng, R.; Yu, Y.; Hu, Z.; Wen, Y.; Song, L. Pressure Effect on Elastic Constants and Related Properties of Ti3Al Intermetallic Compound: A First-Principles Study. Materials 2018, 11, 2015. https://doi.org/10.3390/ma11102015
Zeng X, Peng R, Yu Y, Hu Z, Wen Y, Song L. Pressure Effect on Elastic Constants and Related Properties of Ti3Al Intermetallic Compound: A First-Principles Study. Materials. 2018; 11(10):2015. https://doi.org/10.3390/ma11102015
Chicago/Turabian StyleZeng, Xianshi, Rufang Peng, Yanlin Yu, Zuofu Hu, Yufeng Wen, and Lin Song. 2018. "Pressure Effect on Elastic Constants and Related Properties of Ti3Al Intermetallic Compound: A First-Principles Study" Materials 11, no. 10: 2015. https://doi.org/10.3390/ma11102015
APA StyleZeng, X., Peng, R., Yu, Y., Hu, Z., Wen, Y., & Song, L. (2018). Pressure Effect on Elastic Constants and Related Properties of Ti3Al Intermetallic Compound: A First-Principles Study. Materials, 11(10), 2015. https://doi.org/10.3390/ma11102015






