First Order Reversal Curve Study of SmFe2 Melt-Spun Ribbons
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
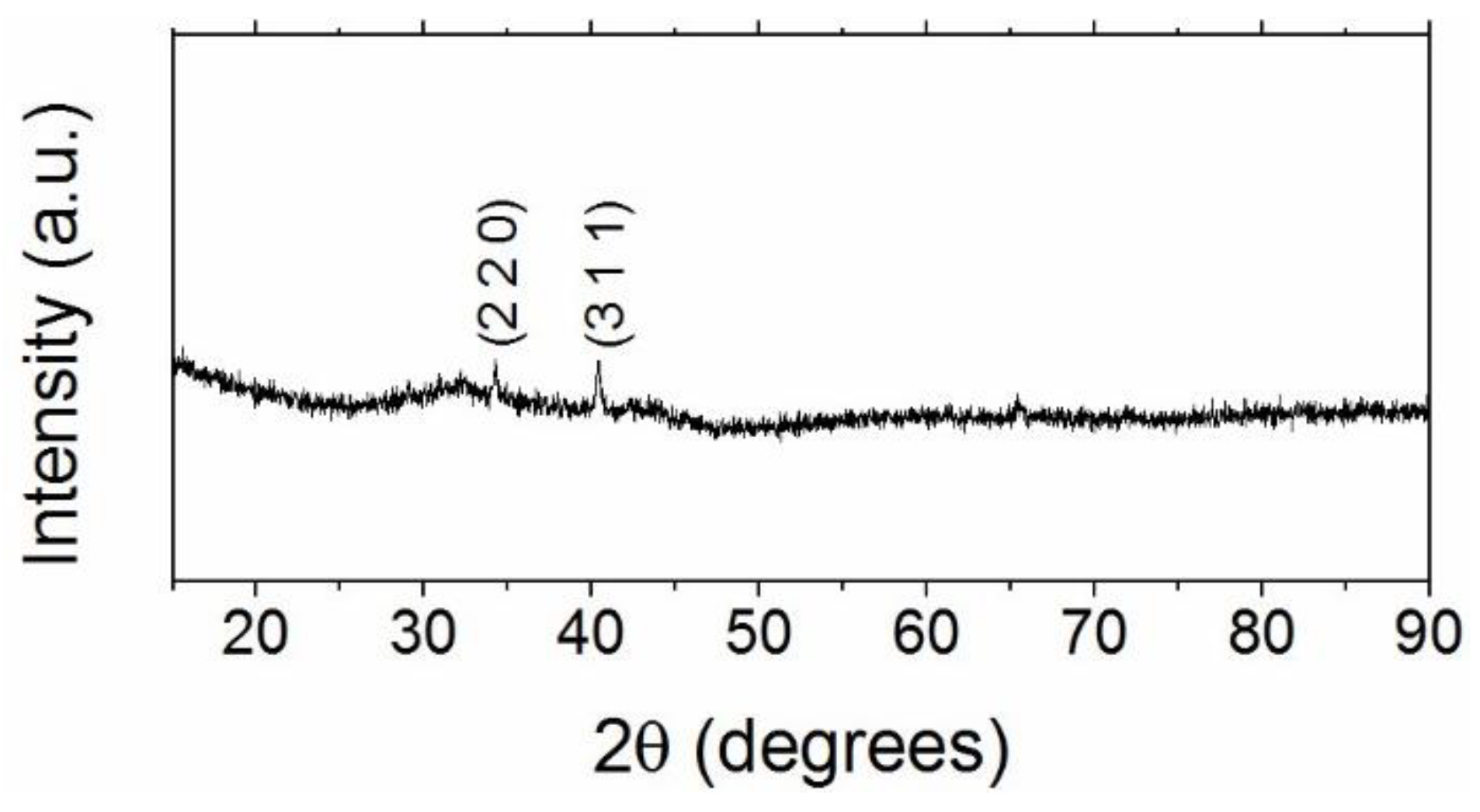
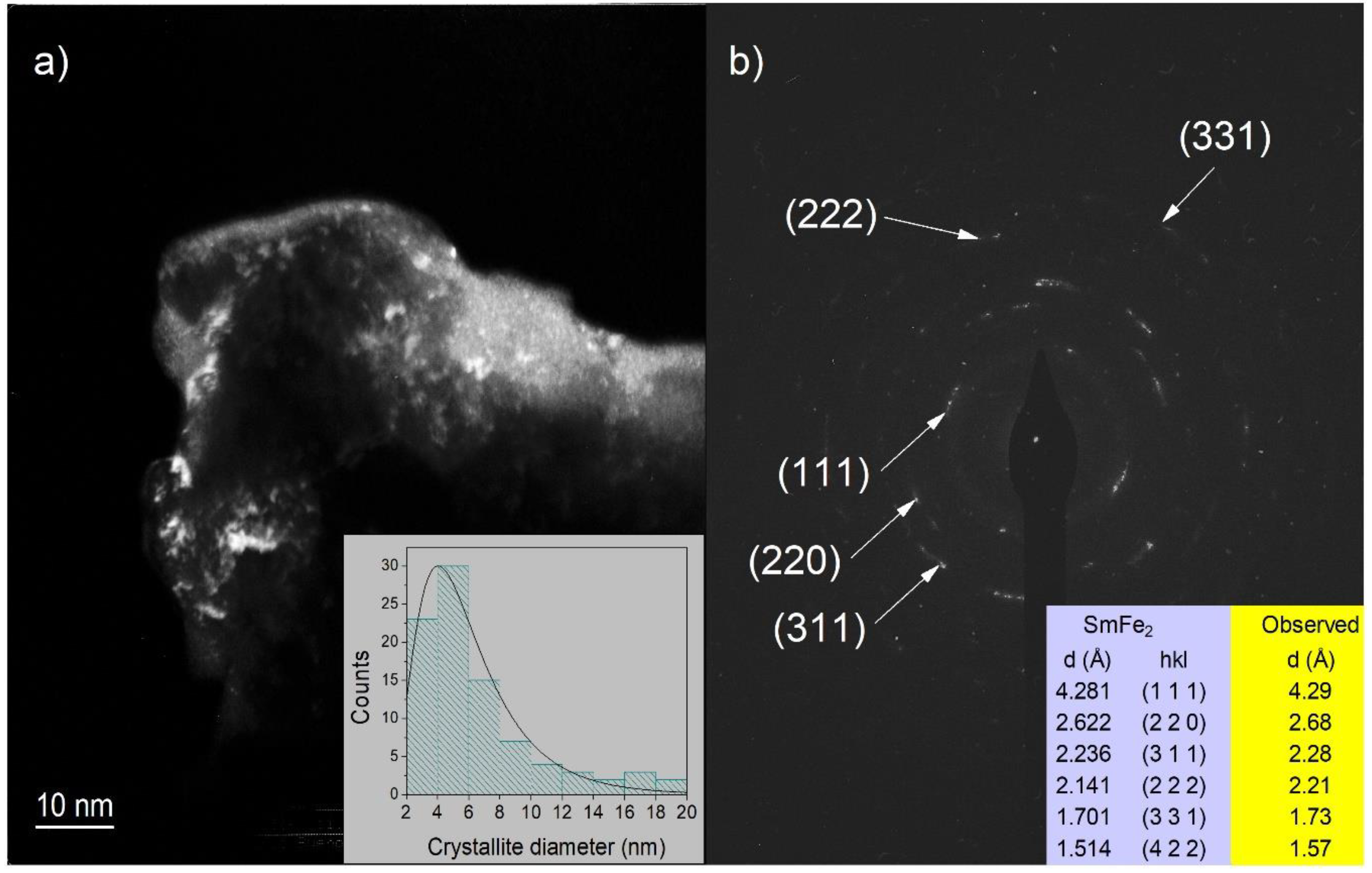
3.1. Microstructure
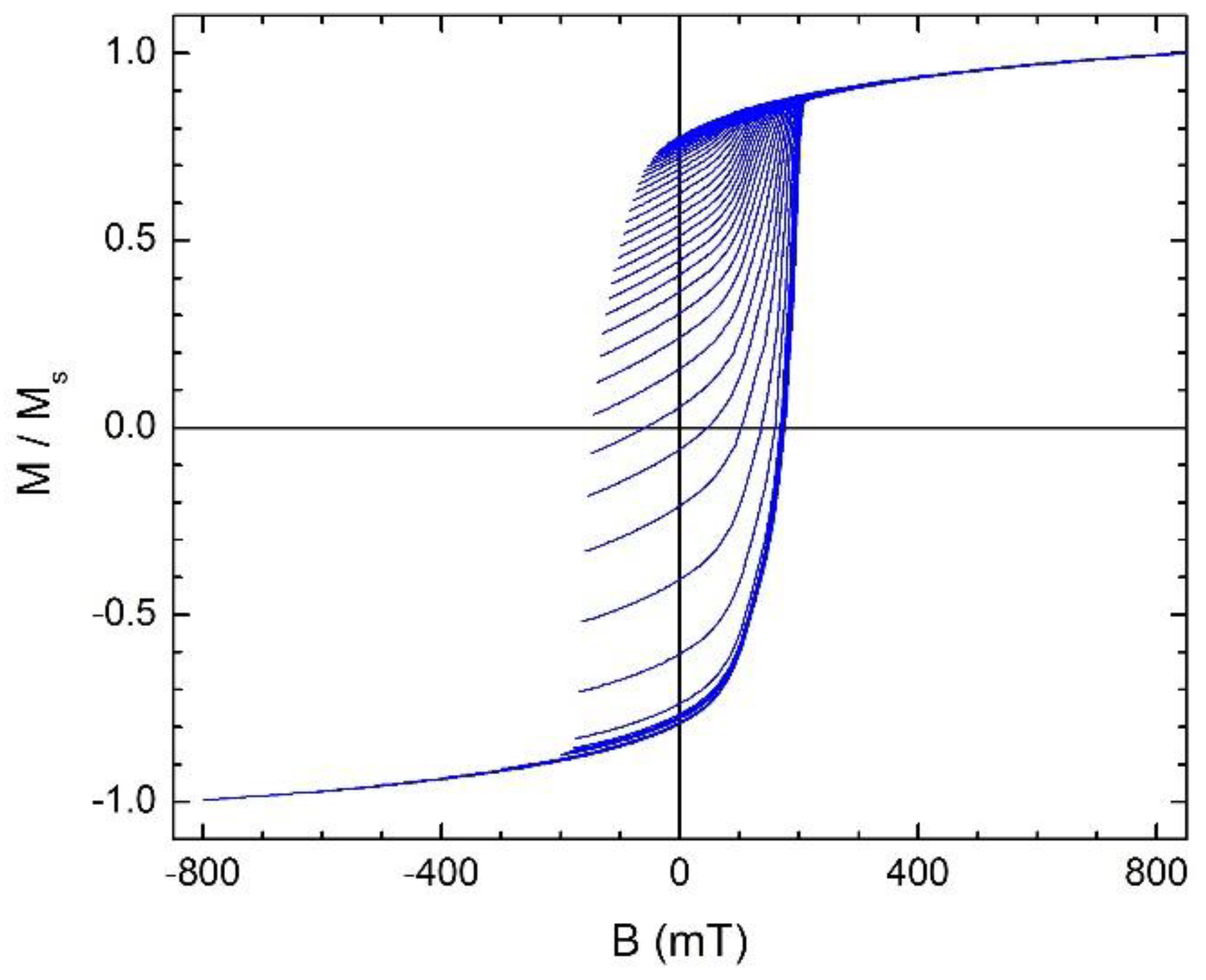
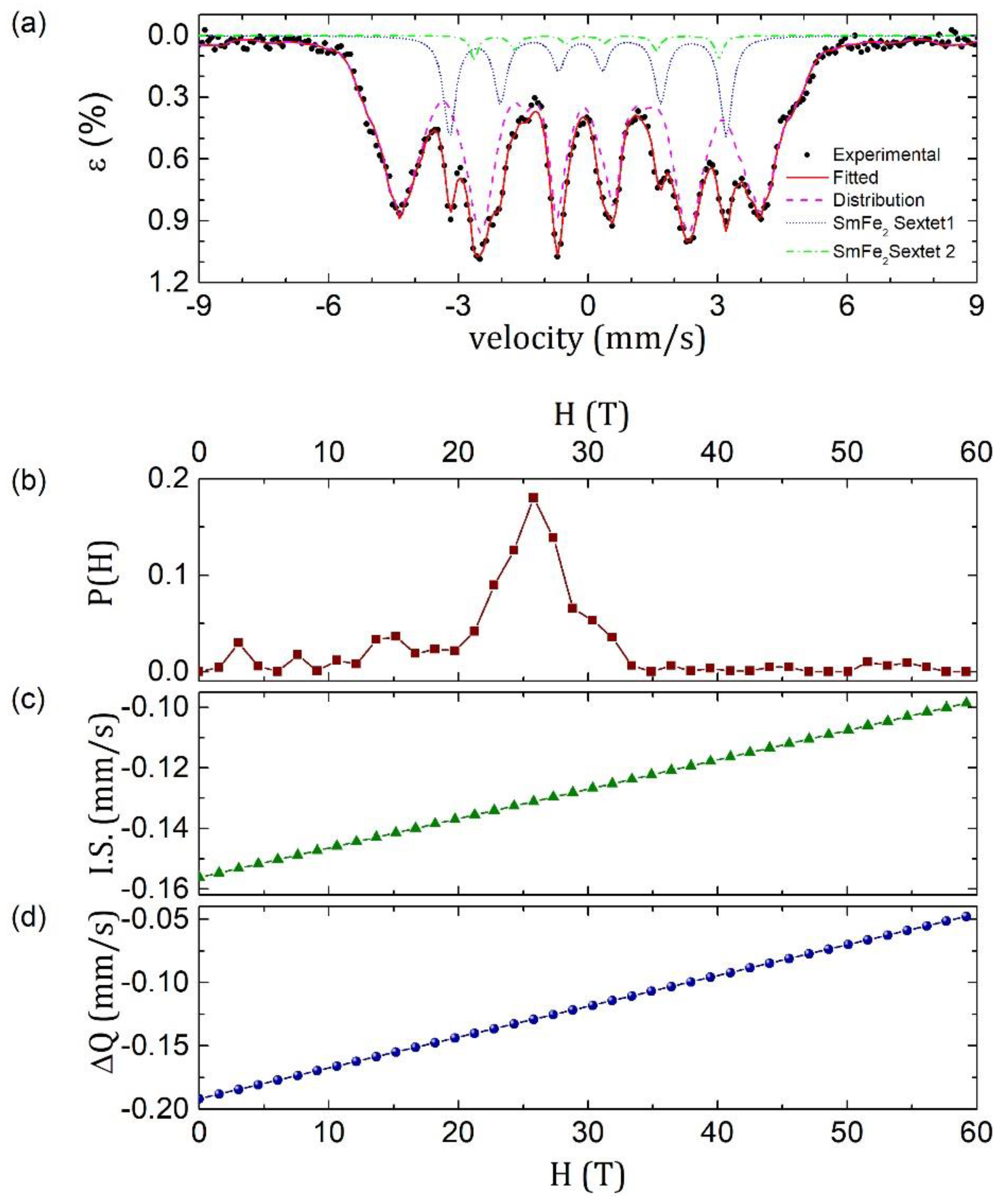
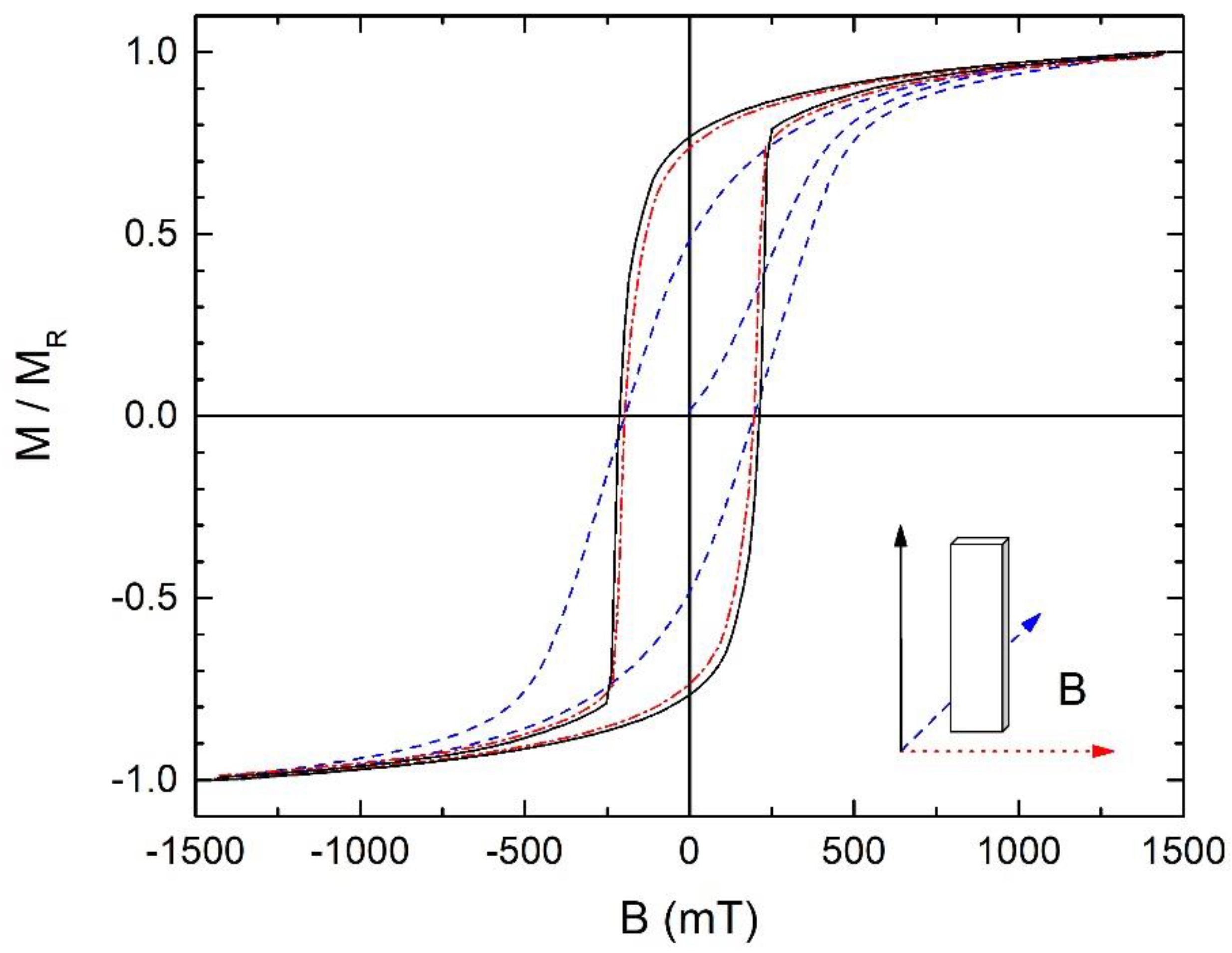
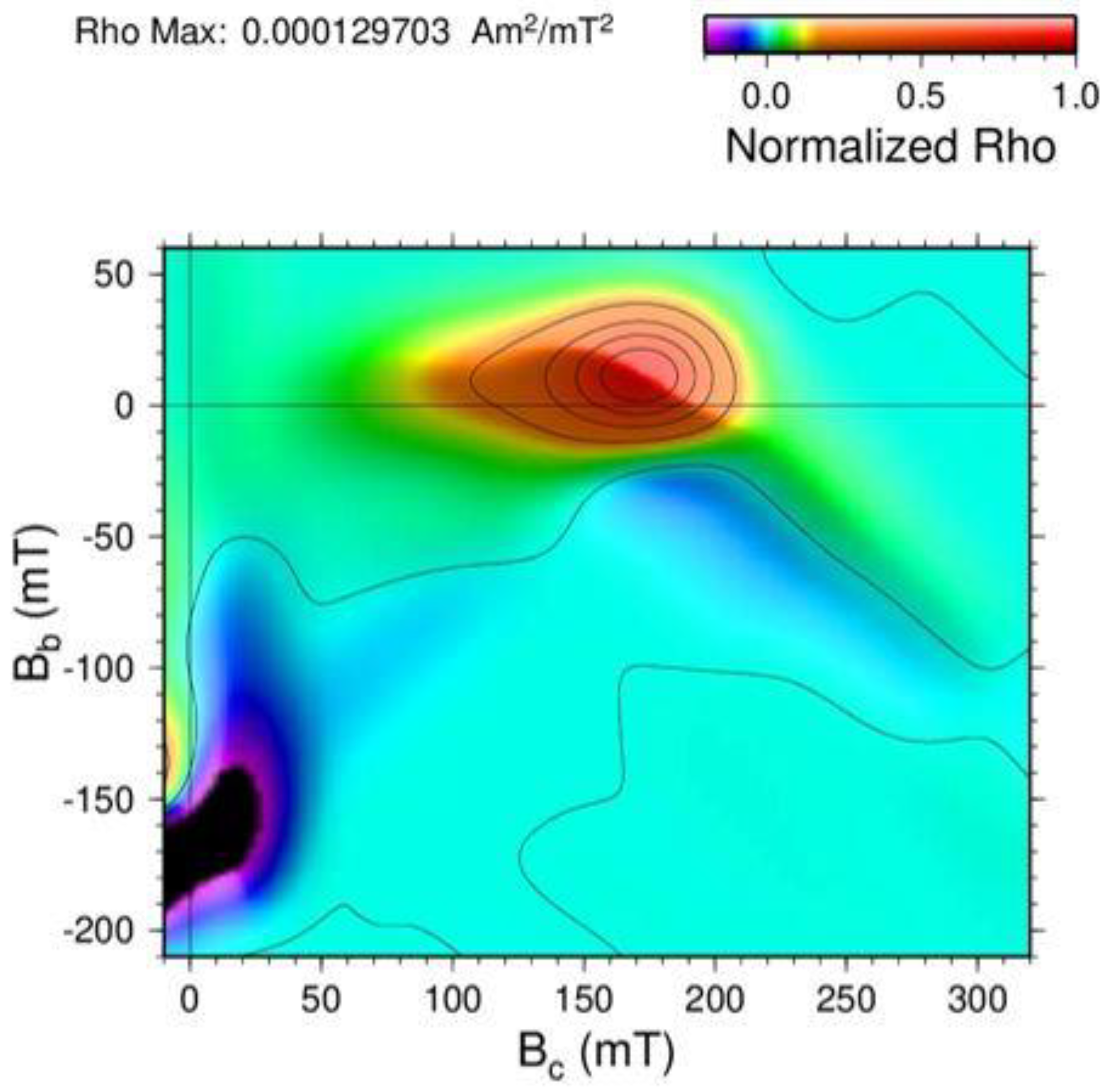
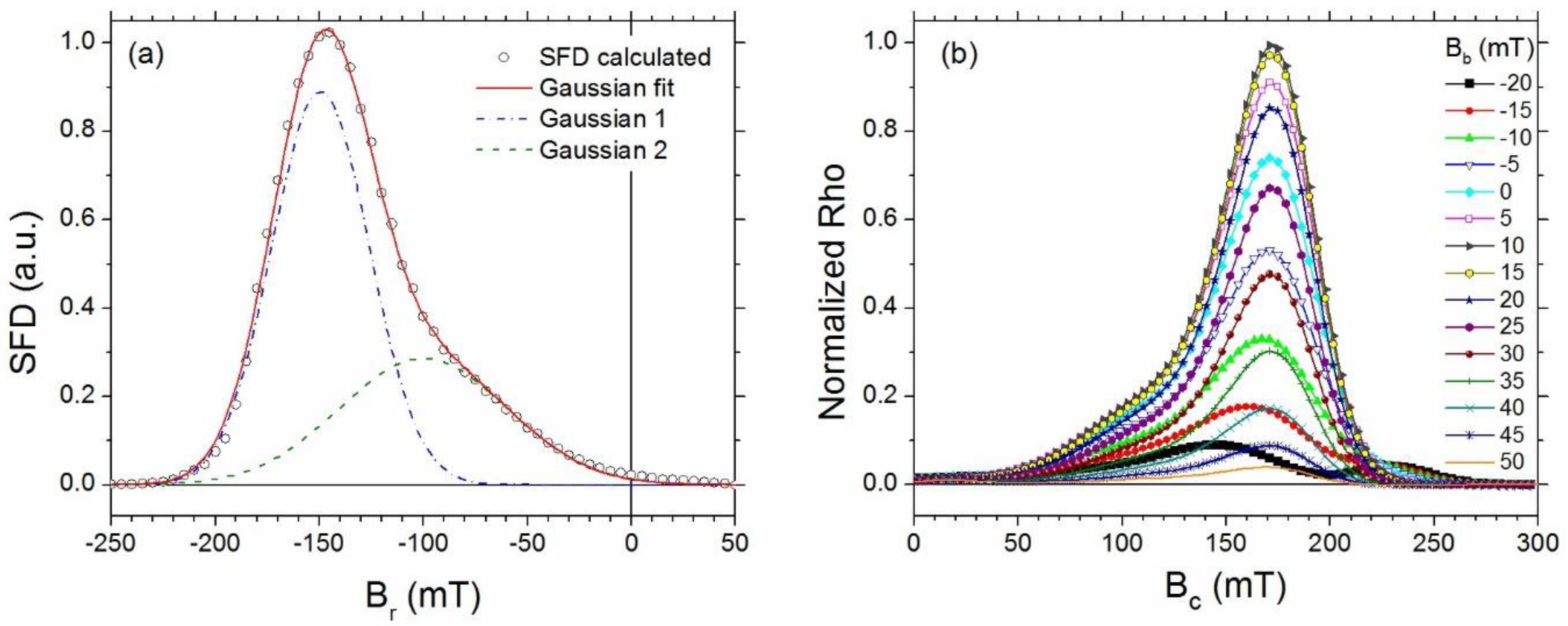
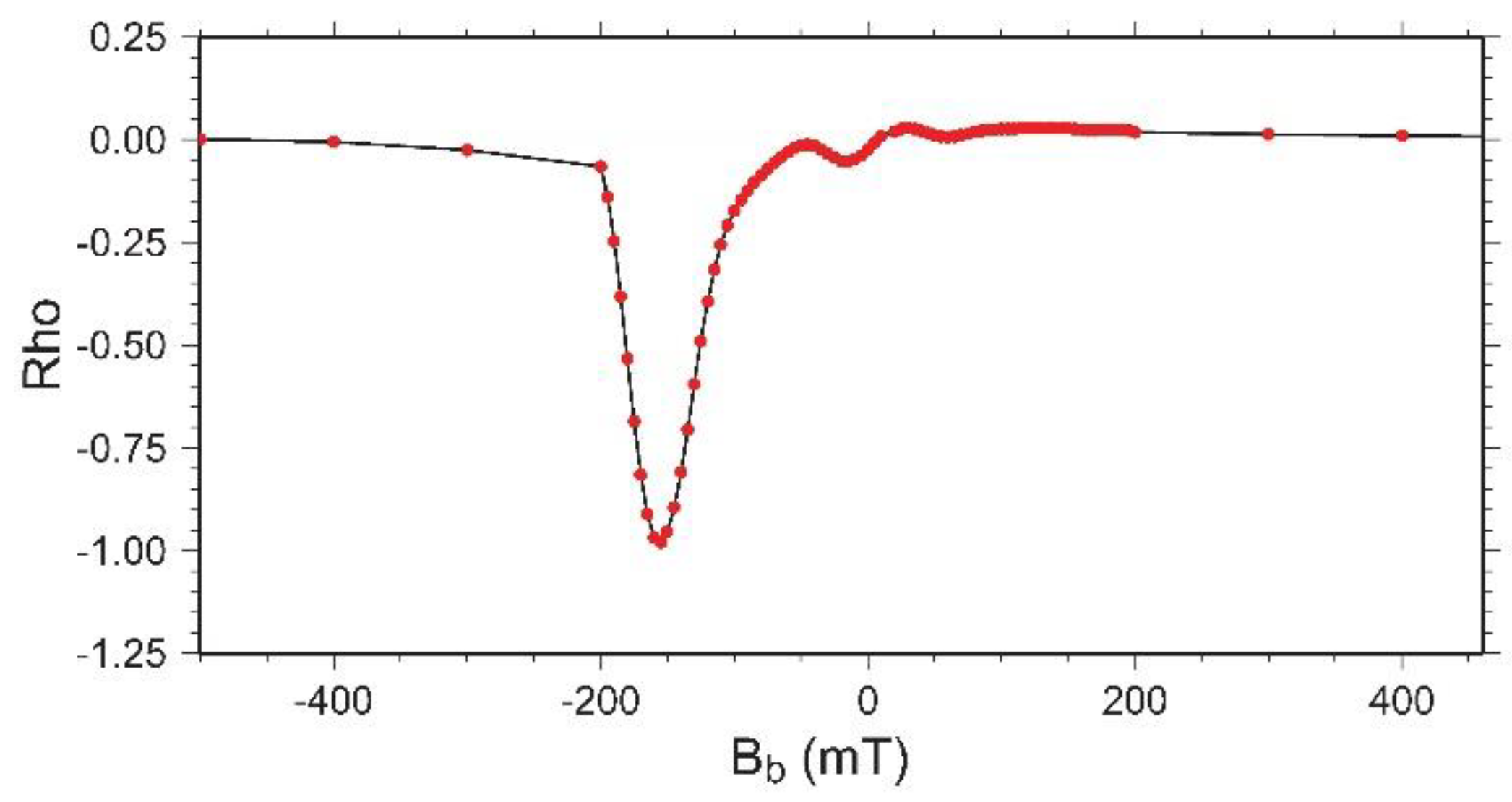
3.2. Magnetic Characterization
4. Conclusions
Supplementary Files
Supplementary File 1Author Contributions
Conflicts of Interest
References
- Nan, C.W.; Weng, G.J. Influence of microstructural features on the effective magnetostriction of composite materials. Phys. Rev. B 1999, 60, 6723–6730. [Google Scholar] [CrossRef]
- Clark, A.E. Magnetostrictive rare earth-Fe2 compounds. In Handbook of Magnetic Materials; Buschow, K.H.J., Wohlfarth, E.P., Eds.; North-Holland: Amsterdam, The Netherlands, 1980; Volume 1, pp. 531–589. ISBN 9780444536907. [Google Scholar]
- Mayergoyz, I.D. Mathematical Models of Hysteresis, 1st ed.; Springer: New York, NY, USA, 2001; pp. 1–63. ISBN 9781461230281. [Google Scholar]
- Gräfe, J.; Weigand, M.; Stahl, C.; Träger, N.; Kopp, M.; Schütz, G.; Wiedwald, U. Combined first-order reversal curve and X-ray microscopy investigation of magnetization reversal mechanisms in hexagonal antidot lattices. Phys. Rev. B 2016, 93, 014406. [Google Scholar] [CrossRef]
- Vaganov, M.V.; Linke, J.; Odenbach, S.; Raikher, Y.L. Model FORC diagrams for hybrid magnetic elastomers. J. Magn. Magn. Mater. 2017, 431, 130–133. [Google Scholar] [CrossRef]
- Cornejo, D.R.; Noce, R.D.; Peixoto, T.R.F.; Barelli, N.; Sumodjo, P.T.A.; Benedetti, A.V. First order reversal curve analysis of nanocrystalline Pd80Co20 alloy films. J. Alloys Compd. 2009, 479, 43–48. [Google Scholar] [CrossRef]
- Katzgraber, H.G.; Hérisson, D.; Östh, M.; Nordblad, P.; Ito, A.; Katori, H.A. Finite versus zero-temperature hysteretic behavior of spin glasses: Experiment and theory. Phys. Rev. B 2007, 76, 092408. [Google Scholar] [CrossRef]
- Katzgraber, H.G.; Pazmandi, F.; Pike, C.R.; Liu, K.; Scalettar, R.T.; Verosub, K.L.; Zimanyi, G.T. Reversal-field memory in the hysteresis of spin glasses. Phys. Rev. Lett. 2002, 89, 257202. [Google Scholar] [CrossRef] [PubMed]
- Pike, C.; Fernandez, A. An investigation of magnetic reversal in submicron-scale Co dots using first order reversal curve diagrams. J. Appl. Phys. 1999, 85, 6668–6676. [Google Scholar] [CrossRef]
- Muxworthy, A.R.; Dunlop, D.J. First-order reversal curve (FORC) diagrams for pseudo-single-domain magnetites at high temperature. Earth Planet. Sci. Lett. 2002, 203, 369–382. [Google Scholar] [CrossRef]
- Basso, V.; Berlotti, G.; Infortuna, A.; Pasquale, M. Preisach model study of the connection between magnetic and microstructural properties of soft magnetic materials. IEEE Trans. Magn. 1995, 31, 4000–4005. [Google Scholar] [CrossRef]
- Pike, C.R. First-order reversal-curve diagrams and reversible magnetization. Phys. Rev. B 2003, 68, 104424. [Google Scholar] [CrossRef]
- Pike, C.R.; Ross, C.A.; Scalettar, R.T.; Zimanyi, G. First-order reversal curve diagram analysis of a perpendicular nickel nanopillar array. Phys. Rev. B 2005, 71, 134407. [Google Scholar] [CrossRef]
- Klencsár, Z.; Kuzmann, E.; Vértes, A. User-Friendly software for Mössbauer spectrum analysis. J. Radioanal. Nucl. Chem. 1996, 210, 105. [Google Scholar] [CrossRef]
- Chen, D.X.; Pardo, E.; Sanchez, A. Demagnetizing factors for rectangular prisms. IEEE Trans. Magn. 2005, 41, 2077–2088. [Google Scholar] [CrossRef]
- Acton, G.; Roth, A.; Verosub, K.L. Analyzing micromagnetic properties with FORCIT software. EOS Trans. 2007, 88, 230. [Google Scholar] [CrossRef]
- Smith, D. (Penn State University, University Park, Pennsylvania, USA). ICDD Grant-in-Aid, 1973.
- Wertheim, G.K. Mössbauer Effect: Principles and Applications, 1st ed.; Academic Press: New York, NY, USA; London, UK, 1964; pp. 80–84. ISBN 9781483228563. [Google Scholar]
- Bowden, G.J.; Bunbury, D.S.P.; Guimarães, A.P.; Snyder, R.E. Mössbauer studies of the cubic Laves iron-rare-earth intermetallic compounds. J. Phys. C. Sol. State Phys. 1968, 1, 1376–1387. [Google Scholar] [CrossRef]
- Davies, J.E.; Hellwig, O.; Fullerton, E.E.; Jiang, J.S.; Bader, S.D.; Zimanyi, G.T.; Liu, K. Anisotropy dependence of irreversible switching in Fe/Sm Co and Fe Ni/Fe Pt exchange spring magnet films. Appl. Phys. Lett. 2005, 86, 262503. [Google Scholar] [CrossRef]
- Cornejo, D.R.; Peixoto, T.R.F.; Reboh, S.; Fichtner, P.F.P.; de Franco, V.C.; Villas-Boas, V.; Missell, F.P. First-order-reversal-curve analysis of Pr–Fe–B-based exchange spring magnets. J. Mater. Sci. 2010, 45, 5077–5083. [Google Scholar] [CrossRef]
| Nominal SmFe2 | Sample Region 1 | Sample Region 2 | Sample Region 3 | Sample Region 4 | |
|---|---|---|---|---|---|
| at% Sm | 33.3 | 34.18 | 32.68 | 33.82 | 34.62 |
| at% Fe | 66.6 | 65.82 | 67.32 | 66.18 | 65.38 |
| Magnetic Field (T) | Isomer Shift (mm s−1) | Quadrupolar Splitting (mm s−1) | Line Width (mm s−1) | Amplitude | |
|---|---|---|---|---|---|
| SmFe2 sextet 1 | 19.8 | −0.089 | 0.172 | 0.33 | 33576.8 |
| SmFe2 sextet 2 | 17.6 | 0.065 | 0.261 | 0.20 | 8286.6 |
| Distribution | 24.4 | −0.130 | −0.132 | 0.35 | 75837.3 |
| m = 0.00097 b = −0.1562 | m = 0.00243 b = −0.1917 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grijalva-Castillo, M.C.; Santillán-Rodríguez, C.R.; Sáenz-Hernández, R.J.; Botello-Zubíate, M.E.; Matutes-Aquino, J.A. First Order Reversal Curve Study of SmFe2 Melt-Spun Ribbons. Materials 2018, 11, 1804. https://doi.org/10.3390/ma11101804
Grijalva-Castillo MC, Santillán-Rodríguez CR, Sáenz-Hernández RJ, Botello-Zubíate ME, Matutes-Aquino JA. First Order Reversal Curve Study of SmFe2 Melt-Spun Ribbons. Materials. 2018; 11(10):1804. https://doi.org/10.3390/ma11101804
Chicago/Turabian StyleGrijalva-Castillo, María C., Carlos R. Santillán-Rodríguez, Renee J. Sáenz-Hernández, María E. Botello-Zubíate, and José A. Matutes-Aquino. 2018. "First Order Reversal Curve Study of SmFe2 Melt-Spun Ribbons" Materials 11, no. 10: 1804. https://doi.org/10.3390/ma11101804
APA StyleGrijalva-Castillo, M. C., Santillán-Rodríguez, C. R., Sáenz-Hernández, R. J., Botello-Zubíate, M. E., & Matutes-Aquino, J. A. (2018). First Order Reversal Curve Study of SmFe2 Melt-Spun Ribbons. Materials, 11(10), 1804. https://doi.org/10.3390/ma11101804






