Power Spectral Density Evaluation of Laser Milled Surfaces
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experiments
2.2. Data Acquisition
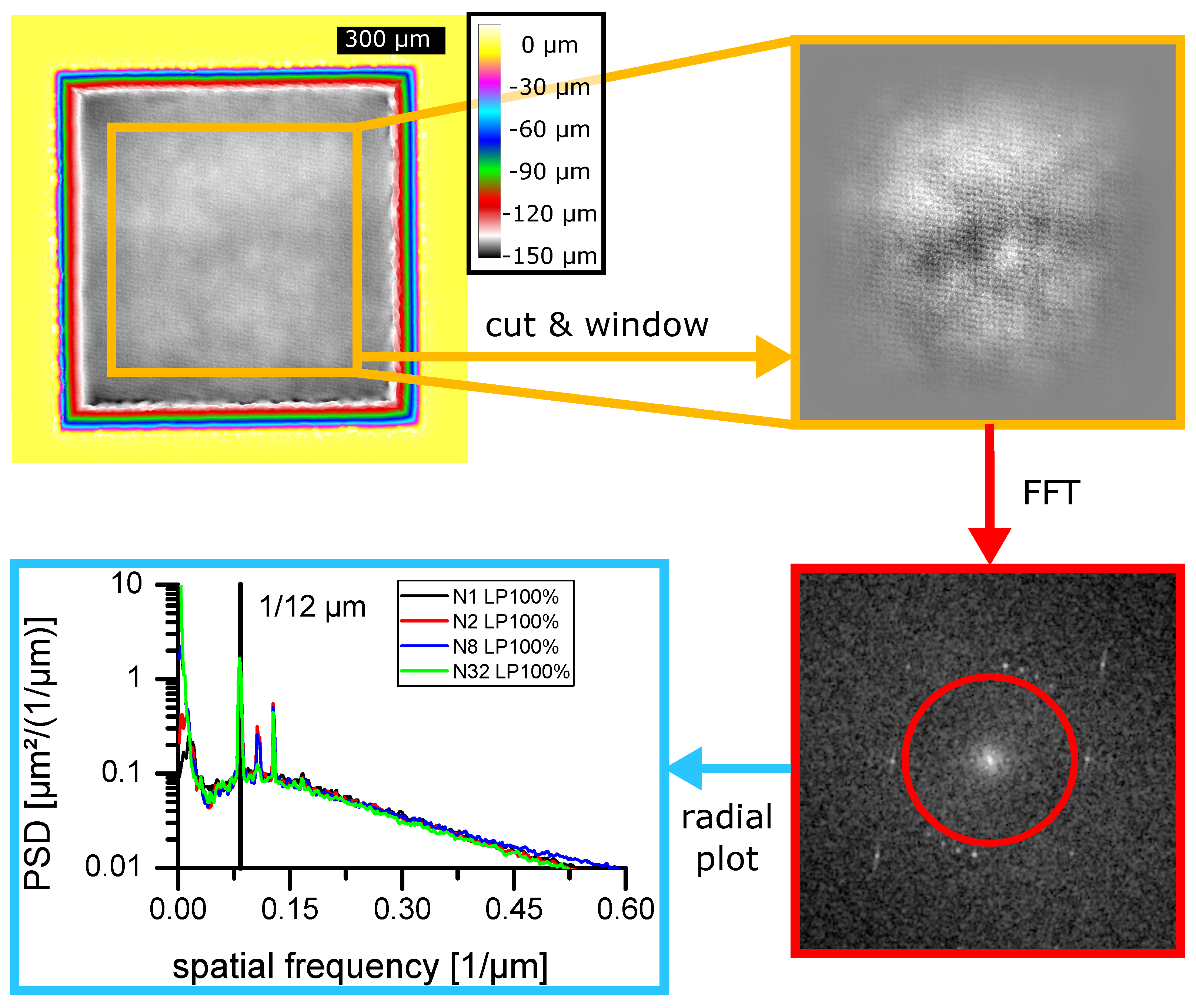
2.3. Power Spectral Density Evaluation
- Selecting a region of interest (ROI) within the cavities. Due to the supported resolution a ROI size of 2048 × 2048 pixels was chosen. Then the image was cropped to the ROI specifications. (compare Figure 3 top left)
- The average value of the new image was subtracted from each value. Afterwards, a PSD conservative (introducing a factor of ) weighting function reproducing a 2-dimensional Hanning window was applied. (compare Figure 3 orange box)with as the range of positions of the cropped image and as image coordinates.
- A fast Fourier transformation (FFT) was applied and the square of the absolute value at each frequency was computed. (compare Figure 3 red box)
- The resulting spectra were summed up to neglect direction-dependent information. Here, two variants came to use.
- (a)
- (b)
- The values within a previously defined circle/frequency range were summed resulting in the “low frequency” roughness as well as all values outside the circle/frequency range resulting in the “high frequency” roughness. (compare Figure 3 red circle)
2.4. Power Spectral Density Variation
- A fast Fourier transformation was applied to the complete profile data set and the low frequencies of the spectrum were removed (compare Section 2.3 step (4b)).
- An inverse fast Fourier transformation was applied resulting in an image containing only “high frequency” surface modulations.
- An identical ROI to the previous methods was chosen and the image was cropped to the ROIs size.
- The image was split into 16 × 16 sub-/sample-images. Standard deviation of every sample-image was calculated and finally the standard deviation of the surfaces standard deviations was taken as an estimate for the uncertainty of HF-STD or rather surface roughness.
2.5. Electron Backscattered Diffraction (EBSD) Analysis
3. Results
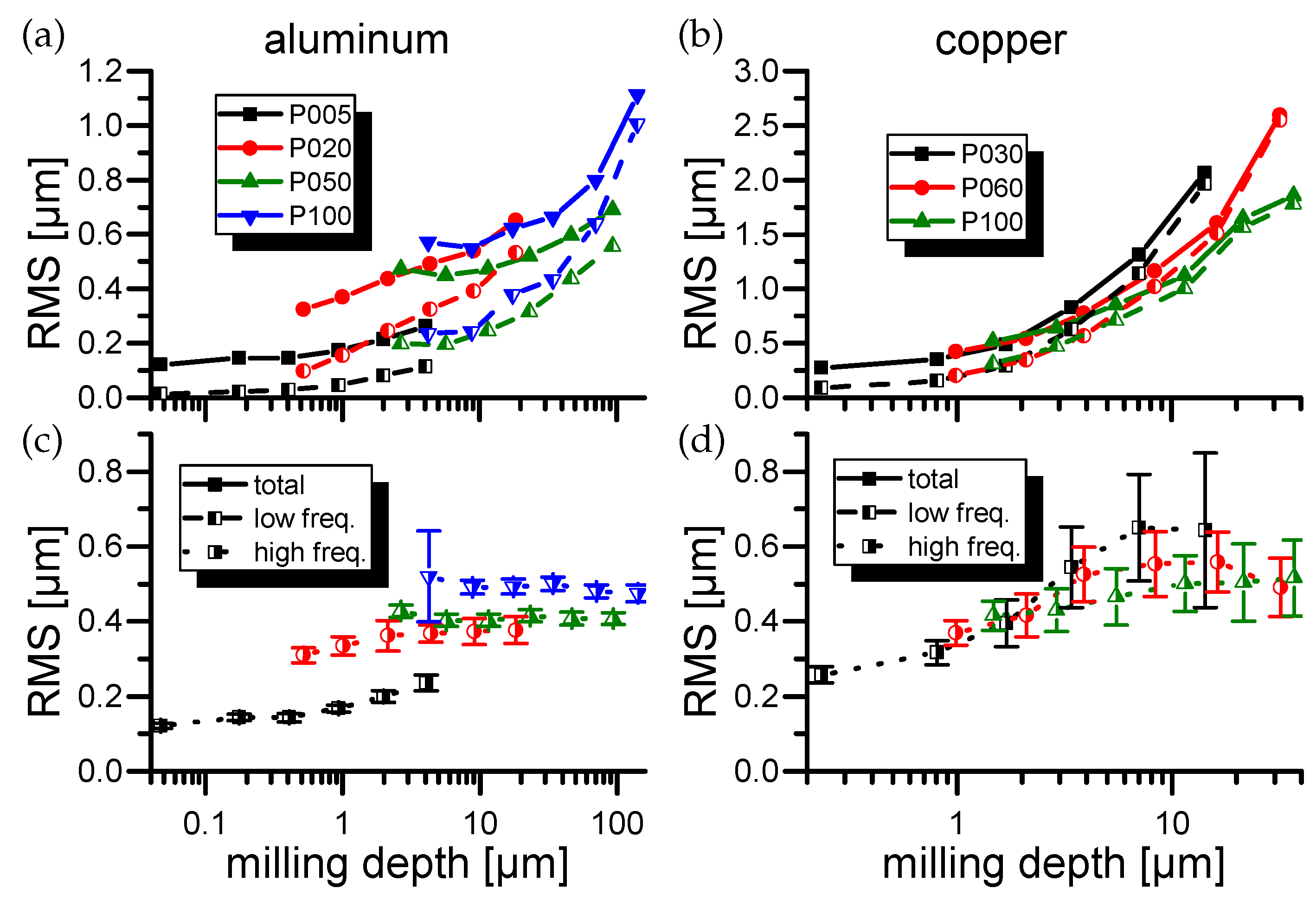
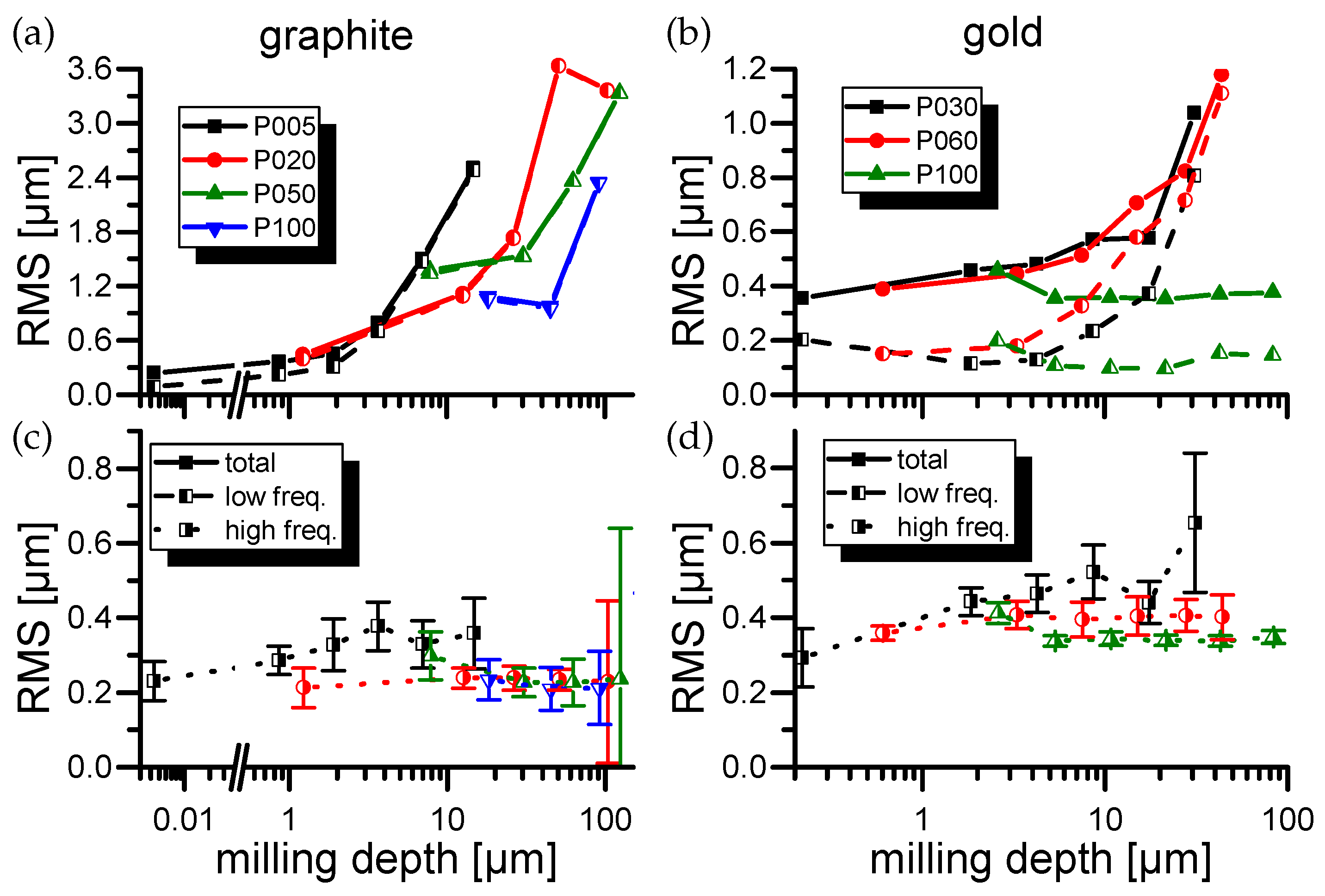
3.1. Roughness Spectra
3.2. Roughness Measurements
4. Discussion
5. Conclusions and Outlook
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| highest wavenumber | |
| circle bin size [px] | |
| beam waist radius | |
| border length [µm] | |
| highest x-position | |
| highest y-position | |
| variance | |
| peak fluence | |
| numerical aperture | |
| smallest wavenumber | |
| lowest x-position | |
| lowest y-position | |
| 2-dimensional Hanning window | |
| number of pixels in x,y direction | |
| circle pixel radius | |
| S | scaling factor |
| EBSD | Electron backscattered diffraction |
| f | focal length |
| FFT | fast Fourier transformation |
| HF | high frequency |
| LF | low frequency |
| PSD | power spectral density |
| RMS | root mean square |
| ROI | region of interest |
| x,y | x,y-coordinate |
References
- Scharring, S.; Lorbeer, R.A.; Eckel, H.A. Numerical Simulations on Laser-Ablative Micropropulsion with Short and Ultrashort Laser Pulses. Trans. Jpn. Soc. Aeronaut. Space Sci. Aerosp. Technol. Jpn. 2016, 14, 69–75. [Google Scholar] [CrossRef]
- Raciukaitis, G.; Brikas, M.; Gecys, P.; Voisiat, B.; Gedvilas, M. Use of high repetition rate and high power lasers in microfabrication: How to keep the efficiency high? JLMN J. Laser Micro/Nanoeng. 2009, 4, 186–191. [Google Scholar] [CrossRef]
- Jaeggi, B.; Neuenschwander, B.; Schmid, M.; Muralt, M.; Zuercher, J.; Hunziker, U. Influence of the Pulse Duration in the ps-Regime on the Ablation Efficiency of Metals. Phys. Procedia 2011, 12, 164–171. [Google Scholar] [CrossRef]
- Cheng, J.; Perrie, W.; Edwardson, S.; Fearon, E.; Dearden, G.; Watkins, K. Effects of laser operating parameters on metals micromachining with ultrafast lasers. Appl. Surf. Sci. 2009, 256, 1514–1520. [Google Scholar] [CrossRef]
- Niso, F.D.; Gaudiuso, C.; Sibillano, T.; Mezzapesa, F.P.; Ancona, A.; Lugarà, P.M. Role of heat accumulation on the incubation effect in multi-shot laser ablation of stainless steel at high repetition rates. Opt. Express 2014, 22, 12200–12210. [Google Scholar] [CrossRef] [PubMed]
- Bauer, F.; Michalowski, A.; Kiedrowski, T.; Nolte, S. Heat accumulation in ultra-short pulsed scanning laser ablation of metals. Opt. Express 2015, 23, 1035–1043. [Google Scholar] [CrossRef] [PubMed]
- Lorbeer, R.A.; Scharring, S.; Karg, S.; Pastow, J.; Pastuschka, L.; Förster, D.J.; Eckel, H.A. Thrust noise minimization in long-term laser ablation of propellant material in the nanosecond and picosecond regime. Opt. Eng. 2017, 56, 011010. [Google Scholar] [CrossRef]
- Danzmann, K.; Prince, T.A.; Binetruy, P.; Bender, P.; Buchman, S.; Centrella, J.; Cerdonio, M.; Cornish, N.; Cruise, M.; Cutler, C.J.; et al. LISA: Unveiling a hidden Universe. Assess. Study Rep. ESA/SRE 2011, 3, 2. [Google Scholar] [CrossRef]
- Leach, R.; Neal, K. Discussion of micro-newton thruster requirements for a drag-free control system. In Proceedings of the 16th Annual/USU Conference on Small Satellites, Logan, UT, USA, 12–15 August 2002. [Google Scholar]
- Scharring, S.; Lorbeer, R.A.; Karg, S.; Pastuschka, L.; Förster, D.J.; Eckel, H.A. The MICROLAS concept: Precise thrust generation in the Micronewton range by laser ablation. In Technology for Small Satellite Research: Payloads and Subsystem Technologies Small Satellite Applications, Missions, and In-Orbit Experiences Small Satellites; IAA Book Series on Small Satellite; International Academy of Astronautics: Stockholm, Sweden, 2016. [Google Scholar]
- Phipps, C.; Birkan, M.; Bohn, W.; Eckel, H.A.; Horisawa, H.; Lippert, T.; Michaelis, M.; Rezunkov, Y.; Sasoh, A.; Schall, W.; et al. Review: Laser-Ablation propulsion. J. Propuls. Power 2010, 26, 609–637. [Google Scholar] [CrossRef]
- Gonzales, D.A.; Baker, R.P. Micropropulsion using a Nd: YAG microchip laser. In Proceedings of the International Symposium on High-Power Laser Ablation, Taos, NM, USA, 21–26 April 2002; International Society for Optics and Photonics (SPIE): Bellingham, WA, USA, 2002; pp. 752–765. [Google Scholar]
- Elson, J.M.; Bennett, J.M. Calculation of the power spectral density from surface profile data. Appl. Opt. 1995, 34, 201–208. [Google Scholar] [CrossRef] [PubMed]
- Duparre, A.; Ferre-Borrull, J.; Gliech, S.; Notni, G.; Steinert, J.; Bennett, J.M. Surface characterization techniques for determining the root-mean-square roughness and power spectral densities of optical components. Appl. Opt. 2002, 41, 154–171. [Google Scholar] [CrossRef] [PubMed]
- Pastow, J. Optimierung Eines Versuchsaufbaus und Untersuchungen des Materialabtrags für Laser-Ablative Mikroantriebe. Master’s Thesis, IFSW, University of Stuttgart, Stuttgart, Germany, 2016. [Google Scholar]
- Preibisch, S.; Saalfeld, S.; Tomancak, P. Globally optimal stitching of tiled 3D microscopic image acquisitions. Bioinformatics 2009, 25, 1463–1465. [Google Scholar] [CrossRef] [PubMed]
- Carl, P. Radial Profile Extended. Available online: https://imagej.nih.gov/ij/plugins/radial-profile-ext.html (accessed on 14 May 2016).
- Lo, C.; Augis, J.; Pinnel, M. Hardening mechanisms of hard gold. J. Appl. Phys. 1979, 50, 6887–6891. [Google Scholar] [CrossRef]
- Plech, A.; Cerna, R.; Kotaidis, V.; Hudert, F.; Bartels, A.; Dekorsy, T. A surface phase transition of supported gold nanoparticles. Nano Lett. 2007, 7, 1026–1031. [Google Scholar] [CrossRef] [PubMed]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lorbeer, R.-A.; Pastow, J.; Sawannia, M.; Klinkenberg, P.; Förster, D.J.; Eckel, H.-A. Power Spectral Density Evaluation of Laser Milled Surfaces. Materials 2018, 11, 50. https://doi.org/10.3390/ma11010050
Lorbeer R-A, Pastow J, Sawannia M, Klinkenberg P, Förster DJ, Eckel H-A. Power Spectral Density Evaluation of Laser Milled Surfaces. Materials. 2018; 11(1):50. https://doi.org/10.3390/ma11010050
Chicago/Turabian StyleLorbeer, Raoul-Amadeus, Jan Pastow, Michael Sawannia, Peter Klinkenberg, Daniel Johannes Förster, and Hans-Albert Eckel. 2018. "Power Spectral Density Evaluation of Laser Milled Surfaces" Materials 11, no. 1: 50. https://doi.org/10.3390/ma11010050
APA StyleLorbeer, R.-A., Pastow, J., Sawannia, M., Klinkenberg, P., Förster, D. J., & Eckel, H.-A. (2018). Power Spectral Density Evaluation of Laser Milled Surfaces. Materials, 11(1), 50. https://doi.org/10.3390/ma11010050




