Metamaterial Waveguide Devices for Integrated Optics
Abstract
:1. Introduction
2. Metamaterial Waveguide Theory and Method of ε-μ Extraction
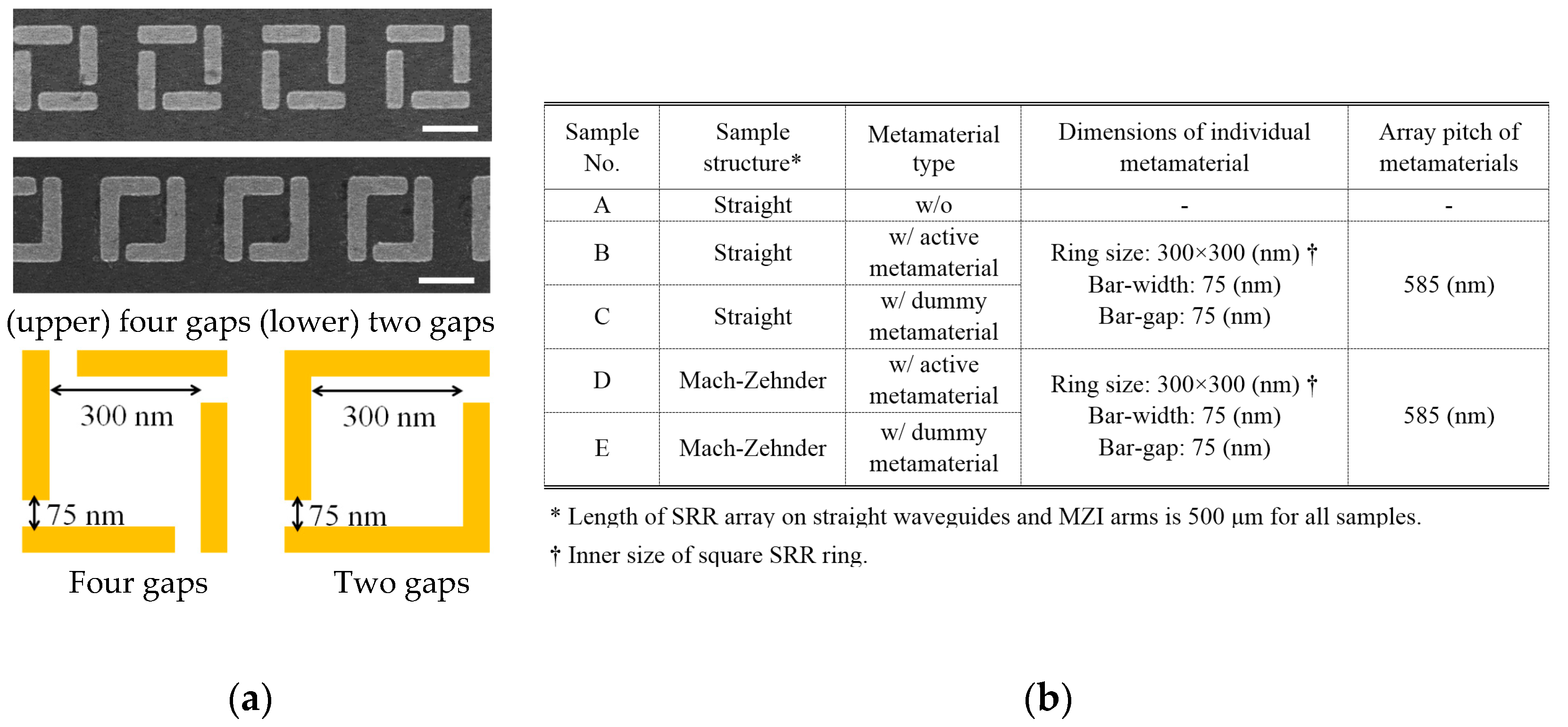
2.1. Split-Ring Metamaterial Compatible with Waveguide Optical Devices
2.2. Analysis of Metamaterial Waveguides Using a Transfer Matrix Method
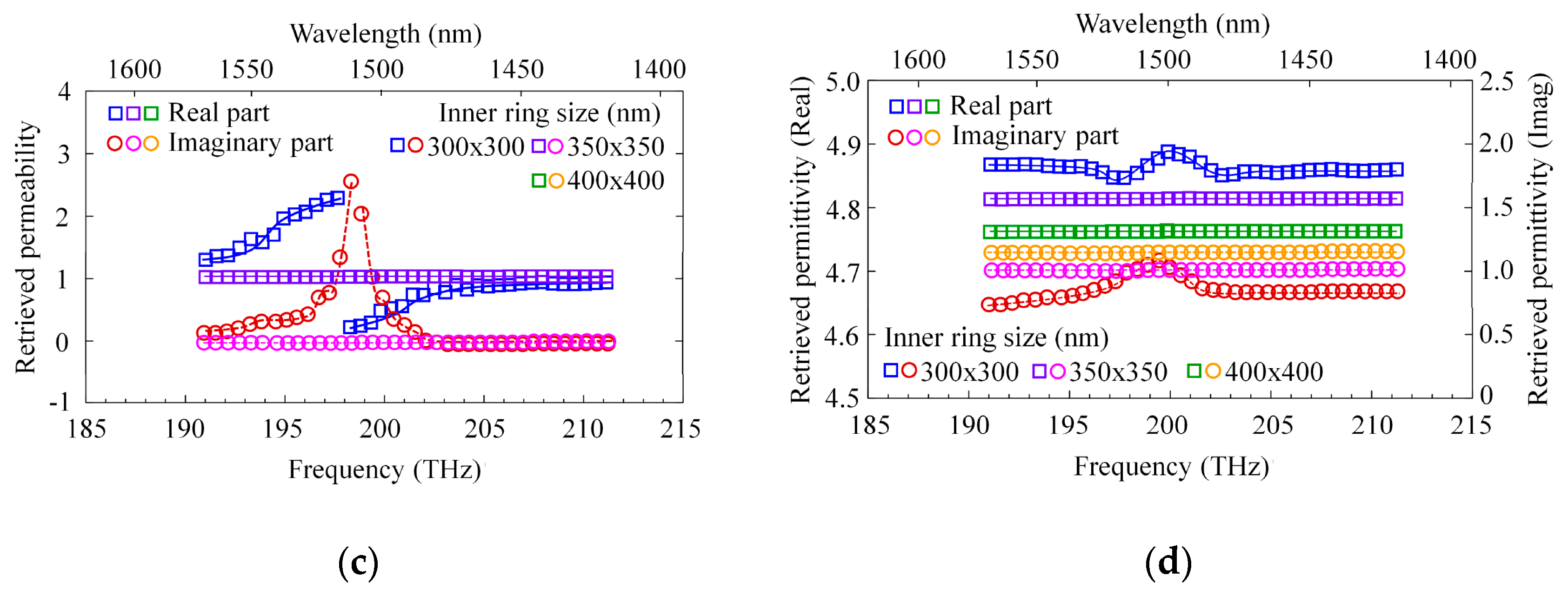
2.3. Permittivity and Permeability of the Metamaterial Uniform Layer
2.4. Example of ε-μ Extraction from Experimental Results
- Complex permittivity εx can be calculated from the transmission data of waveguide a, waveguide c, and MZI e, where μy is set to 1, and
- Complex permeability μy can be calculated from the transmission data of waveguide a, waveguide b, and MZI d, using the value of εx obtained in I.
3. Specific Metamaterial to Control Permeability of Semiconductor Photonic Devices
3.1. Controlling Permeability Using Carrier Accumulation of Semiconductors
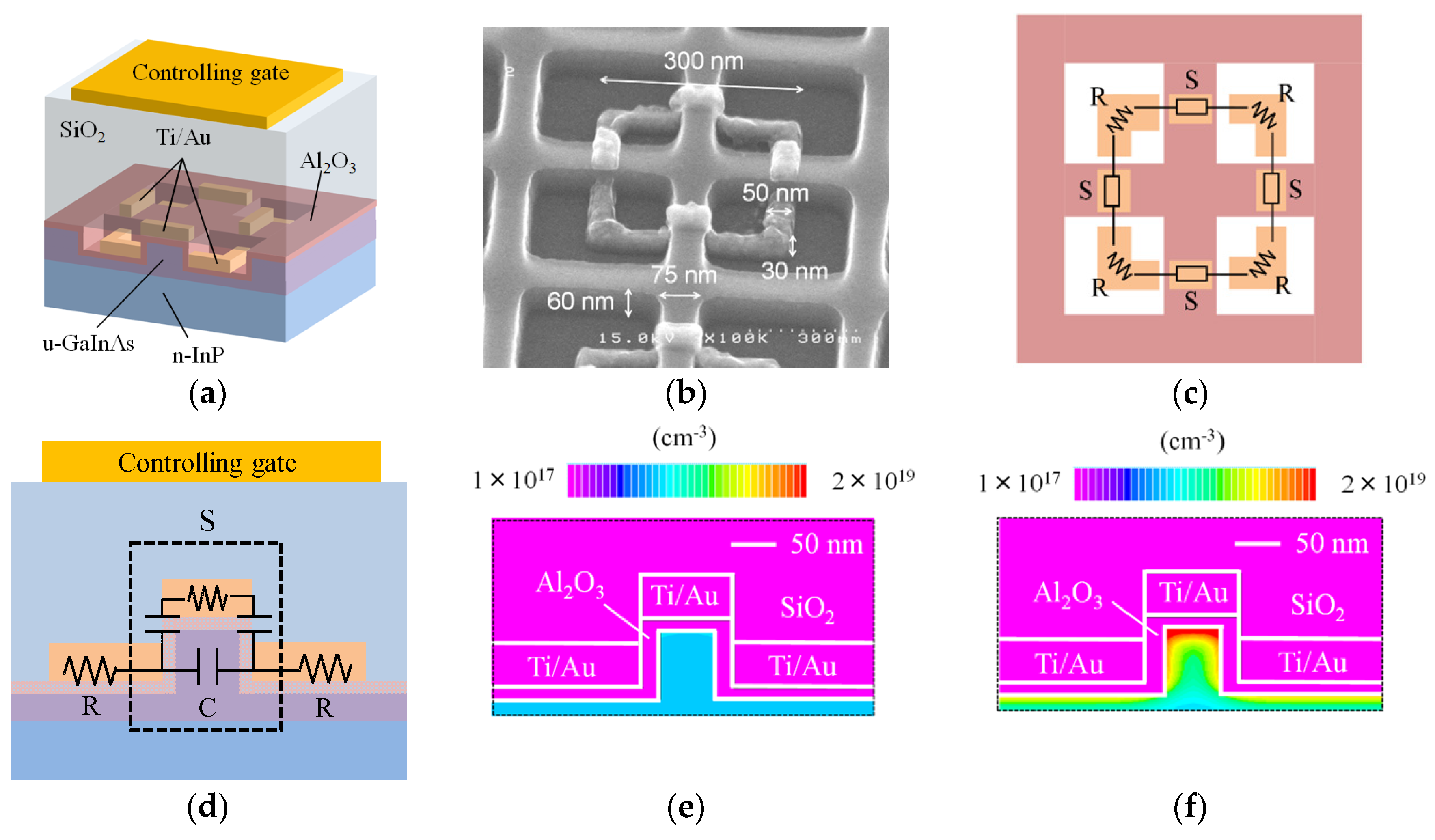
3.2. Specific Metamaterial Suructure for Electrical Control of Permeability
- A GaInAs thin layer is formed on the GaInAsP/InP-based optical waveguide and etched into grid-shaped fins;
- An Al2O3 layer covers the surface of the GaInAs fins;
- To make the SRR, a metal (Ti/Au) ring is formed on the surface in a manner such that it wraps the Al2O3-covered fins and is cut at the edges of the fin. The gap capacitance of the SRR exists at the places where the metal ring is cut (Figure 8c,d). The metal ring and fin form a structure similar to that of a triple-gated, three-dimensional transistor [37,38];
- A controlling gate is placed above the SRR (not illustrated). It is coupled capacitively with the SRR.
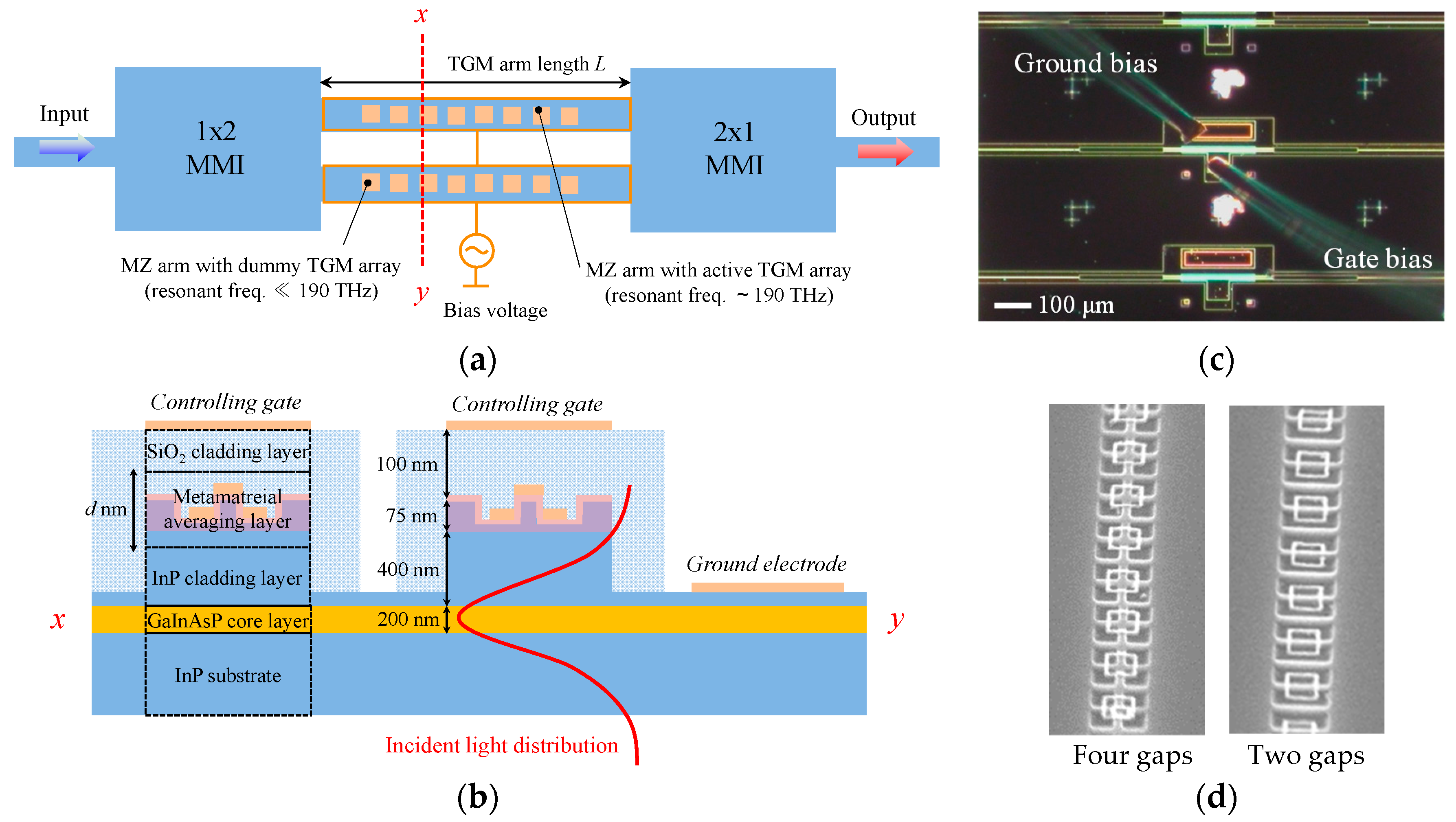
4. Permeability-Controlled Optical Modulator for Integrated Optics
4.1. Fabrication and Concept of Device
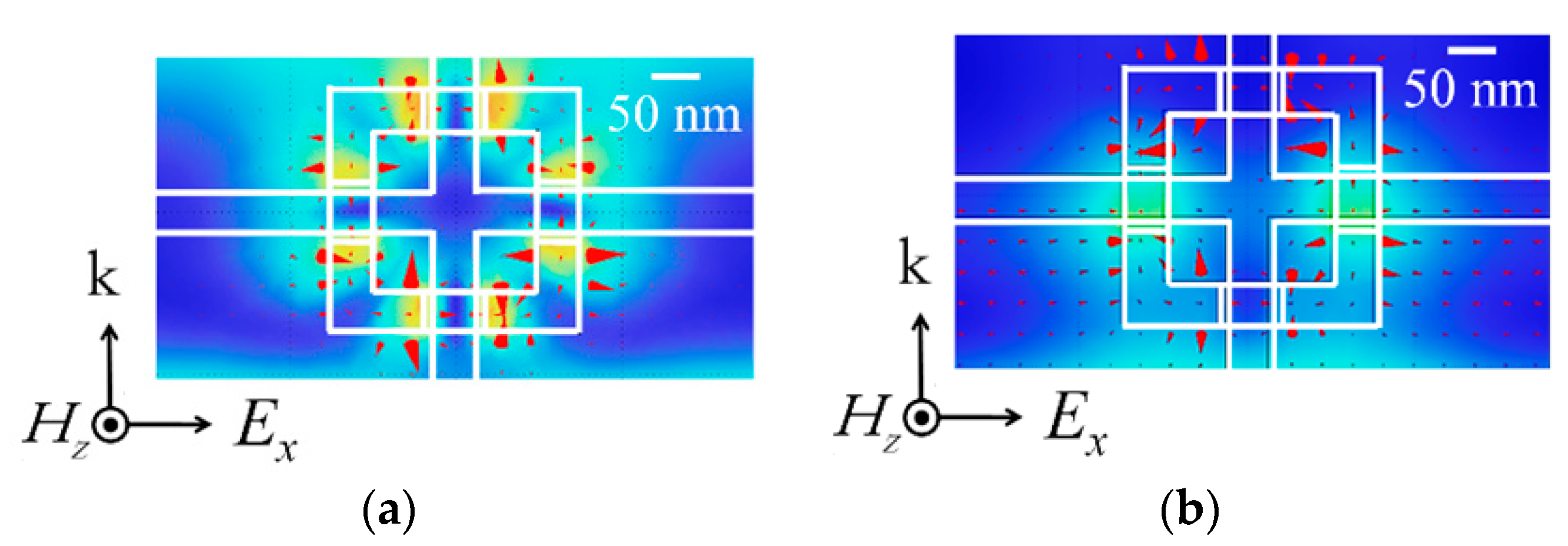
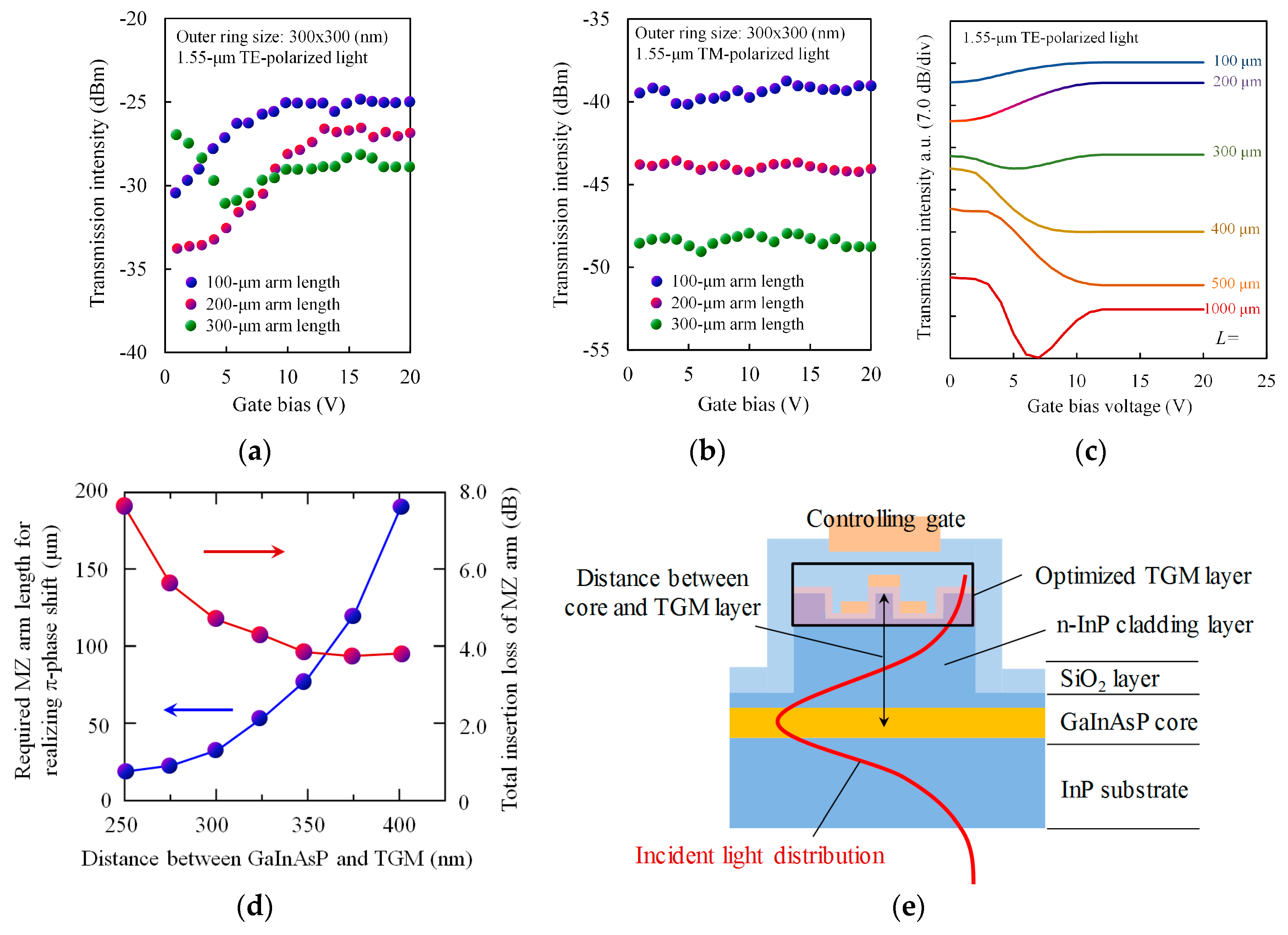
4.2. Operation of Permeability-Controlled Optical Modulator
- Calculate gate-induced electron distribution in the fin as a function of gate voltage, using a three-dimensional semiconductor device simulator (Silvaco Device3D, Santa Clara, CA, USA);
- Calculate the S parameter of one unit cell of the TGM by analysing light propagation over the unit cell with the aid of an electromagnetic simulator (Comsol Multiphysics, Comsol, Burlington, MA, USA);
- The TGM and its neighborhood (its adjacent part of the waveguide) can approximately be considered as a single uniform layer. Under this approximation, calculate the effective permeability and permittivity of the layer from the S parameter obtained in (ii), using the method described in Section 2.3;
- Conduct waveguide analysis to evaluate the transmission characteristics of the permeability-controlled MZ modulator, replacing the TGM and its neighborhood with the single layer. The waveguide analysis can be easily performed using metamaterial waveguide theory described in Section 2.2.
5. Summary
Acknowledgments
Conflicts of Interest
References
- Amemiya, T.; Shindo, T.; Takahashi, D.; Nishiyama, N.; Arai, S. Magnetic interactions at optical frequencies in an InP-based waveguide device with metamaterial. IEEE J. Quantum Electron. 2011, 47, 736–744. [Google Scholar] [CrossRef]
- Amemiya, T.; Shindo, T.; Takahashi, D.; Myoga, S.; Nishiyama, N.; Arai, S. Nonunity Permeability in metamaterial-based GaInAsP/InP multimode interferometers. Opt. Lett. 2011, 36, 2327–2329. [Google Scholar] [CrossRef] [PubMed]
- Walser, R.M. Electromagnetic metamaterials. Proc. SPIE 2001, 4467, 1–15. [Google Scholar] [CrossRef]
- Linden, S.; Enkrich, C.; Dolling, G.; Klein, M.W.; Zhou, J.; Koschny, T.; Soukoulis, C.M.; Burger, S.; Schmidt, F.; Wegener, M. Photonic metamaterials: Magnetism at optical frequencies. IEEE J. Sel. Top. Quantum Electron. 2006, 12, 1097–1105. [Google Scholar] [CrossRef]
- Ni, X.; Emani, N.K.; Kildishev, A.V.; Boltasseva, A.; Shalaev, V.M. Broadband light bending with plasmonic nanoantennas. Science 2012, 335, 427. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Z.H.; Yun, S.; Lin, L.; Bossard, J.A.; Werner, D.H.; Mayer, T.S. Tailoring dispersion for broadband low-loss optical metamaterials using deep-subwavelength inclusions. Sci. Rep. 2012, 3. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.; Ji, D.; Zeng, X.; Liu, K.; Gan, Q. Rainbow trapping in hyperbolic metamaterial waveguide. Sci. Rep. 2013, 3. [Google Scholar] [CrossRef]
- Pryce, I.M.; Aydin, K.; Kelaita, Y.A.; Briggs, R.M.; Atwater, H.A. Highly strained compliant optical metamaterials with large frequency tenability. Nano. Lett. 2014, 10, 4222–4227. [Google Scholar] [CrossRef] [PubMed]
- Fang, X.; Tseng, M.L.; Ou, J.-Y.; MacDonald, K.F.; Tsai, D.P.; Zheludev, N.I. Ultrafast all-optical switching via coherent modulation of metamaterial absorption. Appl. Phys. Lett. 2014, 104. [Google Scholar] [CrossRef]
- Amemiya, T.; Taki, M.; Kanazawa, T.; Hiratani, T.; Arai, S. Optical lattice model towards nonreciprocal invisibility cloaking. IEEE J. Quantum Electron. 2015, 51. [Google Scholar] [CrossRef]
- Zheldev, N.I.; Kivshar, Y.S. From metamaterials to metadevices. Nat. Mater. 2012, 11, 917–924. [Google Scholar] [CrossRef] [PubMed]
- Amemiya, T.; Kanazawa, T.; Urakami, T.; Ishikawa, A.; Hojo, N.; Yasui, A.; Nishiyama, N.; Tanaka, T.; Arai, S. Metafilm: Metamaterial array embedded in organic thin film. In Proceedings of the 2016 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 5–10 June 2016. [Google Scholar]
- Zhai, Y.; Ma, Y.; David, S.N.; Zhao, D.; Lou, R.; Tan, G.; Yang, R.; Yin, X. Scalable-manufactured randomized glass-polymer hybrid metamaterial for daytime radiative cooling. Science 2017, 355, 1062–1066. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Kim, M.-H.; Wang, C.; Han, Z.; Shrestha, S.; Overvig, A.C.; Lu, M.; Stein, A.; Agarwal, A.M.; Lončar, M.; et al. Controlling propagation and coupling of waveguide modes using phase-gradient metasurfaces. Nat. Nanotechnol. 2017, 12, 675–683. [Google Scholar] [CrossRef] [PubMed]
- Tol, J.J.G.M.; Oei, Y.S.; Khalique, U.; Nötzel, R.; Smit, M.K. InP-based photonic circuits: Comparison of monolithic integration techniques. Prog. Quantum Electron. 2010, 34, 135–172. [Google Scholar] [CrossRef]
- Coldren, L.A. High performance InP-based photonic ICs—A tutorial. IEEE J. Lightwave Technol. 2011, 29, 554–570. [Google Scholar] [CrossRef]
- Nagarajan, R.; Kato, M.; Lambert, D.; Evans, P.; Corzine, S.; Lal, V.; Rahn, J.; Nilsson, A.; Fisher, M.; Kuntz, M.; et al. Terabit/s class InP photonic integrated circuits. Semicond. Sci. Technol. 2012, 27, 094003. [Google Scholar] [CrossRef]
- Ishikawa, A.; Tanaka, T.; Kawata, S. Frequency dependence of the magnetic response of split-ring resonators. J. Opt. Soc. Am. B 2006, 24, 510–515. [Google Scholar] [CrossRef]
- Valentine, J.; Zhang, S.; Zentgraf, T.; Ulin-Avila, E.; Genov, D.A.; Bartal, G.; Zhang, X. Three-dimensional optical metamaterial with a negative refractive index. Nature 2008, 455, 376–379. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Sauvan, C.; Liu, H.T.; Lalanne, P. Theory of fishnet negative-index optical metamaterials. Phys. Rev. Lett. 2011, 107, 043903. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.R.; Vier, D.C.; Koschny, T.; Soukoulis, C.M. Electromagnetic parameter retrieval from inhomogeneous metamaterials. Phys. Rev. E 2005, 71, 036617. [Google Scholar] [CrossRef] [PubMed]
- Shadrivov, I.V.; Sukhorukov, A.A.; Kivshar, Y.S. Guided modes in negative-refractive-index waveguides. Phys. Rev. E 2003, 67, 057602. [Google Scholar] [CrossRef] [PubMed]
- Tsakmakidis, K.L.; Boardman, A.D.; Hess, O. Trapped rainbow storage of light in metamaterials. Nature 2007, 450, 397–401. [Google Scholar] [CrossRef] [PubMed]
- Amemiya, T.; Myoga, S.; Shindo, T.; Murai, E.; Nishiyama, N.; Arai, S. Permeability retrieval in InP-based waveguide optical device combined with metamaterial. Opt. Lett. 2012, 37, 2301–2303. [Google Scholar] [CrossRef] [PubMed]
- Ou, J.Y.; Plum, E.; Zhang, J.; Zheludev, N.I. An electromechanically reconfigurable plasmonic metamaterial operating in the near-infrared. Nat. Nanotechnol. 2013, 8, 252–255. [Google Scholar] [CrossRef] [PubMed]
- Dani, K.M.; Ku, Z.; Upadhya, P.C.; Prasankumar, R.P.; Taylor, A.J.; Brueck, S.R. Ultrafast nonlinear optical spectroscopy of a dual-band negative index metamaterial all-optical switching device. Opt. Express 2011, 19, 3973–3983. [Google Scholar] [CrossRef] [PubMed]
- Kocaman, S.; Aras, M.S.; Hsieh, P.; McMillan, J.F.; Biris, C.G.; Panoiu, N.C.; Yu, M.B.; Kwong, D.L.; Stein, A.; Wong, C.W. Zero phase delay in negative-refractive-index photonic crystal superlattices. Nat. Photonics 2011, 5, 499–505. [Google Scholar] [CrossRef]
- Driscoll, T.; Kim, H.-T.; Chae, B.-G.; Kim, B.-J.; Lee, Y.-W.; Jokerst, N.M.; Palit, S.; Smith, D.R.; Di Ventra, M.; Basov, D.N. Memory metamaterials. Science 2009, 325, 1518–1521. [Google Scholar] [CrossRef] [PubMed]
- Jun, Y.C.; Gonzales, E.; Reno, J.; Shaner, E.; Gabbay, A.; Brener, I. Electrically-controlled thermal infrared metamaterial devices. In Proceedings of the 2012 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 6–11 May 2012. [Google Scholar]
- Myoga, S.; Amemiya, T.; Ishikawa, A.; Nishiyama, N.; Tanaka, T.; Arai, S. Carrier-concentration- dependent resonance frequency shift in a metamaterial loaded semiconductor. J. Opt. Soc. Am. B 2012, 29, 2110–2115. [Google Scholar] [CrossRef]
- Jun, Y.C.; Gonzales, E.; Reno, J.; Shaner, E.; Gabbay, A.; Brener, I. Active tuning of mid-infrared metamaterials by electrical control of carrier densities. Opt. Express 2012, 20, 1903–1911. [Google Scholar] [CrossRef] [PubMed]
- Horestani, A.K.; Withayachumnankul, W.; Chahadih, A.; Ghaddar, A.; Zehar, M.; Abbott, D.; Fumeaux, C.; Akalin, T. Metamaterial-inspired bandpass filters for terahertz surface waves on Goubau lines. IEEE Trans. Terahertz Sci. Technol. 2013, 3, 851–858. [Google Scholar] [CrossRef]
- Yamasaki, S.; Yasui, A.; Amemiya, T.; Furusawa, K.; Hara, S.; Watanabe, I.; Kanno, A.; Sekine, N.; Gu, Z.; Nishiyama, N.; et al. Optically-driven terahertz wave modulator using ring-shaped microstripline with GaInAs photoconductive mesa structure. IEEE J. Select. Top. Quantum Electron. 2017, 23, 1–8. [Google Scholar] [CrossRef]
- Bennett, B.R.; Soref, R.A.; Del Alamo, J.A. Carrier-induced change in refractive index of InP, GaAs and GaInAsP. IEEE J. Quantum Electron. 1990, 26, 113–122. [Google Scholar] [CrossRef]
- Bennett, B.R.; Soref, R.A. Electrorefraction and electroabsorption in InP, GaAs, GaSb, InAs, and InSb. IEEE J. Quantum Electron. 1987, 23, 2159–2166. [Google Scholar] [CrossRef]
- Wolff, P.A. Theory of the band structure of very degenerate semiconductors. Phys. Rev. 1962, 126, 405–412. [Google Scholar] [CrossRef]
- Huang, X.; Lee, W.-C.; Kuo, C.; Hisamoto, D.; Chang, L.; Kedzierski, J.; Anderson, E.; Takeuchi, H.; Choi, Y.-K.; Asano, K.; et al. Sub-50 nm P-channel FinFET. IEEE Trans. Electron. Devices 2001, 48, 880–886. [Google Scholar] [CrossRef]
- Auth, C.; Allen, C.; Blattner, A.; Bergstrom, D.; Brazier, M.; Bost, M.; Buehler, M.; Chikarmane, V.; Ghani, T.; Glassman, T.; et al. A 22 nm high performance and low-power CMOS technology featuring fully-depleted tri-gate transistors, self-aligned contacts and high density MIM capacitors. In Proceedings of the 2012 Symposium on VLSI Technology (VLSIT), Honolulu, HI, USA, 12–14 June 2012. [Google Scholar]
- Amemiya, T.; Ishikawa, A.; Kanazawa, T.; Kang, J.; Nishiyama, N.; Miyamoto, Y.; Tanaka, T.; Arai, S. Permeability-controlled optical modulator with tri-gate metamaterial: Control of permeability on InP-based photonic integration platform. Sci. Rep. 2015, 5. [Google Scholar] [CrossRef] [PubMed]






© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amemiya, T.; Kanazawa, T.; Yamasaki, S.; Arai, S. Metamaterial Waveguide Devices for Integrated Optics. Materials 2017, 10, 1037. https://doi.org/10.3390/ma10091037
Amemiya T, Kanazawa T, Yamasaki S, Arai S. Metamaterial Waveguide Devices for Integrated Optics. Materials. 2017; 10(9):1037. https://doi.org/10.3390/ma10091037
Chicago/Turabian StyleAmemiya, Tomohiro, Toru Kanazawa, Satoshi Yamasaki, and Shigehisa Arai. 2017. "Metamaterial Waveguide Devices for Integrated Optics" Materials 10, no. 9: 1037. https://doi.org/10.3390/ma10091037
APA StyleAmemiya, T., Kanazawa, T., Yamasaki, S., & Arai, S. (2017). Metamaterial Waveguide Devices for Integrated Optics. Materials, 10(9), 1037. https://doi.org/10.3390/ma10091037




