Quantifying the Performance of P-Type Transparent Conducting Oxides by Experimental Methods
Abstract
1. Introduction
2. An Assessment of the Commonly Used Figure of Merit
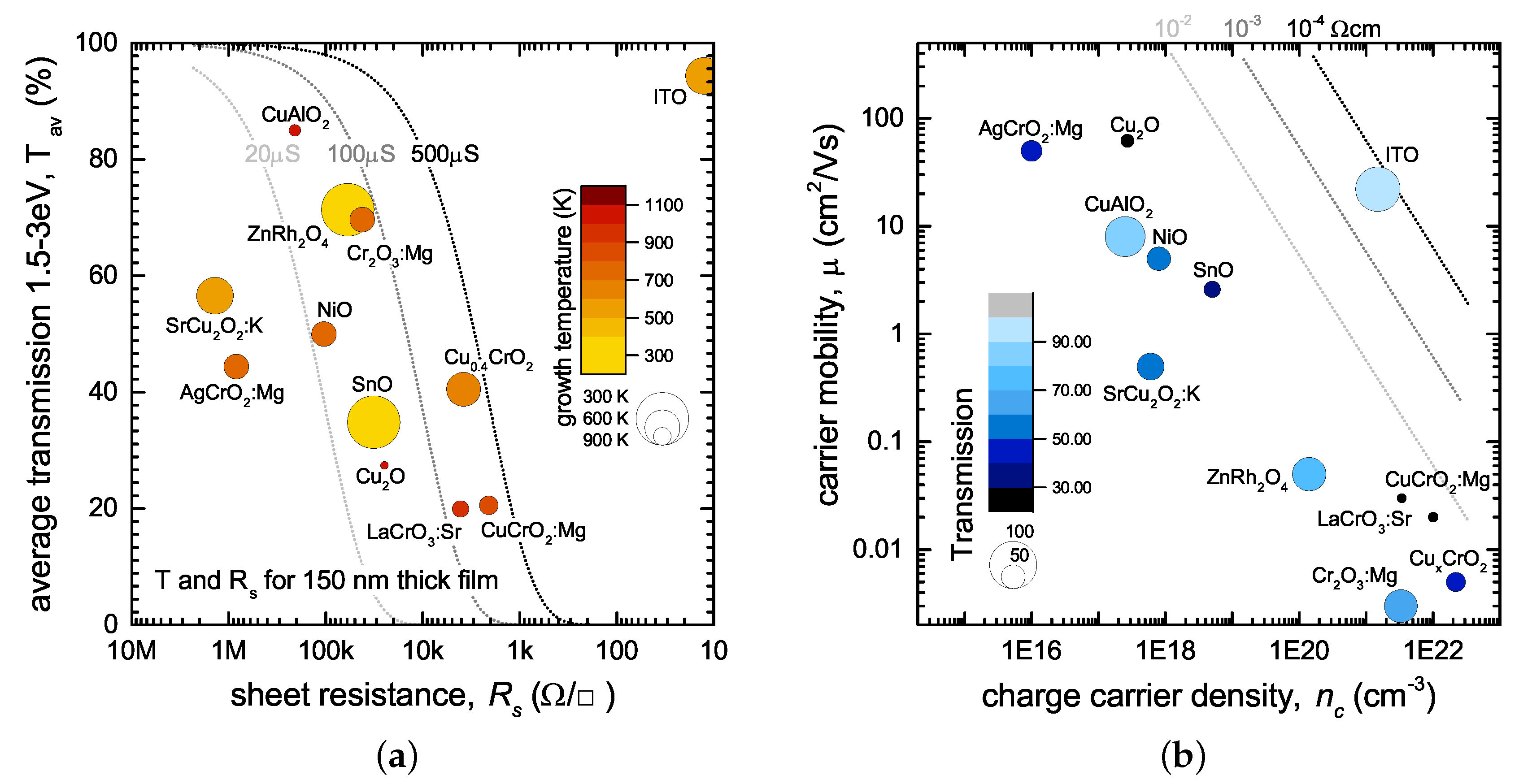
2.1. Comparing Known p-Type TCO Materials—The Issue of Limited Information
2.2. Measuring a Robust Figure of Merit in Screening Methods
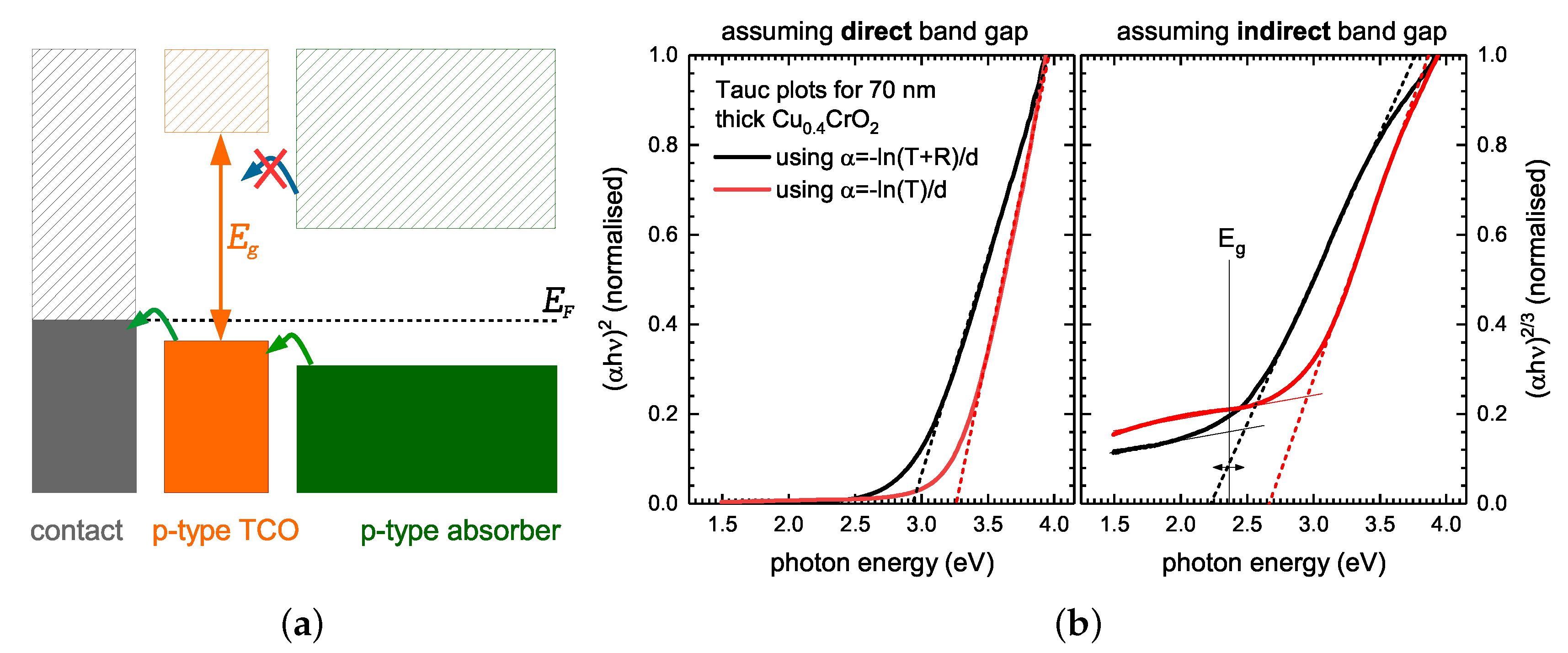
3. Application-Specific Considerations
4. Materials and Methods
5. Conclusions
- If at all possible measure sheet resistance, transmission, and reflection to determine and correctly without systematic thickness-related errors.
- If only transmission data are available:
- -
- estimate the refractive index using methods described in Section 2.2 and calculate
- -
- Measure films of different thickness to evaluate systematic errors in the band gap determination and caused by interference fringes.
- -
- Measure films well above 50 nm thickness to avoid underestimating transparency due to broad reflection maximum
- Check available DFT calculations for consistency of (a) the refractive index n, and (b) the type of band gap. Always assess the possibility of non-direct gaps when using Tauc plots (see Section 3).
- Only give directly measured mobility values (DC-, AC-Hall measurements, or Seebeck measurements for polaronic materials). In all cases, follow rigorous procedures for highly resistive materials [58].
- Explicitly state the assessed films’ sample thickness and check for consistency of the thickness with interference fringes in transmission data.
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| absorption coefficient | |
| AC | alternating current |
| c | speed of light |
| CSD | chemical solution deposition |
| d | sample thickness |
| DFT | density functional theory |
| DFT-LDA | density functional theory in local density approximation |
| DFT-GGA | density functional theory in generalised gradient approximation |
| DC | direct current |
| energetic position of the first interference maxima (for R) or minima (for T) | |
| band gap | |
| FOM | figure of merit |
| FOM based on transmittance and reflectance measurements | |
| simplified FOM based on transmittance measurements | |
| FOM based on transmittance measurement and reflectance estimation | |
| GW | DFT correction based on an expansion of the single-particle |
| Green’s function G with respect to the Coulomb interaction W | |
| h | Plank constant |
| ITO | indium tin oxide |
| k | extinction coefficient |
| LED | light emitting device |
| carrier mobility | |
| MBE | molecular beam epitaxy |
| frequency | |
| n | refractive index |
| carrier concentration | |
| OLED | organic light emitting diode |
| PLD | pulsed laser deposition |
| resistivity | |
| density | |
| r | Tauc exponent |
| R | reflectance |
| bulk material, normal incidence reflectance | |
| measured, average normal incidence reflectance (1.5–3.0 eV) | |
| RF | radio frequency |
| sheet resistance | |
| conductivity | |
| SP | spray pyrolysis |
| measured, average normal incidence transmission (1.5–3.0 eV) | |
| TCO | transparent conducting oxide |
| TFT | thin film transistor |
| TTFT | transparent thin film transistor |
| UV-VIS | ultraviolet-visible |
| XRD | X-ray diffraction |
| XRR | X-ray reflection |
References
- Hosono, H.; Ohta, H.; Orita, M.; Ueda, K.; Hirano, M. Frontier of transparent conductive oxide thin films. Vacuum 2002, 66, 419–425. [Google Scholar] [CrossRef]
- Beyer, W.; Hupkes, J.; Stiebig, H. Transparent conducting oxide films for thin film silicon photovoltaics. Thin Solid Films 2007, 516, 147–154. [Google Scholar] [CrossRef]
- Fortunato, E.; Ginley, D.; Hosono, H.; Paine, D.C. Transparent conducting oxides for photovoltaics. MRS Bull. 2007, 32, 242–247. [Google Scholar] [CrossRef]
- Hosono, H. Recent progress in transparent oxide semiconductors: Materials and device application. Thin Solid Films 2007, 515, 6000–6014. [Google Scholar] [CrossRef]
- Szyszka, B.; Loebmann, P.; Georg, A.; May, C.; Elsaesser, C. Development of new transparent conductors and device applications utilizing a multidisciplinary approach. Thin Solid Films 2010, 518, 3109–3114. [Google Scholar] [CrossRef]
- Morales-Masis, M.; De Wolf, S.; Woods-Robinson, R.; Ager, J.W.; Ballif, C. Transparent Electrodes for Efficient Optoelectronics. Adv. Electron. Mater. 2017, 3, 1600529. [Google Scholar] [CrossRef]
- Stadler, A. Transparent Conducting Oxides-An Up-To-Date Overview. Materials 2012, 5, 661–683. [Google Scholar] [CrossRef] [PubMed]
- Kawazoe, H.; Yasukawa, M.; Hyodo, H.; Kurita, M.; Yanagi, H.; Hosono, H. P-type electrical conduction in transparent thin films of CuAlO2. Nature 1997, 389, 939–942. [Google Scholar] [CrossRef]
- Jayaraj, M.K.; Draeseke, A.D.; Tate, J.; Sleight, A.W. p-type transparent thin films of CuY1−xCaxO2. Thin Solid Films 2001, 397, 244–248. [Google Scholar] [CrossRef]
- Tate, J.; Jayaraj, M.K.; Draeseke, A.D.; Ulbrich, T.; Sleight, A.W.; Vanaja, K.A.; Nagarajan, R.; Wager, J.F.; Hoffman, R.L. p-Type oxides for use in transparent diodes. Thin Solid Films 2002, 411, 119–124. [Google Scholar] [CrossRef]
- Nagarajan, R.; Duan, N.; Jayaraj, M.K.; Li, J.; Vanaja, K.A.; Yokochi, A.; Draeseke, A.; Tate, J.; Sleight, A.W. p-Type conductivity in the delafossite structure. Int. J. Inorg. Mater. 2001, 3, 265–270. [Google Scholar] [CrossRef]
- Narushima, S.; Mizoguchi, H.; Shimizu, K.; Ueda, K.; Ohta, H.; Hirano, M.; Kamiya, T.; Hosono, H. A p-Type Amorphous Oxide Semiconductor and Room Temperature Fabrication of Amorphous Oxide p-n Heterojunction Diodes. Adv. Mater. 2003, 15, 1409. [Google Scholar] [CrossRef]
- Kamiya, T.; Narushima, S.; Mizoguchi, H.; Shimizu, K.; Ueda, K.; Ohta, H.; Hirano, M.; Hosono, H. Electrical properties and structure of p-type amorphous oxide semiconductor ZnO-Rh2O3. Adv. Funct. Mater. 2005, 15, 968–974. [Google Scholar] [CrossRef]
- Peng, H.; Zakutayev, A.; Lany, S.; Paudel, T.R.; d’Avezac, M.; Ndione, P.F.; Perkins, J.D.; Ginley, D.S.; Nagaraja, A.R.; Perry, N.H.; et al. Li-Doped Cr2MnO4: A New p-Type Transparent Conducting Oxide by Computational Materials Design. Adv. Funct. Mater. 2013, 23, 5267–5276. [Google Scholar] [CrossRef]
- Zhang, K.H.L.; Du, Y.; Papadogianni, A.; Bierwagen, O.; Sallis, S.; Piper, L.F.J.; Bowden, M.E.; Shutthanandan, V.; Sushko, P.V.; Chambers, S.A. Perovskite Sr-Doped LaCrO3 as a New p-Type Transparent Conducting Oxide. Adv. Mater. 2015, 27, 5191–5195. [Google Scholar] [CrossRef] [PubMed]
- Holt, A.; Kofstad, P. Electrical conductivity and defect structure of Mg-doped Cr2O3. Solid State Ion. 1997, 100, 201–209. [Google Scholar] [CrossRef]
- Arca, E.; Fleischer, K.; Shvets, I.V. Magnesium, nitrogen codoped Cr2O3: A p-type transparent conducting oxide. Appl. Phys. Lett. 2011, 99, 111910. [Google Scholar] [CrossRef]
- Farrell, L.; Fleischer, K.; Caffrey, D.; Mullarkey, D.; Norton, E.; Shvets, I.V. Conducting mechanism in the epitaxial p-type transparent conducting oxide Cr2O3:Mg. Phys. Rev. B 2015, 91, 125202. [Google Scholar] [CrossRef]
- Perkins, J.D.; Paudel, T.R.; Zakutayev, A.; Ndione, P.F.; Parilla, P.A.; Young, D.L.; Lany, S.; Ginley, D.S.; Zunger, A.; Perry, N.H.; et al. Inverse design approach to hole doping in ternary oxides: Enhancing p-type conductivity in cobalt oxide spinels. Phys. Rev. B 2011, 84, 205207. [Google Scholar] [CrossRef]
- Hautier, G.; Miglio, A.; Ceder, G.; Rignanese, G.M.; Gonze, X. Identification and design principles of low hole effective mass p-type transparent conducting oxides. Nat. Commun. 2013, 4, 2292. [Google Scholar] [CrossRef] [PubMed]
- Sarmadian, N.; Saniz, R.; Partoens, B.; Lamoen, D. Easily doped p-type, low hole effective mass, transparent oxides. Sci. Rep. 2016, 6, 20446. [Google Scholar] [CrossRef] [PubMed]
- Varley, J.B.; Miglio, A.; Ha, V.A.; van Setten, M.J.; Rignanese, G.M.; Hautier, G. High-Throughput Design of Non-oxide p-Type Transparent Conducting Materials: Data Mining, Search Strategy, and Identification of Boron Phosphide. Chem. Mater. 2017, 29, 2568–2573. [Google Scholar] [CrossRef]
- Scanlon, D.O.; Watson, G.W. Understanding the p-type defect chemistry of CuCrO2. J. Mater. Chem. 2011, 21, 3655–3663. [Google Scholar] [CrossRef]
- Zhang, S.B.; Wei, S.H.; Zunger, A. Intrinsic n-type versus p-type doping asymmetry and the defect physics of ZnO. Phys. Rev. B 2001, 63, 075205. [Google Scholar] [CrossRef]
- Lany, S.; Osorio-Guillén, J.; Zunger, A. Origins of the doping asymmetry in oxides: Hole doping in NiO versus electron doping in ZnO. Phys. Rev. B 2007, 75, 241203. [Google Scholar] [CrossRef]
- Godinho, K.G.; Walsh, A.; Watson, G.W. Energetic and electronic structure analysis of intrinsic defects in SnO2. J. Phys. Chem. C 2008, 113, 439–448. [Google Scholar] [CrossRef]
- Exarhos, G.J.; Zhou, X.D. Discovery-based design of transparent conducting oxide films. Thin Solid Films 2007, 515, 7025–7052. [Google Scholar] [CrossRef]
- Gordon, R.G. Criteria for Choosing Transparent Conductors. MRS Bull. 2000, 25, 52. [Google Scholar] [CrossRef]
- Jain, V.K.; Kulshreshtha, A.P. Indium-tin-oxide transparent conducting coatings on silicon solar cells and their “figure of merit”. Sol. Energy Mater. 1981, 4, 151–158. [Google Scholar] [CrossRef]
- Farrell, L.; Norton, E.; O’Dowd, B.J.; Caffrey, D.; Shvets, I.V.; Fleischer, K. Spray pyrolysis growth of a high figure of merit, nano-crystalline, p-type transparent conducting material at low temperature. Appl. Phys. Lett. 2015, 107, 031901. [Google Scholar] [CrossRef]
- Farrell, L.; Norton, E.; Smith, C.M.; Caffrey, D.; Shvets, I.V.; Fleischer, K. Synthesis of nanocrystalline Cu deficient CuCrO2: A high figure of merit p-type transparent semiconductor. J. Mater. Chem. C 2016, 4, 126. [Google Scholar] [CrossRef]
- Popa, P.L.; Crêpellière, J.; Leturcq, R.; Lenoble, D. Electrical and optical properties of Cu–Cr–O thin films fabricated by chemical vapour deposition. Thin Solid Films 2016, 612, 194–201. [Google Scholar] [CrossRef]
- Crêpellière, J.; Popa, P.L.; Bahlawane, N.; Leturcq, R.; Werner, F.; Siebentritt, S.; Lenoble, D. Transparent conductive CuCrO2 thin films deposited by pulsed injection metal organic chemical vapor deposition: up-scalable process technology for an improved transparency/conductivity trade-off. J. Mater. Chem. C 2016, 4, 4278–4287. [Google Scholar] [CrossRef]
- Fleischer, K.; Arca, E.; Shvets, I.V. Improving solar cell efficiency with optically optimised TCO layers. Sol. Energy Mater. Sol. Cells 2012, 101, 262–269. [Google Scholar] [CrossRef]
- Manifacier, J.; Gasiot, J.; Fillard, J. A simple method for the determination of the optical constants n, k and the thickness of a weakly absorbing thin film. J. Phys. E: Sci. Instrum. 1976, 9, 1002. [Google Scholar] [CrossRef]
- Tepehan, F.; Özer, N. A simple method for the determination of the optical constants, n and k of cadmium sulfide films from transmittance measurements. Sol. Energy Mater. Sol. Cells 1993, 30, 353–365. [Google Scholar] [CrossRef]
- Jain, A.; Ong, S.P.; Hautier, G.; Chen, W.; Richards, W.D.; Dacek, S.; Cholia, S.; Gunter, D.; Skinner, D.; Ceder, G.; et al. The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1, 011002. Available online: http://materialsproject.org/ (accessed on 30 August 2017). [CrossRef]
- Saal, J.E.; Kirklin, S.; Aykol, M.; Meredig, B.; Wolverton, C. Materials design and discovery with high-throughput density functional theory: the open quantum materials database (OQMD). JOM 2013, 65, 1501–1509. Available online: http://oqmd.org/ (accessed on 30 August 2017). [CrossRef]
- Lany, S. Band-structure calculations for the 3 d transition metal oxides in GW. Phys. Rev. B 2013, 87, 085112, NREL Materials Database. Available online: http://materials.nrel.gov/ (accessed on 30 August 2017). [CrossRef]
- Hedin, L. New method for calculating the one-particle Green’s function with application to the electron-gas problem. Phys. Rev. 1965, 139, A796. [Google Scholar] [CrossRef]
- Soltani, N.; Hosseini, S.; Kompany, A. Nanoscale ab-initio calculations of optical and electronic properties of LaCrO3 in cubic and rhombohedral phases. Physica B 2009, 404, 4007–4014. [Google Scholar] [CrossRef]
- O’Sullivan, M.; Stamenov, P.; Alaria, J.; Venkatesan, M.; Coey, J.M.D. Magnetoresistance of CuCrO2 -based delafossite films. J. Phys. Conf. Ser. 2010, 200, 052021. [Google Scholar] [CrossRef]
- Dekkers, M.; Rijnders, G.; Blank, D.H. ZnIr2O4, a p-type transparent oxide semiconductor in the class of spinel zinc-d 6-transition metal oxide. Appl. Phys. Lett. 2007, 90, 021903. [Google Scholar] [CrossRef]
- Nagaraja, A.R.; Perry, N.H.; Mason, T.O.; Tang, Y.; Grayson, M.; Paudel, T.R.; Lany, S.; Zunger, A. Band or Polaron: The Hole Conduction Mechanism in the p-Type Spinel Rh2ZnO4. J. Am. Ceram. Soc. 2012, 95, 269–274. [Google Scholar] [CrossRef]
- Lee, Y.S.; Winkler, M.T.; Siah, S.C.; Brandt, R.; Buonassisi, T. Hall mobility of cuprous oxide thin films deposited by reactive direct-current magnetron sputtering. Appl. Phys. Lett. 2011, 98, 192115. [Google Scholar] [CrossRef]
- Guo, W.; Fu, L.; Zhang, Y.; Zhang, K.; Liang, L.Y.; Liu, Z.M.; Cao, H.T.; Pan, X.Q. Microstructure, optical, and electrical properties of p-type SnO thin films. Appl. Phys. Lett. 2010, 96, 042113. [Google Scholar] [CrossRef]
- Guziewicz, M.; Grochowski, J.; Borysiewicz, M.; Kaminska, E.; Domagala, J.Z.; Rzodkiewicz, W.; Witkowski, B.S.; Golaszewska, K.; Kruszka, R.; Ekielski, M.; et al. Electrical and optical properties of NiO films deposited by magnetron sputtering. Optica Applicata 2011, 41, 431–440. [Google Scholar]
- Zou, Y.S.; Wang, H.P.; Zhang, S.L.; Lou, D.; Dong, Y.H.; Song, X.F.; Zeng, H.B. Structural, electrical and optical properties of Mg-doped CuAlO2 films by pulsed laser deposition. RSC Adv. 2014, 4, 41294–41300. [Google Scholar] [CrossRef]
- Kudo, A.; Yanagi, H.; Hosono, H.; Kawazoe, H. SrCu2O2: A p-type conductive oxide with wide band gap. Appl. Phys. Lett. 1998, 73, 220–222. [Google Scholar] [CrossRef]
- Wei, R.; Tang, X.; Hu, L.; Yang, J.; Zhu, X.; Song, W.; Dai, J.; Zhu, X.; Sun, Y. Facile chemical solution synthesis of p-type delafossite Ag-based transparent conducting AgCrO2 films in an open condition. J. Mater. Chem. C 2017, 5, 1885–1892. [Google Scholar] [CrossRef]
- Gladstone, J.; Dale, T. Researches on the Refraction, Dispersion, and Sensitiveness of Liquids. Proc. R. Soc. Lond. 1862, 12, 448–453. [Google Scholar] [CrossRef]
- Eggleton, R.A. Gladstone-Dale constants for the major elements in silicates: Coordination number, polarizability, and the Lorentz-Lorentz relation. Can. Mineral. 1991, 29, 525–532. [Google Scholar]
- Teertstra, D.K. Photon refraction in dielectric crystals using a modified Gladstone-Dale relation. J. Phys. Chem. C 2008, 112, 7757–7760. [Google Scholar] [CrossRef]
- Tauc, J. Optical properties and electronic structure of amorphous Ge and Si. Mater. Res. Bull. 1968, 3, 37–46. [Google Scholar] [CrossRef]
- Yu, P.Y.; Cardona, M. Fundamentals of Semiconductors, 4th ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2010. [Google Scholar]
- Viezbicke, B.D.; Patel, S.; Davis, B.E.; Birnie, D.P. Evaluation of the Tauc method for optical absorption edge determination: ZnO thin films as a model system. Phys. Stat. Sol. (B) 2015, 252, 1700–1710. [Google Scholar] [CrossRef]
- Mok, T.M.; O’Leary, S.K. The dependence of the Tauc and Cody optical gaps associated with hydrogenated amorphous silicon on the film thickness: αl Experimental limitations and the impact of curvature in the Tauc and Cody plots. J. Appl. Phys. 2007, 102, 113525. [Google Scholar] [CrossRef]
- McCloy, J.S.; Ryan, J.V.; Droubay, T.; Kaspar, T.C.; Chambers, S.; Look, D.C. Magnetotransport properties of high quality Co:ZnO and Mn:ZnO single crystal pulsed laser deposition films: Pitfalls associated with magnetotransport on high resistivity materials. Rev. Sci. Instrum. 2010, 81, 063902. [Google Scholar] [CrossRef] [PubMed]
- Norton, E.; Farrell, L.; Callaghan, S.; McGuinness, C.; Shvets, I.; Fleischer, K. X-ray spectroscopic studies of the electronic structure of chromium-based p-type transparent conducting oxides. Phys. Rev. B 2016, 93, 115302. [Google Scholar] [CrossRef]
- Okuda, T.; Jufuku, N.; Hidaka, S.; Terada, N. Magnetic, transport, and thermoelectric properties of the delafossite oxides CuCr1−xMgxO2 (0 = x = 0.04). Phys. Rev. B 2005, 72, 144403. [Google Scholar] [CrossRef]

| Material | Deposition | Thickness (nm) | (%) | (%) | (%) | S | S | S | Ref. |
|---|---|---|---|---|---|---|---|---|---|
| CuCrO:Mg (5%) | RF sputtered | 250 | 22.5 | - | 18.5 | 1600 | 2800 | - | [11] |
| CuCrO:Mg (10%) | PLD | 40 | 40 | - | 18.5 | 350 | 590 | - | [42] |
| CuCrO:Mg (5%) | RF sputtered, annealed | 250 | 35 | - | 18.5 | 25 | 41 | - | [11] |
| CuCrO | Spray pyrolysis | 90 | 54 | 20 | 18.5 | 150 | 290 | 310 | here |
| CrO:Mg (8%) | MBE | 180 | 55 | 15 | 15.5 | 48 | 82 | 80 | [18] |
| CrO:Mg (13%) | DC sputtered metal | 192 | 58 | 16 | 15.5 | 0.4 | 0.6 | 0.6 | here |
| a-CrO:Mg (8%) | RF sputtered ceramic | 50 | 54 | 35 | 15.5 | 0.15 | 0.25 | 0.8 | here |
| LaCrO:Sr (25%) | MBE | 80 | 54 | - | 15.5 | 195 | 330 | - | [15] |
| LaCrO:Sr (12%) | MBE | 67 | 63 | - | 15.5 | 52 | 100 | - | [15] |
| ZnRhO | PLD | 70 | 55 | - | 22 | 32 | 77 | - | [43,44] |
| CuO | DC sputtered | 155 | 26 | - | 17 | 31 | 50 | - | [45] |
| SnO | e-beam evaporated | 100 | 60 | - | 15.5 | 41 | 75 | - | [46] |
| NiO | RF sputtered | 150 | 50 | - | 18 | 14 | 25 | - | [47] |
| CuAlO:Mg (1%) | PLD | 90 | 70 | - | 11 | 10 | 17 | - | [48] |
| SrCuO:K | PLD | 120 | 75 | - | 17 | 2.1 | 7.1 | - | [49] |
| AgCrO:Mg (12%) | CSD | 120 | 60 | - | 21 | 1.9 | 4.6 | - | [50] |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fleischer, K.; Norton, E.; Mullarkey, D.; Caffrey, D.; Shvets, I.V. Quantifying the Performance of P-Type Transparent Conducting Oxides by Experimental Methods. Materials 2017, 10, 1019. https://doi.org/10.3390/ma10091019
Fleischer K, Norton E, Mullarkey D, Caffrey D, Shvets IV. Quantifying the Performance of P-Type Transparent Conducting Oxides by Experimental Methods. Materials. 2017; 10(9):1019. https://doi.org/10.3390/ma10091019
Chicago/Turabian StyleFleischer, Karsten, Emma Norton, Daragh Mullarkey, David Caffrey, and Igor V. Shvets. 2017. "Quantifying the Performance of P-Type Transparent Conducting Oxides by Experimental Methods" Materials 10, no. 9: 1019. https://doi.org/10.3390/ma10091019
APA StyleFleischer, K., Norton, E., Mullarkey, D., Caffrey, D., & Shvets, I. V. (2017). Quantifying the Performance of P-Type Transparent Conducting Oxides by Experimental Methods. Materials, 10(9), 1019. https://doi.org/10.3390/ma10091019





