Modeling Adhesive Anchors in a Discrete Element Framework
Abstract
:1. Introduction
2. Modeling Bonded Anchors at Different Scales
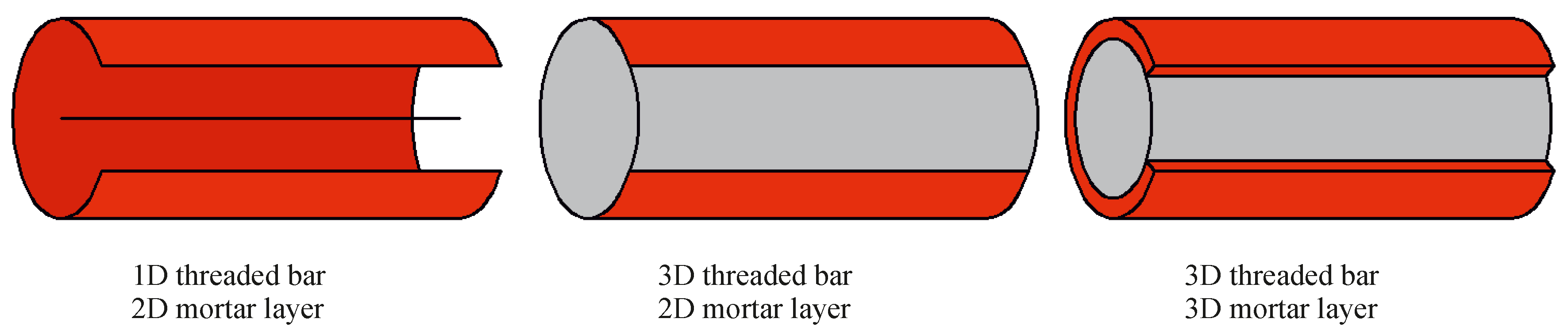
2.1. Threaded Bar
2.2. Lattice Discrete Particle Model
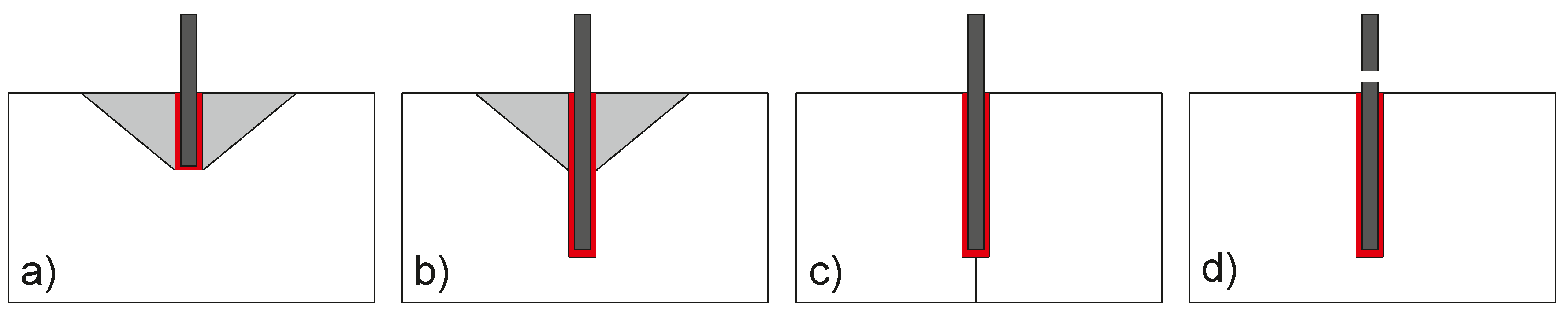
2.3. Particle-Anchor Interaction
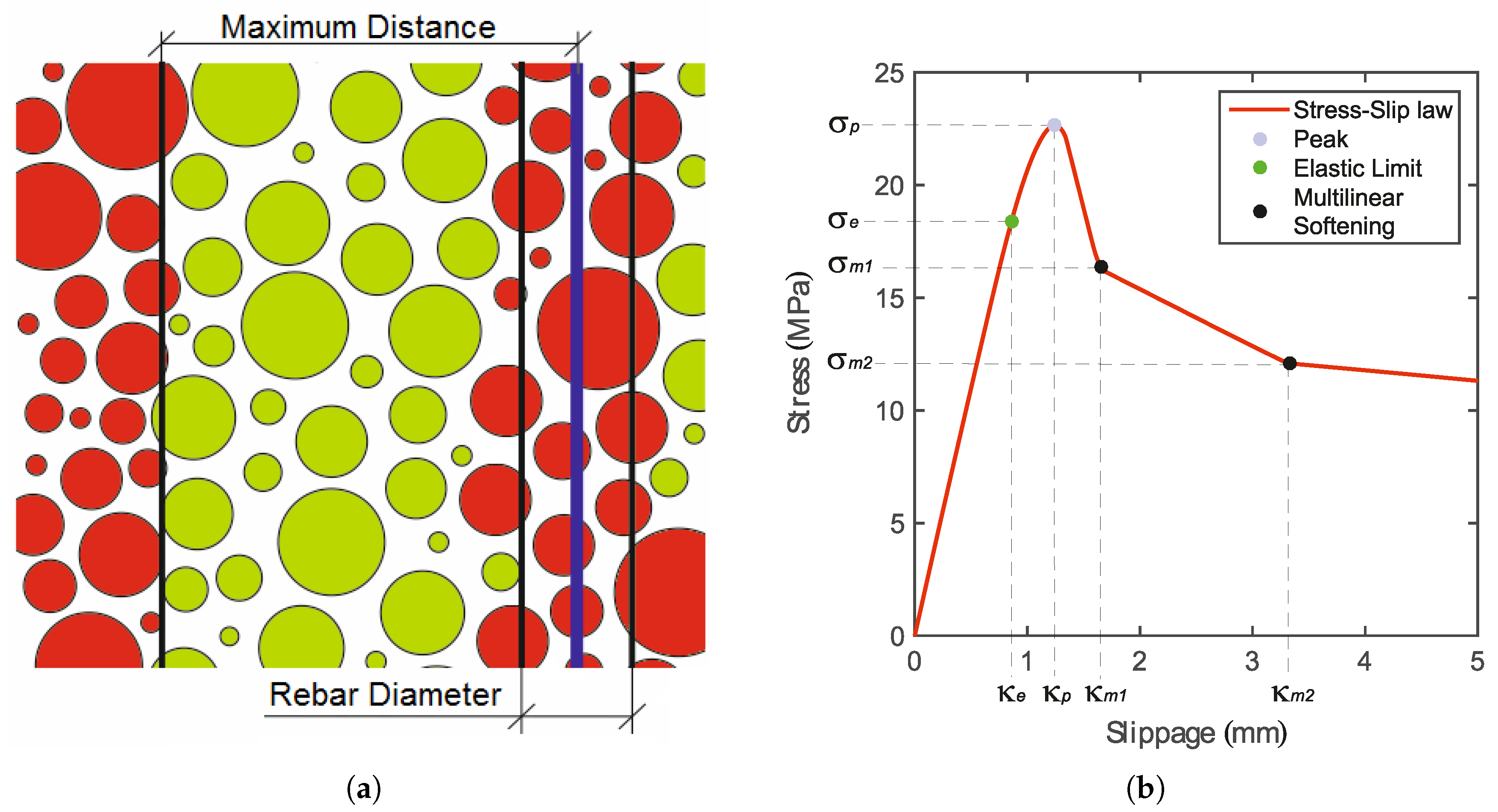
2.4. Bond Law
3. Experimental Campaign
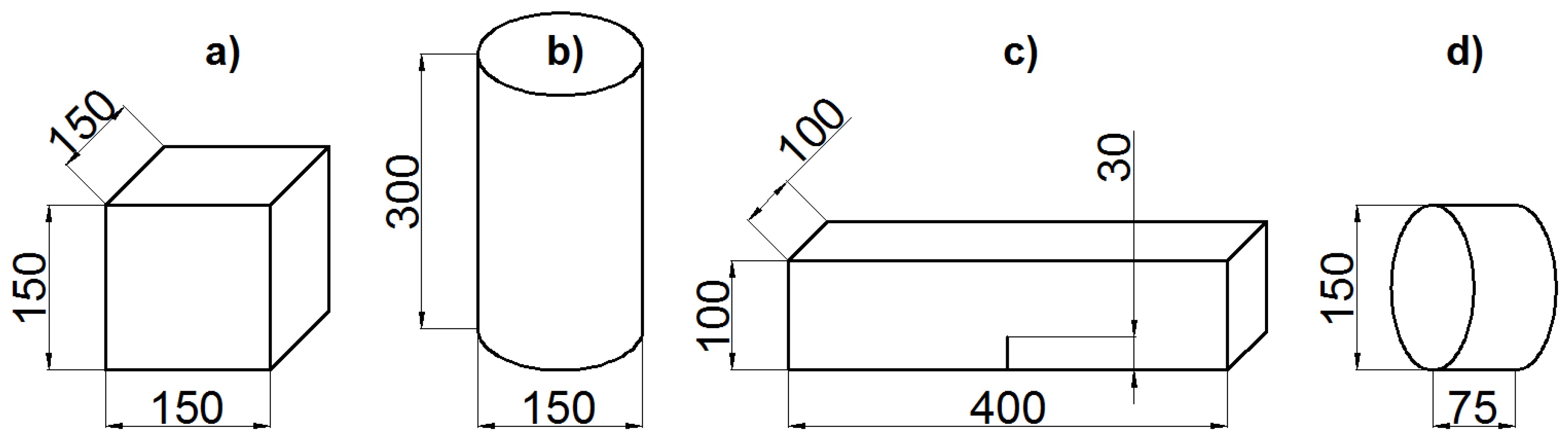
3.1. Concrete Properties
3.2. Bond Properties Determination
3.3. Unconfined Pull-Out Test
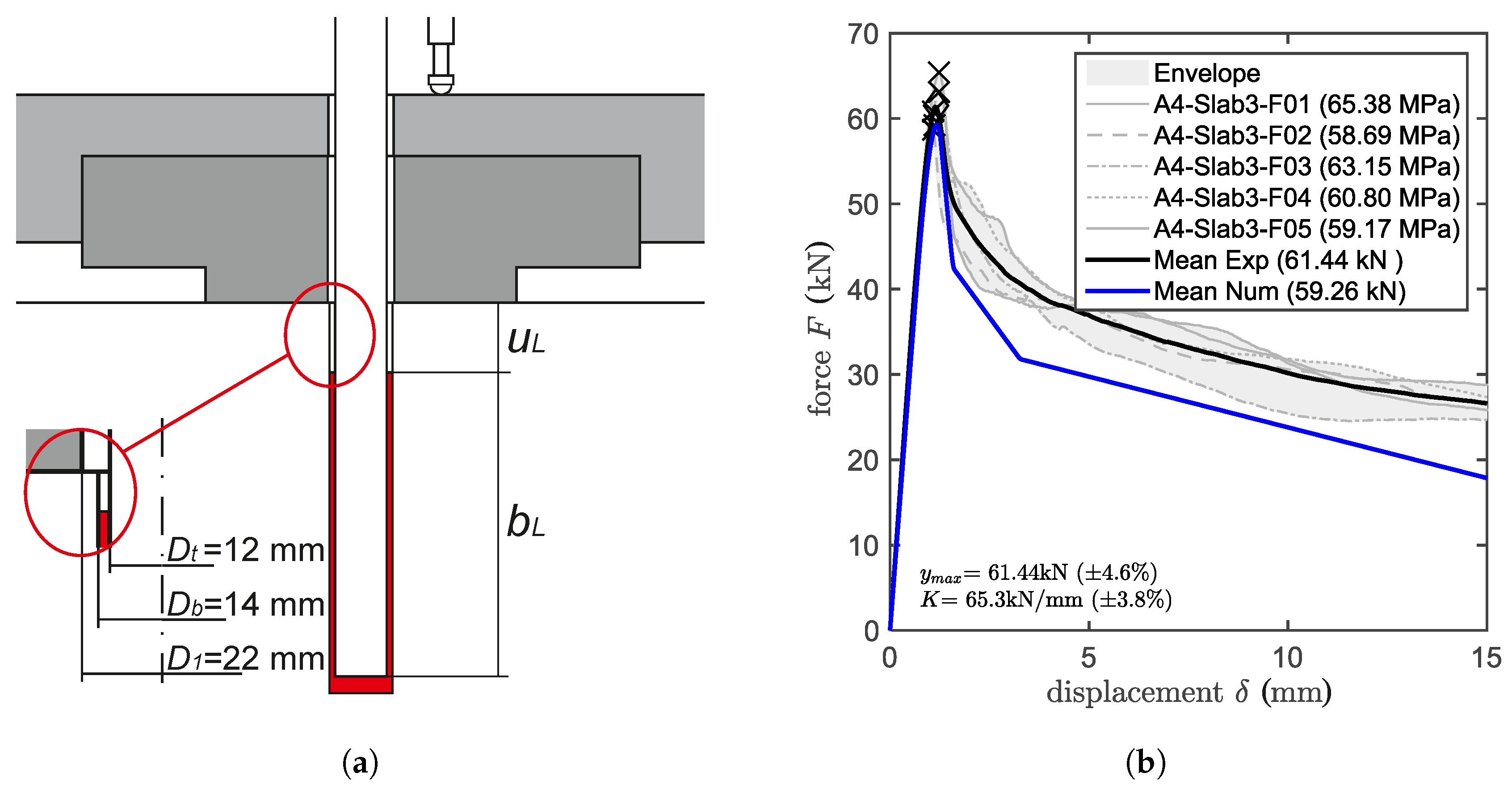
3.4. Confined Pull-Out Tests of Anchors Partially Unbonded at the Loaded End
4. Model Calibration
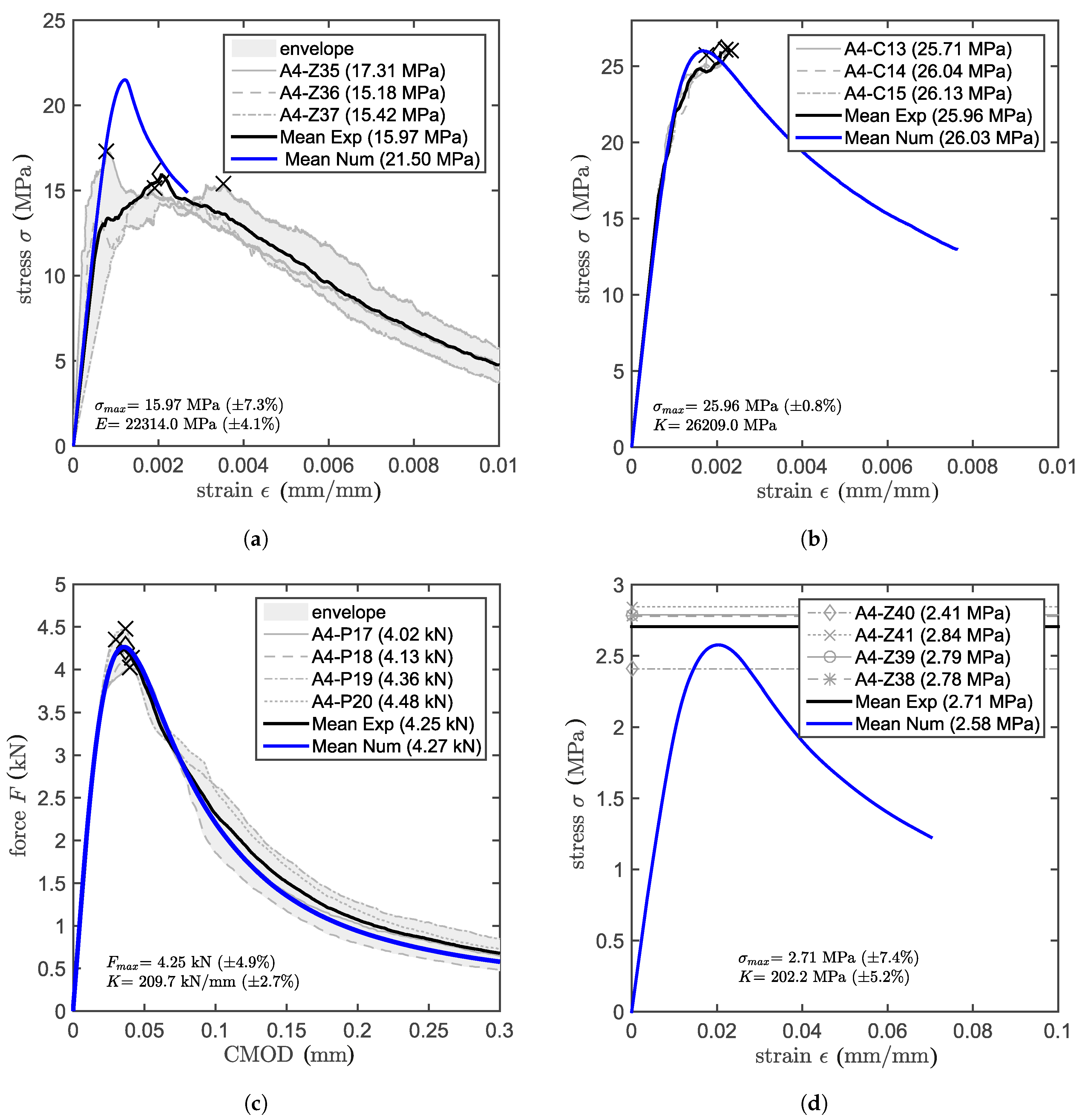
4.1. Calibration and Validation of Concrete Model
4.2. Bond-Law Calibration
5. Model Validation
5.1. Validation on Unconfined Tests
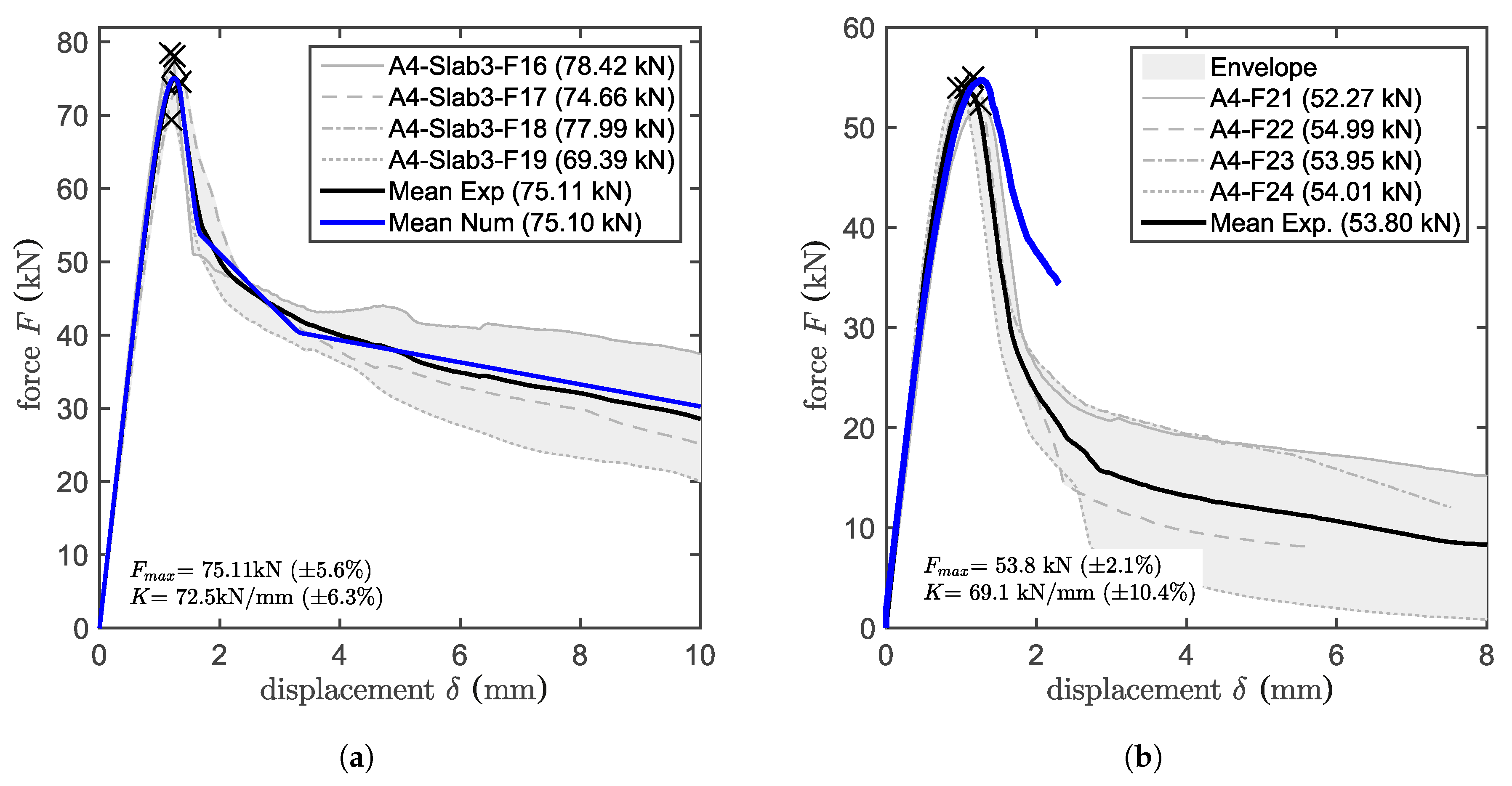
5.2. Validation by Partially-Unbonded Pull-Out Tests
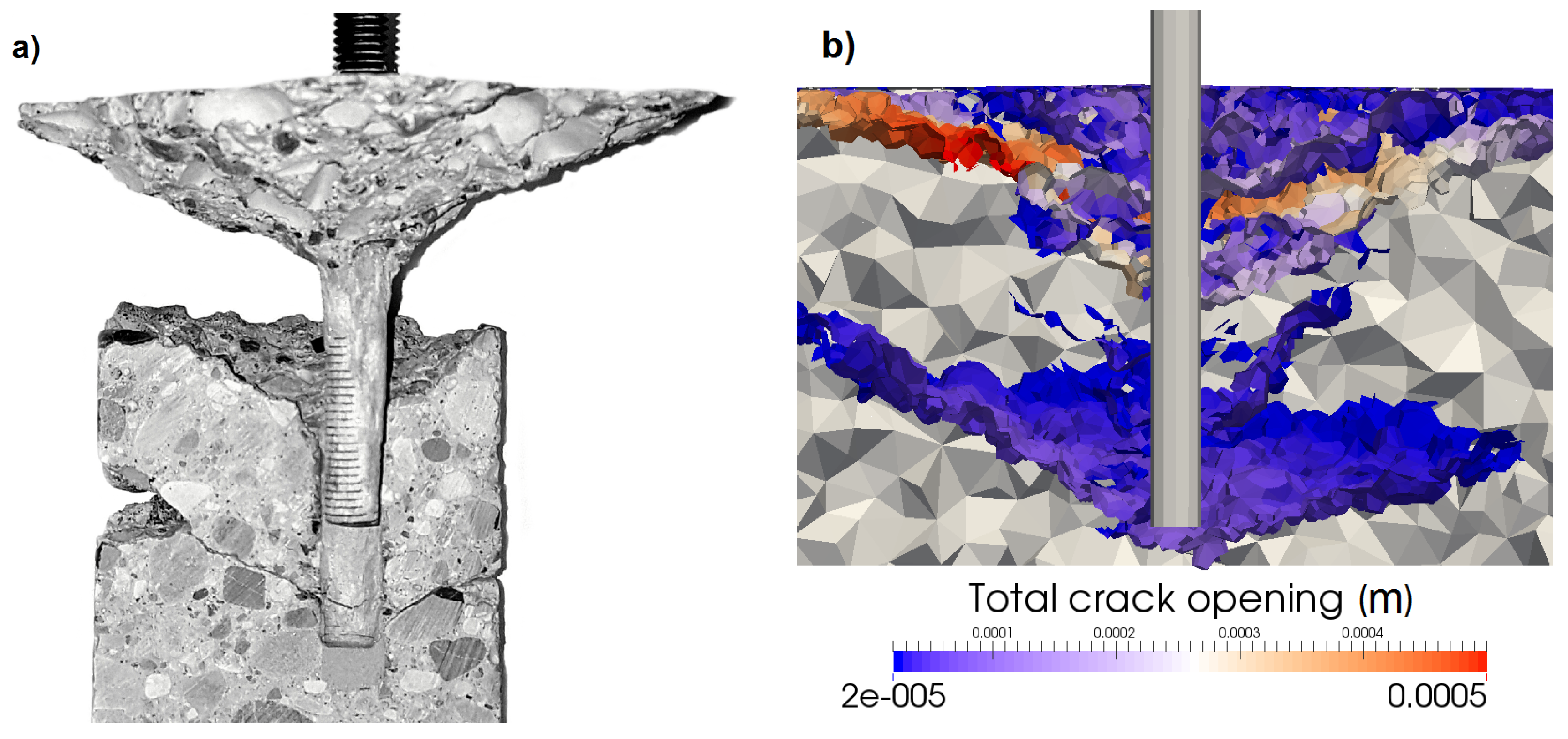
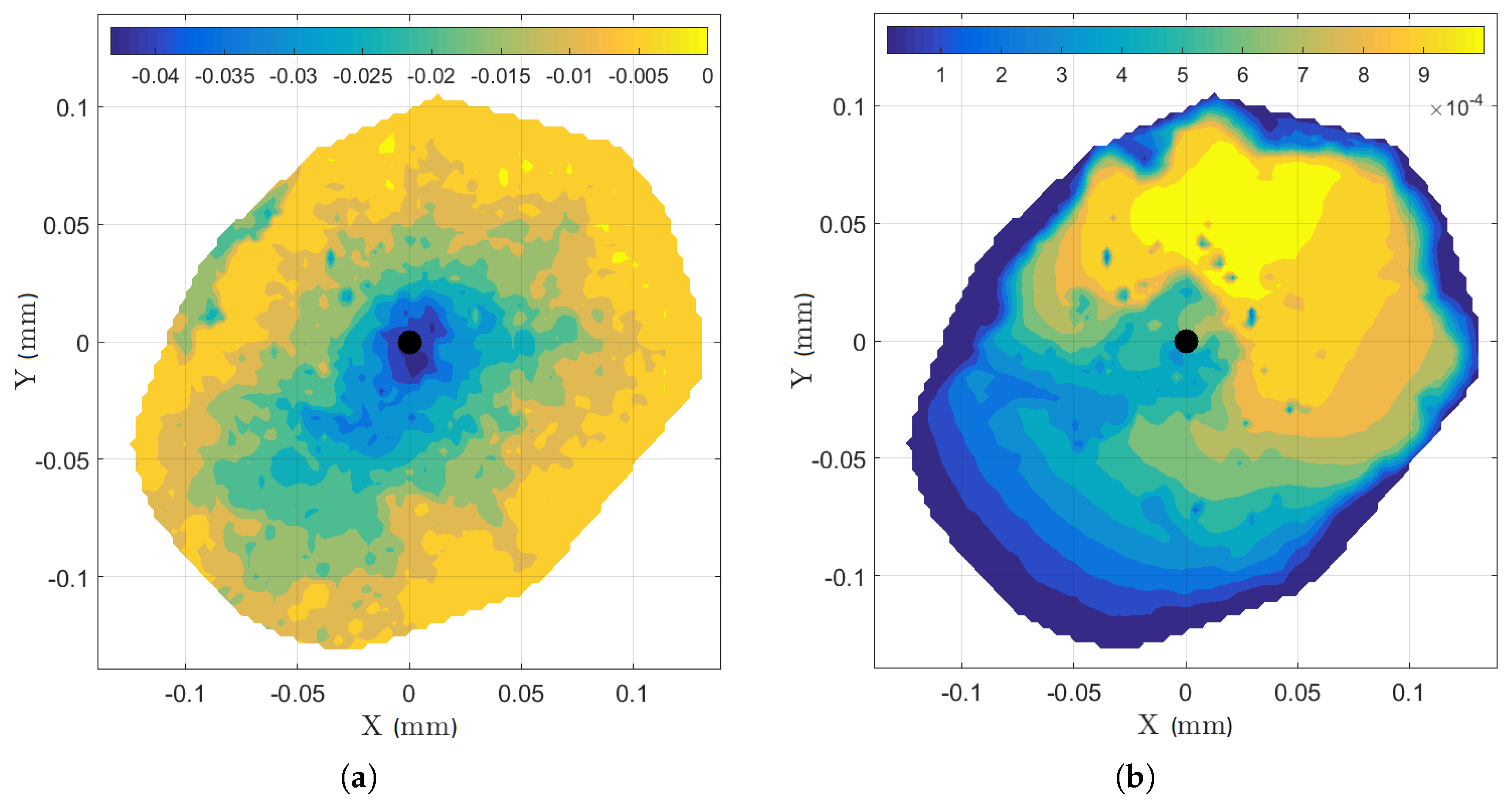
5.3. Photogrammetry
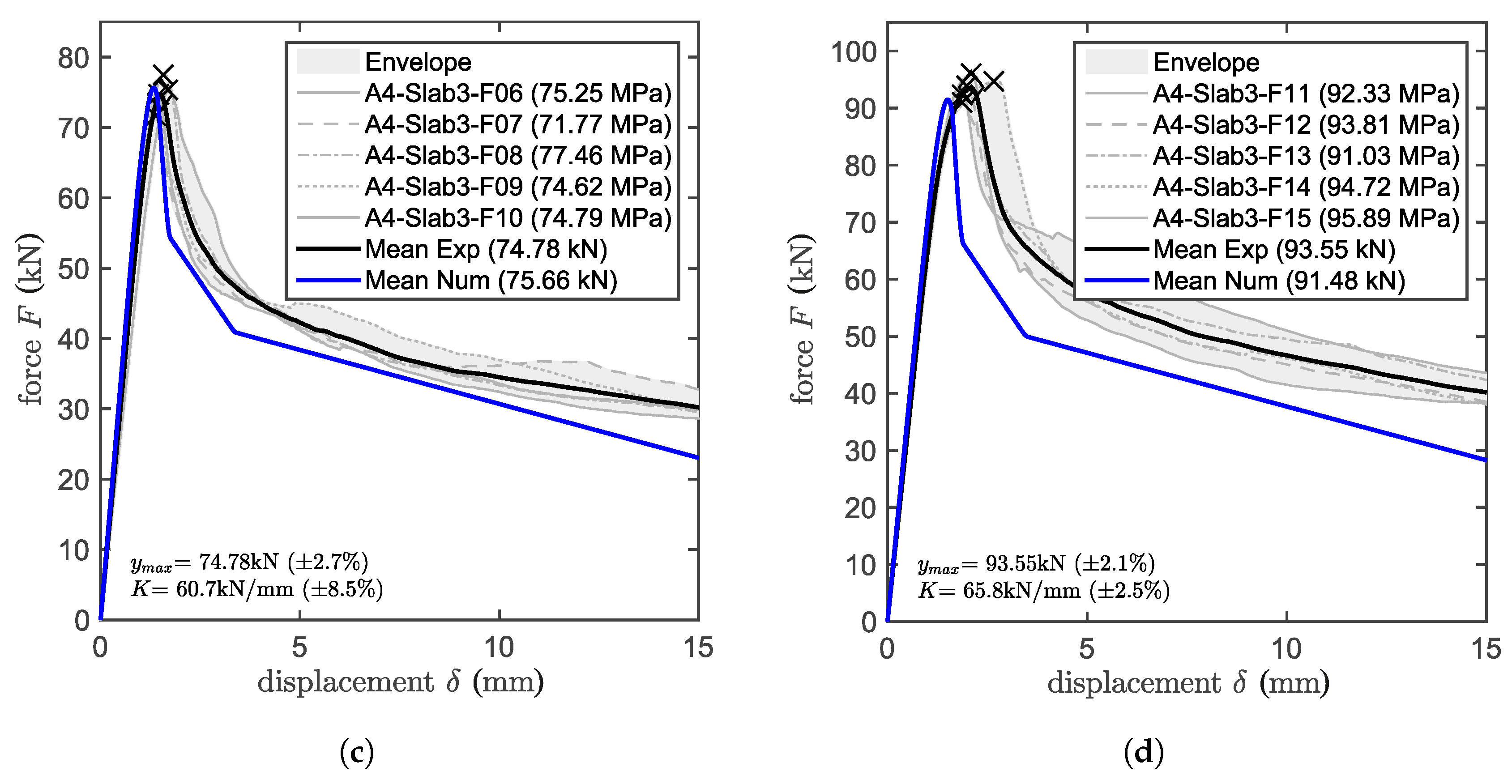
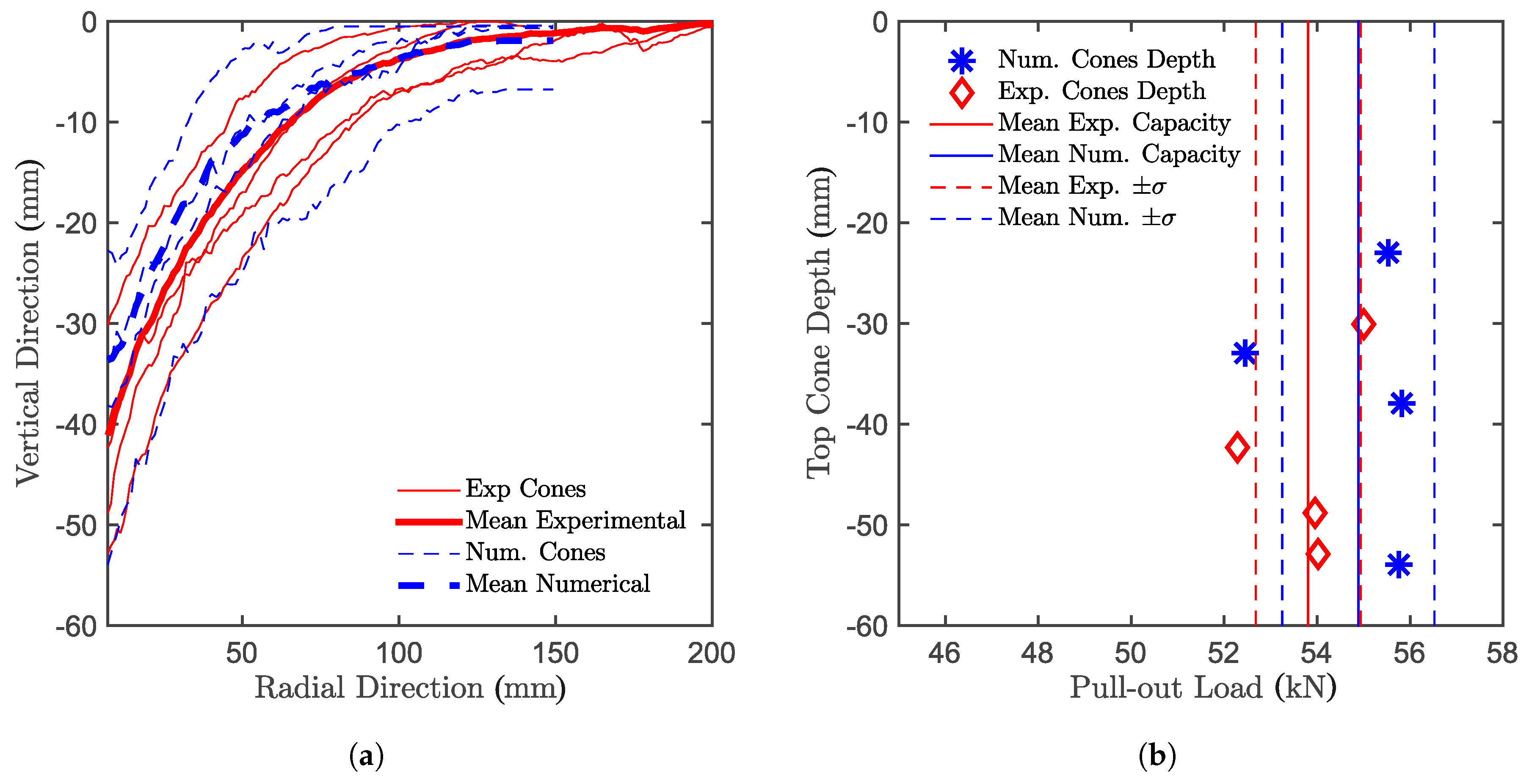
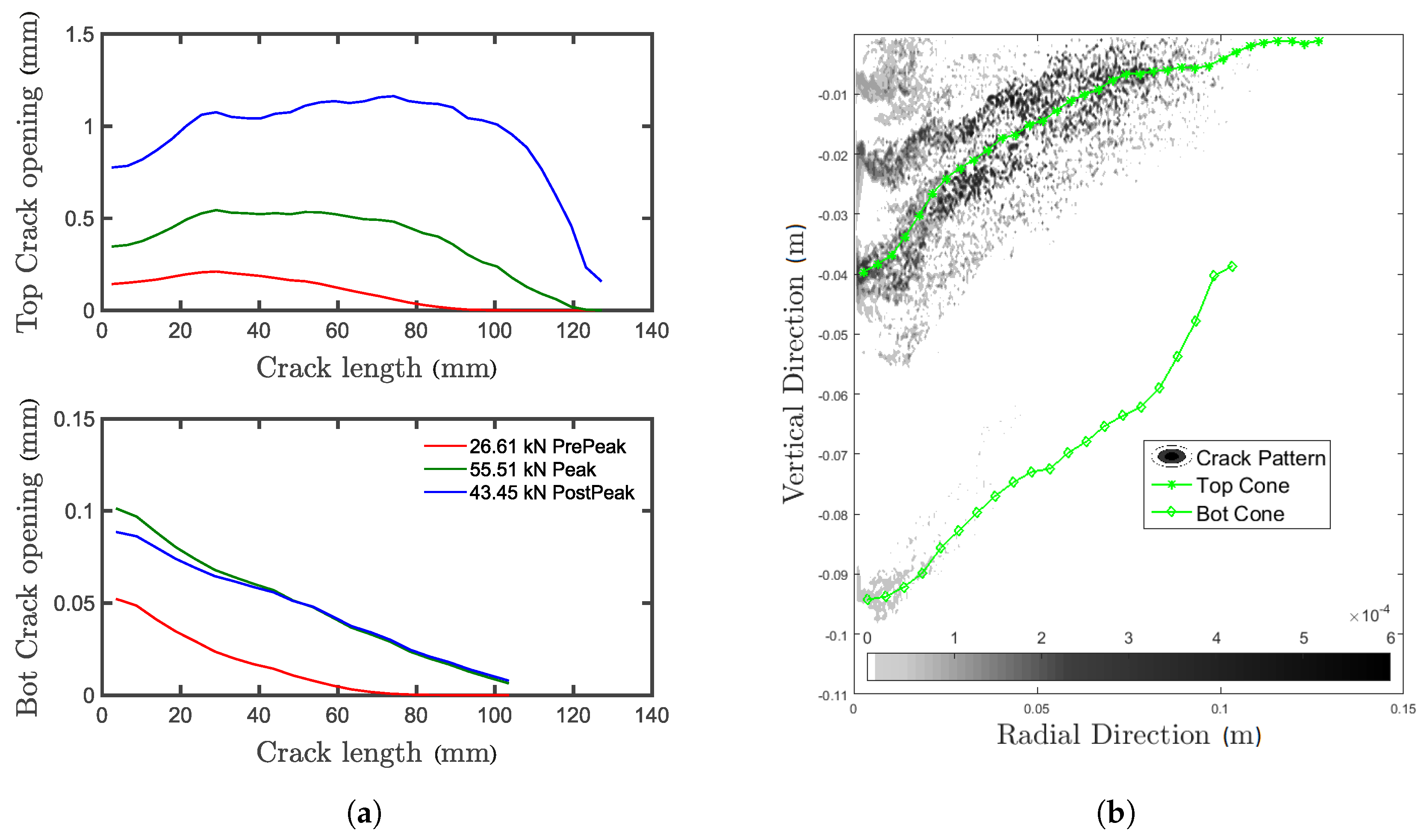
5.4. Multiple Concrete Cones
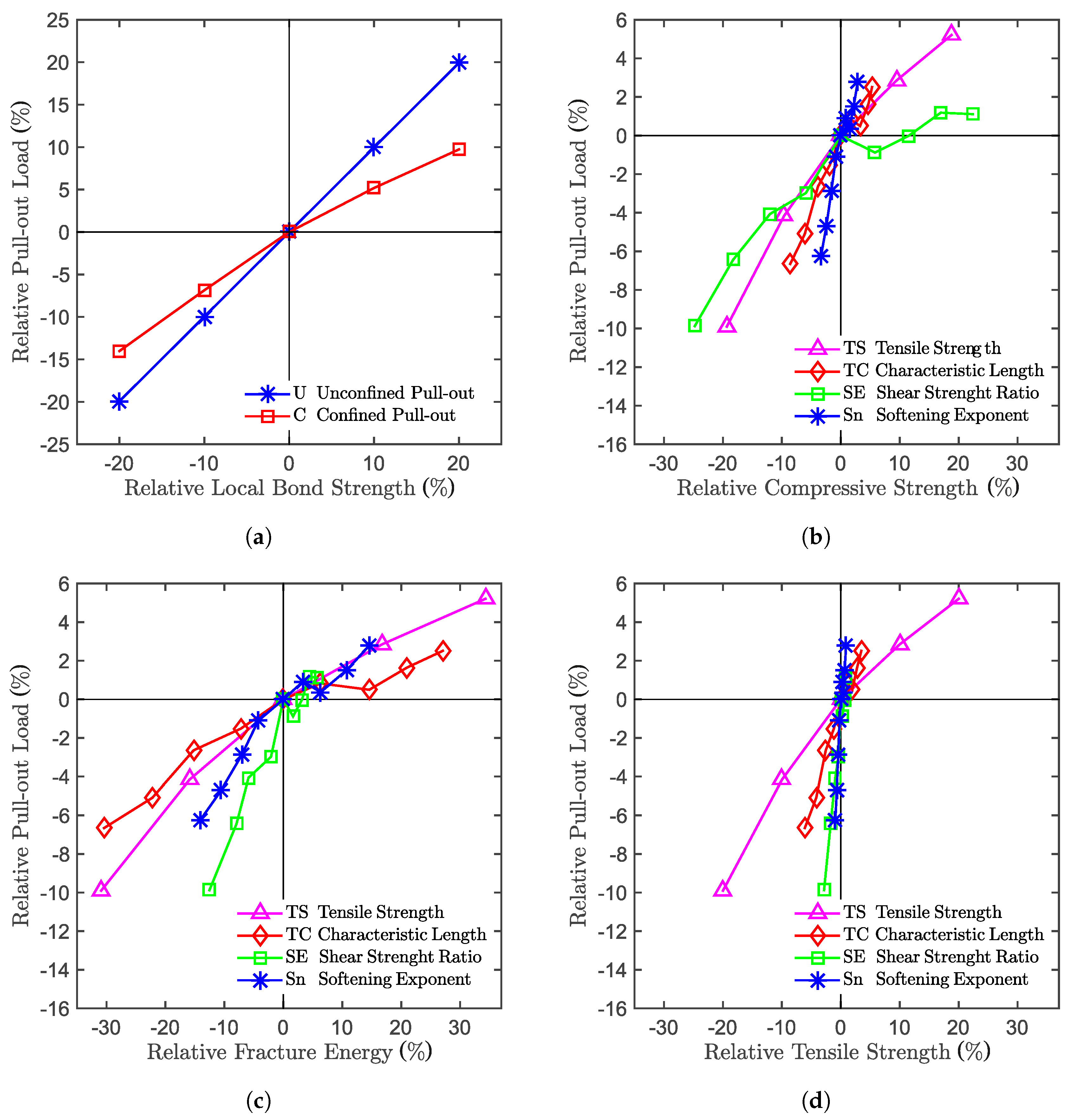
6. Sensitivity Study
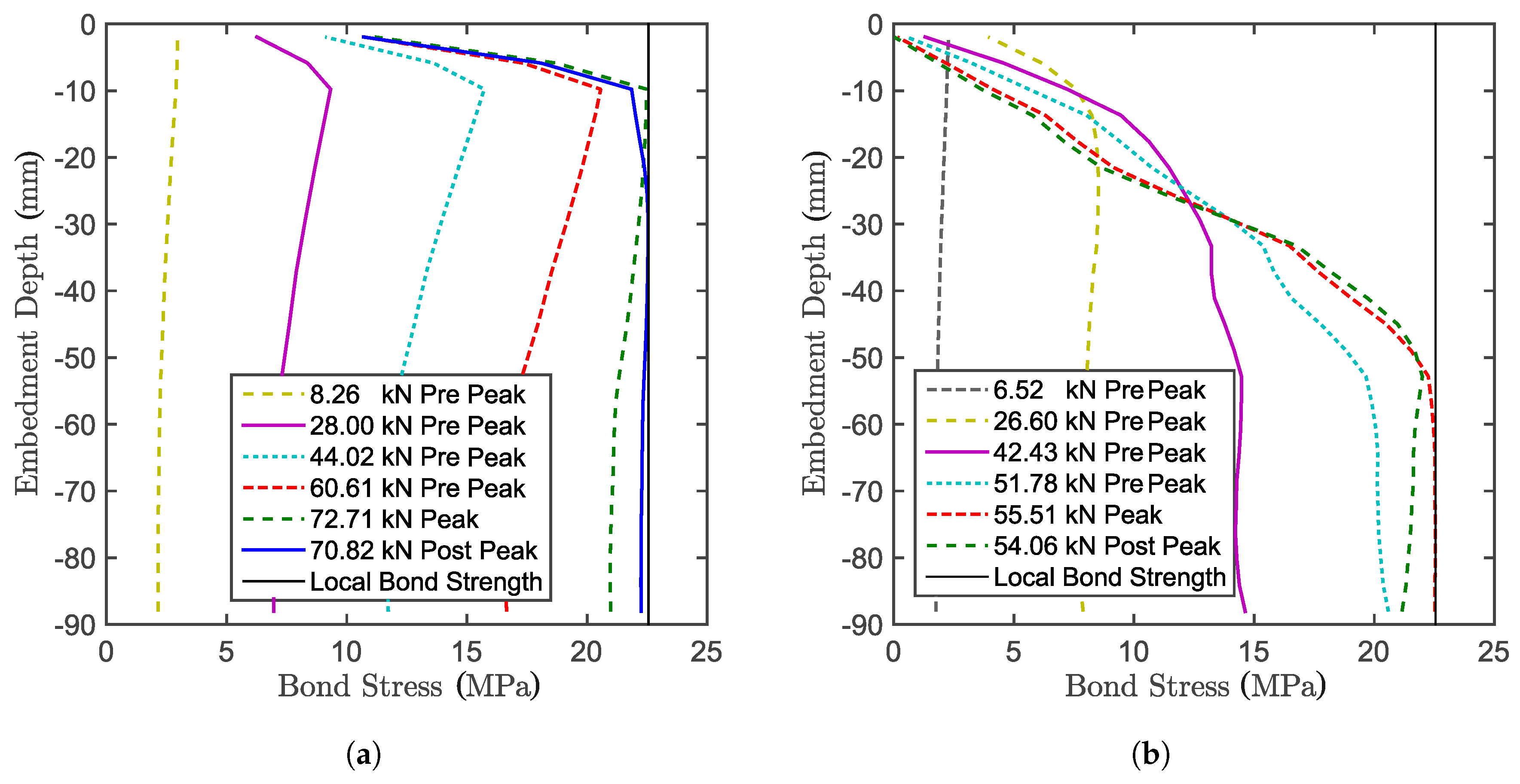
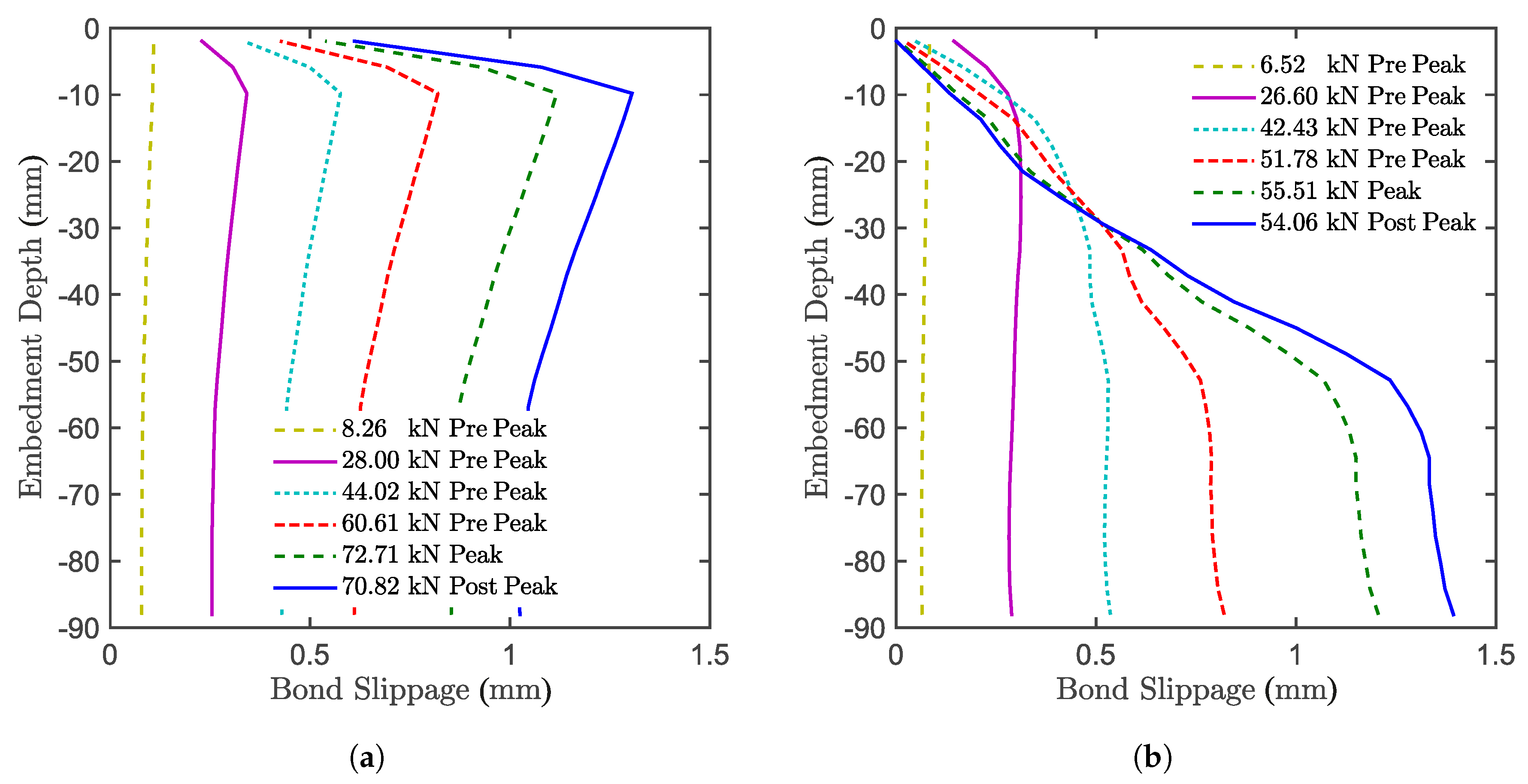
7. Bond Stress along the Anchor
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cook, R.A. Behavior of chemically bonded anchors. J. Struct. Eng. 1993, 119, 2744–2762. [Google Scholar] [CrossRef]
- Cook, R.A.; Kunz, J.; Fuchs, W.; Konz, R.C. Behavior and Design of Single Adhesive Anchors under Tensile Load in Uncracked Concrete. Struct. J. 1998, 95, 9–26. [Google Scholar]
- Ashour, A.; Alqedra, M. Concrete breakout strength of single anchors in tension using neural networks. Adv. Eng. Softw. 2005, 36, 87–97. [Google Scholar] [CrossRef]
- Alqedra, M.; Ashour, A. Prediction of shear capacity of single anchors located near a concrete edge using neural networks. Comput. Struct. 2005, 83, 2495–2502. [Google Scholar] [CrossRef]
- Sakla, S.S.; Ashour, A.F. Prediction of tensile capacity of single adhesive anchors using neural networks. Comput. Struct. 2005, 83, 1792–1803. [Google Scholar] [CrossRef]
- Contrafatto, L.; Cosenza, R. Prediction of the pull-out strength of chemical anchors in natural stone. Frat. Integrità Strutt. 2014, 29, 196–208. [Google Scholar]
- Červenka, V.; Jendele, L. ATENA Program Documentation Part; Cervenka Consulting s.r.o.: Rague, Czech Republic, 2000. [Google Scholar]
- Bajer, M.; Barnat, J. The glue—Concrete interface of bonded anchors. Constr. Build. Mater. 2012, 34, 267–274. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Caner, F.C.; Cedolin, L.; Cusatis, G.; Di Luzio, G. Fracturing material models based on micromechanical concepts: Recent advances. In Proceedings of the Fracture Mechanics of Concrete and Concrete Structures—FraMCoS-5, Vail, CO, USA, 12–16 April 2004; pp. 83–89. [Google Scholar]
- Ožbolt, J.; Li, Y.; Kozar, I. Microplane model with relaxed kinematie constraint. 38, pp. 2683–2711. Available online: http://www.framcos.org/FraMCoS-4/609.pdf (accessed on 3 August 2017).
- Caner, F.C.; Bažant, Z.P. Microplane Model M7 for Plain Concrete: I. Formulation. J. Eng. Mech. 2012, 139, 1714–1723. [Google Scholar] [CrossRef]
- Caner, F.C.; Bažant, Z.P. Microplane Model M7 for Plain Concrete. II: Calibration and Verification. J. Eng. Mech. 2012, 139, 1724–1735. [Google Scholar] [CrossRef]
- Eligehausen, R.; Appl, J. Behavior and Design of Fastenings with Bonded Anchors: Numerical Analysis and Experimental Verification. 2007. Available online: http://framcos.org/FraMCoS-6/418.pdf (accessed on 3 August 2017).
- Li, Y.J.; Eligehausen, R.; Lehr, B.; Ožbolt, J. Fracture Analysis of Quadruple Fastenings with Bonded Anchors. 2001. Available online: http://framcos.org/FraMCoS-4/991.pdf (accessed on 3 August 2017).
- Unterweger, A.; Spyridis, P.; Mihala, R.; Bergmeister, K. Randnahe Vierfachbefestigungen unter Querlast: Experimentelle und numerische Untersuchung. Beton Stahlbetonbau 2008, 103, 741–747. [Google Scholar] [CrossRef]
- McVay, M.; Cook, R.A.; Krishnamurthy, K. Pullout simulation of postinstalled chemically bonded anchors. J. Struct. Eng. 1996, 122, 1016–1024. [Google Scholar] [CrossRef]
- Cusatis, G.; Pelessone, D.; Mencarelli, A. Lattice Discrete Particle Model (LDPM) for failure behavior of concrete. I: Theory. Cem. Concr. Compos. 2011, 33, 881–890. [Google Scholar] [CrossRef]
- Cusatis, G.; Mencarelli, A.; Pelessone, D.; Baylot, J. Lattice Discrete Particle Model (LDPM) for failure behavior of concrete. II: Calibration and validation. Cem. Concr. Compos. 2011, 33, 891–905. [Google Scholar] [CrossRef]
- Abdellatef, M.; Alnaggar, M.; Boumakis, G.; Cusatis, G.; Di-Luzio, G.; Wendner, R. Lattice discrete particle modeling for coupled concrete creep and shrinkage using the solidification microprestress theory. In Proceedings of the 10th International Conference on Mechanics and Physics of Creep, Shrinkage, and Durability of Concrete and Concrete Structures (CONCREEP 10), Vienna, Austria, 21–23 September 2015; pp. 184–193. [Google Scholar]
- Alnaggar, M.; Cusatis, G.; Di Luzio, G. Lattice Discrete Particle Modeling (LDPM) of Alkali Silica Reaction (ASR) deterioration of concrete structures. Cem. Concr. Compos. 2013, 41, 45–59. [Google Scholar] [CrossRef]
- Wendner, R.; Ninčević, K.; Boumakis, I.; Wan, L. Age-Dependent Lattice Discrete Particle Model for Quasi-Static Simulations. In Key Engineering Materials; Trans Tech Publications: Stafa-Zurich, Switzerland, 2016; Volume 711, pp. 1090–1097. [Google Scholar]
- Pukl, R.; Jansta, M.; Červenka, J.; Vořechovský, M.; Novák, D.; Rusina, R. Spatial variability of material properties in nonlinear computer simulation. In Computational Modelling of Concrete Structures; 2006; pp. 891–896. Available online: http://www.fce.vutbr.cz/STM/vorechovsky.m/papers/27z.pdf (accessed on 3 August 2017).
- Amadio, C.; Bedon, C.; Fasan, M.; Pecce, M.R. Refined numerical modelling for the structural assessment of steel-concrete composite beam-to-column joints under seismic loads. Eng. Struct. 2017, 138, 394–409. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Tabbara, M.R.; Kazemi, M.T.; Pijaudier-Cabot, G. Random particle model for fracture of aggregate or fiber composites. J. Eng. Mech. 1990, 116, 1686–1705. [Google Scholar]
- Cusatis, G.; Bažant, Z.P.; Cedolin, L. Confinement-shear lattice model for concrete damage in tension and compression: I. Theory. J. Eng. Mech. 2003, 129, 1439–1448. [Google Scholar] [CrossRef]
- Di Luzio, G.; Cusatis, G. Solidification-microprestress–microplane (SMM) theory for concrete at early age: Theory, validation and application. Int. J. Solids Struct. 2013, 50, 957–975. [Google Scholar] [CrossRef]
- Abdellatef, M.; Salem, E.; Lau, D.; Stenroos, L.; Alnaggar, M. Bond Degradation of Corroded Reinforcement: An Experimental and Numerical Study. In Proceedings of the 9th International Conference on Fracture Mechanics of Concrete and Concrete Structures (IA-FraMCoS), Berkeley, CA, USA, 22–25 May 2016. [Google Scholar]
- Drucker, D.C.; Prager, W. Soil mechanics and plastic analysis or limit design. Q. Appl. Math. 1952, 10, 157–165. [Google Scholar] [CrossRef]
- Schauffert, E.; Cusatis, G. Lattice Discrete Particle Model for Fiber-Reinforced Concrete. I: Theory. J. Eng. Mech. 2011, 138, 826–833. [Google Scholar] [CrossRef]
- Schauffert, E.; Cusatis, G.; Pelessone, D.; O’Daniel, J.; Baylot, J. Lattice Discrete Particle Model for Fiber-Reinforced Concrete. II: Tensile Fracture and Multiaxial Loading Behavior. J. Eng. Mech. 2011, 138, 834–841. [Google Scholar] [CrossRef]
- ASTM. Standard Test Method for Splitting Tensile Strength of Cylindrical Concrete Specimens; ASTM International: West Conshohocken, PA, USA, 2011; Volume C496/C496M-11. [Google Scholar]
- CEN. Eurocode 2: Design of Concrete Structures, Part 1-1: General Rules and Rules for Buildings; British Standards Institution: London, UK, 2004. [Google Scholar]
- Podroužek, J.; Vorel, J.; Boumakis, I.; Cusatis, G.; Wendner, R. Implications of spatial variability characterization in discrete particle models. In Proceedings of the 9th International Conference on Fracture Mechanics of Concrete and Concrete Structures (IA-FraMCoS), Berkeley, CA, USA, 22–25 May 2016. [Google Scholar]
- Podroužek, J.; Vorel, J.; Cusatis, G.; Wendner, R. Imposed Correlation Between Random Field and Discrete Particle Placement. In Proceedings of the 14th International Probabilistic Workshop, Ghent, Belgium, 5–7 December 2016; pp. 245–252. [Google Scholar]

| (MPa) | (MPa) | E (GPa) | (N/m) |
|---|---|---|---|
| (kN) | (kN) | (kN) | (kN) | (kN) |
|---|---|---|---|---|
| (MPa) | (MPa) | (MPa) | (MPa) | (MPa) |
| Mix design | c (kg/m) | (-) | (-) | (mm) | (mm) |
| 240 | 4 | 18 | |||
| LDPM parameters | (MPa) | (GPa) | (mm) | (-) | n (-) |
| 200 | 1 | ||||
| Stress-slip law parameters | (MPa) | (MPa) | (MPa) | (MPa) | (MPa) |
| (mm) | (mm) | (mm) | (mm) | (mm) | |
| 3 | 30 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marcon, M.; Vorel, J.; Ninčević, K.; Wan-Wendner, R. Modeling Adhesive Anchors in a Discrete Element Framework. Materials 2017, 10, 917. https://doi.org/10.3390/ma10080917
Marcon M, Vorel J, Ninčević K, Wan-Wendner R. Modeling Adhesive Anchors in a Discrete Element Framework. Materials. 2017; 10(8):917. https://doi.org/10.3390/ma10080917
Chicago/Turabian StyleMarcon, Marco, Jan Vorel, Krešimir Ninčević, and Roman Wan-Wendner. 2017. "Modeling Adhesive Anchors in a Discrete Element Framework" Materials 10, no. 8: 917. https://doi.org/10.3390/ma10080917
APA StyleMarcon, M., Vorel, J., Ninčević, K., & Wan-Wendner, R. (2017). Modeling Adhesive Anchors in a Discrete Element Framework. Materials, 10(8), 917. https://doi.org/10.3390/ma10080917





