Characterization of OT4-1 Alloy by Multi-Dome Forming Test
Abstract
:1. Introduction
2. Material and Experiments
2.1. Material
2.2. Tensile Testing
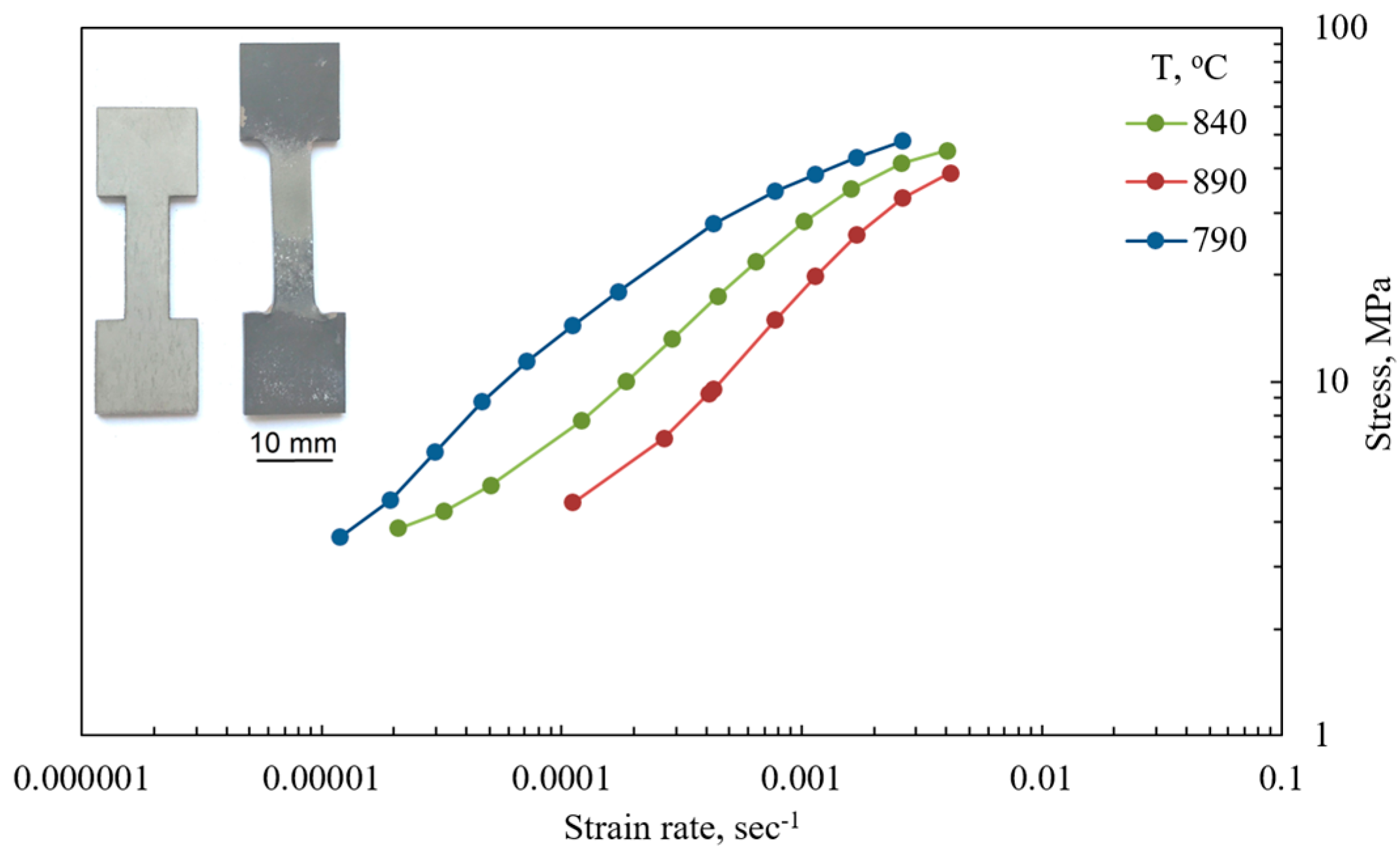
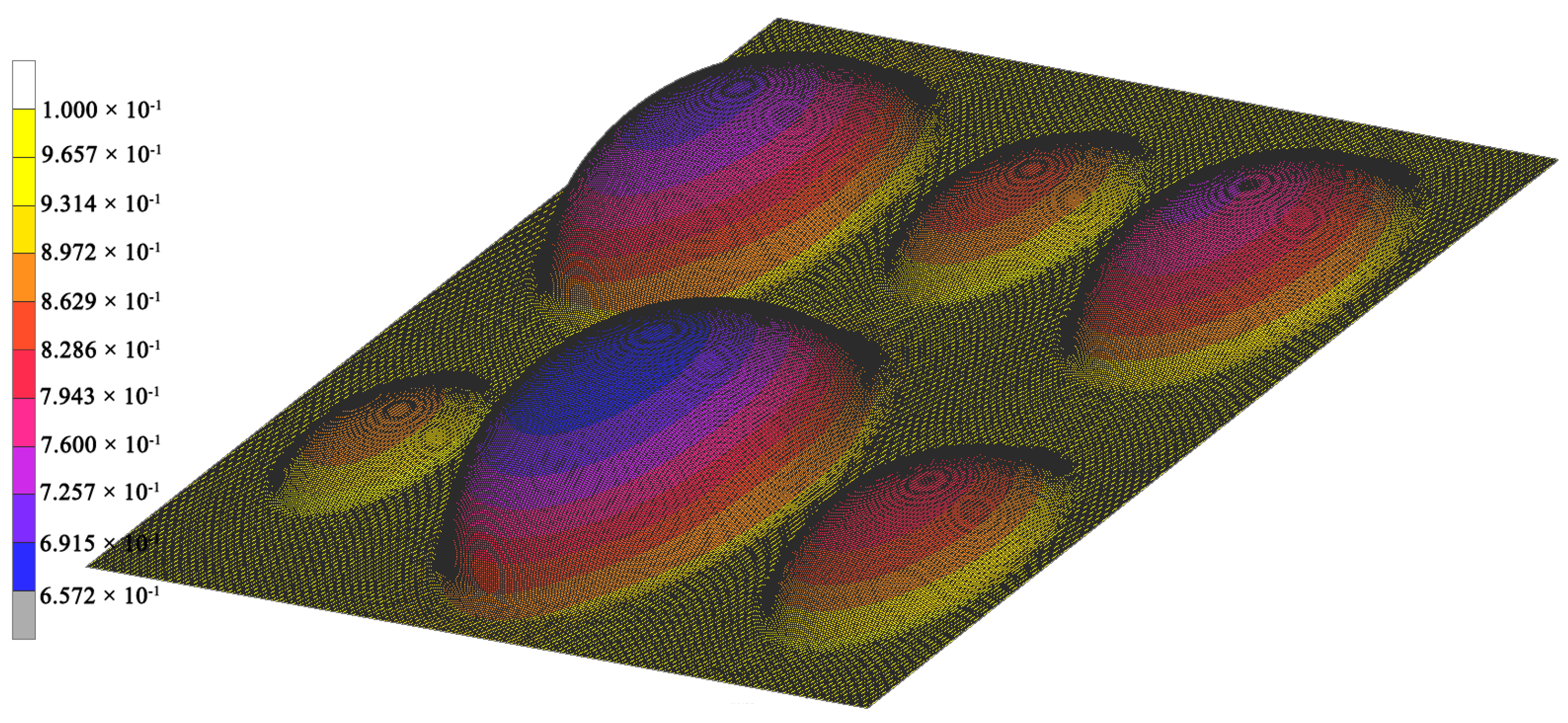
2.3. Multi-Dome Forming Testing
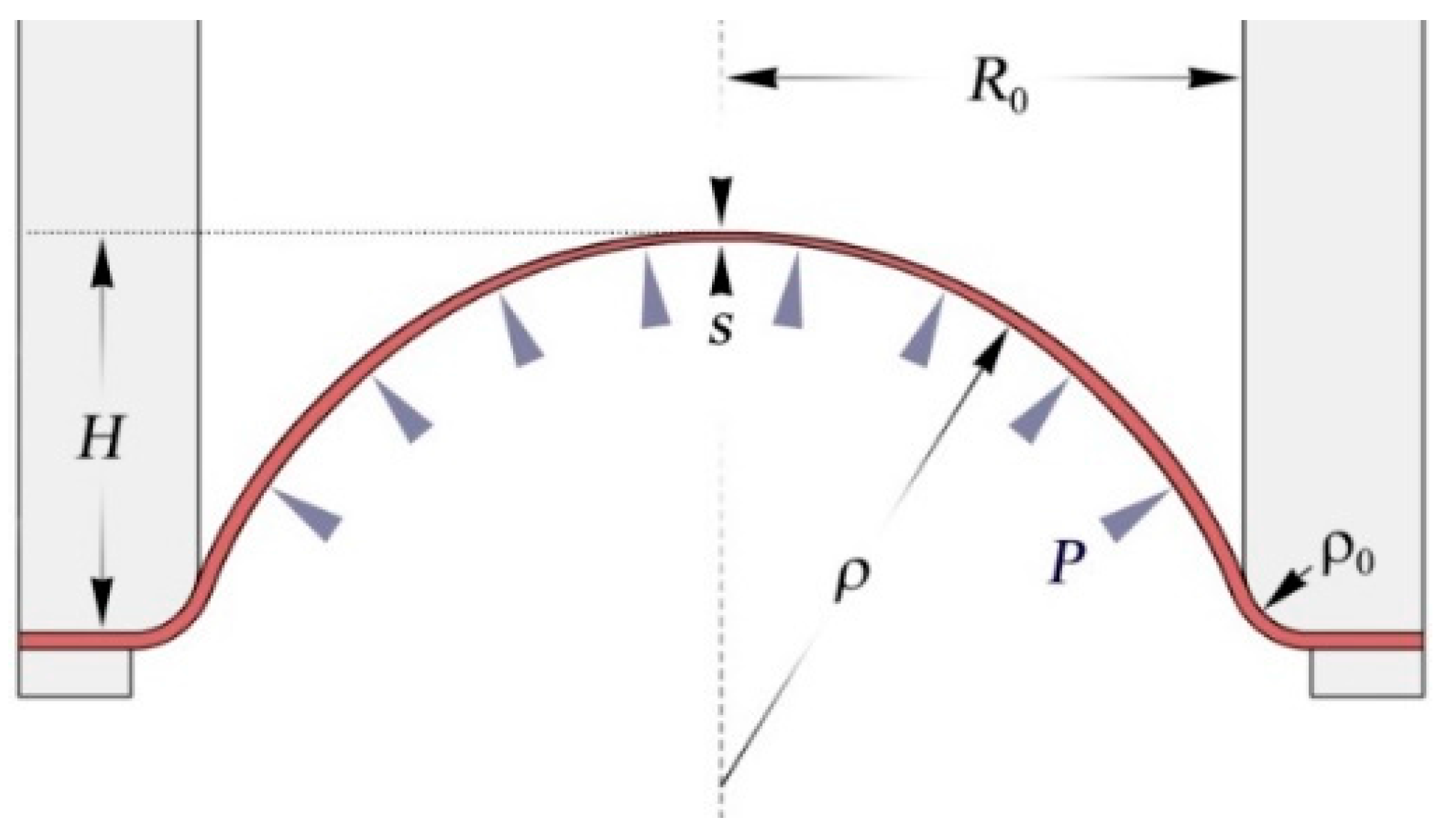
3. Mathematical Model and Characterization Technique
- The material is isotropic
- Elastic strains are negligible
- At any given time, the metal sheet is shaped as a part of the sphere
- The sheet is rigidly clamped
4. Results and Discussion
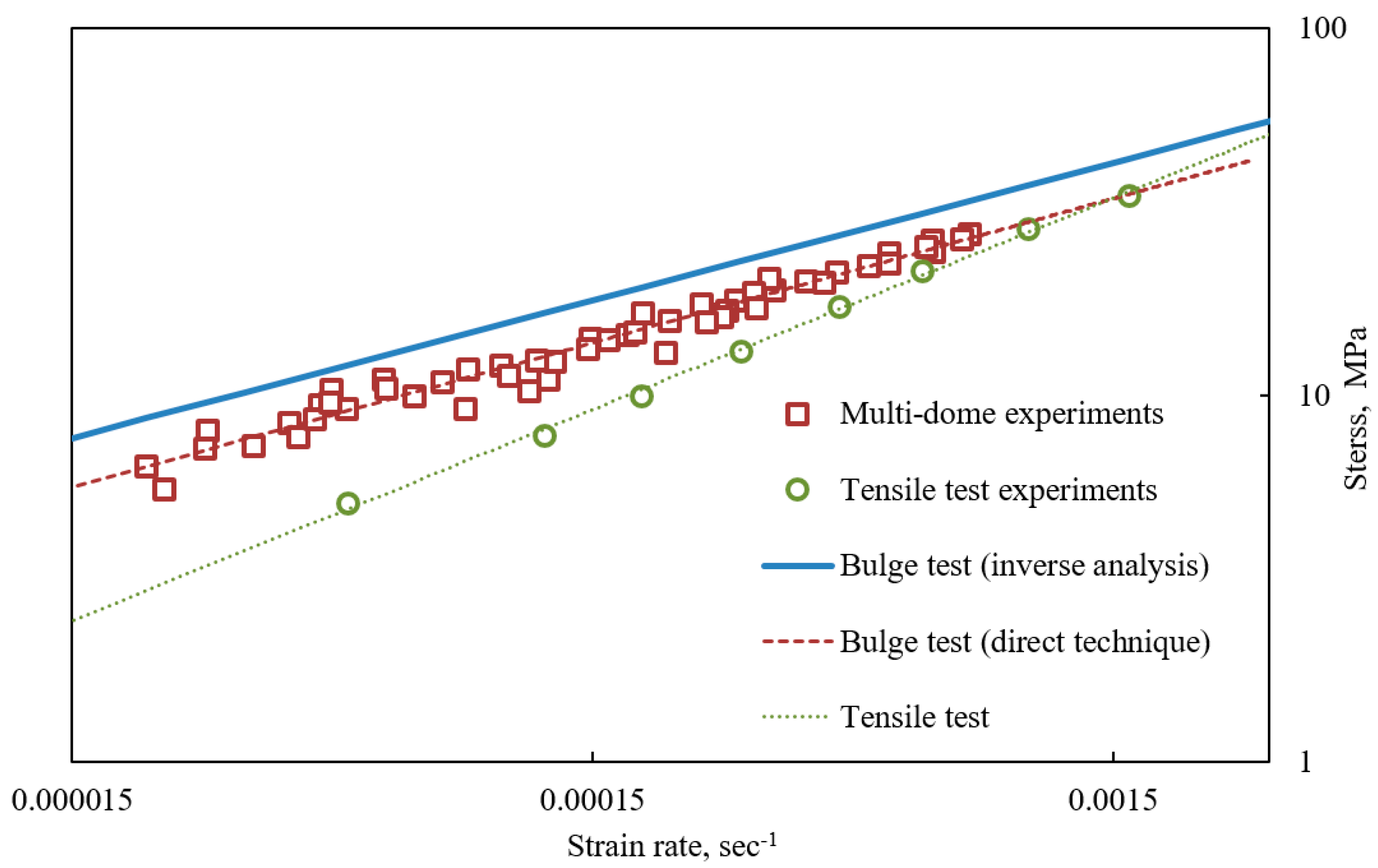
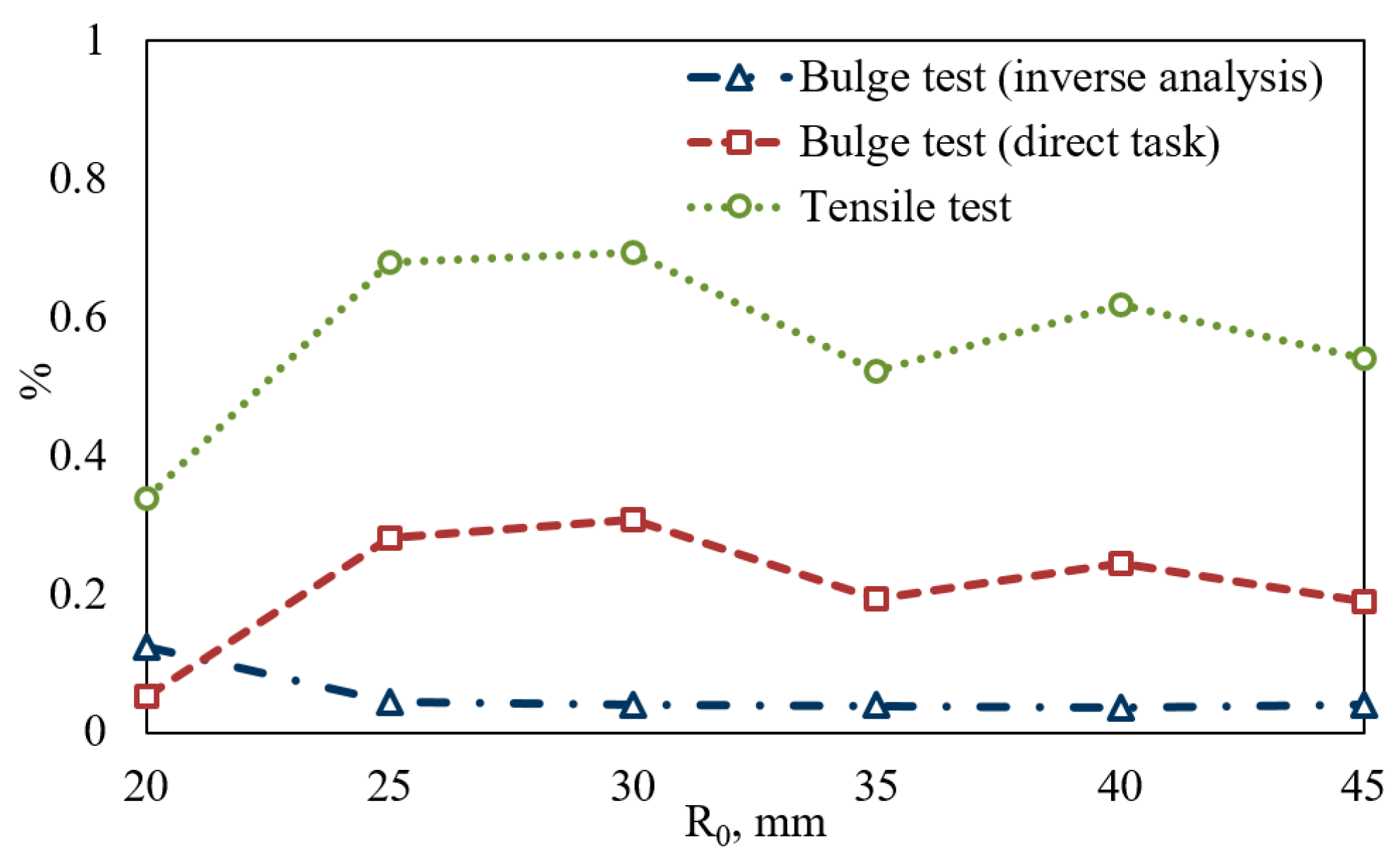
4.1. Material Characterization
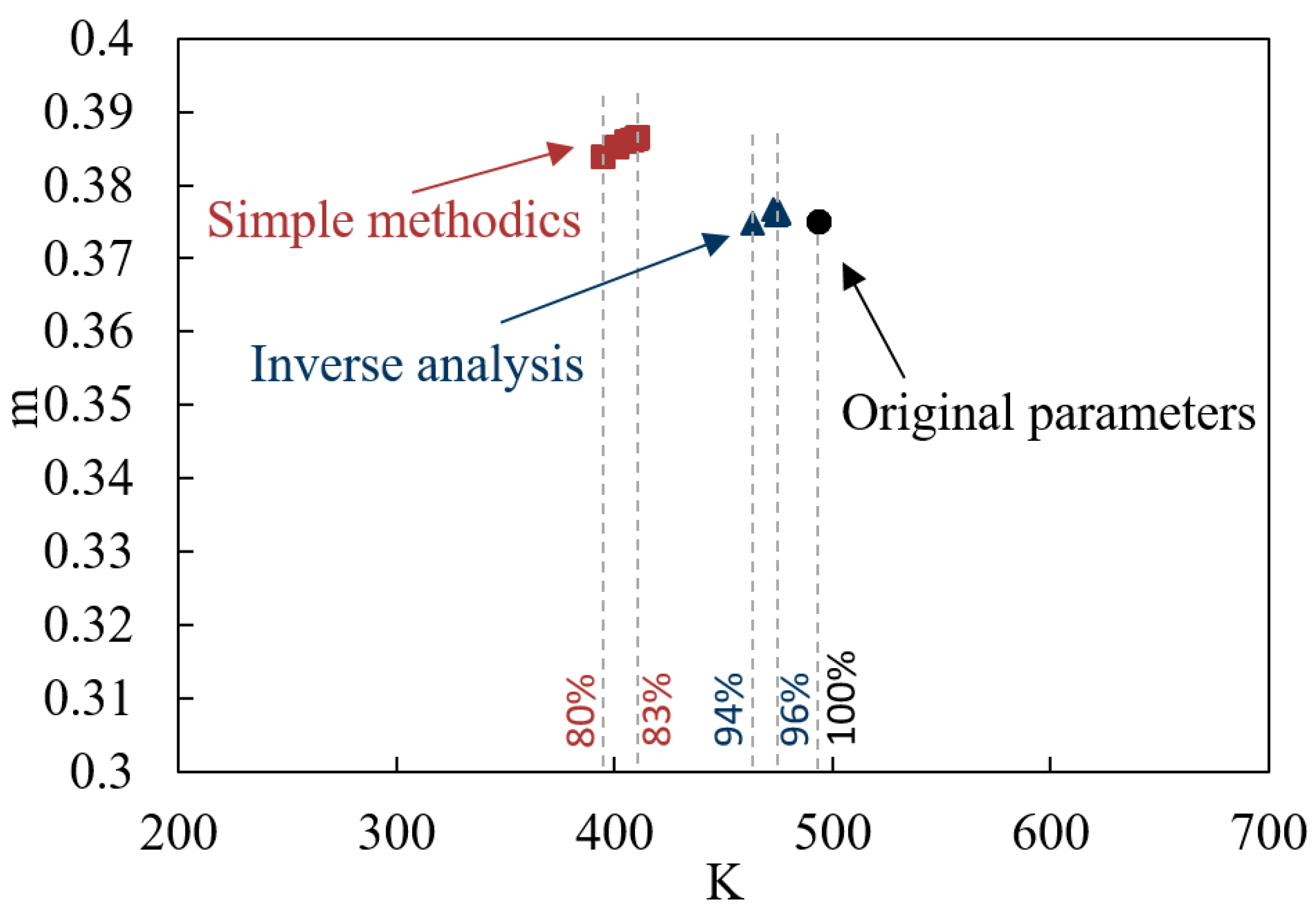
4.2. Finite Element Verification
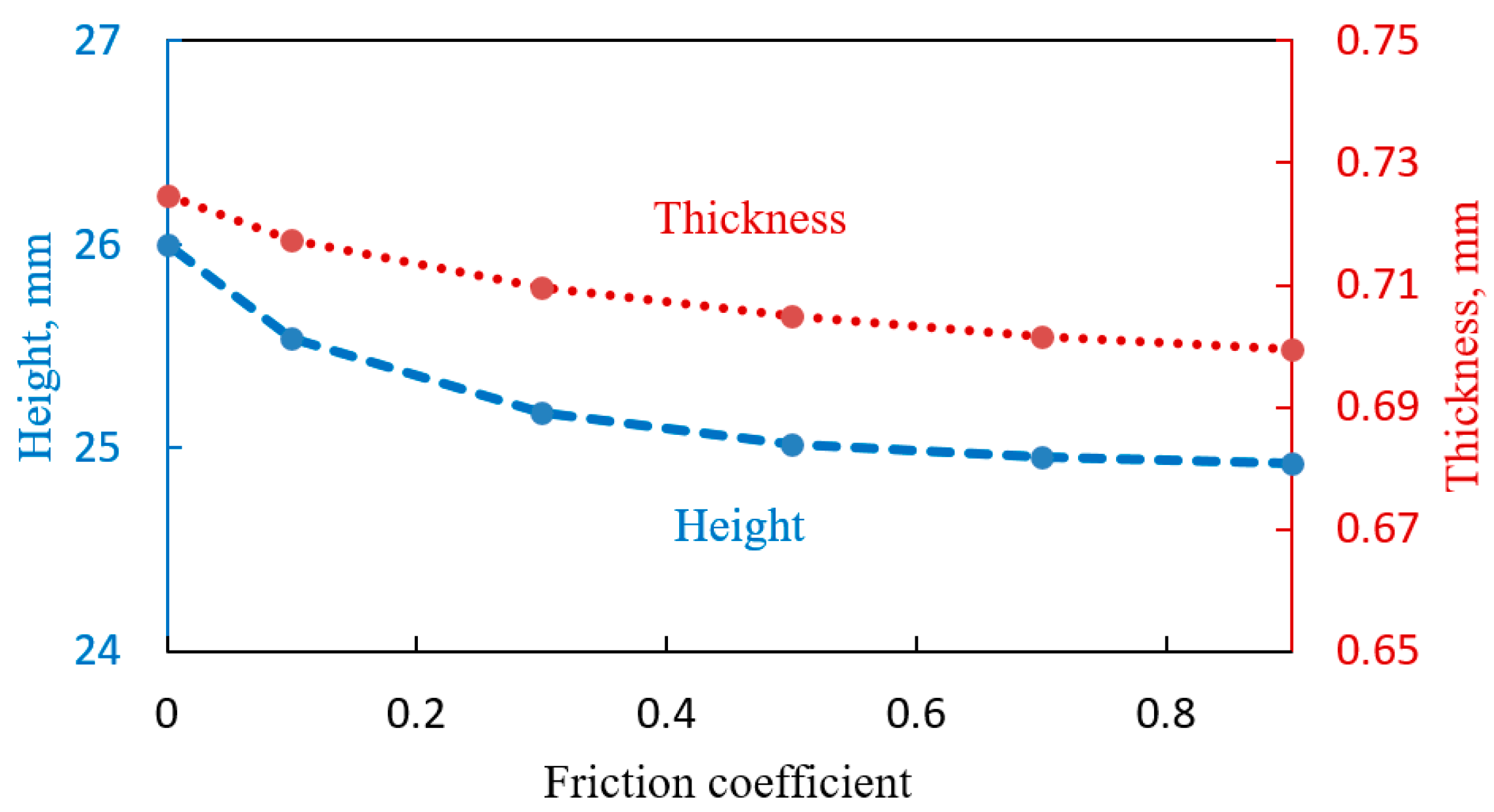
4.3. Effect of Friction
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Pearson, C.E. The viscous properties of extruded eutectic alloys of lead-tin and bismuth-tin. J. Inst. Met. 1934, 54, 111–123. [Google Scholar]
- Backofen, W.A.; Turner, I.R.; Avery, D.H. Superplasticity in an Al-Zn Alloy. Trans. ASM 1964, 57, 980–990. [Google Scholar]
- Jarrar, F.; Jafar, R.; Tulupova, O.; Enikeev, F.; Al-Hunti, N. Constitutive modeling for the simulation of the superplastic forming of AA5083. Mater. Sci. Forum 2016, 838, 512–517. [Google Scholar] [CrossRef]
- Langdon, T.G. Forty-five tears of superplastic research: Recent developments and future prospects. Mater. Sci. Forum 2016, 838, 3–12. [Google Scholar] [CrossRef]
- Yang, W.-P.; Guo, X.-F.; Yang, K.-J. Low temperature quasi-superplasticity of ZK60 alloy prepared by reciprocating extrusion. Trans. Nonferrous Met. Soc. China 2012, 22, 255–261. [Google Scholar] [CrossRef]
- Taleff, E.M.; Hector, L.G.; Verma, R.; Krajewski, P.E.; Chang, J.K. Material Models for Simulation of Superplastic Mg Alloy Sheet Forming. J. Mater. Eng. Perform. 2010, 19, 488–494. [Google Scholar] [CrossRef]
- Taleff, E.M.; Hector, L.G.; Bradley, J.R.; Verma, R.; Krajewski, P.E. The effect of stress state on high-temperature deformation of fine-grained aluminum-magnesium alloy AA5083 sheet. Acta Mater. 2009, 57, 2812–2822. [Google Scholar] [CrossRef]
- El-Morsy, A.; Akkus, N.; Manabe, K.; Nishimura, H. Superplastic characteristics of Ti-alloy and Al-alloy sheets by multi-dome forming test. Mater. Trans. 2001, 42, 2332–2338. [Google Scholar] [CrossRef]
- Aksenov, S.A.; Kolesnikov, A.V.; Mikhaylovskaya, A.V. Design of a gas forming technology using the material constants obtained by tensile and free bulging testing. J. Mater. Process. Technol. 2016, 237, 88–95. [Google Scholar] [CrossRef]
- Enikeev, F.U.; Kruglov, A.A. An analysis of the superplastic forming of a thin circular diagram. Int. J. Mech. Sci. 1995, 37, 473–483. [Google Scholar] [CrossRef]
- Giuliano, G. Constitutive modelling of superplastic AA-5083. Tech. Mech. 2012, 32, 221–226. [Google Scholar]
- Sorgente, D.; Tricarico, L. Characterization of a superplastic aluminium alloy ALNOVI-U through free inflation tests and inverse analysis. Int. J. Mater. Form. 2014, 7, 179–187. [Google Scholar] [CrossRef]
- Sorgente, D.; Palumbo, G.; Piccininni, A.; Guglielmi, P.; Tricarico, L. Modelling the superplastic behaviour of the Ti6Al4V-ELI by means of a numerical/experimental approach. Int. J. Adv. Manuf. Technol. 2016, 90, 1–10. [Google Scholar] [CrossRef]
- Li, G.Y.; Tan, M.J.; Liew, K.M. Three-dimensional modelling and simulation of superplastic forming. J. Mater. Process. Technol. 2004, 150, 76–83. [Google Scholar] [CrossRef]
- Aksenov, S.A.; Cumachenko, E.N.; Kolesnikov, A.V.; Osipov, S.A. Determination of optimal gas forming conditions from free bulging tests at constant pressure. J. Mater. Process. Technol. 2015, 217, 158–164. [Google Scholar] [CrossRef]
- Kumaresan, G.; Kalaichelvan, K. Multi-dome forming test for determining the strain rate sensitivity index of a superplastic 7075Al alloy sheet. J. Alloys Compd. 2014, 583, 226–230. [Google Scholar] [CrossRef]
- El-Morsy, A.; Manabe, K. FE simulation of rectangular box forming using material characteristics from the multi-dome forming test. J. Mater. Process. Technol. 2002, 125, 772–777. [Google Scholar] [CrossRef]
- Bhattacharya, S.S.; Padmanabhan, K.A. Similarities and differences in the approaches to structural superplasticity and high temperature creep. Trans. Indian Inst. Met. 1989, 42, S123–S137. [Google Scholar]
- Yogesha, B.; Bhattacharya, S.S. Superplastic hemispherical Bulge Forming of a Ti-Al-Mn Alloy. Int. J. Sci. Eng. Res. 2011, 2, 1–4. [Google Scholar]
- Aksenov, S.A.; Zakhariev, I.Y.; Kolesnikov, A.V.; Osipov, S.A. Characterization of superplastic materials by results of free bulging tests. Mater. Sci. 2016, 838, 552–556. [Google Scholar] [CrossRef]

| Fe % | C % | Si % | Mn % | N % | O % | Al % | Zr % | Ti % |
|---|---|---|---|---|---|---|---|---|
| 0.3 | 0.1 | 0.12 | 2 | 0.05 | 0.15 | 2.5 | 0.3 | Balance |
| Pressure, MPa | , s | , s | , s |
|---|---|---|---|
| P, MPa | Equation | Deviations | |||||
|---|---|---|---|---|---|---|---|
| 0.3 | Inverse analysis | 0.1501 | 0.0521 | 0.0367 | 0.0199 | 0.0299 | 0.0333 |
| 0.3 | Direct technique | 0.0371 | 0.3106 | 0.3117 | 0.1984 | 0.2349 | 0.1829 |
| 0.3 | Tensile test | 0.4556 | 1.006 | 0.9658 | 0.7084 | 0.8454 | 0.7349 |
| 0.5 | Inverse analysis | 0.1532 | 0.0177 | 0.0291 | 0.0345 | 0.0237 | 0.0332 |
| 0.5 | Direct technique | 0.0204 | 0.2470 | 0.2978 | 0.1584 | 0.2258 | 0.1665 |
| 0.5 | Tensile test | 0.2779 | 0.5881 | 0.6641 | 0.4550 | 0.5617 | 0.4861 |
| 0.7 | Inverse analysis | 0.0653 | 0.0604 | 0.0566 | 0.0623 | 0.0564 | 0.0515 |
| 0.7 | Direct technique | 0.0971 | 0.2875 | 0.3125 | 0.2245 | 0.2726 | 0.2196 |
| 0.7 | Tensile test | 0.2799 | 0.4412 | 0.4532 | 0.4012 | 0.4443 | 0.3976 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zakhariev, I.; Aksenov, S.; Kotov, A.; Kolesnikov, A. Characterization of OT4-1 Alloy by Multi-Dome Forming Test. Materials 2017, 10, 899. https://doi.org/10.3390/ma10080899
Zakhariev I, Aksenov S, Kotov A, Kolesnikov A. Characterization of OT4-1 Alloy by Multi-Dome Forming Test. Materials. 2017; 10(8):899. https://doi.org/10.3390/ma10080899
Chicago/Turabian StyleZakhariev, Ivan, Sergey Aksenov, Anton Kotov, and Aleksey Kolesnikov. 2017. "Characterization of OT4-1 Alloy by Multi-Dome Forming Test" Materials 10, no. 8: 899. https://doi.org/10.3390/ma10080899
APA StyleZakhariev, I., Aksenov, S., Kotov, A., & Kolesnikov, A. (2017). Characterization of OT4-1 Alloy by Multi-Dome Forming Test. Materials, 10(8), 899. https://doi.org/10.3390/ma10080899





