Adsorption of Milk Proteins (β-Casein and β-Lactoglobulin) and BSA onto Hydrophobic Surfaces
Abstract
1. Introduction
2. Results and Discussion
2.1. MD Simulations of -Casein
2.2. Comparison of Simulation Results for -Casein, -Lactoglobulin and BSA
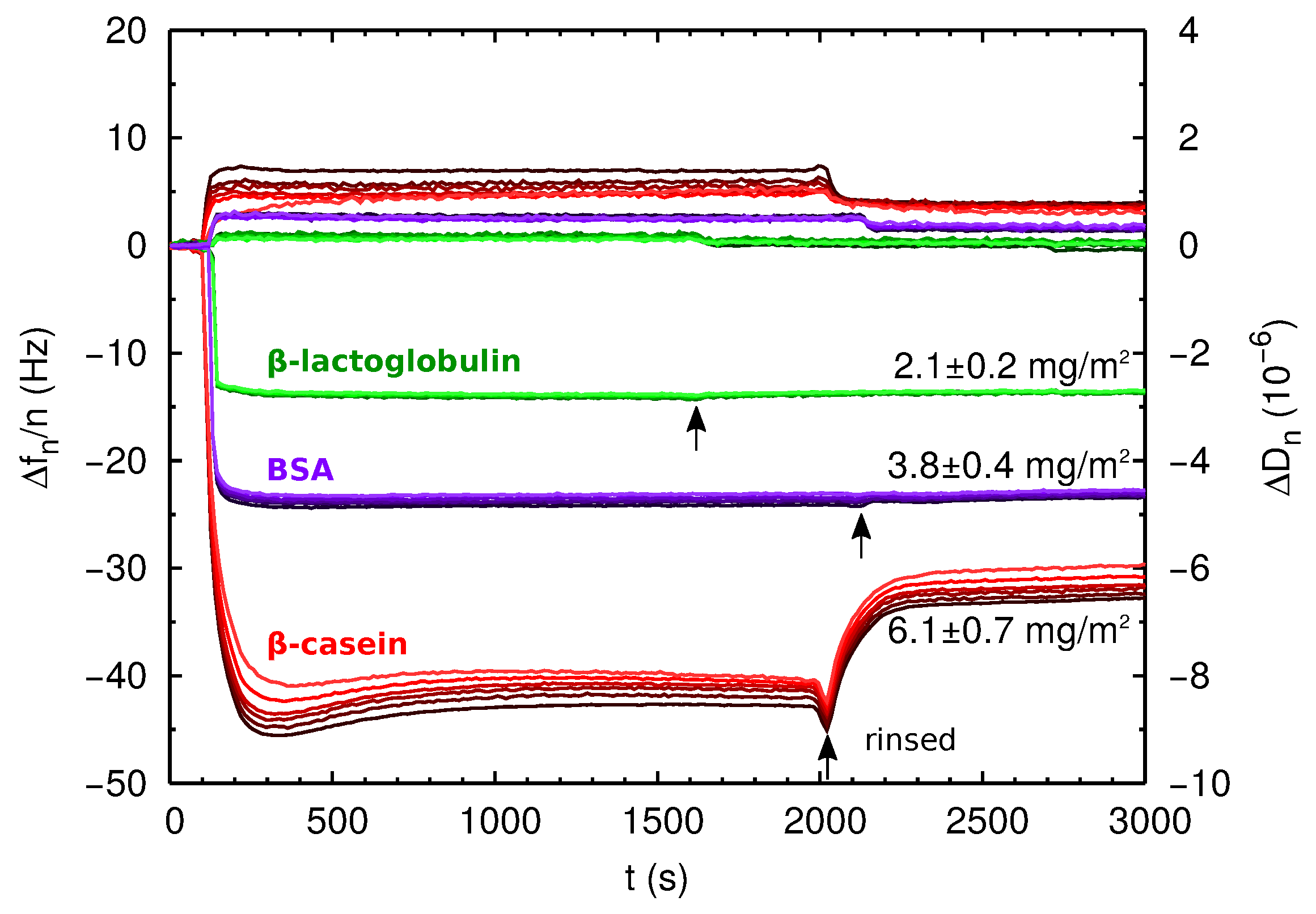
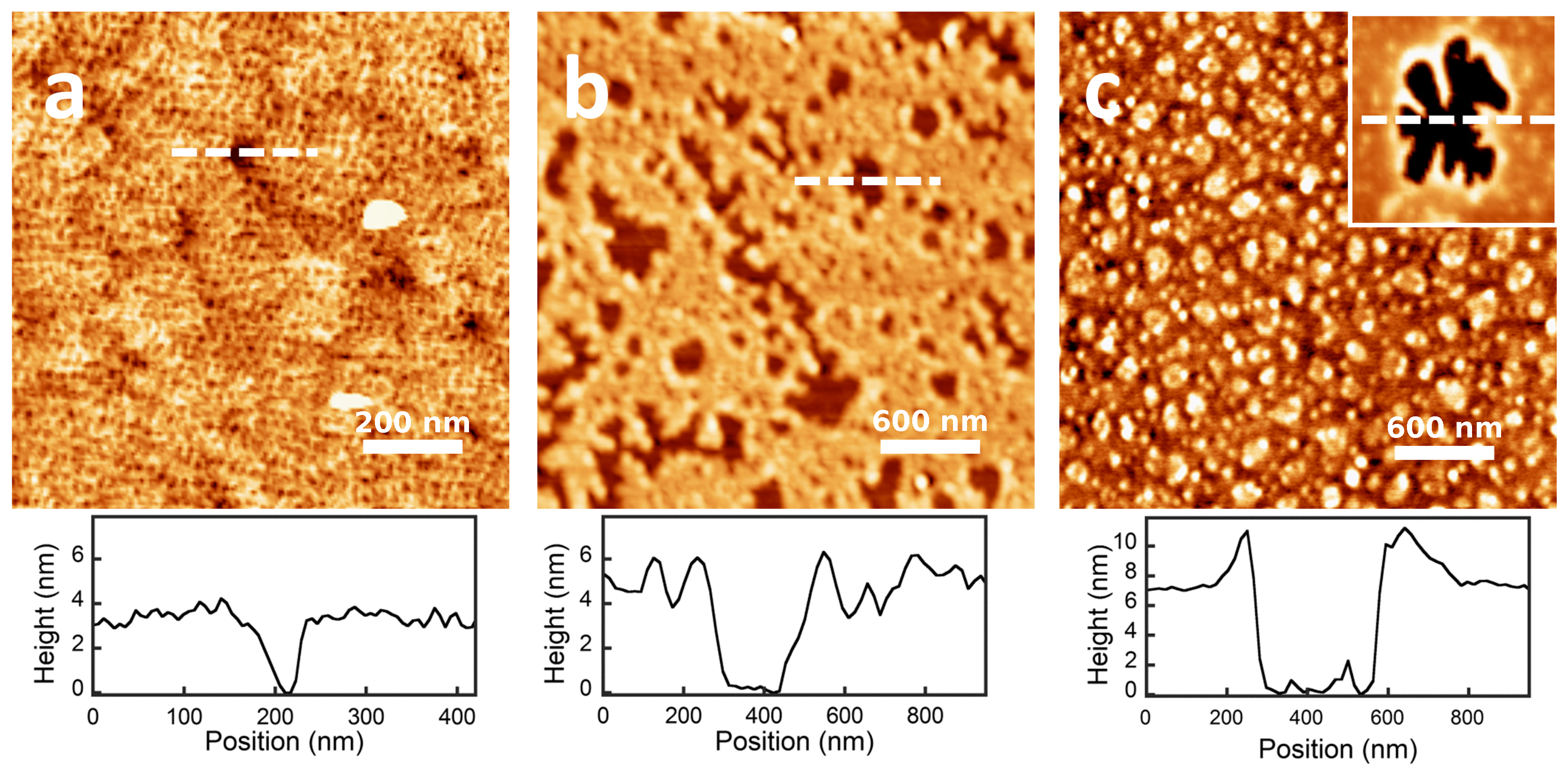
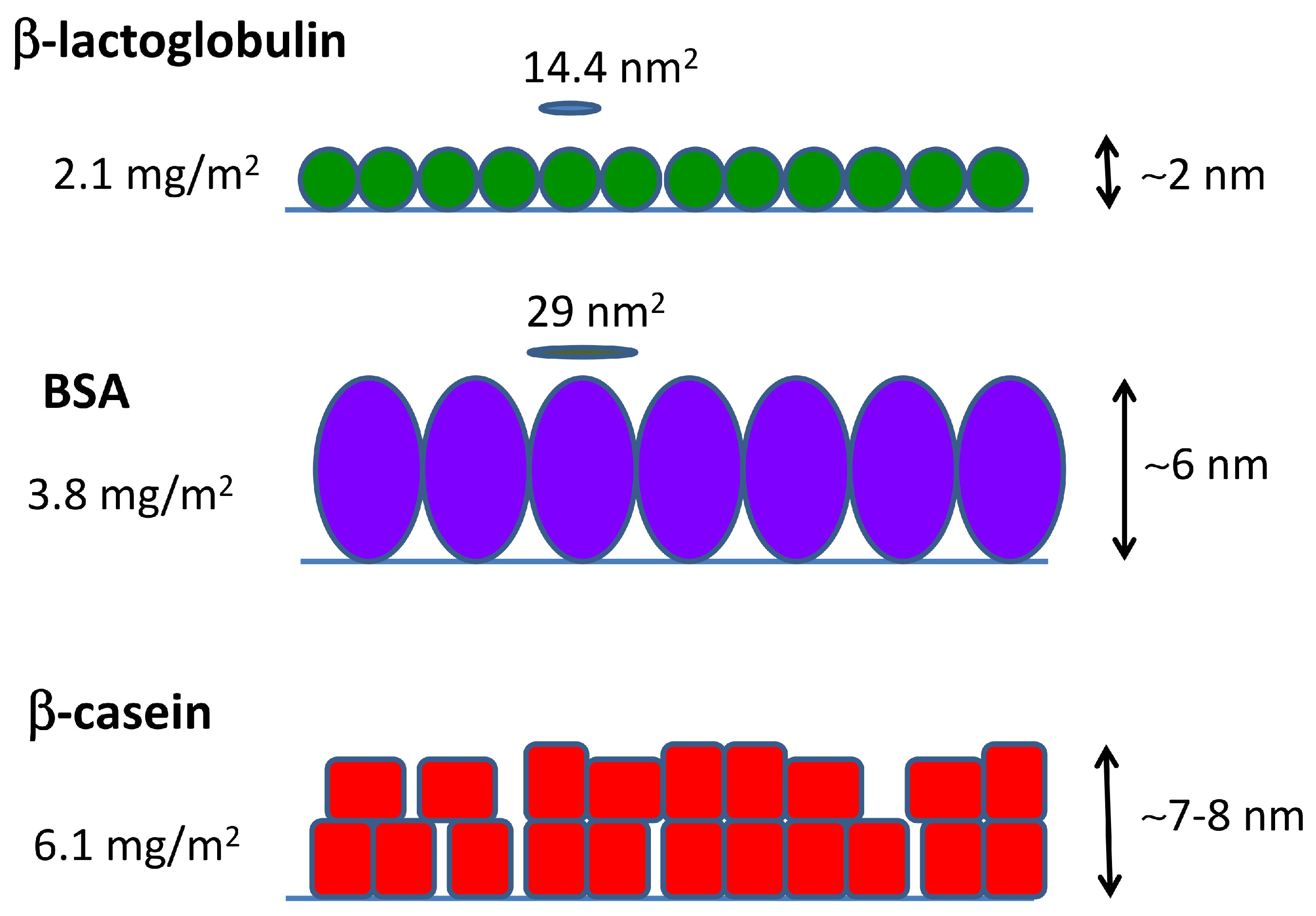
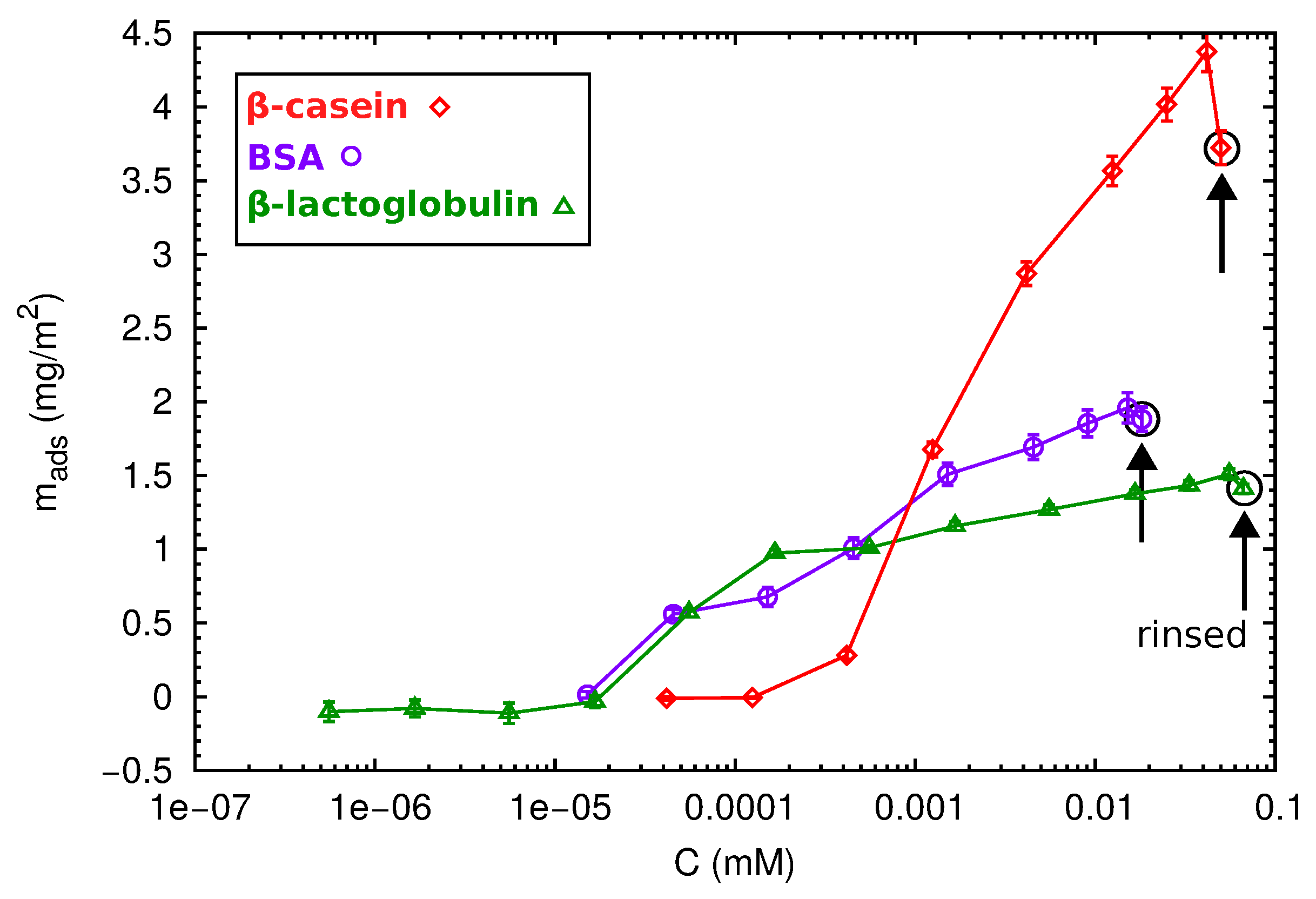
2.3. QCM-D and AFM Study of Protein Adsorption onto a Planar Surface
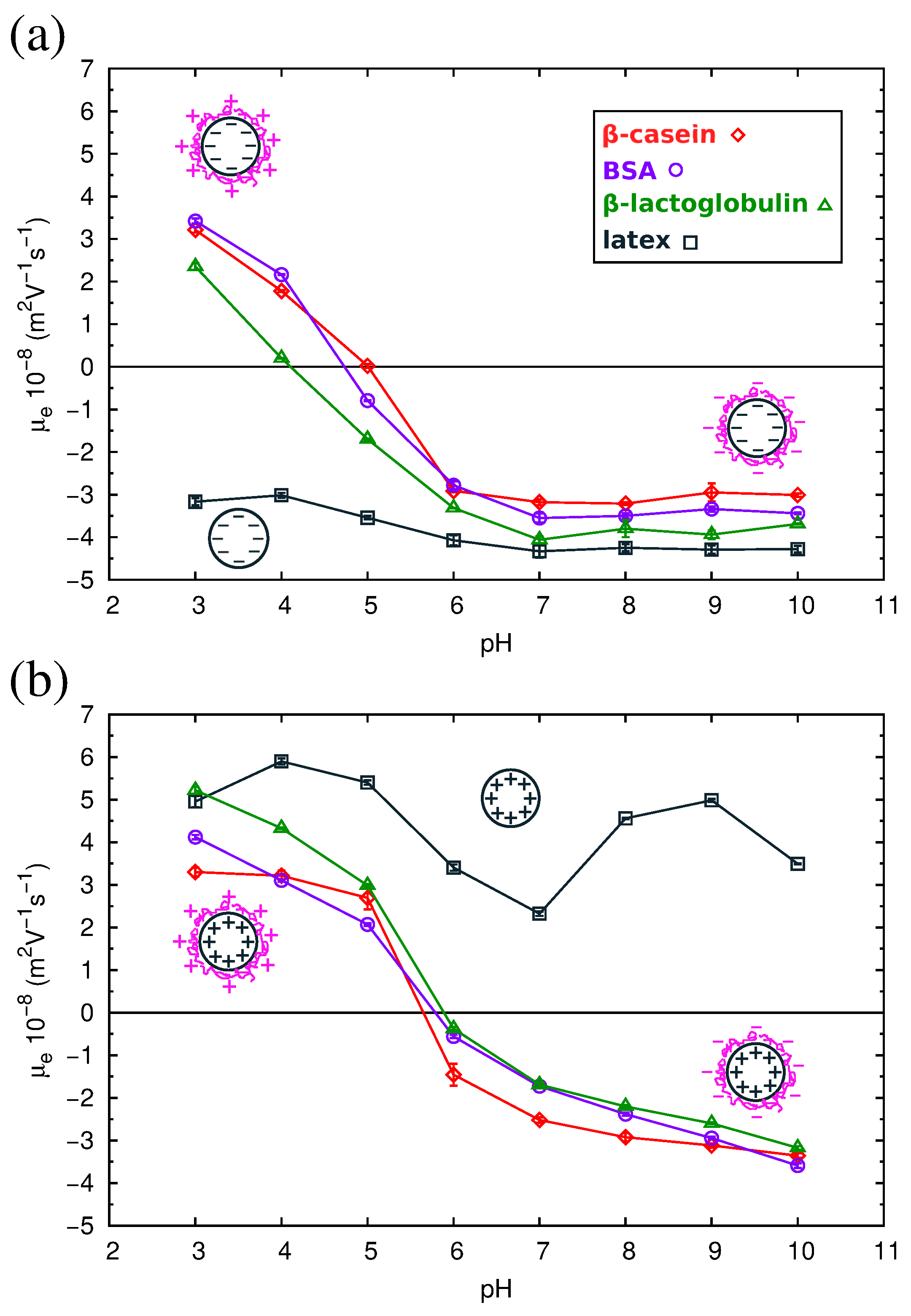
2.4. Electrokinetics of Adsorbed Protein Layers
3. Materials and Methods
3.1. Experimental
3.1.1. Reagents
3.1.2. Polystyrene Latex Microspheres
3.1.3. Protein Adsorption onto Latex Microspheres
3.1.4. Electrokinetics
3.1.5. Quartz Crystal Microbalance
3.1.6. Atomic Force Microscopy
3.2. MD Simulations
3.2.1. Models and Force Fields
3.2.2. MD Simulations of Proteins in Implicit Water
3.2.3. MD Simulations of -Casein Adsorption
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| MD | Molecular dynamics |
| AFM | Atomic force microscopy |
| QCM-D | Quartz crystal microbalance with dissipation monitoring |
| BSA | Bovine serum albumin |
| -lg | -lactoglobulin |
| -cas | -casein |
References
- Monopoli, M.P.; Åberg, C.; Salvati, A.; Dawson, K.A. Biomolecular coronas provide the biological identity of nanosized materials. Nat. Nanotechnol. 2012, 7, 779–786. [Google Scholar] [CrossRef] [PubMed]
- Wee, K.W.; Kang, G.Y.; Park, J.; Kang, J.Y.; Yoon, D.S.; Park, J.H.; Kim, T.S. Novel electrical detection of label-free disease marker proteins using piezoresistive self-sensing micro-cantilevers. Biosens. Bioelectron. 2005, 20, 1932–1938. [Google Scholar] [CrossRef] [PubMed]
- Vollmer, F.; Arnold, S. Whispering-gallery-mode biosensing: Label-free detection down to single molecules. Nat. Methods 2008, 5, 591–596. [Google Scholar] [CrossRef] [PubMed]
- Cai, K.; Bossert, J.; Jandt, K.D. Does the nanometre scale topography of titanium influence protein adsorption and cell proliferation? Colloids Surf. B 2006, 49, 136–144. [Google Scholar] [CrossRef] [PubMed]
- Ellingsen, J.E. A study on the mechanism of protein adsorption to TiO2. Biomaterials 1991, 12, 593–596. [Google Scholar] [CrossRef]
- Pavithra, D.; Doble, M. Biofilm formation, bacterial adhesion and host response on polymeric implants—Issues and prevention. Biomed. Mater. 2008, 3, 034003. [Google Scholar] [CrossRef] [PubMed]
- Hucknall, A.; Rangarajan, S.; Chilkoti, A. In pursuit of zero: Polymer brushes that resist the adsorption of proteins. Adv. Mater. 2009, 21, 2441–2446. [Google Scholar] [CrossRef]
- Wei, Q.; Becherer, T.; Angioletti-Uberti, S.; Dzubiella, J.; Wischke, C.; Neffe, A.T.; Lendlein, A.; Ballauff, M.; Haag, R. Protein interactions with polymer coatings and biomaterials. Angew. Chem. 2014, 53, 8004–8031. [Google Scholar] [CrossRef] [PubMed]
- Norde, W. Adsorption of proteins from solution at the solid-liquid interface. Adv. Colloid Interface Sci. 1986, 25, 267–340. [Google Scholar] [CrossRef]
- Norde, W.; Lyklema, J. Why proteins prefer interfaces. J. Biomater. Sci. 1991, 2, 183–202. [Google Scholar] [CrossRef]
- Gray, J.J. The interaction of proteins with solid surfaces. Curr. Opin. Struct. Biol. 2004, 14, 110–115. [Google Scholar] [CrossRef] [PubMed]
- Rabe, M.; Verdes, D.; Seeger, S. Understanding protein adsorption phenomena at solid surfaces. Adv. Colloid Interface Sci. 2011, 162, 87–106. [Google Scholar] [CrossRef] [PubMed]
- Nakanishi, K.; Sakiyama, T.; Imamura, K. On the adsorption of proteins on solid surfaces, a common but very complicated phenomenon. J. Biosci. Bioeng. 2001, 91, 233–244. [Google Scholar] [CrossRef]
- Roussel, T.J.; Barrena, E.; Ocal, C.; Faraudo, J. Predicting supramolecular self-assembly on reconstructed metal surfaces. Nanoscale 2014, 6, 7991–8001. [Google Scholar] [CrossRef] [PubMed]
- Hagiwara, T.; Sakiyama, T.; Watanabe, H. Molecular simulation of bovine β-lactoglobulin adsorbed onto a positively charged solid surface. Langmuir 2008, 25, 226–234. [Google Scholar] [CrossRef] [PubMed]
- Huppertz, T. Chemistry of the Caseins. In Advanced Dairy Chemistry; Springer: Boston, MA, USA, 2013; pp. 135–160. [Google Scholar]
- Hamada, D.; Segawa, S.; Goto, Y. Non-native α-helical intermediate in the refolding of β-lactoglobulin, a predominantly β-sheet protein. Nat. Struct. Mol. Biol. 1996, 3, 868–873. [Google Scholar] [CrossRef]
- Loch, J.; Polit, A.; Gorecki, A.; Bonarek, P.; Kurpiewska, K.; Dziedzicka-Wasylewska, M.; Lewiński, K. Two modes of fatty acid binding to bovine β-lactoglobulin—Crystallographic and spectroscopic studies. J. Mol. Recognit. 2011, 24, 341–349. [Google Scholar] [CrossRef] [PubMed]
- Docena, G.; Fernandez, R.; Chirdo, F.; Fossati, C. Identification of casein as the major allergenic and antigenic protein of cow’s milk. Allergy 1996, 51, 412–416. [Google Scholar] [CrossRef] [PubMed]
- Goldman, A.; Anderson, D.; Sellers, W.; Saperstein, S.; Kniker, W.; Halpern, S. Milk allergy I. Oral challenge with milk and isolated milk proteins in allergic children. Pediatrics 1963, 32, 425–443. [Google Scholar] [PubMed]
- Hammann, F.; Schmid, M. Determination and Quantification of Molecular Interactions in Protein Films: A Review. Materials 2014, 7, 7975–7996. [Google Scholar] [CrossRef]
- Pérez-Fuentes, L.; Drummond, C.; Faraudo, J.; Bastos-González, D. Interaction of organic ions with proteins. Soft Matter 2017, 13, 1120–1131. [Google Scholar] [CrossRef] [PubMed]
- Wright, A.; Thompson, M. Hydrodynamic structure of bovine serum albumin determined by transient electric birefringence. Biophys. J. 1975, 15, 137–141. [Google Scholar] [CrossRef]
- Demanèche, S.; Chapel, J.P.; Monrozier, L.J.; Quiquampoix, H. Dissimilar pH-dependent adsorption features of bovine serum albumin and α-chymotrypsin on mica probed by AFM. Colloids Surf. B 2009, 70, 226–231. [Google Scholar] [CrossRef] [PubMed]
- Barbosa, L.R.; Ortore, M.G.; Spinozzi, F.; Mariani, P.; Bernstorff, S.; Itri, R. The importance of protein-protein interactions on the pH-induced conformational changes of bovine serum albumin: A small-angle X-ray scattering study. Biophys. J. 2010, 98, 147–157. [Google Scholar] [CrossRef] [PubMed]
- Bujacz, A.; Zielinski, K.; Sekula, B. Structural studies of bovine, equine, and leporine serum albumin complexes with naproxen. Proteins 2014, 82, 2199–2208. [Google Scholar] [CrossRef] [PubMed]
- Yu, S.; Perálvarez-Marín, A.; Minelli, C.; Faraudo, J.; Roig, A.; Laromaine, A. Albumin-coated SPIONs: An experimental and theoretical evaluation of protein conformation, binding affinity and competition with serum proteins. Nanoscale 2016, 8, 14393–14405. [Google Scholar] [CrossRef] [PubMed]
- Pieper, U.; Webb, B.M.; Dong, G.Q.; Schneidman-Duhovny, D.; Fan, H.; Kim, S.J.; Khuri, N.; Spill, Y.G.; Weinkam, P.; Hammel, M.; et al. ModBase: A database of annotated comparative protein structure models and associated resources. Nucleic Acids Res. 2014, 42, D336–D346. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Rawat, N.; Biswas, P. Size, shape, and flexibility of proteins and DNA. J. Chem. Phys. 2009, 131, 165104. [Google Scholar] [CrossRef] [PubMed]
- Vilhena, J.G.; Rubio-Pereda, P.; Vellosillo, P.; Serena, P.A.; Pérez, R. Albumin (BSA) Adsorption over Graphene in Aqueous Environment: Influence of Orientation, Adsorption Protocol, and Solvent Treatment. Langmuir 2016, 32, 1742–1755. [Google Scholar] [CrossRef] [PubMed]
- Siretanu, I. Nanostructuration Contrôlée de Films de Polymères. Ph.D. Thesis, University of Bordeaux 1, Talence, France, 2011. [Google Scholar]
- Johannsmann, D.; Reviakine, I.; Rojas, E.; Gallego, M. Effect of sample heterogeneity on the interpretation of QCM(-D) data: Comparison of combined quartz crystal microbalance/atomic force microscopy measurements with finite element method modeling. Anal. Chem. 2008, 80, 8891–8899. [Google Scholar] [CrossRef] [PubMed]
- Graham, D.; Phillips, M. Proteins at liquid interfaces: II. Adsorption isotherms. J. Colloid Interface Sci. 1979, 70, 415–426. [Google Scholar] [CrossRef]
- Pandey, L.M.; Pattanayek, S.K.; Delabouglise, D. Properties of adsorbed bovine serum albumin and fibrinogen on self-assembled monolayers. J. Phys. Chem. C 2013, 117, 6151–6160. [Google Scholar] [CrossRef]
- Atkinson, P.J.; Dickinson, E.; Horne, D.S.; Richardson, R.M. Neutron reflectivity of adsorbed β-casein and β-lactoglobulin at the air/water interface. J. Chem. Soc. Faraday Trans. 1995, 91, 2847–2854. [Google Scholar] [CrossRef]
- Lebec, V.; Landoulsi, J.; Boujday, S.; Poleunis, C.; Pradier, C.M.; Delcorte, A. Probing the orientation of β-lactoglobulin on gold surfaces modified by alkyl thiol self-assembled monolayers. J. Phys. Chem. C 2013, 117, 11569–11577. [Google Scholar] [CrossRef]
- Graham, D.; Phillips, M. Proteins at liquid interfaces: I. Kinetics of adsorption and surface denaturation. J. Colloid Interface Sci. 1979, 70, 403–414. [Google Scholar] [CrossRef]
- Lee, M.; Park, S.K.; Chung, C.; Kim, H. QCM study of β-casein adsorption on the hydrophobic surface: Effect of ionic strength and cations. Bull. Korean Chem. Soc. 2004, 25, 1031–1035. [Google Scholar]
- Murray, B.S.; Cros, L. Adsorption of β-lactoglobulin and β-casein to metal surfaces and their removal by a non-ionic surfactant, as monitored via a quartz crystal microbalance. Colloids Surf. B 1998, 10, 227–241. [Google Scholar] [CrossRef]
- Mackie, A.R.; Mingins, J.; North, A.N. Characterisation of adsorbed layers of a disordered coil protein on polystyrene latex. J. Chem. Soc. Faraday Trans. 1991, 87, 3043–3049. [Google Scholar] [CrossRef]
- Brooksbank, D.V.; Davidson, C.M.; Horne, D.S.; Leaver, J. Influence of electrostatic interactions on β-casein layers adsorbed on polystyrene latices. J. Chem. Soc. Faraday Trans. 1993, 89, 3419–3425. [Google Scholar] [CrossRef]
- Nylander, T.; Wahlgren, N.M. Competitive and sequential adsorption of β-casein and β-lactoglobulin on hydrophobic surfaces and the interfacial structure of β-casein. J. Colloid Interface Sci. 1994, 162, 151–162. [Google Scholar] [CrossRef]
- Nylander, T.; Tiberg, F.; Wahlgren, N.M. Evaluation of the structure of adsorbed layers of β//this should be curled beta, -casein from ellipsometry and surface force measurements. Int. Dairy J. 1999, 9, 313–317. [Google Scholar] [CrossRef]
- Fang, F.; Szleifer, I. Kinetics and thermodynamics of protein adsorption: A generalized molecular theoretical approach. Biophys. J. 2001, 80, 2568–2589. [Google Scholar] [CrossRef]
- Shirahama, H.; Ohno, H.; Suzawa, T. Preparation, characterization, and albumin adsorption of amphoteric polymer latices. Colloids Surf. 1991, 60, 1–17. [Google Scholar] [CrossRef]
- Galisteo-González, F.; Martín-Rodríguez, A.; Hidalgo-Álvarez, R. Adsorption of monoclonal IgG on polystyrene microspheres. Colloid Polym. Sci. 1994, 272, 352–358. [Google Scholar] [CrossRef]
- Delgado, Á.V. Interfacial Electrokinetics and Electrophoresis; CRC Press: New York, NY, USA, 2001; Volume 106. [Google Scholar]
- Martín, A.; Puig, J.; Galisteo, F.; Serra, J.; Hidalgo-Álvarez, R. On some aspects of the adsorption of immunoglobulin-G molecules on polystyrene microspheres. J. Dispers. Sci. Technol. 1992, 13, 399–416. [Google Scholar] [CrossRef]
- Ortega-Vinuesa, J.L.; Bastos-Gónzalez, D.; Hidalgo-Álvarez, R. Comparative studies on physically adsorbed and chemically bound IgG to carboxylated latexes, II. J. Colloid Interface Sci. 1995, 176, 240–247. [Google Scholar] [CrossRef]
- Pace, C.N.; Vajdos, F.; Fee, L.; Grimsley, G.; Gray, T. How to measure and predict the molar absorption coefficient of a protein. Protein Sci. 1995, 4, 2411–2423. [Google Scholar] [CrossRef] [PubMed]
- Farrell, H.; Jimenez-Flores, R.; Bleck, G.; Brown, E.; Butler, J.; Creamer, L.; Hicks, C.; Hollar, C.; Ng-Kwai-Hang, K.; Swaisgood, H. Nomenclature of the proteins of cows’ milk—Sixth revision. J. Dairy Sci. 2004, 87, 1641–1674. [Google Scholar] [CrossRef]
- Li, H.; Robertson, A.D.; Jensen, J.H. Very fast empirical prediction and rationalization of protein pKa values. Proteins 2005, 61, 704–721. [Google Scholar] [CrossRef] [PubMed]
- Bas, D.C.; Rogers, D.M.; Jensen, J.H. Very fast prediction and rationalization of pKa values for protein–ligand complexes. Proteins 2008, 73, 765–783. [Google Scholar] [CrossRef] [PubMed]
- Olsson, M.H.; Søndergaard, C.R.; Rostkowski, M.; Jensen, J.H. PROPKA3: Consistent treatment of internal and surface residues in empirical pKa predictions. J. Chem. Theory Comput. 2011, 7, 525–537. [Google Scholar] [CrossRef] [PubMed]
- Oosawa, F. Polyelectrolytes; Dekker: New York, NY, USA, 1971. [Google Scholar]
- Manning, G.S. Limiting laws and counterion condensation in polyelectrolyte solutions. J. Chem. Phys. 1969, 51, 924–933. [Google Scholar] [CrossRef]
- Belloni, L. Ionic condensation and charge renormalization in colloidal suspensions. Colloids Surf. A 1998, 140, 227–243. [Google Scholar] [CrossRef]
- Manning, G.S. Counterion condensation on charged spheres, cylinders, and planes. J. Phys. Chem. B 2007, 111, 8554–8559. [Google Scholar] [CrossRef] [PubMed]
- Bocquet, L.; Trizac, E.; Aubouy, M. Effective charge saturation in colloidal suspensions. J. Chem. Phys. 2002, 117, 8138–8152. [Google Scholar] [CrossRef]
- Calero, C.; Faraudo, J. The interaction between electrolyte and surfaces decorated with charged groups: A molecular dynamics simulation study. J. Chem. Phys. 2010, 132, 024704. [Google Scholar] [CrossRef] [PubMed]
- Maldonado-Valderrama, J.; Terriza, J.H.; Torcello-Gómez, A.; Cabrerizo-Vílchez, M. In vitro digestion of interfacial protein structures. Soft Matter 2013, 9, 1043–1053. [Google Scholar] [CrossRef]
- López-León, T.; Jódar-Reyes, A.B.; Bastos-González, D.; Ortega-Vinuesa, J.L. Hofmeister effects in the stability and electrophoretic mobility of polystyrene latex particles. J. Phys. Chem. B 2003, 107, 5696–5708. [Google Scholar] [CrossRef]
- López-León, T.; Santander-Ortega, M.J.; Ortega-Vinuesa, J.L.; Bastos-González, D. Hofmeister effects in colloidal systems: Influence of the surface nature. J. Phys. Chem. C 2008, 112, 16060–16069. [Google Scholar] [CrossRef]
- Payens, T.; Brinkhuis, J.; Van Markwijk, B. Self-association in non-ideal systems. Combined light scattering and sedimentation measurements in β-casein solutions. Biochim. Biophys. Acta 1969, 175, 434–437. [Google Scholar] [CrossRef]
- Portnaya, I.; Ben-Shoshan, E.; Cogan, U.; Khalfin, R.; Fass, D.; Ramon, O.; Danino, D. Self-assembly of bovine β-casein below the isoelectric pH. J. Agric. Food Chem. 2008, 56, 2192–2198. [Google Scholar] [CrossRef] [PubMed]
- López-León, T.; Jódar-Reyes, A.; Ortega-Vinuesa, J.L.; Bastos-González, D. Hofmeister effects on the colloidal stability of an IgG-coated polystyrene latex. J. Colloid Interface Sci. 2005, 284, 139–148. [Google Scholar] [CrossRef] [PubMed]
- Ohshima, H. Approximate analytic expression for the electrophoretic mobility of a spherical colloidal particle. J. Colloid Interface Sci. 2001, 239, 587–590. [Google Scholar] [CrossRef] [PubMed]
- Makino, K.; Ohshima, H. Electrophoretic mobility of a colloidal particle with constant surface charge density. Langmuir 2010, 26, 18016–18019. [Google Scholar] [CrossRef] [PubMed]
- Reviakine, I.; Johannsmann, D.; Richter, R.P. Hearing what you cannot see and visualizing what you hear: Interpreting quartz crystal microbalance data from solvated interfaces. Anal. Chem. 2011, 83, 8838–8848. [Google Scholar] [CrossRef] [PubMed]
- Sauerbrey, G. Use of quartz vibration for weighing thin films on a microbalance. J. Phys. 1959, 155, 206–212. [Google Scholar]
- Sekar, S.; Giermanska, J.; Chapel, J.P. Reusable and recyclable quartz crystal microbalance sensors. Sens. Actuator B-Chem. 2015, 212, 196–199. [Google Scholar] [CrossRef]
- Hegner, M.; Wagner, P.; Semenza, G. Ultralarge atomically flat template-stripped Au surfaces for scanning probe microscopy. Surf. Sci. 1993, 291, 39–46. [Google Scholar] [CrossRef]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The protein data bank. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef] [PubMed]
- MacKerell, A.D., Jr.; Bashford, D.; Bellott, M.; Dunbrack, R.L., Jr.; Evanseck, J.D.; Field, M.J.; Fischer, S.; Gao, J.; Guo, H.; Ha, S.; et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B 1998, 102, 3586–3616. [Google Scholar] [CrossRef] [PubMed]
- MacKerell, A.D.; Feig, M.; Brooks, C.L. Extending the treatment of backbone energetics in protein force fields: Limitations of gas-phase quantum mechanics in reproducing protein conformational distributions in molecular dynamics simulations. J. Comput. Chem. 2004, 25, 1400–1415. [Google Scholar] [CrossRef] [PubMed]
- Tanner, D.E.; Chan, K.Y.; Phillips, J.C.; Schulten, K. Parallel generalized Born implicit solvent calculations with NAMD. J. Chem. Theory Comput. 2011, 7, 3635–3642. [Google Scholar] [CrossRef] [PubMed]
- Weiser, J.; Shenkin, P.S.; Still, W.C. Approximate atomic surfaces from linear combinations of pairwise overlaps (LCPO). J. Comput. Chem. 1999, 20, 217–230. [Google Scholar] [CrossRef]
- Anandakrishnan, R.; Drozdetski, A.; Walker, R.C.; Onufriev, A.V. Speed of Conformational Change: Comparing Explicit and Implicit Solvent Molecular Dynamics Simulations. Biophys. J. 2015, 108, 1153–1164. [Google Scholar] [CrossRef] [PubMed]
- Calero, C.; Faraudo, J.; Bastos-González, D. Interaction of monovalent ions with hydrophobic and hydrophilic colloids: Charge inversion and ionic specificity. J. Am. Chem. Soc. 2011, 133, 15025–15035. [Google Scholar] [CrossRef] [PubMed]
- Huang, D.M.; Cottin-Bizonne, C.; Ybert, C.; Bocquet, L. Aqueous electrolytes near hydrophobic surfaces: Dynamic effects of ion specificity and hydrodynamic slip. Langmuir 2008, 24, 1442–1450. [Google Scholar] [CrossRef] [PubMed]
- Werder, T.; Walther, J.H.; Jaffe, R.; Halicioglu, T.; Koumoutsakos, P. On the water-carbon interaction for use in molecular dynamics simulations of graphite and carbon nanotubes. J. Phys. Chem. B 2003, 107, 1345–1352. [Google Scholar] [CrossRef]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kale, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef] [PubMed]
- Giorgino, T. Computing 1-D atomic densities in macromolecular simulations: The density profile tool for VMD. Comutput. Phys. Commun. 2014, 185, 317–322. [Google Scholar] [CrossRef]
- Raffaini, G.; Ganazzoli, F. Simulation study of the interaction of some albumin subdomains with a flat graphite surface. Langmuir 2003, 19, 3403–3412. [Google Scholar] [CrossRef]
- Mücksch, C.; Urbassek, H.M. Molecular dynamics simulation of free and forced BSA adsorption on a hydrophobic graphite surface. Langmuir 2011, 27, 12938–12943. [Google Scholar] [CrossRef] [PubMed]
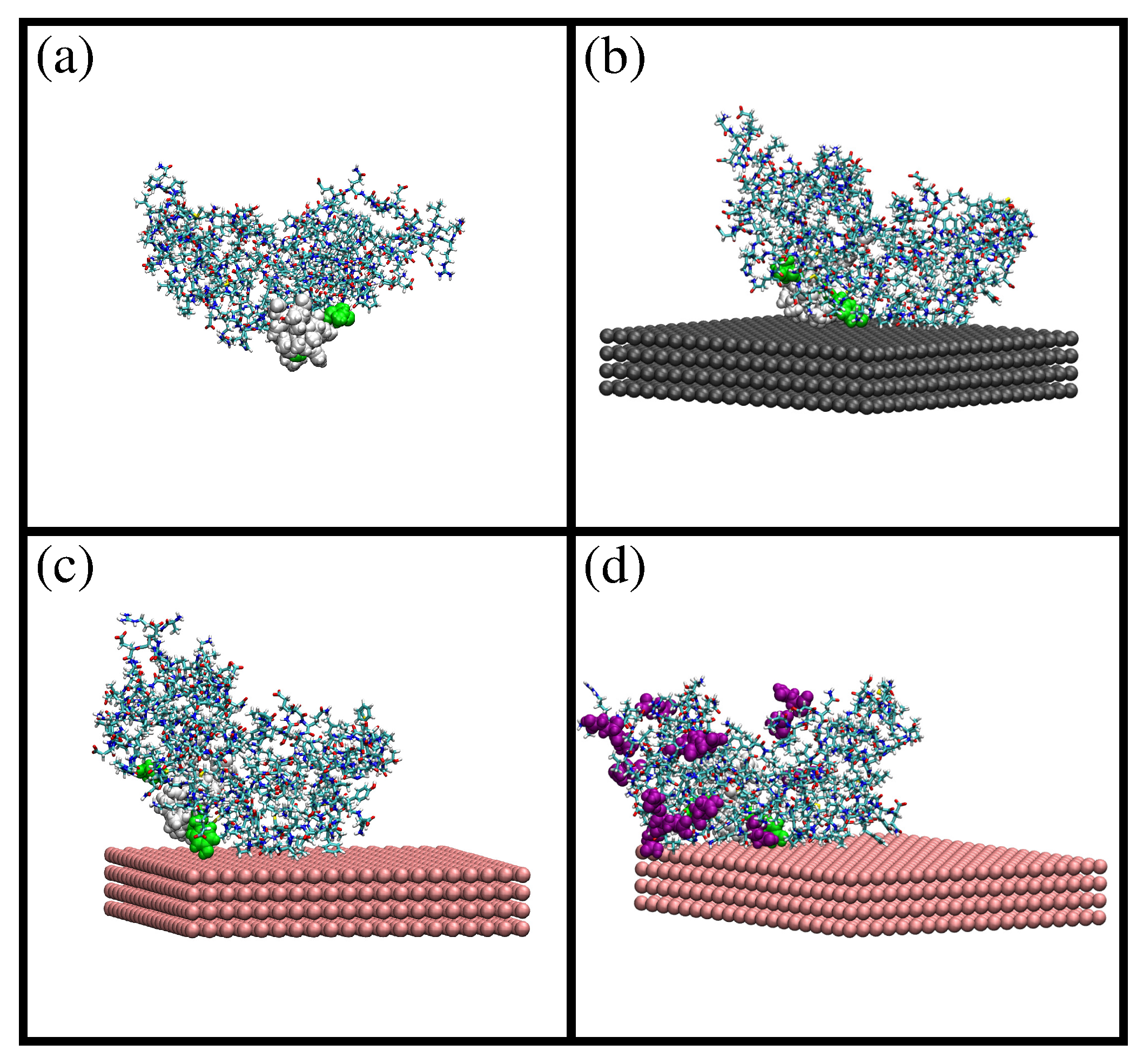
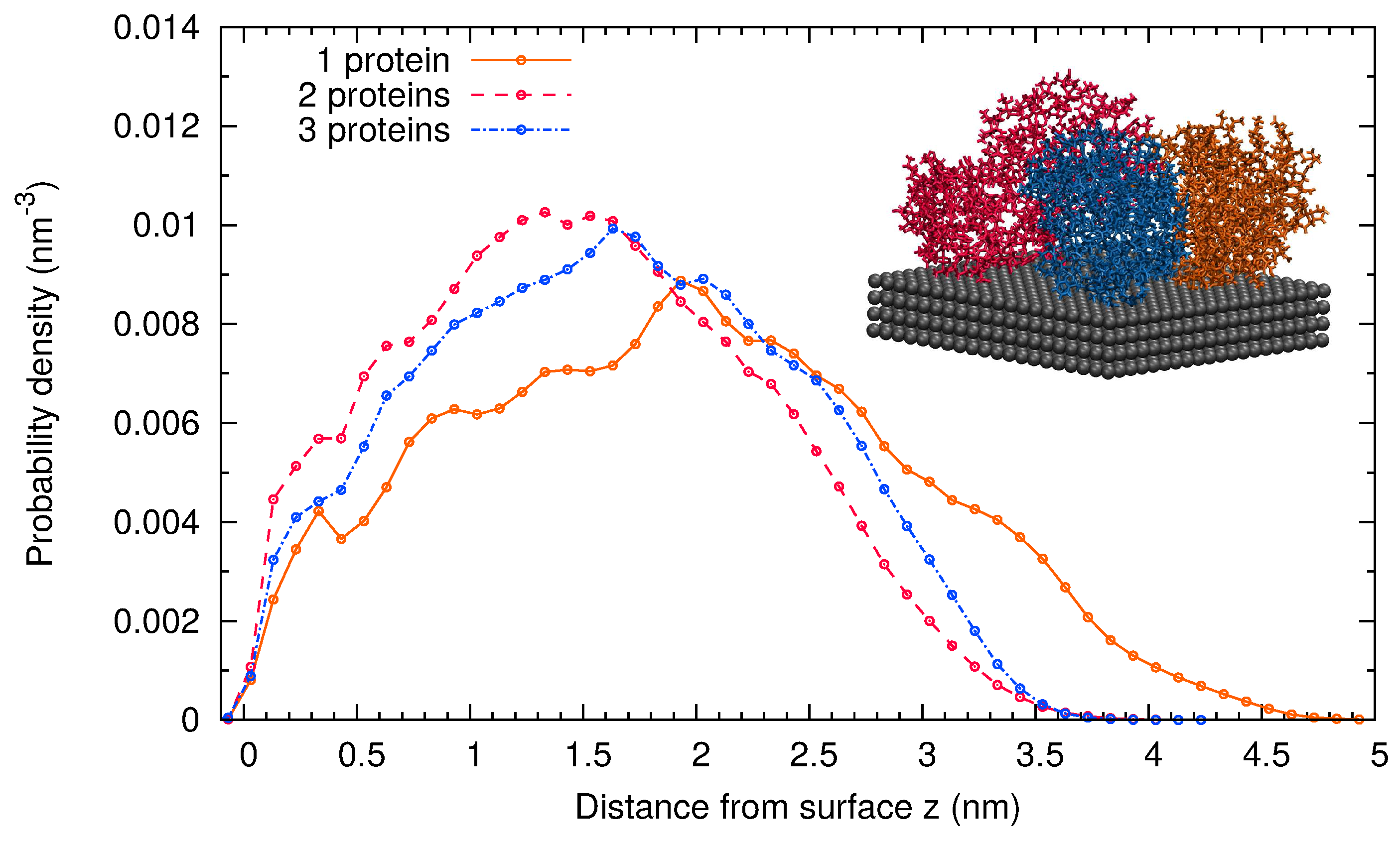
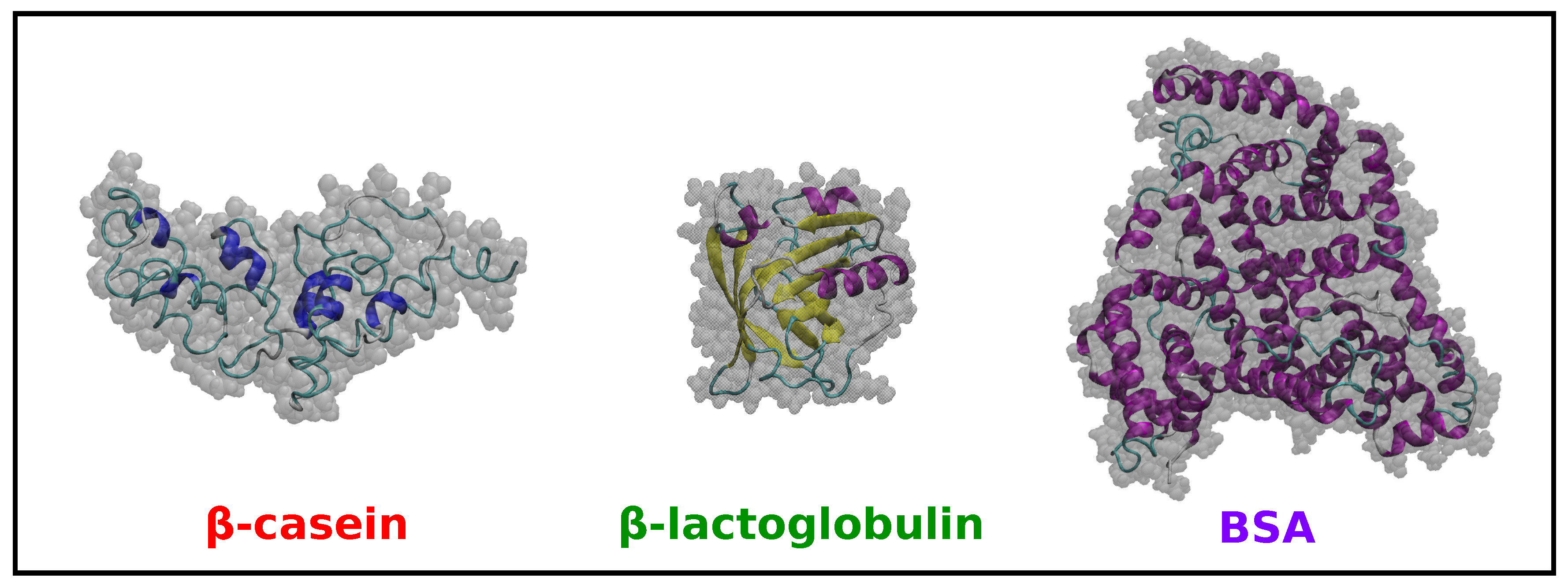
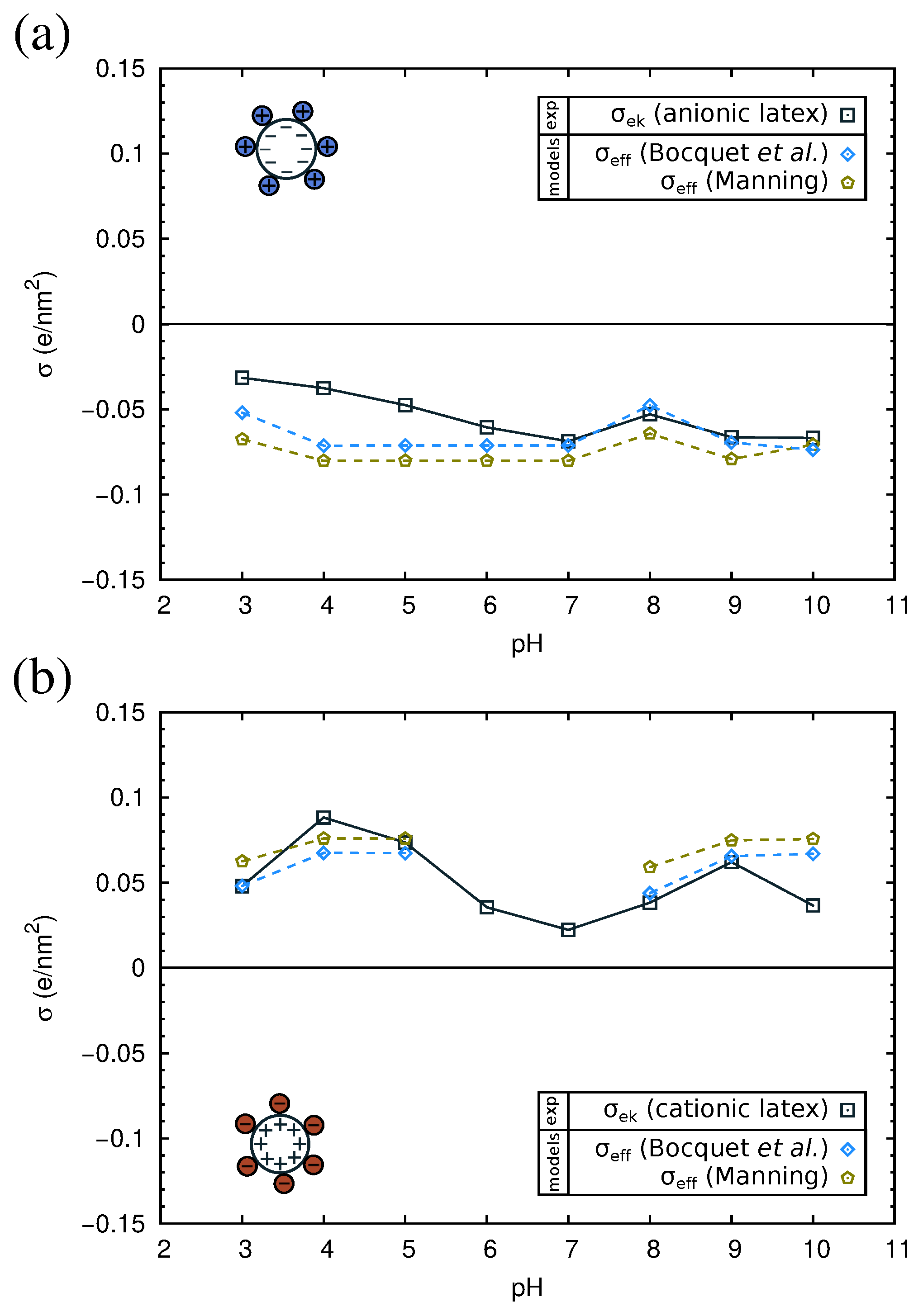
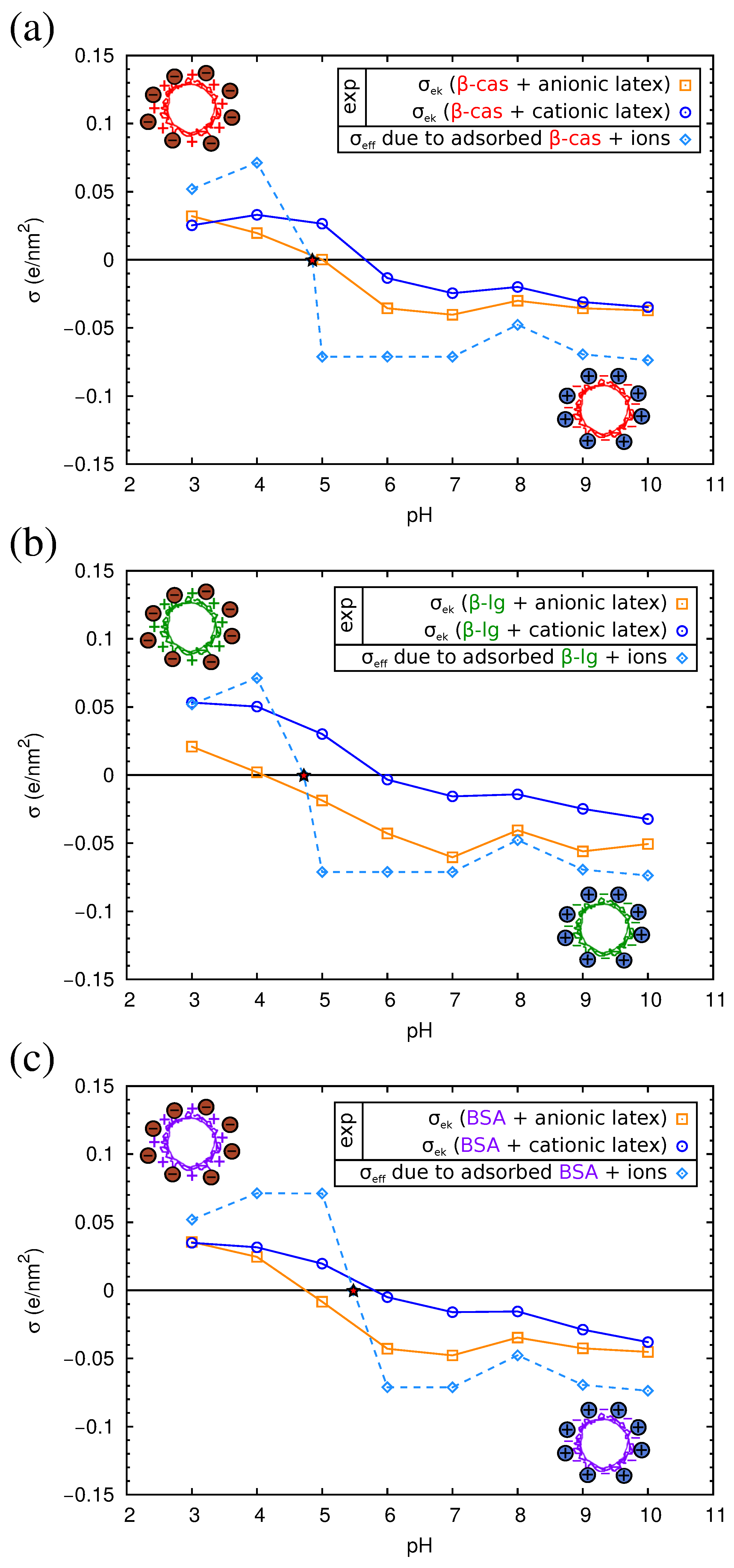
| Protein | Number of Amino Acids | RMSD (nm) | (nm2) | (nm2) | (nm) | (nm2) | (nm2) | (nm2) | S | pI (Sim) | pI (Exp) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| -cas | 195 | 1.0 | 118 | 124 | 2.73 | 3.2 | 3.0 | 1.3 | 6 × | −3 × | 4.9 | 4.6–5.1 |
| -lg | 162 | 0.3 | 87 | 96 | 2.14 | 1.6 | 1.5 | 1.4 | 8 × | −3 × | 4.7 | 5.1 |
| BSA | 582 | 0.4 | 284 | 317 | 3.86 | 6.4 | 4.7 | 3.9 | 2 × | +4 × | 5.5 | 5.3 |
| Protein Film | Isotherm (mg/m2) | Direct ads (mg/m2) | (nm2) | (nm) |
|---|---|---|---|---|
| PS--lg | 1.41 ± 0.03 | 2.1 ± 0.2 | 14.4 | ∼3 |
| PS-BSA | 1.88 ± 0.08 | 3.8 ± 0.4 | 29 | ∼5 |
| PS--cas | 3.7 ± 0.1 | 6.1 ± 0.7 | – | ∼7 |
| Protein | pI (Complex) Anionic Latex | pI (Complex) Cationic Latex | pI (Protein) Simulation | pI (Protein) Experimental |
|---|---|---|---|---|
| -cas | 4.9 | 5.7 | 4.9 | 4.6–5.1 |
| -lg | 4.1 | 6.0 | 4.7 | 5.1 |
| BSA | 4.8 | 5.9 | 5.5 | 5.3 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pérez-Fuentes, L.; Drummond, C.; Faraudo, J.; Bastos-González, D. Adsorption of Milk Proteins (β-Casein and β-Lactoglobulin) and BSA onto Hydrophobic Surfaces. Materials 2017, 10, 893. https://doi.org/10.3390/ma10080893
Pérez-Fuentes L, Drummond C, Faraudo J, Bastos-González D. Adsorption of Milk Proteins (β-Casein and β-Lactoglobulin) and BSA onto Hydrophobic Surfaces. Materials. 2017; 10(8):893. https://doi.org/10.3390/ma10080893
Chicago/Turabian StylePérez-Fuentes, Leonor, Carlos Drummond, Jordi Faraudo, and Delfi Bastos-González. 2017. "Adsorption of Milk Proteins (β-Casein and β-Lactoglobulin) and BSA onto Hydrophobic Surfaces" Materials 10, no. 8: 893. https://doi.org/10.3390/ma10080893
APA StylePérez-Fuentes, L., Drummond, C., Faraudo, J., & Bastos-González, D. (2017). Adsorption of Milk Proteins (β-Casein and β-Lactoglobulin) and BSA onto Hydrophobic Surfaces. Materials, 10(8), 893. https://doi.org/10.3390/ma10080893






