Abstract
Cation substitutional doping is an effective approach to modifying the electronic and thermal transports in Bi2Te3-based thermoelectric alloys. Here we present a comprehensive analysis of the electrical and thermal conductivities of polycrystalline Pb-doped p-type bulk Bi0.48Sb1.52Te3. Pb doping significantly increased the electrical conductivity up to ~2700 S/cm at x = 0.02 in Bi0.48-xPbxSb1.52Te3 due to the increase in hole carrier concentration. Even though the total thermal conductivity increased as Pb was added, due to the increased hole carrier concentration, the thermal conductivity was reduced by 14–22% if the contribution of the increased hole carrier concentration was excluded. To further understand the origin of reduction in the thermal conductivity, we first estimated the contribution of bipolar conduction to thermal conductivity from a two-parabolic band model, which is an extension of the single parabolic band model. Thereafter, the contribution of additional point defect scattering caused by Pb substitution (Pb in the cation site) was analyzed using the Debye–Callaway model. We found that Pb doping significantly suppressed both the bipolar thermal conduction and lattice thermal conductivity simultaneously, while the bipolar contribution to the total thermal conductivity reduction increased at high temperatures. At Pb doping of x = 0.02, the bipolar thermal conductivity decreased by ~30% from 0.47 W/mK to 0.33 W/mK at 480 K, which accounts for 70% of the total reduction.
1. Introduction
The thermoelectric (TE) effect offers the direct conversion of a temperature gradient into electrical energy, and vice-versa. Among the many TE materials, (Bi,Sb)2(Te,Se)3-based alloys (p-type (Bi,Sb)2Te3 and n-type Bi2(Te,Se)3) have been intensively investigated because they exhibit the highest TE performance near room temperature [1,2]. However, current TE applications are limited due to low conversion efficiency, which is evaluated from a dimensionless TE figure of merit, zT = S2·σ·T/κ (S: Seebeck coefficient, σ: electrical conductivity, and κ: thermal conductivity) at a given absolute temperature (T). The zT value can be improved by reducing the κ and enhancing the S while maintaining the σ. Low κ maintains the temperature difference between the hot and cold sides of a material, and high S associates the high voltages generated at a certain temperature gradient.
zT can be enhanced by reducing the lattice thermal conductivity (κlatt) caused by interface phonon scattering in nanostructured materials, which effectively scatter low-frequency phonons. For example, Poudel et al. [1] reported a peak zT of 1.4 at 100 °C in nanograin composite Bi0.5Sb1.5Te3. Additionally, it has been recently found that dense dislocations formed at grain boundaries can intensify phonon scattering by the additional scattering of mid-frequency phonons [3]. Substitutional doping is another effective approach to reducing the κlatt by introducing point defects for phonon scattering, which target high-frequency phonons. It has been experimentally found that certain elements, such as Al, Ga, In, Cu, Ag, and Fe, reduce κlatt effectively [4,5,6,7,8]. However, the substitutional doping approach is inherently accompanied with the modification of electronic structure, resulting in the variation of power factor (σ·S2) and bipolar conduction.
We have recently demonstrated that the substitutional doping of Pb in Bi0.48Sb1.52Te3 can reduce κlatt and increase power factor (σ·S2) [9]. In this study, the TE transport properties, including S, σ, and κlatt of Pb-doped Bi0.48Sb1.52Te3 polycrystalline samples, were further analyzed by using the single parabolic band (SPB) model [10] and Callaway model [11], and compared with a Bi0.48Sb1.52Te3 polycrystalline sample in order to closely examine the effect of Pb substitution on bipolar conduction and κlatt reduction. The S and σ were fitted to experimental values by adjusting the deformation potentials and the effective masses of both the conduction and valence bands by the two-parabolic band model based on the SPB model. Through this model, the bipolar conduction (κbp) was estimated, while the κlatt was analyzed using the Callaway model.
2. Results and Discussion
The temperature dependence of σ and S of the Pb-doped samples (Bi0.48-xPbxSb1.52Te3, x = 0.0025, 0.005, 0.01, 0.015, and 0.02) and undoped Bi0.48Sb1.52Te3 (x = 0) is shown in Figure 1. The value of σ of Bi0.48Sb1.52Te3 at 300 K is about 640 S/cm, which increased significantly to 2700 S/cm (x = 0.02) with an increase in Pb content. The hole concentrations (Np) at 300 K were 2.47, 3.54, 4.96, 6.60, 8.76, and 11.96 × 1019/cm3 for x = 0, 0.0025, 0.005, 0.01, 0.015, and 0.02, respectively. Therefore, the substitution of Pb for Sb induces significant hole carriers by the introduction of acceptor defects. The value of S decreased from 215 μV/K to 117 μV/K, revealing a clear trade-off relationship with the σ value. It is noteworthy that while the maximum value of S is obtained at 360 K for x = 0, it shifts to a higher temperature of 480 K for x = 0.02; this implies that the charge compensation from bipolar conduction is reduced due to the significant increase in Np as Pb is added.
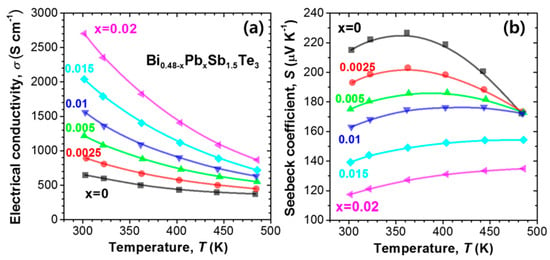
Figure 1.
Temperature dependence of (a) electrical conductivity (σ) and (b) Seebeck coefficient (S) for Bi0.48-xPbxSb1.52Te3 (x = 0, 0.0025, 0.005, 0.01, 0.015, and 0.02). The σ and S data were taken from Reference [9].
Figure 2 shows the temperature dependence of κtot and (κtot-κelec) of the Pb-doped samples (Bi0.48-xPbxSb1.52Te3, x = 0.0025, 0.005, 0.01, 0.015, and 0.02) and undoped Bi0.48Sb1.52Te3 (Bi0.48-xPbxSb1.52Te3, x = 0), where κtot is the measured total thermal conductivity and κelec is the electronic thermal conductivity without considering the bipolar conduction. Thus, (κtot-κelec) is the thermal conductivity excluding the contribution of the increased Np. The κelec was estimated using the Wiedemann–Franz law, and the Lorenz number was calculated using Equation (1) [12] which is deduced under the assumption of a single parabolic band (plus acoustic phonon scattering),
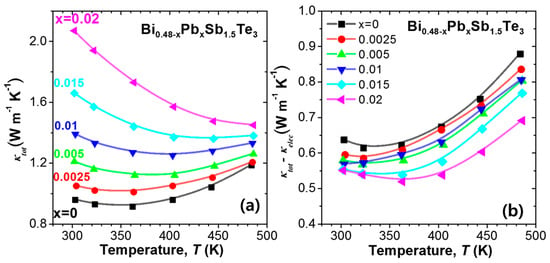
Figure 2.
Temperature dependence of (a) total thermal conductivity (κtot) and (b) (κtot-κelec) for Bi0.48-xPbxSb1.52Te3 (x = 0, 0.0025, 0.005, 0.01, 0.015, and 0.02). The κtot data are taken from [9].
Indeed, the κtot increased with Pb content due to a significantly enhanced Np value (Figure 2a). As seen in Figure 2b, the (κtot-κelec) value decreased by over 14% to 0.55 W/mK for x = 0.02, as compared to 0.64 W/mK of the undoped sample at 300 K. Furthermore, the amount of reduction in the (κtot-κelec) value increased with increasing temperature and reduced up to 22% for x = 0.02 at 480 K. For x = 0.02, which is only a 1% substitution for the cation site, a significant reduction of 14–22% in (κtot-κelec) was achieved.
Figure 3a shows the temperature dependence of power factor, which shows ~40% increase to 4.11 mW/mK2 for x = 0.01 from 2.97 mW/mK2 for x = 0. The Np value of 4.96 × 1019/cm3 at x = 0.01 seems to be the optimum value for the highest power factor. For x = 0.015 and 0.02, the power factor decreased due to a significant reduction in the S value. Figure 3b,c exhibit zT values of the samples. The zT values at temperatures above 400 K increased as the substitution increased to x = 0.01, as shown in the inset of Figure 3b. For x = 0.02, the zT value reduced up to 440 K due to a significant increase in the σ value, which results in a significant rise in κtot. The optimal σ range is 700–1200 S/cm for a high zT in this case.
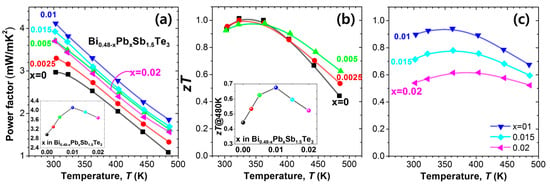
Figure 3.
(a) Temperature dependence of power factor (σS2) for Bi0.48-xPbxSb1.52Te3 (x = 0, 0.0025, 0.005, 0.01, 0.015, and 0.02). Inset shows the power factor value at 300 K for the samples; (b,c) Temperature dependence of a dimensionless figure of merit, zT, for Bi0.48-xPbxSb1.52Te3 for (b) x = 0, 0.0025, and 0.005 and (c) x = 0.01, 0.015, and 0.02. Inset in (b) shows the zT value at 480 K. The power factor and zT data are taken from [9].
Pb substitutional doping significantly increases σ due to an increase in Np and reduces the (κtot-κelec) value, which includes the bipolar thermal conductivity (κbp) and lattice thermal conductivity (κlatt). In order to further understand the origin of (κtot-κelec) reduction, we first estimated the κbp from a two parabolic band model, which is an extension of the SPB model that considers acoustic phonon scattering. Thereafter, the contribution of additional point defect scattering to κlatt was closely analyzed using the Debye–Callaway model and compared with the point defect contribution from its native cation disorder. The Pb substitutes are additional point defects in the native cation disorder of (Bi0.48Sb1.52) in their mother compound Bi0.48Sb1.52Te3.
In the two-band model, the thermoelectric parameters of valence and conduction bands computed from the Boltzmann transport equations [10] can be substituted into Equations (2)–(5),
Here, σi, Si, and RHi in Equations (2)–(5) are the electrical conductivity, Seebeck coefficient, and Hall coefficient of an individual band, respectively. The parameters with subscript “total” include contributions from all the participating bands (these variables can be measured directly). Equation (5) describes the contribution of κelec, κlatt, and κbp to the κtot. In order to estimate κbp, the calculated σtotal and Stotal of one sample were fitted to the experimental σ and S of the sample by adjusting the deformation potentials and density-of-states (DOS) effective masses (m*) of its valence and conduction bands (Table 1). Since it is nontrivial to extract a single band’s contribution to TE transport (band parameters) experimentally, we estimated each band’s contribution via modelling. For this purpose, we referred to the values of m* and the mobility of Bi2Te3 reported in literature. For example, the m* of holes (or electrons) in Bi2Te3 reported in the literature can elucidate the band structure of Bi0.48Sb1.52Te3 when two bands (valence and conduction) are assumed to participate in the transport. Due to the high crystal symmetry of BixSb2-xTe3, more than one pocket of Fermi surface contributes to m* as m* = NV2/3mb*, where NV and mb* are the valley (pocket) degeneracy and band mass of a single valley, respectively. The NV of the highest valence band of BixSb2-xTe3 is 6, while that of the lowest conduction band is 2, as listed in Table 1 [13]. Similarly, the mobility of holes and electrons in Bi2Te3 reported in the literature along with m* can help us estimate reasonable deformation potentials. Moreover, RHi was calculated from the measured Hall carrier concentration (=1/(e RHtotal)) and other band parameters computed above (deformation potential and m*). The Fermi level of each band obtained from RHi was used to crosscheck that it calculated from Si. Because the band gap between the valence and conduction bands are given, we only needed to calculate the Fermi level of either band.

Table 1.
Band parameters used to estimate the bipolar contribution to thermal conductivity, κbp, of the Pb-doped samples using the two-band model.
The estimated κbp is plotted in Figure 4a,b. In Figure 4b, the plot of ln(κbp) vs. (1/T) reveals that the bipolar conduction increases exponentially with temperature. It is clearly seen that the estimated κbp decreases systematically with Pb doping, as inferred from Figure 1a and Figure 2. The inset in Figure 4b shows that the κbp decreases by ~30% from 0.47 W/mK to 0.33 W/mK at 480 K for x = 0.02. The Pb doping of Bi0.48Sb1.52Te3 effectively suppresses the κbp by increasing the concentration of the major carrier (holes) and reducing the concentration of the minor carrier (electrons), which partly accounts for the reduced κlatt values at high temperatures in Pb-doped Bi0.48Sb1.52Te3.
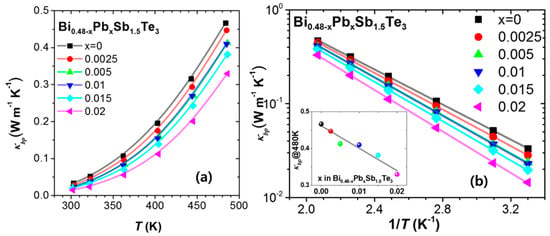
Figure 4.
(a) Temperature dependence of bipolar thermal conductivity, κbp, of Bi0.48-xPbxSb1.52Te3 (x = 0, 0.0025, 0.005, 0.01, 0.015, and 0.02) estimated from the two-parabolic band model [10]; (b) ln(κbp) vs. (1/T). Inset shows that the κbp at 480 K decreases as the Pb substitution increases.
The estimated κbp for each sample was added to the theoretical κlatt, which is calculated below, to compare with the experimentally determined κlatt. Heat flow (q) is defined as a product of thermal conductivity (κ) and temperature gradient (ΔT). The negative sign of the product (q = −κ ΔT) indicates that heat flows from hot to cold. κ can be expressed as arising from the heat capacity (CV), velocity (v), and distance between the collisions (l) according to the kinetic gas model presented in Equation (6).
The l in Equation (6) is a product of v and the relaxation time, τ. Here, κ can also be described in terms of CV, v, and τ (Equation (6)). By applying Equation (6) to the phonons in solids instead of gas particles, we obtain the Callaway equation for κlatt (Equation (7)).
Because each parameter is dependent on frequency (ω), the product of each parameter is integrated over the frequency. Here, vg refers to the phonon group velocity (vg = dω/dk). By treating the vg and phase velocity (vp = ω/k) as equivalent to the speed of sound, v, Equation (7) can be written as Equation (8) (Debye–Callaway model).
where kB, ћ, θ, and z are the Boltzmann constant, reduced Planck’s constant, Debye temperature θa, and ћω/kBT, respectively [11]. The values of Debye temperature θa (94 K) [14] and average phonon velocity (2147 m/s) [15] were obtained from experimental literature data. The κlatt of a material can be calculated using Equation (8) once its τtotal (z) is determined from the individual relaxation times (τi) for different scattering processes, according to Matthiessen’s rule (Equation (9)),
The parameter for relaxation times is associated with Umklapp scattering (τU), boundary scattering (τB), and point-defect scattering (τPD). Here, point-defect scattering arises from atomic disorders in alloys, and is described in terms of a scattering parameter (Г) within the τPD formula as:
and
In Equations (10) and (11), P is the fitting parameter and Г is a scattering parameter related to the difference in mass (ΔM) and lattice constant (Δa) between two constituents of an alloy. The parameters f, ΔM, G, , r, and Δa are the fractional concentration of either constituents, difference in mass, parameter representing a ratio of the fractional change of bulk modulus to that of local bond length, Grüneisen parameter, Poisson ratio, and the difference in lattice constant, respectively. The parameter (G) represents material dependent (ΔK/K) (R/ΔR), where ΔK and ΔR are the changes in bulk modulus and local bond length, respectively. We used the same parameters used in reference [16] for estimating the relaxation times for Umklapp scattering (τU) and boundary scattering (τB).
For estimating the relaxation time for point-defect scattering (τPD), we regard P and f (or ) in Equation (10) as adjustable parameters in the calculation; these parameters were fitted to experimental κlatt varying with f for the (Bi1-fSbf)2Te3 alloy by Stordeur and Sobotta [17] to model the κlatt of the undoped sample in Figure 2b with f = 0.48/2 = 0.24 (Bi fraction in the cation site). The P and were fitted to 28.19 × 10−41 s3 and 5.142 × 10−41 s3 and the result is represented as a black solid line in Figure 5. For the Pb-doped samples, the additional scattering due to Pb point defects was estimated with separated relaxation time for Pb disorder, τPD(Pb), using the fractional concentration of Pb in the cation site, which is fPb = x/2 (0.0013, 0.0025, 0.005, 0.0075, and 0.001 for x = 0.0025, 0.005, 0.01, 0.015, and 0.02, respectively). The fitting parameter for the scattering of Pb defects, PPb, is 208.8 × 10−41 s3, and thus, the values are 0.229, 0.521, 1.039, 1.553 and 2.067 × 10−41 s3 for x = 0.0025, 0.005, 0.01, 0.015, and 0.02, respectively (Table 2). The solid lines in Figure 5 exhibit the results of the calculation to which the estimated κbp was added. It is noteworthy that PPb is ~7.4 times higher than P for its native cation disorder. The effect of Pb substitution on κlatt reduction appears to be much greater than that of the native cation disorder between Bi and Sb. It seems that the interaction of disorders within the matrix, for example, bonding nature and structure, is important to the inducing of strong point-defect scattering, thus influencing the local vibration mode around the point defects.
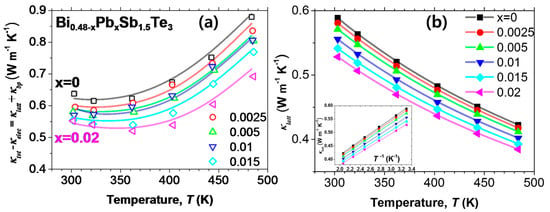
Figure 5.
(a) (κtot-κelec) values of the samples (Figure 2b) with fitted values (lines); (b) Calculated value (κlatt estimated by the Callaway model). The further 10% reduction is achieved by Pb doping (x = 0.02). Inset shows the linear relationship between κlatt and (1/T).

Table 2.
Point defect contributions to the total relaxation rate () used to model κlatt of the samples.
Although no meaningful enhancement in the maximum zT was observed since Pb doping induced excessive hole carriers, it was evident that Pb doping effectively suppressed both κlatt and κbp simultaneously. The bipolar contribution to the thermal conductivity decreased by ~30% from 0.47 W/mK to 0.33 W/mK at 480 K for x = 0.02, while the bipolar contribution to the reduction in total thermal conductivity increased at higher temperatures. At 480 K, the contribution of bipolar conduction suppression to thermal conductivity reduction increased up to 0.13 W/mK, which is 70% of the total reduction of 0.19 W/mK, due to Pb doping (x = 0.02). Therefore, the substitutional doping approach should be considered not only for the introduction of additional point defects for phonon scattering, but also for the suppression of bipolar conduction in BixSb1-xTe alloys, especially at high temperatures.
3. Materials and Methods
High-purity elemental Bi (99.999%, 5N Plus), Sb (99.999%, 5N Plus), Te (99.999%, 5N Plus), and Pb (99.999%, Sigma Aldrich, St. Louis, MO, USA) were used as starting materials. According to the formula, the mixed elements were loaded into a quartz tube and vacuum-sealed under 10−4 Torr. The stoichiometrically mixed elements were vacuum sealed and the contents were melted in a box furnace for 10 h at 1273 K, and then water quenched. The ingots were ground in a ball mill and consolidated by spark plasma sintering (SPS) using a graphite die (diameter = 10.4 mm) under a dynamic vacuum with the application of 50 MPa uniaxial pressure at 753 K. Room temperature Hall measurements were carried out in a constant magnetic field (1 T) and electric current (50 mA) using a Keithley 7065 system. The S and σ values were measured using a ZEM-3 system (M8, Advanced RIKO, Inc., Yokohama, Japan) in the temperature range from 300 K to 480 K. The κ values (κ = ρsCpλ) were calculated from separated measurements of sample density (ρs), heat capacity (Cp), and thermal diffusivity (λ). The Cp values obtained using a Quantum Design physical property measurement system were almost constant at ~0.187 J·g−1·K−1, and the λ values were collected by a laser-flash method (TC-9000, Advanced RIKO, Inc., Yokohama, Japan). The TE properties were measured perpendicular to the SPS press direction for polycrystalline Bi0.48Sb1.52Te3 and Pb-doped Bi0.48Sb1.52Te3 samples.
4. Conclusions
In this study, the electrical and thermal conductivities and Seebeck coefficient of a series of polycrystalline bulk Pb-doped p-type Bi0.48Sb1.52Te3 were comprehensively analyzed using the single parabolic band model and Debye–Callaway model, and compared with that of Bi0.48Sb1.52Te3 polycrystalline alloys to closely examine the effect of Pb substitution on bipolar conduction and lattice thermal conductivity. A two-band model based on the single parabolic band model showed that Pb doping effectively suppressed the bipolar thermal conduction. The bipolar contribution to thermal conductivity decreased by ~30% from 0.47 W/mK to 0.33 W/mK at 480 K for x = 0.02 in Bi0.48-xPbxSb1.52Te3. By using the Debye–Callaway model, it was found that the phonon scattering effect of Pb substitutes was much greater than the native alloy disorder in Bi0.48Sb1.52Te3. The interaction of disorders with the matrix, for example, bonding nature and structure, appeared to be important in inducing strong point-defect scattering. Therefore, we conclude that Pb doping is effective in suppressing both the bipolar thermal conduction and lattice thermal conductivity simultaneously in Bi0.48Sb1.52Te3 alloys. In addition, the bipolar contribution to thermal conductivity reduction increased at high temperatures in Pb doping. At 480 K, the contribution of bipolar conduction suppression to thermal conductivity reduction increased up to 0.13 W/mK, which is 70% of the total reduction of 0.19 W/mK, due to Pb doping (x = 0.02).
Acknowledgments
This study was supported by the 2016 Research Grant from Kangwon National University (No. 520160493) and the National Research Foundation of Korea Grant funded by the Korean Government (MSIP) (NRF-2015R1A5A1036133).
Author Contributions
Sang-il Kim and Sung Wng Kim organized the research and wrote the paper; Hyun-sik Kim and Kyu Hyoung Lee analyzed the data; Hyun-sik Kim and Kyu Hyoung Lee contributed equally to this work; Joonyeon Yoo, Jehun Youn, and Jong Wook Roh discussed the analysis and the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Poudel, B.; Hao, Q.; Ma, Y.; Lan, Y.; Minnich, A.; Yu, B.; Yan, X.; Wang, D.; Muto, A.; Vashaee, D.; et al. High-thermoelectric performance of nanostructured bismuth antimony telluride bulk alloys. Science 2008, 320, 634–638. [Google Scholar] [CrossRef] [PubMed]
- Snyder, G.; Toberer, E. Complex thermoelectric materials. Nat. Mater. 2008, 7, 105–114. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.I.; Lee, K.H.; Mun, H.A.; Kim, H.S.; Hwang, S.W.; Roh, J.W.; Yang, D.J.; Shin, W.H.; Li, X.S.; Lee, Y.H.; et al. Dense dislocation arrays embedded in grain boundaries for high-performance bulk thermoelectrics. Science 2015, 348, 109–114. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.H.; Hwang, S.; Ryu, B.; Ahn, K.; Roh, J.; Yang, D.; Lee, S.-M.; Kim, H.; Kim, S.-I. Enhancement of the thermoelectric performance of Bi0.4Sb1.6Te3 alloys by In and Ga doping. J. Electron. Mater. 2013, 42, 1617–1621. [Google Scholar] [CrossRef]
- Cui, J.L.; Xiu, W.J.; Xue, H.F. Preparation and thermoelectric properties of p-type (Ga2Te3)x–(Bi0.5Sb1.5Te3)1−x (x = 0–0.2) alloys prepared by spark plasma sintering. Intermetallics 2007, 15, 1466–1470. [Google Scholar] [CrossRef]
- Cui, J.L.; Xiu, W.J.; Xue, H.F. High thermoelectric properties of p-type pseudobinary (Cu4Te3)x-(Bi0.5Sb1.5Te3)1-x alloys prepared by spark plasma sintering. J. Appl. Phys. 2007, 101. [Google Scholar] [CrossRef]
- Lee, K.H.; Choi, S.M.; Roh, J.W.; Hwang, S.W.; Kim, S.I.; Shin, W.H.; Park, H.J.; Lee, J.H.; Kim, S.W.; Yang, D.J. Enhanced thermoelectric performance of p-type Bi–Sb–Te alloys by codoping with Ga and Ag. J. Electron. Mater. 2015, 44, 1531–1535. [Google Scholar] [CrossRef]
- Mun, H.; Lee, K.H.; Kim, S.J.; Kim, J.-Y.; Lee, J.H.; Lim, J.-H.; Park, H.J.; Roh, J.W.; Kim, S.W. Fe-doping effect on thermoelectric properties of p-type Bi0.48Sb1.52Te3. Materials 2015, 8, 959–965. [Google Scholar] [CrossRef]
- Moon, S.P.; Kim, T.W.; Kim, S.W.; Jeon, W.M.; Kim, J.H.; Kim, J.H.; Lee, K.H. Effect of Pb Doping on the Thermoelectric Properties of Bi0.48Sb1.52Te3. J. Korean Inst. Electr. Electron. Mater. Eng. 2017, in press. [Google Scholar]
- May, A.F.; Snyder, G.J. Materials, Preparation, and Characterization in Thermoelectric; CRC Press: Boca Raton, FL, USA, 2012; pp. 1–18. [Google Scholar]
- Callaway, J. Model for lattice thermal conductivity at low temperatures. Phys. Rev. 1959, 113, 1046–1051. [Google Scholar] [CrossRef]
- Kim, H.S.; Gibbs, Z.M.; Tang, Y.; Wang, H.; Snyder, G.J. Characterization of Lorenz number with Seebeck coefficient. APL Mater. 2015, 3, 041506. [Google Scholar] [CrossRef]
- Larson, P. Effect of p1/2 correction in the electronic structure of Bi2Te3 compounds. Phys. Rev. B 2003, 68. [Google Scholar] [CrossRef]
- Bessas, D.; Sergueev, I.; Wille, H.C.; Perßon, J.; Ebling, D.; Hermann, R.P. Lattice dynamics in Bi2Te3 and Sb2Te3: Te and Sb density of phonon states. Phys. Rev. B 2012, 86. [Google Scholar] [CrossRef]
- Yang, F.; Ikeda, T.; Snyder, G.J.; Dames, C. Effective thermal conductivity of polycrystalline materials with randomly oriented superlattice grains. J. Appl. Phys. 2010, 108. [Google Scholar] [CrossRef]
- Kim, H.-S.; Kim, S.I.; Lee, K.H.; Kim, S.W.; Snyder, G.J. Phonon scattering by dislocations at grain boundaries in polycrystalline Bi0.5Sb1.5Te3. Phys. Status Solidi B 2016, 254. [Google Scholar] [CrossRef]
- Stordeur, M.; Sobotta, H. Valence band structure and thermoelectric figure of merit of (Bi1-xSbx)2Te3. In First European Conference on Thermoelectrics (IEE Materials and Devices Series 7); Peregrinus Ltd.: London, UK, 1988; pp. 209–212. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).