An Ab Initio and Kinetic Monte Carlo Simulation Study of Lithium Ion Diffusion on Graphene
Abstract
:1. Introduction
2. Methods
3. Results of DFT and KMC Calculations
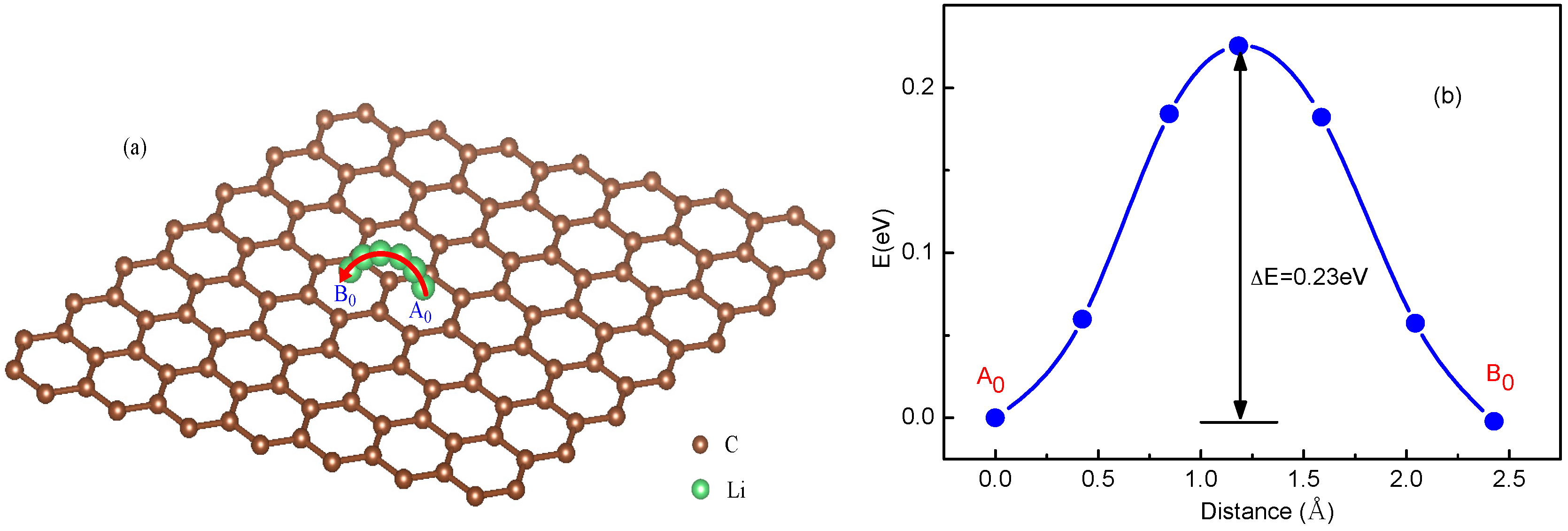
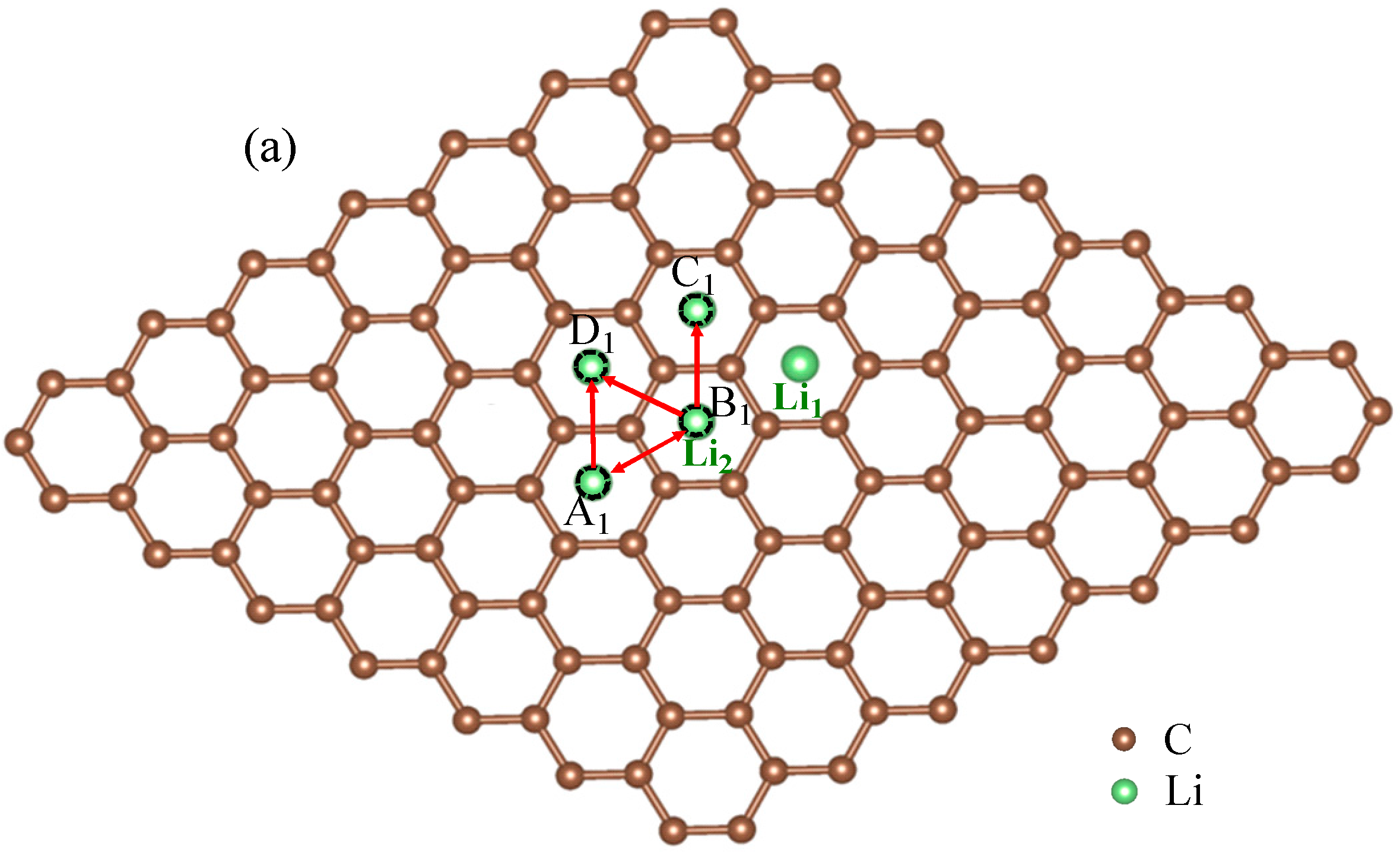
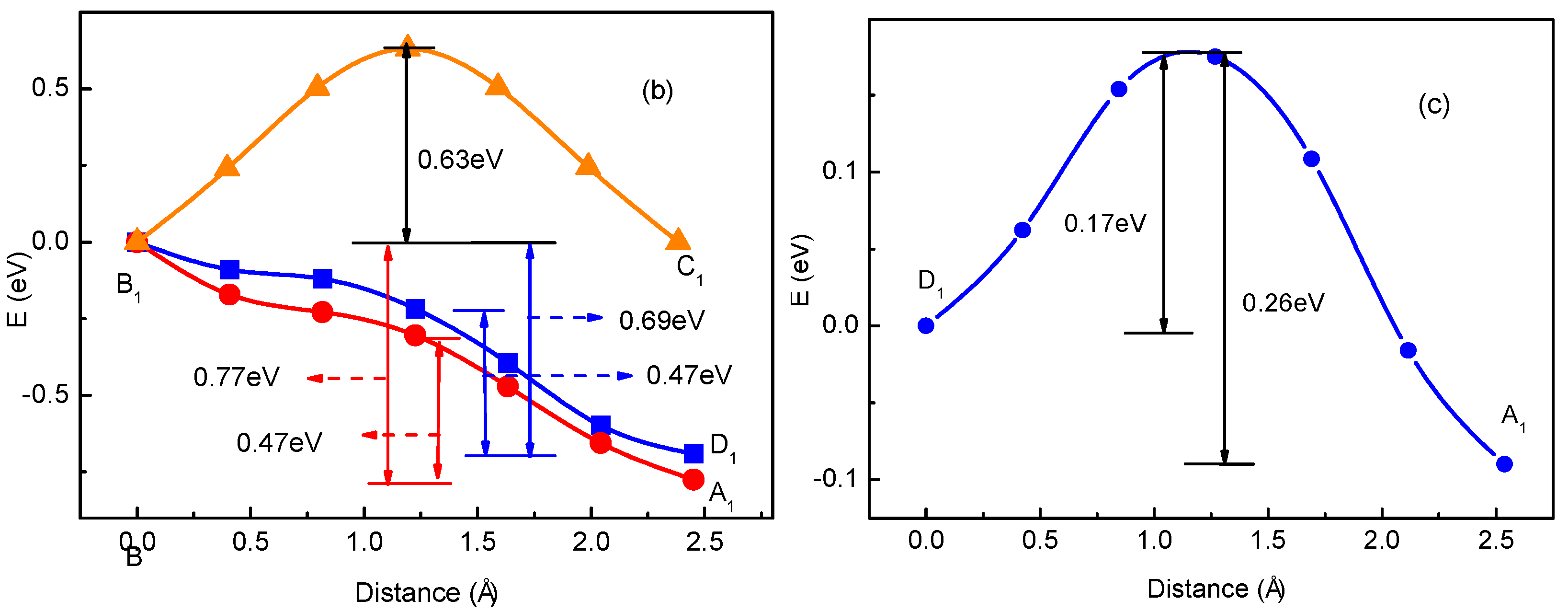
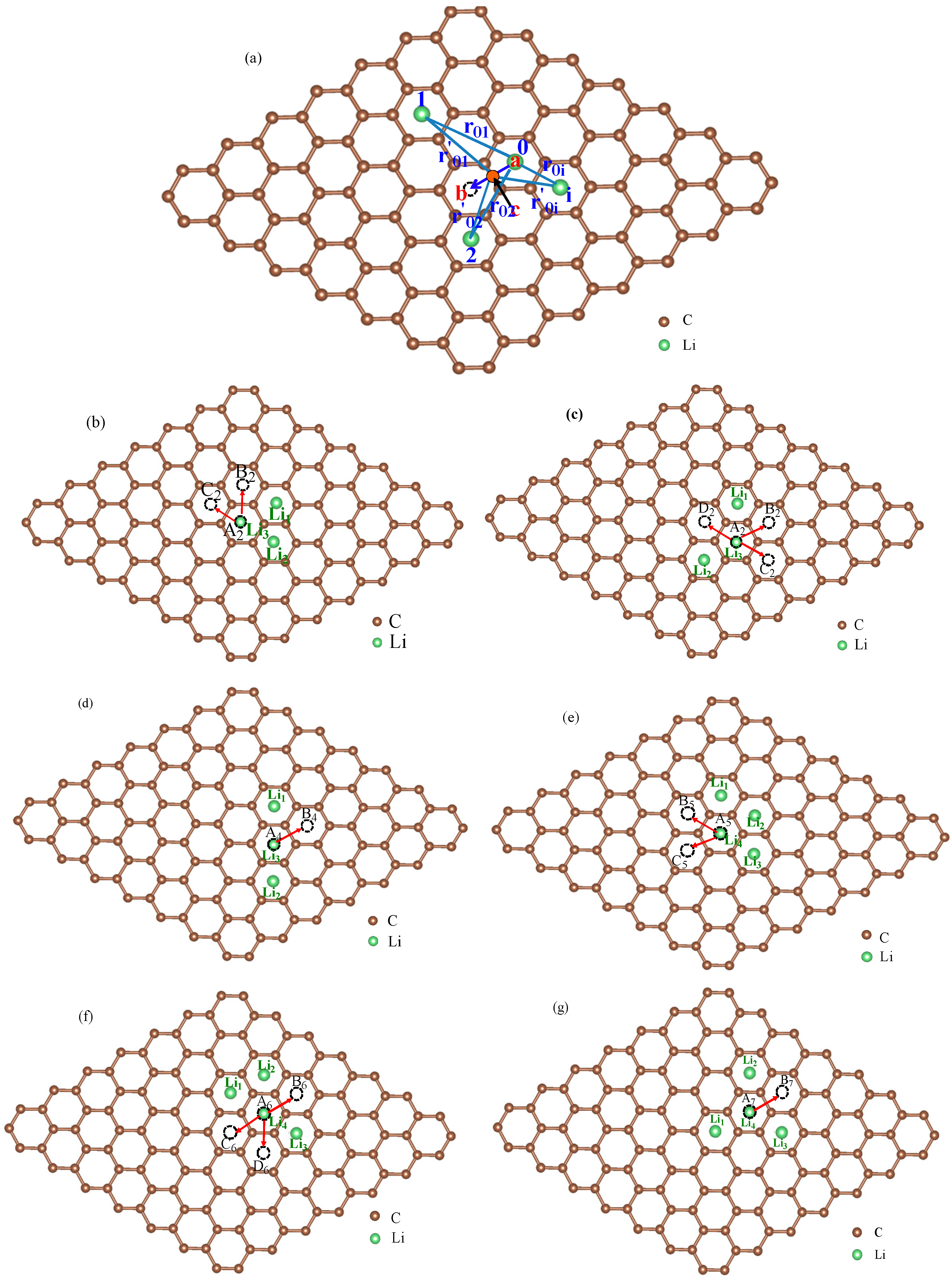
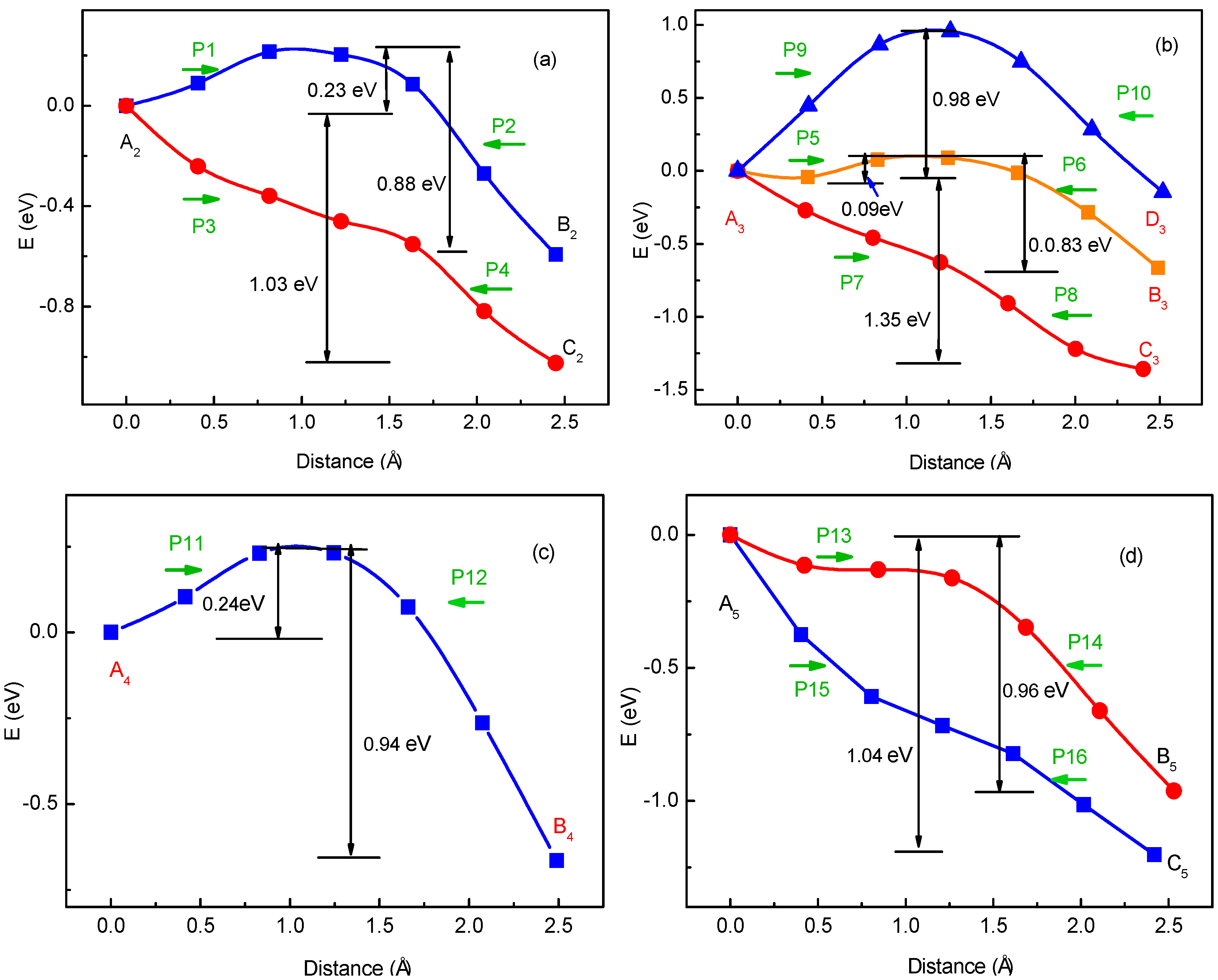
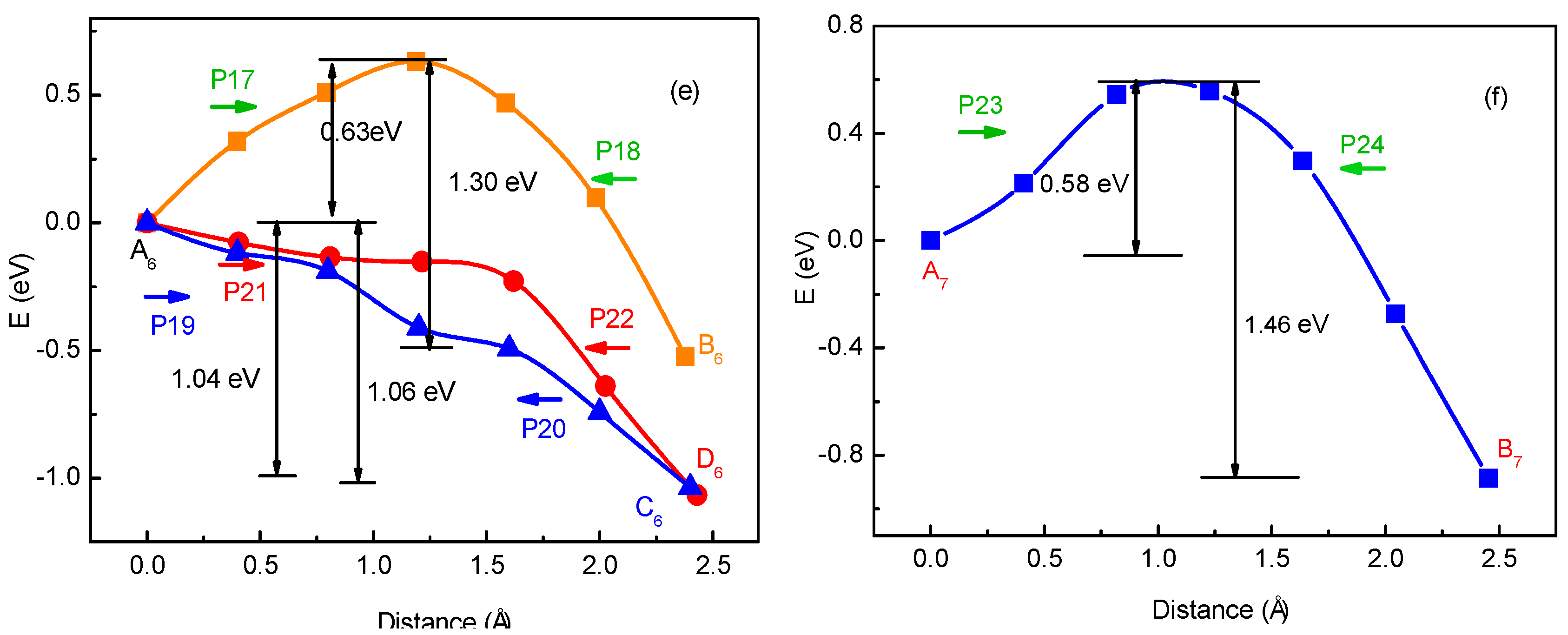
3.1. Migration Energy Barrier in Single-Li+ and Two-Li+ Adsorbed Graphene Systems
3.2. Method for Energy Barrier Estimation
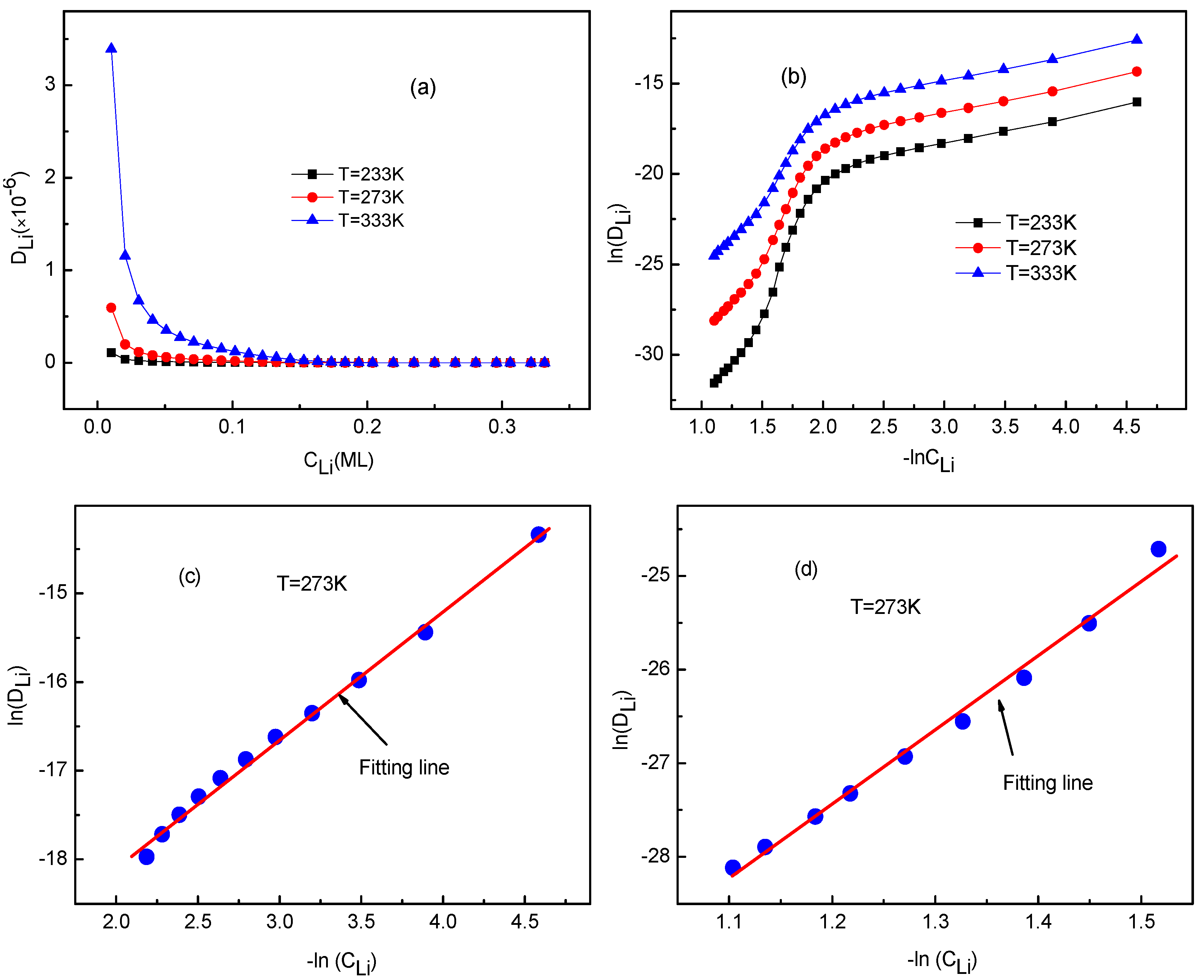
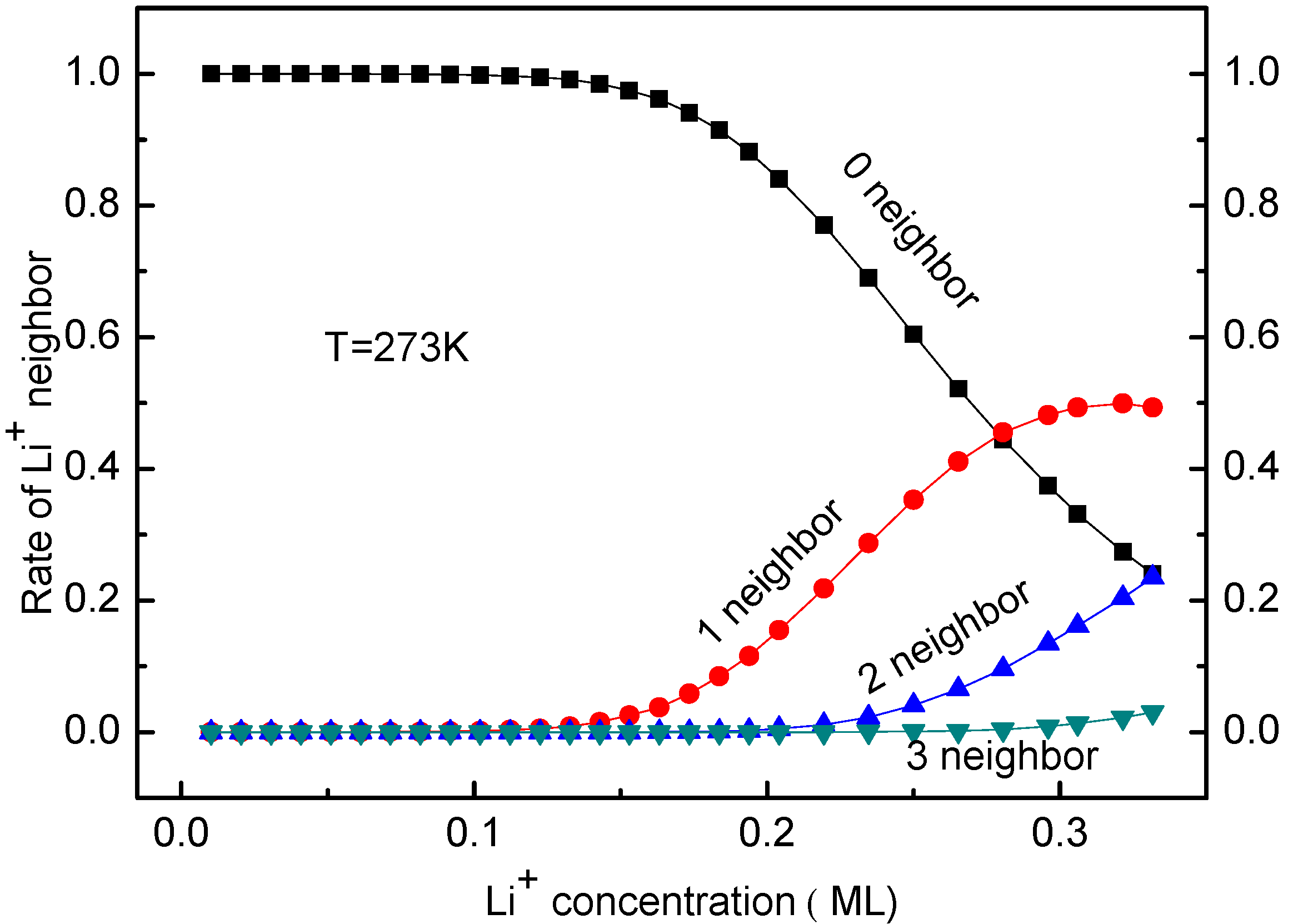
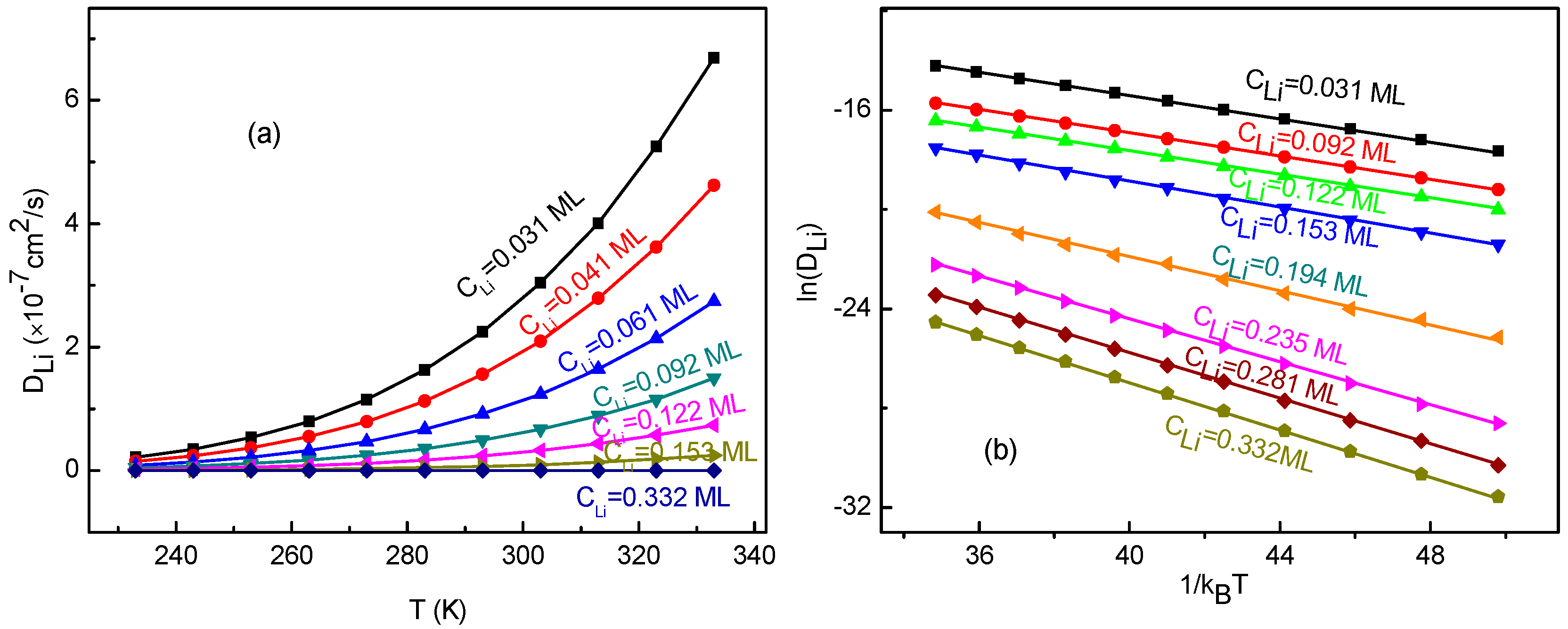
3.3. Concentration Effects on Li+ Diffusion Coefficient
3.4. Temperature Effects on Li+ Diffusion Coefficient
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Castro Neto, A.; Guinea, F.; Peres, N.; Novoselov, K.; Geim, A. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef]
- Geim, A.K. Graphene: Status and prospects. Science 2009, 324, 1530–1534. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless dirac fermions in graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Tan, J.W.; Stormer, H.L.; Kim, P. Experimental observation of quantum hall effect and berry’s phase in graphene. Nature 2005, 438, 201–204. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Lv, W.; Tang, D.-M.; He, Y.-B.; You, C.-H.; Shi, Z.-Q.; Chen, X.-C.; Chen, C.-M.; Hou, P.-X.; Liu, C.; Yang, Q.-H. Low-temperature exfoliated graphenes: Vacuum-promoted exfoliation and electrochemical energy storage. ACS Nano 2009, 3, 3730–3736. [Google Scholar] [CrossRef] [PubMed]
- Yoo, E.; Kim, J.; Hosono, E.; Zhou, H.-S.; Kudo, T.; Honma, I. Large reversible Li storage of graphene nanosheet families for use in rechargeable lithium ion batteries. Nano. Lett. 2008, 8, 2277–2282. [Google Scholar] [CrossRef] [PubMed]
- Jang, B.Z.; Liu, C.; Neff, D.; Yu, Z.; Wang, M.C.; Xiong, W.; Zhamu, A. Graphene surface-enabled lithium ion-exchanging cells: Next-generation high-power energy storage devices. Nano. Lett. 2011, 11, 3785–3791. [Google Scholar] [CrossRef] [PubMed]
- Lee, E.; Persson, K.A. Li Absorption and intercalation in single layer graphene and few layer graphene by First Principles. Nano. Lett. 2012, 12, 4624–4628. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Shen, X.; Yao, J.; Park, J. Graphene nanosheets for enhanced lithium storage in lithium ion batteries. Carbon 2009, 47, 2049–2053. [Google Scholar] [CrossRef]
- Atabaki, M.M.; Kovacevic, R. Graphene composites as anode materials in lithium-ion batteries. Electron. Mater. Lett. 2013, 2, 133–153. [Google Scholar] [CrossRef]
- Su, C.; Bu, X.; Xu, L.; Liu, J.; Zhang, C. A novel LiFePO4/graphene/carbon composite as a performance-improved cathode material for lithium-ion batteries. Electrochim. Acta 2012, 64, 190–195. [Google Scholar] [CrossRef]
- Park, M.; Zhang, X.; Chung, M.; Less, G.B.; Sastry, A.M. A review of conduction phenomena in Li-ion batteries. J. Power Sources 2010, 195, 7904–7929. [Google Scholar] [CrossRef]
- Dokko, K.; Mohamedi, M.; Fujita, Y.; Itoh, T.; Nishizawa, M.; Umeda, M.I. Uchida kinetic characterization of single particles of LiCoO2 by AC impedance and potential step methods. J. Electrochem. Soc. 2001, 148, A422–A426. [Google Scholar] [CrossRef]
- Montoro, L.A.; Rosolen, J.M. The role of structural and electronic alterations on the lithium diffusion in LixCo0.5Ni0.5O2. Electrochim. Acta 2004, 49, 3243–3249. [Google Scholar] [CrossRef]
- Tang, A.; Wang, X.; Xu, G.; Zhou, Z.; Nie, H. Determination of the chemical diffusion coefficient of lithium in Li3V2(PO4)3. Mater. Lett. 2009, 63, 1439–1441. [Google Scholar] [CrossRef]
- Xia, H.; Lu, L.; Ceder, G. Li diffusion in LiCoO2 thin films prepared by pulsed laser deposition. J. Power Sources 2006, 159, 1422–1427. [Google Scholar] [CrossRef]
- Jang, Y., II; Neudecker, B.J.; Dudney, N.J. Lithium diffusion in LixCoO2 (0.45 < x < 0.7) intercalation cathodes. Electrochem. Solid-State Lett. 2001, 4, A74–A77. [Google Scholar]
- Tang, X.-C.; Li, L.-X.; Lai, Q.-L.; Song, X.-W.; Jiang, L.-H. Investigation on diffusion behavior of Li+ in LiFePO4 by capacity intermittent titration technique (CITT). Electrochim. Acta 2009, 54, 2329–2334. [Google Scholar] [CrossRef]
- Liu, G.Q.; Kuo, H.T.; Liu, R.S.; Shen, C.H.; Shy, D.S.; Xing, X.K.; Chen, J.M. Study of electrochemical properties of coating ZrO2 on LiCoO2. J. Alloys Compd. 2010, 496, 512–516. [Google Scholar] [CrossRef]
- Cao, Q.; Zhang, H.P.; Wang, G.J.; Xia, Q.; Wu, Y.P.; Wu, H.Q. A novel carbon-coated LiCoO2 as cathode material for lithium ion battery. Electrochem. Commun. 2007, 9, 1228–1232. [Google Scholar] [CrossRef]
- Zhu, Y.R.; Xie, Y.; Zhu, R.-S.; Shu, J.; Jiang, L.-J.; Qiao, H.-B.; Yi, T.-F. Kinetic study on LiFePO4-positive electrode material of lithium-ion battery. Ionics 2011, 17, 437–441. [Google Scholar] [CrossRef]
- Takami, N.; Satoh, A.; Hara, M.; Ohsaki, T. Structural and kinetic characterization of lithium intercalation into carbon anodes for secondary lithium batteries. J. Electrochem. Soc. 1995, 142, 371–379. [Google Scholar] [CrossRef]
- Yu, P.; Popov, B.N.; Ritter, J.A.; White, R.E. Determination of the lithium ion diffusion coefficient in graphite. J. Electrochem. Soc. 1999, 146, 8–14. [Google Scholar] [CrossRef]
- Umeda, M.; Dokko, K.; Fujita, Y.; Mohamedi, M.; Uchida, I.; Selman, J.R. Electrochemical impedance study of li-ion insertion into mesocarbon microbead single particle electrode. Part I. Graphitized carbon. Electrochim. Acta 2001, 47, 885–890. [Google Scholar] [CrossRef]
- Dokko, K.; Fujita, Y.; Mohamedi, M.; Umeda, M.; Uchida, I.; Selman, J.R. Electrochemical impedance study of Li-ion insertion into mesocarbon microbead single particle electrode: Part II. Disordered carbon. Electrochim. Acta 2001, 47, 933–938. [Google Scholar] [CrossRef]
- Shim, J.; Striebel, K.A. Electrochemical Characterization of thermally oxidized natural graphite anodes in Lithium-ion batteries. J. Power Sources 2007, 164, 862–867. [Google Scholar] [CrossRef]
- Levi, M.D.; Aurbach, D. The Mechanism of Lithium intercalation in graphite film electrodes in aprotic media. Part 1. High resolution slow scan rate cyclic voltammetric studies and modeling. J. Electroanal. Chem. 1997, 421, 79–88. [Google Scholar] [CrossRef]
- Verbrugge, M.W.; Koch, B.J. Electrochemical analysis of lithiated graphite anodes. J. Electrochem. Soc. 2003, 150, A374–A384. [Google Scholar] [CrossRef]
- Levi, M.D.; Markevich, E.; Aurbach, D. The effect of slow interfacial kinetics on the chronoamperometric response of composite lithiated graphite electrodes and on the calculation of the chemical diffusion coefficient of Li ions in graphite. J. Phys. Chem. B 2005, 109, 7420–7427. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Bang, H.J.; Prakash, J. Evaluation of electrochemical interface area and lithium diffusion coefficient for a composite graphite anode. J. Electrochem. Soc. 2004, 151, A1247–A1250. [Google Scholar] [CrossRef]
- Tachikawa, H. A direct molecular orbital-molecular dynamics study on the diffusion of the Li ion on a fluorinated graphene surface. J. Phys. Chem. C 2008, 112, 10193–10199. [Google Scholar] [CrossRef]
- Das, D.; Kim, S.; Lee, K.-R.; Singh, A.K. Li diffusion through doped and defected graphene. Phys. Chem. Chem. Phys. 2013, 15, 15128–15134. [Google Scholar] [CrossRef] [PubMed]
- Uthaisar, C.; Barone, V. Edge effects on the characteristics of Li diffusion in graphene. Nano. Lett. 2010, 10, 2838–2842. [Google Scholar] [CrossRef] [PubMed]
- Fan, X.; Zheng, W.T.; Kuo, J.-L. Adsorption and diffusion of Li on pristine and defective graphene. ACS Appl. Mater. Interfaces 2012, 4, 2432–2438. [Google Scholar] [CrossRef] [PubMed]
- Zheng, J.; Ren, Z.; Guo, P.; Fang, L.; Fan, J. Diffusion of Li+ ion on graphene: A DFT study. Applied Surf. Sci. 2011, 258, 1651–1655. [Google Scholar] [CrossRef]
- Petrova, N.V.; Yakovkin, I.N.; Ptushinskii, Yu.G. Monte-Carlo simulation of kinetics of H2 molecular adsorption. Surf. Sci. 2002, 497, 349–355. [Google Scholar] [CrossRef]
- Becquart, C.S.; Domain, C. An object kinetic Monte Carlo simulation of the dynamics of helium and point defects in tungsten. J. Nucl. Mater. 2009, 385, 223–227. [Google Scholar] [CrossRef]
- Du, Y.A.; Rogal, J.; Drautz, R. Diffusion of hydrogen within idealized grains of bcc Fe: A kinetic Monte Carlo study. Phys. Rev. B 2012, 86, 174110. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Xu, G.G.; Wu, Q.Y.; Chen, Z.G.; Huang, Z.G.; Wu, R.Q.; Feng, Y.P. Disorder and surface effects on work function of Ni-Pt metal gates. Phys. Rev. B 2008, 78, 115420. [Google Scholar] [CrossRef]
- Zhong, K.H.; Xu, G.G.; Cheng, Y.M.; Tang, K.Q.; Chen, Z.G.; Huang, Z.G. A novel spin modulation of work function for C adsorbed Cr/Fe(001) metal gate. AIP Adv. 2012, 2, 042134. [Google Scholar] [CrossRef]
- Zhong, K.H.; Xu, G.G.; Zhang, J.-M.; Huang, Z.G. Effects of strain on effective work function for Ni/HfO2 interfaces. J. Appl. Phys. 2014, 116, 063707. [Google Scholar] [CrossRef]
- Xu, G.G.; Wu, Q.Y.; Chen, Z.G.; Huang, Z.G.; Feng, Y.P. Effects of surface alloying and orientation on work function of MoTa metal gate. J. Appl. Phys. 2009, 106, 043708. [Google Scholar] [CrossRef]
- Zhang, J.-M.; Ming, W.; Huang, Z.G.; Liu, G.-B.; Kou, X.; Fan, Y.; Wang, K.L.; Yao, Y. Stability, electronic, and magnetic properties of the magnetically doped topological insulators Bi2Se3, Bi2Te3, and Sb2Te3. Phys. Rev. B 2013, 88, 235131. [Google Scholar] [CrossRef]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671–6687. [Google Scholar] [CrossRef]
- Sevinçli, H.; Topsakal, M.; Durgun, E.; Ciraci, S. Electronic and magnetic properties of 3D transition-metal atom adsorbed graphene and graphene nanoribbons. Phys. Rev. B 2008, 77, 195434. [Google Scholar] [CrossRef]
- Larsson, M.I.; Sabiryanov, R.F.; Cho, K.; Clemens, B.M. Nanopatterning of periodically strained surfaces: Predictive kinetic Monte Carlo simulation study. J. Appl. Phys. 2003, 94, 3470–3484. [Google Scholar] [CrossRef]
- Ramanarayanan, P.; Cho, K.; Clemens, B.M. Effect of composition on vacancy mediated diffusion in random binary alloys: First principles study of the Si1−xGex system. J. Appl. Phys. 2003, 94, 174–185. [Google Scholar] [CrossRef]
- Moon, J.; Lee, B.; Cho, M.; Cho, K. Ab initio and kinetic Monte Carlo simulation study of lithiation in crystalline and amorphous silicon. J. Power Sources 2014, 272, 1010–1017. [Google Scholar] [CrossRef]
- Yang, X.; Hassanein, A. Kinetic Monte Carlo simulation of hydrogen diffusion on tungsten reconstructed (001) surface. Fusion Eng. Des. 2014, 89, 2545–2549. [Google Scholar] [CrossRef]
- Takachi, M.; Fukuzumi, Y.; and Moritomo, Y. Concentration dependence of Li+/Na+ diffusion in manganese hexacyanoferrates. Jpn. J. Appl. Phys. 2016, 55, 067101. [Google Scholar] [CrossRef]
- Pollak, E.; Geng, B.; Jeon, K.J.; Lucas, I.T.; Richardson, T.J.; Wang, F.; Kostecki, R. The interaction of Li+ with single-layer and few-layer graphene. Nano. Lett. 2010, 10, 3386–3388. [Google Scholar] [CrossRef] [PubMed]
- Malyi, O.I.; Tan, T.L.; Manzhos, S. A comparative computational study of structures, diffusion, and dopant interactions between Li and Na insertion into Si. Appl. Phys. Express 2013, 6, 027301. [Google Scholar] [CrossRef]
- Fan, X.; Zheng, W.T.; Kuo, J.-L.; Singh, D.J. Adsorption of single Li and the formation of small Li clusters on graphene for the anode of lithium-ion batteries. ACS Appl. Mater. Interfaces 2013, 5, 7793–7797. [Google Scholar] [CrossRef] [PubMed]
- Persson, K.; Sethuraman, V.A.; Hardwick, L.J.; Hinuma, Y.; Meng, Y.S.; van der Ven, A.; Srinivasan, V.; Kostecki, R.; Ceder, G. Lithium diffusion in graphitic carbon. J. Phys. Chem. Letts. 2010, 1, 1176–1180. [Google Scholar] [CrossRef]
- Piao, T.; Park, S.M.; Doh, C.H.; Moonb, S.I. Intercalation of Lithium ions into graphite electrodes studied by AC impedance measurements. J. Electrochem. Soc. 1999, 146, 2794–2798. [Google Scholar] [CrossRef]
- Wu, S.L.; Zhang, W.; Song, X.Y.; Shukla, A.K.; Liu, G.; Battaglia, V.; Srinivasan, V. High rate capability of Li(Ni1/3Mn1/3Co1/3)O2 electrode for Li-ion batteries. J. Electrochem. Soc. 2012, 159, A438–A444. [Google Scholar] [CrossRef]
- Amina, R.; Chianga, Y.M. Characterization of electronic and ionic transport in Li1-xNi0.33Mn0.33Co0.33O2 (NMC333) and Li1-xNi0.50Mn0.20Co0.30O2 (NMC523) as a function of Li content. J. Electrochem. Soc. 2016, 163, A1512–A1517. [Google Scholar] [CrossRef]
- Chou, C.Y.; Hwang, G.S. On the origin of the significant difference in lithiation behavior between silicon and germanium. J. Power Sources 2014, 263, 252–258. [Google Scholar] [CrossRef]
- Yang, X.-Y.; Lu, Y.; Zhang, P. The temperature-dependent diffusion coefficient of helium in zirconium carbide studied with first-principles calculations. J. Appl. Phys. 2015, 117, 164903. [Google Scholar] [CrossRef]
- Bouar, Y.L.; Soisson, F. Kinetic pathways from embedded-atom-method potentials: Influence of the activation barriers. Phys. Rev. B 2002, 65, 094103. [Google Scholar] [CrossRef]

| Concentration CLi (ML) | Temperature T (K) | ||||||
|---|---|---|---|---|---|---|---|
| T = 233 | T = 243 | T = 253 | T = 263 | T = 273 | T = 283 | ||
| 0.01–0.11 | 1.46 ± 0.04 | 1.46 ± 0.0 | 1.45 ± 0.04 | 1.45 ± 0.03 | 1.44 ± 0.03 | 1.44 ± 0.03 | |
| r1 | 0.9936 | 0.9947 | 0.9942 | 0.9953 | 0.9949 | 0.9953 | |
| 0.21–0.33 | 8.94 ± 0.38 | 8.69 ± 0.35 | 8.34 ± 0.34 | 8.04 ± 0.30 | 7.95 ± 0.28 | 7.80 ± 0.25 | |
| r1 | 0.9859 | 0.9871 | 0.9866 | 0.9892 | 0.9899 | 0.9916 | |
| T = 293 | T = 303 | T = 313 | T = 323 | T = 333 | |||
| 0.01–0.11 | 1.43 ± 0.03 | 1.43 ± 0.03 | 1.44 ± 0.03 | 1.43 ± 0.03 | 1.42 ± 0.03 | ||
| r1 | 0.9956 | 0.9963 | 0.9957 | 0.9960 | 0.9961 | ||
| 0.16–0.33 | 7.58 ± 0.28 | 7.29 ± 0.28 | 7.16 ± 0.21 | 7.08 ± 0.20 | 6.88 ± 0.16 | ||
| r1 | 0.9886 | 0.9884 | 0.9915 | 0.99354 | 0.9954 | ||
| Concentration CLi (ML) | Slope (eV) | Correlation Coefficient r2 |
|---|---|---|
| 0.031 | −0.2295 ± 0.0003 | 0.9999 |
| 0.092 | −0.2332 ± 0.0004 | 0.9999 |
| 0.153 | −0.261 ± 0.002 | 0.9995 |
| 0.235 | −0.432 ± 0.002 | 0.9998 |
| 0.281 | −0.457 ± 0.001 | 0.9999 |
| 0.332 | −0.473 ± 0.001 | 0.9999 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, K.; Yang, Y.; Xu, G.; Zhang, J.-M.; Huang, Z. An Ab Initio and Kinetic Monte Carlo Simulation Study of Lithium Ion Diffusion on Graphene. Materials 2017, 10, 761. https://doi.org/10.3390/ma10070761
Zhong K, Yang Y, Xu G, Zhang J-M, Huang Z. An Ab Initio and Kinetic Monte Carlo Simulation Study of Lithium Ion Diffusion on Graphene. Materials. 2017; 10(7):761. https://doi.org/10.3390/ma10070761
Chicago/Turabian StyleZhong, Kehua, Yanmin Yang, Guigui Xu, Jian-Min Zhang, and Zhigao Huang. 2017. "An Ab Initio and Kinetic Monte Carlo Simulation Study of Lithium Ion Diffusion on Graphene" Materials 10, no. 7: 761. https://doi.org/10.3390/ma10070761
APA StyleZhong, K., Yang, Y., Xu, G., Zhang, J.-M., & Huang, Z. (2017). An Ab Initio and Kinetic Monte Carlo Simulation Study of Lithium Ion Diffusion on Graphene. Materials, 10(7), 761. https://doi.org/10.3390/ma10070761




