Crack Identification in CFRP Laminated Beams Using Multi-Resolution Modal Teager–Kaiser Energy under Noisy Environments
Abstract
:1. Introduction
2. Fundamental Theories
2.1. MRA
2.2. TKE Operator
3. MRM-TKE for Identifying Cracks in Beams under Noisy Environments
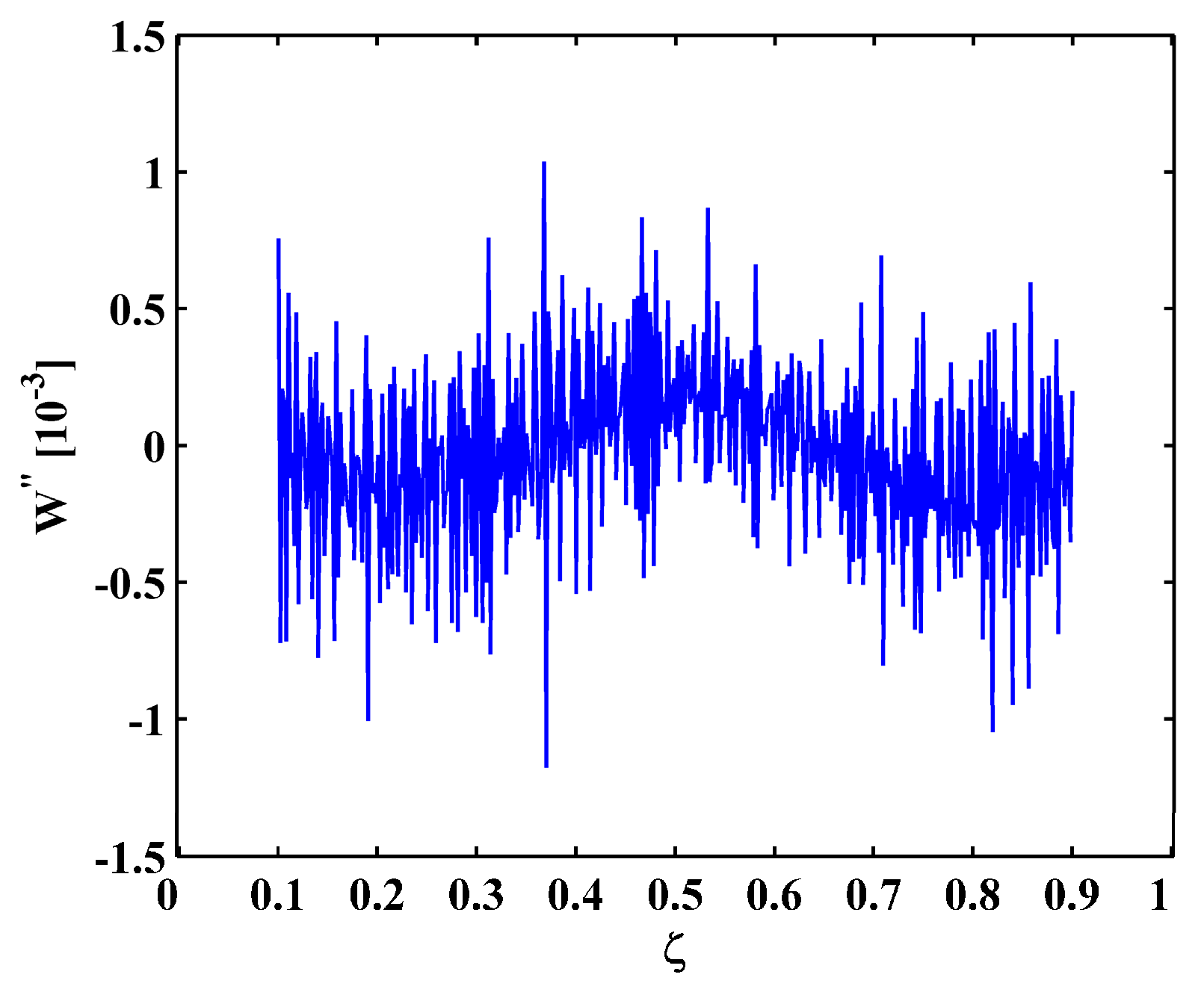
3.1. M-TKE
3.2. MRM-TKE
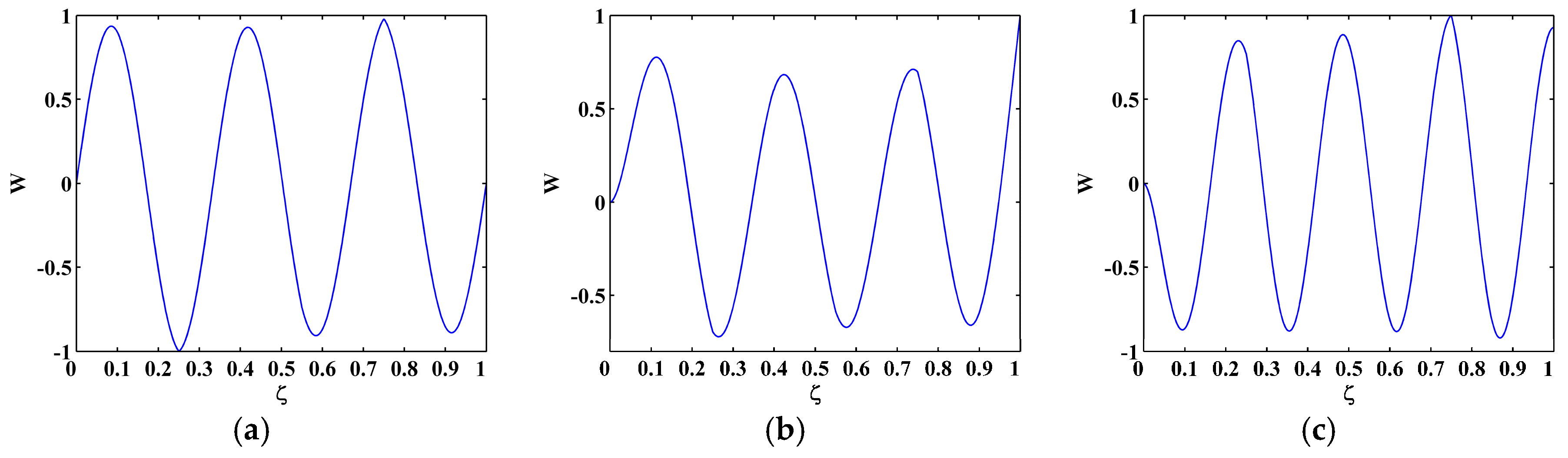
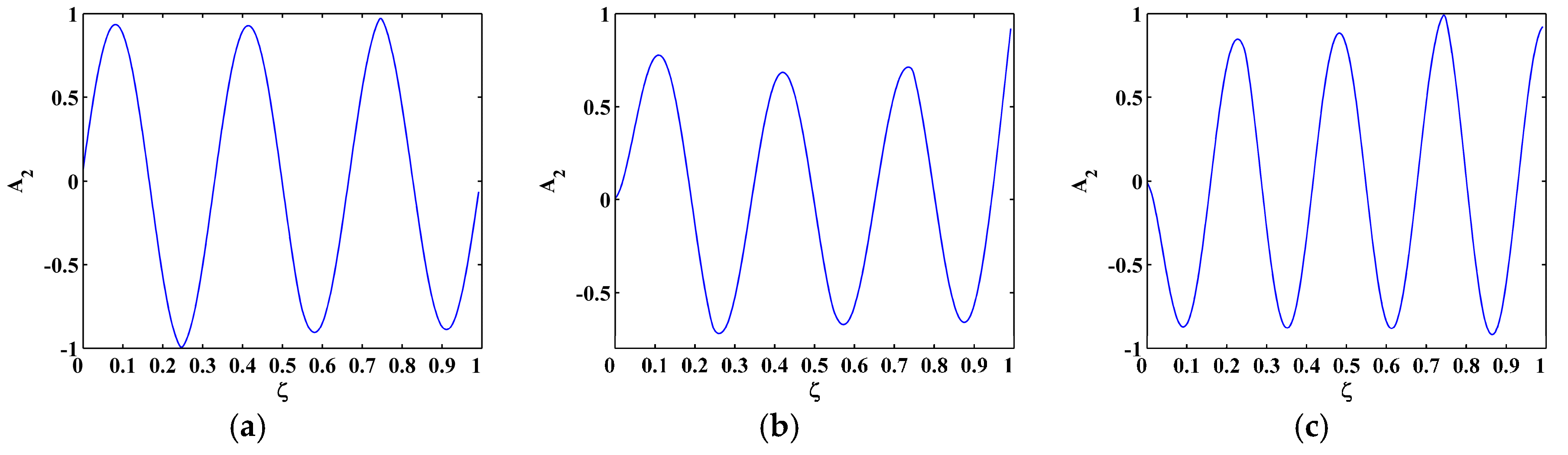
4. Proof of Concept
4.1. Free Vibration of Timoshenko Beams with Cracks
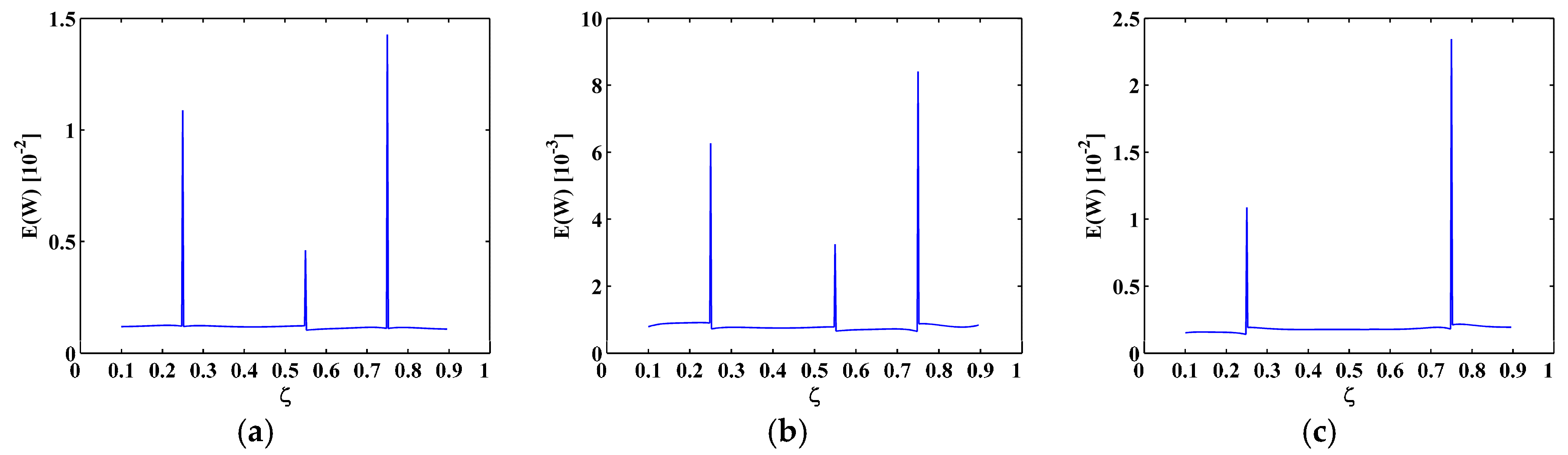
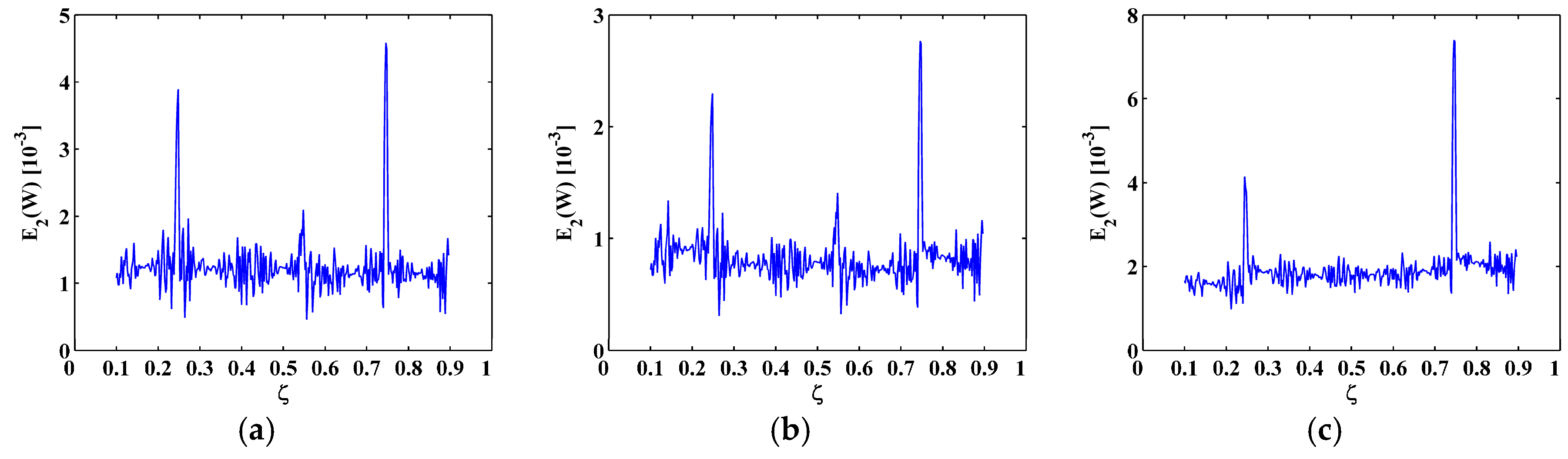
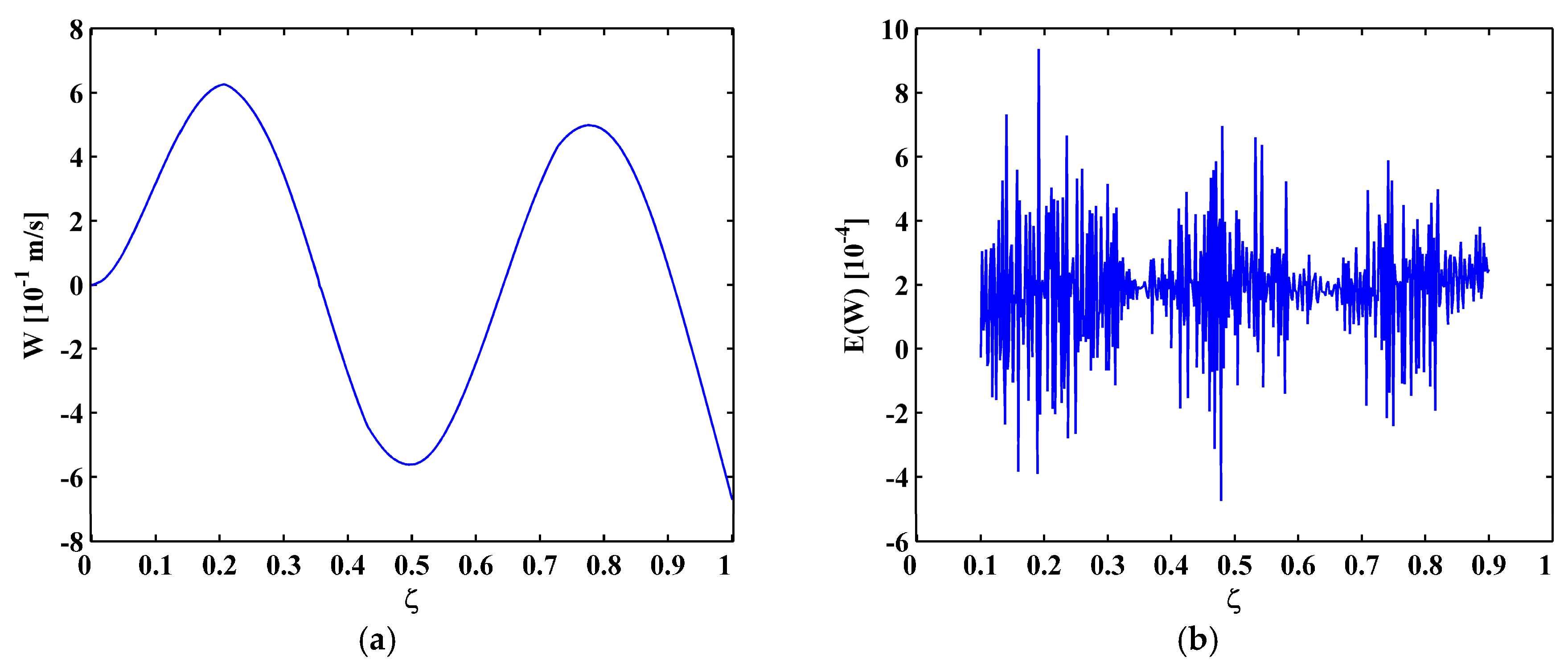
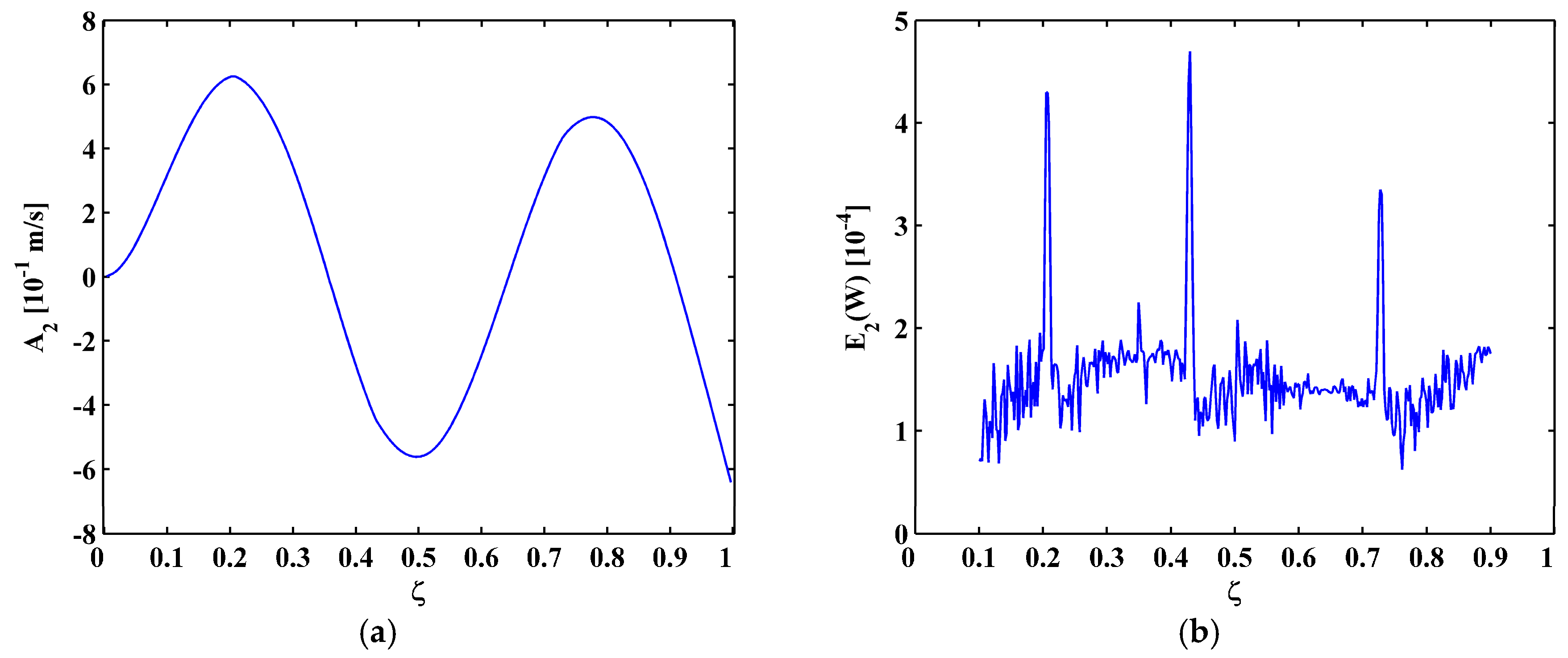
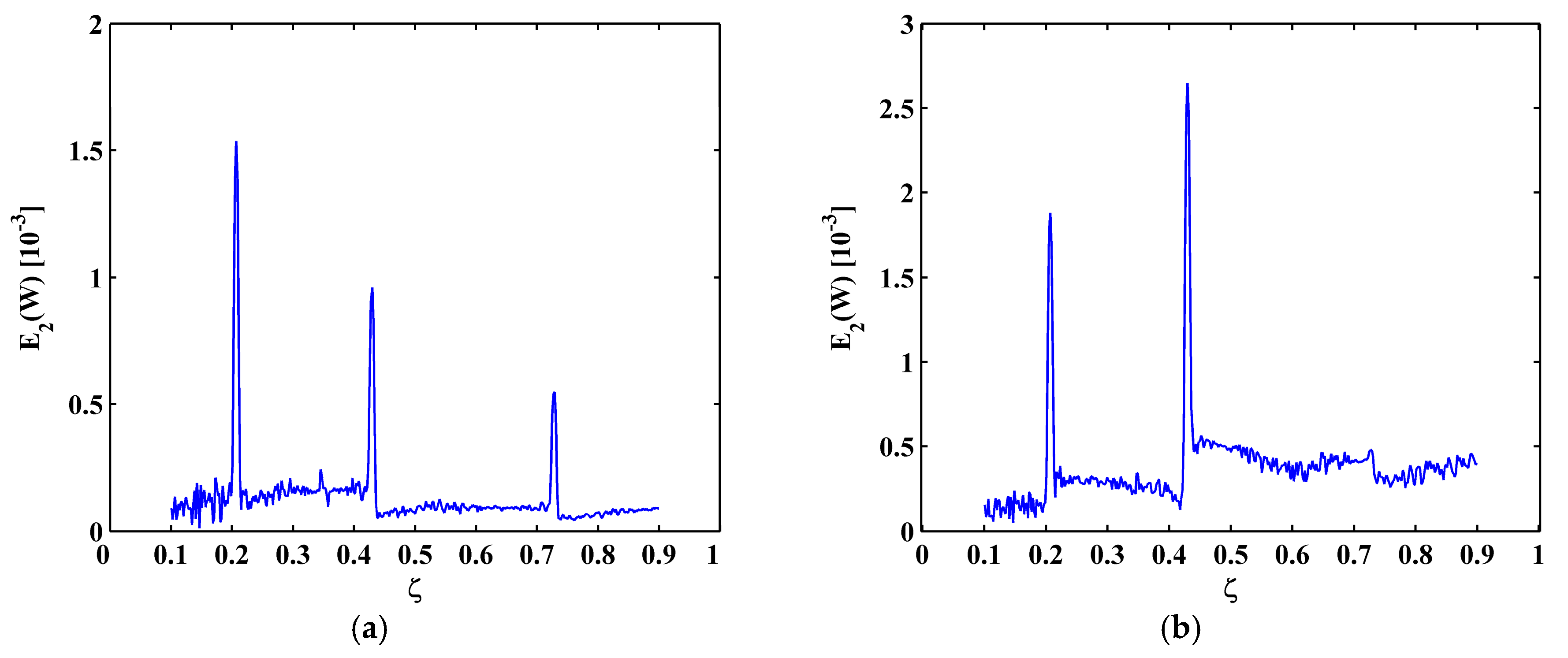
4.2. Crack Identification
4.3. Noise Tolerance
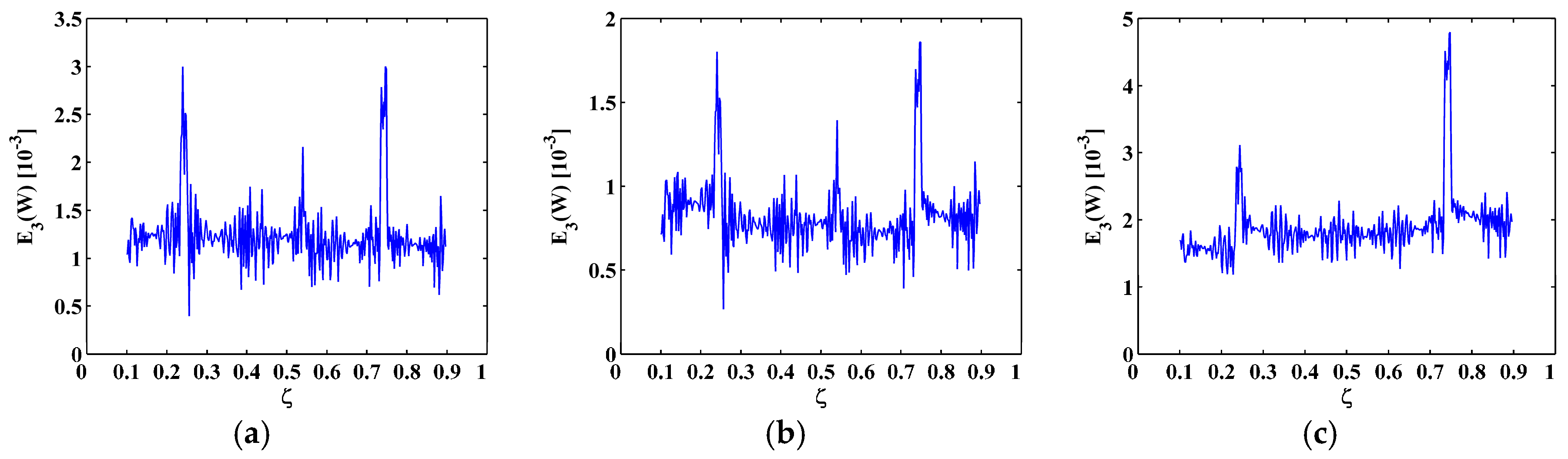
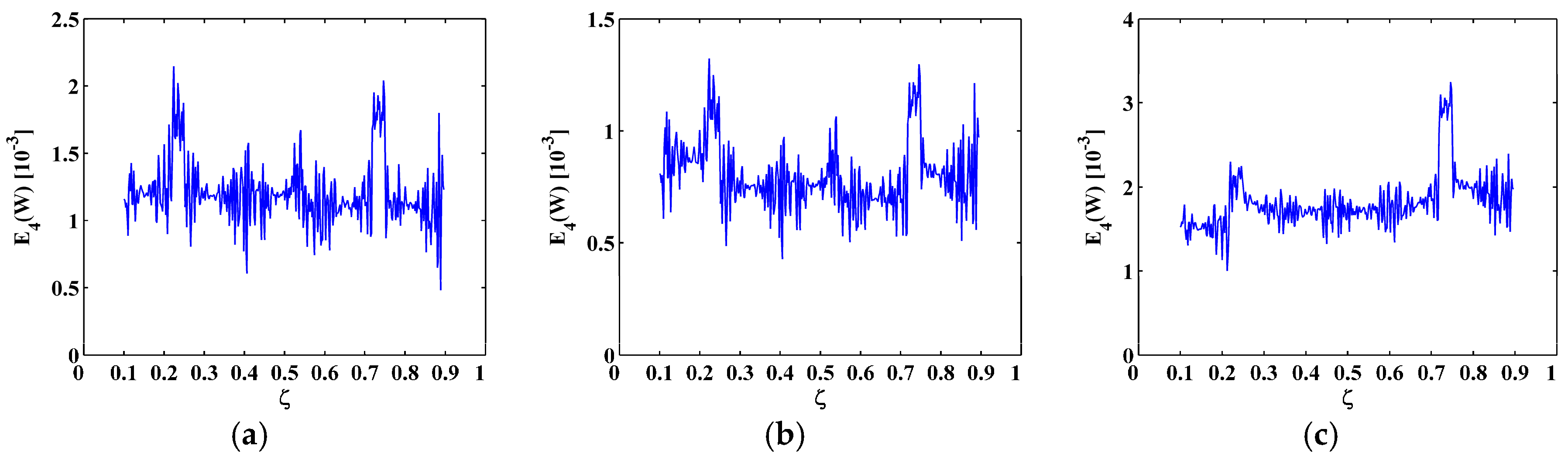
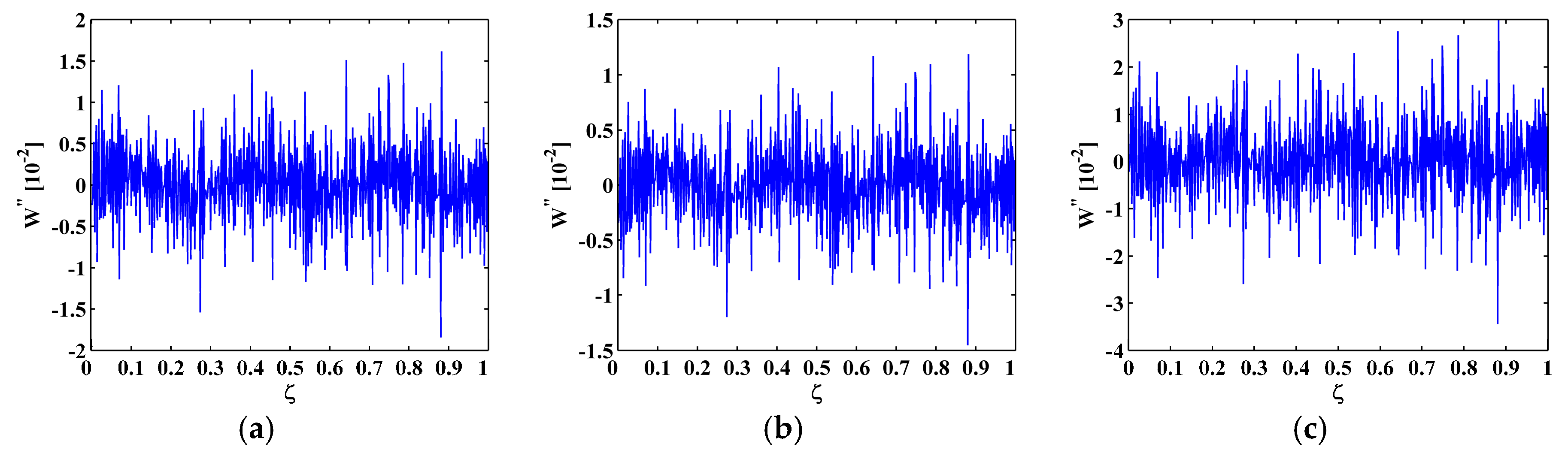
5. Experimental Validation
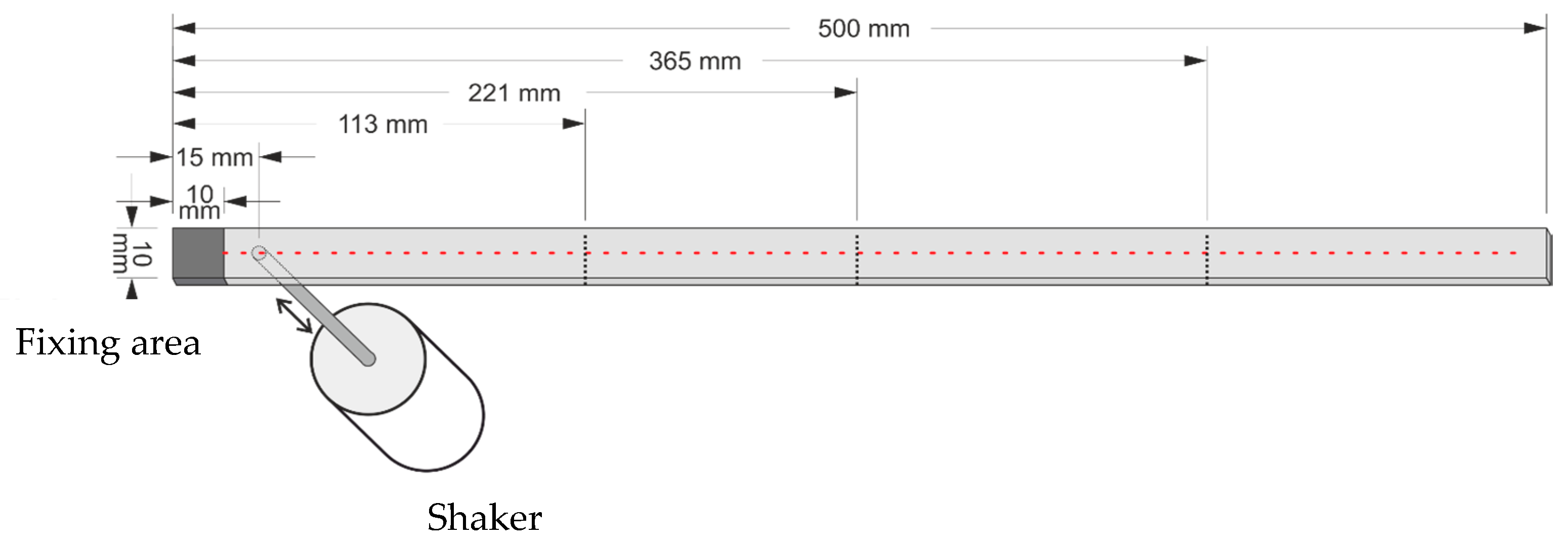
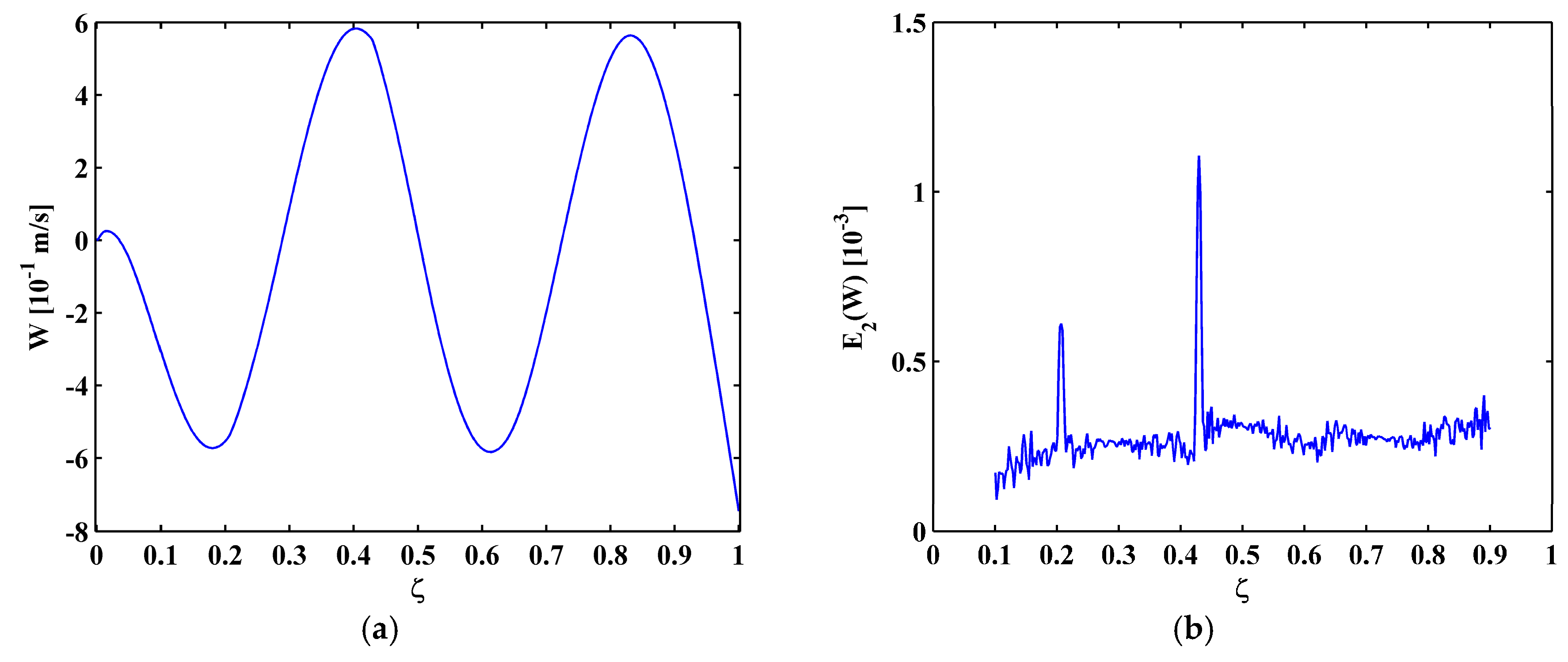
5.1. Setup
5.2. Experimental Results
6. Conclusions
- Cracks can cause rapid changes in the M-TKE because the TKE operator is sensitive to slight changes in the local frequency and amplitude of a mode shape. However, the M-TKE is very prone to noise interference and therefore lacks the robustness to identify cracks under noise environments.
- To enhance the noise robustness of the M-TKE, the MRM-TKE is developed from the M-TKE with the WT-based MRA, whereby noise components in the M-TKE can be eliminated at a satisficing level in the MRM-TKE; synchronously, damage-caused change in the M-TKE can be retained in the MRM-TKE. Thus, the MRM-TKE is capable of identifying cracks in CFRP laminated beams under noisy environments.
- The MRM-TKE method is a non-baseline method, requiring no structural baseline information such as temperature, materials, geometry, and boundary conditions. The only requirement for the MRM-TKE method is that high-order modes are needed for small boundary-effect intervals.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mohee, F.M.; Al-Mayah, A.; Plumtree, A. Anchors for CFRP plates: State-of-the-art review and future potential. Compos. Part B-Eng. 2016, 90, 432–442. [Google Scholar] [CrossRef]
- Xie, X.; Li, X.; Shen, Y. Static and dynamic characteristics of a long-span cable-stayed bridge with CFRP cables. Materials 2014, 7, 4854–4877. [Google Scholar] [CrossRef]
- Prakash, R.; Krishnaraj, V.; Zitoune, R.; Sheikh-Ahmad, J. High-speed edge trimming of CFRP and online monitoring of performance of router tools using acoustic emission. Materials 2016, 9, 798. [Google Scholar] [CrossRef]
- Jeong, Y.; Lee, J.; Kim, W. Modeling and measurement of sustained loading and temperature-dependent deformation of carbon fiber-reinforced polymer bonded to concrete. Materials 2015, 8, 435–450. [Google Scholar] [CrossRef]
- Maier, A.; Schmidt, R.; Oswald-Tranta, B.; Schledjewski, R. Non-destructive thermography analysis of impact damage on large-scale CFRP automotive parts. Materials 2014, 7, 413–429. [Google Scholar] [CrossRef]
- Zuluaga-Ramírez, P.; Frövel, M.; Belenguer, T.; Salazar, F. Surface irregularity factor as a parameter to evaluate the fatigue damage state of CFRP. Materials 2015, 8, 7524–7535. [Google Scholar] [CrossRef]
- Yuan, S.; Bao, Q.; Qiu, L.; Zhong, Y. A single frequency component-based re-estimated MUSIC algorithm for impact localization on complex composite structures. Smart Mater. Struct. 2015, 24, 105021. [Google Scholar] [CrossRef]
- Qiu, L.; Yuan, S.; Bao, Q.; Mei, H.; Ren, Y. Crack propagation monitoring in a full-scale aircraft fatigue test based on guided wave-Gaussian mixture model. Smart Mater. Struct. 2016, 25, 055048. [Google Scholar] [CrossRef]
- Giurgiutiu, V.; Yu, L.; Kendall, J.R.I.; Jenkins, C. In situ imaging of crack growth with piezoelectric-wafer active sensors. AIAA J. 2007, 45, 2758–2769. [Google Scholar] [CrossRef]
- Lam, H.F.; Yin, T. Application of two-dimensional spatial wavelet transform in the detection of an obstructed crack on a thin plate. Struct. Control Health Monit. 2012, 19, 260–277. [Google Scholar] [CrossRef]
- Liu, P.; Sohn, H.; Kundu, T.; Yang, S. Noncontact detection of fatigue cracks by laser nonlinear wave modulation spectroscopy (LNWMS). NDT E Int. 2014, 66, 106–116. [Google Scholar] [CrossRef]
- Parvasi, S.M.; Xu, C.; Kong, Q.; Song, G. Detection of multiple thin surface cracks using vibrothermography with low-power piezoceramic-based ultrasonic actuator—A numerical study with experimental verification. Smart Mater. Struct. 2016, 25, 055042. [Google Scholar] [CrossRef]
- Okabe, Y.; Tanaka, N.; Takeda, N. Effect of fiber coating on crack detection in carbon fiber reinforced plastic composites using fiber Bragg grating sensors. Smart Mater. Struct. 2002, 11, 892–898. [Google Scholar] [CrossRef]
- Aratama, S.; Hashizume, R.; Takenaka, K.; Koga, K.; Tsumura, Y.; Miyake, T.; Nishikawa, M.; Hojo, M. Microscopic observation of voids and transverse crack initiation in CFRP laminates. Adv. Compos. Mater. 2016, 25, 115–130. [Google Scholar] [CrossRef]
- Matsuzaki, R.; Todoroki, A. Wireless detection of internal delamination cracks in CFRP laminates using oscillating frequency changes. Compos. Sci. Technol. 2006, 66, 407–416. [Google Scholar] [CrossRef]
- Todoroki, A.; Omagari, K.; Shimamura, Y.; Kobayashi, H. Matrix crack detection of CFRP using electrical resistance change with integrated surface probes. Compos. Sci. Technol. 2006, 66, 1539–1545. [Google Scholar] [CrossRef]
- Cheng, L.; Tian, G.Y. Surface crack detection for carbon fiber reinforced plastic (CFRP) materials using pulsed eddy current thermography. IEEE Sens. J. 2011, 11, 3261–3268. [Google Scholar] [CrossRef]
- Wu, J.; Zhou, D.; Wang, J. Surface crack detection for carbon fiber reinforced plastic materials using pulsed eddy current based on rectangular differential probe. J. Sens. 2014, 2014, 727269. [Google Scholar] [CrossRef]
- Fan, W.; Qiao, P. Vibration-based damage identification methods: A review and comparative study. Struct. Health Monit. 2011, 10, 83–111. [Google Scholar] [CrossRef]
- Cao, M.S.; Ostachowicz, W.; Radzienski, M.; Xu, W. Multiscale shear-strain gradient for detecting delamination in composite laminates. Appl. Phys. Lett. 2013, 103, 101910. [Google Scholar] [CrossRef]
- Pandey, A.K.; Biswas, M.; Samman, M.M. Damage detection from changes in curvature mode shapes. J. Sound Vib. 1991, 145, 321–332. [Google Scholar] [CrossRef]
- Ratcliffe, C.P.; Bagaria, W.J. Vibration technique for locating delamination in a composite beam. AIAA J. 1998, 36, 1074–1077. [Google Scholar] [CrossRef]
- Abdel Wahab, M.M.; De Roeck, G. Damage detection in bridges using modal curvatures: Application to a real damage scenario. J. Sound Vib. 1999, 226, 217–235. [Google Scholar] [CrossRef]
- Ratcliffe, C.P. A frequency and curvature based experimental method for locating damage in structures. J. Vib. Acoust. 2000, 122, 324–329. [Google Scholar] [CrossRef]
- Hu, N.; Fukunaga, H.; Kameyama, M.; Aramaki, Y.; Chang, F.K. Vibration analysis of delaminated composite beams and plates using a higher-order finite element. Int. J. Mech. Sci. 2002, 44, 1479–1503. [Google Scholar] [CrossRef]
- Hamey, C.S.; Lestari, W.; Qiao, P.Z.; Song, G.B. Experimental damage identification of carbon/epoxy composite beams using curvature mode shapes. Struct. Health Monit. 2004, 3, 333–353. [Google Scholar] [CrossRef]
- Lestari, W.; Qiao, P.; Hanagud, S. Curvature mode shape-based damage assessment of carbon/epoxy composite beams. J. Intell. Mater. Syst. Struct. 2007, 18, 189–208. [Google Scholar] [CrossRef]
- Cao, M.; Qiao, P. Novel Laplacian scheme and multiresolution modal curvatures for structural damage identification. Mech. Syst. Signal Process. 2009, 23, 1223–1242. [Google Scholar] [CrossRef]
- Sung, S.H.; Jung, H.J.; Jung, H.Y. Damage detection for beam-like structures using the normalized curvature of a uniform load surface. J. Sound Vib. 2013, 332, 1501–1519. [Google Scholar] [CrossRef]
- Cao, M.; Radzienski, M.; Xu, W.; Ostachowicz, W. Identification of multiple damage in beams based on robust curvature mode shapes. Mech. Syst. Signal Process. 2014, 46, 468–480. [Google Scholar] [CrossRef]
- Cao, M.; Xu, W.; Ostachowicz, W.; Su, Z. Damage identification for beams in noisy conditions based on Teager energy operator-wavelet transform modal curvature. J. Sound Vib. 2014, 333, 1543–1553. [Google Scholar] [CrossRef]
- Sazonov, E.; Klinkhachorn, P. Optimal spatial sampling interval for damage detection by curvature or strain energy mode shapes. J. Sound Vib. 2005, 285, 783–801. [Google Scholar] [CrossRef]
- Cao, M.; Xu, W.; Ren, W.; Ostachowicz, W.; Sha, G.; Pan, L. A concept of complex-wavelet modal curvature for detecting multiple cracks in beams under noisy conditions. Mech. Syst. Signal Process. 2016, 76, 555–575. [Google Scholar] [CrossRef]
- Yang, Z.; Radzienski, M.; Kudela, P.; Ostachowicz, W. Fourier spectral-based modal curvature analysis and its application to damage detection in beams. Mech. Syst. Signal Process. 2017, 84, 763–781. [Google Scholar] [CrossRef]
- Li, Y.Y.; Cheng, L.; Yam, L.H.; Wong, W.O. Identification of damage locations for plate-like structures using damage sensitive indices: Strain modal approach. Comput. Struct. 2002, 80, 1881–1894. [Google Scholar] [CrossRef]
- Stubbs, N.; Kim, J.T. Damage localization in structures without baseline modal parameters. AIAA J. 1996, 34, 1644–1649. [Google Scholar] [CrossRef]
- Law, S.S.; Shi, Z.Y.; Zhang, L.M. Structural damage detection from incomplete and noisy modal test data. J. Eng. Mech. 1998, 124, 1280–1288. [Google Scholar] [CrossRef]
- Cornwell, P.; Doebling, S.W.; Farrar, C.R. Application of the strain energy damage detection method to platelike structures. J. Sound Vib. 1999, 224, 359–374. [Google Scholar] [CrossRef]
- Shi, Z.Y.; Law, S.S.; Zhang, L.M. Structural damage detection from modal strain energy change. J. Eng. Mech. 2000, 126, 1216–1223. [Google Scholar] [CrossRef]
- Rucka, M.; Wilde, K. Crack identification using wavelets on experimental static deflection profiles. Eng. Struct. 2006, 28, 279–288. [Google Scholar] [CrossRef]
- Mallat, S.; Hwang, W.L. Singularity detection and processing with wavelets. IEEE Trans. Inf. Theory 1992, 38, 617–643. [Google Scholar] [CrossRef]
- Liew, K.M.; Wang, Q. Application of wavelet theory for crack identification in structures. J. Eng. Mech. 1998, 124, 152–157. [Google Scholar] [CrossRef]
- Wang, Q.; Deng, X.M. Damage detection with spatial wavelets. Int. J. Solids Struct. 1999, 36, 3443–3468. [Google Scholar] [CrossRef]
- Hong, J.C.; Kim, Y.Y.; Lee, H.C.; Lee, Y.W. Damage detection using the Lipschitz exponent estimated by the wavelet transform: Applications to vibration modes of a beam. Int. J. Solids Struct. 2002, 39, 1803–1816. [Google Scholar] [CrossRef]
- Douka, E.; Loutridis, S.; Trochidis, A. Crack identification in beams using wavelet analysis. Int. J. Solids Struct. 2003, 40, 3557–3569. [Google Scholar] [CrossRef]
- Kim, H.S.; Melhem, H. Damage detection of structures by wavelet analysis. Eng. Struct. 2004, 26, 347–362. [Google Scholar] [CrossRef]
- Chang, C.C.; Chen, L.W. Damage detection of a rectangular plate by spatial wavelet based approach. Appl. Acoust. 2004, 65, 819–832. [Google Scholar] [CrossRef]
- Rucka, M.; Wilde, K. Application of continuous wavelet transform in vibration based damage detection method for beams and plates. J. Sound Vib. 2006, 297, 536–550. [Google Scholar] [CrossRef]
- Cao, M.; Qiao, P. Integrated wavelet transform and its application to vibration mode shapes for the damage detection of beam-type structures. Smart Mater. Struct. 2008, 17, 055014. [Google Scholar] [CrossRef]
- Hadjileontiadis, L.J.; Douka, E.; Trochidis, A. Fractal dimension analysis for crack identification in beam structures. Mech. Syst. Signal Process. 2005, 19, 659–674. [Google Scholar] [CrossRef]
- Wang, J.; Qiao, P. Improved damage detection for beam-type structures using a uniform load surface. Struct. Health Monit. 2007, 6, 99–110. [Google Scholar] [CrossRef]
- Qiao, P.; Cao, M. Waveform fractal dimension for mode shape-based damage identification of beam-type structures. Int. J. Solids Struct. 2008, 45, 5946–5961. [Google Scholar] [CrossRef]
- Bai, R.; Cao, M.; Su, Z.; Ostachowicz, W.; Xu, H. Fractal dimension analysis of higher-order mode shapes for damage identification of beam structures. Math. Probl. Eng. 2012, 2012, 454568. [Google Scholar] [CrossRef]
- Bai, R.B.; Ostachowicz, W.; Cao, M.S.; Su, Z. Crack detection in beams in noisy conditions using scale fractal dimension analysis of mode shapes. Smart Mater. Struct. 2014, 23, 065014. [Google Scholar] [CrossRef]
- Xu, W.; Cao, M.S.; Radzienski, M.; Xia, N.; Su, Z.; Ostachowicz, W.; Wang, S.S. Detecting multiple small-sized damage in beam-type structures by Teager energy of modal curvature shape. J. Vibroeng. 2015, 17, 275–286. [Google Scholar]
- Montanari, L.; Spagnoli, A.; Basu, B.; Broderick, B. On the effect of spatial sampling in damage detection of cracked beams by continuous wavelet transform. J. Sound Vib. 2015, 345, 233–249. [Google Scholar] [CrossRef]
- Kaiser, J.F. On a simple algoritm to calculate the energy of a signal. In Proceedings of the Acoustics, Speech and Signal Processing, Albuquerque, NM, USA, 3–6 April 1990. [Google Scholar]
- Mallat, S.G. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Timoshenko, S.P.X. On the transverse vibrations of bars of uniform cross-section. Philos. Mag. 1922, 43, 125–131. [Google Scholar] [CrossRef]
- Dugundji, J. Simple expressions for higher vibration modes of uniform Euler beams. AIAA J. 1988, 26, 1013–1014. [Google Scholar] [CrossRef]
- Pai, P.F.; Young, L.G. Damage detection of beams using operational deflection shapes. Int. J. Solids Struct. 2001, 38, 3161–3192. [Google Scholar] [CrossRef]
- Rizos, P.F.; Aspragathos, N.; Dimarogonas, A.D. Identification of crack location and magnitude in a cantilever beam from the vibration modes. J. Sound Vib. 1990, 138, 381–388. [Google Scholar] [CrossRef]
- Ostachowicz, W.M.; Krawczuk, M. Analysis of the effect of cracks on the natural frequencies of a cantilever beam. J. Sound Vib. 1991, 150, 191–201. [Google Scholar] [CrossRef]
- Huang, T.C. The effect of rotatory inertia and of shear deformation on the frequency and normal mode equations of uniform beams with simple end conditions. J. Appl. Mech. 1961, 28, 579–584. [Google Scholar] [CrossRef]
- Lin, H.P. Direct and inverse methods on free vibration analysis of simply supported beams with a crack. Eng. Struct. 2004, 26, 427–436. [Google Scholar] [CrossRef]
- Greco, A.; Pau, A. Damage identification in Euler frames. Comput. Struct. 2012, 92–93, 328–336. [Google Scholar] [CrossRef]
- Khaji, N.; Shafiei, M.; Jalalpour, M. Closed-form solutions for crack detection problem of Timoshenko beams with various boundary conditions. Int. J. Mech. Sci. 2009, 51, 667–681. [Google Scholar] [CrossRef]
- Abbas, B. Vibrations of Timoshenko beams with elastically restrained ends. J. Sound Vib. 1984, 97, 541–548. [Google Scholar] [CrossRef]
- Cao, M.S.; Xu, W.; Su, Z.; Ostachowicz, W.; Xia, N. Local coordinate systems-based method to analyze high-order modes of n-step Timoshenko beam. J. Vib. Control 2017, 23, 89–102. [Google Scholar] [CrossRef]
- Xu, W.; Zhu, W.D.; Smith, S.A.; Cao, M.S. Structural damage detection using slopes of longitudinal vibration shapes. J. Vib. Acoust. 2016, 138, 034501. [Google Scholar] [CrossRef]
- Schwarz, B.J.; Richardson, M.H. Introduction to Operating Deflection Shapes; CSI Reliability Week: Orlando, FL, USA, 1999; Volume 10, pp. 121–126. [Google Scholar]





© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, W.; Cao, M.; Ding, K.; Radzieński, M.; Ostachowicz, W. Crack Identification in CFRP Laminated Beams Using Multi-Resolution Modal Teager–Kaiser Energy under Noisy Environments. Materials 2017, 10, 656. https://doi.org/10.3390/ma10060656
Xu W, Cao M, Ding K, Radzieński M, Ostachowicz W. Crack Identification in CFRP Laminated Beams Using Multi-Resolution Modal Teager–Kaiser Energy under Noisy Environments. Materials. 2017; 10(6):656. https://doi.org/10.3390/ma10060656
Chicago/Turabian StyleXu, Wei, Maosen Cao, Keqin Ding, Maciej Radzieński, and Wiesław Ostachowicz. 2017. "Crack Identification in CFRP Laminated Beams Using Multi-Resolution Modal Teager–Kaiser Energy under Noisy Environments" Materials 10, no. 6: 656. https://doi.org/10.3390/ma10060656
APA StyleXu, W., Cao, M., Ding, K., Radzieński, M., & Ostachowicz, W. (2017). Crack Identification in CFRP Laminated Beams Using Multi-Resolution Modal Teager–Kaiser Energy under Noisy Environments. Materials, 10(6), 656. https://doi.org/10.3390/ma10060656





