Optical Absorption Enhancement in CdTe Thin Films by Microstructuration of the Silicon Substrate
Abstract
:1. Introduction
2. Materials and Methods
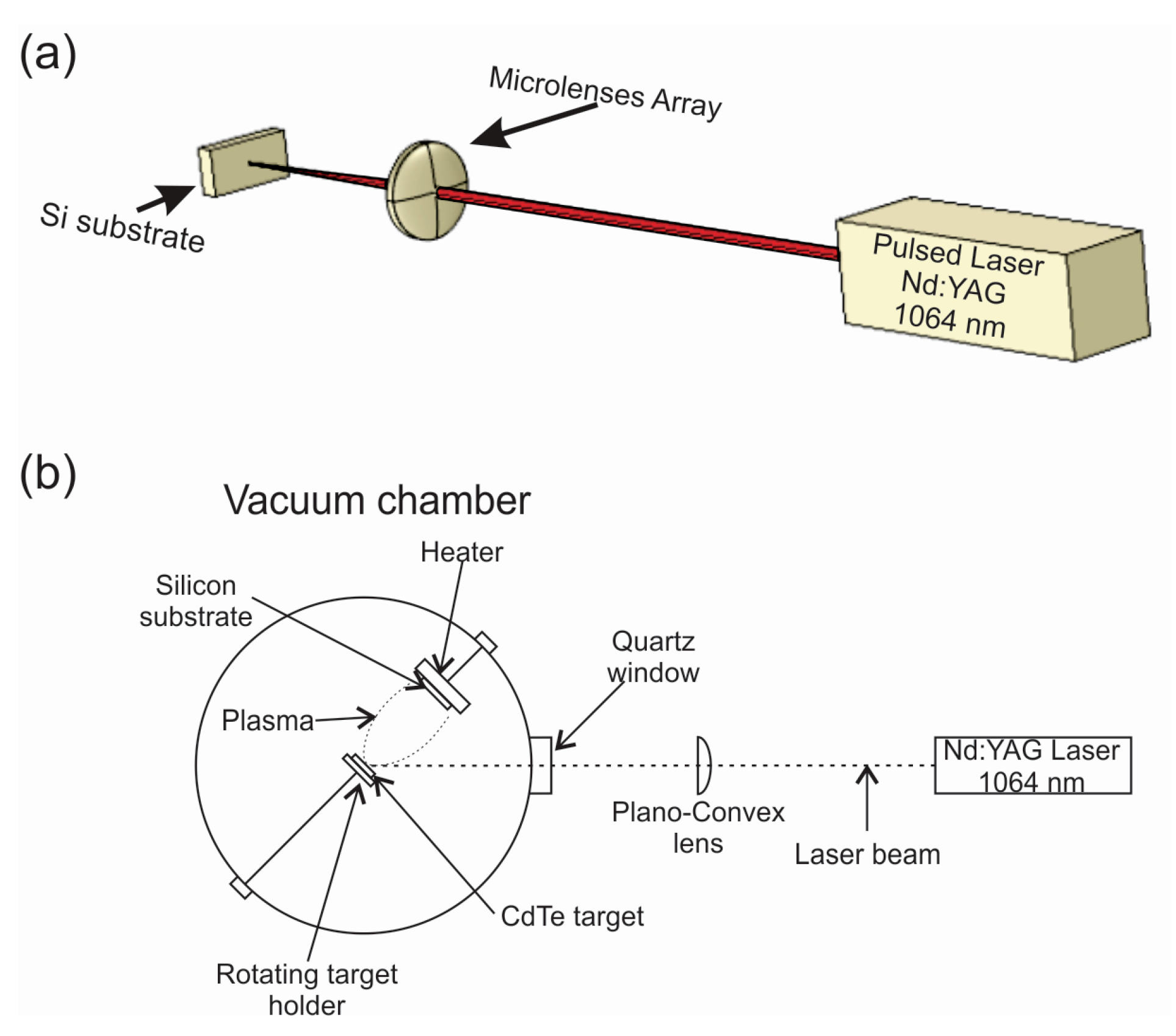
2.1. Substrate Modification
2.2. Thin Film Synthesis
2.3. Characterization of CdTe Thin Films
3. Results and Discussion
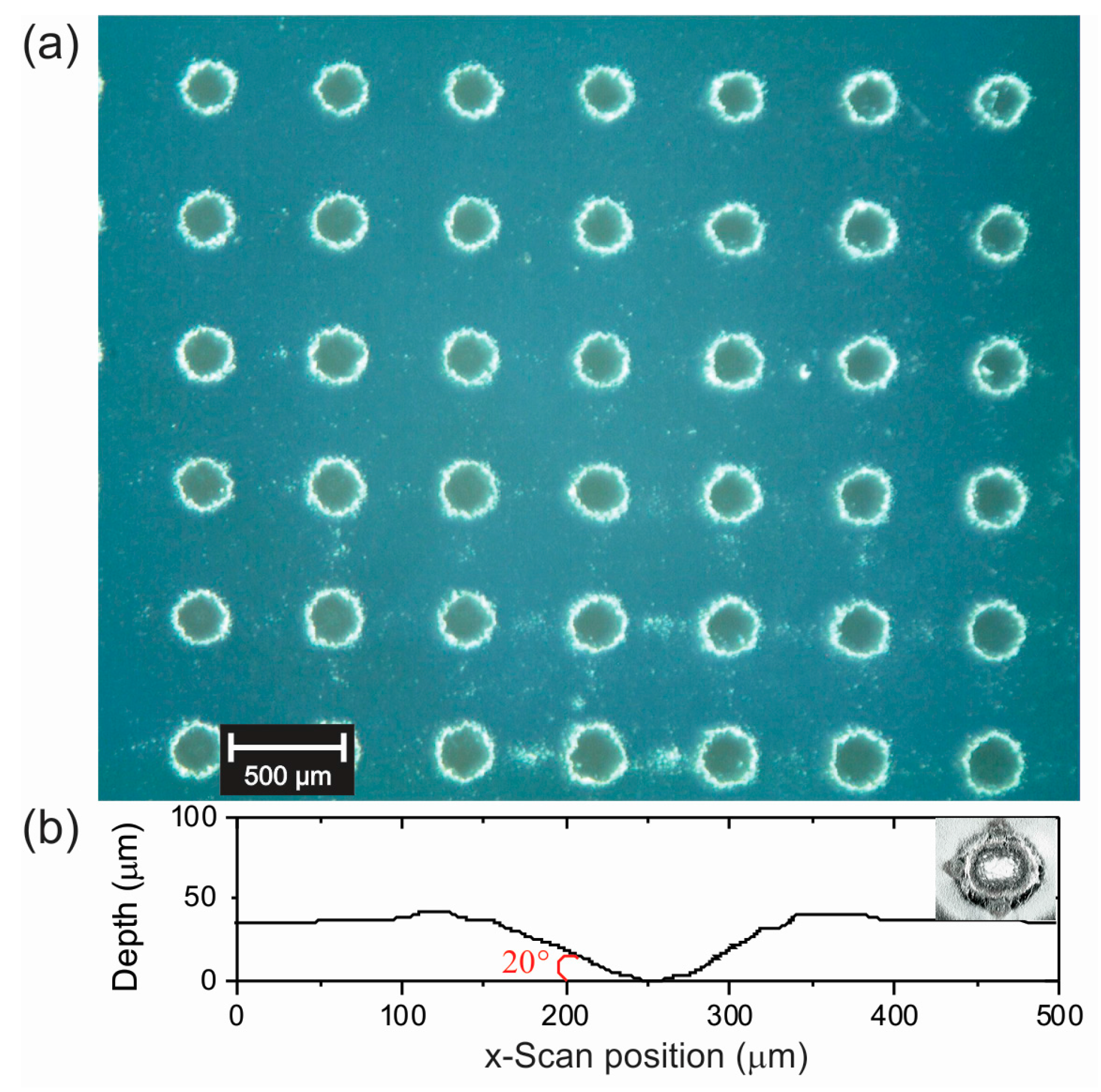
3.1. Optical Microscopy
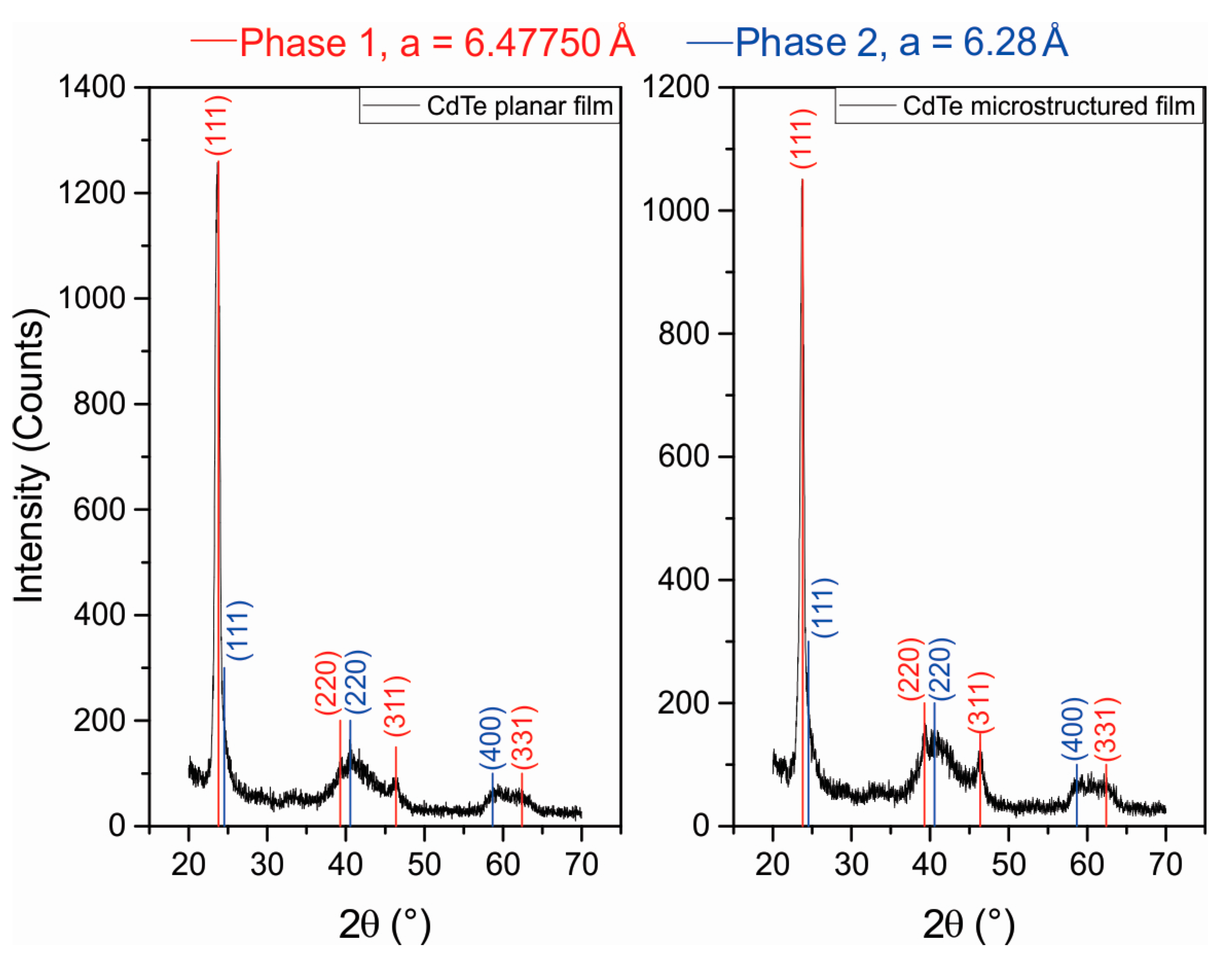
3.2. X-ray Diffraction Analysis
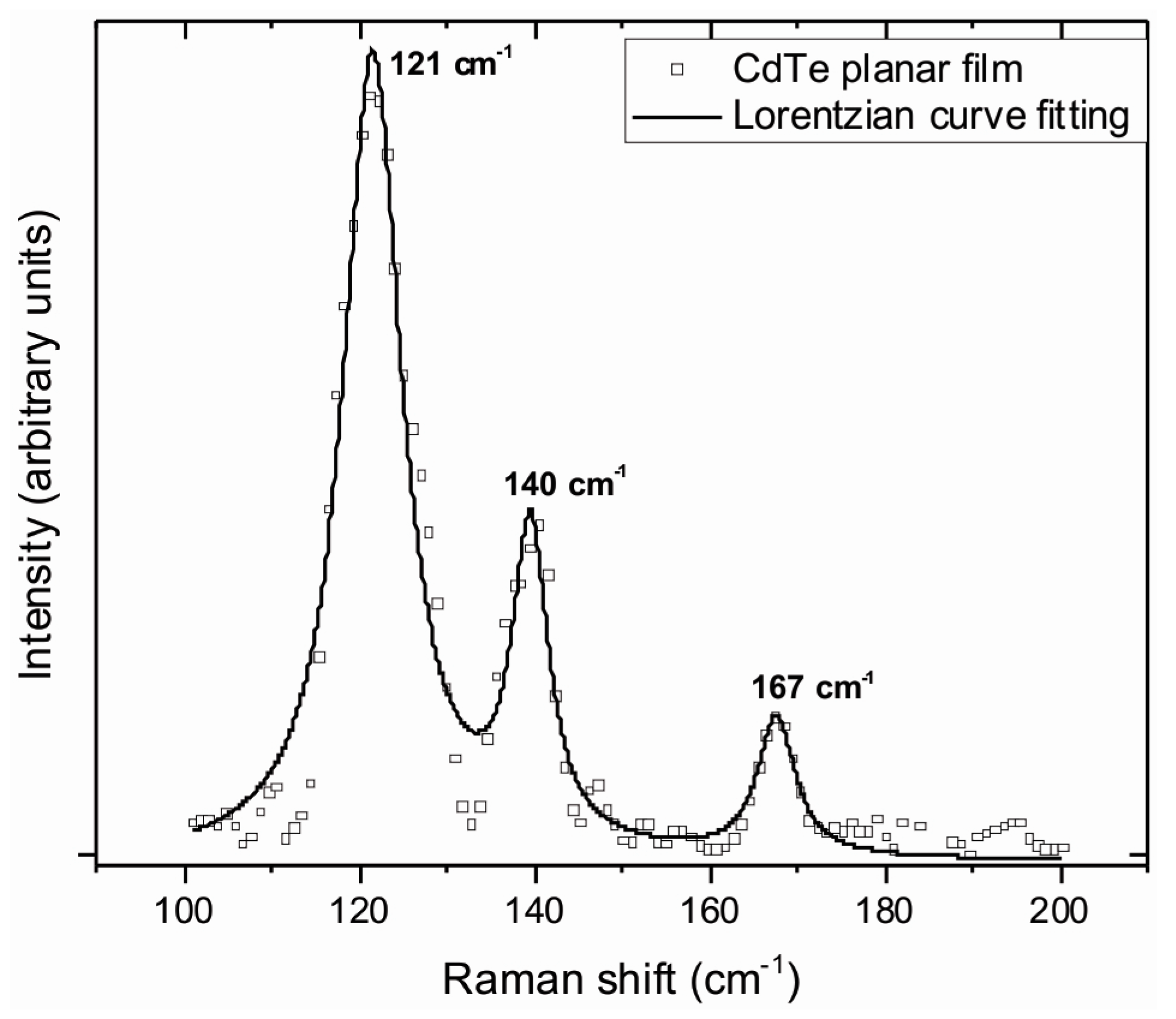
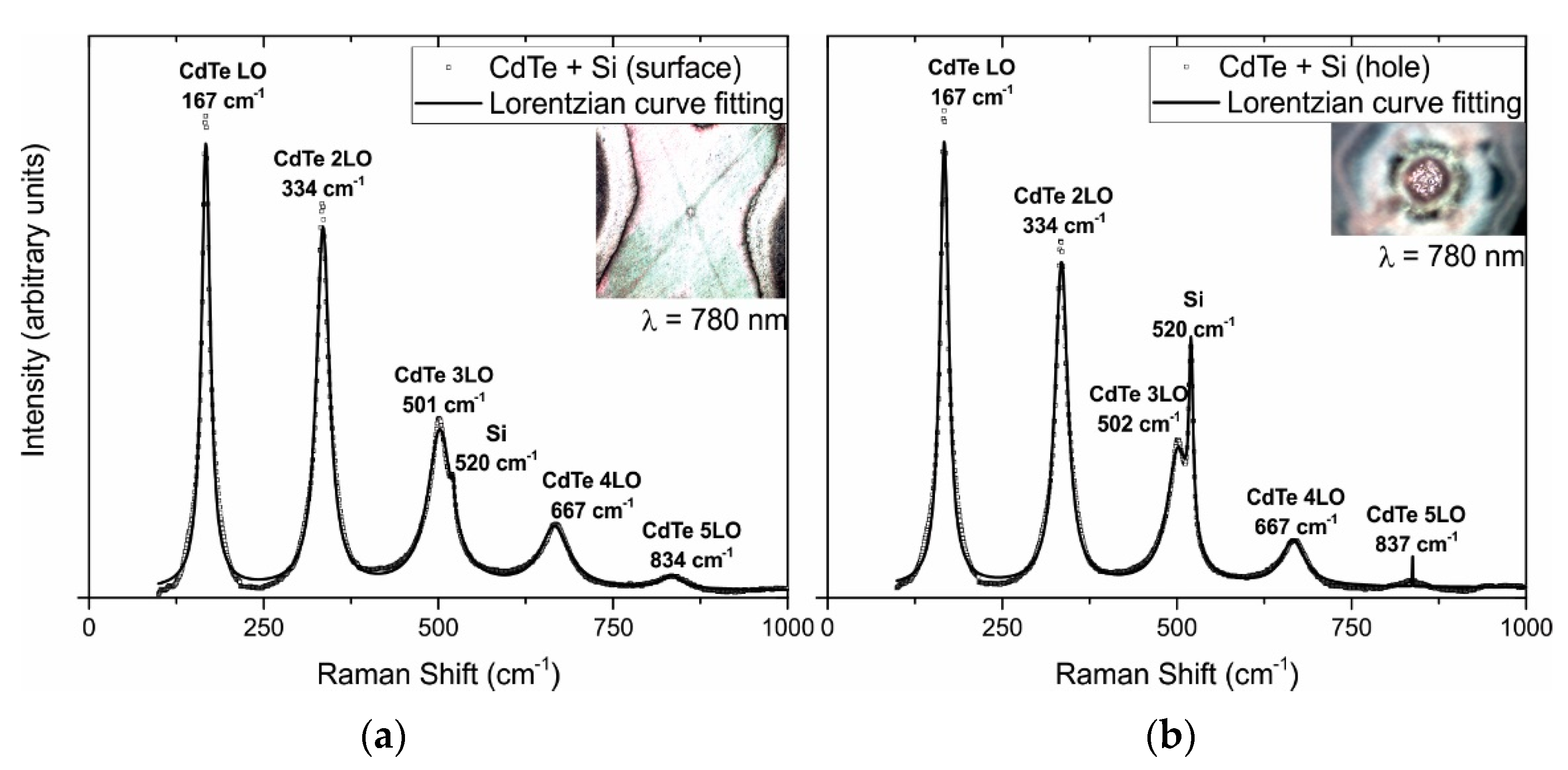
3.3. Raman Spectroscopy
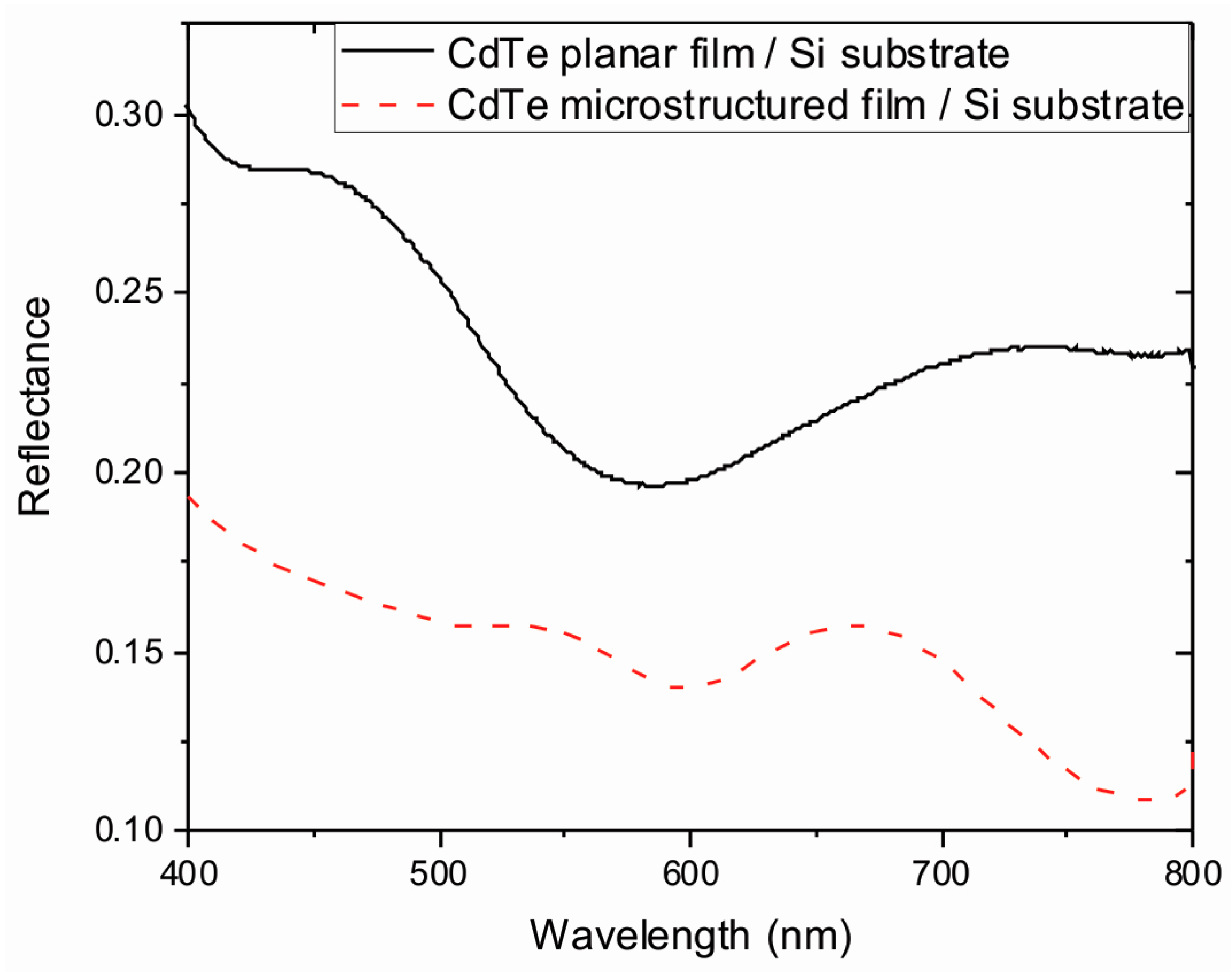
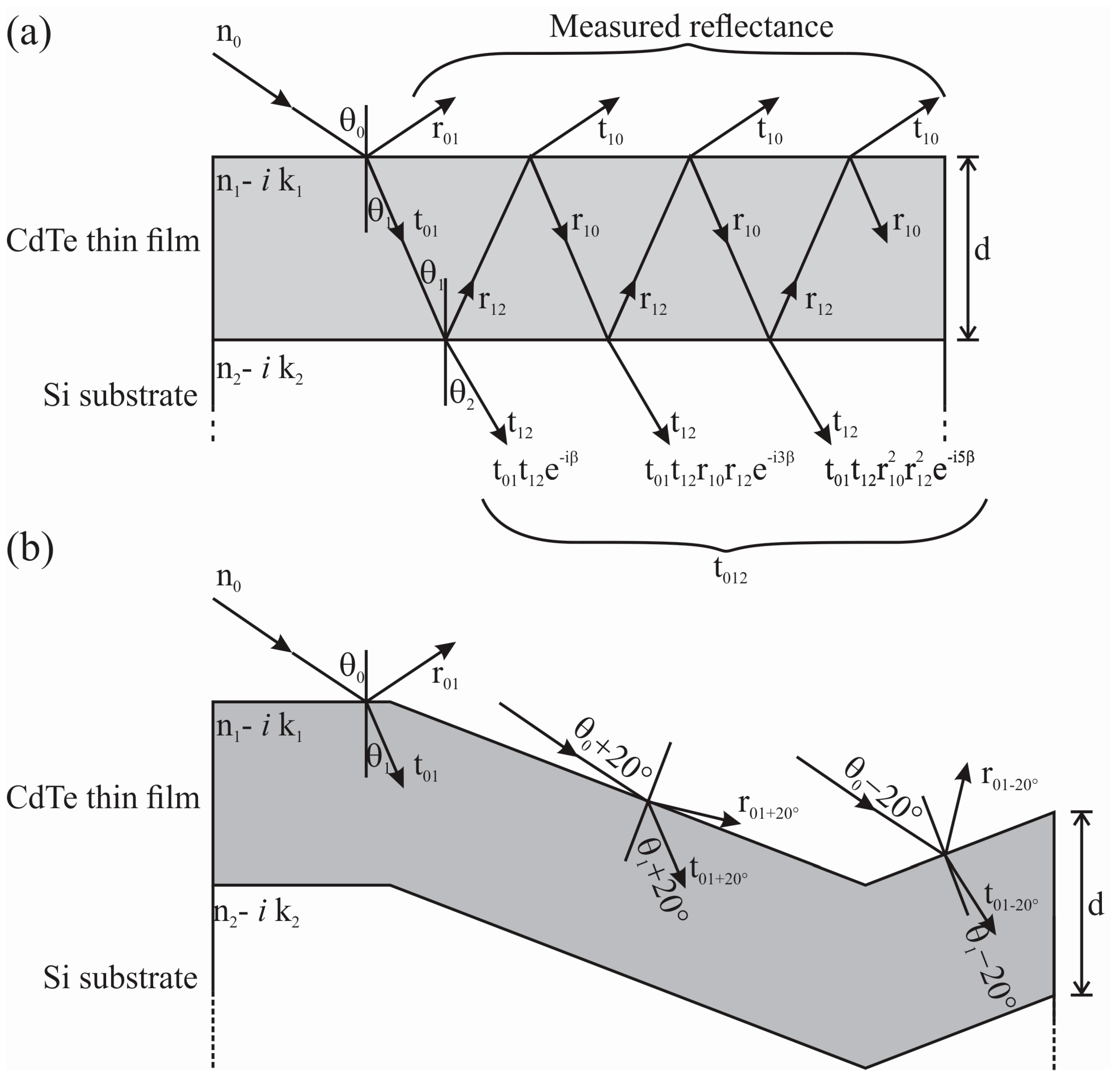
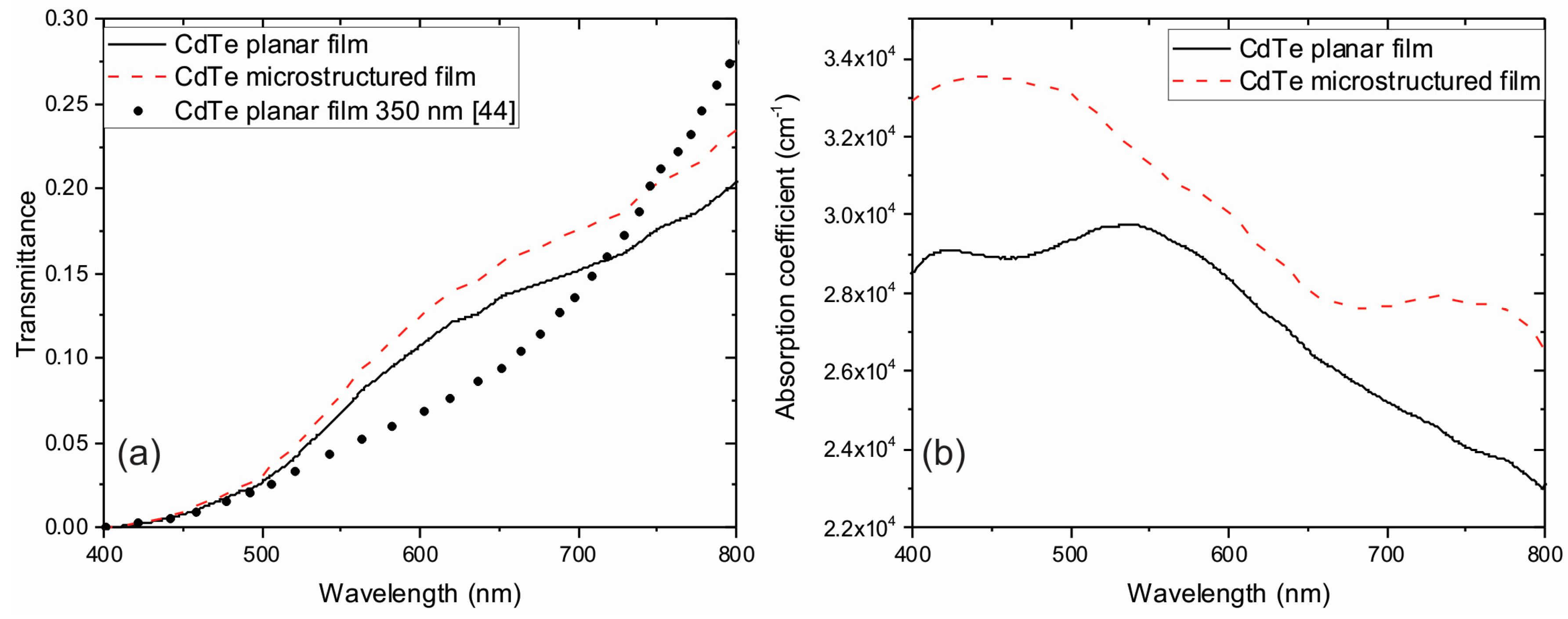
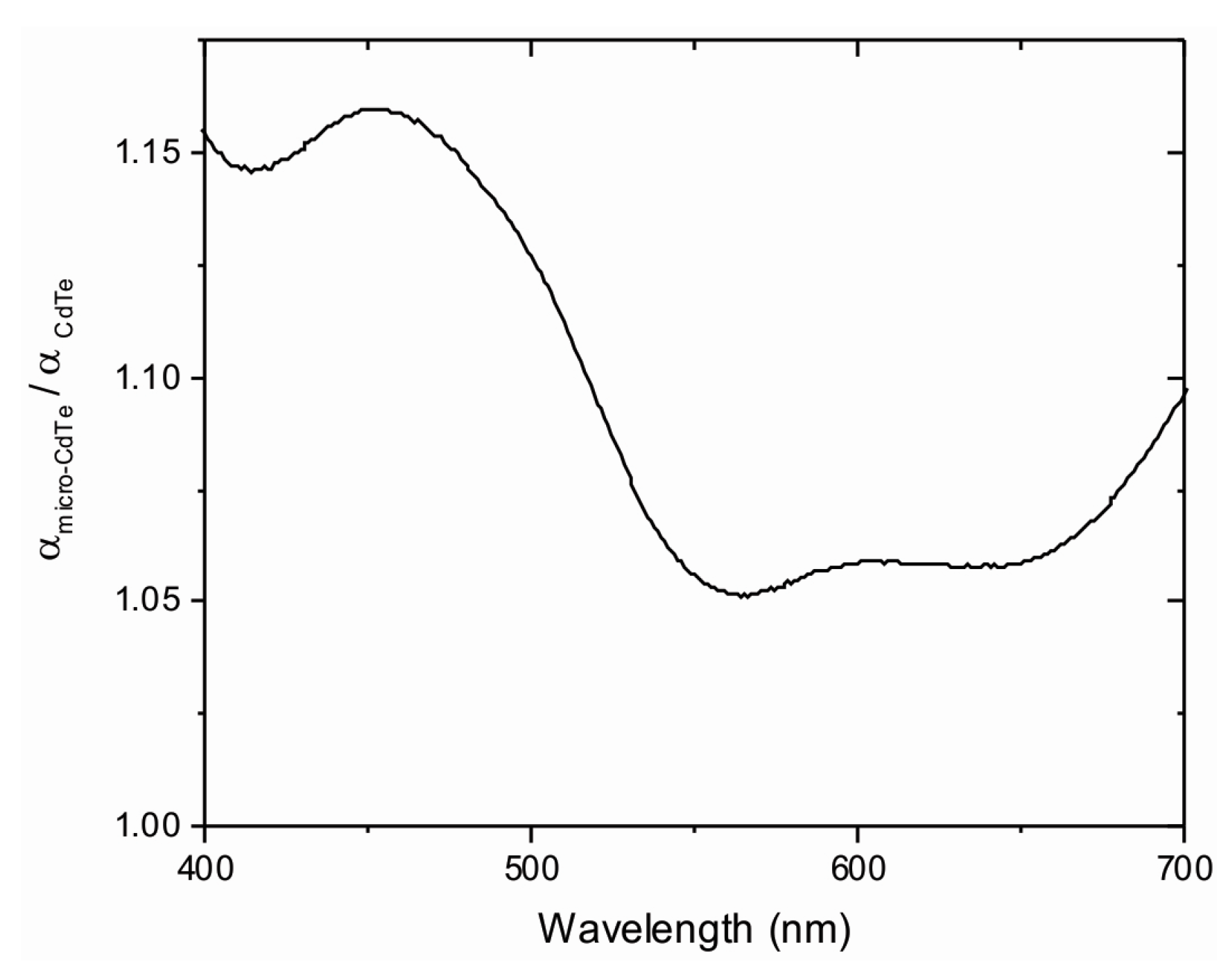
3.4. Optical Properties
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Green, M.A. Commercial progress and challenges for photovoltaics. Nat. Energy 2016, 1, 1–4. [Google Scholar] [CrossRef]
- Chen, W.; Grouquist, D.; Roark, J. Voltage Tunable Electroluminescence of CdTe Nanoparticle Light-Emitting Diodes. J. Nanosci. Nanotechnol. 2002, 2, 47–53. [Google Scholar] [CrossRef] [PubMed]
- Gaponik, N.P.; Talapin, D.V.; Rogach, A.L. A light-emitting device based on a CdTe nanocrystal/polyaniline composite. Phys. Chem. Chem. Phys. 1999, 1, 1787–1789. [Google Scholar] [CrossRef]
- Poplawsky, J.D. Cadmium telluride solar cells: Record-breaking voltages. Nat. Energy 2016, 1, 16021. [Google Scholar] [CrossRef]
- Burst, J.M.; Duenow, J.N.; Albin, D.S.; Colegrove, E.; Reese, M.O.; Aguiar, J.A.; Jiang, C.-S.; Patel, M.K.; Al-Jassim, M.M.; Kuciauskas, D.; et al. CdTe solar cells with open-circuit voltage greater than 1 V. Nat. Energy 2016, 1. in press. [Google Scholar]
- Eisen, Y.; Shor, A.; Mardor, I. CdTe and CdZnTe X-ray and gamma-ray detectors for imaging systems. IEEE Trans. Nucl. Sci. 2004, 51, 1191–1198. [Google Scholar] [CrossRef]
- Courtney, C.M.; Goodman, S.M.; McDaniel, J.A.; Madinger, N.E.; Chatterjee, A.; Nagpal, P. Photoexcited quantum dots for killing multidrug-resistant bacteria. Nat. Mater. 2016, 15, 485–588. [Google Scholar] [CrossRef] [PubMed]
- Du, T.; Cai, K.; Han, H.; Fang, L.; Liang, J.; Xiao, S. Probing the interactions of CdTe quantum dots with pseudorabies virus. Sci. Rep. 2015, 5, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Burgelman, M. Cadmium Telluride Thin Film Solar Cells: Characterization, Fabrication and Modeling. In Thin Film Solar Cells Fabrication, Characterization and Applications; Poortmans, J., Arkhipov, V., Eds.; John Wiley & Sons Ltd: Leuven, Belgium, 2006; Volume 1. [Google Scholar]
- Deivanayaki, S.; Jayamurugan, P.; Mariappan, R.; Ponnuswamy, V. Optical and structural characterization of CdTe thin films by chemical bath deposition technique. Chalcogenide Lett. 2010, 7, 159–163. [Google Scholar]
- Gunjal, S.D.; Khollam, Y.B.; Jadkar, S.R.; Shripathi, T.; Sathe, V.G.; Shelke, P.N.; Takwale, M.G.; Mohite, K.C. Spray pyrolysis deposition of p-CdTe films: Structural, optical and electrical properties. Sol. Energy 2014, 106, 56–62. [Google Scholar] [CrossRef]
- Chander, S.; Dhaka, M.S. Optimization of physical properties of vacuum evaporated CdTe thin films with the application of thermal treatment for solar cells. Mater. Sci. Semicond. Process. 2015, 40, 708–712. [Google Scholar] [CrossRef]
- Rajeshwar, K.; Bhattacharya, R.N. Electrodeposition of Cdte Thin Films. J. Electrochem. Soc. Soc. 1984, 131, 2032–2037. [Google Scholar]
- Kim, S.-H.; Lee, J.-Y.; Han, W.-K.; Lee, J.-H. Electrochemical deposition of CdSe/CdTe multilayer nanorods for hybrid solar cell. Thin Solid Films 2010, 518, 7222–7224. [Google Scholar] [CrossRef]
- Khalaf, M.K.; Alhilli, B.A.M.; Khudiar, A.I.; Alzahra, A.A. Influence of nanocrystalline size on optical band gap in CdSe thin films prepared by DC sputtering. Photonics Nanostruct. Fundam. Appl. 2016, 18, 59–66. [Google Scholar] [CrossRef]
- Bylica, A.; Sagan, P.; Virt, I.; Wisz, G.; Bester, M.; Stefaniuk, I.; Kuzma, M. Layers of CdTe and CdS obtained by PLD on ITO substrates. Thin Solid Films 2006, 511–512, 439–442. [Google Scholar] [CrossRef]
- Martín-Tovar, E.A.; Castro-Rodríguez, R.; Iribarren, A. Isoelectronic CdTe-doped ZnO thin films grown by PLD. Mater. Lett. 2015, 139, 352–354. [Google Scholar] [CrossRef]
- Hu, P.; Li, B.; Feng, L.; Jiang, H.; Yang, H.; Xiao, X. Effects of the substrate temperature on the properties of CdTe thin films deposited by pulsed laser deposition. Surf. Coat. Technol. 2012, 213, 84–89. [Google Scholar] [CrossRef]
- Richards, B.S. Comparison of TiO2 and other dielectric coatings for buried-contact solar cells: A review. Prog. Photovoltaics Res. Appl. 2004, 12, 253–281. [Google Scholar] [CrossRef]
- Edman Jonsson, G.; Fredriksson, H.; Sellappan, R.; Chakarov, D. Nanostructures for enhanced light absorption in solar energy devices. Int. J. Photoenergy 2011, 2011, 1–11. [Google Scholar] [CrossRef]
- Shir, D.; Yoon, J.; Chanda, D.; Ryu, J.H.; Rogers, J.A. Performance of ultrathin silicon solar microcells with nanostructures of relief formed by soft imprint lithography for broad band absorption enhancement. Nano Lett. 2010, 10, 3041–3046. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.H.; Kwon, J.Y.; Maldonado, S.; Tuteja, A.; Boukai, A. Extreme light absorption by multiple plasmonic layers on upgraded metallurgical grade silicon solar cells. Nano Lett. 2014, 14, 1961–1967. [Google Scholar] [CrossRef] [PubMed]
- Müller, J.; Rech, B.; Springer, J.; Vanecek, M. TCO and light trapping in silicon thin film solar cells. Sol. Energy 2004, 77, 917–930. [Google Scholar] [CrossRef]
- Berginski, M.; Hüpkes, J.; Schulte, M.; Schöpe, G.; Stiebig, H.; Rech, B.; Wuttig, M. The effect of front ZnO:Al surface texture and optical transparency on efficient light trapping in silicon thin-film solar cells. J. Appl. Phys. 2007, 101, 1–11. [Google Scholar] [CrossRef]
- Garnett, E.; Yang, P. Light trapping in silicon nanowire solar cells. Nano Lett. 2010, 10, 1082–1087. [Google Scholar] [CrossRef] [PubMed]
- Jeong, S.; McGehee, M.D.; Cui, Y. All-back-contact ultra-thin silicon nanocone solar cells with 13.7% power conversion efficiency. Nat. Commun. 2013, 4, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Nalwa, K.S.; Chaudhary, S. Design of light-trapping microscale-textured surfaces for efficient organic solar cells. Opt. Express 2010, 18, 5168–5178. [Google Scholar] [CrossRef] [PubMed]
- Branham, M.S.; Hsu, W.-C.; Yerci, S.; Loomis, J.; Boriskina, S.V.; Hoard, B.R.; Han, S.E.; Chen, G. 15.7% Efficient 10-μm-Thick Crystalline Silicon Solar Cells Using Periodic Nanostructures. Adv. Mater. 2015, 27, 2182–2188. [Google Scholar] [CrossRef] [PubMed]
- Information, O.; Science, E.; Society, O.; Ocis, A. Cosine light-trapping nanostructures for thin film solar cells. Opt. Lett. 2015, 40, 3866–3868. [Google Scholar]
- Guo, X.; Wang, D.; Xu, W.; Li, S.; Tang, P. Absorption enhancement in thin-film silicon solar cells with a Fourier-series based periodic array. Opt. Mater. Express 2017, 7, 793–798. [Google Scholar] [CrossRef]
- Baik, S.J.; Lee, Y.; Lim, K.S.; Kim, K.-T. Thin film solar cells on honeycomb-structured substrates for photovoltaic building blocks. Renew. Energy 2014, 64, 98–104. [Google Scholar] [CrossRef]
- Abrikosov, N.K. Semiconducting II–VI, IV–VI, and V–VI Compounds; Springer: Boston, MA, USA, 2013. [Google Scholar]
- Ochoa, O.R.; Witkowski, E.J., III; Colajacomo, C.; Simmons, J.H.; Potter, B.G., Jr. Raman characterization of CdTe nanocrystallites embedded in a glass matrix. J. Mater. Sci. Lett. 1997, 16, 613–616. [Google Scholar] [CrossRef]
- Amirtharaj, P.M.; Pollak, F.H. Raman scattering study of the properties and removal of excess Te on CdTe surfaces. Appl. Phys. Lett. 1984, 45, 789–791. [Google Scholar] [CrossRef]
- Artamonov, V.V.; Valakh, M.Y.; Strel’chuk, V.V.; Baidullaeva, A.; Mozol, P.E. Raman scattering by tellurium films on CdTe single crystals. J. Appl. Spectrosc. 1988, 48, 653–655. [Google Scholar] [CrossRef]
- Schreder, B.; Schmidt, T.; Ptatschek, V.; Spanhel, L.; Materny, A.; Kiefer, W. Raman characterization of CdTe/CdS core-shell clusters in colloids and films. J. Crys. Growth 2000, 214, 782–786. [Google Scholar] [CrossRef]
- Dzhagan, V.; Lokteva, I.; Himcinschi, C.; Jin, X.; Kolny-Olesiak, J.; Zahn, D.R. Phonon Raman spectra of colloidal CdTe nanocrystals: Effect of size, non-stoichiometry and ligand exchange. Nanoscale Res. Lett. 2011, 6, 79. [Google Scholar] [CrossRef] [PubMed]
- Tuschel, D. Practical Group Theory and Raman Spectroscopy, Part II: Application of Polarization. Spectroscopy 2014, 29, 15–22. [Google Scholar]
- Parker, J.H., Jr.; Feldman, D.W.; Ashkin, M. Raman scattering by silicon and germanium. Phys. Rev. 1967, 155, 712. [Google Scholar] [CrossRef]
- Filmetrics, I. Calculate Spectral Reflectance of Thin-Film Stacks. Available online: http://www.filmetrics.com/reflectance-calculator (accessed on 31 March 2017).
- Fujiwara, H. Spectroscopic Ellipsometry: Principles and Applications; John Wiley & Sons Ltd: Chischester, UK, 2007. [Google Scholar]
- Palik, E.D. (Ed.) Handbook of Optical Constants of Solids; Academic Press: San Diego, CA, USA, 1985; Volume 1. [Google Scholar]
- Optical Data from Sopra SA. Available online: http://sspectra.com/sopra.html (accessed on 23 March 2017).
- Rajesh Kumar, B.; Hymavathi, B.; Subba Rao, T. Studies on optoelectronic properties of DC reactive magnetron sputtered CdTe thin films. AIP Conf. Proc. 2014, 1576, 73–75. [Google Scholar]
- Tauc, J.; Grigorovici, R.; Vancu, A. Optical properties and eletronic structure of amorphous germanium. Phys. Stat. Sol. 1966, 15, 627–637. [Google Scholar] [CrossRef]
- De Moure-Flores, F.; Quiñones-Galván, J.G.; Guillén-Cervantes, A.; Arias-Cerón, J.S.; Contreras-Puente, G.; Hernández-Hernández, A.; Santoyo-Salazar, J.; De La, M.; Santana-Aranda, M.A.; Zapata-Torres, M.; et al. Physical properties of CdTe:Cu films grown at low temperature by pulsed laser deposition. J. Appl. Phys. 2012, 112, 1–6. [Google Scholar] [CrossRef]
- Britt, J.; Ferekides, C. Thin-film CdS/CdTe solar cell with 15.8% efficiency. Appl. Phys. Lett. 1993, 62, 2851–2852. [Google Scholar] [CrossRef]
- Battaglia, C.; Hsu, C.M.; Söderström, K.; Escarré, J.; Haug, F.J.; Charrière, M.; Boccard, M.; Despeisse, M.; Alexander, D.T.L.; Cantoni, M.; et al. Light trapping in solar cells: Can periodic beat random? ACS Nano 2012, 6, 2790–2797. [Google Scholar] [CrossRef] [PubMed]
- Dewan, R.; Jovanov, V.; Hamraz, S.; Knipp, D. Analyzing periodic and random textured silicon thin film solar cells by Rigorous Coupled Wave Analysis. Sci. Rep. 2014, 4, 1–7. [Google Scholar] [CrossRef] [PubMed]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rangel-Cárdenas, J.; Sobral, H. Optical Absorption Enhancement in CdTe Thin Films by Microstructuration of the Silicon Substrate. Materials 2017, 10, 607. https://doi.org/10.3390/ma10060607
Rangel-Cárdenas J, Sobral H. Optical Absorption Enhancement in CdTe Thin Films by Microstructuration of the Silicon Substrate. Materials. 2017; 10(6):607. https://doi.org/10.3390/ma10060607
Chicago/Turabian StyleRangel-Cárdenas, Jesús, and Hugo Sobral. 2017. "Optical Absorption Enhancement in CdTe Thin Films by Microstructuration of the Silicon Substrate" Materials 10, no. 6: 607. https://doi.org/10.3390/ma10060607
APA StyleRangel-Cárdenas, J., & Sobral, H. (2017). Optical Absorption Enhancement in CdTe Thin Films by Microstructuration of the Silicon Substrate. Materials, 10(6), 607. https://doi.org/10.3390/ma10060607




