Artificial Neural Network Modeling and Genetic Algorithm Optimization for Cadmium Removal from Aqueous Solutions by Reduced Graphene Oxide-Supported Nanoscale Zero-Valent Iron (nZVI/rGO) Composites
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Preparation of nZVI/rGO Composites
2.3. Characterization of nZVI/rGO Composites
2.4. Batch Experimental Program
2.5. Modeling and Optimization
2.5.1. RSM Modeling and Optimization
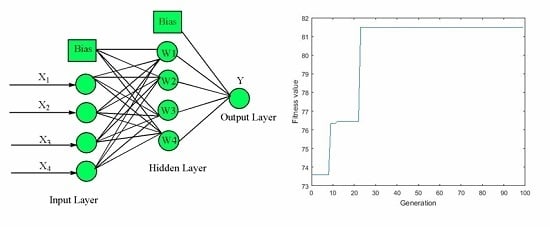
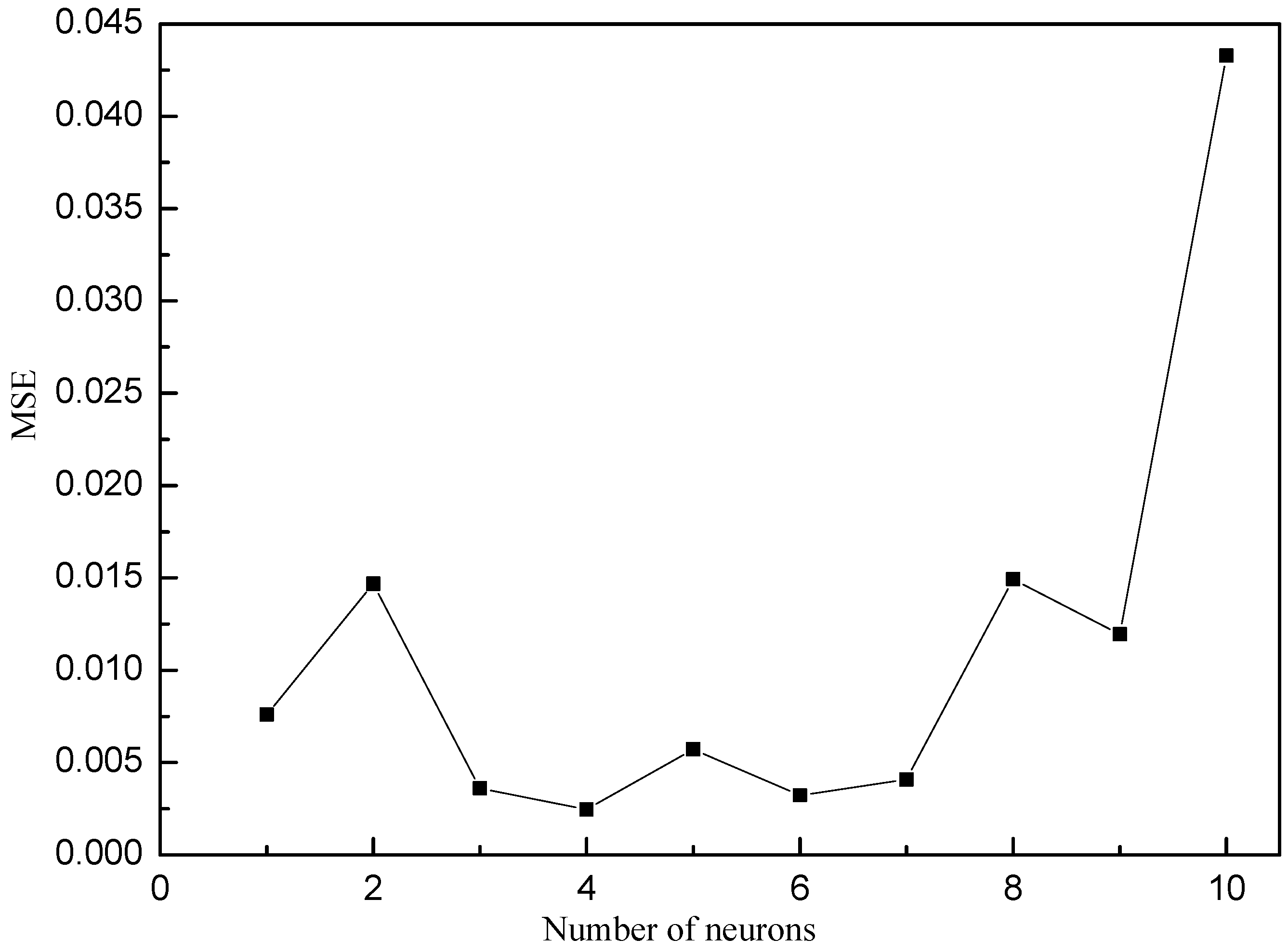
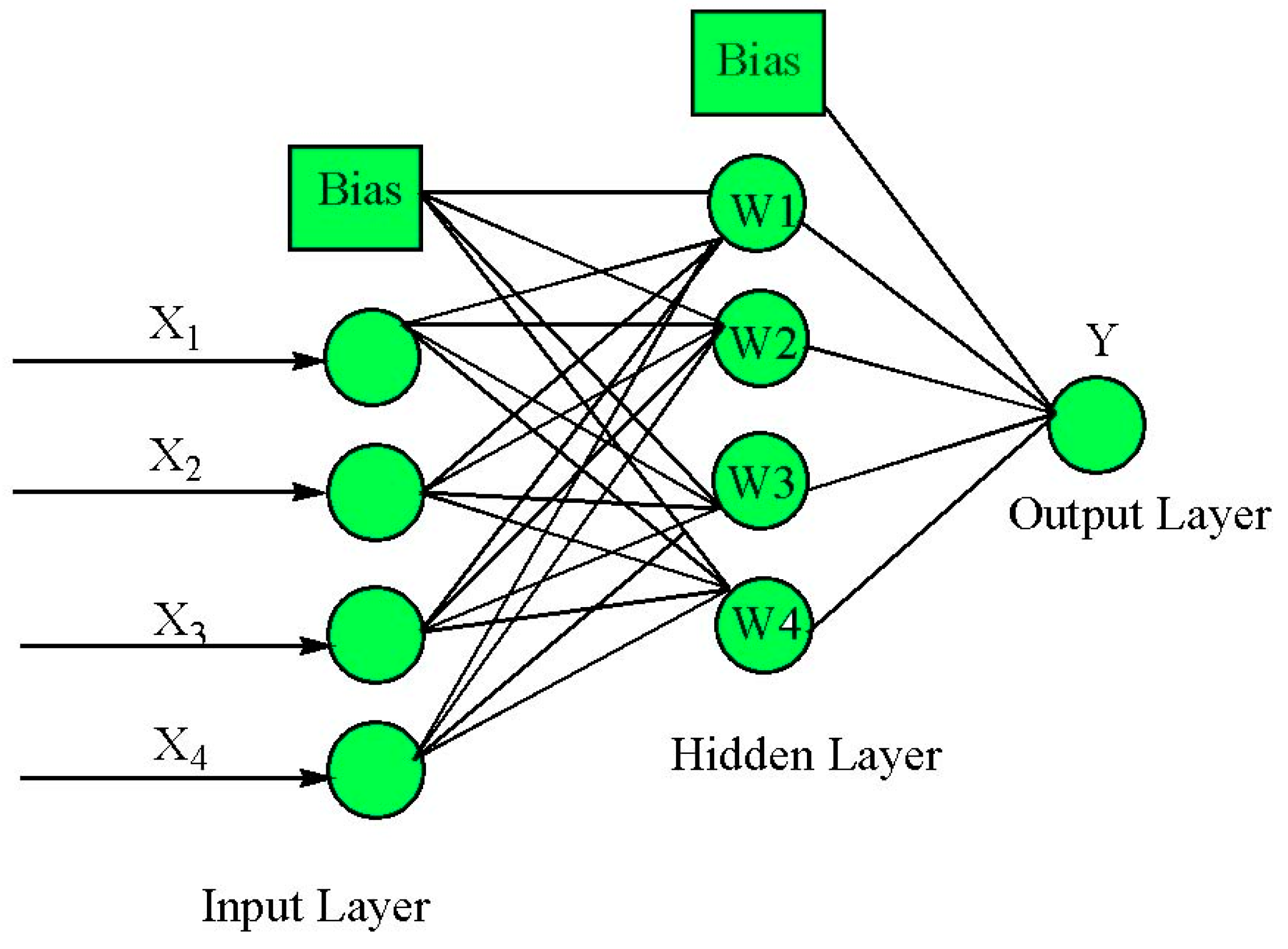
2.5.2. ANN-GA Modeling and Optimization
2.6. Adsorption Isotherm Study
2.7. Thermodynamic Study
2.8. Removal Kinetics
3. Results and Discussion
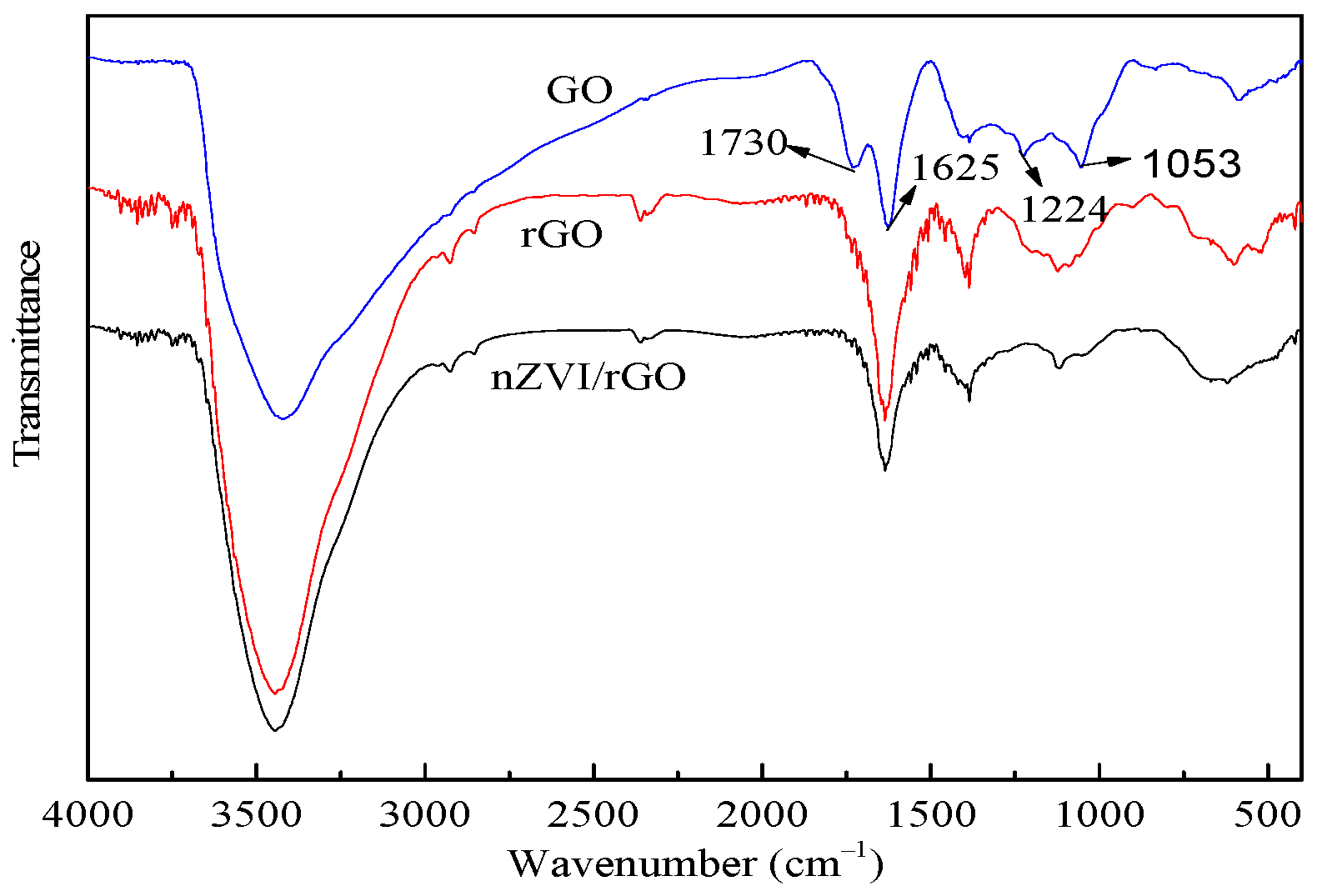
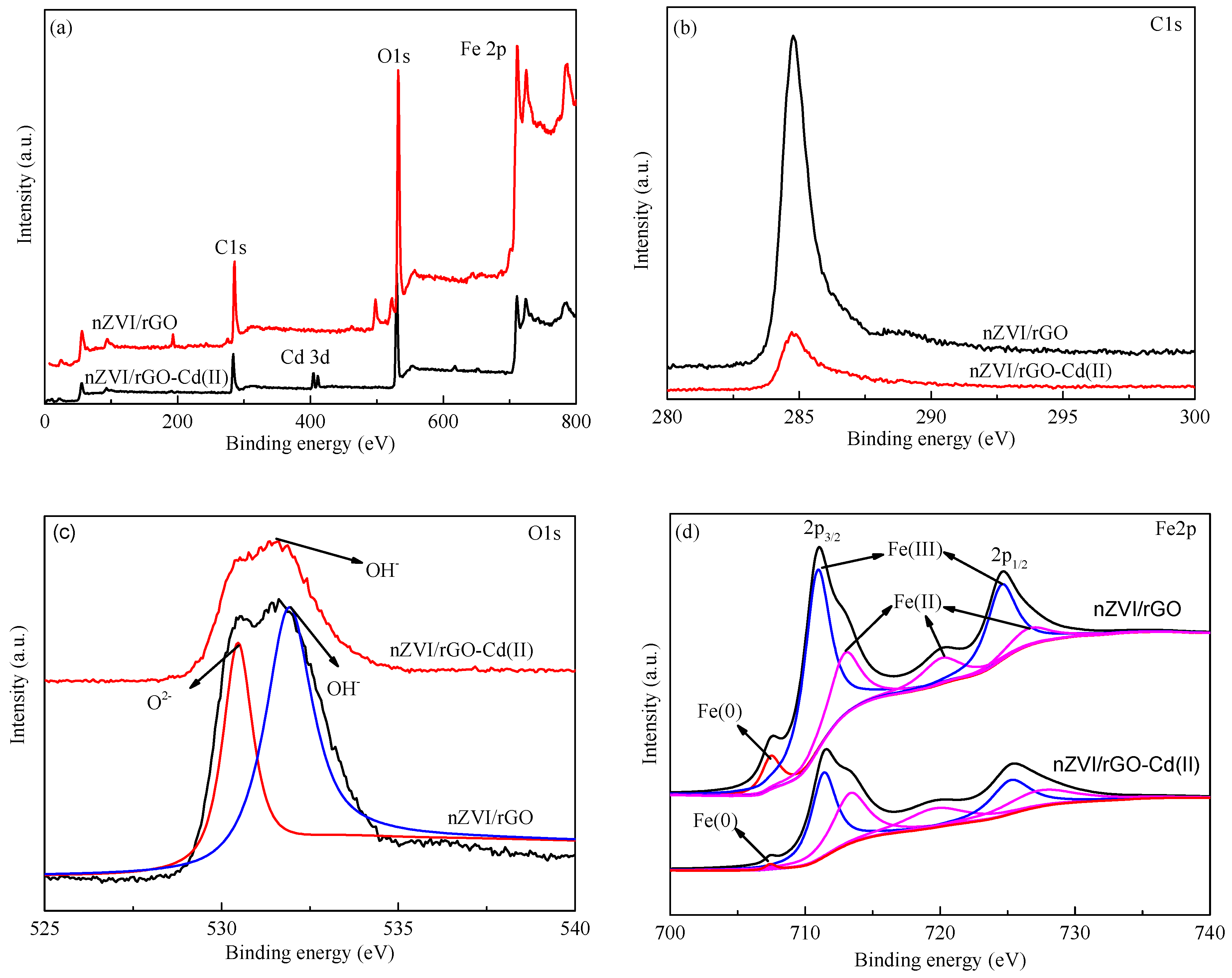
3.1. Characterization of nZVI/rGO Composites
3.2. RSM Optimization
0.29X2X3 + 0.36X2X4 + 0.03X3X4 − 0.03X12 − 3.33X22 − 0.02X32 − 0.03X42
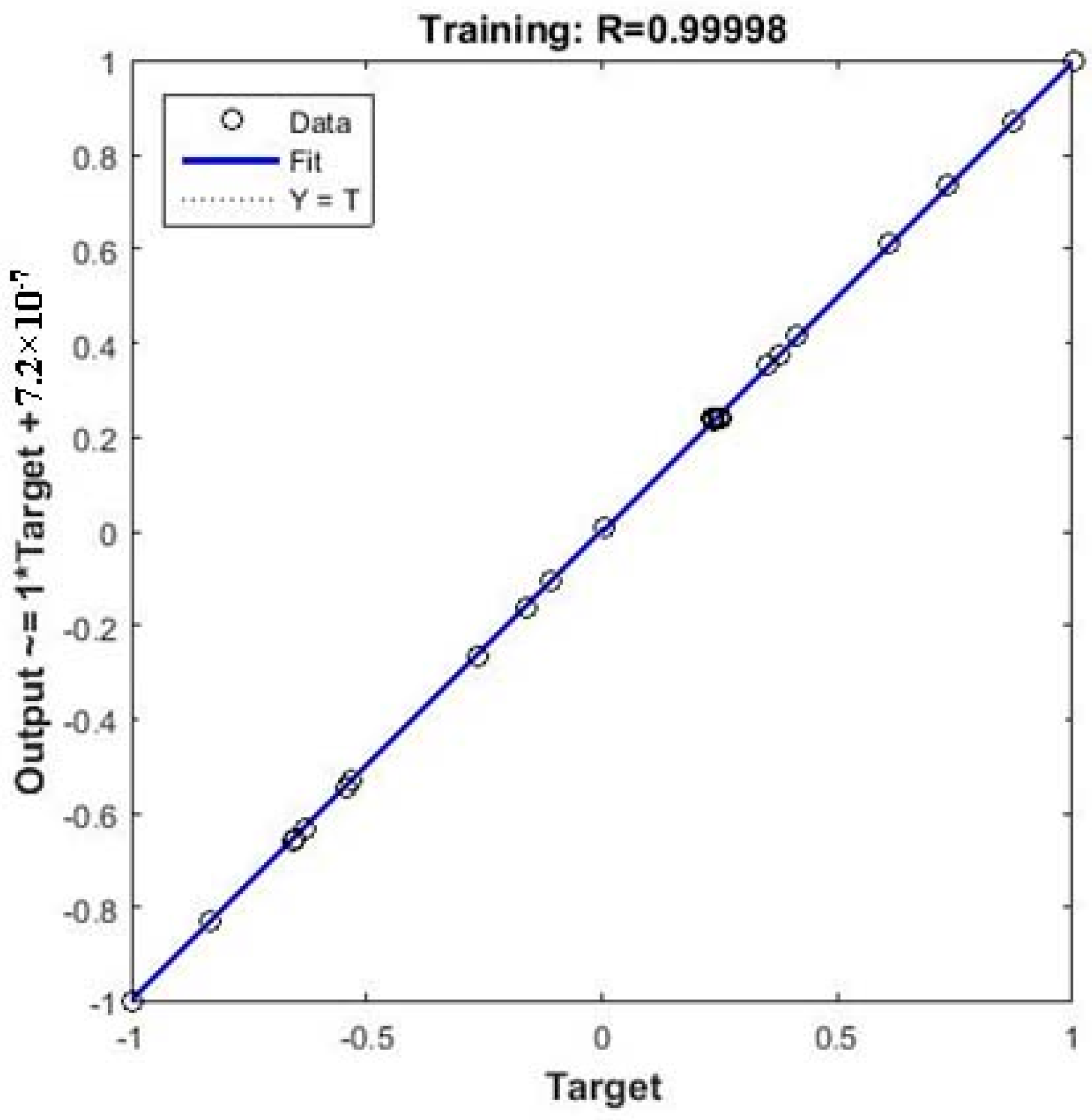
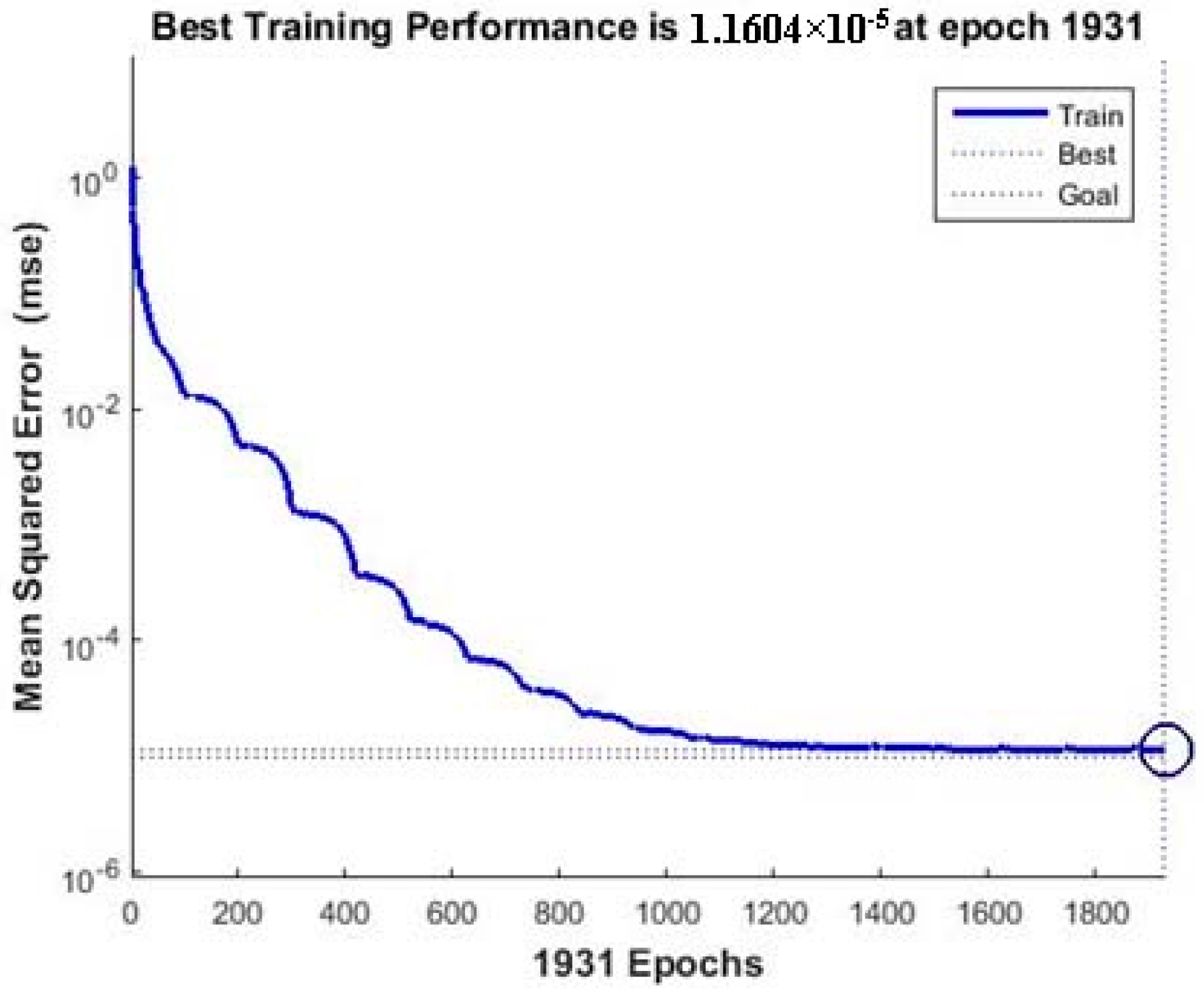
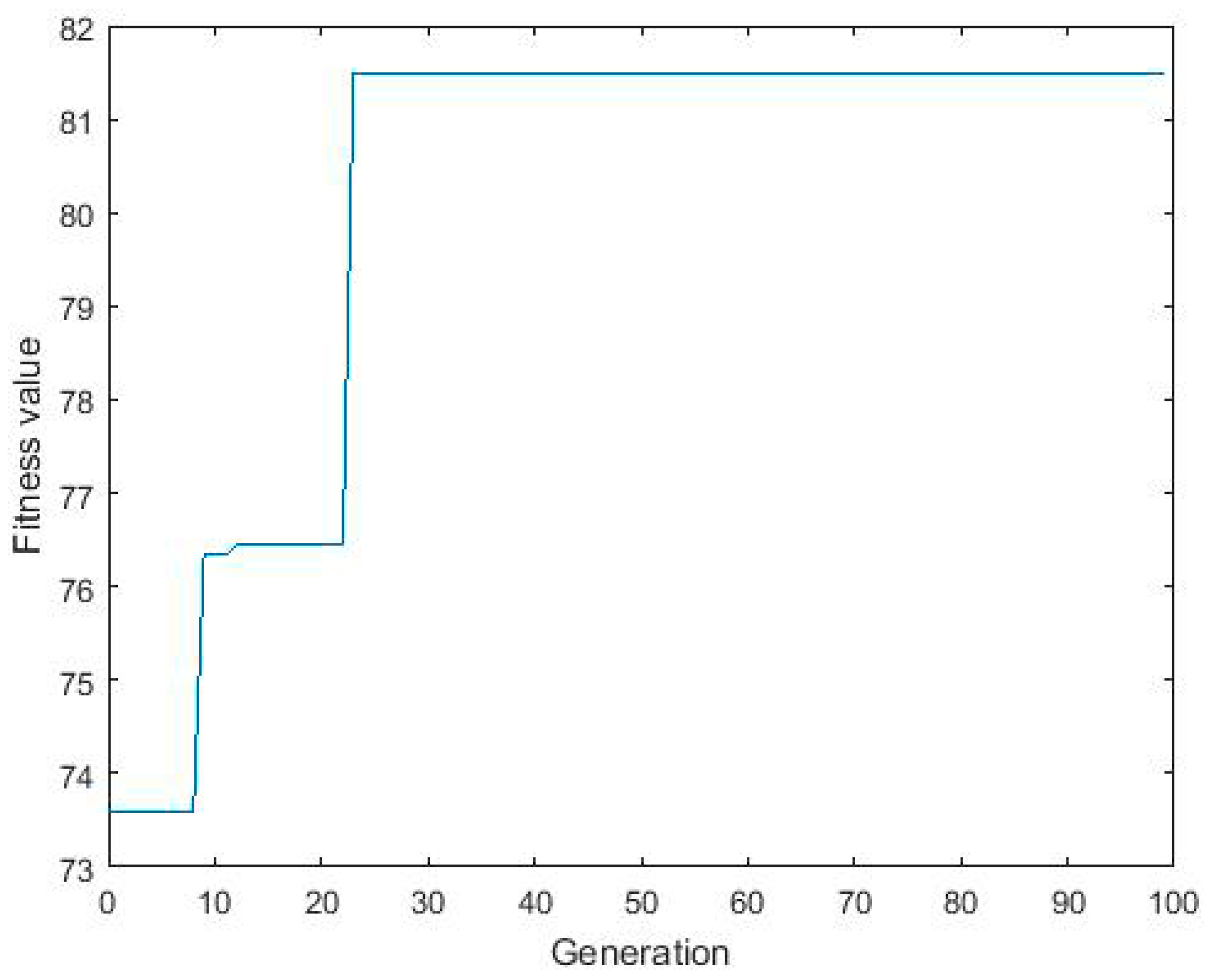
3.3. ANN-GA Optimization
3.4. Comparison of RSM and Hybrid ANN-GA
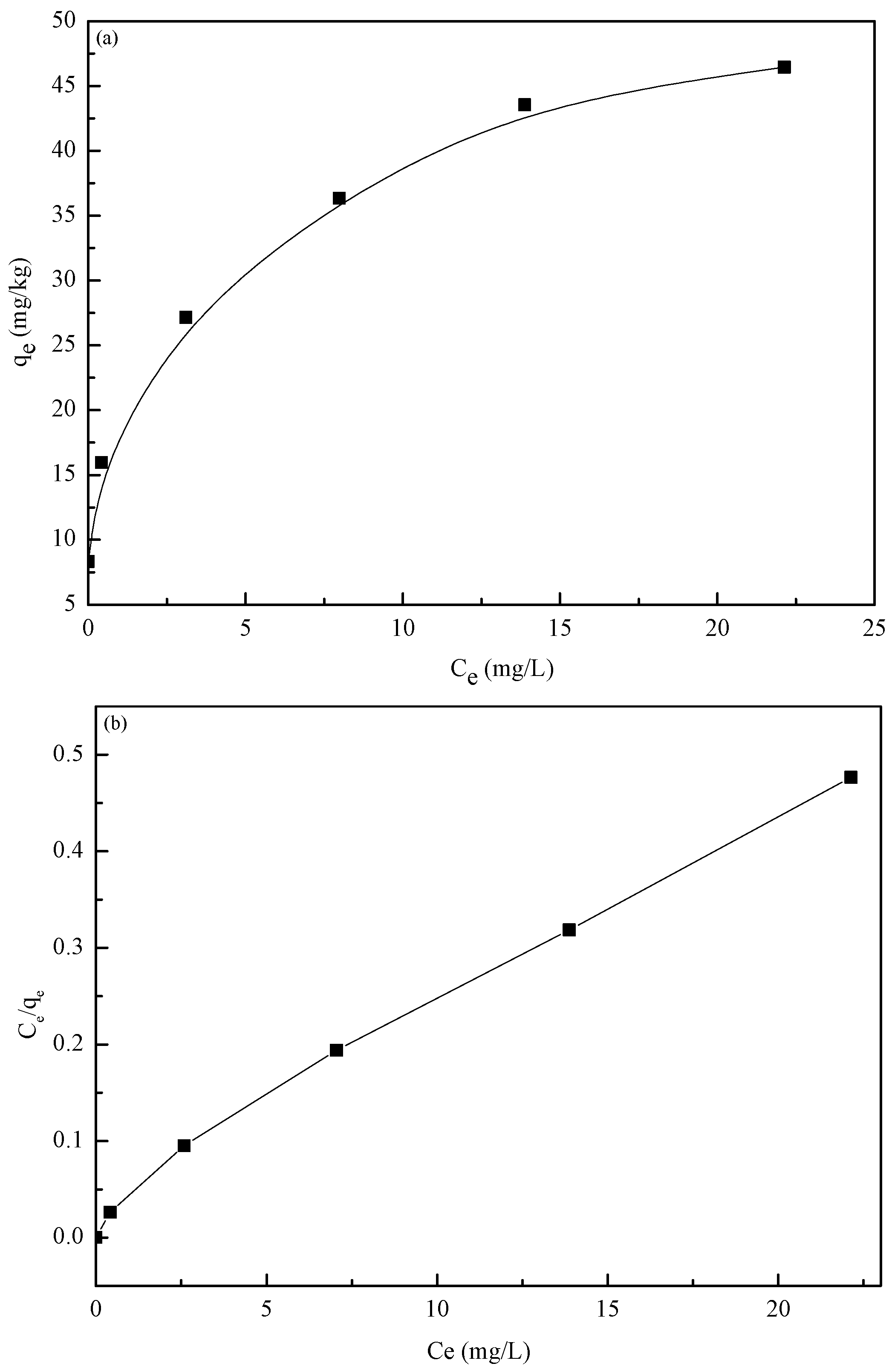
3.5. Adsorption Isotherms
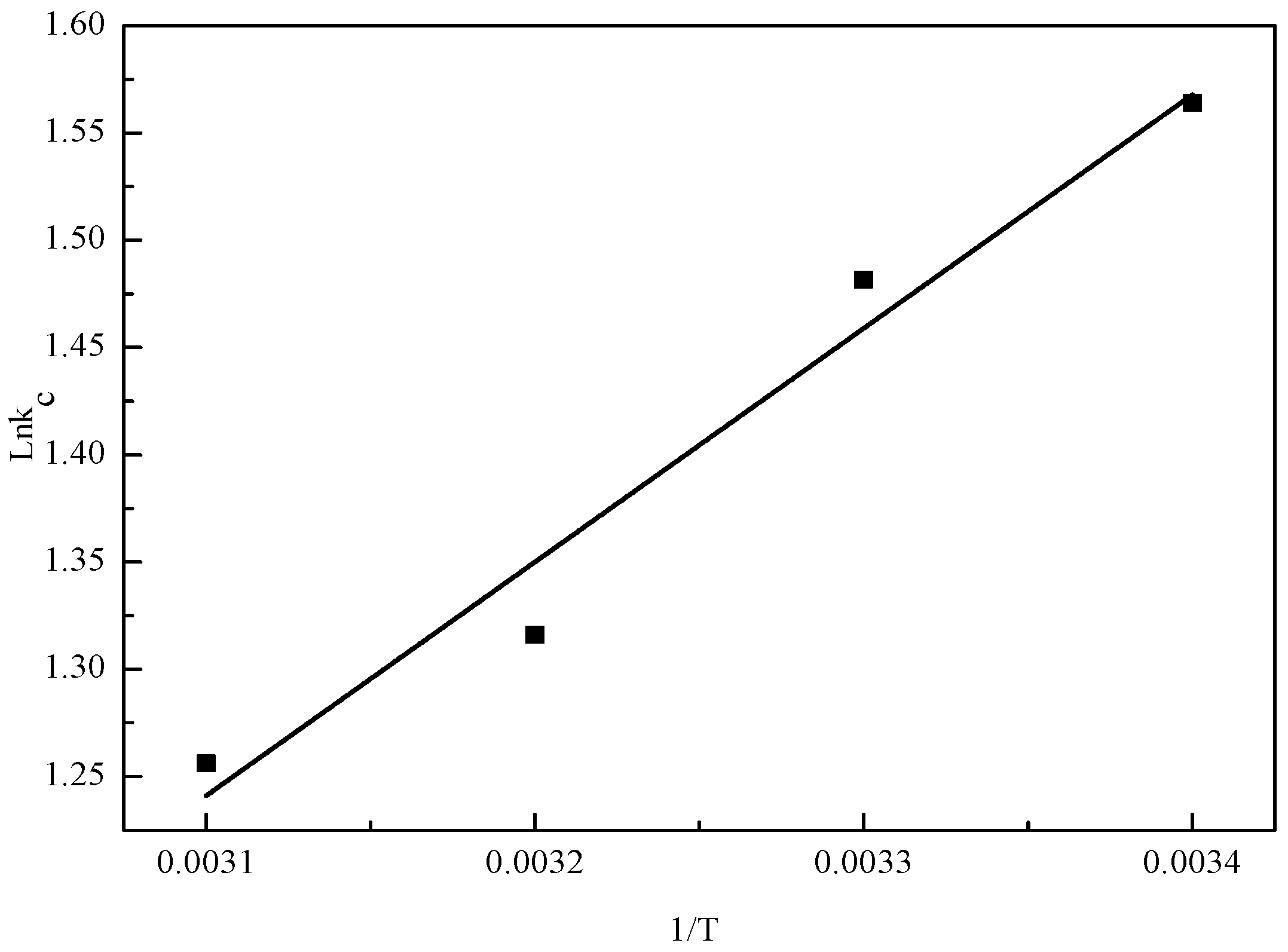
3.6. Thermodynamic Study
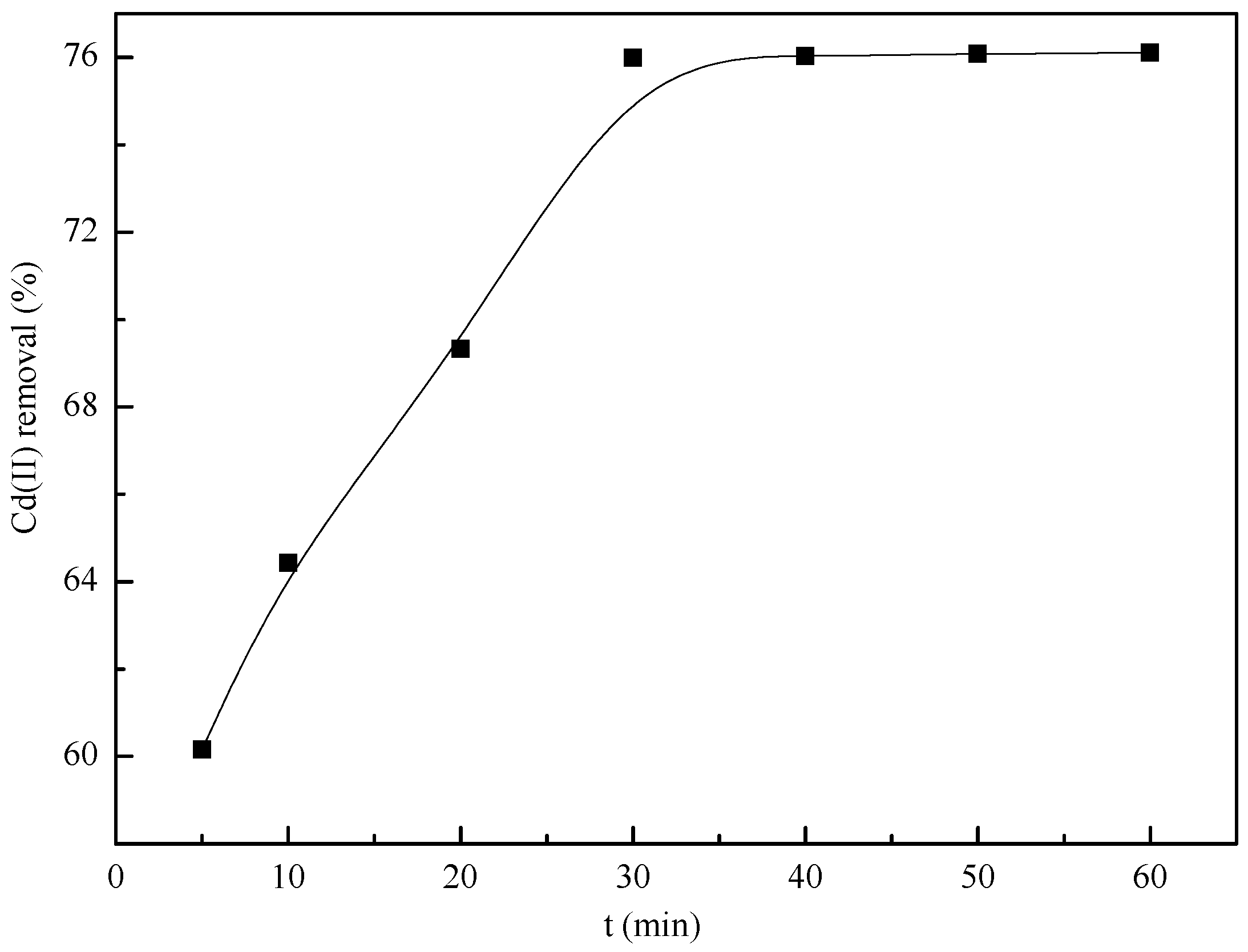
3.7. Removal Kinetics
3.8. Cd(II) Removal Mechanisms
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflict of Interest
References
- Xu, M.; Hadi, P.; Chen, G.; Mckay, G. Removal of cadmium ions from wastewater using innovative electronic waste-derived material. J. Hazard. Mater. 2014, 273, 118–123. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, N.K.; Majumder, C.B. Novel biofiltration methods for the treatment of heavy metals from industrial wastewater. J. Hazard. Mater. 2008, 151, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Kaewsarn, P.; Yu, Q. Cadmium (II) removal from aqueous solutions by pre-treated biomass of marine alga Padina sp. Environ. Pollut. 2001, 112, 209–213. [Google Scholar] [CrossRef]
- Hu, Y.; Cheng, H.; Tao, S. The Challenges and Solutions for Cadmium-contaminated Rice in China: A Critical Review. Environ. Int. 2016, 515, 92–93. [Google Scholar] [CrossRef] [PubMed]
- Kula, I.; Uğurlu, M.; Karaoğlu, H.; Celik, A. Adsorption of Cd(II) ions from aqueous solutions using activated carbon prepared from olive stone by ZnCl2 activation. Bioresour. Technol. 2008, 99, 492–501. [Google Scholar] [CrossRef] [PubMed]
- Mohan, D.; Pittman, C.U., Jr.; Bricka, M.; Smith, F.; Yancey, B.; Mohammad, J.; Steele, P.H.; Alexandrefranco, M.F.; Gómezserrano, V.; Gong, H. Sorption of arsenic, cadmium, and lead by chars produced from fast pyrolysis of wood and bark during bio-oil production. J. Colloid Interface Sci. 2007, 310, 57–73. [Google Scholar] [CrossRef] [PubMed]
- Dong, T.; Yang, L.; Zhu, M.; Liu, Z.; Sun, X.; Yu, J.; Liu, H. Removal of cadmium(II) from wastewater with gas-assisted magnetic separation. Chem. Eng. J. 2015, 280, 426–432. [Google Scholar] [CrossRef]
- Gao, J.; Sun, S.P.; Zhu, W.P.; Chung, T.S. Green modification of outer selective P84 nanofiltration (NF) hollow fiber membranes for cadmium removal. J. Membr. Sci. 2016, 499, 361–369. [Google Scholar] [CrossRef]
- Pérez-Marín, A.B.; Zapata, V.M.; Ortuño, J.F.; Aguilar, M.; Sáez, J.; Lloréns, M. Removal of cadmium from aqueous solutions by adsorption onto orange waste. J. Hazard. Mater. 2007, 139, 122–131. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Zhou, Y.; Tang, L.; Zeng, G.; Zhang, J.; Peng, B.; Xie, X.; Lai, C.; Long, B.; Zhu, J. Determination of Cd2+ and Pb2+ based on mesoporous carbon nitride/self-doped polyaniline nanofibers and square wave anodic stripping voltammetry. Nanomaterials 2016, 6, 7. [Google Scholar] [CrossRef] [PubMed]
- Zeng, L.; Zhang, Y.; Liu, Q.; Yang, L.; Xiao, J.; Liu, X.; Yang, Y. Determination of mass transfer coefficient for continuous removal of cadmium by emulsion liquid membrane in a modified rotating disc contactor. Chem. Eng. J. 2016, 289, 452–462. [Google Scholar] [CrossRef]
- Yetilmezsoy, K.; Demirel, S. Artificial neural network (ANN) approach for modeling of Pb(II) adsorption from aqueous solution by Antep pistachio (Pistacia Vera L.) shells. J. Hazard. Mater. 2008, 153, 1288–1300. [Google Scholar] [CrossRef] [PubMed]
- Assefi, P.; Ghaedi, M.; Ansari, A.; Habibi, M.H.; Momeni, M.S. Artificial neural network optimization for removal of hazardous dye Eosin Y from aqueous solution using Co2O3-NP-AC: Isotherm and kinetics study. J. Ind. Eng. Chem. 2014, 20, 2905–2913. [Google Scholar] [CrossRef]
- Zhang, Y.; Pan, B. Modeling batch and column phosphate removal by hydrated ferric oxide-based nanocomposite using response surface methodology and artificial neural network. Chem. Eng. J. 2014, 249, 111–120. [Google Scholar] [CrossRef]
- Johnson, R.; Nurmi, J.T.; Johnson, G.S.O.; Fan, D.; Johnson, R.L.O.; Shi, Z.Q.; Salter-Blanc, A.J.; Tratnyek, P.G.; Lowry, G.V. Field-scale transport and transformation of carboxymethylcellulose-stabilized nano zero-valent iron. Environ. Sci. Technol. 2013, 47, 1573–1580. [Google Scholar] [CrossRef] [PubMed]
- Li, L.Y.; Hu, J.W.; Shi, X.D.; Fan, M.Y.; Luo, J.; Wei, X. Nanoscale zero-valent metals: A review of synthesis, characterization, and applications to environmental remediation. Environ. Sci. Pollut. Res. 2016, 23, 17880–17900. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Phenrat, T.; Lowry, G.V. Effect of TCE concentration and dissolved groundwater solutes on nZVI-promoted TCE dechlorination and H2 evolution. Environ. Sci. Technol. 2007, 41, 7881–7887. [Google Scholar] [CrossRef] [PubMed]
- Yan, S.; Hua, B.; Bao, Z.; Yang, J.; Liu, C.; Deng, B. Uranium(VI) removal by nanoscale zerovalent iron in anoxic batch systems. Environ. Sci. Technol. 2010, 44, 7783–7789. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Chen, C.; Zhu, K.; Wang, X. Nanoscale zero-valent iron particles modified on reduced graphene oxides using a plasma technique for Cd(II) removal. J. Taiwan Inst. Chem. Eng. 2015, 59, 389–394. [Google Scholar] [CrossRef]
- Song, W.C.; Wang, X.X.; Wang, Q.; Shao, D.D.; Wang, X.K. Plasma-induced grafting of polyacrylatmide on graphene oxide nanosheets for simultaneous removal of radionuclides. Phys. Chem. Chem. Phys. 2015, 17, 398–406. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.T.; Chang, Y.L.; Wang, H.F.; Liu, G.B.; Chen, S.; Wang, Y.W. Folding/aggregation of graphene oxide and its application in Cu2+ removal. J. Colloid Interface Sci. 2010, 351, 122–127. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Li, Y.; Zhang, L.; Huang, H.; Hu, J.J.; Shah, S.M.; Su, X.G. Adsorption and removal of tetracycline antibiotics from aqueous solution by graphene oxide. J. Colloid Interface Sci. 2012, 368, 540–546. [Google Scholar] [CrossRef] [PubMed]
- Chandra, V.; Park, J.; Chun, Y.; Lee, J.W.; Hwang, I.C.; Kim, K.S. Water-dispersible magnetite-reduced graphene oxide composites for arsenic removal. ACS Nano 2010, 4, 3979–3986. [Google Scholar] [CrossRef] [PubMed]
- Fan, M.Y.; Li, T.J.; Hu, J.W.; Cao, R.S.; Wu, Q.; Wei, X.H.; Li, L.Y.; Shi, X.D.; Ruan, W.Q. Synthesis and characterization of reduced graphene oxide-supported nanoscale zero-valent iron (nZVI/rGO) composites used for Pb(II) removal. Materials 2016, 9, 687. [Google Scholar] [CrossRef]
- Jabeen, H.; Kemp, K.C.; Chandra, V. Synthesis of nano zerovalent iron nanoparticles—Graphene composite for the treatment of lead contaminated water. J. Eviron. Manag. 2013, 130, 429–435. [Google Scholar] [CrossRef] [PubMed]
- Sreeprasad, T.S.; Maliyekkal, S.M.; Lisha, K.P.; Pradeep, T. Reduced graphene oxide-metal/metal oxide composites: Facile synthesis and application in water purification. J. Hazard. Mater. 2011, 186, 921–931. [Google Scholar] [CrossRef] [PubMed]
- Pan, B.J.; Qiu, H.; Pan, B.C.; Nie, G.Z.; Xiao, L.L.; Lv, L.; Zhang, W.M.; Zhang, Q.X.; Zheng, S.R. Highly efficient removal of heavy metals by polymer-supported nanosized hydrated Fe(III) oxides: Behavior and XPS study. Water Res. 2010, 44, 815–824. [Google Scholar] [CrossRef] [PubMed]
- Pan, B.J.; Wu, J.; Pan, B.C.; Lv, L.; Zhang, W.M.; Xiao, L.L.; Wang, X.S.; Tao, X.C.; Zheng, S.R. Develoment of polymer-based nanosized hydrated ferric oxides (HFOs) for enhanced phosphate removal from waste effluents. Water Res. 2009, 43, 4421–4429. [Google Scholar] [CrossRef] [PubMed]
- Avramovic, J.M.; Veličkovic, A.V.; Stamenkovic, O.S.; Rajkovic, K.M.; Milic, P.S.; Veljkovic, V.B. Optimization of sunflower oil ethanolysis catalyzed by calcium oxide: RSM versus ANN-GA. Energy Convers. Manag. 2015, 105, 1149–1156. [Google Scholar] [CrossRef]
- He, X.; Guan, H.; Qin, J. A hybrid wavelet neural network model with mutual information and particle swam optimization for forecasting monthly rainfall. J. Hrdrol. 2015, 527, 88–100. [Google Scholar] [CrossRef]
- Desai, K.M.; Survase, S.A.; Saudagar, P.S.; Lele, S.S.; Singhal, R.S. Comparison of artificial neural network (ANN) and response surface methodology (RSM) in fermentation media optimization: Case study of fermentative production of scleroglucan. Biochem. Eng. J. 2008, 41, 266–273. [Google Scholar] [CrossRef]
- Kundu, P.; Paul, V.; Kumar, V.; Mishra, I.M. Formulation development, modeling and optimization of emulsification process using evolving RSM coupled hybrid ANN-GA framework. Chem. Eng. Res. Des. 2015, 104, 773–790. [Google Scholar] [CrossRef]
- Li, M.; Feng, C.; Zhang, Z.; Chen, R.; Xue, Q.; Gao, C.; Sugiura, N. Optimization of process parameters for electrochemical nitrate removal using Box-Behnken design. Electrochim. Acta 2010, 56, 265–270. [Google Scholar] [CrossRef]
- Singh, K.P.; Gupta, S.; Singh, A.K.; Sinha, S. Experimental design and response surface modeling for optimization of Rhodamine B removal from water by magnetic nanocomposite. Chem. Eng. J. 2010, 165, 151–160. [Google Scholar] [CrossRef]
- Tripathi, P.; Srivastava, V.; Kumar, A. Optimization of an azo dye batch adsorption parameters using Box-Behnken design. Desalination 2009, 249, 1273–1279. [Google Scholar] [CrossRef]
- Huang, M.; Ma, Y.; Wan, J.; Zhang, H.; Wang, Y.; Chen, Y.; Yoo, C.; Guo, W. A hybrid genetic-neural algorithm for modeling the biodegradation process of DnBP in AAO system. Bioresour. Technol. 2011, 102, 8907–8913. [Google Scholar] [CrossRef] [PubMed]
- Rajendra, M.; Jena, P.C.; Raheman, H. Prediction of optimized pretreatment process parameters for biodiesel production using ANN and GA. Fuel 2009, 88, 868–875. [Google Scholar] [CrossRef]
- Bhatti, M.S.; Kapoor, D.; Kalia, R.K.; Reddy, A.S.; Thukral, A.K. RSM and ANN modeling for electrocoagulation of copper from simulated wastewater: Multi objective optimization using genetic algorithm approach. Desalination 2011, 274, 74–80. [Google Scholar] [CrossRef]
- Koc, A.B.; Heinemann, P.H.; Ziegler, G.R. Optimization of whole milk powder processing variables with neural networks and genetic algorithms. Food Bioprod. Process. 2007, 85, 336–343. [Google Scholar] [CrossRef]
- Çelekli, A.; Bozkurt, H.; Geyik, F. Use of artificial neural networks and genetic algorithms for prediction of sorption of an azo-metal complex dye onto lentil straw. Bioresour. Technol. 2012, 129, 396–401. [Google Scholar] [CrossRef] [PubMed]
- Mohan, S.; Singh, Y.; Verma, D.K.; Hasan, S.H. Synthesis of CuO nanoparticles through green route using Citrus limon juice and its application as nanosorbent for Cr(VI) remediation: Process optimization with RSM and ANN-GA based model. Process Saf. Environ. 2015, 96, 156–166. [Google Scholar] [CrossRef]
- Singh, A.; Majumder, A.; Goyal, A. Artificial intelligence based optimization of exocellular glucansucrase production from Leuconostoc dextranicum NRRL B-1146. Bioresour. Technol. 2008, 99, 8201–8206. [Google Scholar] [CrossRef] [PubMed]
- Zafar, M.; Kumar, S.; Kumar, S.; Dhiman, A.K. Artificial intelligence based modeling and optimization of poly(3-hydroxybutyrate-co-3-hydroxyvalerate) production process by using Azohydromonas lata MTCC 2311 from cane molasses supplemented with volatile fatty acids: A genetic algorithm paradigm. Bioresour. Technol. 2012, 104, 631–641. [Google Scholar] [CrossRef] [PubMed]
- Baughman, D.R.; Liu, Y.A. Neural Networks in Bioprocessing and Chemical Engineering; Academic Press: Cambridge, MA, USA, 1995; ISBN 978-0-12-083030-5. [Google Scholar]
- Ghanbary, F.; Modirshahla, N.; Khosravi, M.; Behnajady, M.A. Synthesis of TiO2 nanoparticles in different thermal conditions and modeling its photocatalytic activity with artificial neural network. J. Environ. Sci. 2012, 24, 750–756. [Google Scholar] [CrossRef]
- Langmuir, I. The adsorption of gases on plane surfaces of glass, mica and platinum. J. Am. Chem. Soc. 1918, 143, 1361–1403. [Google Scholar] [CrossRef]
- Freundlich, H.; Heller, W. The adsorption of cis- and trans-Azobenzene. J. Am. Chem. Soc. 2002, 61, 861–870. [Google Scholar] [CrossRef]
- Baig, J.A.; Kazi, T.G.; Shah, A.Q.; Kandhro, G.A.; Afridi, H.I.; Khan, S.; Kolachi, N.F. Biosorption studies on powder of stem of Acacia nilotica: Removal of arsenic from surface water. J. Hazard. Mater. 2010, 178, 941–948. [Google Scholar] [CrossRef] [PubMed]
- Aldegs, Y.S.; Elbarghouthi, M.I.; Issa, A.A.; Khraisheh, M.A.; Walker, G.M. Sorption of Zn(II), Pb(II), and Co(II) using natural sorbents: Equilibrium and kinetic studies. Water Res. 2006, 40, 2645–2658. [Google Scholar] [CrossRef] [PubMed]
- Xu, P.; Zeng, G.M.; Huang, D.L.; Lai, C.; Zhao, M.H.; Wei, Z.; Li, N.J.; Huang, C.; Xie, G.X. Adsorption of Pb(II) by iron oxide nanoparticles immobilized Phanerochaete chrysosporium: Equilibrium, kinetic, thermodynamic and mechanisms analysis. Chem. Eng. J. 2012, 203, 423–431. [Google Scholar] [CrossRef]
- Dubey, R.; Bajpai, J.; Bajpai, A.K. Green synthesis of graphene sand composite (GSC) as novel adsorbent for efficient removal of Cr (VI) ions from aqueous solution. J. Water Process Eng. 2015, 5, 83–94. [Google Scholar] [CrossRef]
- Bhatnagar, A.; Kumar, E.; Sillanpää, M. Nitrate removal from water by nano-alumina: Characterization and sorption studies. Chem. Eng. J. 2010, 163, 317–323. [Google Scholar] [CrossRef]
- Aghaii, M.D.; Pakizeh, M.; Ahmadpour, A. Synthesis and characterization of modified UZM-5 as adsorbent for nitrate removal from aqueous solution. Sep. Purif. Technol. 2013, 113, 24–32. [Google Scholar] [CrossRef]
- Ma, X.; Li, Y.; Li, X.; Yang, L.; Wang, X. Preparation of novel polysulfone capsules containing zirconium phosphate and their properties for Pb2+ removal from aqueous solution. J. Hazard. Mater. 2011, 188, 296–303. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.W.; Zhuang, Y.; Luo, J.; Wei, X.H. A quantitative structure-property relationship study on reaction rate constants for reductive debromination of polybrominated diphenyl ether by zero-valent iron. Adv. Mater. Res. 2012, 550, 2668–2675. [Google Scholar] [CrossRef]
- Singh, Y.; Srivastav, S.K. Statistical and evolutionary optimization for enhanced production of an antileukemic enzyme, l-asparaginase, in a protease-deficient Bacillus aryabhattai ITBHU02 isolated from the soil contaminated with hospital waste. Indian J. Exp. Biol. 2013, 51, 322–335. [Google Scholar] [PubMed]
- Amirov, A.; Gerget, O.; Devjatyh, D.; Gazaliev, A. Medical data processing system based on neural network and genetic algorithm. Procedia Soc. Behav. Sci. 2014, 131, 149–155. [Google Scholar] [CrossRef]
- Azouaou, N.; Sadaoui, Z.; Djaafri, A.; Mokaddem, H. Adsorption of cadmium from aqueous solution onto untreated coffee grounds: Equilibrium, kinetics and thermodynamics. J. Hazard. Mater. 2010, 184, 126–134. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, V.C.; Mall, I.D.; Mishra, I.M. Equilibrium modelling of single and binary adsorption of cadmium and nickel onto bagasse fly ash. Chem. Eng. J. 2006, 117, 79–91. [Google Scholar] [CrossRef]
- Wasewar, K.L. Adsorption of cadmium ions from aqueous solution using granular activated carbon and activated clay. CLEAN Soil Air Water 2015, 38, 649–656. [Google Scholar] [CrossRef]
- Heidari, A.; Younesi, H.; Mehraban, Z. Removal of Ni(II), Cd(II), and Pb(II) from a ternary aqueous solution by amino functionalized mesoporous and nano mesoporous silica. Chem. Eng. J. 2009, 153, 70–79. [Google Scholar] [CrossRef]
- Sengil, I.A.; Ozacar, M. Competitive biosorption of Pb2+, Cu2+ and Zn2+ ions from aqueous solutions onto valonia tannin resin. J. Hazard. Mater. 2009, 166, 1488–1494. [Google Scholar] [CrossRef] [PubMed]
- Ahmaruzzaman, M.; Sharma, D.K. Adsorption of phenols from wastewater. J. Colloid Interface Sci. 2005, 287, 14–24. [Google Scholar] [CrossRef] [PubMed]
- Verma, D.K.; Hasan, S.H.; Ranjan, D.; Banik, R.M. Modified biomass of Phanerochaete chrysosporium immobilized on luffa sponge for biosorption of hexavalent chromium. Int. J. Environ. Sci. Te. 2014, 11, 1927–1938. [Google Scholar] [CrossRef]
- Ranjan, D.; Talat, M.; Hasan, S.H. Biosorption of arsenic from aqueous solution using agricultural residue ‘rice polish’. J. Hazard. Mater. 2009, 166, 1050–1059. [Google Scholar] [CrossRef] [PubMed]
- Barkat, M.; Nibou, D.; Chegrouche, S.; Mellah, A. Kinetics and thermodynamics studies of chromium(VI) ions adsorption onto activated carbon from aqueous solutions. Chem. Eng. Process. 2009, 48, 38–47. [Google Scholar] [CrossRef]
- Ngomsik, A.F.; Bee, A.; Siaugue, J.M.; Cabuil, V.; Cote, G. Nickel adsorption by magnetic alginate microcapsules containing an extractant. Water Res. 2006, 40, 1848–1856. [Google Scholar] [CrossRef] [PubMed]
- Namasivayam, C.; Ranganathan, K. Removal of Cd(II) from wastewater by adsorption on “waste” Fe(III)Cr(III) hydroxide. Water Res. 1995, 29, 1737–1744. [Google Scholar] [CrossRef]
- Pandey, P.K.; Sharma, S.K.; Sambi, S.S. Kinetics and equilibrium study of chromium adsorption on zeoliteNaX. Int. J. Environ. Sci. Technol. 2010, 7, 395–404. [Google Scholar] [CrossRef]
- Jabeen, H.; Chandra, V.; Jung, S.; Lee, J.W.; Kim, K.S.; Kim, S.B. Enhanced Cr(VI) removal using iron nanoparticle decorated graphene. Nanoscale 2011, 3, 3583–3585. [Google Scholar] [CrossRef] [PubMed]
- Bhunia, P.; Kim, G.; Baik, C.; Lee, H. A strategically designed porous iron-iron oxide matrix on graphene for heavy metal adsorption. Chem. Commun. 2012, 48, 9888. [Google Scholar] [CrossRef] [PubMed]
- Boparai, H.K.; Joseph, M.; O’Carroll, D.M. Cadmium (Cd2+) removal by nano zerovalent iron: Surface analysis, effects of solution chemistry and surface complexation modeling. Environ. Sci. Pollut. Res. 2013, 20, 6210–6221. [Google Scholar] [CrossRef] [PubMed]

| Parameters | Unit | Lower Level (−1) | Middle Level (0) | Upper Level (+1) |
|---|---|---|---|---|
| Initial concentration | mg/L | 20 | 30 | 40 |
| Initial pH | 5 | 6 | 7 | |
| contact time | min | 10 | 20 | 30 |
| operating temperature | °C | 20 | 30 | 40 |
| Run | X1 | X2 | X3 | X4 | YExperimental | YRSM,pred | YANN,pred |
|---|---|---|---|---|---|---|---|
| mg/L | min | °C | % | % | % | ||
| 1 | 40 | 7 | 20 | 30 | 51.77 ± 0.52 | 52.48 | 51.77 |
| 2 | 40 | 5 | 20 | 30 | 47.05 ± 0.36 | 46.17 | 47.05 |
| 3 | 30 | 5 | 20 | 40 | 50.32 ± 0.42 | 51.09 | 50.32 |
| 4 | 20 | 6 | 20 | 40 | 67.58 ± 0.78 | 68.35 | 67.58 |
| 5 | 30 | 6 | 20 | 30 | 64.88 ± 0.22 | 64.72 | 64.74 |
| 6 | 40 | 6 | 30 | 30 | 50.01 ± 0.57 | 50.97 | 50.01 |
| 7 | 30 | 6 | 20 | 30 | 64.89 ± 0.55 | 64.72 | 64.74 |
| 8 | 30 | 7 | 20 | 20 | 58.97 ± 0.68 | 58.19 | 58.97 |
| 9 | 40 | 6 | 20 | 20 | 44.26 ± 0.15 | 43.53 | 44.26 |
| 10 | 30 | 5 | 10 | 30 | 52.01 ± 0.25 | 53.01 | 52.01 |
| 11 | 30 | 6 | 30 | 40 | 66.97 ± 0.38 | 65.99 | 66.97 |
| 12 | 30 | 6 | 30 | 20 | 58.11 ± 0.21 | 58.91 | 58.11 |
| 13 | 20 | 7 | 20 | 30 | 77.25 ± 0.88 | 78.09 | 77.25 |
| 14 | 30 | 6 | 20 | 30 | 64.62 ± 0.74 | 64.72 | 64.74 |
| 15 | 40 | 6 | 10 | 30 | 49.92 ± 0.28 | 50.67 | 49.92 |
| 16 | 20 | 6 | 20 | 20 | 66.58 ± 0.33 | 67.43 | 66.58 |
| 17 | 30 | 7 | 20 | 40 | 70.85 ± 0.53 | 71.94 | 70.85 |
| 18 | 40 | 6 | 20 | 40 | 56.37 ± 0.45 | 55.56 | 56.37 |
| 19 | 30 | 6 | 20 | 30 | 64.67 ± 0.56 | 64.72 | 64.74 |
| 20 | 30 | 6 | 20 | 30 | 64.52 ± 0.72 | 64.72 | 64.74 |
| 21 | 20 | 6 | 30 | 30 | 75.12 ± 0.52 | 74.36 | 75.12 |
| 22 | 30 | 6 | 10 | 40 | 60.87 ± 0.32 | 60.04 | 60.86 |
| 23 | 30 | 7 | 30 | 30 | 72.88 ± 0.76 | 71.92 | 72.88 |
| 24 | 30 | 7 | 10 | 30 | 61.66 ± 0.11 | 60.76 | 64.66 |
| 25 | 20 | 6 | 10 | 30 | 64.94 ± 0.29 | 63.98 | 65.14 |
| 26 | 30 | 5 | 20 | 20 | 52.98 ± 0.07 | 51.89 | 53.79 |
| 27 | 30 | 5 | 30 | 30 | 51.58 ± 0.26 | 52.52 | 55.34 |
| 28 | 30 | 6 | 10 | 20 | 53.23 ± 0.54 | 54.18 | 51.08 |
| 29 | 20 | 5 | 20 | 30 | 57.99 ± 0.37 | 57.25 | 57.28 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | Remarks |
|---|---|---|---|---|---|---|
| Model | 2109.55 | 14 | 150.68 | 113.96 | <0.0001 | significant |
| X1 | 1009.80 | 1 | 1009.80 | 763.73 | <0.0001 | |
| X2 | 552.84 | 1 | 552.84 | 418.13 | <0.0001 | |
| X3 | 85.55 | 1 | 85.55 | 64.70 | <0.0001 | |
| X4 | 125.65 | 1 | 125.65 | 95.03 | <0.0001 | |
| X1X2 | 52.85 | 1 | 52.85 | 39.97 | <0.0001 | |
| X1X3 | 25.45 | 1 | 25.45 | 19.25 | 0.0006 | |
| X1X4 | 30.86 | 1 | 30.86 | 23.34 | 0.0003 | |
| X2X3 | 33.93 | 1 | 33.93 | 25.66 | 0.0002 | |
| X2X4 | 52.85 | 1 | 52.85 | 39.97 | <0.0001 | |
| X3X4 | 0.37 | 1 | 0.37 | 0.28 | 0.6041 | |
| X12 | 54.15 | 1 | 54.15 | 40.95 | <0.0001 | |
| X22 | 71.95 | 1 | 71.95 | 54.42 | <0.0001 | |
| X32 | 21.76 | 1 | 21.76 | 16.46 | 0.0012 | |
| X42 | 62.66 | 1 | 62.66 | 47.39 | <0.0001 | |
| Residual | 18.51 | 14 | 1.32 | |||
| Lack of Fit | 18.51 | 10 | 1.84 | 68.85 | 0.0005 | not significant |
| Pure Error | 0.11 | 4 | 0.027 | |||
| Total | 2128.07 | 28 |
| Independent Variable | Order | Relative Importance (%) |
|---|---|---|
| Initial concentration | 1 | 43.33 |
| Initial pH | 2 | 30.71 |
| Contact time | 4 | 10.57 |
| Operating temperature | 3 | 15.39 |
| Process Parameters | RSM | ANN-GA | ||
|---|---|---|---|---|
| Optimized Values | Experimental Values | Optimized Values | Experimental Values | |
| Initial Cd(II) concentration (mg/L) | 20.00 | 20.00 | 20.16 | 20.00 |
| Initial pH | 7.00 | 7.00 | 6.48 | 6.50 |
| Contact time (min) | 30.00 | 30.00 | 30.00 | 30.00 |
| Operating temperature (°C) | 37.13 | 37.10 | 25.31 | 25.30 |
| Removal efficiency (%) | 85.92 | 80.36 ± 0.46% | 81.50 | 82.38 ± 0.82% |
| Average values of prediction errors (%) | 6.47 | 1.08 | ||
| R2 | 0.9913 | 0.9999 | ||
| Isotherms | Equation | Parameters | Values of Parameters |
|---|---|---|---|
| Langmuir | k (L/mg) | 0.96 | |
| qm (mg/g) | 47.84 | ||
| R2 | 0.9909 | ||
| Freundlich | Kf (mg/g) | 20.02 | |
| n 1/n | 3.54 0.28 | ||
| R2 | 0.9852 | ||
| D–R | β (mol2/J2) | 10−7 | |
| qm (mol/g) E (kJ/mol) | 0.34 2.24 | ||
| R2 | 0.8226 |
| Initial Concentration (mg/L) | RL Value |
|---|---|
| 5 | 0.172 |
| 10 | 0.094 |
| 20 | 0.050 |
| 30 | 0.034 |
| 40 | 0.025 |
| 50 | 0.020 |
| T (K) | Equation | ΔS (kJ/mol/K) | ΔH (kJ/mol) | ΔG (kJ/mol) |
|---|---|---|---|---|
| 293 | 0.0587 | −8.5759 | −25.7752 | |
| 303 | −26.3622 | |||
| 313 | −26.9492 | |||
| 323 | −27.5363 |
| Model | Equation | Parameters | Value of Parameters |
|---|---|---|---|
| Pseudo-first-order kinetics | k1 (1/min) | 2.23 × 10−1 | |
| qe (mg/g) | 53.43 | ||
| R2 | 0.8729 | ||
| Pseudo-second-order kinetics | k2 (g/mg/min) | 3.41 × 10−1 | |
| qe (mg/g) | 26.32 | ||
| R2 | 0.996 | ||
| Intraparticle diffusion | k3 (mg/g/min1/2) | 1.03 | |
| b (mg/g) | 18.37 | ||
| R2 | 0.8841 | ||
| experimental qe (mg/g) | 25.37 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, M.; Li, T.; Hu, J.; Cao, R.; Wei, X.; Shi, X.; Ruan, W. Artificial Neural Network Modeling and Genetic Algorithm Optimization for Cadmium Removal from Aqueous Solutions by Reduced Graphene Oxide-Supported Nanoscale Zero-Valent Iron (nZVI/rGO) Composites. Materials 2017, 10, 544. https://doi.org/10.3390/ma10050544
Fan M, Li T, Hu J, Cao R, Wei X, Shi X, Ruan W. Artificial Neural Network Modeling and Genetic Algorithm Optimization for Cadmium Removal from Aqueous Solutions by Reduced Graphene Oxide-Supported Nanoscale Zero-Valent Iron (nZVI/rGO) Composites. Materials. 2017; 10(5):544. https://doi.org/10.3390/ma10050544
Chicago/Turabian StyleFan, Mingyi, Tongjun Li, Jiwei Hu, Rensheng Cao, Xionghui Wei, Xuedan Shi, and Wenqian Ruan. 2017. "Artificial Neural Network Modeling and Genetic Algorithm Optimization for Cadmium Removal from Aqueous Solutions by Reduced Graphene Oxide-Supported Nanoscale Zero-Valent Iron (nZVI/rGO) Composites" Materials 10, no. 5: 544. https://doi.org/10.3390/ma10050544
APA StyleFan, M., Li, T., Hu, J., Cao, R., Wei, X., Shi, X., & Ruan, W. (2017). Artificial Neural Network Modeling and Genetic Algorithm Optimization for Cadmium Removal from Aqueous Solutions by Reduced Graphene Oxide-Supported Nanoscale Zero-Valent Iron (nZVI/rGO) Composites. Materials, 10(5), 544. https://doi.org/10.3390/ma10050544