3.1. Fatigue Crack Growth Rate
A feasible theory and methodology for using the three MLAs for fatigue crack growth rate calculation has been introduced. In this section, various experimental data of different materials and characteristics are employed to validate the practical effectiveness of MLAs. The three MLAs are compared with each other to demonstrate the advantages and disadvantages. The training results of MLAs listed in this paper are the best choosing from a number of trial and error. Additionally, the predictions of classical
approach are also utilized to compare with the results of MLAs with respect. The
α value in
formula of different materials references the results of Kujawski’s researches for
approach [
14,
43].
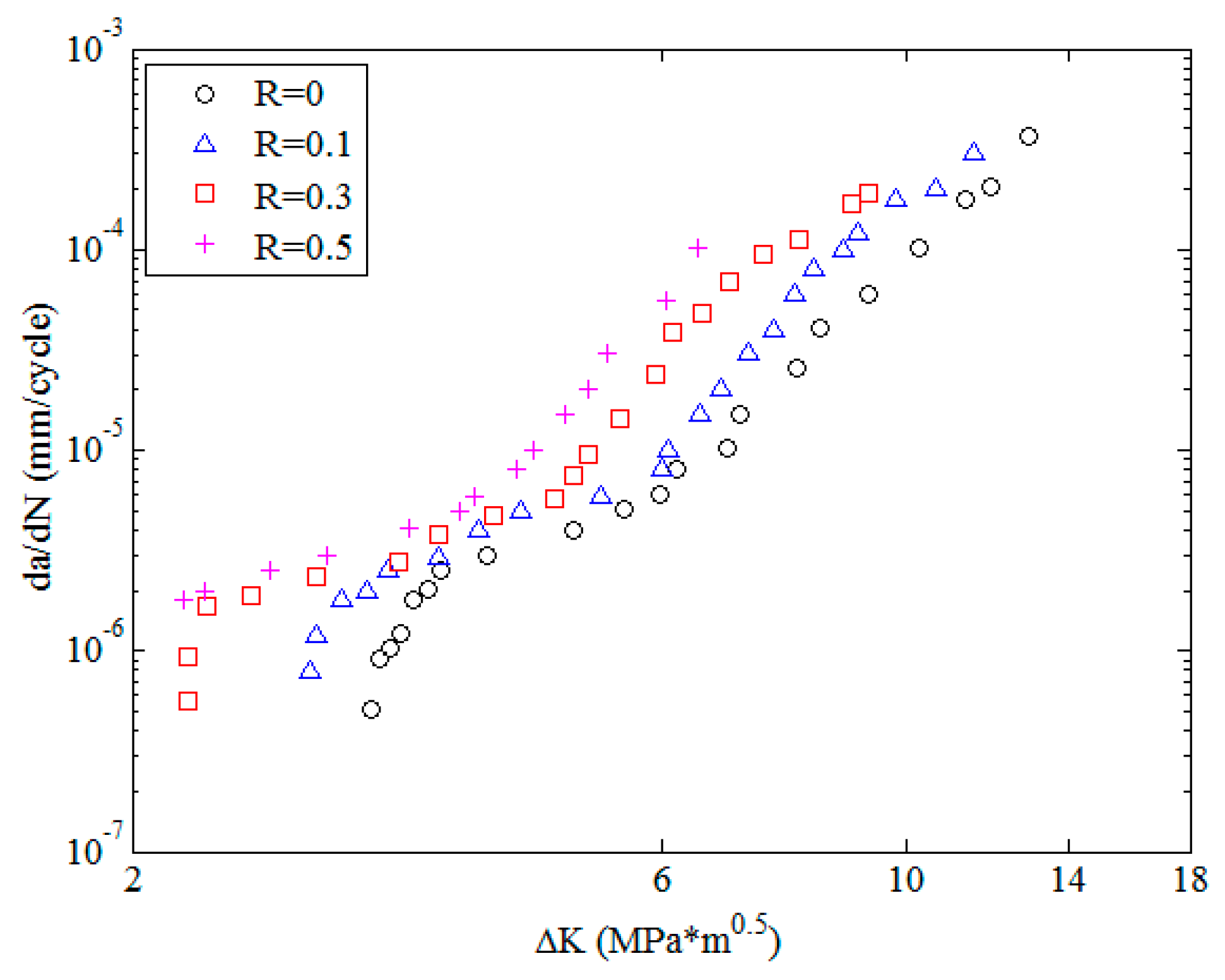
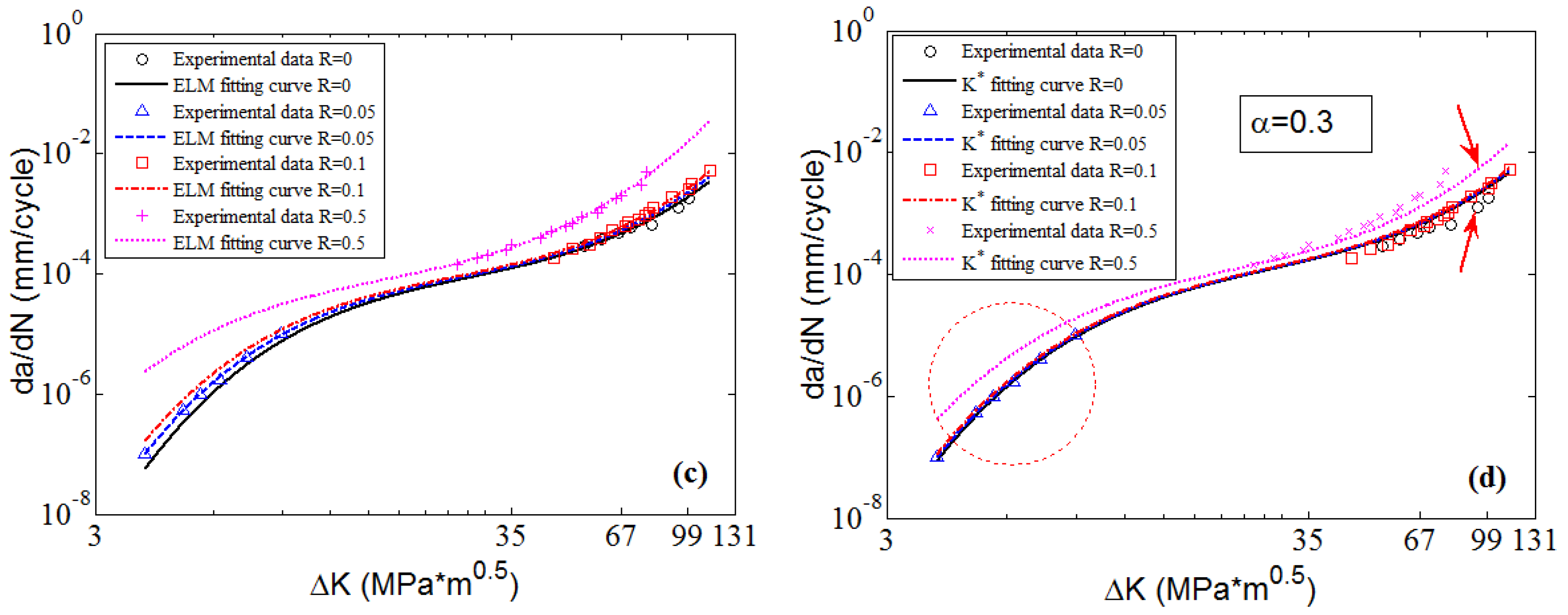
The experimental data of 2024-T351 aluminum alloy [
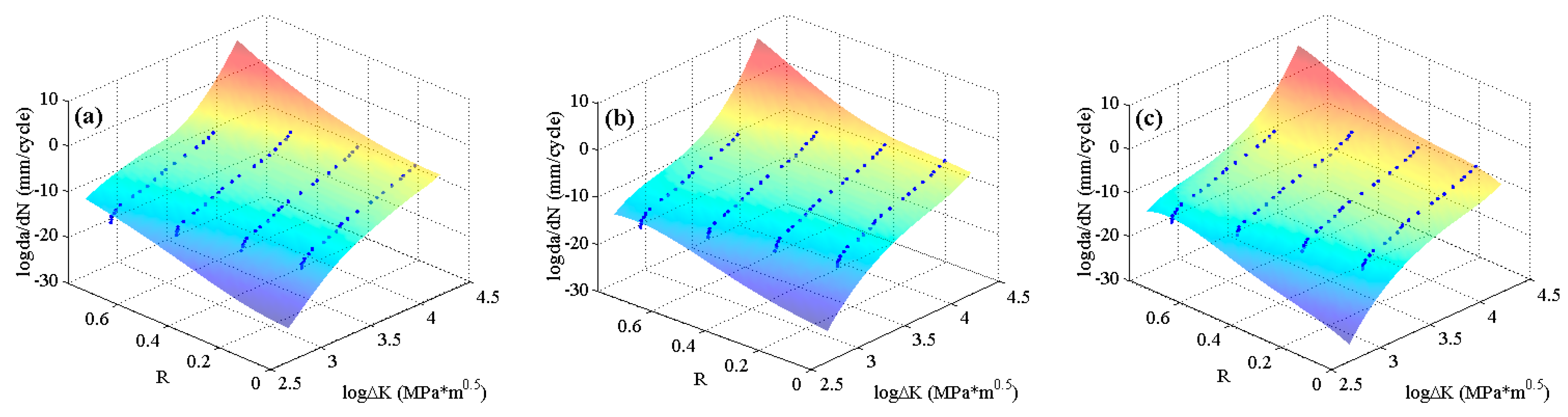
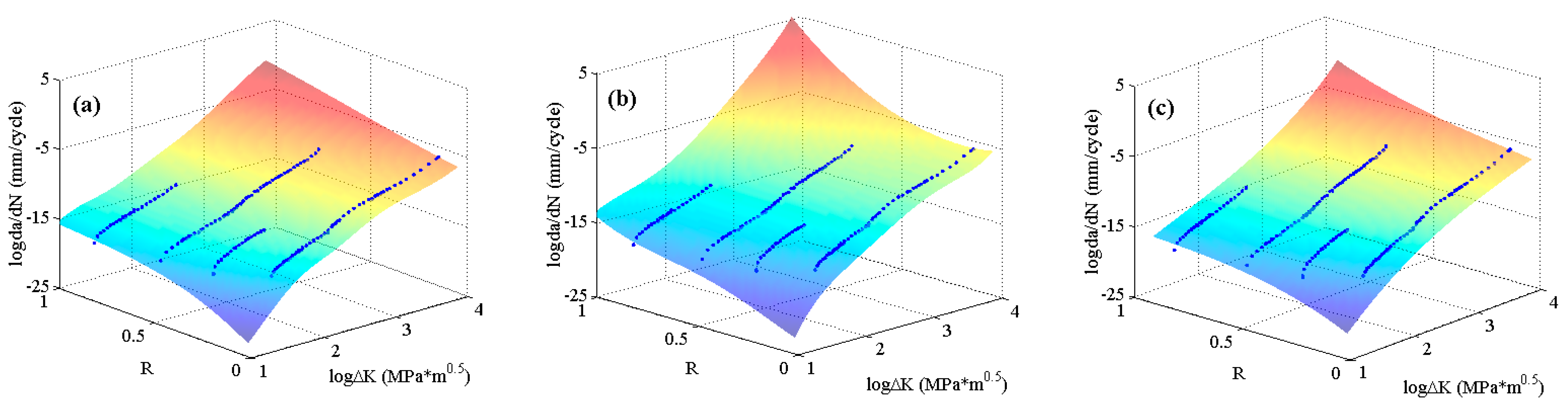
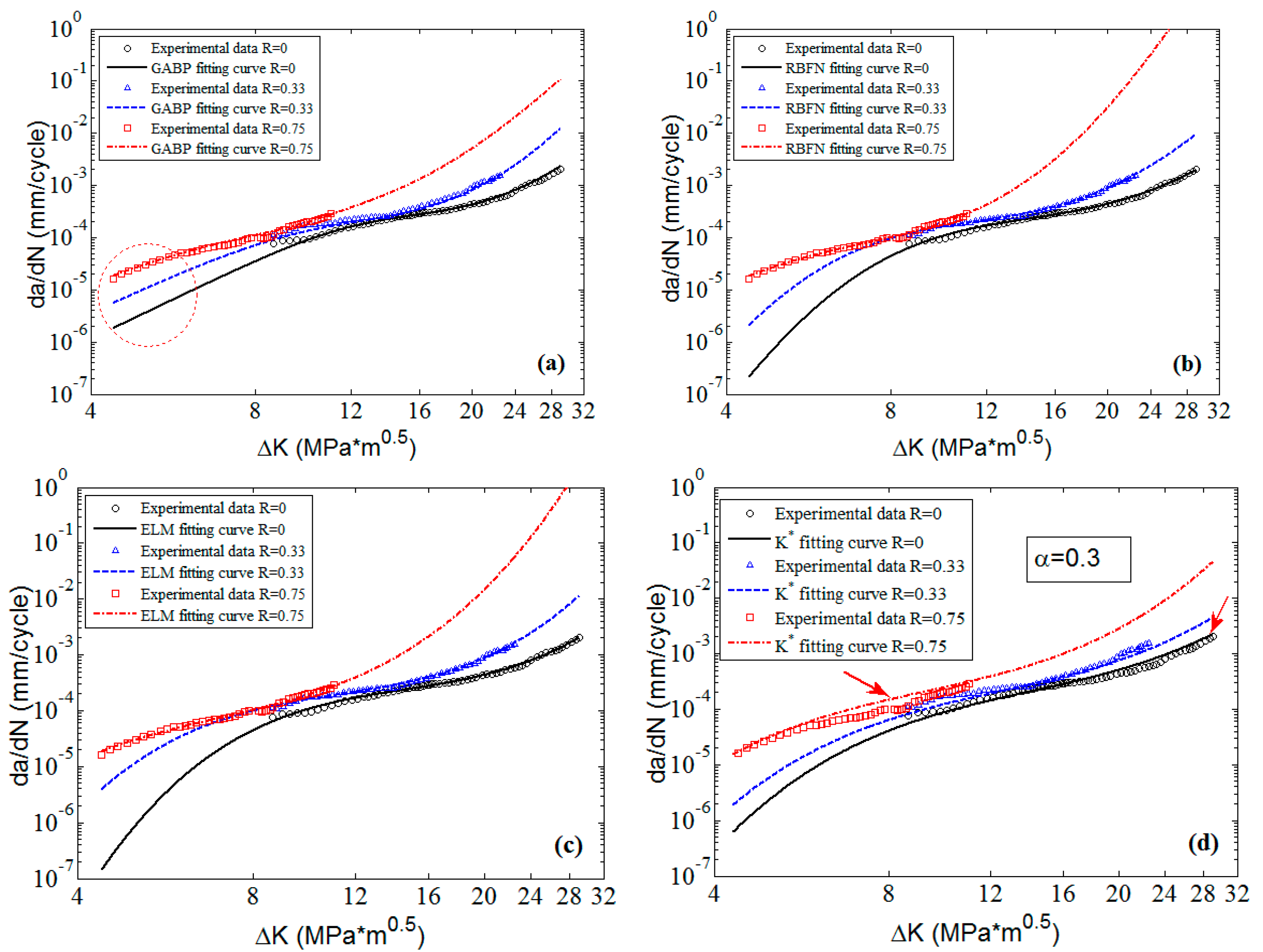
42] with four stress ratios in the threshold region and the Paris region are employed to train the MLAs as shown in
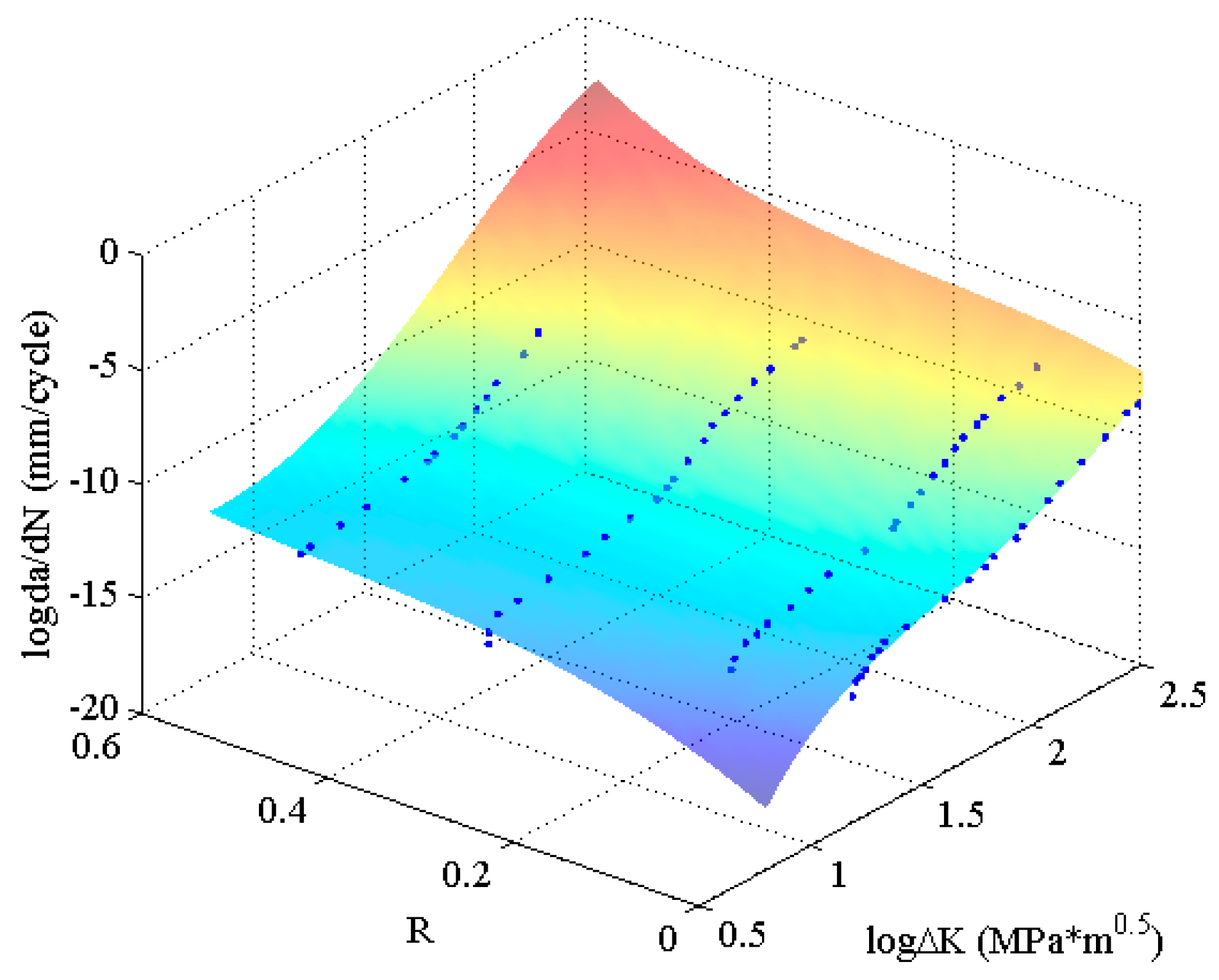
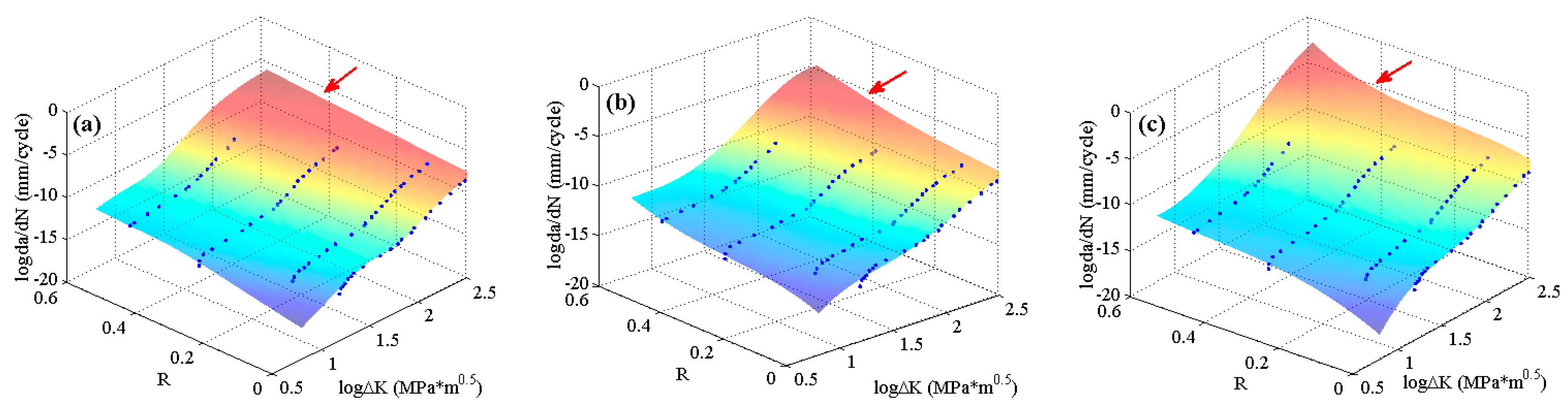
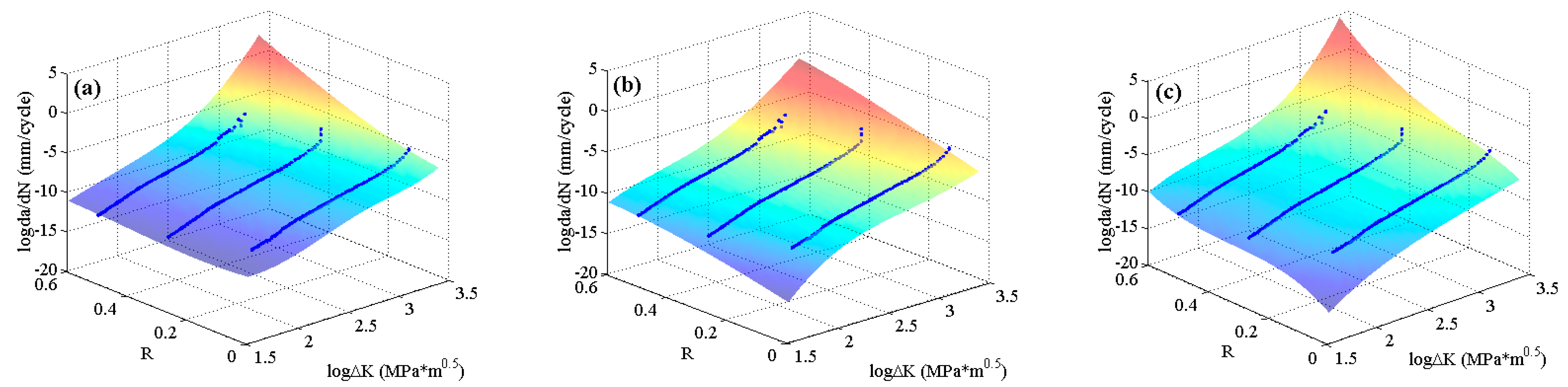
Figure 4. In the figure, it can be seen that the experimental data of 2024-T351 aluminum alloy show typically nonlinear characteristics even in the Paris region which is different from Paris’ law. The predicted results are shown in
Figure 7. The three MLAs all can output the continuous and smooth surfaces, and all the surfaces show perfect nonlinearities which fit the experimental data very well as a whole. However, the three predicted surfaces have some differences on the tendencies in both the threshold region and the Paris region. The downward tendency of ELM is more obvious than that of RBFN and GABP in the threshold region. As the red arrows show in
Figure 7, the tendency in the Paris region of ELM is upward, which is more consistent with the experiments, while that of RBFN is almost flat and the GABP is a little downward.
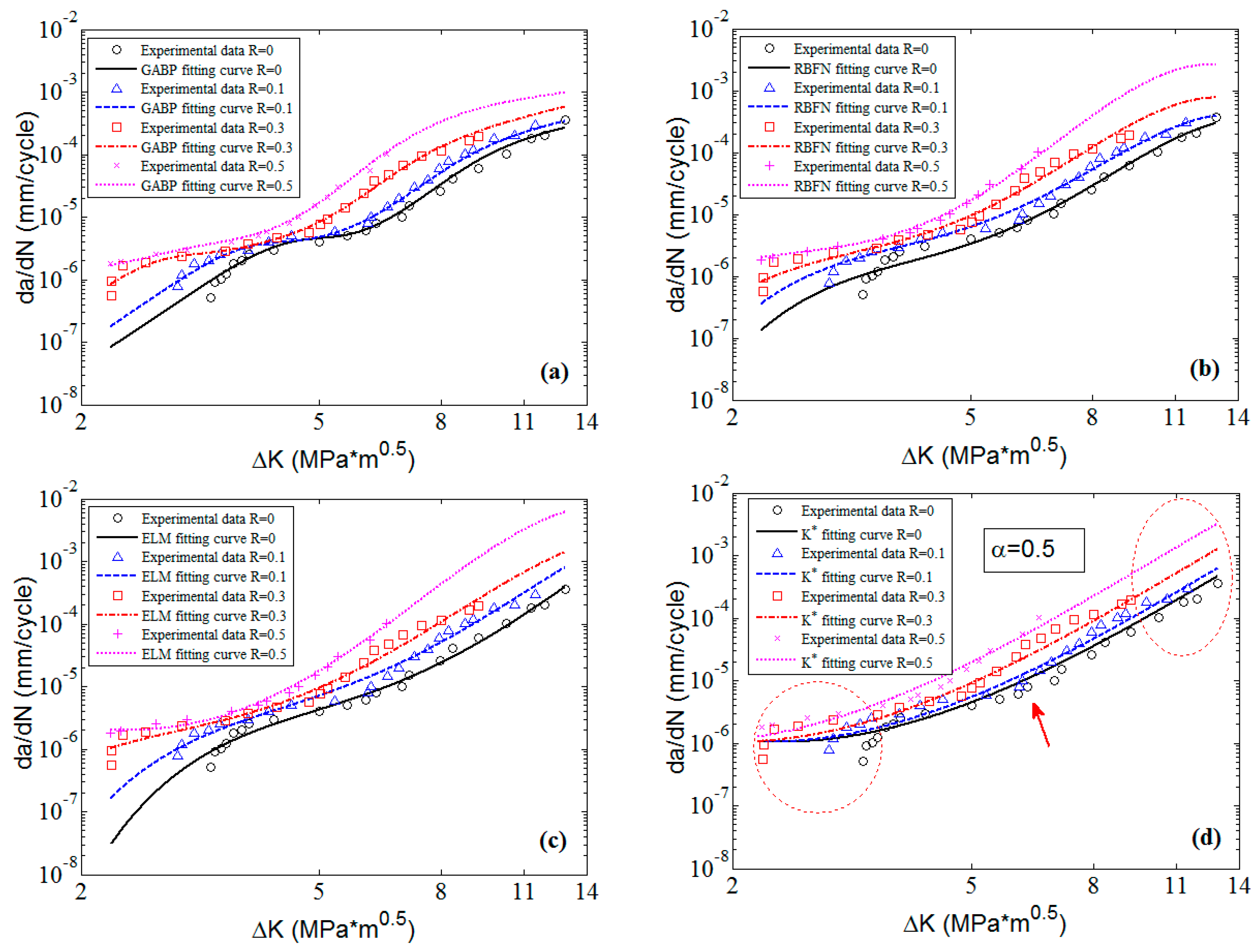
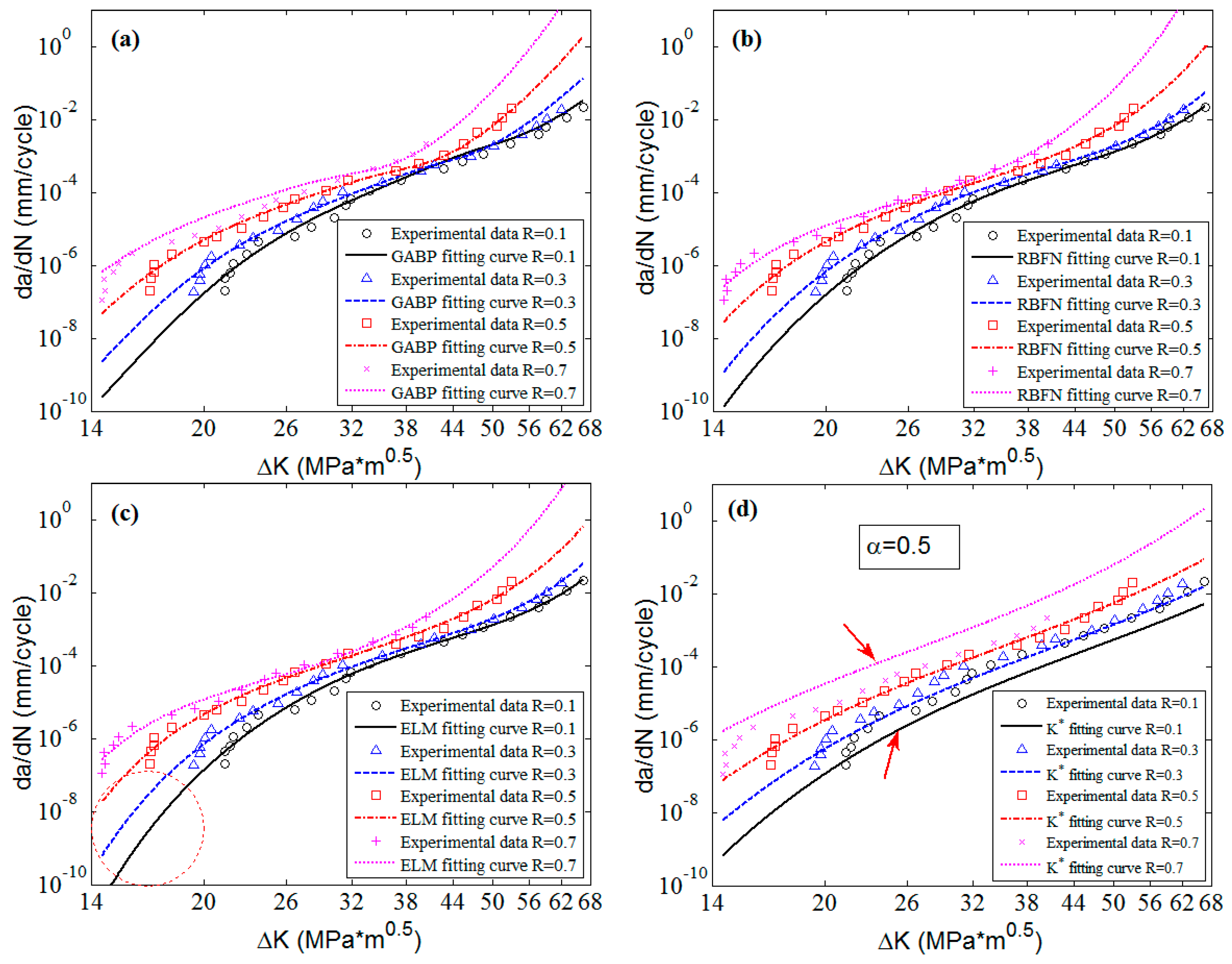
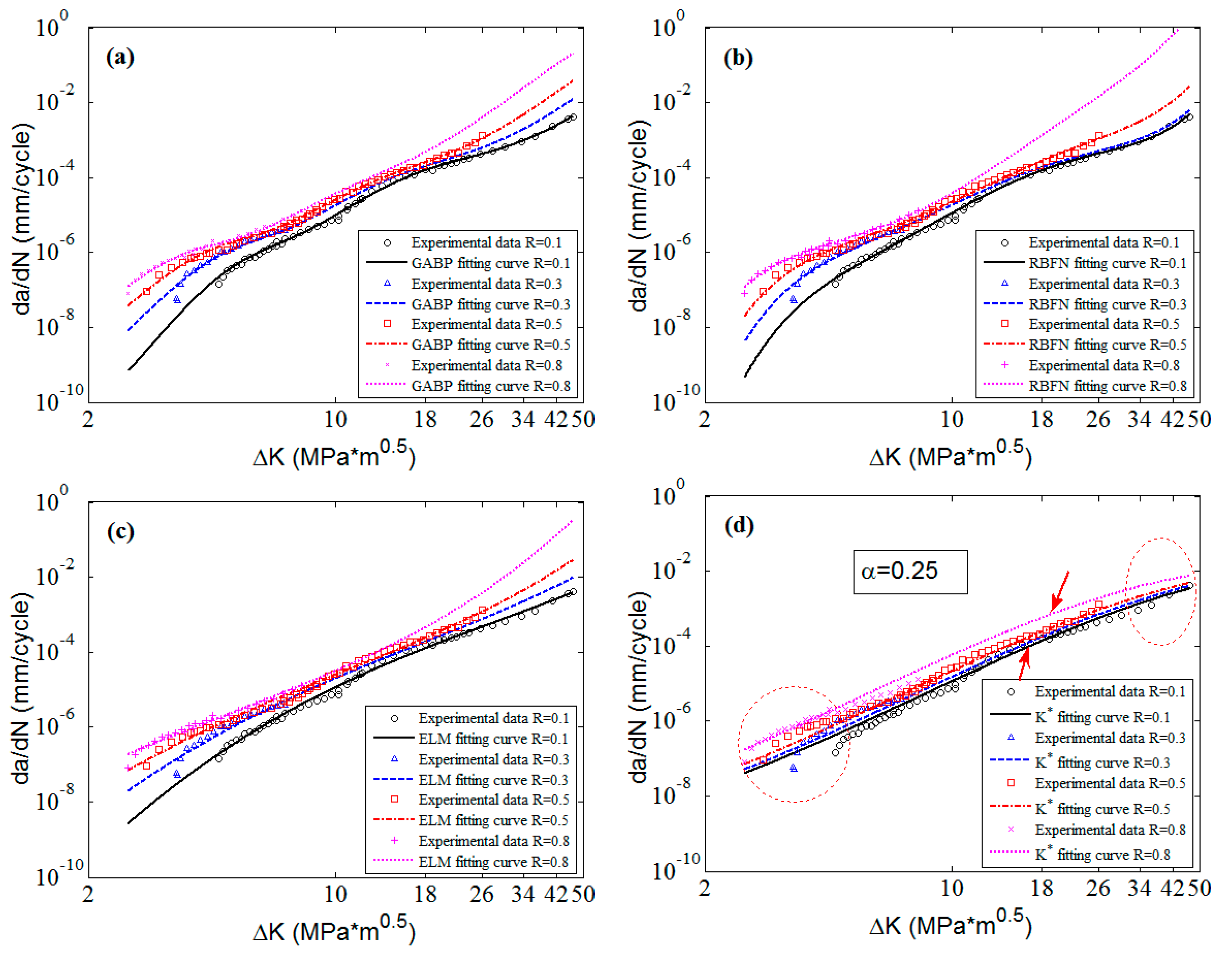
To clearly check the effectiveness and accuracy of the predicted results,
Figure 8 shows the predicted curves and the corresponding experimental data in 2D graphs. It is obvious that the predicted curves of the three MLAs all can perfectly fit the nonlinearities of the experimental data as a whole, and the performance of MLAs are much better than that of
approach in nonlinearity and accuracy, especially in the threshold region as the red circle shows in
Figure 8. Furthermore, in the Paris region, the MLAs match the experimental data with more excellent nonlinearity than
approach. However, the MLAs show different performance in dealing with some details. In the Paris region, though the three MLAs all fit the experimental data very well, the GABP is better than the RBFN and the ELM as the GABP can fit any nonlinear characteristics of the experimental data, while the other two MLAs are meet with the global tendencies. Actually, in the threshold region, the
will quickly decrease with the
closing to the threshold value. In the end of the Paris region, the
will keep the stable increasing tendency, similar to the whole Paris region. It is obvious that the ELM performs best in handling both tendencies. In other words, the ELM can fit the nonlinear characteristics of the experimental data by globally learning and optimizing the nonlinearities while the other two MLAs may be affected by some of the data points in the both ends of the curves.
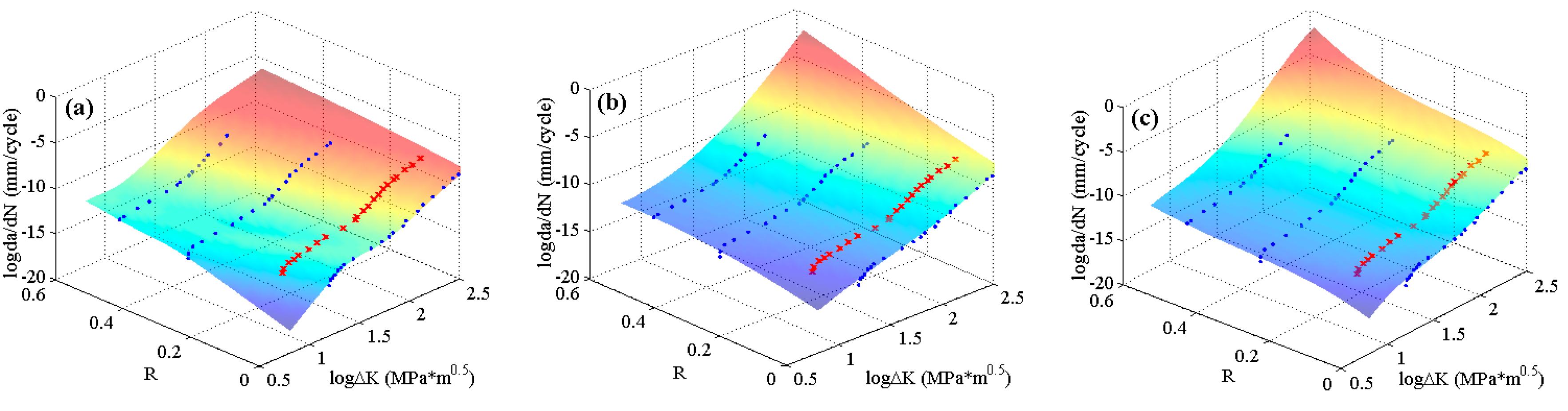
In this part, the cross-validation is conducted to investigate the predictive capacity of the MLAs by using the same experimental data of 2024-T351 aluminum alloy [
42]. This time only three sets of the experimental data with stress ratios 0, 0.3 and 0.5 are utilized to train the MLAs. The experimental data with stress ratio 0.1 are used for validation. The predicted surfaces and experimental data are shown in
Figure 9. The blue dots are the training data, and the red crosses represent the validation data. It can be seen that the accuracy is still satisfactory compared with the predictions in
Figure 7. The predicted MSEs of the GABP, RBFN and ELM are 3.07 × 10
−7, 9.91 × 10
−8 and 1.33 × 10
−8, respectively.
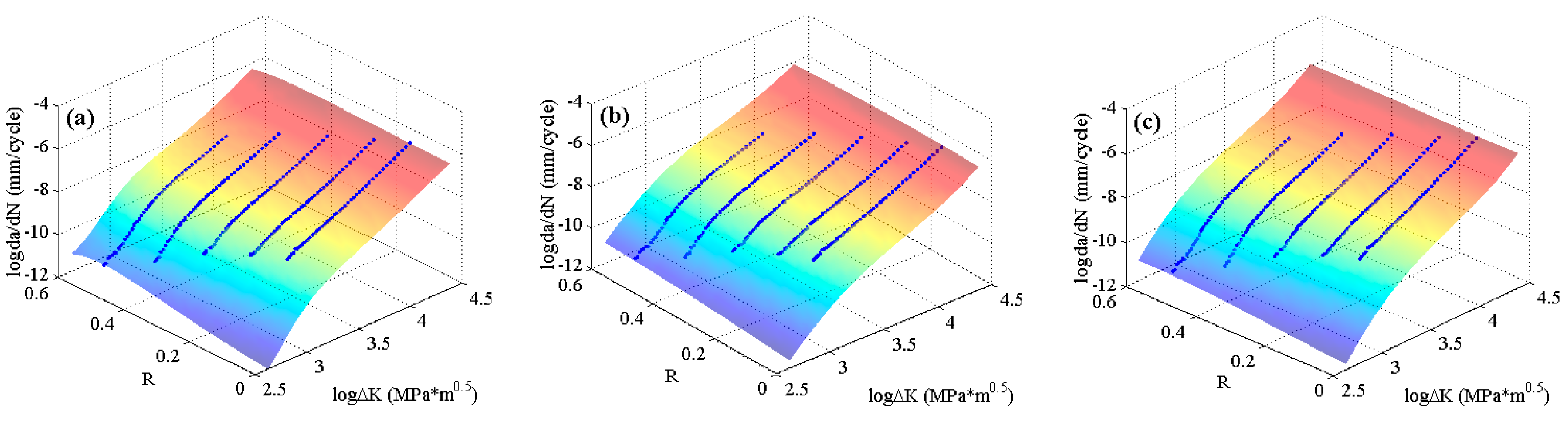
To further validate the globally optimizing characteristics of the MLAs, the experimental data of 6013-T651 aluminum alloy [
5], which include all three regions of
curves, are employed. The predicted surfaces are shown in
Figure 10. It can be seen that there is no obvious distinction for the surfaces predicted by the three MLAs, all of which describe the crack growth rate variation under different stress ratios very well.
The corresponding 2D graphs of 6013-T651 aluminum alloy with different stress ratios are plotted in
Figure 11. It is clear that the predicted curves of the three MLAs match the experimental data of each stress ratio with perfect nonlinearity. However, the fitting curves of the
approach are approximate “parallel linear” which cannot fit the nonlinearities of the experimental data, especially when the stress ratios are 0.1 and 0.7. It indicates that the stability of MLAs are better than that of the
approach. Though the three MLAs can all fit the experimental data in the Paris region, the ELM can fit the fast change tendencies of
in the threshold region and the high
region better than the GABP, and the RBFN is almost comparable with the ELM. Additionally, the ELM extrapolates the nonlinearities of the experimental data better than the GABP and the RBFN when the predicted curves are beyond the
ranges of experimental data as the red circle shows in
Figure 11. That is to say, the excellent generalization performance of ELM means it can globally fit the nonlinearities of the experimental data, which is superior to the RBFN and the GABP.
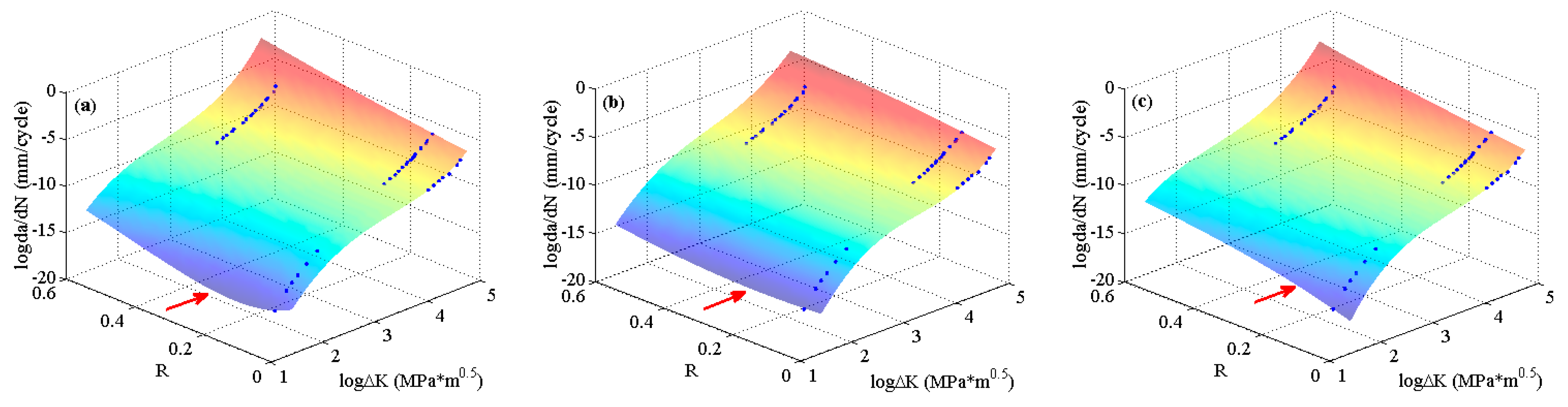
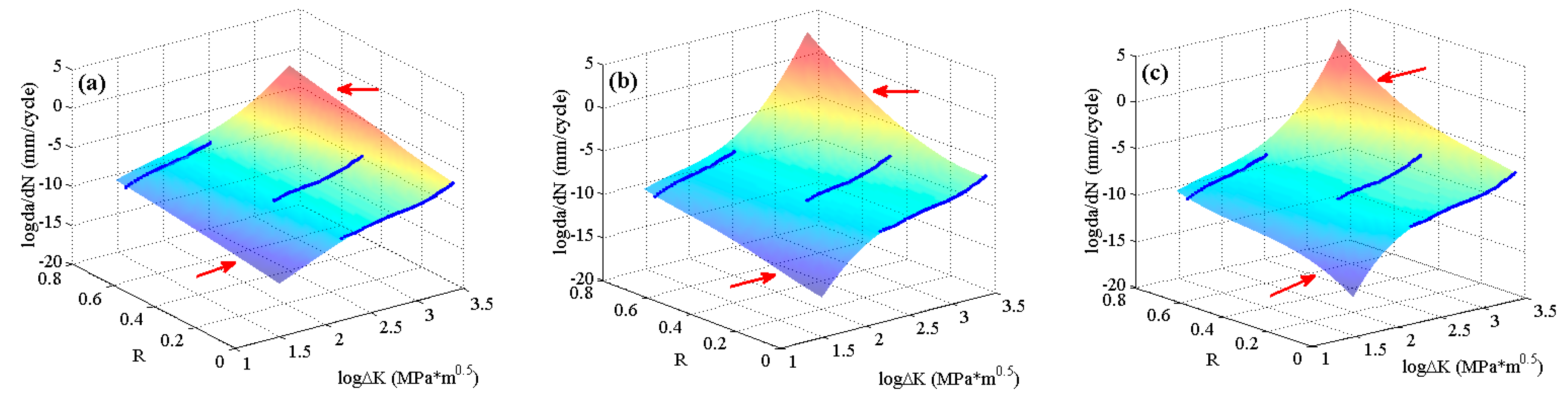
In order to more clearly contrast the extrapolating performance of each MLA, the experimental data of 4340 steel [
44] with narrow
ranges for each stress ratios are employed. The predicted surfaces are shown in
Figure 12. The results reveal that the three MLAs can output satisfactory surfaces by using the small size experimental data without considering the accuracy and effectiveness. However, the tendencies of the predicted surfaces are different in the threshold region as the red arrows show. It can be seen that the ELM can extrapolate the nonlinearities better than the RBFN and the GABP.
To validate the accuracy and effectiveness of the three MLAs, the predicted curves and experimental data of 4340 steel in 2D graphs are shown in
Figure 13. Since it is not easy to distinguish the goodness-of-fit of the three MLAs visually, the MSEs of the three MLAs’ fittings are given. The MSEs of the GABP, RBFN and ELM are 7.32 × 10
−5, 8.89 × 10
−8 and 3.12 × 10
−8, respectively, which indicates that the three MLAs all can match the experimental data very well, and the ELM is the best one. The
approach cannot fit the experimental data when the stress ratios are 0 and 0.5, which indicates that the three MLAs are more accurate than
approach. However, the effectiveness of the three MLAs are totally different. When the
is in the range where there are many training data with different stress ratios, as the red ellipse shows in
Figure 13, the tendencies of the predicted curves are almost the same, which fit the experimental data very well. When the
is in the extrapolating range where there is no or a few training data with different stress ratios as the red circles show in
Figure 13, the predicted curves of MLAs are quite different. The GABP curves of
R = 0 and 0.1 cross with each other and the RBFN curves of
R = 0, 0.05 and 0.1 almost converge to one in the extrapolating range, which is impossible in experiments for 4340 steel. Therefore, ELM is the only one of the three MLAs not only can excellently fit the experimental data, but also extrapolate the nonlinear tendencies very well. In other words, when dealing with small size fatigue crack growth data such as for 4340 steel, ELM is the best one, although all the three MLAs can learn and predict the nonlinearities of experimental data very well.
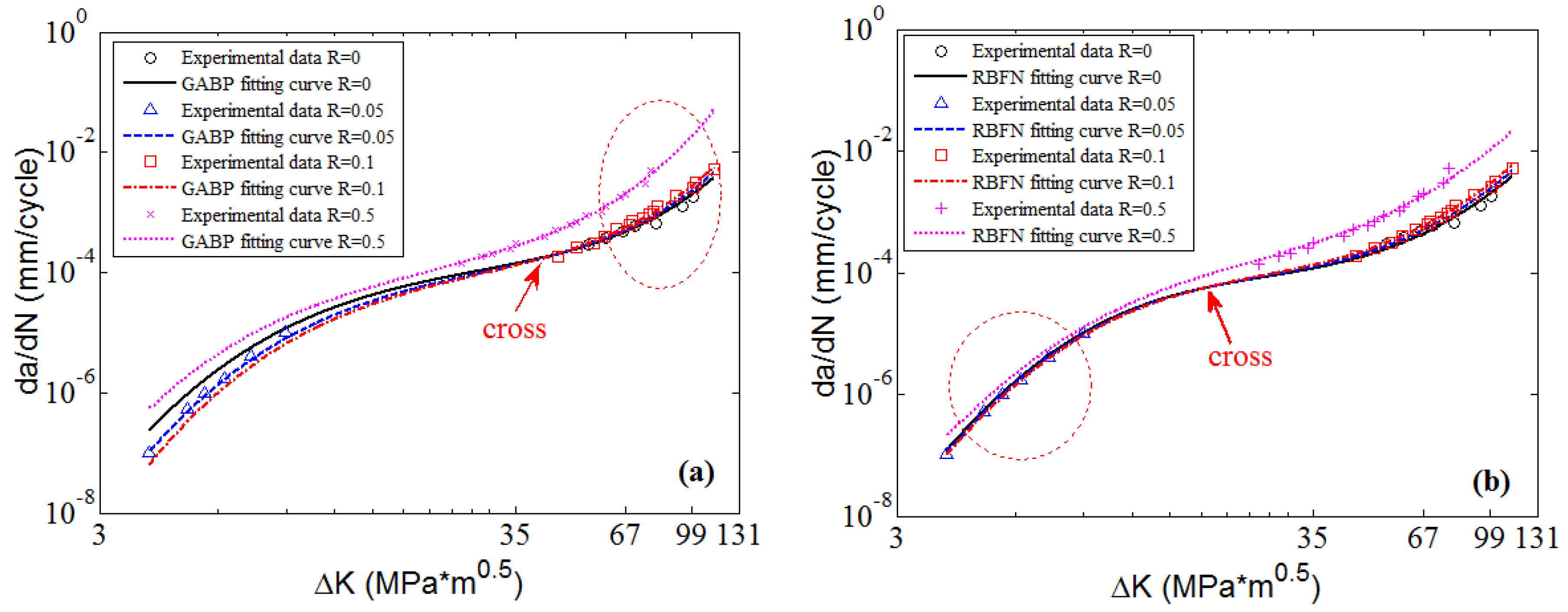
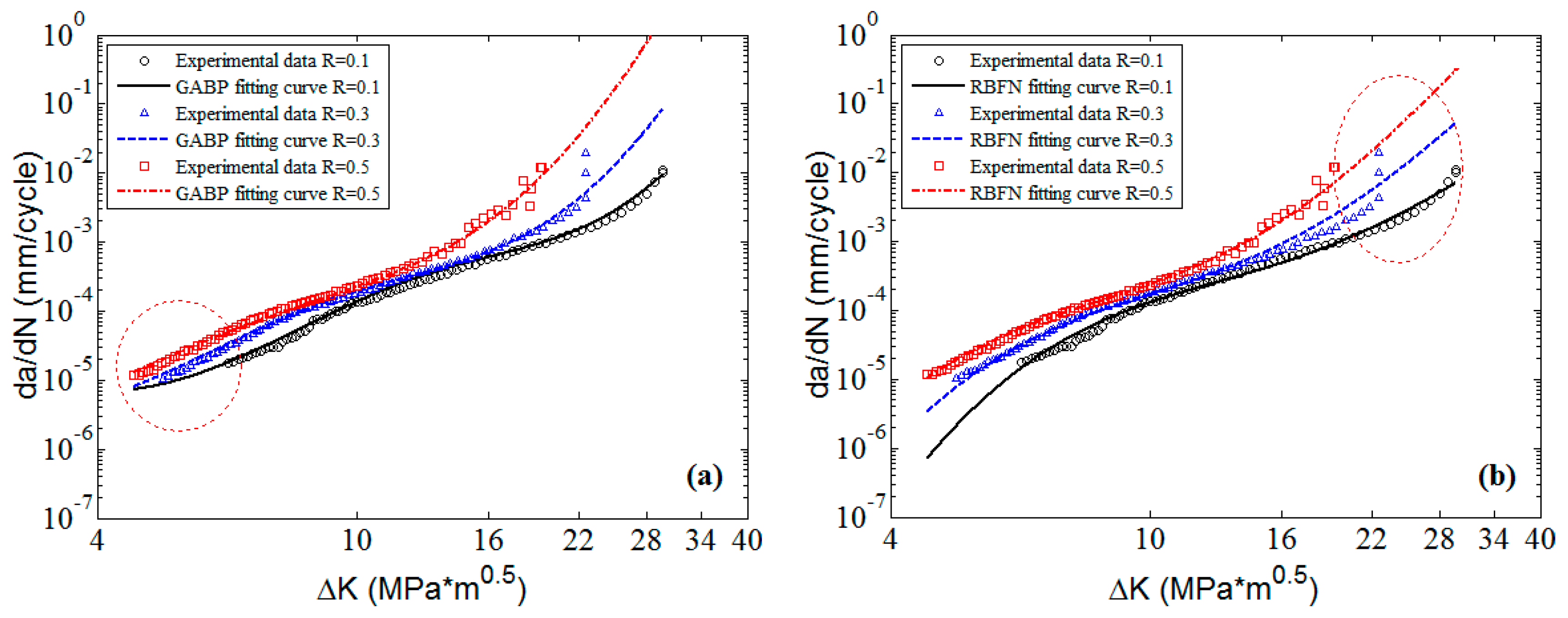
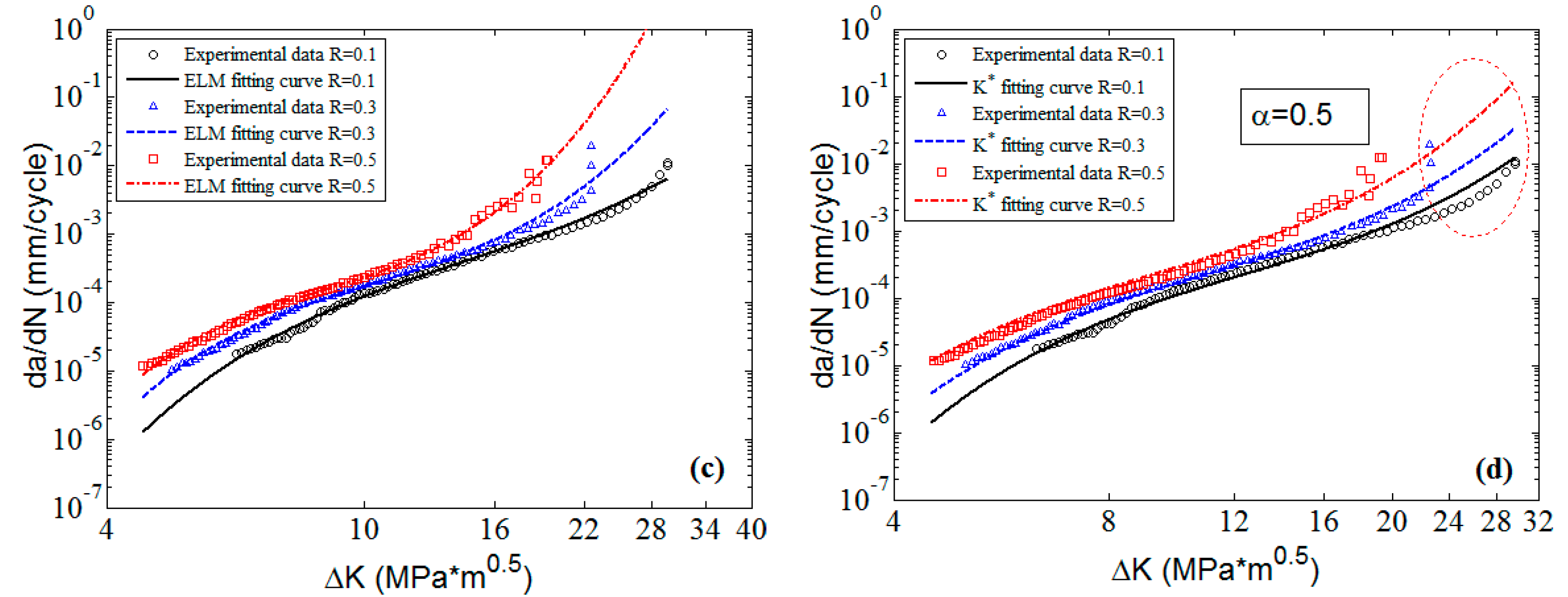
In the following part, the flexibility and applicability of the three MLAs are further validated and compared with
approach by using different kinds of materials including 7050-T7451 aluminum alloy, Ti6Al4V titanium alloy [
45], ADB610 steel [
7] and D16 aluminum alloy [
46]. The predicted surfaces and 2D graphs are shown in
Figure 14,
Figure 15,
Figure 16,
Figure 17,
Figure 18,
Figure 19,
Figure 20 and
Figure 21, respectively. The results reveal that though the employed materials are of different fatigue crack growth characteristics, the three MLAs all can fit the experimental data very well with excellent nonlinearities, which is better than that of
approach. Besides, the effectiveness and accuracy of MLAs are not affected by materials, which is superior to classical formula methods as the red arrows show in
Figure 14,
Figure 15,
Figure 16,
Figure 17,
Figure 18,
Figure 19,
Figure 20 and
Figure 21. Considering the extrapolating ability in the threshold region and the high
region as the red circles and ellipses show in
Figure 14,
Figure 15,
Figure 16,
Figure 17,
Figure 18,
Figure 19,
Figure 20 and
Figure 21, the results of ELM are better than those of GABP and RBFN.
A comparison study of the three MLAs using different kinds of fatigue crack growth rate data indicates that it is feasible to apply the MLAs to fatigue crack growth calculation. The accuracy and effectiveness of MLAs compared well to those of
approach. Additionally, the MLAs overcome the disadvantages of classical models (such as
approach) that the applicability are affected by material parameters, such as
and
. Therefore, the MLAs can be applied to a wider scope of materials, and the nonlinearities of MLAs are superior to those of
approach. However, the three MLAs have their own advantages and limitations when used for fatigue crack growth calculation. The detailed comparisons based on the training results are summarized in
Table 2. As a whole, the ELM is the best one used for fatigue crack growth calculation for its outstanding global optimization and generalization performance. Meanwhile, the ELM is the most convenient method to be trained, because it just have to tune the hidden neurons whose values are integer, while the adjustment parameters of GABP and RBFN can be more or any values which are hard to trial and error to find out the optimal combination. Moreover, when handling fatigue problems with less experimental data or stress ratios, such as 4340 steel, 7050-T7451 and D16 aluminum alloy in this paper, the GABP and the RBFN will be much more difficult and time-consuming than the ELM to obtain the satisfactory target outputs, especially the GABP whose results are not so good.
3.2. Fatigue Life Prediction
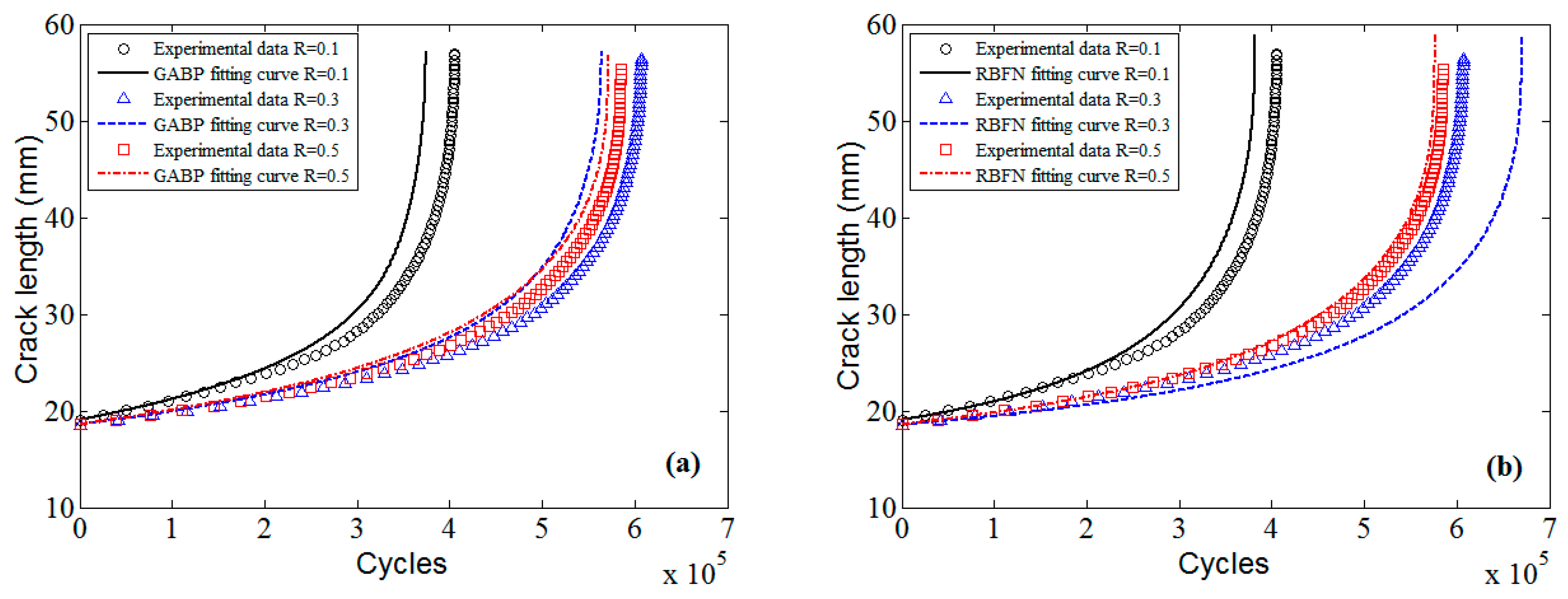
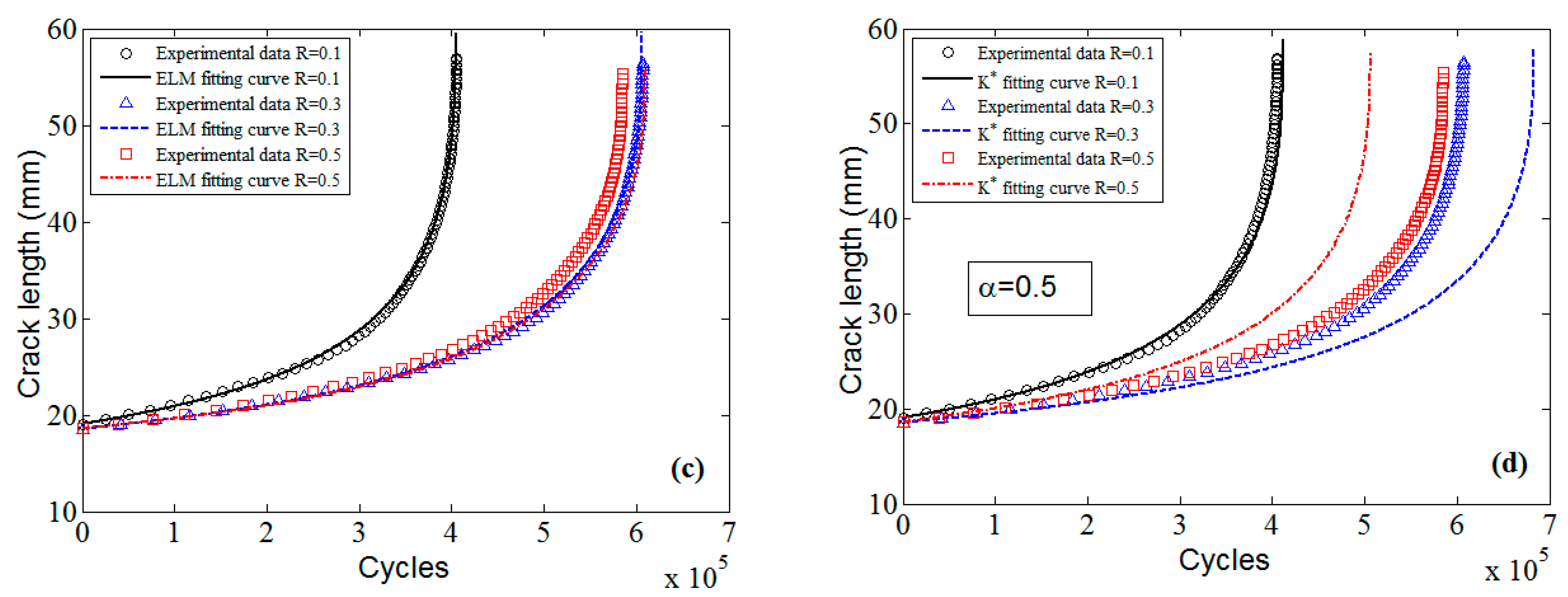
In order to validate the MLA based fatigue life prediction method, experimental data of 7050-T7451 aluminum alloy are employed. The experimental information is listed in
Table 3. The well trained MLAs with the
data, as shown in
Figure 14 and
Figure 15, will be used to predict the fatigue life (a-N curves). Additionally, the classical
approach will be also used to compare with the MLAs.
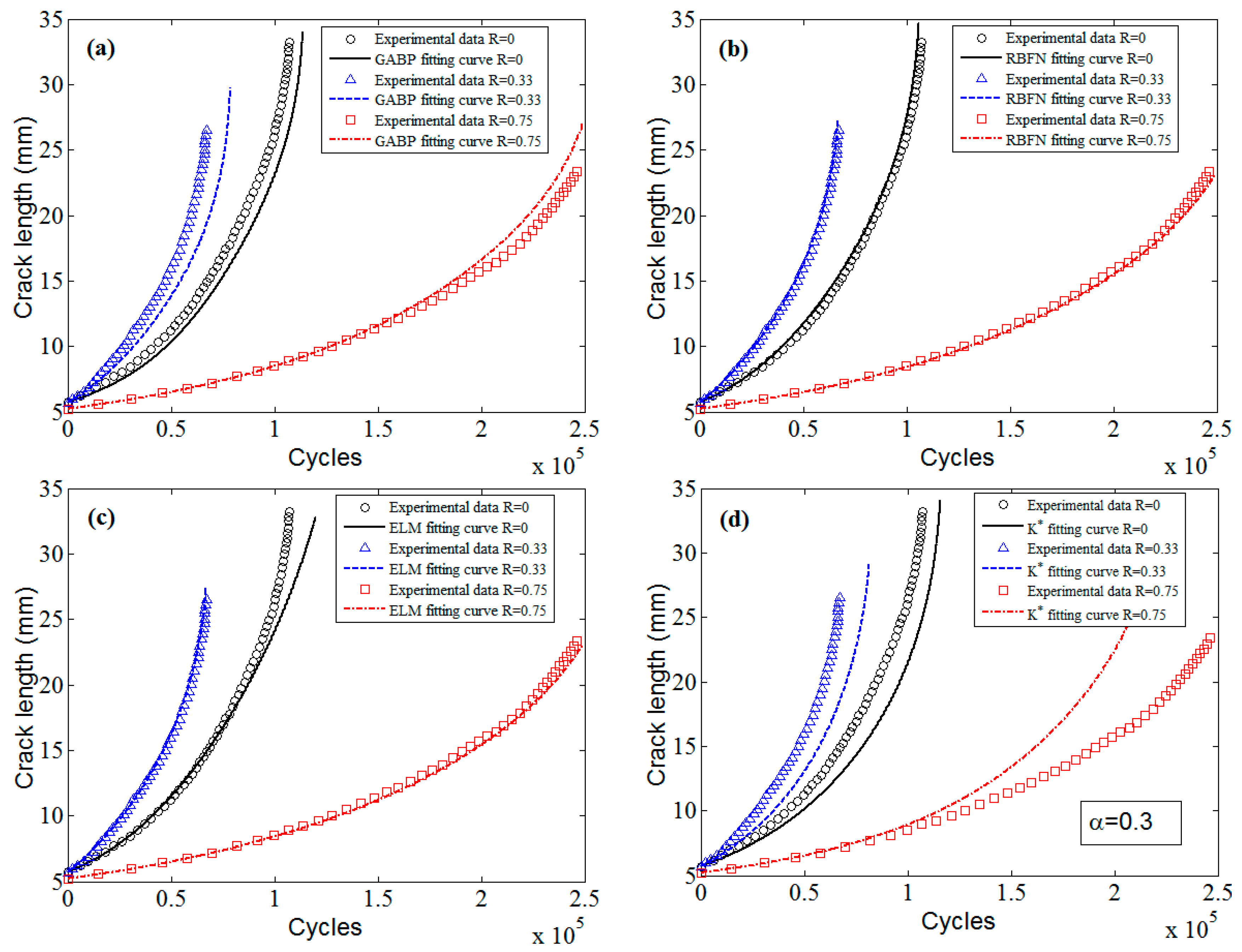
The predicted a-N curves of 7050-T7451 aluminum alloy by MLAs and
approach are displayed in
Figure 22. The
x-axis is the cycle number, and the
y-axis is the crack length. By comparing to the experimental data, it can be seen that the predictions of MLAs are superior to those of
approach, and the predictions of ELM are much better than those of GABP and RBFN.
The fatigue life can be calculated once the failure criterion is determined by using the predictions. To compare the prediction accuracy of MLAs with that of
approach, the errors of the four methods when the critical crack length
is 35 mm, 45 mm and 55 mm are listed in
Table 4, where the positive value means that the predicted fatigue life is more than the experimental life, and the negative value represents that the predicted fatigue life is less than the experimental life. It is obvious that the accuracy of MLAs is globally much better than that of
approach, especially the ELM whose accuracy and stability is the best.
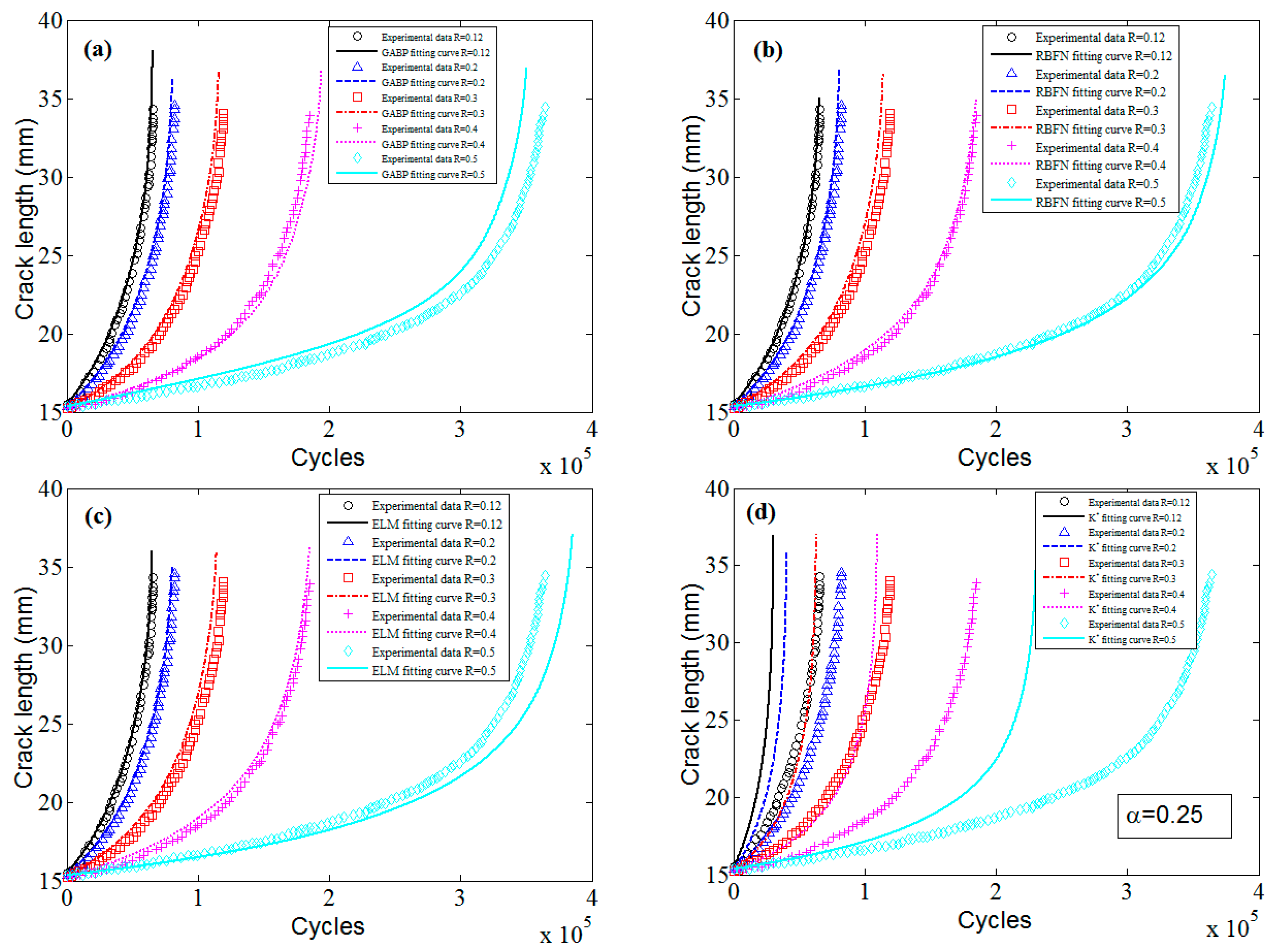
To validate the flexibility and applicability of MLAs to different materials, ADB610 steel [
7] is used to predict the fatigue life by using the well trained MLAs shown in
Figure 18 and
Figure 19. The results are compared with the classical
approach. The experimental information of ADB610 steel is listed in
Table 5.
The predicted a-N curves of ADB610 steel are shown in
Figure 23. It can be seen that the predictions of MLAs are much better than those of the
approach, and the three MLAs all show good accuracy.
The prediction errors of ADB610 steel when the critical crack length is 25 mm and 32 mm are listed in
Table 6. The results show that the MLAs are better than
approach in global accuracy and stability.
Furthermore, different experimental data of D16 aluminum alloy [
46] are also used for model validation. The experimental information is listed in
Table 7. Similarly, the surfaces and
curves predicted by the MLAs shown in
Figure 20 and
Figure 21 are utilized for fatigue life prediction, and the
approach is also employed as a comparison.
Figure 24 displays the predicted a-N curves of D16 aluminum alloy. It is obvious that the three MLAs all show pretty good performance, which are better than
approach, especially the ELM and the RBFN.
The prediction errors of D16 aluminum alloy when the critical crack length is 15 mm, 18 mm and 22 mm are calculated in
Table 8. The errors indicate the same conclusion that the MLAs are of excellent accuracy and stability, especially the ELM.