Modeling Time-Dependent Behavior of Concrete Affected by Alkali Silica Reaction in Variable Environmental Conditions
Abstract
:1. Introduction
2. Multi-Physics Formulation
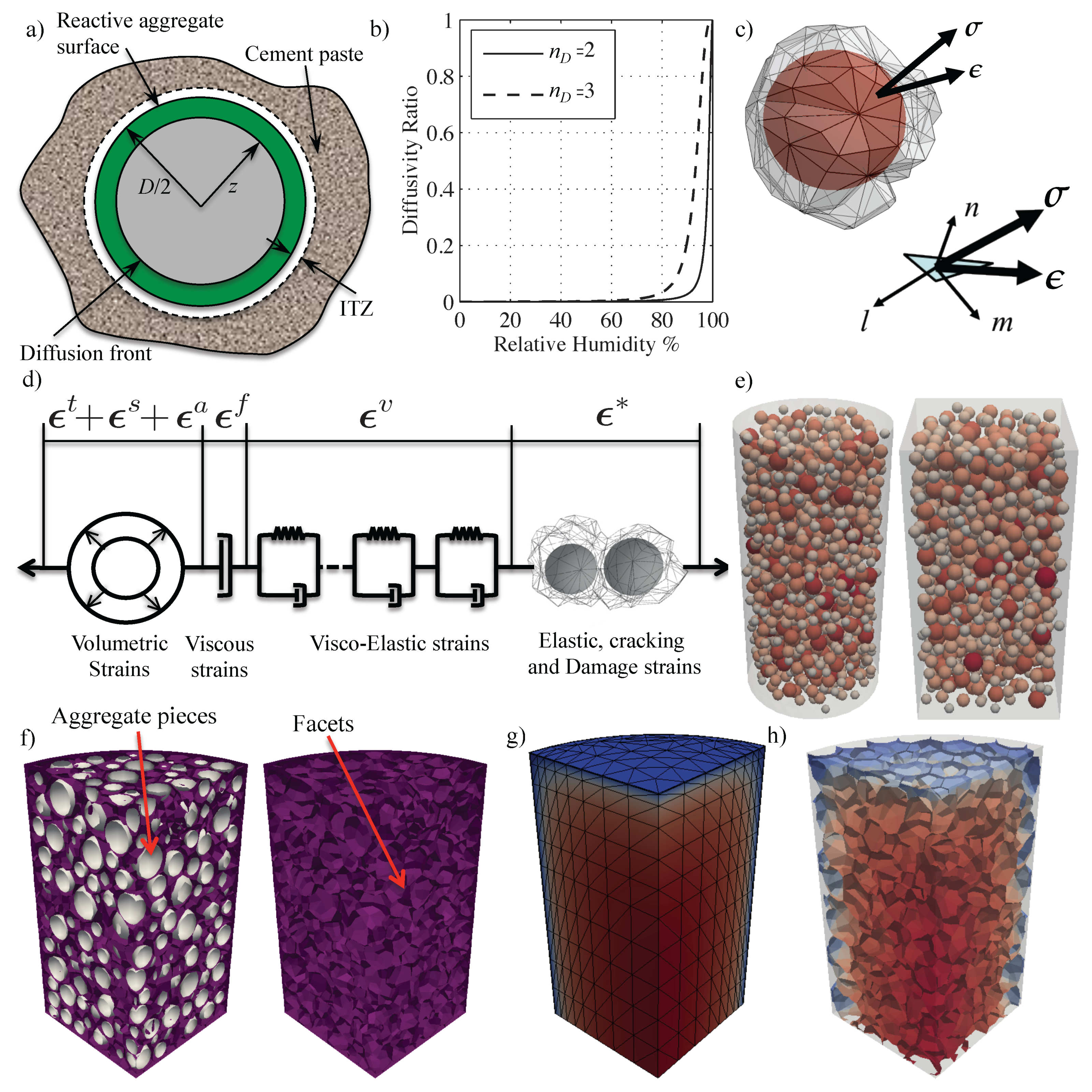
2.1. Modeling ASR Expansion
2.2. Hygro-Thermo-Chemical (HTC) Model
2.3. Mechanical Behavior
2.3.1. LDPM for Concrete Elastic, Cracking and Damage Behavior
2.4. Microprestress-Solidification Theory for Viscous and Visco-Elastic Deformations
2.5. ASR Induced Deformation
2.6. Thermal and Hygral Deformations
3. Numerical Implementation
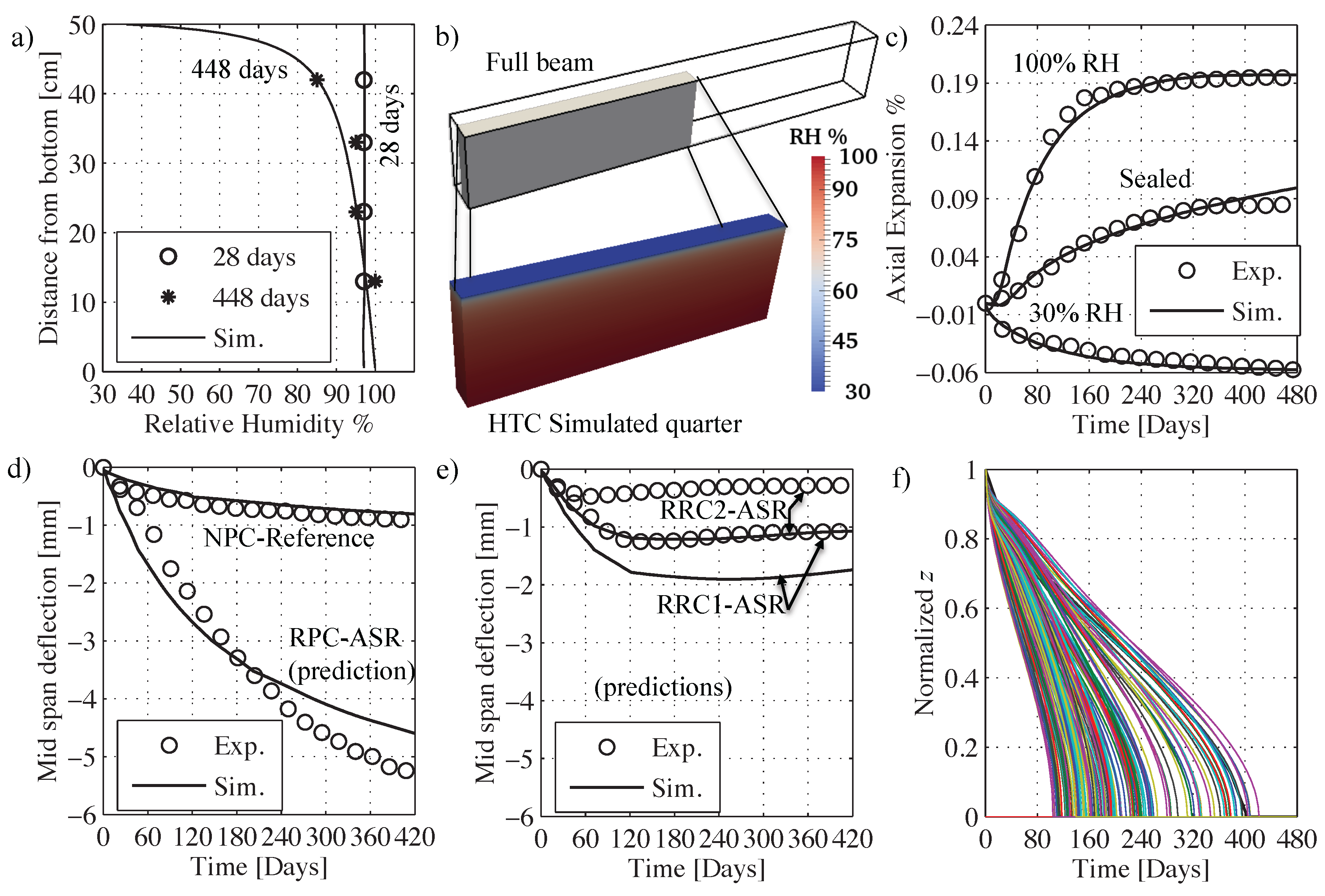
4. Numerical Simulations and Comparison with Experimental Data
4.1. Identification of Cement Hydration Parameters
4.2. Identification of HTC Parameters
4.3. Identification of Shrinkage and Creep Parameters
4.4. Calibration of LDPM Concrete Parameters
4.5. Calibration of ASR Model Parameters
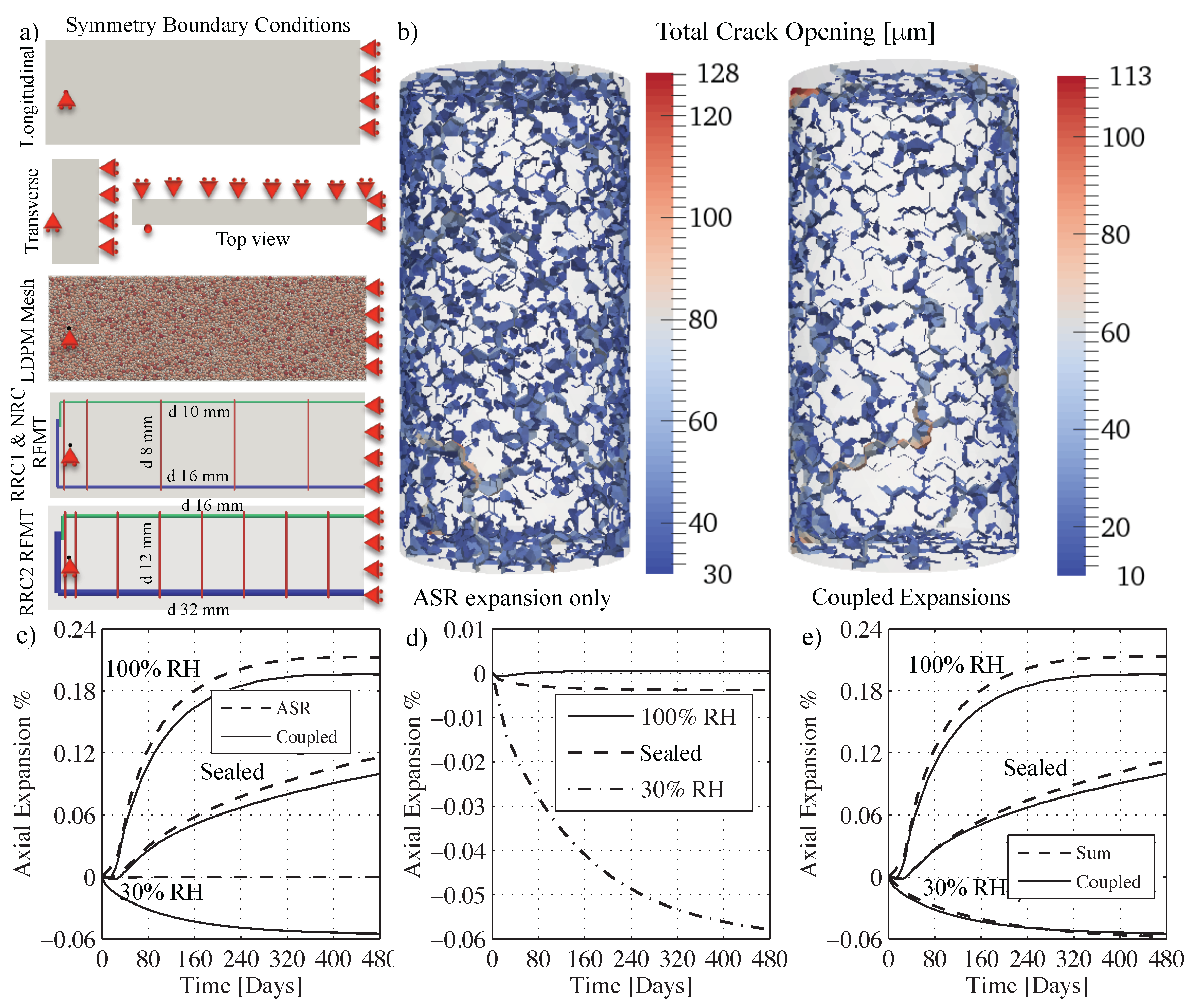
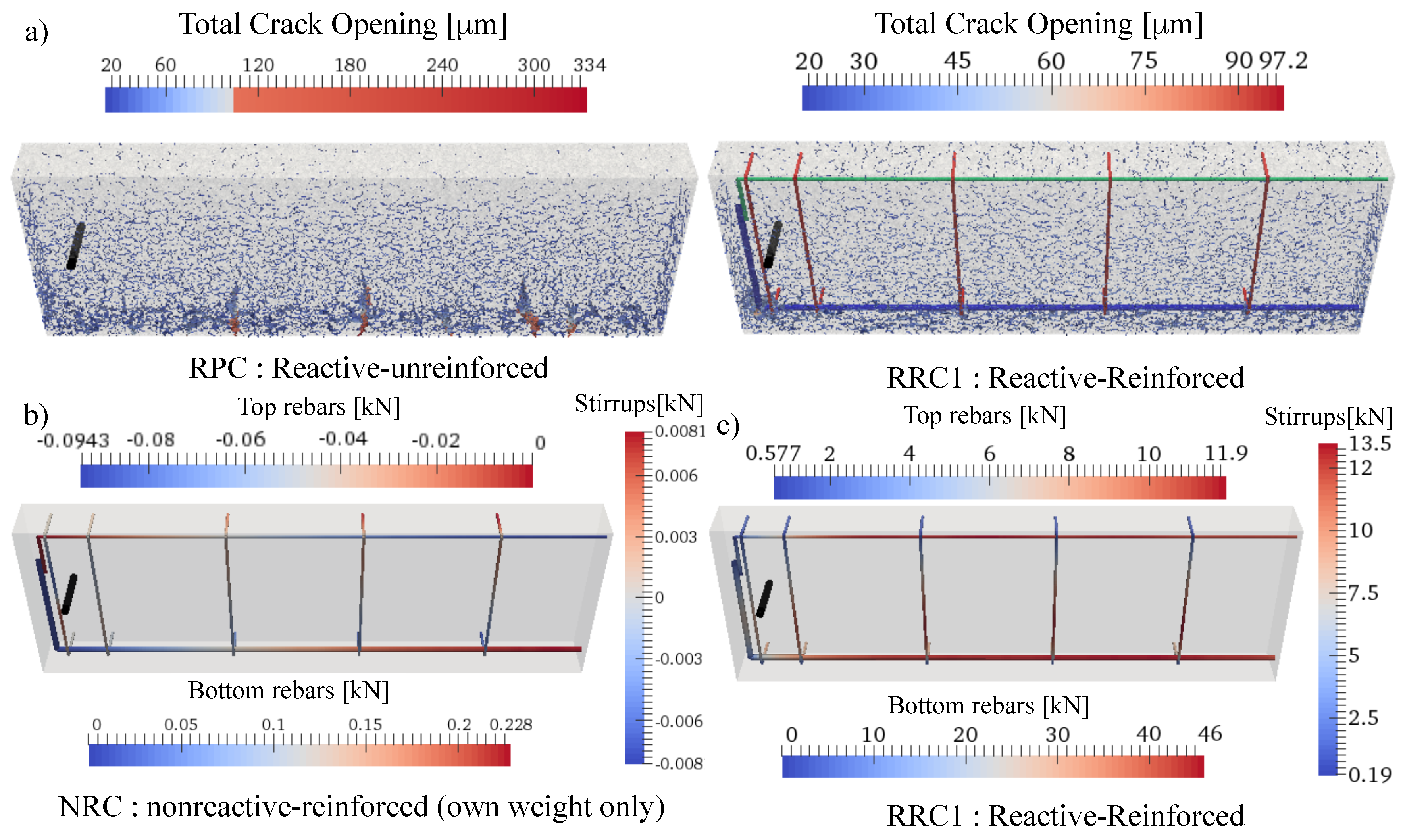
4.6. Validation through Full Scale Beam Simulations
5. Discussion of Results
6. Conclusions
- ASR progression is a process that takes a few years to multi-decades depending on moisture and temperature conditions as well as cement chemistry and aggregate mineralogy. This makes ASR in full interaction with other aging and deterioration phenomena like creep, shrinkage and thermal expansions. Simple addition of the deformation induced by these phenomena is incorrect because the different phenomena are nonlinearly coupled.
- Meso-scale modeling reveals the sub-scale interactions between coupled phenomena that are not seen at the macroscopic length scale. Namely, for the case of ASR induced free expansion, only modeling of deformations at the meso-scale can capture meso-scale creep deformations and relaxation of meso-scale stress build up that are not seen at the macroscopic scale because the macroscopic stress is zero.
- Relative humidity effect on ASR expansion is essentially a moisture diffusion controlled process that can be modeled similarly to relative humidity effects on moisture diffusivity in concrete.
- Simplified average section models that describe creep and shrinkage can lead to large inaccuracy in predicting ASR deformations for nonsaturated conditions. The humidity profile has a significant effect on ASR expansions that can not be averaged.
- ASR expansions in reinforced concrete elements can lead to large internal forces build up and may lead to reinforcement yielding, reinforcement slippage, and partial bond loss.
- For any complex framework to be predictive, its calibration needs to depend on uncoupled phenomena, then, it must be validated clearly. This was accomplished here by a multi-step calibration procedure on companion specimens with no ASR expansion, followed by ASR expansion calibration, then finally validation on full scale beams. A key factor here is the degree of scatter in the experimental data which is reflected directly in the prediction results of the model.
- To the best knowledge of the authors, this is the only framework in literature that was calibrated on individual lab size specimens and was able to predict structural behavior. Other models are either directly calibrated based on structural response to simulate structural behavior, or are calibrated and validated based on individual lab size specimens.
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Model Parameters
| Param. (Units) | Modeled Chemical Reaction | Test for Calibration | Value | Source |
|---|---|---|---|---|
| (h) | Cement hydration | Calorimetric tests | 1.41 | [79] |
| (-) | Cement hydration | Calorimetric tests | 5 | [79] |
| (-) | Cement hydration | Calorimetric tests | 8 | [79] |
| Param. (Units) | Modeled Behavior or Mechanism | Test for Calibration | Value | Source |
|---|---|---|---|---|
| (GPa) | Elasticity | Any in the linear range | 133 | Calibrated |
| (-) | Poisson’s effect | 0.25 | [67] | |
| (MPa) | Short term visco-elasticity | Basic creep tests with short load duration (≈1 year) | 1.75 | Calibrated |
| (MPa) | Long term viscocity | Basic creep tests with long load duration (≈10 year) | 7 | Calibrated |
| (-) | Aging visco-elasticity | Basic creep tests at different age of loading | 1.9 | [96] |
| (MPa) | Evolution of the microprestress at variable temperature and relative humidity | Drying creep test or transitional thermal creep tests | 19 | [96] |
| (MPa) | Tensile fracture | Fracture tests or tensile strength tests | 4.75 | Calibrated |
| (mm) | Tensile fracture | Fracture tests or size effect tests | 75 | Calibrated |
| (-) | Cohesive behavior in shear | Unconfined compression test | 3.07 | Calibrated |
| (-) | Frictional behavior | Triaxial compression tests at low confinement | 0.2 | [67] |
| (MPa) | Frictional behavior | Triaxial tests at high confinement | 600 | [67] |
| (MPa) | Yielding and pore collapse | Hydrostatic compression test | 150 | [67] |
| (-) | Yielding and pore collapse | Hydrostatic compression test | 0.3 | [90] |
| (-) | Yielding and pore distorsion | Passively confined tests | 0.1 | [90] |
| (-) | Material densification after pore collapse | Hydrostatic compression test | 4 | [90] |
| (-) | Material densification after pore collapse | Hydrostatic compression test at very high pressure or with unloading | 1 | [67] |
| Param. (Units) | Modeled Behavior or Mechanism | Test for Calibration | Value | Source |
|---|---|---|---|---|
| (J/kgC) | Heat transfer | Thermal conductivity tests | 1100 | [79] |
| (W/mC) | Heat transfer | Thermal conductivity tests | 2.3 | [79] |
| (-) | Moisture content | Sorption/desorption isotherms relevant to two different values of hydration degree | 1.7 | [79] |
| (-) | Moisture content in C-S-H pores | Sorption/desorption isotherms relevant to two different values of hydration degree | 0.2 | [79] |
| (kg/mm h) | Moisture transport | Humidity profile during drying tests | 2 | Calibrated |
| (kg/mm h) | Moisture transport | Humidity profile during drying tests | 4 | Calibrated |
| n (-) | Moisture transport | Humidity profile during drying tests | 2.35 | Calibrated |
| Param. (Units) | Modeled Behavior or Mechanism | Test for Calibration | Value | Source |
|---|---|---|---|---|
| (-) | Shrinkage and swelling due to moisture content change | Shrinkage tests | 9 | Calibrated |
| (-) | Thermal expansion and contraction | Thermal expansion tests | 1 | [96] |
| Param. (Units) | Modeled Behavior or Mechanism | Test for Calibration | Value | Source |
|---|---|---|---|---|
| (kg/m) | ASR gel density | Free ASR expansion tests at 100 % relative humidity | 689 | [65,68] |
| (cmkgday) | ASR gel formation | Free ASR expansion tests at 100 % relative humidity | 2.62 | Calibrated |
| (-) | Water imbibition | Free ASR expansion tests at 100 % relative humidity | 1.45 | Calibrated |
| (mm/day) | Water imbibition | Free ASR expansion tests at 100 % relative humidity | 7.78 | Calibrated |
| (m) | ITZ porosity effect on ASR imposed strain | Free ASR expansion tests at 100 % relative humidity | 6.0 | Calibrated |
| (kg/m) | Alkali content effect | Free ASR expansion tests at 100 % relative humidity and different alkali contents | 2.7 | [65] |
| (kg/m) | Alkali content effect | Free ASR expansion tests at 100 % relative humidity and different alkali contents | 4.37 | [65] |
| (-) | Relative humidity effect | Free ASR expansion at different levels of relative humidity | 3600 | Calibrated |
| (-) | Relative humidity effect | Free ASR expansion at different levels of relative humidity | 2 | Calibrated |
References
- Saouma, V.; Xi, Y. Literature Review of Alkali Aggregate Reactions in Concrete Dams; Report cu/sa-xi-2004/001; Department of Civil, Environmental, & Architectural Engineering University of Colorado: Boulder, CO, USA, 2004. [Google Scholar]
- Kawabata, Y.; Seignol, J.F.; Martin, R.P.; Toutlemonde, F. Macroscopic chemo-mechanical modeling of alkali-silica reaction of concrete under stresses. Constr. Build. Mater. 2017, 137, 234–245. [Google Scholar] [CrossRef]
- Bažant, Z.; Steffens, A. Mathematical model for kinetics of alkali-silica reaction in concrete. Cem. Concr. Res. 2000, 30, 419–428. [Google Scholar] [CrossRef]
- Kurihara, T.; Katawaki, K. Effects of moisture control and inhibition on alkali silica reaction. In Proceedings of the 8th International Conference on Alkali Aggregate Reaction in Concrete, Kyoto, Japan, 17–20 July 1989; pp. 629–634. [Google Scholar]
- Tomosawa, F.; Tamura, K.; Abe, M. Influence of water content of concrete on alkali—Aggregate reaction. In Proceedings of the 8th International Conference on Alkali Aggregate Reaction in Concrete, Kyoto, Japan, 17–20 July 1989; pp. 881–885. [Google Scholar]
- Nilsson, L. Moisture effects on the alkali silica reaction. In Proceedings of the 6th International Conference on Alkali Aggregate Reaction in Concrete, Denmark, Copenhagen, 22–25 June 1983; pp. 201–208. [Google Scholar]
- Ludwig, U. Effects of environmental conditions on alkali aggregate reaction and preventive measures. In Proceedings of the 8th International Conference on Alkali Aggregate Reaction in Concrete, Kyoto, Japan, 17–20 July 1989; pp. 583–596. [Google Scholar]
- Larive, C. Apports Combin’es de l’Experimentation et de la Modélisation à la Comprehension del Alcali-Réaction et de ses Effets Mécaniques. Ph.D. Thesis, Laboratoire Central des Ponts et Chaussées, Paris, France, 1998. [Google Scholar]
- Alnaggar, M. Multiscale Modeling of Aging and Deterioration of Reinforced Concrete Structures. Ph.D. Thesis, Northwestern University, Evanston, IL, USA, 2014. [Google Scholar]
- Bažant, Z.P.; Rahimi-Aghdam, S. Diffusion-Controlled and Creep-Mitigated ASR Damage via Microplane Model. I: Mass Concrete. J. Eng. Mech. 2016. [Google Scholar] [CrossRef]
- Giorla, A.B.; Scrivener, K.L.; Dunant, C.F. Influence of visco-elasticity on the stress development induced by alkali-silica reaction. Cem. Concr. Res. 2015, 70, 1–8. [Google Scholar] [CrossRef]
- Bouzabata, H.; Multon, S.; Sellier, A.; Houari, H. Swellings due to alkali-silica reaction and delayed ettringite formation: Characterisation of expansion isotropy and effect of moisture conditions. Cem. Concr. Compos. 2012, 34, 349–356. [Google Scholar] [CrossRef]
- Karthik, M.M.; Mander, J.B.; Hurlebaus, S. ASR/DEF related expansion in structural concrete: Model development and validation. Constr. Build. Mater. 2016, 128, 238–247. [Google Scholar] [CrossRef]
- Wood, S.G.; Dunn, J.R.; Giannini, E.R. Development of Specimens with Freeze-Thaw and ASR for Non-Destructive Evaluation. In Proceedings of the 10th fib International Ph.D. Symposium in Civil Engineering, Québec City, QC, Canada, 21–23 July 2014. [Google Scholar]
- Rajabipour, F.; Giannini, E.; Dunant, C.; Ideker, J.H.; Thomas, M.D. Alkali-silica reaction: Current understanding of the reaction mechanisms and the knowledge gaps. Cem. Concr. Res. 2015, 76, 130–146. [Google Scholar] [CrossRef]
- Glasser, L.D.; Kataoka, N. The chemistry of alkali-aggregate reaction. Cem. Concr. Res. 1981, 11, 1–9. [Google Scholar] [CrossRef]
- Kim, T.; Olek, J. Chemical Sequence and Kinetics of Alkali-Silica Reaction Part I. Experiments. J. Am. Ceram. Soc. 2014, 97, 2195–2203. [Google Scholar] [CrossRef]
- Ponce, J.; Batic, O. Different manifestations of the alkali-silica reaction in concrete according to the reaction kinetics of the reactive aggregate. Cem. Concr. Res. 2006, 36, 1148–1156. [Google Scholar] [CrossRef]
- Chatterji, S.; Jensen, A.; Thaulow, N.; Christensen, P. Studies of alkali-silica reaction. Part 3. Mechanisms by which NaCl and Ca(OH)2 affect the reaction. Cem. Concr. Res. 1986, 16, 246–254. [Google Scholar] [CrossRef]
- Diamond, S.; Barneyback, R.S., Jr.; Struble, L.J. On the physics and chemistry of Alkali-Silica Reactions. In Proceedings of the 5th International Conference on Alkali-Aggregate Reaction in Concrete, Capetown, South Africa, 30 March–3 April 1981. [Google Scholar]
- Jones, T. A new interpretation of alkali-silica reaction and expansion mechanisms in concrete. Chem. Ind. 1988, 18, 40–44. [Google Scholar]
- Wilson, M.; Cabrera, J.G.; Zou, y. The process and mechanism of alkali-silica reaction using fused silica as the reactive aggregate. Adv. Cem. Res. 1994, 6, 117–125. [Google Scholar]
- Chatterji, S.; Thaulow, N.; Jensen, A. Studies of alkali-silica reaction. Part 4. Effect of different alkali salt solutions on expansion. Cem. Concr. Res. 1987, 17, 777–783. [Google Scholar] [CrossRef]
- Dron, R.; Brivot, F. Thermodynamic and kinetic approach to the alkali-silica reaction: Part 1. Cem. Concr. Res. 1992, 22, 941–948. [Google Scholar] [CrossRef]
- Prince, W.; Perami, R. Mise en evidence du role essentiel des ions OH− dans les reactions alcali silice. Cem. Concr. Res. 1993, 23, 1121–1129. [Google Scholar] [CrossRef]
- Larive, C.; Laplaud, A.; Coussy, O. The role of water in alkali-silica reaction. In Proceedings of the 11th International Conference on Alkali-Aggregate Reaction, Québec City, QC, Canada, 11–16 June 2000; pp. 61–69. [Google Scholar]
- Multon, S.; Toutlemonde, F. Effect of moisture conditions and transfers on alkali silica reaction damaged structures. Cem. Concr. Res. 2010, 40, 924–934. [Google Scholar] [CrossRef]
- Glasser, L. Osmotic pressure and the swelling of gels. Cem. Concr. Res. 1979, 9, 515–517. [Google Scholar] [CrossRef]
- Šachlová, S.; PřAikryl, R.; Pertold, Z. Alkali-silica reaction products: Comparison between samples from concrete structures and laboratory test specimens. Mater. Charact. 2010, 61, 1379–1393. [Google Scholar] [CrossRef]
- Haha, B. Mechanical Effects of Alkali Silica Reaction in Concrete Studied by SEM-Image Analysis. Ph.D. Thesis, EPFL, Lausanne, France, 2006. [Google Scholar]
- Sanchez, L.; Fournier, B.; Jolin, M.; Duchesne, J. Reliable quantification of {AAR} damage through assessment of the Damage Rating Index (DRI). Cem. Concr. Res. 2015, 67, 74–92. [Google Scholar] [CrossRef]
- Hobbs, D.W. The alkali-silica reaction—A model for predicting expansion in mortar. Mag. Concr. Res. 1981, 33, 208–220. [Google Scholar] [CrossRef]
- Groves, G.W.; Zhang, X. A dilatation model for the expansion of silica glass/OPC mortars. Cem. Concr. Res. 1990, 20, 453–460. [Google Scholar] [CrossRef]
- Furusawa, Y.; Ohga, H.; Uomoto, T. An analytical study concerning prediction of concrete expansion due to alkali-silica reaction. In Proceedings of the Third International Conference on Durability of Concrete, Nice, France, 22–28 May 1994; pp. 757–780. [Google Scholar]
- Meyer, C.; Baxter, S. Use of Recycled Glass and Fly Ash for Precast Concrete; Report NYSERDA 98-18 (4292-IABR-IA-96) to New York State Energy Research and Developement Authority; Department of Civil Engineering and Engineering Mechanics, Columbia University: New York, NY, USA, 1998. [Google Scholar]
- Suwito, A.; Jin, W.; Xi, Y.; Meyer, C. A Mathematical Model for the Pessimum size Effect of ASR in Concrete. Concr. Sci. Eng. 2002, 4, 23–34. [Google Scholar]
- Xi, Y.; Suwito, A.; Wen, X.; Meyer, C.; Jin, W. Testing and modeling alkali-silica reaction and the associated expansion of concrete. In Mechanics of Quasi-Brittle Materials and Structures, Proceedings of International Workshop in Honor of Prof Z P Bazant 60th Birthday; Hermes Science Publications: Paris, France, 1998. [Google Scholar]
- Xi, Y.; Jennings, H.M. Shrinkage of cement paste and concrete modelled by a multiscale effective homogeneous theory. Mater. Struct. 1997, 30, 329–339. [Google Scholar] [CrossRef]
- Fick, A. Ueber Diffusion. Ann. Phys. 1855, 170, 59–86. [Google Scholar] [CrossRef]
- Bazănt, Z.P.; Zi, G.; Meyer, C. Fracture mechanics of ASR in concretes with waste glass particles of different sizes. J. Eng. Mech. 2000, 126, 226–232. [Google Scholar] [CrossRef]
- Gao, X.X.; Multon, S.; Cyr, M.; Sellier, A. Alkali silica reaction (ASR) expansion: Pessimum effect versus scale effect. Cem. Concr. Res. 2013, 44, 25–33. [Google Scholar] [CrossRef]
- Dunant, C.F.; Scrivener, K.L. Effects of aggregate size on alkali-silica-reaction induced expansion. Cem. Concr. Res. 2012, 42, 745–751. [Google Scholar] [CrossRef]
- Charlwood, R.G.; Solymar, S.V.; Curtis, D.D. A review of alkali aggregate reactions in hydroelectric plants and dams. In Proceedings of the International Conference of Alkali-Aggregate Reactions in Hydroelectric Plants and Dams, Fredericton, NB, Canada, 28 September–2 October 1992; Volume 129. [Google Scholar]
- Thompson, G.; Charlwood, R.; Steele, R.; Curtis, D. Mactaquac generating station Intake and spillway remedial measures. In Proceedings of the Eighteenth International Congress on Large Dams, Durban, South Africa, 7–11 November 1994; Volume 1, pp. 347–368. [Google Scholar]
- Léger, P.; Côté, P.; Tinawi, R. Finite element analysis of concrete swelling due to alkali-aggregate reactions in dams. Comput. Struct. 1996, 60, 601–611. [Google Scholar] [CrossRef]
- Herrador, M.F.; Martínez-Abella, F.; Fernández-Gago, R.H. Mechanical behavior model for ASR-affected dam concrete under service load: Formulation and verification. Mater. Struct. 2009, 42, 201–212. [Google Scholar] [CrossRef]
- Pietruszczak, S. On the mechanical behaviour of concrete subjected to alkali-aggregate reaction. Comput. Struct. 1996, 58, 1093–1097. [Google Scholar] [CrossRef]
- Huang, M.; Pietruszczak, S. Numerical analysis of concrete structures subjected to alkali-aggregate reaction. Mech. Cohesive-Frict. Mater. 1996, 1, 305–319. [Google Scholar] [CrossRef]
- Ulm, F.; Coussy, O.; Kefei, L.; Larive, C. Thermo-Chemo-Mechanics Of ASR Expansion In Concrete Structures. J. Eng. Mech. 2000, 126, 233–242. [Google Scholar] [CrossRef]
- Farage, M.; Alves, J.L.D.; Fairbairn, E.M.R. Macroscopic model of concrete subjected to alkali–aggregate reaction. Cem. Concr. Res. 2004, 34, 495–505. [Google Scholar] [CrossRef]
- Fairbairn, E.M.R.; Ribeiro, F.L.B.; Lopes, L.E.; Toledo-Filho, R.D.; Silvoso, M.M. Modelling the structural behaviour of a dam affected by alkali-silica reaction. Commun. Numer. Methods. Eng. 2005, 22, 1–12. [Google Scholar] [CrossRef]
- Saouma, V.; Perotti, L. Constitutive model for alkali-aggregate reactions. ACI Mater. J. 2006, 103, 194–202. [Google Scholar]
- Multon, S.; Seignol, J.F.; Toutlemonde, F. Chemo-mechanical assessment of beams damaged by alkali-silica reaction. J. Mater. Civ. Eng. 2006, 18, 500–509. [Google Scholar] [CrossRef]
- Comi, C.; Fedele, R.; Perego, U. A chemo-thermo-damage model for the analysis of concrete dams affected by alkali-silica reaction. Mech. Mater. 2009, 41, 210–230. [Google Scholar] [CrossRef]
- Comi, C.; Perego, U. Anisotropic damage model for concrete affected by alkali-aggregate reaction. Int. J. Damage Mech. 2011, 20, 598–617. [Google Scholar] [CrossRef]
- Poyet, S.; Sellier, A.; Capra, B.; Foray, G.; Torrenti, J.M.; Cognon, H.; Bourdarot, E. Chemical modelling of alkali silica reaction: Influence of the reactive aggregate size distribution. Mater. Struct. 2007, 40, 229–239. [Google Scholar] [CrossRef]
- Pesavento, F.; Gawin, D.; Wyrzykowski, M.; Schrefler, B.A.; Simoni, L. Modeling alkali silica reaction in non-isothermal, partially saturated cement based materials. Comput. Methods Appl. Mech. Eng. 2012, 225–228, 95–115. [Google Scholar] [CrossRef]
- Capra, B.; Sellier, A. Orthotropic modelling of alkali-aggregate reaction in concrete structures: Numerical simulations. Mech. Mater. J. 2003, 35, 817–830. [Google Scholar] [CrossRef]
- Pan, J.; Feng, Y.; Wang, J.; Sun, Q.; Zhang, C.; Owen, D. Modeling of alkali-silica reaction in concrete: A review. Front. Struct. Civ. Eng. 2012, 6, 1–18. [Google Scholar]
- Dunant, C.F.; Scrivener, K.L. Physically based models to study the alkali-silica reaction. Proc. Inst. Civ. Eng. Constr. Mater. 2016, 169, 136–144. [Google Scholar] [CrossRef]
- Comby-Peyrot, I.; Bernard, F.; Bouchard, P.O.; Bay, F.; Garcia-Diaz, E. Development and validation of a 3D computational tool to describe concrete behaviour at mesoscale. Application to the alkali-silica reaction. Comput. Mater. Sci. 2009, 46, 1163–1177. [Google Scholar] [CrossRef]
- Dunant, C.F.; Scrivener, K.L. Micro-mechanical modelling of alkali-silica-reaction-induced degradation using the AMIE framework. Cem. Concr. Res. 2010, 40, 517–525. [Google Scholar] [CrossRef]
- Shin, J.H.; Struble, L.J.; Kirkpatrick, R.J. Modeling alkali-silica reaction using image analysis and finite element analysis. In Proceedings of the 6th International Symposium on Cement and Concrete and Canmet/Aci International Symposium on Concrete Technology for Sustainable Development, Xi’an, China, 19–22 September 2006; Volume 3. [Google Scholar]
- Shin, J.H. Modeling Alkali-Silica Reaction Using Image Analysis and Finite Element Analysis; DissertationTip, University of Illinois at Urbana-Champaign: Champaign, IL, USA, 2009. [Google Scholar]
- Alnaggar, M.; Cusatis, G.; Di Luzio, G. Lattice Discrete Particle Modeling (LDPM) of Alkali Silica Reaction (ASR) deterioration of concrete structures. Cem. Concr. Compos. 2013, 41, 45–59. [Google Scholar] [CrossRef]
- Cusatis, G.; Pelessone, D.; Mencarelli, A. Lattice Discrete Particle Model (LDPM) for Concrete failure Behavior of Concrete. I: Theory. Cem. Concr. Compos. 2011, 33, 881–890. [Google Scholar] [CrossRef]
- Cusatis, G.; Mencarelli, A.; Pelessone, D.; Baylot, J. Lattice Discrete Particle Model (LDPM) for Failure Behavior of Concrete. II: Calibration and Validation. Cem. Concr. Compos. 2011, 33, 891–905. [Google Scholar] [CrossRef]
- Alnaggar, M.; Liu, M.; Qu, J.; Cusatis, G. Lattice Discrete Particle Modeling of acoustic nonlinearity change in accelerated alkali silica reaction (ASR) tests. Mater. Struct. 2015, 1–23. [Google Scholar] [CrossRef]
- Multon, S.; Sellier, A. Multi-scale analysis of alkali-silica reaction (ASR): Impact of alkali leaching on scale effects affecting expansion tests. Cem. Concr. Res. 2016, 81, 122–133. [Google Scholar] [CrossRef]
- Hong, S.Y.; Glasser, F. Alkali binding in cement pastes Part I. The C-S-H phase. Cem. Concr. Res. 1999, 29, 1893–1903. [Google Scholar] [CrossRef]
- Chatterji, S. Transportation of ions through cement based materials. Part 3 experimental evidence for the basic equations and some important deductions. Cem. Concr. Res. 1994, 24, 1229–1236. [Google Scholar] [CrossRef]
- Arnold, J.; Kosson, D.; Garrabrants, A.; Meeussen, J.; van der Sloot, H. Solution of the nonlinear Poisson Boltzmann equation: Application to ionic diffusion in cementitious materials. Cem. Concr. Res. 2013, 44, 8–17. [Google Scholar] [CrossRef]
- Martin, R.P.; Metalssi, O.O.; Toutlemonde, F. Importance of considering the coupling between transfer properties, alkali leaching and expansion in the modelling of concrete beams affected by internal swelling reactions. Constr. Build. Mater. 2013, 49, 23–30. [Google Scholar] [CrossRef]
- Rahimi-Aghdam, S.; Bažant, Z.P.; Caner, F.C. Diffusion-Controlled and Creep-Mitigated ASR Damage via Microplane Model. II: Material Degradation, Drying, and Verification. J. Eng. Mech. 2017, 143. [Google Scholar] [CrossRef]
- Alnaggar, M.; Cusatis, G.; Luzio, G.D. A discrete model for Alkali-Silica-Reaction in concrete. In Proceedings of the 8th International Conference on Fracture Mechanics of Concrete and Concrete Structures, FraMCoS 2013, Toledo, Spain, 10–14 March 2013; pp. 1315–1326. [Google Scholar]
- Di Luzio, G.; Cusatis, G. Hygro-thermo-chemical modeling of high performance concrete. I: Theory. Cem. Concr. Compos. 2009, 31, 301–308. [Google Scholar] [CrossRef]
- Pantazopoulou, S.J.; Mills, R.H. Microstructural Aspects of the Mechanical Response of Plain Concrete. Mater. J. 1995, 92, 605–616. [Google Scholar]
- Norling Mjonell, K. A model on self-desiccation in high-performance concrete. In Self-Desiccation and its Importance in Concrete Technology, Proceedings of the International Research Seminar, Lund, Sweden, 10 June 1997; 1997; pp. 141–157. [Google Scholar]
- Di Luzio, G.; Cusatis, G. Hygro-thermo-chemical modeling of high performance concrete. II: Numerical implementation, calibration, and validation. Cem. Concr. Compos. 2009, 31, 309–324. [Google Scholar] [CrossRef]
- Feldman, R. Sorption and length-change scanning isotherms of methanol and water on hydrated Portland cement. In Proceedings of the 5th International Congress on the Chemistry of Cement, Tokyo, Japan, 7–11 October 1968; pp. 53–66. [Google Scholar]
- Baroghel-Bounya, V.; Mainguya, M.; Lassabatereb, T.; Coussya, O. Characterization and identification of equilibrium and transfer moisture properties for ordinary and high-performance cementitious materials. Cem. Concr. Res. 1999, 29, 1225–1238. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Bažant, M.Z. Theory of Sorption Hysteresis in Nanoporous Solids: Part I. Snap-through Instabilities; Part II. Molecular Condensation; Collaborative Structural Engineering Report; Departement of Civil Engineering Northwestern University: Evanston, IL, USA, 2011. [Google Scholar]
- Kawabata, Y.; Martin, R.P.; Seignol, J.F.; Toutlemonde, F. Modelling of evolution of transfer properties due to expansion of concrete induced by internal swelling reaction. In Proceedings of the 15th International Conference on Alkali-Aggregate Reaction in Concrete, São Paulo, Brazil, 3–7 July 2016. [Google Scholar]
- Ulm, F.J.; Coussy, O. Modeling of thermochemomechanical couplings of concrete at early ages. J. Eng. Mech. 1995, 121, 785–794. [Google Scholar] [CrossRef]
- Cervera, M.; Oliver, J.; Prato, T. Thermo-chemo-mechanical model for concrete. I: Hydration and aging. J. Eng. Mech. 1999, 125, 1018–1027. [Google Scholar] [CrossRef]
- Gawin, D.; Pesanto, F.; Schrefler, B.A. Hygro-thermo-chemo-mechanical modelling of concrete at early ages and beyond. Part I: hydration and hygro-thermal phenomena. Int. J. Numer. Methods Eng. 2006, 67, 299–331. [Google Scholar] [CrossRef]
- Cusatis, G.; Schauffert, E. Discontinuous cell method (DCM) for cohesive fracture propagation. In Proceedings of the 7th international conference on fracture mechanics of concrete and concrete structures (FraMCos 7), Jeju, Korea, 23–28 May 2010; pp. 23–28. [Google Scholar]
- Rezakhani, R.; Cusatis, G. Asymptotic expansion homogenization of discrete fine-scale models with rotational degrees of freedom for the simulation of quasi-brittle materials. J. Mech. Phys. Solids 2016, 88, 320–345. [Google Scholar] [CrossRef]
- Cusatis, G.; Zhou, X. High-Order Microplane Theory for Quasi-Brittle Materials with Multiple Characteristic Lengths. J. Eng. Mech. 2014, 140, 04014046. [Google Scholar] [CrossRef]
- Ceccato, C.; Salviato, M.; Pellegrino, C.; Cusatis, G. Simulation of concrete failure and fiber reinforced polymer fracture in confined columns with different cross sectional shape. Int. J. Solids Struct. 2017, 108, 216–229. [Google Scholar] [CrossRef]
- Schauffert, E.A.; Cusatis, G. Lattice discrete particle model for fiber reinforced concrete (LDPM-F): I. Theory. J. Eng. Mech. 2011, 138, 826–833. [Google Scholar]
- Schauffert, E.A.; Cusatis, G.; Pelessone, D.; O’Daniel, J.; Baylot, J. Lattice discrete particle model for fiber reinforced concrete (LDPM-F): II. Tensile fracture and multiaxial loading behavior. J. Eng. Mech. 2011, 138, 834–841. [Google Scholar]
- Smith, J.; Cusatis, G.; Pelessone, D.; Landis, E.; O’Daniel, J.; Baylot, J. Discrete modeling of ultra-high-performance concrete with application to projectile penetration. Int. J. Impact Eng. 2014, 65, 13–32. [Google Scholar] [CrossRef]
- Alnaggar, M.; Cusatis, G. Automatic Parameter Identification of Discrete Mesoscale Models with Application to the Coarse-Grained Simulation of Reinforced Concrete Structures. In Proceedings of the 20th Analysis and Computation Specialty Conference, Chicago, IL, USA, 29–31 March 2012; Volume 36, pp. 406–417. [Google Scholar]
- Cusatis, G.; Rezakhani, R.; Alnaggar, M.; Zhou, X.; Pelessone, D. Multiscale computational models for the simulation of concrete materials and structures. In Computational Modelling of Concrete Structures; CRC Press: Boca Raton, FL, USA, 2014; pp. 23–38. [Google Scholar]
- Di Luzio, G.; Cusatis, G. Solidification–microprestress–microplane (SMM) theory for concrete at early age: Theory, validation and application. Int. J. Solids Struct. 2013, 50, 957–975. [Google Scholar] [CrossRef]
- Prasannan, S.; Bažant, Z.P. Solidification Theory for Concrete Creep. I: Formulation. J. Eng. Mech. 1989, 115, 1691–1703. [Google Scholar]
- Hauggaard, A.B.; Bažant, Z.P.; Baweja, S.; Ulm, F.J. Microprestress-Solidification Theory for Concrete Creep. I: Aging and Drying Effects. J. Eng. Mech. 1997, 123, 1188–1194. [Google Scholar]
- Bažant, Z.P.; Cusatis, G.; Cedolin, L. Temperature Effect on Concrete Creep Modeled by Microprestress-Solidification Theory. J. Eng. Mech. 2004, 130, 691–699. [Google Scholar] [CrossRef]
- Havlasek, P.; Jirasek, M. Multiscale modeling of drying shrinkage and creep of concrete. Cem. Concr. Res. 2016, 85, 55–74. [Google Scholar] [CrossRef]
- Jirásek, M.; Bažant, Z. Inelastic Analysis of Structures; John Wiley & Sons: Somerset, NJ, USA, 2002. [Google Scholar]
- Bazant, Z.P.; Xi, Y. Continuous retardation spectrum for solidification theory of concrete creep. J. Eng. Mech. 1995, 121, 281–288. [Google Scholar] [CrossRef]
- Pelessone, D. MARS: Modeling and Analysis of the Response of Structures—User’s Manual; ES3: Solana Beach, CA, USA, 2009. [Google Scholar]
- Multon, S.; Seignol, J.F.; Toutlemonde, F. Structural behavior of concrete beams affected by alkali-silica reaction. ACI Mater. J. 2005, 102, 67–76. [Google Scholar]
- Hubler, M.H.; Wendner, R.; Bažant, Z.P. Statistical justification of Model B4 for drying and autogenous shrinkage of concrete and comparisons to other models. Mater. Struct. 2015, 48, 797–814. [Google Scholar] [CrossRef]
- Wendner, R.; Hubler, M.H.; Bažant, Z.P. Statistical justification of model B4 for multi-decade concrete creep using laboratory and bridge databases and comparisons to other models. Mater. Struct. 2015, 48, 815–833. [Google Scholar] [CrossRef]
- Standard Test Method for Static Modulus of Elasticity and Poisson’s Ratio of Concrete in Compression; Technical Report; ASTM International: West Conshohocken, PA, USA, 2014; ASTM C469/C469M-14.
- Multon, S.; Toutlemonde, F. Effect of applied stresses on alkali-silica reaction-induced expansions. Cem. Concr. Res. 2006, 36, 912–920. [Google Scholar] [CrossRef]
- Standard Test Method for Concrete Aggregates by Determination of Length Change of Concrete Due to Alkali-Silica Reaction; Annual Book of ASTM Standards: Philadelphia, PA, USA, 2002; 1293-01 AC.
- SPotential Expansivity of Aggregates (Procedure for Length Change Due to Alkali-Aggregate Reaction in Concrete Prisms); Methods of Test for Concrete; Canadian Standards Association: Mississauga, ON, USA, 2000; pp. 207–216, CSA A23.2-00.
- Abdellatef, M.; Salem, E.; Lau, D.; Stenroos, L.; Alnaggar, M. Bond degradation of corroded reinforcement: An experimental and numerical study. In Proceedings of the 9th International Conference on Fracture Mechanics of Concrete and Concrete Structures, FraMCoS 9, Berkeley, CA, USA, 29 May–1 June 2016. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alnaggar, M.; Di Luzio, G.; Cusatis, G. Modeling Time-Dependent Behavior of Concrete Affected by Alkali Silica Reaction in Variable Environmental Conditions. Materials 2017, 10, 471. https://doi.org/10.3390/ma10050471
Alnaggar M, Di Luzio G, Cusatis G. Modeling Time-Dependent Behavior of Concrete Affected by Alkali Silica Reaction in Variable Environmental Conditions. Materials. 2017; 10(5):471. https://doi.org/10.3390/ma10050471
Chicago/Turabian StyleAlnaggar, Mohammed, Giovanni Di Luzio, and Gianluca Cusatis. 2017. "Modeling Time-Dependent Behavior of Concrete Affected by Alkali Silica Reaction in Variable Environmental Conditions" Materials 10, no. 5: 471. https://doi.org/10.3390/ma10050471
APA StyleAlnaggar, M., Di Luzio, G., & Cusatis, G. (2017). Modeling Time-Dependent Behavior of Concrete Affected by Alkali Silica Reaction in Variable Environmental Conditions. Materials, 10(5), 471. https://doi.org/10.3390/ma10050471






