Analysis of the Mechanical Behavior, Creep Resistance and Uniaxial Fatigue Strength of Martensitic Steel X46Cr13
Abstract
:1. Introduction
2. Experimental Procedures
2.1. Tested Material
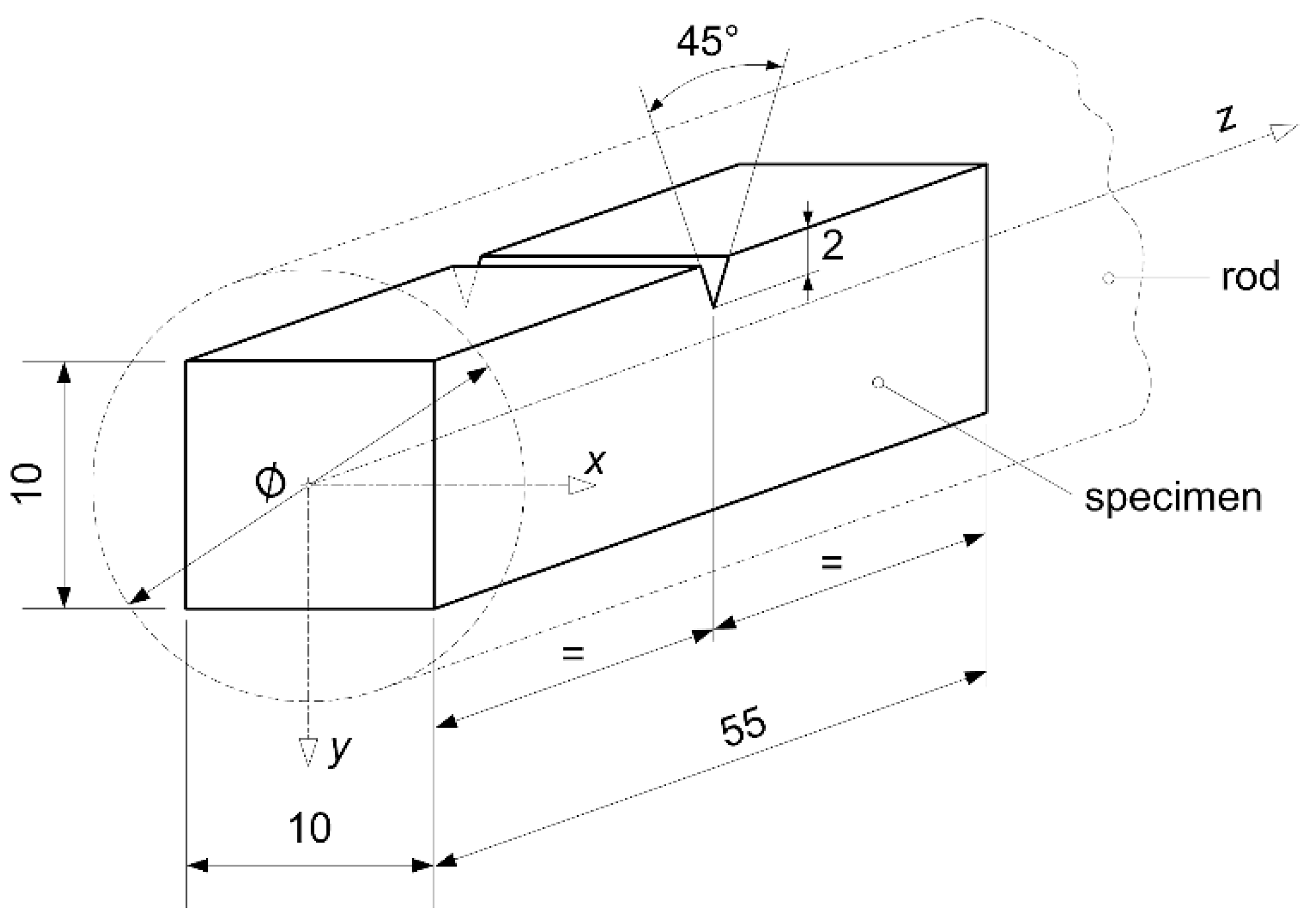
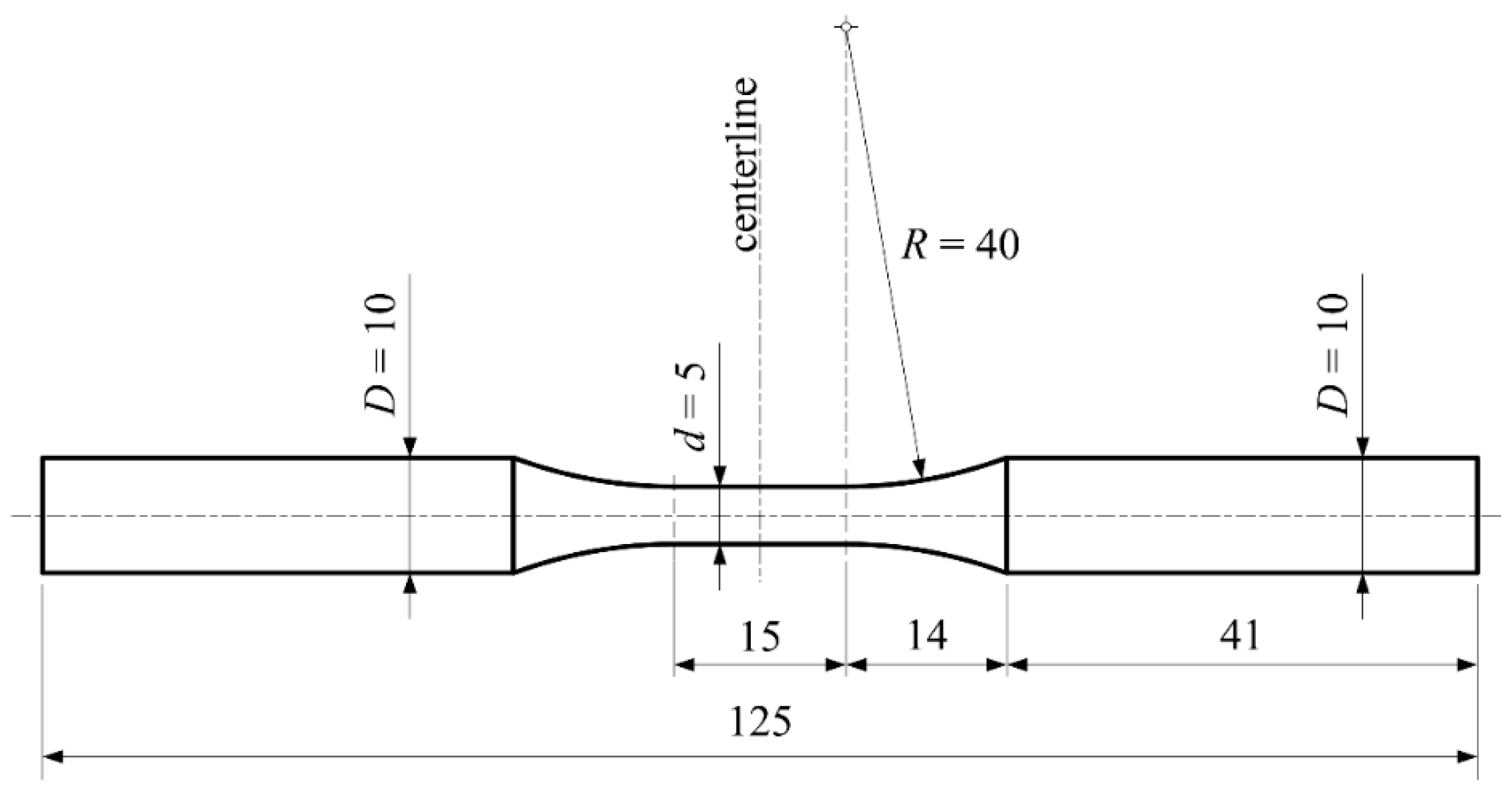
2.2. Equipment, Specimens, Testing Procedures and Standards
3. Experimental Results and Discussion
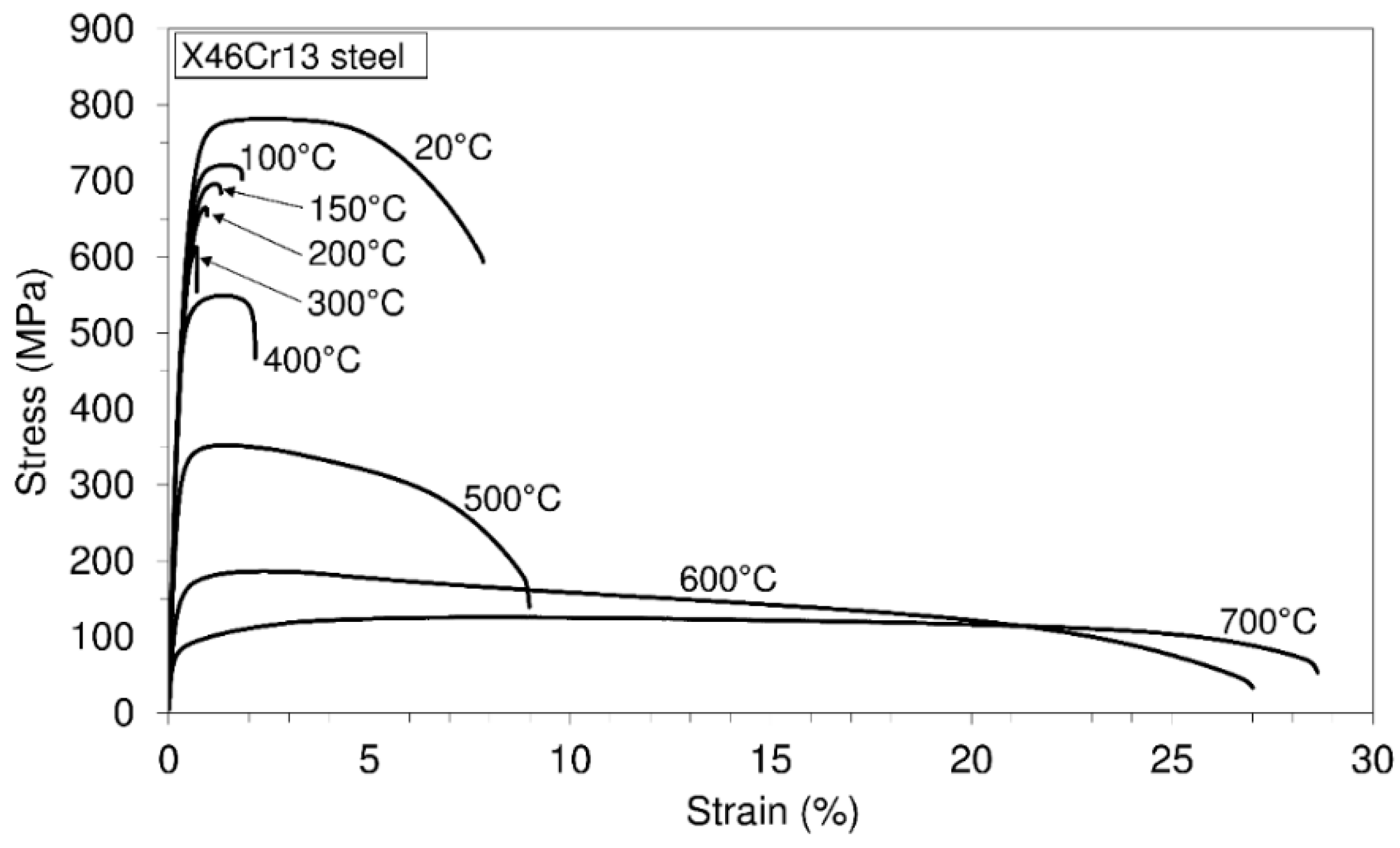
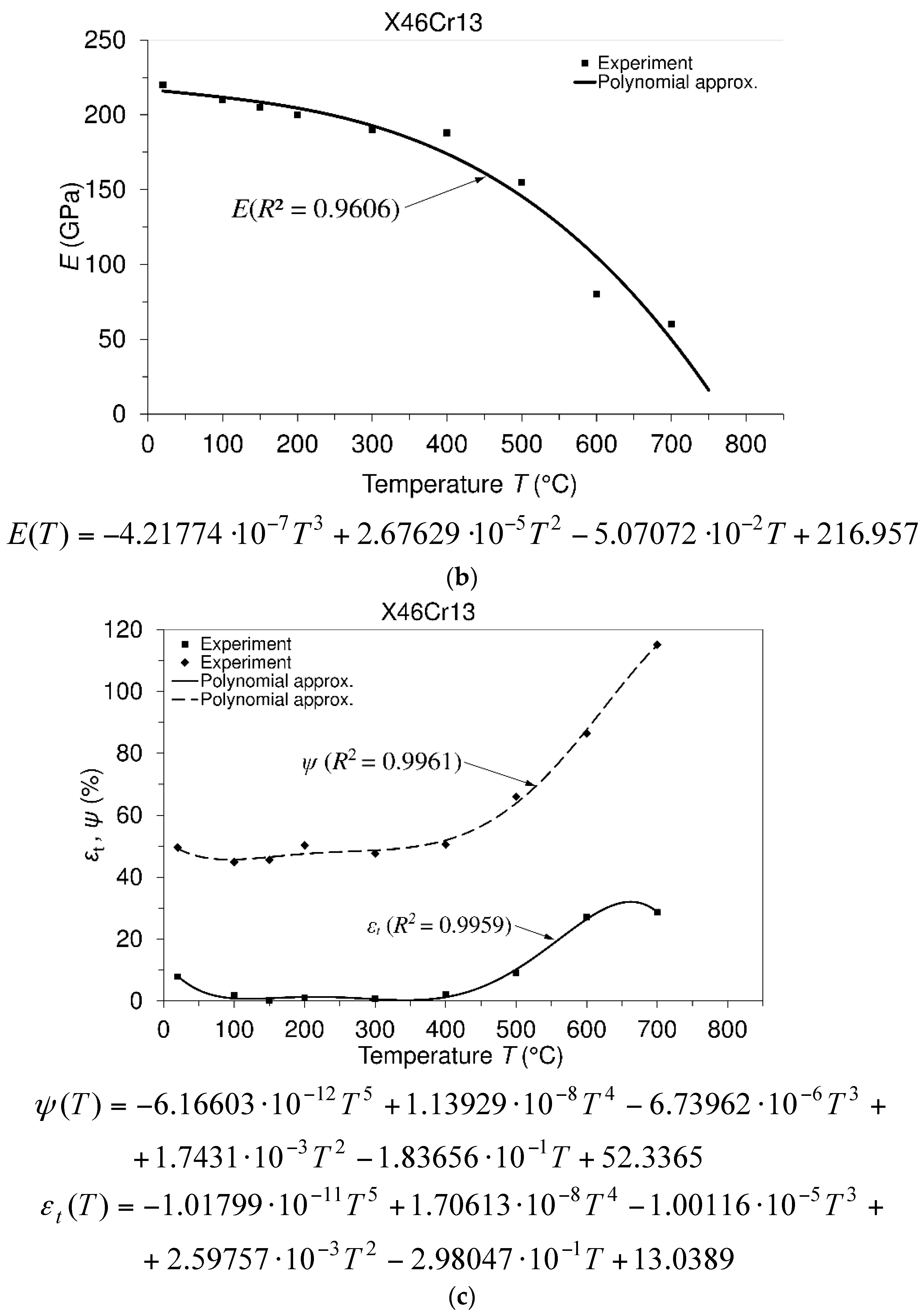
3.1. Uniaxial Tensile Tests
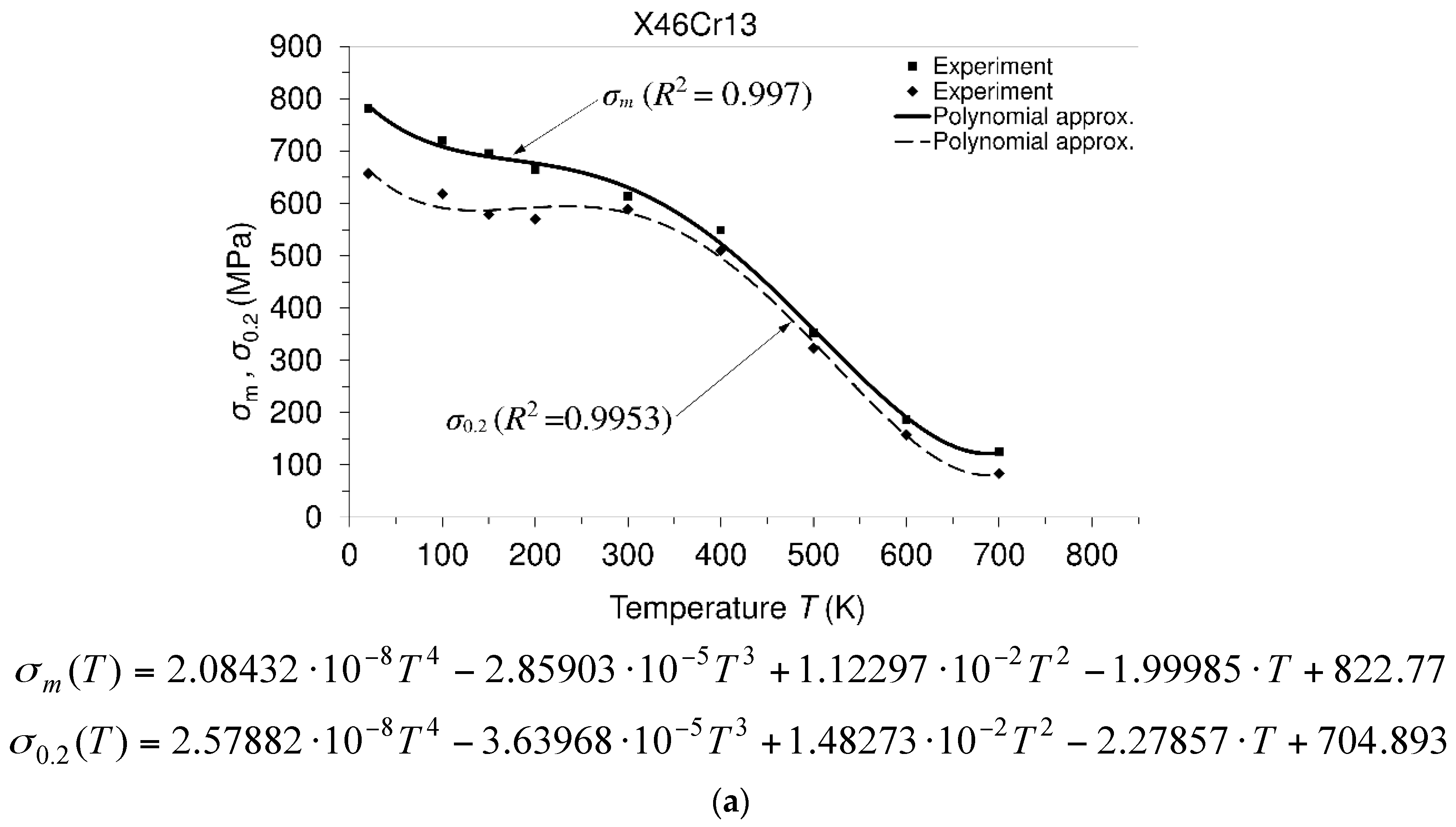
Engineering Stress-Strain Diagrams and Mechanical Properties versus Temperature
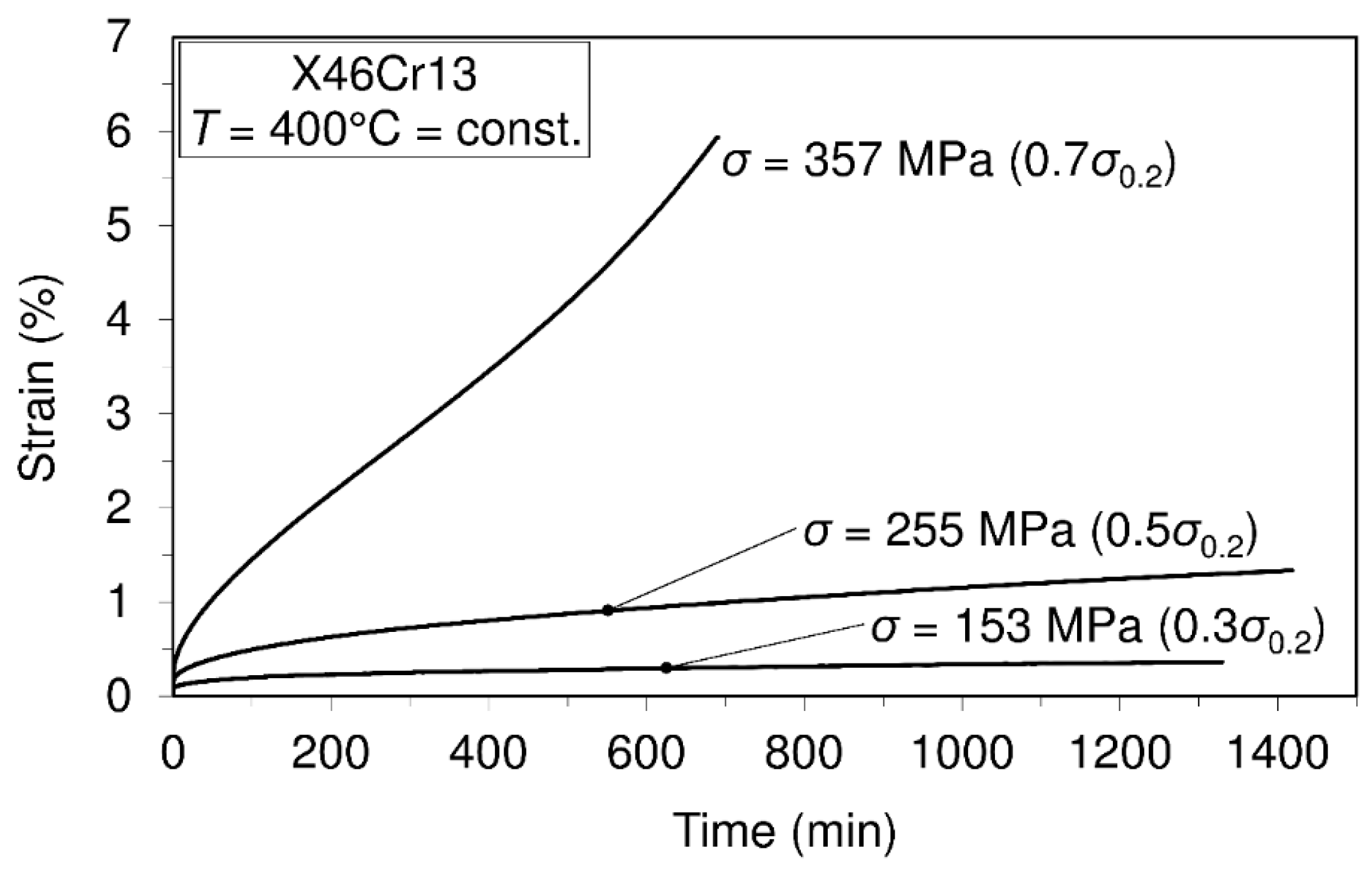
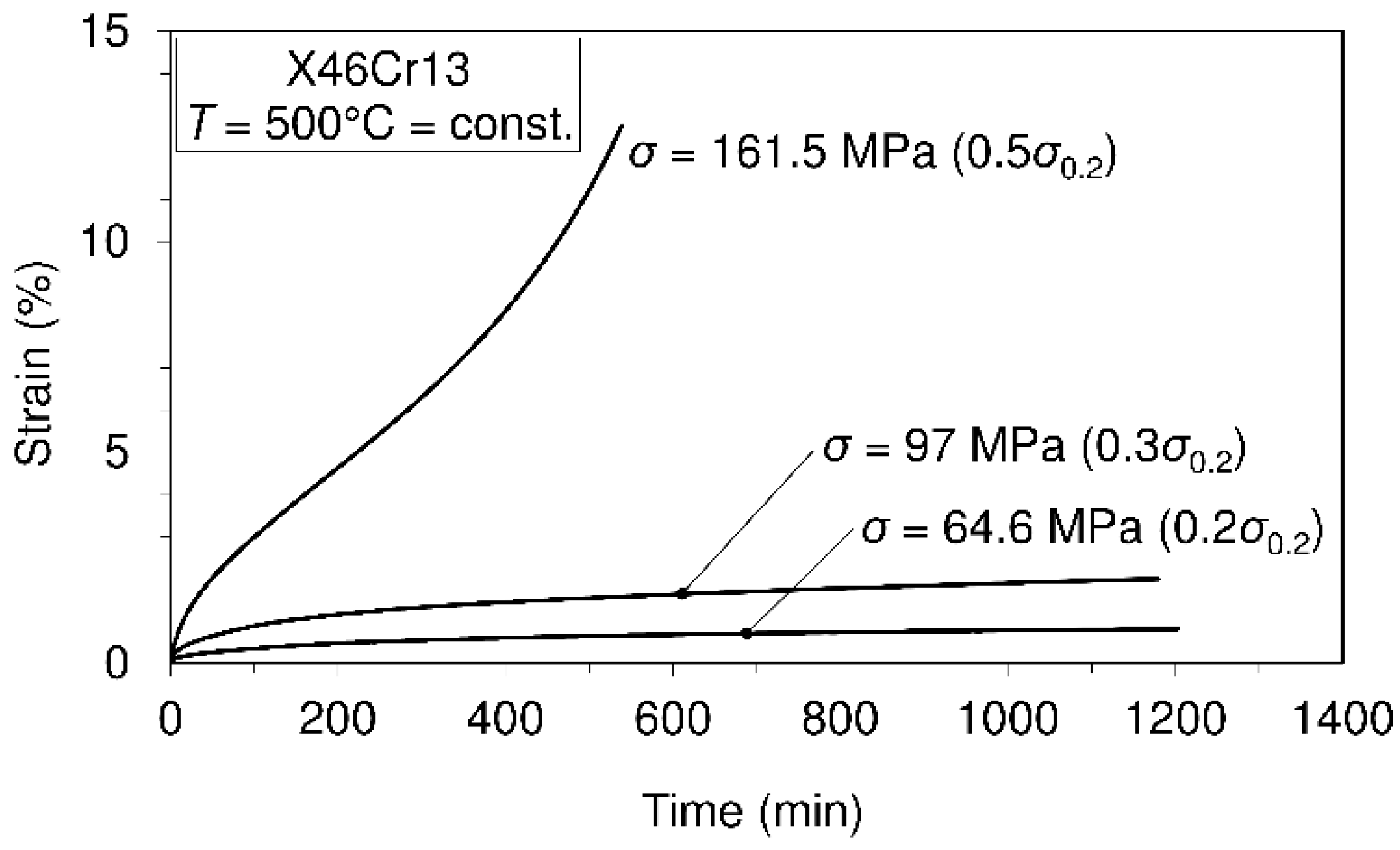
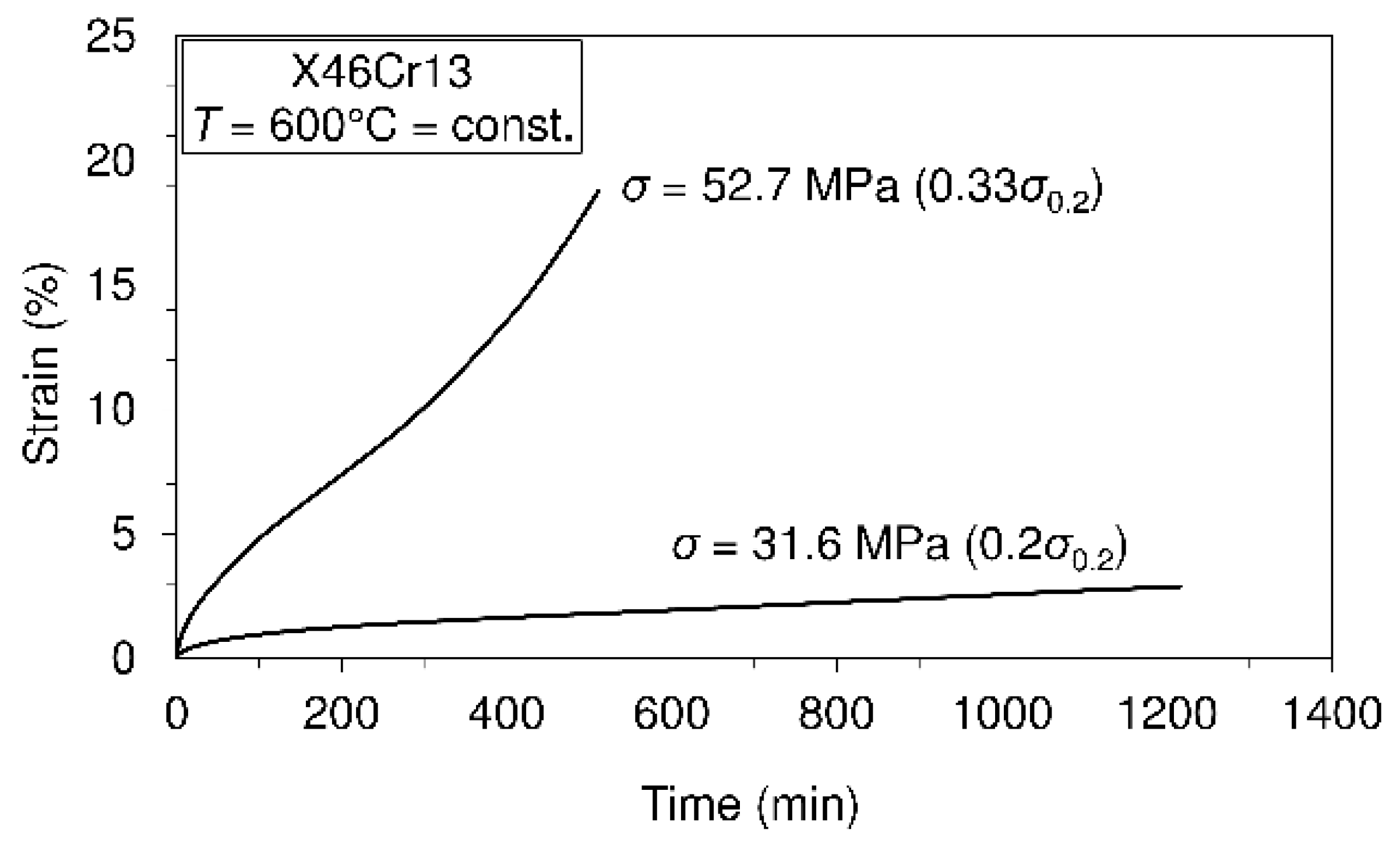
3.2. Uniaxial Short-Time Creep Tests and Creep Modeling
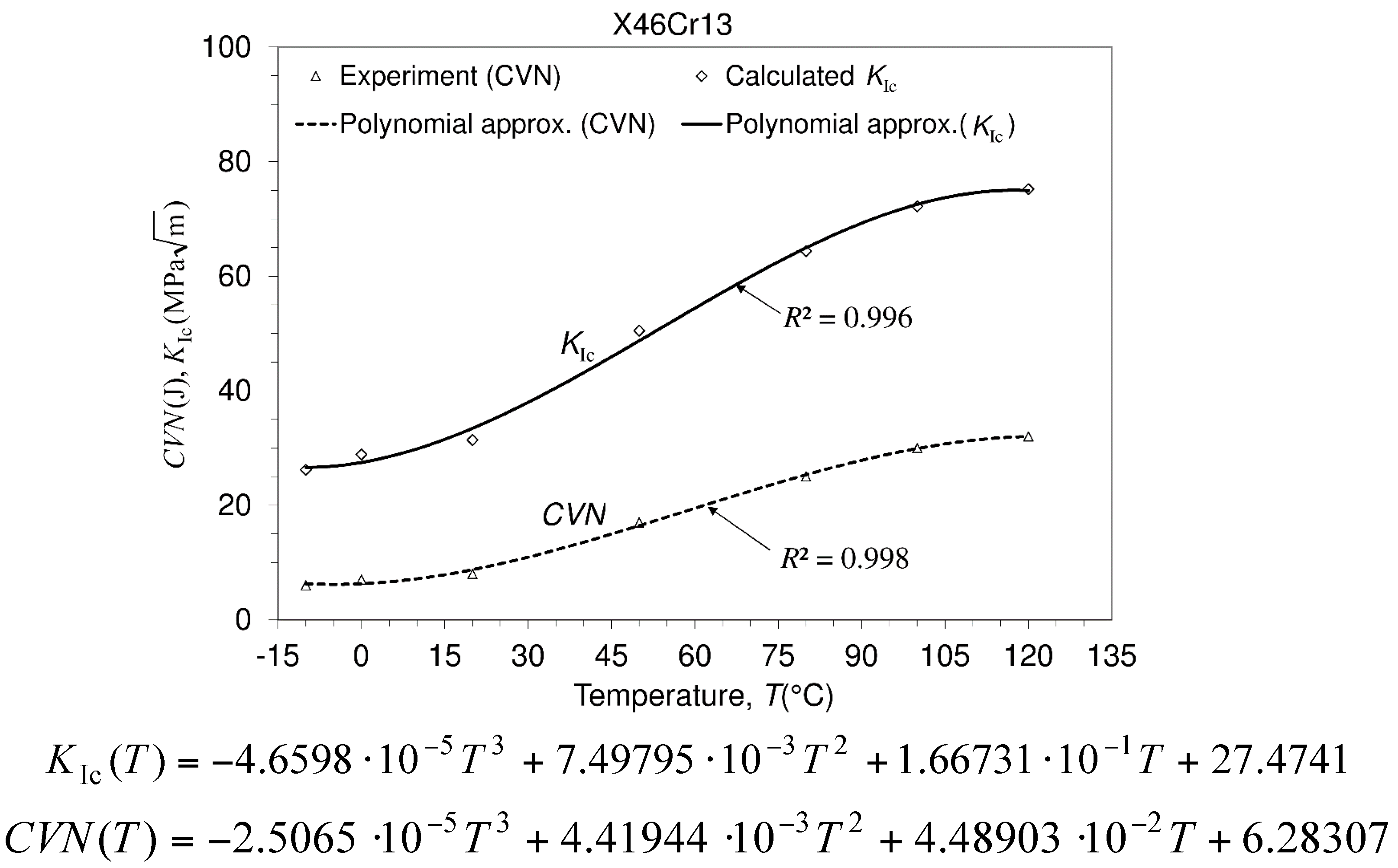
3.3. Charpy V-notch Impact Energy and Fracture Toughness Calculation
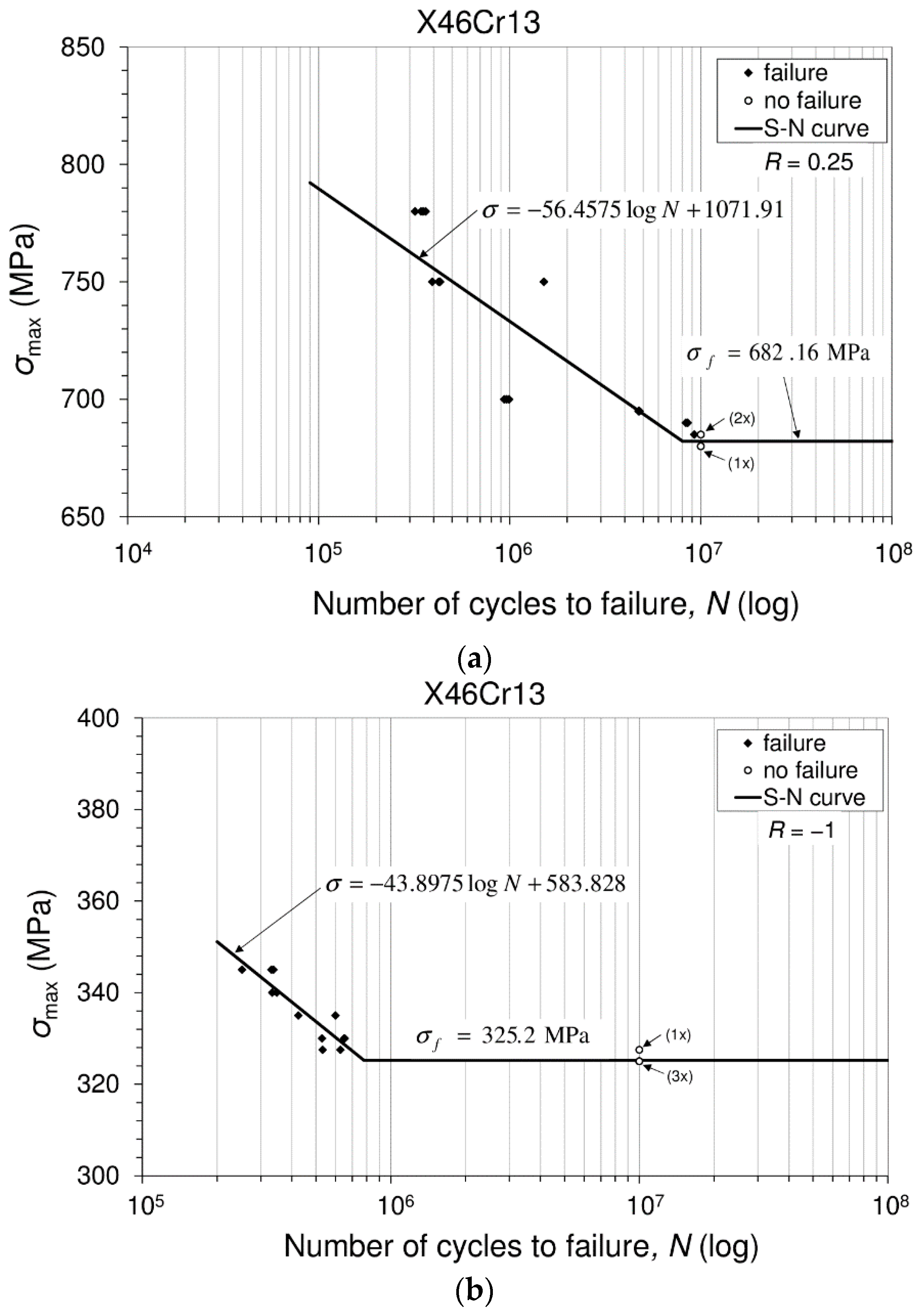
3.4. Fatigue Tests and Fatigue Limit Calculation
Fatigue Limit Calculation
- -
- , the mean fatigue strength, which is defined as:where “d” is the stress step (i.e., the difference between the neighboring stress levels) (Table 5).
- -
- , the coefficient for the one-sided tolerance limit for a normal distribution
- -
- , the estimated standard deviation of the fatigue strength, which is calculated as:
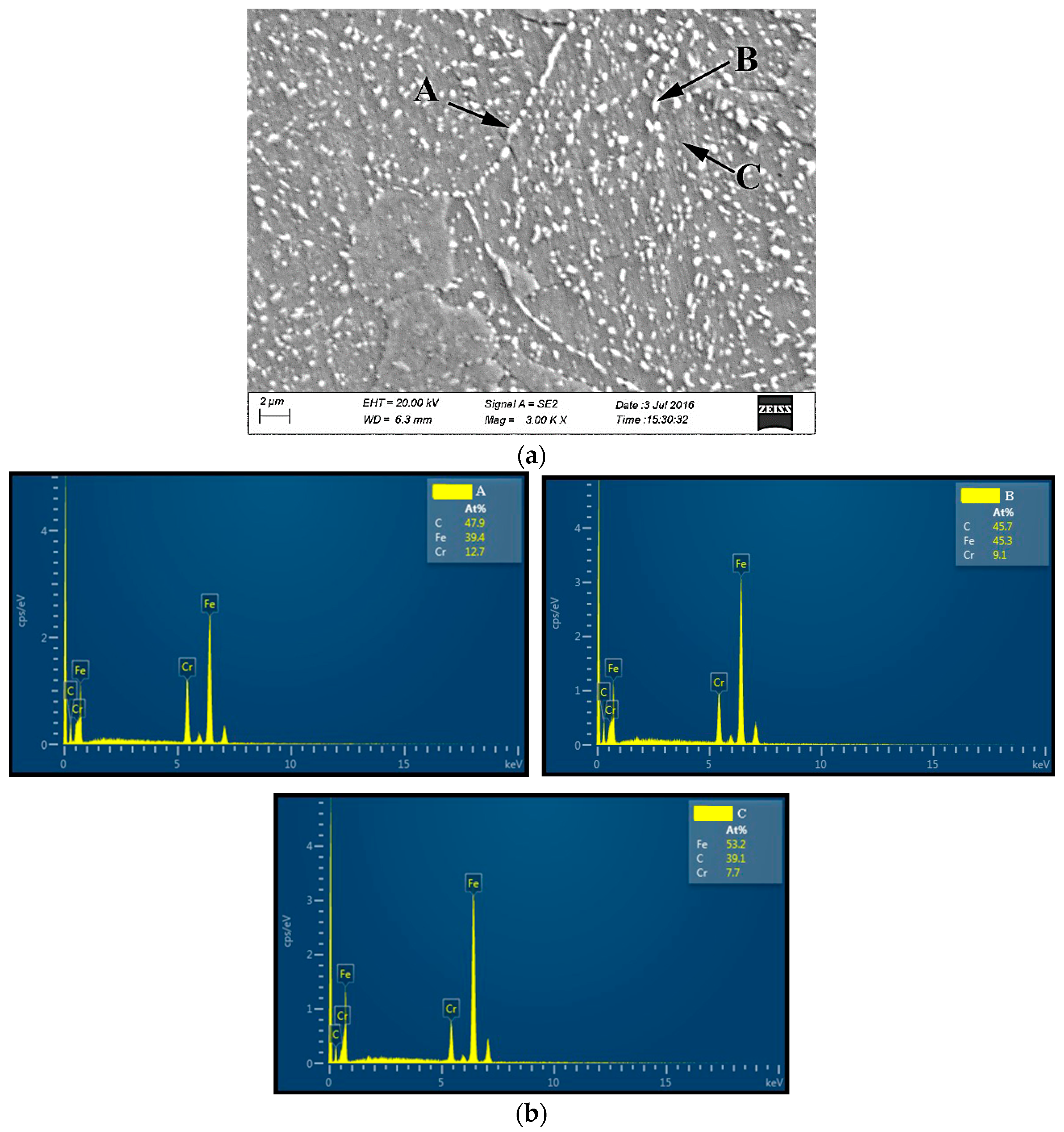
3.5. Microstructure Analysis
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bramfitt, B.L. Effect of composition, processing and structure on properties of iron and steels. In ASM Handbook, Materials Selection and Design; ASM International: Materials Park, OH, USA, 2001; Volume 20, p. 355. [Google Scholar]
- Brooks, C.R.; Choudhury, A. Failure Analysis of Engineering Materials; McGraw-Hill: New York, NY, USA, 2002. [Google Scholar]
- Farahmand, B.; Bockrath, G.; Glassco, J. Fatigue and Fracture Mechanics of High Risk Parts; Chapman & Hall: New York, NY, USA, 1997. [Google Scholar]
- Collins, J.A. Failure of Materials in Mechanical Design, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Raghavan, V. Materials Science and Engineering; Prentice-Hall of India: New Delhi, India, 2004. [Google Scholar]
- Pfennig, A.; Wiegand, R.; Wolf, M.; Bork, C.P. Corrosion and corrosion fatigue of AISI 420C (X46Cr13) at 60 degrees C in CO2-saturated artificial geothermal brine. Corros. Sci. 2013, 68, 134–143. [Google Scholar] [CrossRef]
- Rosemann, P.; Kauss, N.; Muller, C.; Halle, T. Influence of solution annealing temperature and cooling medium on microstructure, hardness and corrosion resistance of martensitic stainless steel X46Cr13. Mater. Corros. 2015, 66, 1068–1076. [Google Scholar] [CrossRef]
- Mueller, T.; Heyn, A.; Babutzka, M.; Rosemann, P. Examination of the influence of heat treatment on the corrosion resistance of martensitic stainless steels. Mater. Corros. 2015, 66, 656–662. [Google Scholar] [CrossRef]
- Rosemann, P.; Mueller, Th.; Babutzka, M.; Heyn, A. Influence of microstructure and surface treatment on the corrosion resistance of martensitic stainless steels 1.4116, 1.4034, and 1.4021. Mater. Corros. 2015, 66, 45–53. [Google Scholar] [CrossRef]
- Schiefler Filho, M.F.O.; Buschinelli, A.J.A.; Gärtner, F.; Kirsten, J.; Voyer, J.; Kreye, H. Influence of process parameters on the quality of thermally sprayed X46Cr13 stainless steel coatings. J. Braz. Soc. Mech. Sci. Eng. 2004, 26, 98–106. [Google Scholar] [CrossRef]
- Scendo, M.; Radek, N.; Konstanty, J.; Staszewska, K. Sliding Wear Behaviour and Corosion Resistance to Ringer’s Solution of Uncoated and DLC Coated X46Cr13 Steel. Arch. Metall. Mater. 2016, 61, 1895–1900. [Google Scholar] [CrossRef]
- Metals—Mechanical Testing; Elevated and Low- Temperature Tests; Metallography. In Annual Book of ASTM Standards; ASTM International: Baltimore, MD, USA, 2015; Volume 03.01.
- Draper, N.R.; Smith, H. Applied Regression Analysis; Wiley–Interscience Publications: New York, NY, USA, 1998. [Google Scholar]
- Brnic, J.; Turkalj, G.; Canadija, M.; Lanc, D.; Brcic, M. Study of the Effects of High Temperatures on the Engineering Properties of Steel 42CrMo4. High Temp. Mater. Processes 2015, 34, 27–34. [Google Scholar] [CrossRef]
- Brnic, J.; Canadija, M.; Turkalj, G.; Lanc, D. 50CrMo4 Steel-Determination of Mechanical Properties at Lowered and Elevated Temperatures, Creep Behavior and Fracture Toughness Calculation. J. Eng. Mater. Technol. 2010, 132, 021004-1–021004-6. [Google Scholar] [CrossRef]
- Brnic, J.; Turkalj, G.; Niu, J.; Canadija, M.; Lanc, D. Analysis of experimental data on the behavior of steel S275JR—Reliability of modern design. Mater. Des. 2013, 47, 497–504. [Google Scholar] [CrossRef]
- Findley, W.N.; Lai, J.S.; Onaran, K. Creep and Relaxation if Nonlinear Viscoelastic Materials; Dover Publications, Inc.: New York, NY, USA, 1989. [Google Scholar]
- Boresi, A.P.; Schmidt, R.J.; Sidebotom, O.M. Advances Mechanics of Materials; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Chao, Y.J.; Ward, J.D.; Sands, R.G. Charpy impact energy, fracture toughness and ductile–brittle transition temperature of dual-phase 590 Steel. Mater. Des. 2007, 28, 551–557. [Google Scholar] [CrossRef]
- Roberts, R.; Newton, C. Interpretive Report on Small Scale Test Correlation with KIc Data. Weld. Res. Counc. Bull. 1981, 265, 1–16. [Google Scholar]
- Brnic, J.; Turkalj, G.; Lanc, D.; Canadija, M.; Brcic, M.; Vukelic, G. Comparison of material properties: Steel 20MnCr5 and similar steels. J. Constr. Steel Res. 2014, 95, 81–89. [Google Scholar] [CrossRef]
- Pollak, R.D. Analysis of Methods for Determining High Cycle Fatigue Strength of a Material with Investigation of Ti-6Al-4V Gigacycle Fatigue Behavior. Ph.D. Dissertation, Air Force Institute of Technology, Wright-Patterson Air Force Base, OH, USA, 2005. [Google Scholar]
- 12107:2012-Metallic Materials-Fatigue Testing-Statistical Planning and Analysis of Data; International Organization for Standardization: Geneva, Switzerland, 2012.




| Material: X46Cr13 Steel (Chromium Martensitic Stainless Steel) | |||||||
|---|---|---|---|---|---|---|---|
| Designation | |||||||
| Steel name | Steel number (Mat. No; W. Nr; Mat. Code) | ||||||
| EN 10088-3-2005/DIN 17440: X46Cr13; AISI 420; BS: 420S45. | 1.4034 | ||||||
| Chemical composition of considered material Mass (%) | |||||||
| C | Si | Mn | P | S | Cr | V | Rest |
| 0.442 | 0.375 | 0.381 | 0.0121 | 0.0192 | 13.05 | 0.201 | 85.2997 |
| Mo | Cu | Al | Ti | Pb | Sn | Co | |
| 0.0493 | 0.108 | 0.0026 | 0.0044 | 0.0004 | 0.0243 | 0.031 | |
| Temperature T (°C) | Material Properties | Reduction Factors | ||||
|---|---|---|---|---|---|---|
| (MPa) | (MPa) | E (GPa) | ||||
| 20 | 781.7 | 657.5 | 220 | 1 | 1 | 1 |
| 100 | 720.6 | 618.4 | 210 | 0.922 | 0.940 | 0.955 |
| 150 | 695.7 | 578.5 | 205 | 0.889 | 0.879 | 0.932 |
| 200 | 664.8 | 570.1 | 200 | 0.850 | 0.867 | 0.909 |
| 300 | 613 | 588.8 | 190 | 0.784 | 0.896 | 0.864 |
| 400 | 549 | 510 | 188 | 0.702 | 0.776 | 0.855 |
| 500 | 352.3 | 323.3 | 155 | 0.451 | 0.492 | 0.705 |
| 600 | 186.5 | 158 | 80 | 0,239 | 0.240 | 0.364 |
| 700 | 125.7 | 83 | 60 | 0.161 | 0.126 | 0.273 |
| Material | X46Cr13 (1.4034) | ||||
|---|---|---|---|---|---|
| Creep strain-time dependence models: (Equation (1)); and (Equation (1c)) where Time (min) = 1200, for all creep processes Creep processes were carried out at the temperatures and stresses listed below | |||||
| Constant temperature ( °C) | 400 | 500 | 600 | ||
| Constant stress level | 153 | 255 | 64 | 97 | 31 |
| Parameters | Parameters and valid for: | ||||
| x = 0.1–0.6 | x = 0.1–0.4 | x = 0.1–0.3 | |||
In accordance with Equation (1) | |||||
In accordance with Equation (1c) | |||||
| R = 0.25 | |||||||
| Stress/max MPa | Number of Specimens | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 690 | ♦ | ♦ | ♦ | ||||
| 685 | ♦ | ○ | ○ | ||||
| 680 | ○ | ||||||
| R = | |||||||
| Stress/max MPa | Number of Specimens | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 330 | ♦ | ♦ | ♦ | ||||
| 327.5 | ♦ | ○ | ♦ | ||||
| 325 | ○ | ||||||
| R = 0.25 | ||||
| Stress/max (MPa) | Number of the level of stress i | |||
| 690 | 2 | 3 | 6 | 12 |
| 685 | 1 | 1 | 1 | 1 |
| 680 | 0 | 0 | 0 | 0 |
| 4 | 7 | 13 | ||
| R = | ||||
| Stress/max (MPa) | Number of the level of stress i | |||
| 330 | 2 | 3 | 6 | 12 |
| 327.5 | 1 | 2 | 2 | 2 |
| 325 | 0 | 0 | 0 | 0 |
| 5 | 8 | 14 | ||
| R = 0.25 | |
| Equation | Material: X46Cr13 (1.4034) |
| 7 | |
| 13 | |
| 4 | |
| 0.1875 | |
| R = | |
| Equation | Material: X46Cr13 (1.4034) |
| 8 | |
| 14 | |
| 5 | |
| 0.24 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brnic, J.; Krscanski, S.; Lanc, D.; Brcic, M.; Turkalj, G.; Canadija, M.; Niu, J. Analysis of the Mechanical Behavior, Creep Resistance and Uniaxial Fatigue Strength of Martensitic Steel X46Cr13. Materials 2017, 10, 388. https://doi.org/10.3390/ma10040388
Brnic J, Krscanski S, Lanc D, Brcic M, Turkalj G, Canadija M, Niu J. Analysis of the Mechanical Behavior, Creep Resistance and Uniaxial Fatigue Strength of Martensitic Steel X46Cr13. Materials. 2017; 10(4):388. https://doi.org/10.3390/ma10040388
Chicago/Turabian StyleBrnic, Josip, Sanjin Krscanski, Domagoj Lanc, Marino Brcic, Goran Turkalj, Marko Canadija, and Jitai Niu. 2017. "Analysis of the Mechanical Behavior, Creep Resistance and Uniaxial Fatigue Strength of Martensitic Steel X46Cr13" Materials 10, no. 4: 388. https://doi.org/10.3390/ma10040388
APA StyleBrnic, J., Krscanski, S., Lanc, D., Brcic, M., Turkalj, G., Canadija, M., & Niu, J. (2017). Analysis of the Mechanical Behavior, Creep Resistance and Uniaxial Fatigue Strength of Martensitic Steel X46Cr13. Materials, 10(4), 388. https://doi.org/10.3390/ma10040388



.JPG)





