Numerical Studies on the Failure Process of Heterogeneous Brittle Rocks or Rock-Like Materials under Uniaxial Compression
Abstract
:1. Introduction
2. The Numerical Approach
2.1. Brief Review of the Existing Numerical Approaches for Brittle Fracturing of Materials
2.2. The Approach Used in this Study
3. Description of the Heterogeneous Material Models and the Uniaxial Compression Tests
3.1. The Heterogeneous Material Models
3.2. Description of the Numerical Uniaxial Compression Tests
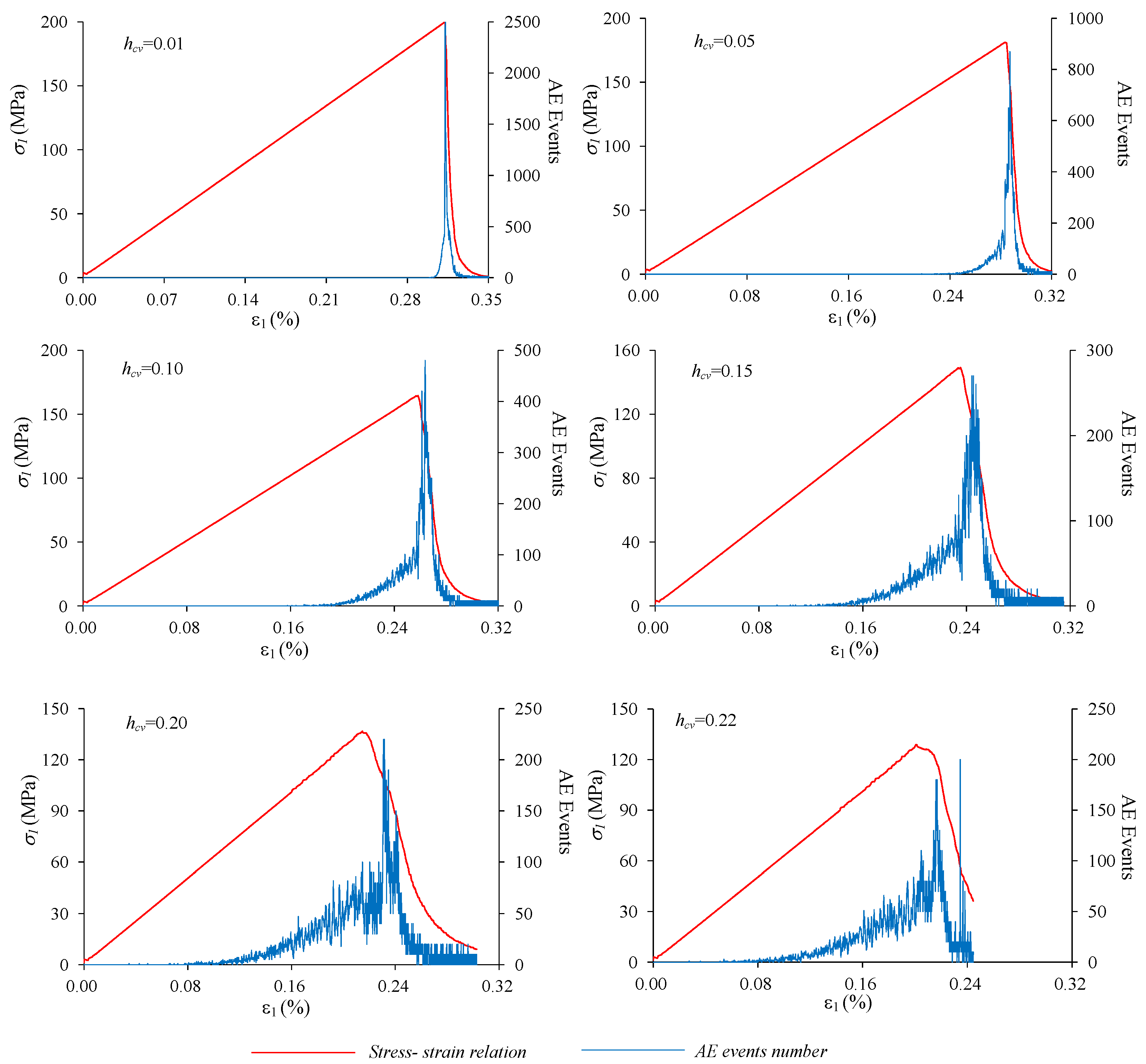
4. The Stress and Fracturing Process of Heterogeneous Material under Uniaxial Compression
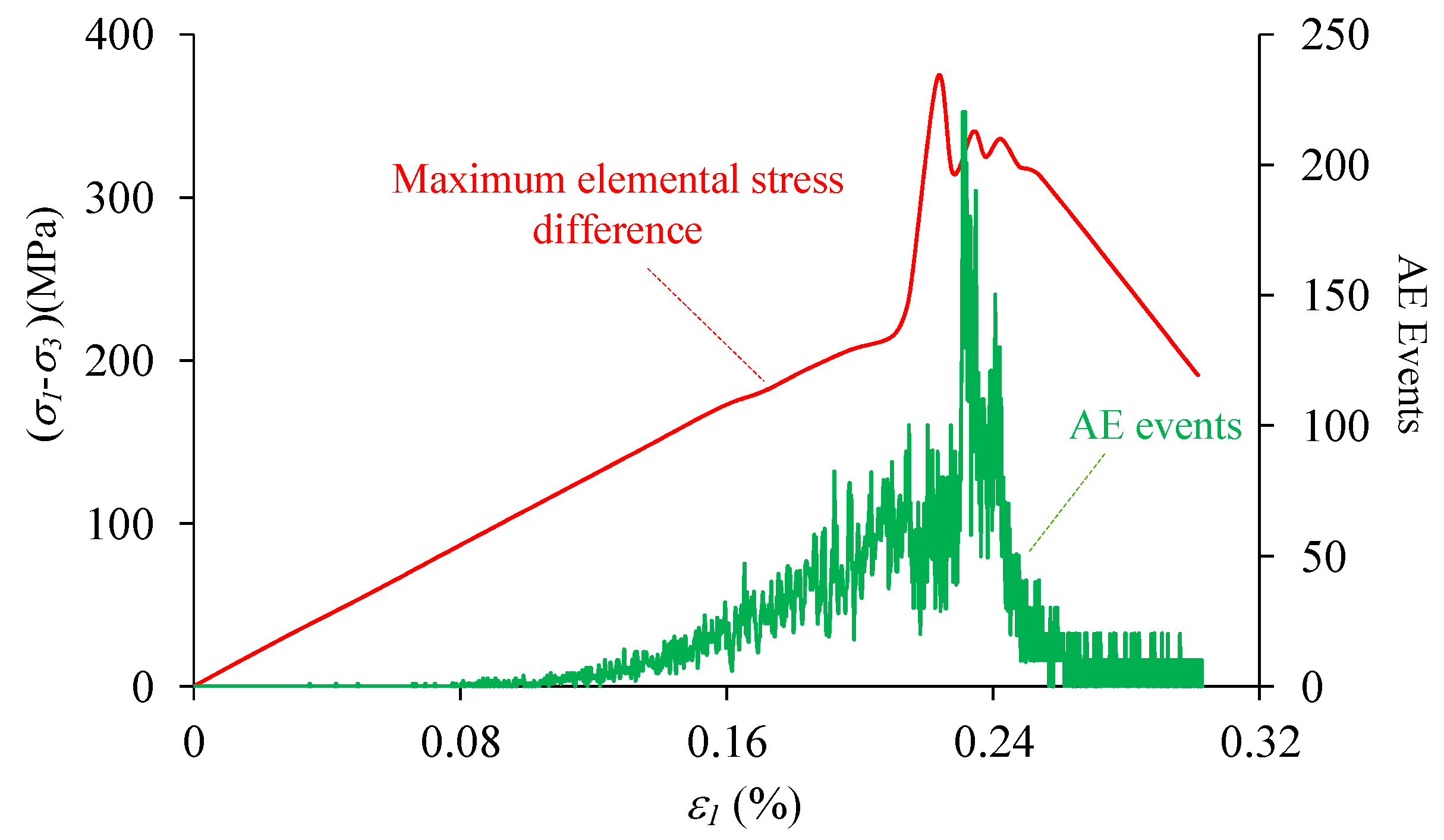
4.1. The Failure Process
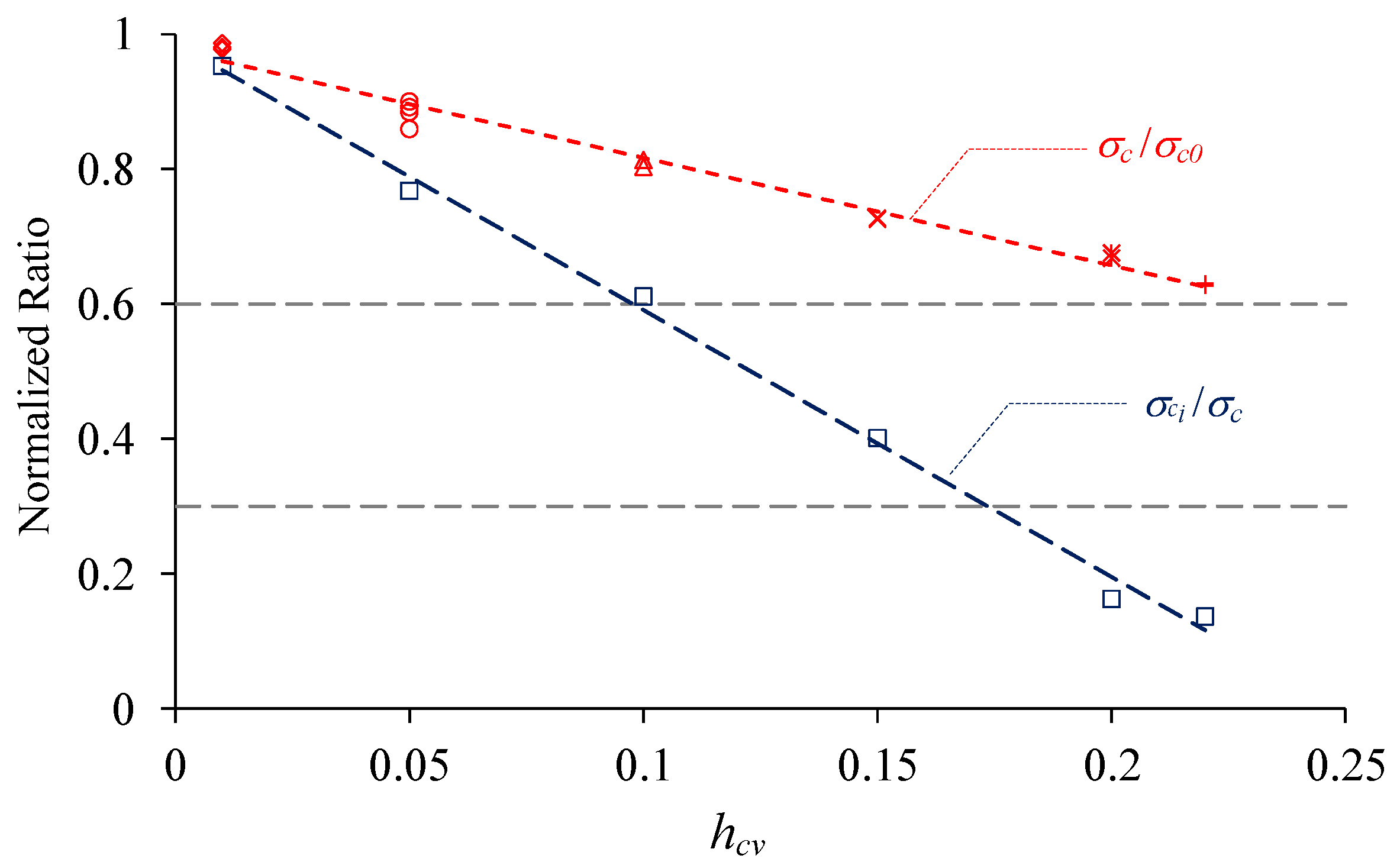
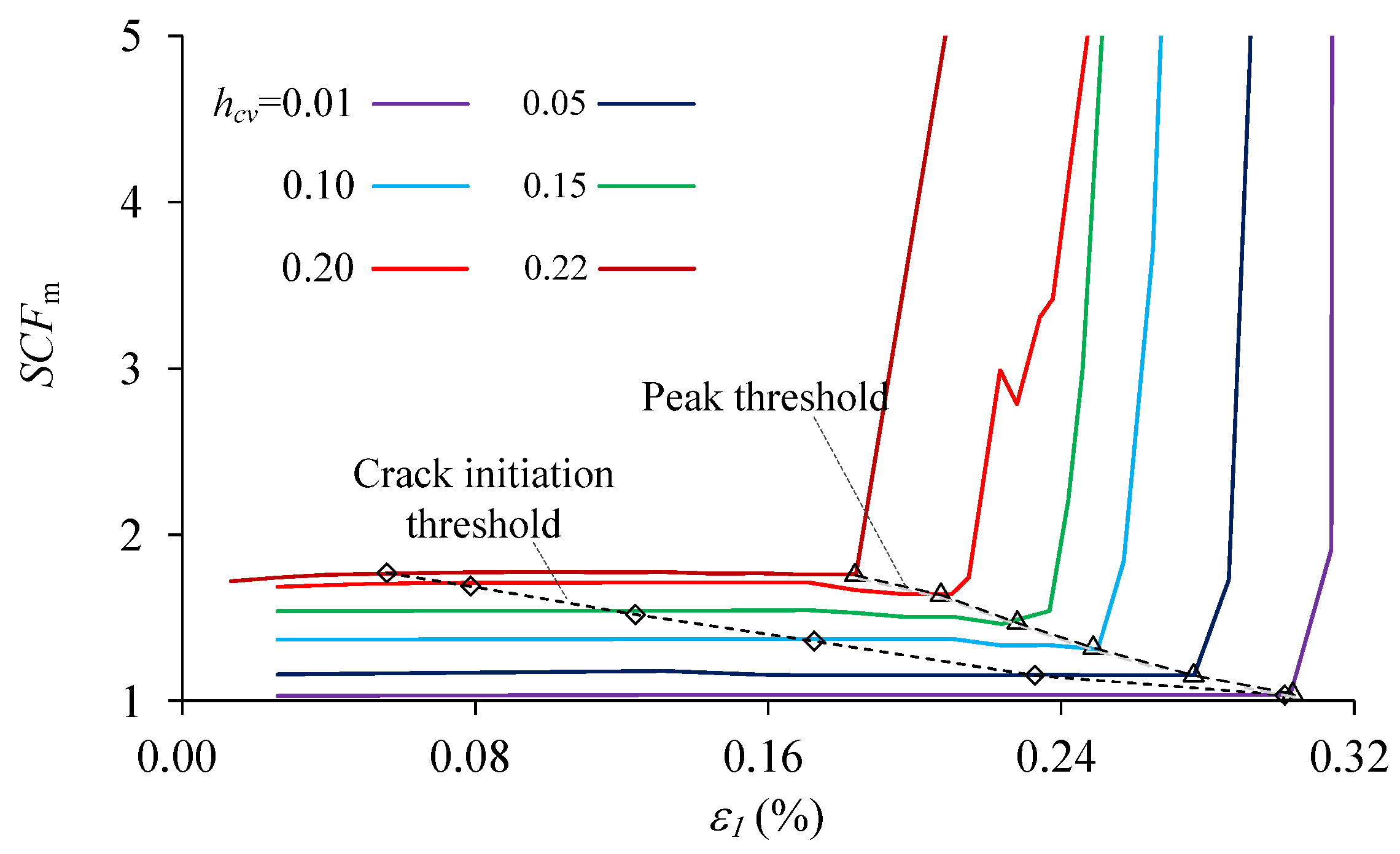
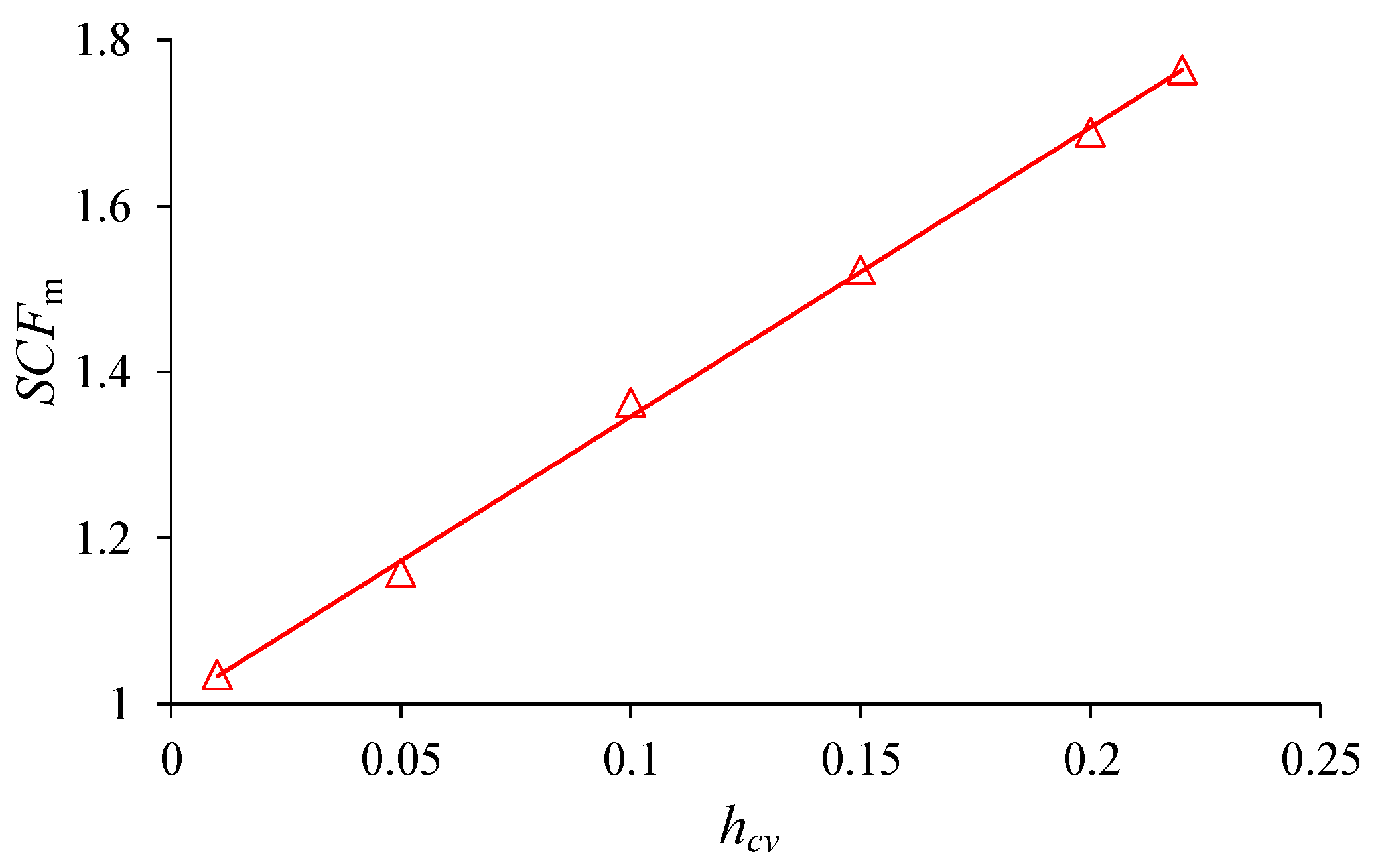
4.2. The Influence of Material Heterogeneity
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hoek, E.; Bieniawski, Z.T. Brittle fracture propagation in rock under compression. Int. J. Fracture 1965, 1, 137–155. [Google Scholar] [CrossRef]
- Brace, W.F.; Paulding, B.W.; Scholz, C.H. Dilatancy in the fracture of crystalline rocks. J. Geophys. Res. 1966, 71, 3939–3953. [Google Scholar] [CrossRef]
- Bieniawski, Z.T. Mechanism of brittle fracture of rock: Part I—Theory of the fracture process. Int. J. Rock Mech. Min. 1967, 4, 395–406. [Google Scholar] [CrossRef]
- Bieniawski, Z.T. Mechanism of brittle fracture of rock: Part II—Experimental studies. Int. J. Rock Mech. Min. 1967, 4, 407–423. [Google Scholar] [CrossRef]
- Bieniawski, Z.T. Mechanism of brittle fracture of rock: Part III—Fracture in tension and under long-term loading. Int. J. Rock Mech. Min. 1967, 4, 424–430. [Google Scholar] [CrossRef]
- Cai, M.; Kaiser, P.K.; Tasaka, Y.; Maejima, T.; Morioka, H.; Minami, M. Generalized crack initiation and crack damage stress thresholds of brittle rock masses near underground excavations. Int. J. Rock Mech. Min. 2004, 41, 833–847. [Google Scholar] [CrossRef]
- Martin, C.D. Seventeenth Canadian geotechnical colloquium: The effect of cohesion loss and stress path on brittle rock strength. Can. Geotech. J. 1997, 34, 698–725. [Google Scholar] [CrossRef]
- Nicksiar, M.; Martin, C.D. Crack initiation stress in low porosity crystalline and sedimentary rocks. Eng. Geol. 2013, 154, 64–76. [Google Scholar] [CrossRef]
- Emsley, S.; Olsson, O.; Stenberg, L.; Alheid, H.J.; Falls, S. ZEDEX: A Study of Damage and Disturbance from Tunnel Excavation by Blasting and Tunnel Boring; Technical Report for Swedish Nuclear Fuel and Waste Management Co.: Figeholm, Sweden, December 1997. [Google Scholar]
- Košťák, B.; Bielenstein, H.U. Strength distribution in hard rock. Int. J. Rock Mech. Min. 1971, 8, 501–521. [Google Scholar] [CrossRef]
- You, M.; Zou, Y. Discussion on heterogeneity of rock material and size effect on specimen strength. Chin. J. Rock Mech. Eng. 2000, 19, 391–395. (In Chinese) [Google Scholar]
- Liu, H.Y.; Roquete, M.; Kou, S.Q.; Lindqvist, P.A. Characterization of rock heterogeneity and numerical verification. Eng. Geol. 2004, 72, 89–119. [Google Scholar] [CrossRef]
- Jing, L.; Hudson, J.A. Numerical methods in rock mechanics. Int. J. Rock Mech. Min. 2002, 39, 409–427. [Google Scholar] [CrossRef]
- Cundall, P.A.; Hart, R.D. Numerical modelling of discontinua. Eng. Computation. 1992, 9, 101–113. [Google Scholar] [CrossRef]
- Itasca Consulting Group Inc. UDEC (universal distinct element code). Available online: http://www.itascacg.com/software/udec (accessed on 1 April 2017).
- Itasca Consulting Group Inc. PFC2D (particle flow code in 2 dimensions). Available online: http://www.itascacg.com/software/pfc (accessed on 1 April 2017).
- Shi, G.; Goodman, R.E. Discontinuous deformation analysis—A new method for computing stress, strain and sliding of block systems. In Proceedings of the 29th US Symposium on Rock Mechanics (USRMS), Minneapolis, MN, USA, 13–15 June 1988. [Google Scholar]
- Potyondy, D.O.; Cundall, P.A.; Lee, C.A. Modelling rock using bonded assemblies of circular particles. In Proceedings of the 2nd North American Rock Mechanics symposium, Montreal, QC, Canada, June 1996. [Google Scholar]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Hazzard, J.F.; Young, R.P. Simulating acoustic emissions in bonded-particle models of rock. Int. J. Rock Mech. Min. 2000, 37, 867–872. [Google Scholar] [CrossRef]
- Jia, L.; Chen, M.; Zhang, W.; Xu, T.; Zhou, Y.; Hou, B.; Jin, Y. Experimental study and numerical modeling of brittle fracture of carbonate rock under uniaxial compression. Mech. Res. Commun. 2013, 50, 58–62. [Google Scholar] [CrossRef]
- Koyama, T.; Jing, L. Effects of model scale and particle size on micro-mechanical properties and failure processes of rocks—A particle mechanics approach. Eng. Anal. Bound. Elem. 2007, 31, 458–472. [Google Scholar] [CrossRef]
- Diederichs, M.S. Manuel rocha medal recipient rock fracture and collapse under low confinement conditions. Rock Mech. Rock Eng. 2003, 36, 339–381. [Google Scholar] [CrossRef]
- Asadi, M.S.; Rasouli, V.; Barla, G. A bonded particle model simulation of shear strength and asperity degradation for rough rock fractures. Rock Mech. Rock Eng. 2012, 45, 649–675. [Google Scholar] [CrossRef]
- Rasouli, V.; Harrison, J.P. Assessment of rock fracture surface roughness using Riemannian statistics of linear profiles. Int. J. Rock Mech. Min. 2010, 47, 940–948. [Google Scholar] [CrossRef]
- Zhao, Z. Gouge particle evolution in a rock fracture undergoing shear: A microscopic DEM study. Rock Mech. Rock Eng. 2013, 46, 1461–1479. [Google Scholar] [CrossRef]
- Zhang, X.P.; Wong, L.N.Y. Cracking processes in rock-like material containing a single flaw under uniaxial compression: A numerical study based on bonded-particle model approach. Rock Mech. Rock Eng. 2012, 45, 711–737. [Google Scholar] [CrossRef]
- Zhang, X.P.; Wong, L.N.Y. Crack initiation, propagation and coalescence in rock-like material containing two flaws: A numerical study based on bonded-particle model approach. Rock Mech. Rock Eng. 2013, 46, 1001–1021. [Google Scholar] [CrossRef]
- Manouchehrian, A.; Marji, M.F. Numerical analysis of confinement effect on crack propagation mechanism from a flaw in a pre-cracked rock under compression. Acta Mech. Sinica 2012, 28, 1389–1397. [Google Scholar] [CrossRef]
- Lan, H.; Martin, C.; Hu, B. Effect of heterogeneity of brittle rock on micromechanical extensile behaviour during compression loading. J. Geophys. Res. 2010, 115, 1–14. [Google Scholar] [CrossRef]
- Kazerani, T.; Zhao, J. Micromechanical parameters in bonded particle method for modelling of brittle material failure. Int. J. Numer. Anal. Met. 2010, 34, 1877–1895. [Google Scholar] [CrossRef]
- Yan, M. Numerical modelling of brittle fracture and step-path failure: From laboratory to rock slope scale. Ph.D. Thesis, Simon Fraser University, Burnaby, Canada, 2008. [Google Scholar]
- Lisjak, A.; Grasselli, G. A review of discrete modeling techniques for fracturing processes in discontinuous rock masses. J. Rock Mech. Geotech. Eng. 2014, 6, 301–314. [Google Scholar] [CrossRef]
- Ke, T.C. Application of DDA to simulate fracture propagation in solid. In Proceedings of the Second International Conference on Analysis of Discontinuous Deformation, Kyoto, Japan, 9–12 July 1997. [Google Scholar]
- Koo, C.Y.; Chern, J.C. Modeling of progressive fracture in jointed rock by DDA method. In In Proceedings of the Second International Conference on Analysis of Discontinuous Deformation, Kyoto, Japan, 9–12 July 1997. [Google Scholar]
- Cai, M.; Kaiser, P.K. Numerical simulation of the Brazilian test and the tensile strength of anisotropic rocks and rocks with pre-existing cracks. Int. J. Rock Mech. Min. 2004, 41, 478–483. [Google Scholar] [CrossRef]
- Rockfield Software Ltd. ELFEN 2D/3D Numerical Modelling Software. Available online: http://www.rockfieldglobal.com/software/advanced-finite-element/ (accessed on 1 April 2017).
- Mahabadi, O.K. Investigating the influence of micro-scale heterogeneity and microstructure on the failure and mechanical behaviour of geomaterials. Ph.D. Thesis, University of Toronto, Toronto, Canada, 2012. [Google Scholar]
- Munjiza, A. The Combined Finite-Discrete Element Method; John Wiley & Sons Ltd.: Chichester, UK, 2004. [Google Scholar]
- Klerck, P.A.; Sellers, E.J.; Owen, D.R.J. Discrete fracture in quasi-brittle materials under compressive and tensile stress states. Comput. Method Appl. M. 2004, 193, 3035–3056. [Google Scholar] [CrossRef]
- Cai, M. Influence of intermediate principal stress on rock fracturing and strength near excavation boundaries-insight from numerical modeling. Int. J. Rock Mech. Min. 2008, 45, 763–772. [Google Scholar] [CrossRef]
- Cai, M. Fracture initiation and propagation in a Brazilian disc with a plane interface: A numerical study. Rock Mech. Rock Eng. 2013, 46, 289–302. [Google Scholar] [CrossRef]
- Mahabadi, O.K.; Randall, N.X.; Zong, Z.; Grasselli, G. A novel approach for micro-scale characterization and modeling of geomaterials incorporating actual material heterogeneity. Geophys. Res. Lett. 2012, 39, L01303. [Google Scholar] [CrossRef]
- Lisjak, A.; Tatone, B.S.; Grasselli, G.; Vietor, T. Numerical modelling of the anisotropic mechanical behaviour of Opalinus Clay at the laboratory-scale using FEM/DEM. Rock Mech. Rock Eng. 2014, 47, 187–206. [Google Scholar] [CrossRef]
- Jing, L.; Stephansson, O. Fundamentals of Discrete Element Methods for Rock Engineering: Theory and Applications; Elsevier Science: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Bobet, A.; Fakhimi, A.; Johnson, S.; Morris, J.; Tonon, F.; Yeung, M.R. Numerical models in discontinuous media: Review of advances for rock mechanics applications. J. Geotech. Geoenviron. 2009, 135, 1547–1561. [Google Scholar] [CrossRef]
- Yuan, S.C.; Harrison, J.P. A review of the state of the art in modelling progressive mechanical breakdown and associated fluid flow in intact heterogeneous rocks. Int. J. Rock Mech. Min. 2006, 43, 1001–1022. [Google Scholar] [CrossRef]
- Tang, C. Numerical simulation of progressive rock failure and associated seismicity. Int. J. Rock Mech. Min. 1997, 34, 249–261. [Google Scholar] [CrossRef]
- Tang, C.; Xu, X.; Kou, S.Q.; Lindqvist, P.A.; Liu, H.Y. Numerical investigation of particle breakage as applied to mechanical crushing—Part I: Single-particle breakage. Int. J. Rock Mech. Min. 2001, 38, 1147–1162. [Google Scholar] [CrossRef]
- Tang, C.; Liu, B.; Lee, P.K.K.; Tsui, y.; Than, L.G. Numerical studies of the influence of microstructure on rock failure in uniaxial compression—Part I: Effect of heterogeneity. Int. J. Rock Mech. Min. 2000, 37, 555–569. [Google Scholar] [CrossRef]
- Liu, H.Y.; Kou, S.Q.; Lindqvist, P.A.; Tang, C. Numerical studies on the failure process and associated microseismicity in rock under triaxial compression. Tectonophysics 2004, 384, 149–174. [Google Scholar] [CrossRef]
- Tang, C.; Liu, H.; Qin, S.; Yang, z. Influence of heterogeneity on crack propagation mode in brittle rock. Chin. J. Geophys. 2000, 43, 117–125. (In Chinese) [Google Scholar] [CrossRef]
- Liang, Z.; Tang, C.; Li, H.; Xu, T.; Zhang, Y. Numerical simulation of 3-D failure process in heterogeneous rocks. Int. J. Rock Mech. Min. 2004, 41, 323–328. [Google Scholar] [CrossRef]
- Zhu, W.; Liu, J.; Tang, C.; Zhao, X.; Brady, B.H. Simulation of progressive fracturing processes around underground excavations under biaxial compression. Tunn. Undergr. Space Technol. 2005, 20, 231–247. [Google Scholar] [CrossRef]
- Tang, C.; Lin, P.; Wong, R.H.C.; Chau, K.T. Analysis of crack coalescence in rock-like materials containing three flaws—Part II: Numerical approach. Int. J. Rock Mech. Min. 2001, 38, 925–939. [Google Scholar] [CrossRef]
- Tang, C.; Tham, L.G.; Lee, P.K.K.; Yang, T.; Li, L. Coupled analysis of flow, stress and damage (FSD) in rock failure. Int. J. Rock Mech. Min. 2002, 39, 477–489. [Google Scholar] [CrossRef]
- Tang, C.; Xu, T.; Yang, T.; Liang, Z. Numerical investigation of the mechanical behavior of rock under confining pressure and pore pressure. Int. J. Rock Mech. Min. 2004, 41, 336–341. [Google Scholar] [CrossRef]
- Zhu, W.; Liu, J.; Yang, T.; Sheng, J.; Elsworth, D. Effects of local rock heterogeneities on the hydromechanics of fractured rocks using a digital-image-based technique. Int. J. Rock Mech. Min. 2006, 43, 1182–1199. [Google Scholar] [CrossRef]
- Zhu, W.; Tang, C.; Huang, Z.; Liu, J. A numerical study of the effect of loading conditions on the dynamic failure of rock. Int. J. Rock Mech. Min. 2004, 41, 348–353. [Google Scholar] [CrossRef]
- Xu, T.; Tang, C.; Zhao, J.; Li, L.; Heap, M.J. Modelling the time-dependent rheological behaviour of heterogeneous brittle rocks. Geophys. J. Int. 2012, 189, 1781–1796. [Google Scholar] [CrossRef]
- Fang, Z.; Harrison, J.P. A mechanical degradation index for rock. Int. J. Rock Mech. Min. 2001, 38, 1193–1199. [Google Scholar] [CrossRef]
- Fang, Z.; Harrison, J.P. Development of a local degradation approach to the modelling of brittle fracture in heterogeneous rocks. Int. J. Rock Mech. Min. 2002, 39, 443–457. [Google Scholar] [CrossRef]
- Fang, Z.; Harrison, J.P. Application of a local degradation model to the analysis of brittle fracture of laboratory scale rock specimens under triaxial conditions. Int. J. Rock Mech. Min. 2002, 39, 459–476. [Google Scholar] [CrossRef]
- Fang, Z.; Harrison, J.P. Numerical analysis of progressive fracture and associated behaviour of mine pillars by use of a local degradation model. Trans. Inst. Min. Metall. 2002, 111, 59–72. [Google Scholar] [CrossRef]
- Ma, G.; Wang, X.; Ren, F. Numerical simulation of compressive failure of heterogeneous rock-like materials using SPH method. Int. J. Rock Mech. Min. Sci. 2011, 48, 353–363. [Google Scholar] [CrossRef]
- Feng, X.; Pan, P.; Zhou, H. Simulation of the rock microfracturing process under uniaxial compression using an elasto-plastic cellular automaton. Int. J. Rock Mech. Min. Sci. 2006, 43, 1091–1108. [Google Scholar] [CrossRef]
- Pan, P.; Feng, X.; Hudson, J.A. Numerical simulations of Class I and Class II uniaxial compression curves using an elasto-plastic cellular automaton and a linear combination of stress and strain as the control method. Int. J. Rock Mech. Min. Sci. 2006, 43, 1109–1117. [Google Scholar] [CrossRef]
- Blair, S.C.; Cook, N.G.W. Analysis of compressive fracture in rock using statistical techniques: Part I. A non-linear rule-based model. Int. J. Rock Mech. Min. Sci. 1998, 35, 837–848. [Google Scholar] [CrossRef]
- Leite, J.P.B.; Slowik, V.; Mihashi, H. Computer simulation of fracture processes of concrete using mesolevel models of lattice structures. Cem. Concr. Res. 2004, 34, 1025–1033. [Google Scholar] [CrossRef]
- Hajiabdolmajid, V.; Kaiser, P.K.; Martin, C.D. Modelling brittle failure of rock. Int. J. Rock Mech. Min., 2002, 39, 731–741. [Google Scholar] [CrossRef]
- Guo, S.; Qi, S.; Zheng, B.; Li, X. The deformation and strength properties of Jinping marble with different confining pressures under cyclic loading—Unloading tests. In Proceedings of the International Symposium and 9th Asian Regional Conference of IAEG, Beijing, China, 24–25 September 2013. [Google Scholar]
- Guo, S.; Qi, S.; Cai, M. Influence of tunnel wall roughness and localized stress concentrations on the initiation of brittle spalling. Bull. Eng. Geol. Environ. 2016, 75, 1597–1607. [Google Scholar] [CrossRef]
- Guo, S.; Qi, S.; Huang, X. Anisotropy of rock mass strength and its transformation critical confining stress. Chin. J. Rock Mech. Eng. 2013, s2, 3222–3227. (In Chinese) [Google Scholar]
- Guo, S.; Qi, S.; Li, X.; Zou, Y.; Zhang, S. Strength and deformation characteristics of rock sample with discontinuities under numerical uniaxial compression simulation tests. J. Eng. Geol. 2016, 24, 891–898. (In Chinese) [Google Scholar]
- Guo, S.; Qi, S. Numerical study on progressive failure of hard rock samples with an unfilled undulate joint. Eng. Geol. 2015, 193, 173–182. [Google Scholar] [CrossRef]
- Amitrano, D.; Grasso, J.R.; Hantz, D. From diffuse to localised damage through elastic interaction. Geophys. Res. Lett. 1999, 26, 2109–2112. [Google Scholar] [CrossRef]
- Cundall, P.A. FLAC 3D Manual: A Computer Program for Fast Lagrangian Analysis of Continua, Version 4.0; Itasca Consulting Group Inc.: Minneapolis, MN, USA, 2008. [Google Scholar]
- Byerlee, J. Friction of rocks. Pure Appl. Geophys. 1978, 116, 615–626. [Google Scholar] [CrossRef]
- Brown, E. Rock Characterization, Testing & Monitoring: ISRM Suggested Methods; Pergamon Press: Oxford, UK, 1981. [Google Scholar]
- Wawersik, W.R.; Fairhurst, C. A study of brittle rock fracture in laboratory compression experiments. Int. J. Rock Mech. Min. Sci. 1970, 7, 561–575. [Google Scholar] [CrossRef]
- Stavrogin, A.N.; Tarasov, B.G.; Shirkes, O.A.; Pevzner, E.D. Strength and deformation of rocks before and after the breakdown point. Soviet Min. 1981, 17, 487–493. [Google Scholar] [CrossRef]
- Van Mier, J.G.M.; Shah, S.P.; Arnaud, M.; Balayssac, J.P.; Bascoul, A.; Choi, S.; Dasenbrock, D.; Ferrara, G.; French, C.; Gobbi, M.E.; et al. Strain-softening of concrete in uniaxial compression. Mater. Struct. 1997, 30, 195–209. [Google Scholar] [CrossRef]
- Zhou, J.; Xu, W.; Yang, X. A microcrack damage model for brittle rocks under uniaxial compression. Mech. Res. Commun. 2010, 37, 399–405. [Google Scholar] [CrossRef]
- McClintock, F.A.; Argon, A.S. Mechanical Behavior of Materials; Addison-Wesley: Reading, MA, USA, 1966. [Google Scholar]
- Feng, X.T.; Chen, B.R.; Zhang, C.Q.; Li, S.J.; Wu, S.Y. Mechanism, Warning and Dynamic Control of Rockburst Development Processes; Science Press Ltd.: Beijing, China, 2013. [Google Scholar]
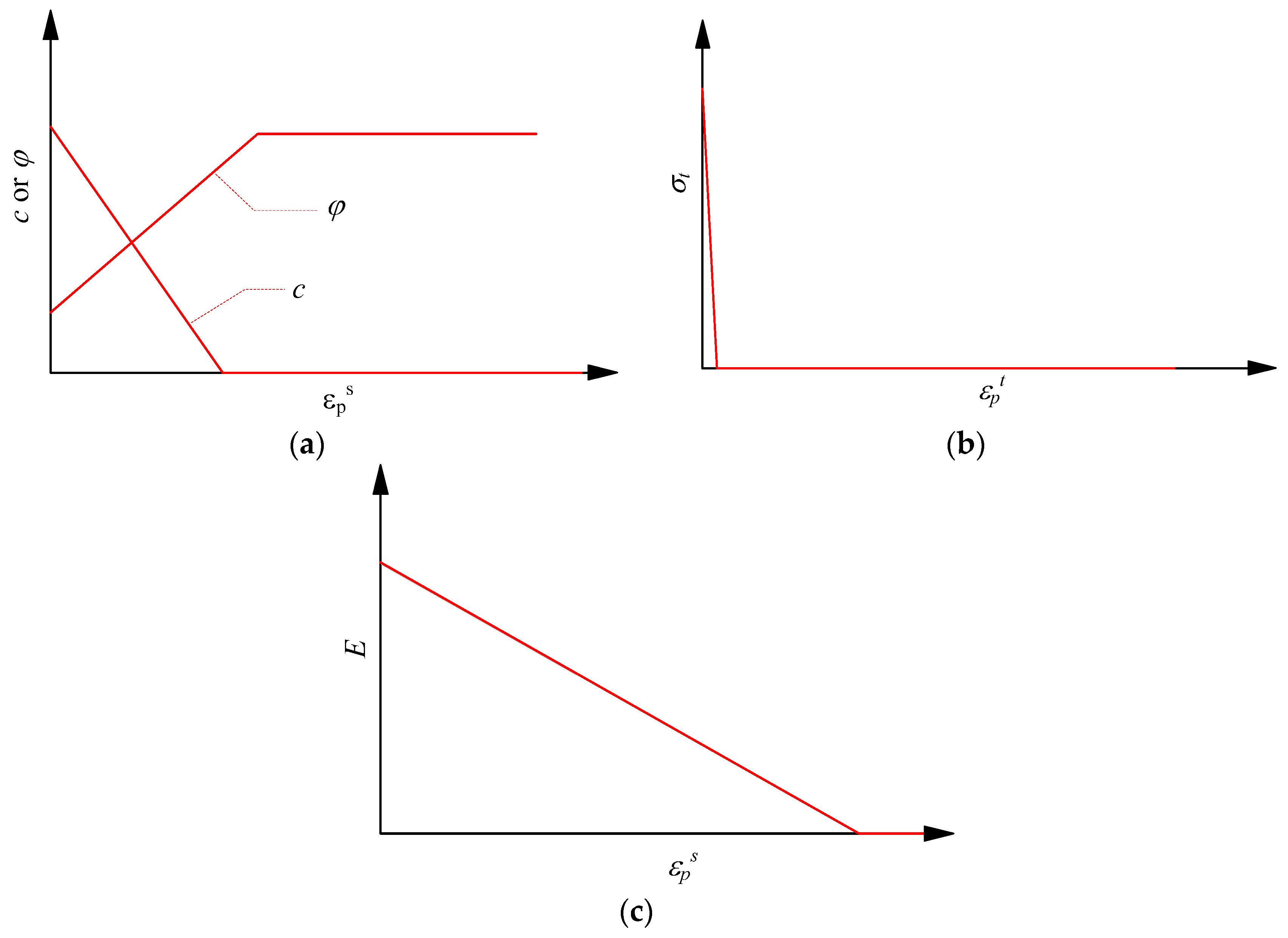
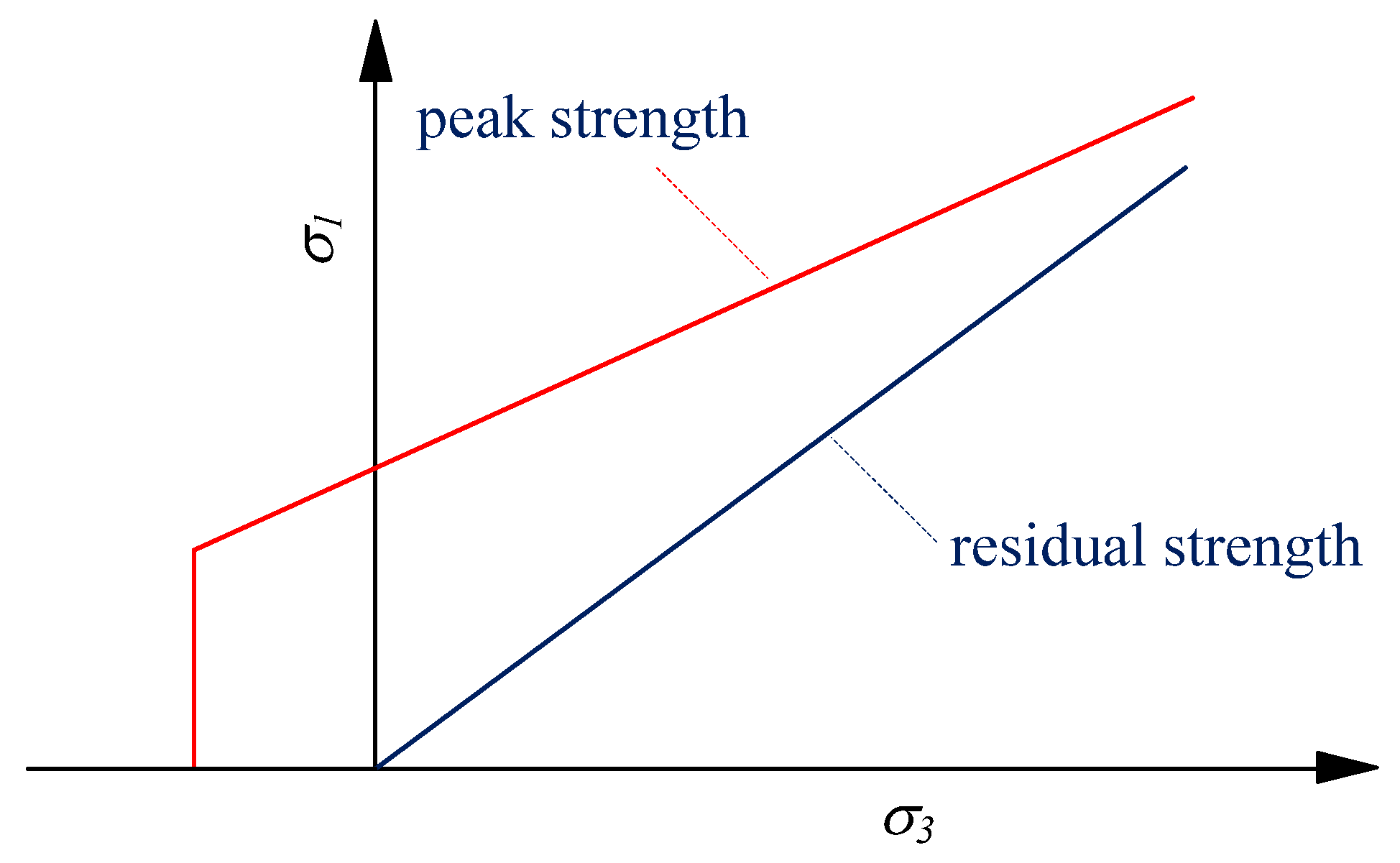
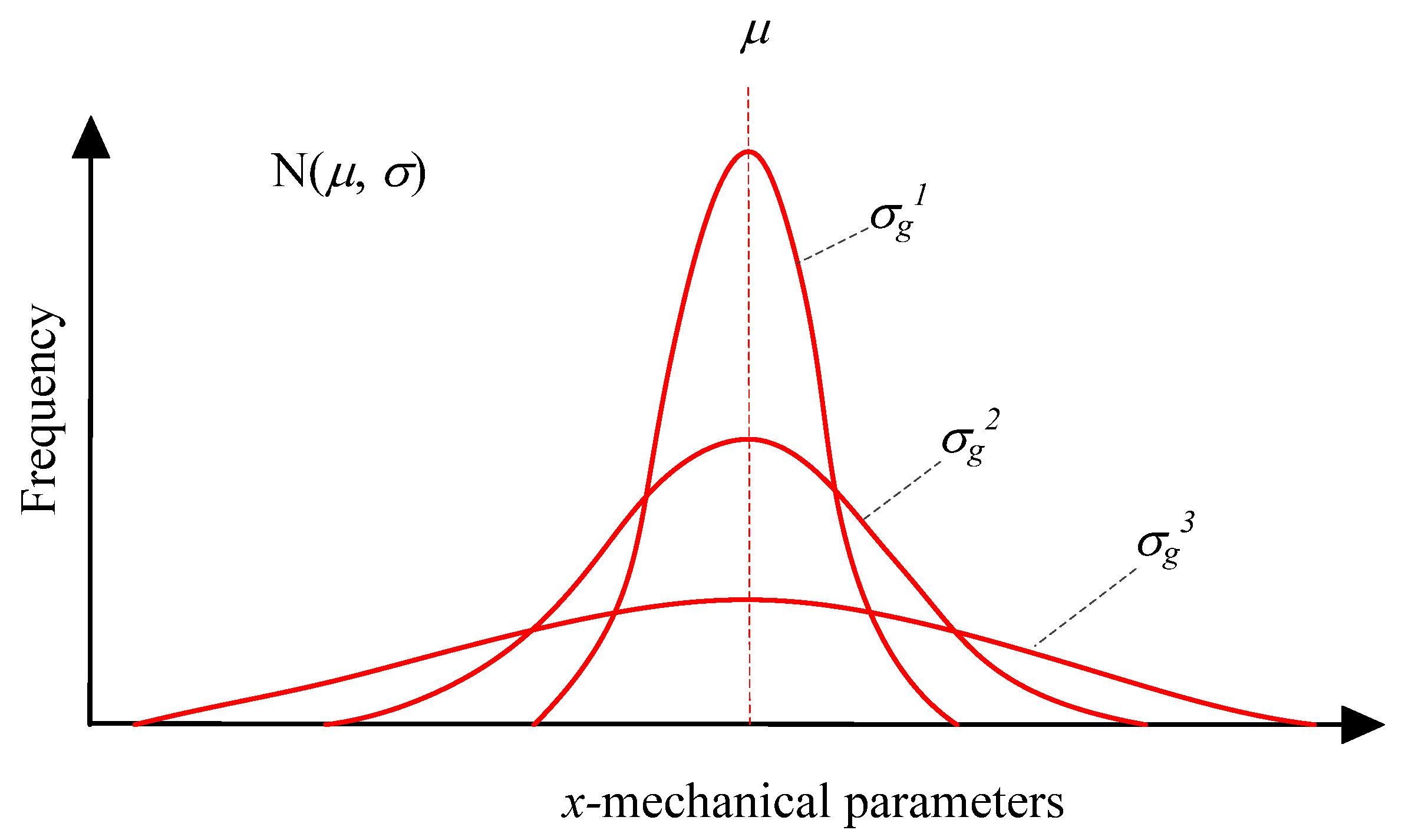


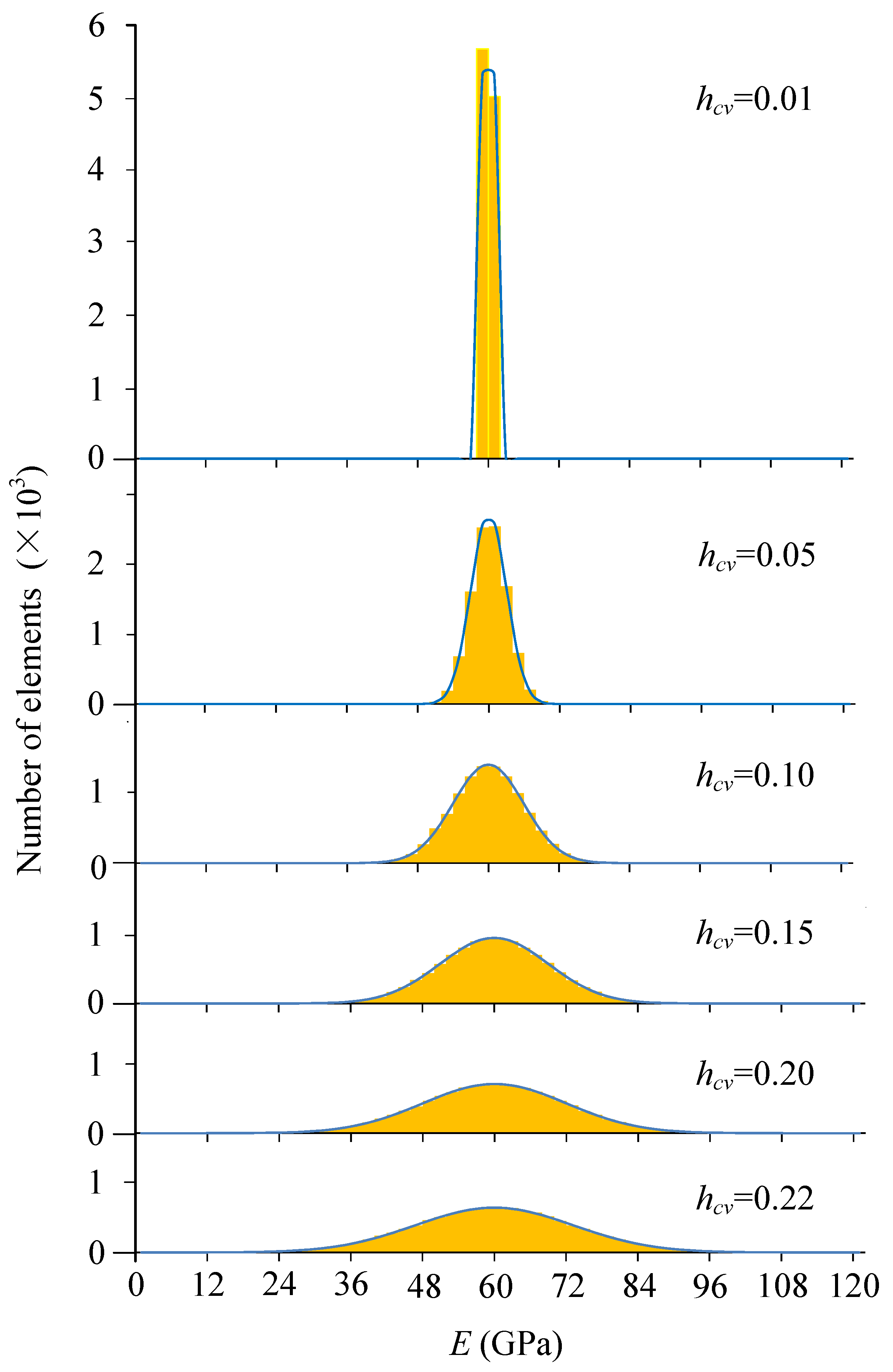
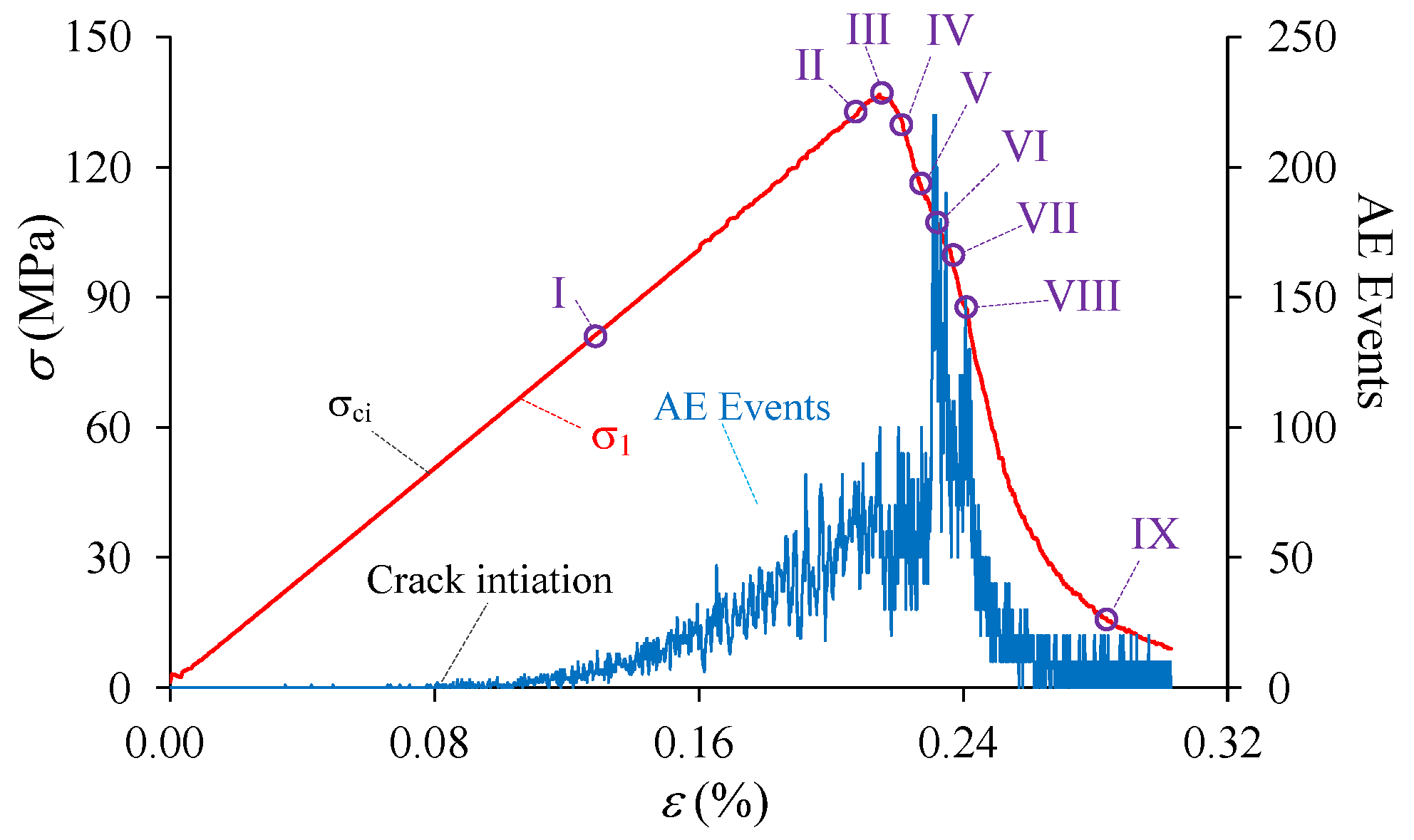
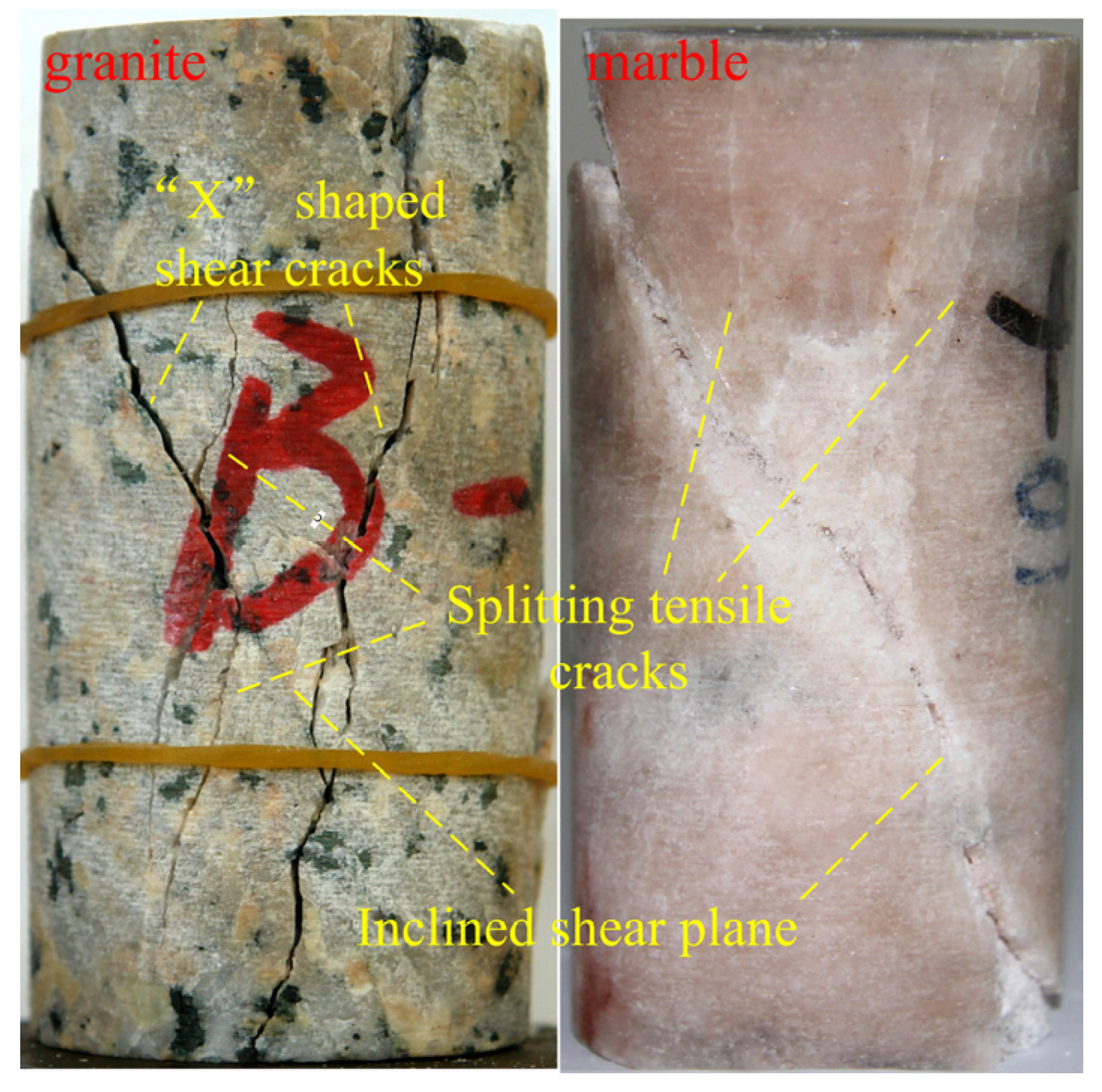

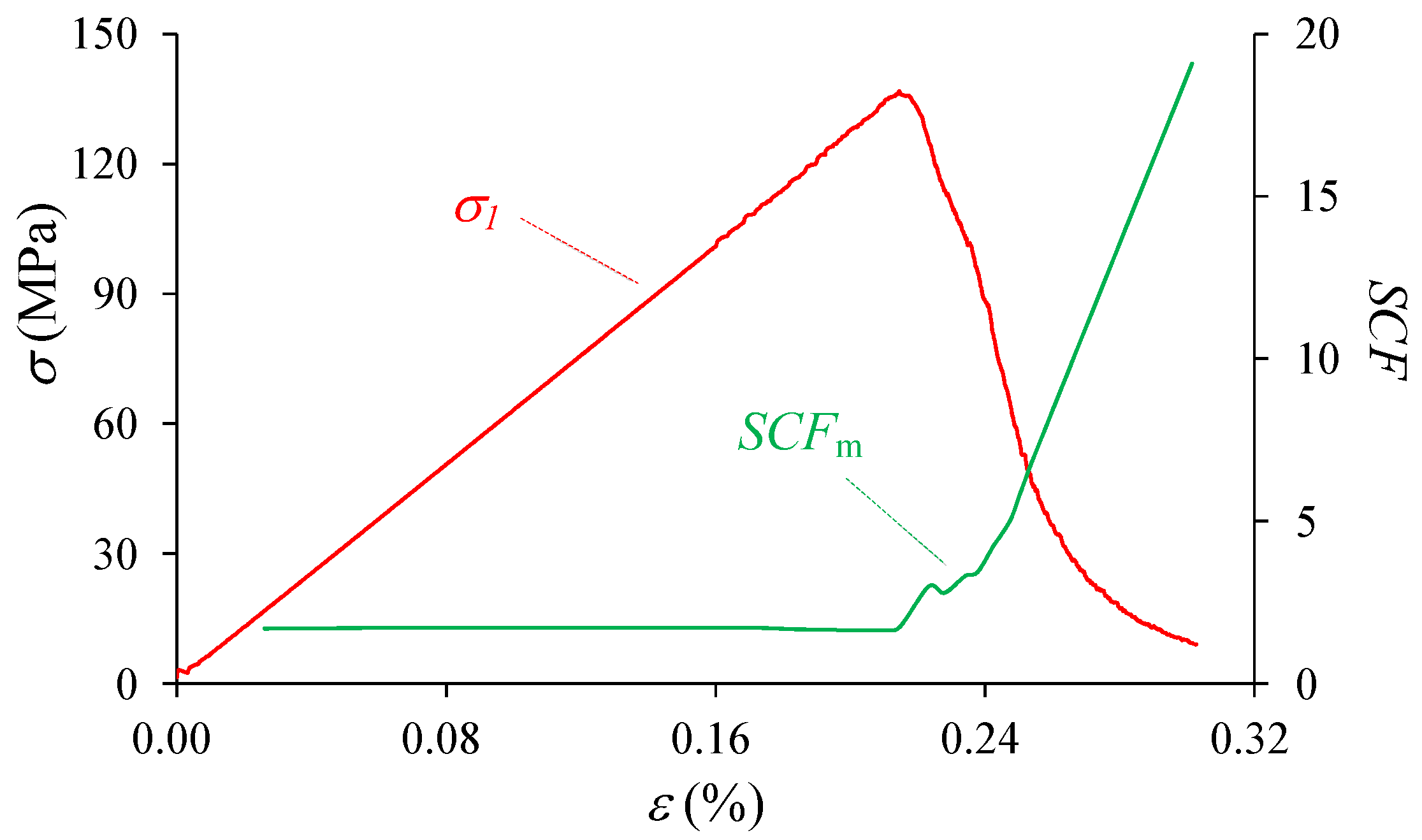

| Plastic Strain Parameters | |||
| Elastic Modulus (Gpa) | 60 | 0 | |
| Poisson’s Ratio | 0.25 | 0.25 | 0.25 |
| Cohesion (MPa) | 50 | 0 | |
| Friction Angle (°) | 38 | 40 | |
| Tensile Strength (MPa) | |||
| 20 | 0 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, S.; Qi, S.; Zou, Y.; Zheng, B. Numerical Studies on the Failure Process of Heterogeneous Brittle Rocks or Rock-Like Materials under Uniaxial Compression. Materials 2017, 10, 378. https://doi.org/10.3390/ma10040378
Guo S, Qi S, Zou Y, Zheng B. Numerical Studies on the Failure Process of Heterogeneous Brittle Rocks or Rock-Like Materials under Uniaxial Compression. Materials. 2017; 10(4):378. https://doi.org/10.3390/ma10040378
Chicago/Turabian StyleGuo, Songfeng, Shengwen Qi, Yu Zou, and Bowen Zheng. 2017. "Numerical Studies on the Failure Process of Heterogeneous Brittle Rocks or Rock-Like Materials under Uniaxial Compression" Materials 10, no. 4: 378. https://doi.org/10.3390/ma10040378
APA StyleGuo, S., Qi, S., Zou, Y., & Zheng, B. (2017). Numerical Studies on the Failure Process of Heterogeneous Brittle Rocks or Rock-Like Materials under Uniaxial Compression. Materials, 10(4), 378. https://doi.org/10.3390/ma10040378





