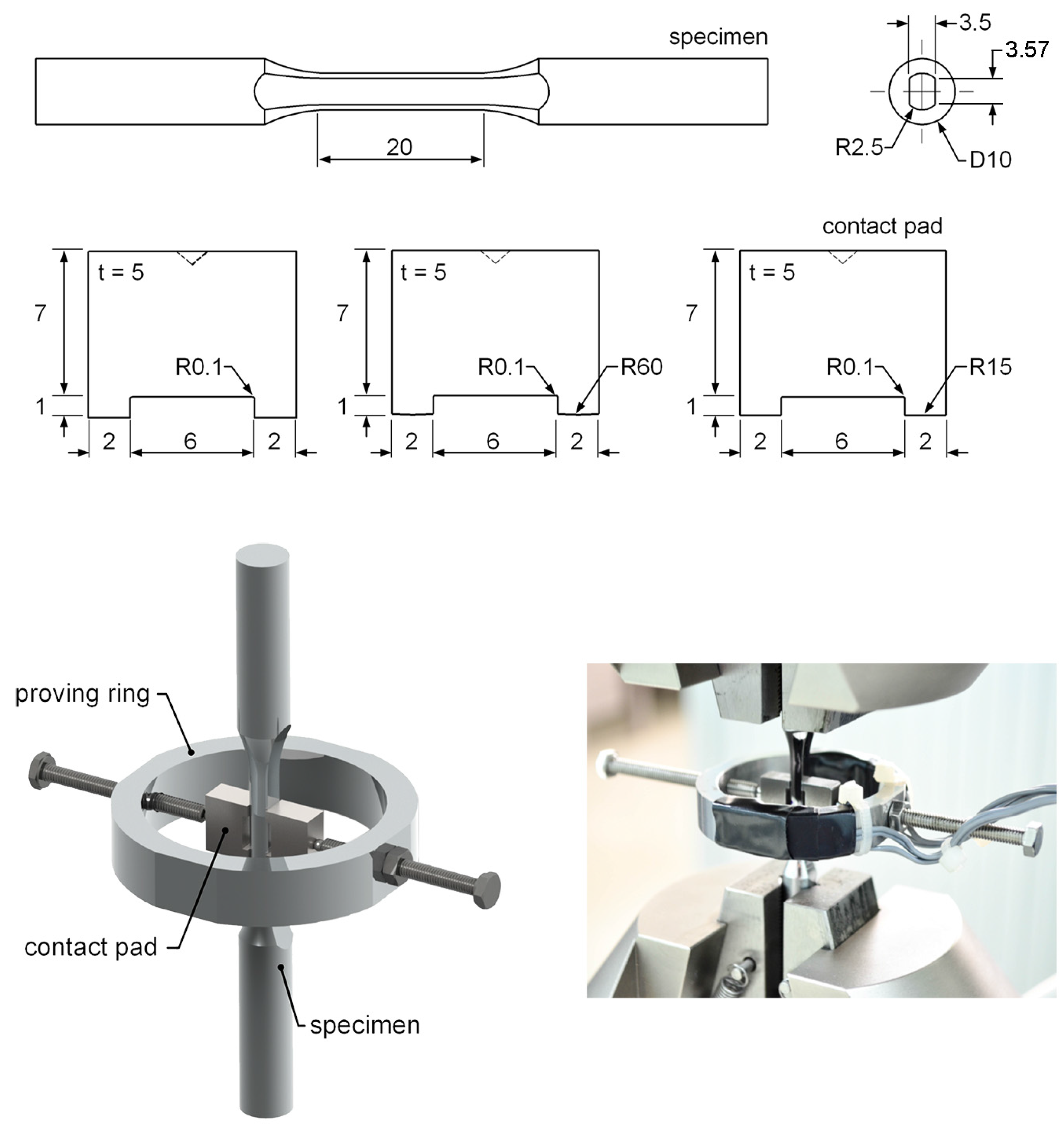
3.1. Fretting Fatigue Life and Fretting Fatigue Crack
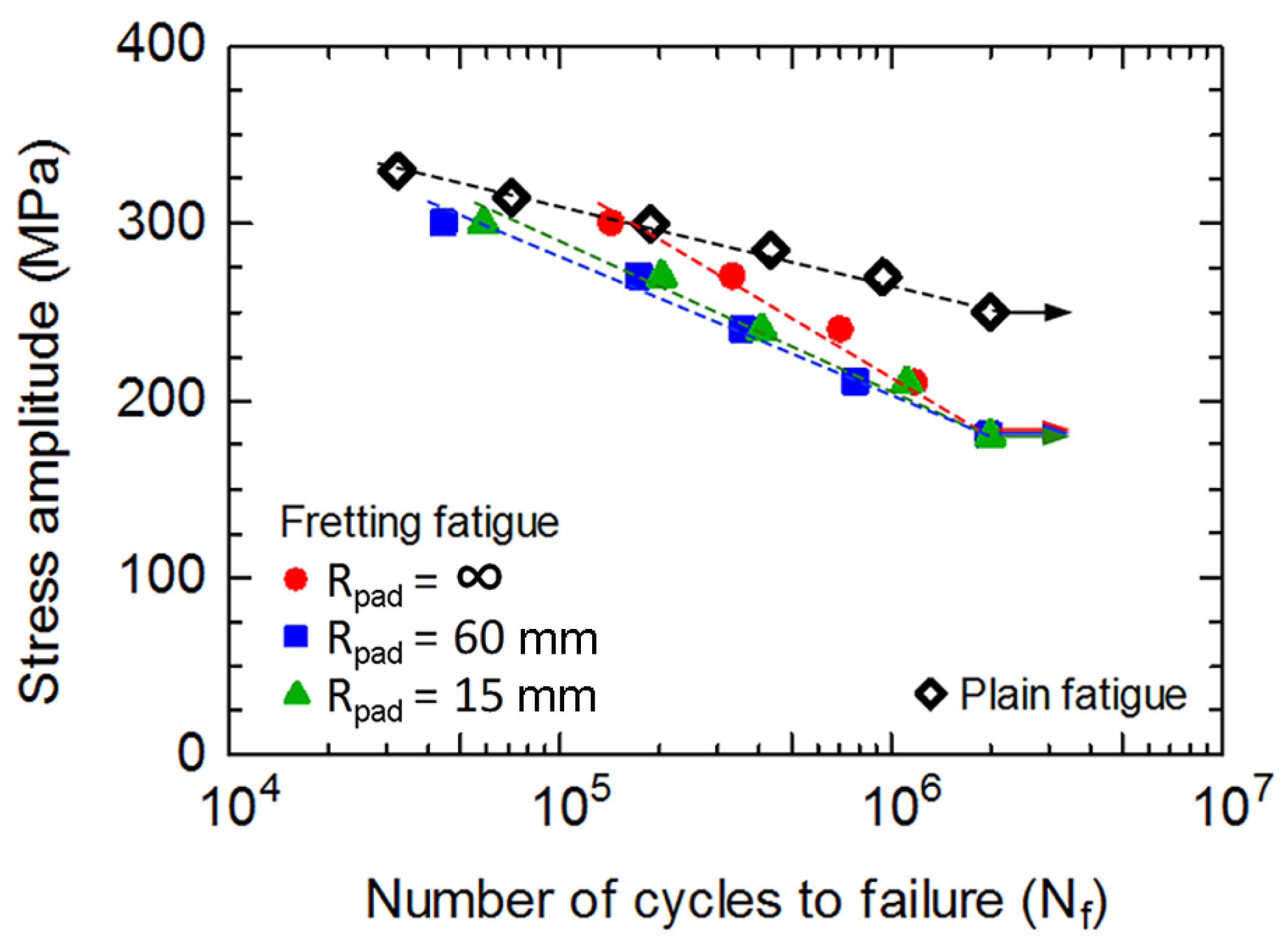
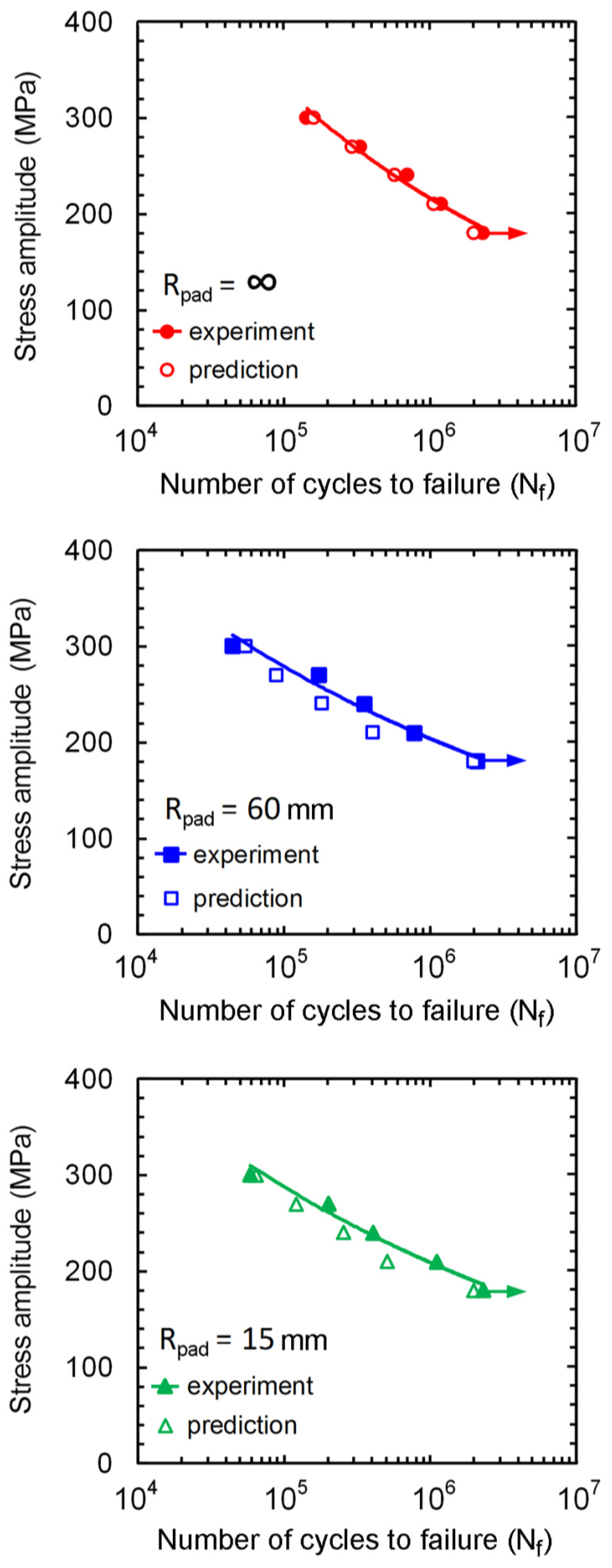
Stress amplitude (σ
a) versus fatigue life (
Nf) curve is shown in
Figure 2. Fatigue life increased with decreasing stress amplitude, which is a typical S-N curve. Fretting fatigue resistances were lower than that of plain fatigue. The specimens with
Rpad = ∞ (flat-on-flat contact) had the highest fatigue resistance following by those with
Rpad = 15 and 60 mm (cylindrical-on-flat contact), respectively. Although similar mean contact pressure was applied for fretting fatigue experiments with various radii of contact pad, the contacts were smaller for the specimens with cylindrical contact pads compared to that with flat contact pad. Thus, the contact pressures at cylindrical-on-flat contacts were higher than that at flat-on-flat contact. High contact pressures of specimens with cylindrical contact pads are the reason for shorter fretting fatigue lives. However, the fatigue limits of fretting fatigue experiments with various radii of contact pad were similar, which is approximately 180 MPa. With the supports for numerical calculations, the influence of contact stress fields with various geometries of contact pad on the crack nucleation and propagation was discussed in the later section.
Satoh et al. [
32] investigated the influence of contact pad geometry (flat contact,
R = 2, 4, 8 and 20 mm cylindrical contacts) and mean contact pressure (30 MPa to 1.5 GPa) on fretting fatigue behavior. The contact pad was 12Cr-Mo-W-V steel, while fretting fatigue specimen was 11Cr-Mo-V-Nb steel. They found that the cylindrical contact was plastically deformed due to contact load, and also worn with repeated fretting cycles to become a flat contact. In the present work, some specimens were interrupted, and observed under a scanning electron microscope to evaluate the contacts. The contact marks on fretting fatigue specimens (
Rpad = 15 mm) tested at low and high stress amplitudes (180 MPa and 300 MPa) were observed at
N/
Nf = 0.2 and 1, as shown in
Figure 3. The contact widths at six locations were measured using image analysis software (DinoCapture 2.0, AnMo Electronics Corporation, New Taipei City, Taiwan), and the average contact width (
w) was determined. Because the high stress amplitude causes large deformation of specimen and large slip amplitude, the contact width of specimen with stress amplitudes of 300 MPa was larger than that of specimen with stress amplitudes of 180 MPa. At same stress amplitude, the contacts without crack at
Nf = 0.2 and
Nf = 1 had similar width. On the other hand, because of the crack opening of specimen tested at stress amplitudes of 300 MPa, the contact with crack was slightly larger than the contact without crack. Because the contact wear was not severe enough to transform the cylindrical-on-flat contact into flat-on-flat contact, the assumption of Hertzian contact stress was applied for the present cylindrical-on-flat contacts.
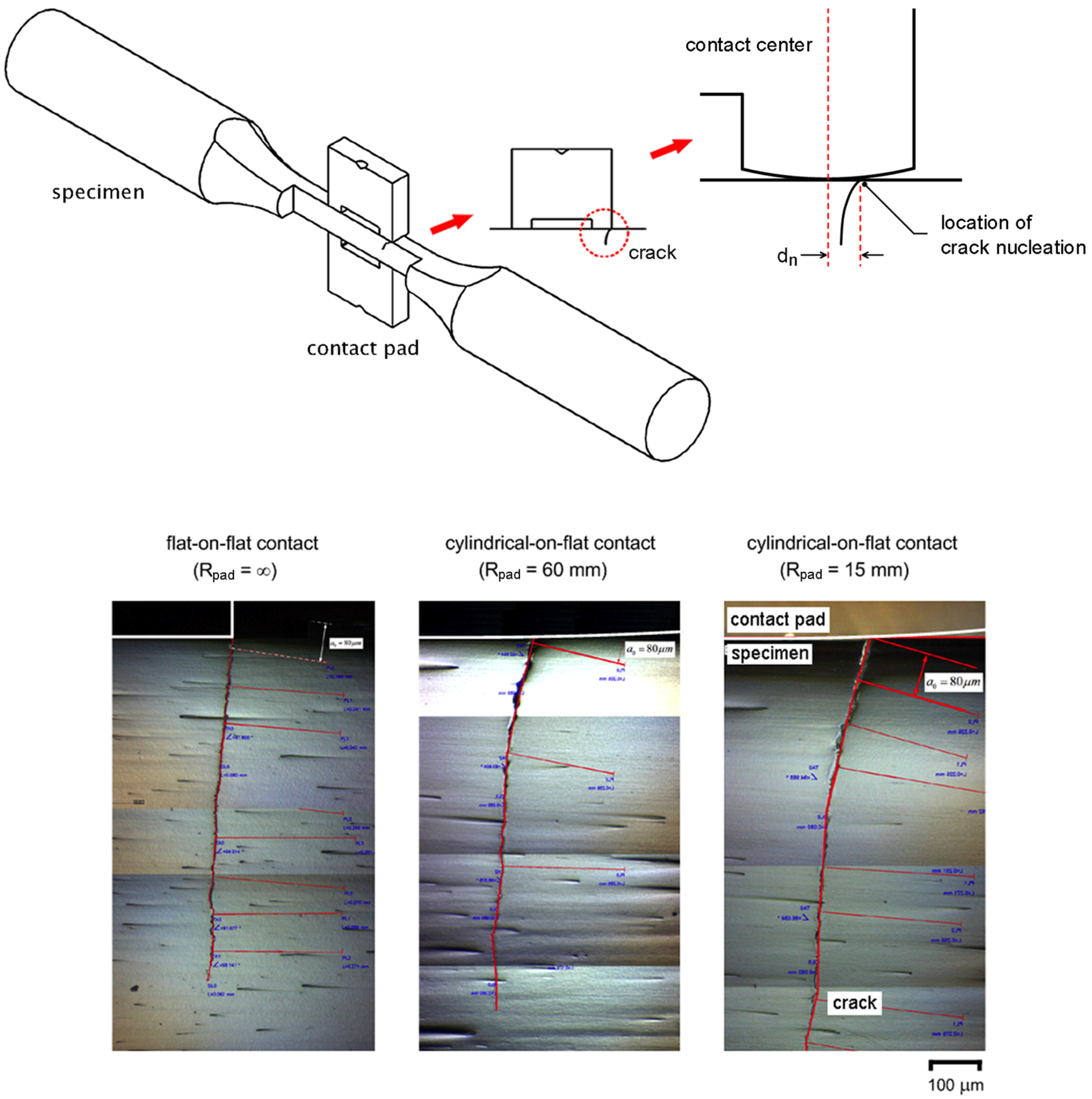
Fretting fatigue experiments at stress amplitude of 300 MPa were interrupted just before complete fracture (
N/
Nf > 0.9), sectioned along the longitudinal axis using an electrical discharge machine (EDM), and observed under an optical microscope. Micrographs of the longitudinal sections of specimens with
Rpad = ∞, 60 and 15 mm are shown in
Figure 4. All fretting fatigue cracks were found to nucleate near the contact trailing edge and propagate at the inclined angle beneath the contact pad. As a reference for the location of crack nucleation, the contact centers of four pad legs were marked on the surface of specimen before fretting fatigue experiment. Distance (
dn) from the contact center to the crack nucleation was measured using image analysis software (DinoCapture 2.0). At stress amplitude of 300 MPa,
dn were approximately 1000, 210 and 180 μm for specimens with
Rpad = ∞, 60 and 15 mm, respectively.
Nucleation of fretting fatigue crack involves contact stress as well as slip displacement [
33]. After crack nucleation, the influence of contact stress on the stress intensity factor at crack tip decreased with crack extension, and then the fretting fatigue crack path gradually changed to the direction normal to the applied bulk alternating stress [
4,
5,
6,
7]. To understand the influence of contact geometries on fretting fatigue resistance, the numerical analysis of crack nucleation, crack path, and crack propagation were performed and described in the following sections.
3.2. Fretting Fatigue Crack Nucleation
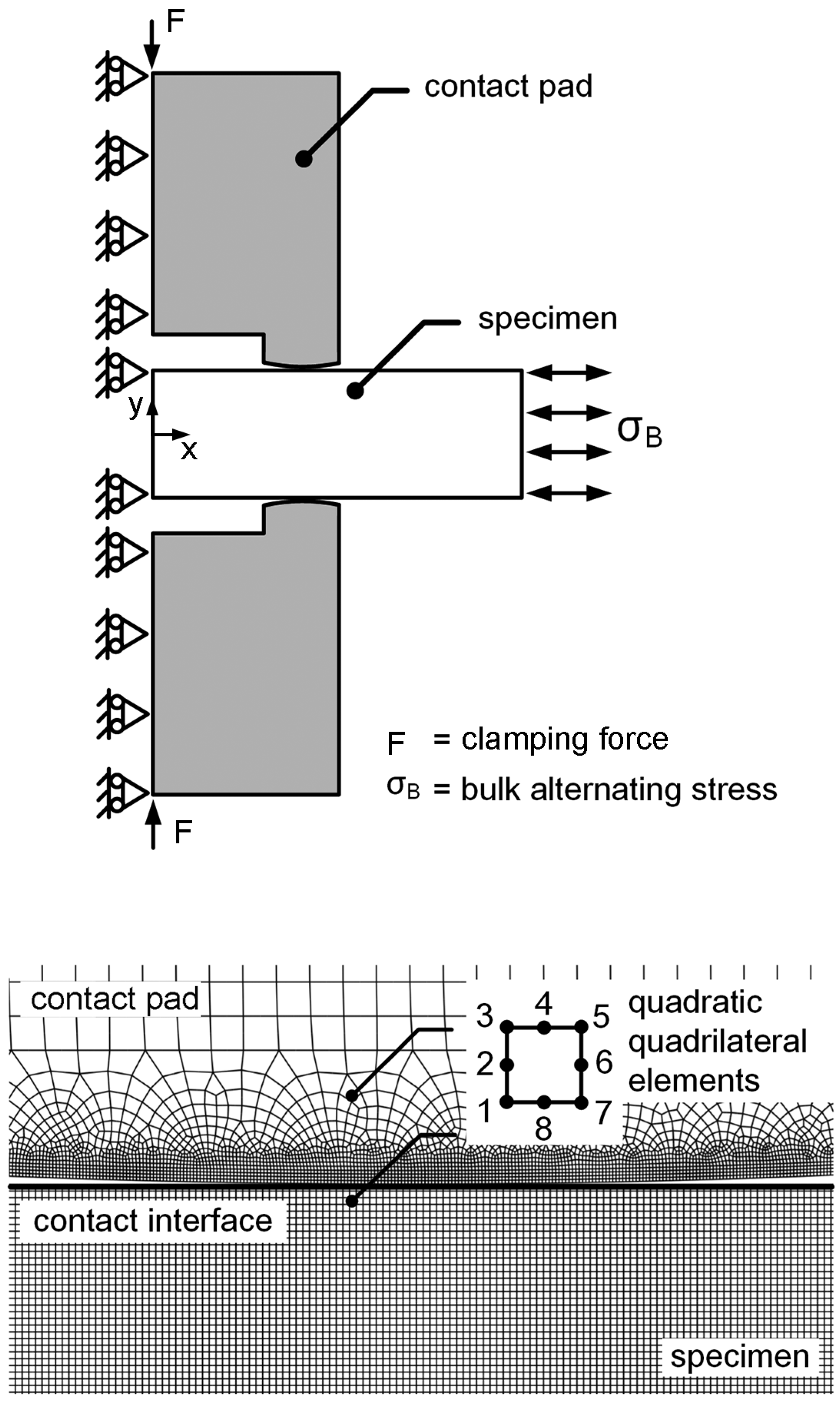
To evaluate the location of crack nucleation, the model of fretting fatigue experiment without crack was used. Plane-strain linear-elastic FEA, i.e., ABAQUS [
34], was applied to determine the stresses and strains around contact. Symmetry model was applied to reduce the calculation time, i.e., a half of the fretting fatigue specimen was used for FEA (
Figure 5). Boundary conditions were applied at the middle of fretting fatigue specimen and contact pads, i.e., the displacement in
x direction and the rotations around
y-axis were constrained. Frictional-contact elements (quadratic-quadrilateral elements), master-slave algorithm, and penalty method [
34] were applied to the contact. The slip of contact is assumed to occur when the shear stress is greater than the critical shear stress (τ
c), i.e.,
where σ
n and μ are the normal stress and the friction coefficient, respectively. Friction coefficient was measured as μ = 0.6 via a completely sliding wear test [
35].
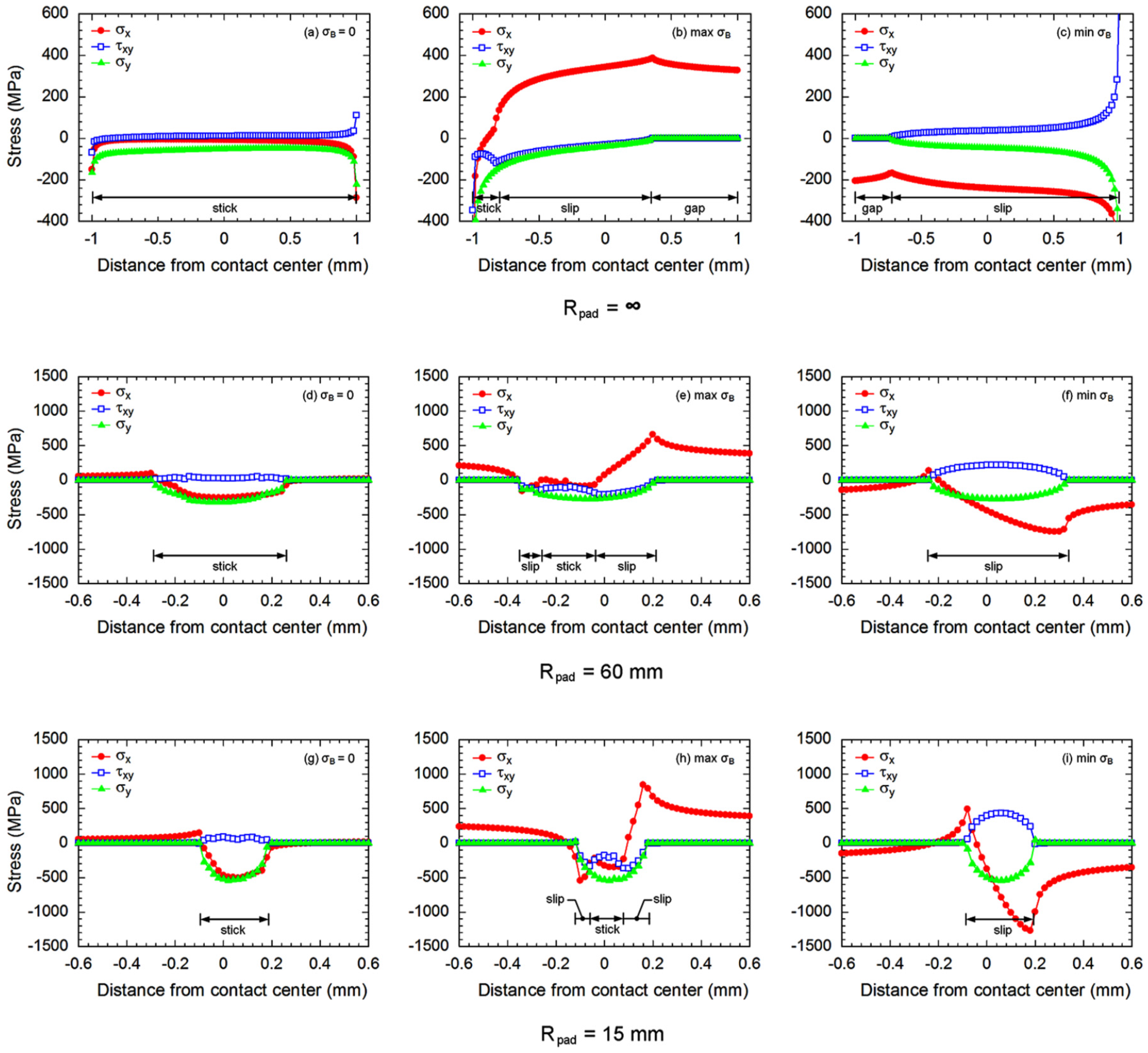
Initially, a mean contact pressure (
P) of 60 MPa was applied to the contact pad. Then, the bulk stress was gradually increased from zero to the maximum σ
B. Subsequently, the bulk stress was gradually decreased to the minimum σ
B. Finally, the bulk stress was increased to the zero bulk stress to complete one loading cycle. Bulk stress was varied with intervals of 80 steps for one loading cycle. To minimize the influence of element size, the size of elements was adjusted until the variation of the Von Mises stress around the contact was below 5%. The smallest size of element along contact was 5 μm. Stress distributions along contact at zero σ
B, the maximum σ
B (tension) and the minimum σ
B (compression) of fretting fatigue experiment at stress amplitude of 300 MPa are shown in
Figure 6.
After applying a mean contact pressure (σ
B = 0 of
Figure 6), the contact is defined as the region where the σ
y is not zero. For flat-on-flat contact, the contact width was similar to the width of contact pad’s leg, i.e., 2 mm. While, the cylindrical-on-flat contact widths were approximately 550 and 290 μm for fretting fatigues with
Rpad = 60 and 15 mm, respectively. These numerical estimations of cylindrical-on-flat contact widths correspond to the theoretical Hertzian contact widths [
31], i.e., 564 and 282 μm for fretting fatigues with
Rpad = 60 and 15 mm, respectively. On the other hand, the maximum compressive stresses (σ
y) were observed at contact centers of cylindrical-on-flat contacts, i.e., 300 and 540 MPa for fretting fatigues with
Rpad = 60 and 15 mm, respectively. These numerical estimations correspond to the theoretical maximum contact pressures [
31], i.e., 271 and 542 MPa for fretting fatigues with
Rpad = 60 and 15 mm, respectively.
After applying bulk alternating stress (σ
B), three types of deformation were observed at contact, i.e., gapping, slipping and sticking. Existences of gapping, slipping and sticking depend on bulk alternating stress, contact pressure, geometries of contact, as well as frictional coefficient. Gapping is defined as the situation when the normal stress perpendicular to contact (σ
y) and shear stress at contact (τ
xy) become zero. In the region where the contact between pad and specimen occurs but the friction is not enough to stick the pad onto specimen, the slipping exists. On the other hand, the sticking between pad and specimen is possible in the region where the friction becomes high enough. Accordingly, the gapping, slipping and sticking could be identified by considering the stress behavior at contact, as shown in
Figure 6.
As the differences between stresses at the maximum σ
B and those at the minimum σ
B, the distributions of stress range along contacts of fretting fatigue experiments at a stress amplitude of 300 MPa are shown in
Figure 7. Contact can be defined as the region where the Δ
σy is not zero. As an example, the contact width on fretting fatigue specimen (
Rpad = 15 mm) tested at stress amplitude of 300 MPa is 350 μm. However, this contact width is about 22% shorter than that of experiment (
Figure 3), i.e., an average contact width of 450 μm. Difference may relate to the plastic deformation of asperities under contact, which was not considered for the present linear-elastic FEA.
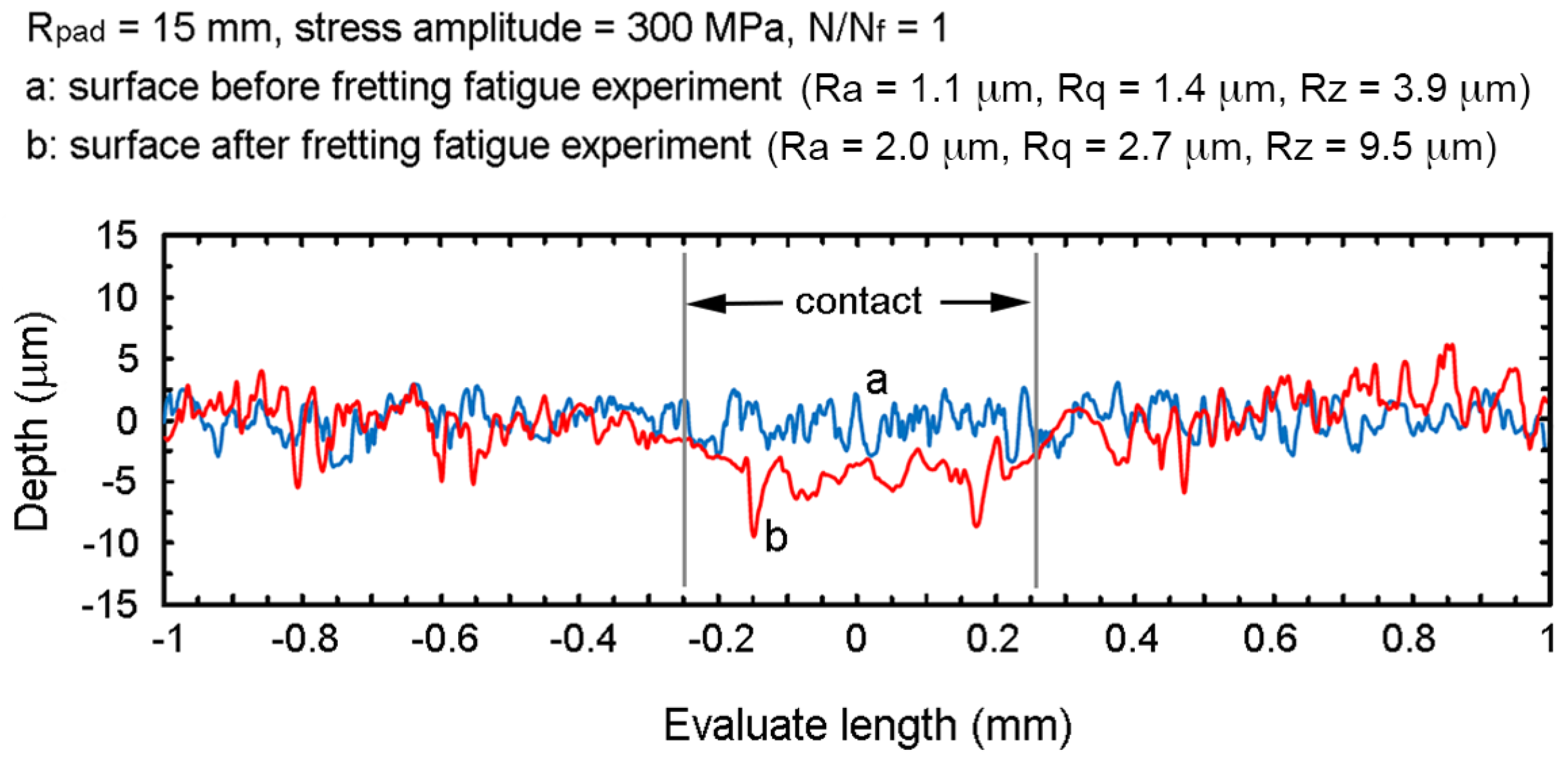
To investigate the influence of surface asperities on contact, the surface roughness of specimen before and after fretting fatigue experiment (
Rpad = 15 mm and stress amplitude = 300 MPa) were measured using a surface roughness tester (Mitutoyo: SJ-310), as shown in
Figure 8. The asperities around the contact center were compressed and plastically deformed during fretting fatigue experiment. Moreover, the grooves were observed near the contact trailing edges. Without the consideration of asperities, the contact width from linear-elastic FEA is shorter than that of experiment with deformed asperities. However, it is believed that the stress distributions along contacts without asperities and contact with deformed asperities are marginally different, especially at the early stage of fretting fatigue life. Therefore, the assumption of specimen without asperities was used for the present FEA of crack nucleation.
3.2.1. Maximum Shear Stress Range Criterion
It is known that the cycle stress causes the irreversibility of shear displacement at the surface of alloy, i.e., intrusions and extrusions. The stress concentration at these sites can promote fatigue crack nucleation [
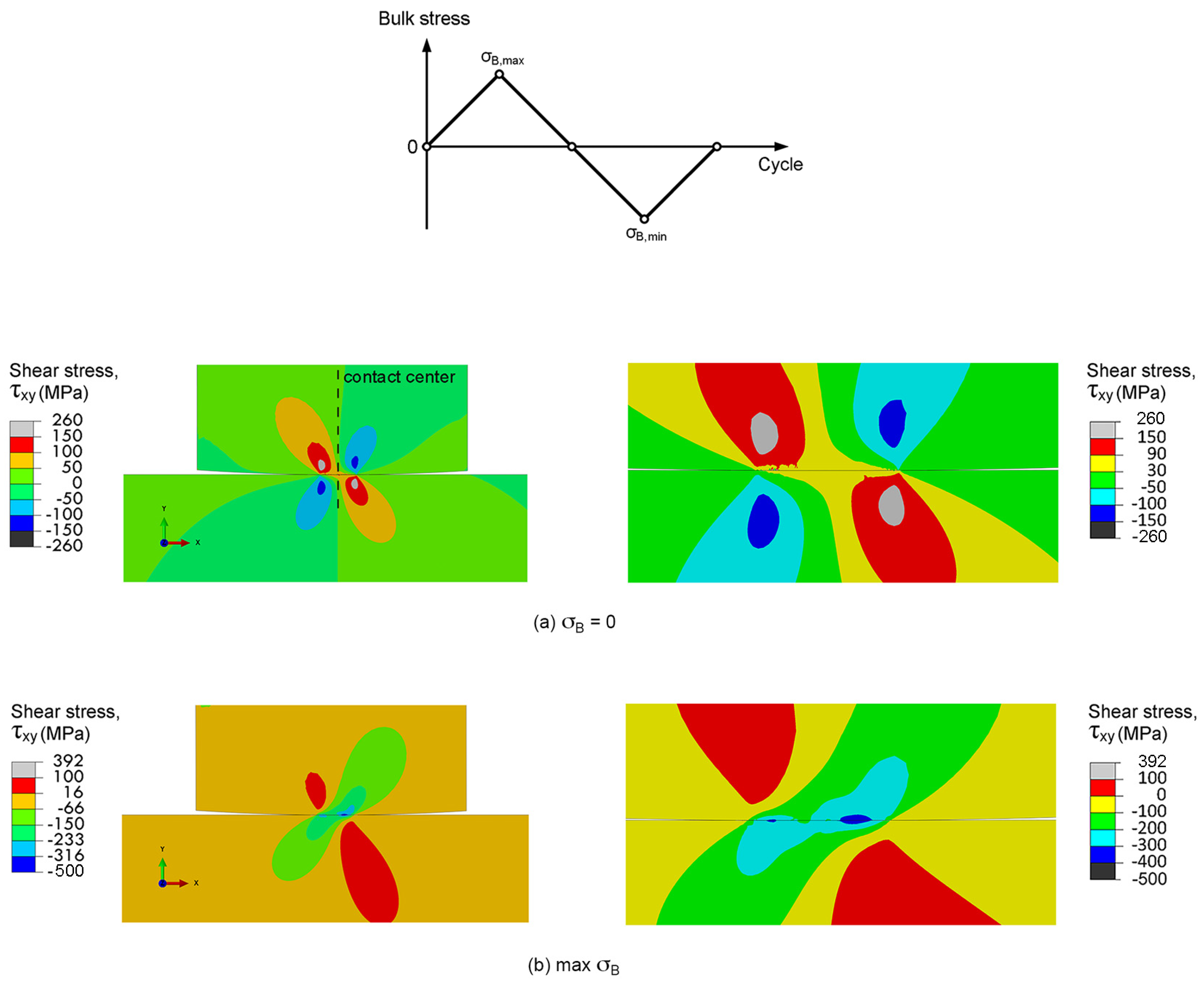
36]. Thus, the fretting fatigue crack is assumed to nucleate at the location of the maximum shear stress range, i.e., the maximum shear stress range criterion. The shear stress range at contact was evaluated using plane-strain linear-elastic FEA. The distributions of shear stresses around contact of right leg of contact pad during fretting fatigue experiment (
Rpad = 15 mm and
σB = 300 MPa) are shown in
Figure 9. After applying of a contact pressure (
σB = 0), the highest shear stress occurred below the contact (
Figure 9a), which is the typical Hertzian contact stress for cylindrical-on-flat contact. However, the highest shear stress moved to the contact with the contributions of bulk alternating stress and friction at contact. The highest shear stress at the maximum
σB was observed on the contact and at the right side of contact center (
Figure 9b), while that at minimum
σB was observed on the contact and at the left side of contact center (
Figure 9c). As the difference between shear stresses at the maximum and minimum σ
B, the distribution of shear stress ranges is shown in
Figure 9d. The maximum shear stress range was observed on the contact and at the right side of contact center, i.e., near the contact trailing edge. The distributions of shear stresses around contacts of fretting fatigue specimens (
σB = 300 MPa) with various radii of contact pads were numerically calculated. Distances from the contact center to the location of the maximum shear stress (
dn) were approximately 1000, 20 and 80 μm for specimens with
Rpad = ∞, 60 and 15 mm, respectively.
3.2.2. Maximum Relative Slip Amplitude Criterion
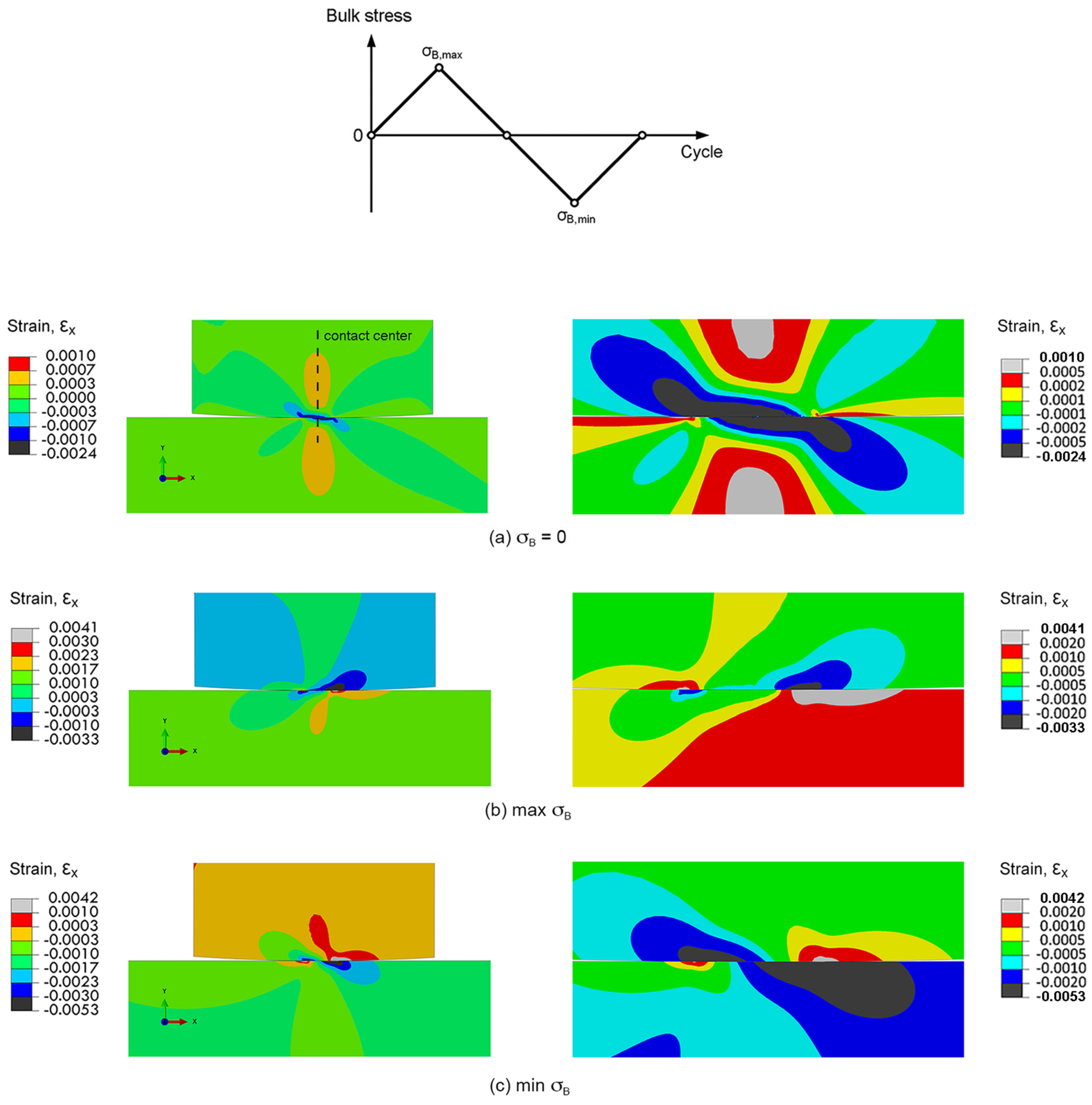
Slipping at contact can cause contact wear, which enhance the stress concentration at wear track. The stress concentration at these sites may promote fatigue crack nucleation. Thus, the fretting fatigue crack is assumed to nucleate at the location of the maximum relative slip amplitude, i.e., the maximum relative slip amplitude criterion. The slipping of contact was evaluated using plane-strain linear-elastic FEA. To understand the slipping of contact, the distributions of normal strains in
x-direction (ε
x) during fretting fatigue experiment (
Rpad = 15 mm and σ
a = 300 MPa) are shown in
Figure 10. After applying a contact pressure (σ
B = 0), the distributions of ε
x along contact of contact pad and specimen were similar (
Figure 10a), i.e., sticking. At the maximum σ
B, the highest ε
x along contact of specimen was observed at the right side of contact center (
Figure 10b), while that at minimum σ
B was observed at the left side of contact center (
Figure 10c). The mismatches in ε
x between contact pad and specimen, i.e., slipping, were observed along contacts (
Figure 10b,c), especially at the outer regions of contacts.
As a difference in deformations in
x-direction between the contact points on contact pad and on specimen, the relative slips at the maximum and minimum σ
B were obtained. Subsequently, the relative slip range, i.e., a total slip from the minimum to the maximum of σ
B, and the relative slip amplitude, i.e., a half of relative slip range, could be determined. To verify the FEA of relative slip amplitude, the relative slip amplitude at external contact edge of flat-on-flat contact (
Rpad = ∞) was measured using an extensometer, and compared with that from FEA. Both the FEA and the experimental results were in good agreement [
6]. Under stress amplitude of 300 MPa, the relative slip amplitudes along various contacts are shown in
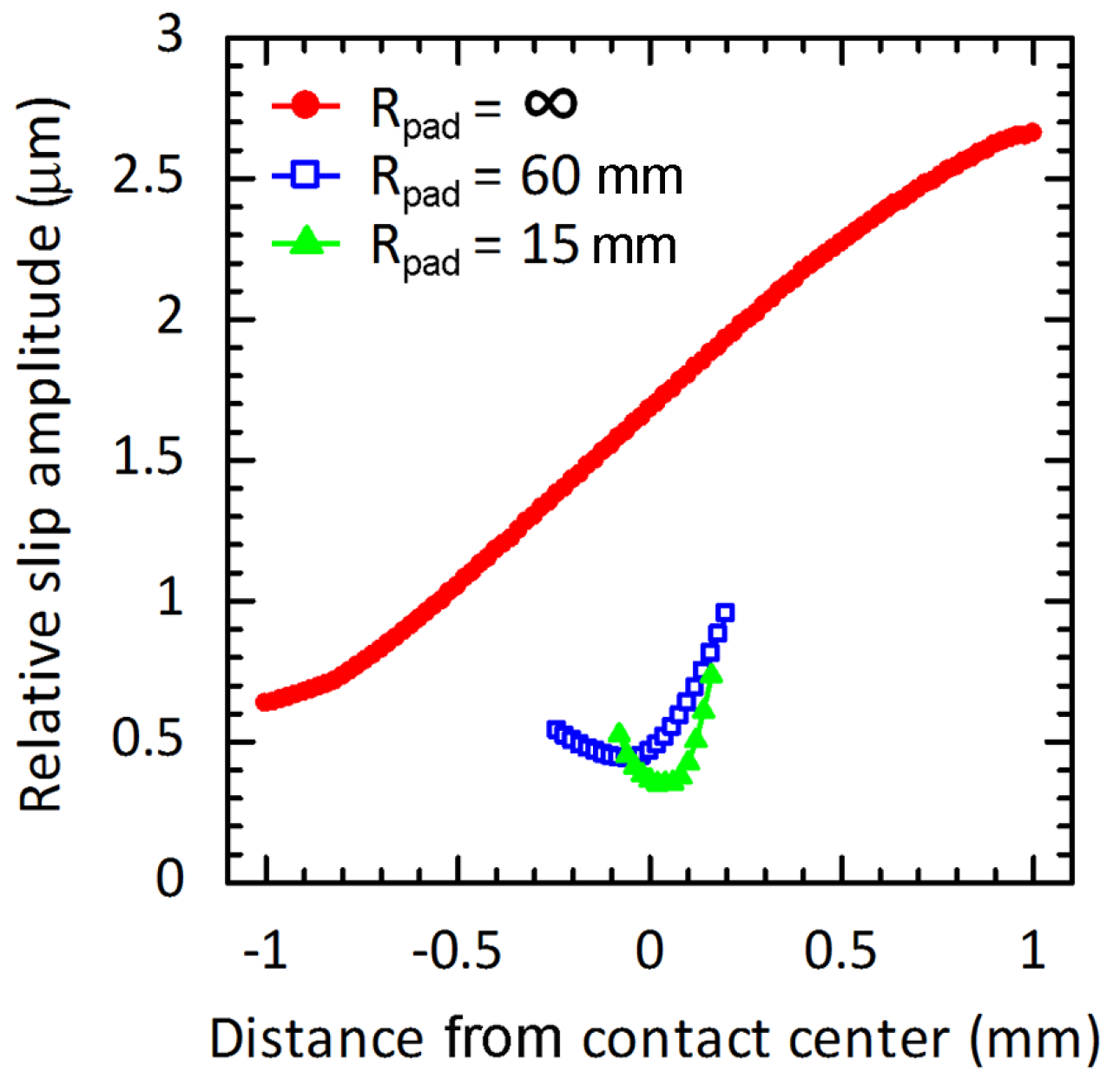
Figure 11. The influence of radius of contact pad on the relative slip amplitudes could be clearly observed in the figure. Distances from the contact center to the location of the maximum relative slip amplitude (
dn) were approximately 1000, 200 and 160 μm for specimens with
Rpad = ∞, 60 and 15 mm, respectively.
Distances from the contact center to the location of crack nucleation (
dn) obtained from experiments and FEAs, i.e., the maximum shear stress range criterion and the maximum relative slip amplitude criterion, were compared, as shown in
Figure 12. The locations of crack nucleation of flat-on-flat contact (
Rpad = ∞) using the maximum shear stress range criterion and the maximum relative slip amplitude criterion were similar and correspond to that of experiment, i.e., crack nucleated at the external contact edge. On the other hand, the locations of crack nucleation of cylindrical-on-flat contacts (
Rpad = 60 and 15 mm) using the maximum shear stress range criterion and the maximum relative slip amplitude criterion were different. The predicted locations of crack nucleation using the maximum relative slip amplitude criterion were in better agreement with the experimental results. Therefore, the maximum relative slip amplitude criterion should be used for the prediction of the location of fretting fatigue crack nucleation under cylindrical-on-flat contact.
3.3. Fretting Fatigue Crack Path
The effect that the model’s geometry has on fretting fatigue life predictions was studied by Vazquez et al. [
37], where the crack initiation and crack-propagation phases were combined to obtain the total fatigue life. Their results showed solid predictions for both 2D and 3D FEM models when considering a semi-elliptical surface crack. The use of a 2D FEM model, while incorporating a semi-elliptical surface crack, is therefore justified because it provides the advantage of lower computational cost compared with 3D FEM model. In the present study, the fretting fatigue crack could be observed in the early stage of fatigue life; the crack nucleation life was significantly short and the fretting fatigue life was dominated by the crack propagation [
1,
7,
38]. Accordingly, the 2D FEA model of fretting fatigue experiment with through-thickness crack was used for the evaluation of crack path and crack propagation.
As an initial propagating crack, a crack in the direction of the maximum tangential stress range (Δσ
θmax) was introduced at the location of the maximum relative slip amplitude. Subsequently, it is assumed to propagate in the direction of Δσ
θmax, i.e., the maximum tangential stress range criterion [
39]. Stresses at crack tip were evaluated using plane-strain linear-elastic FEA (
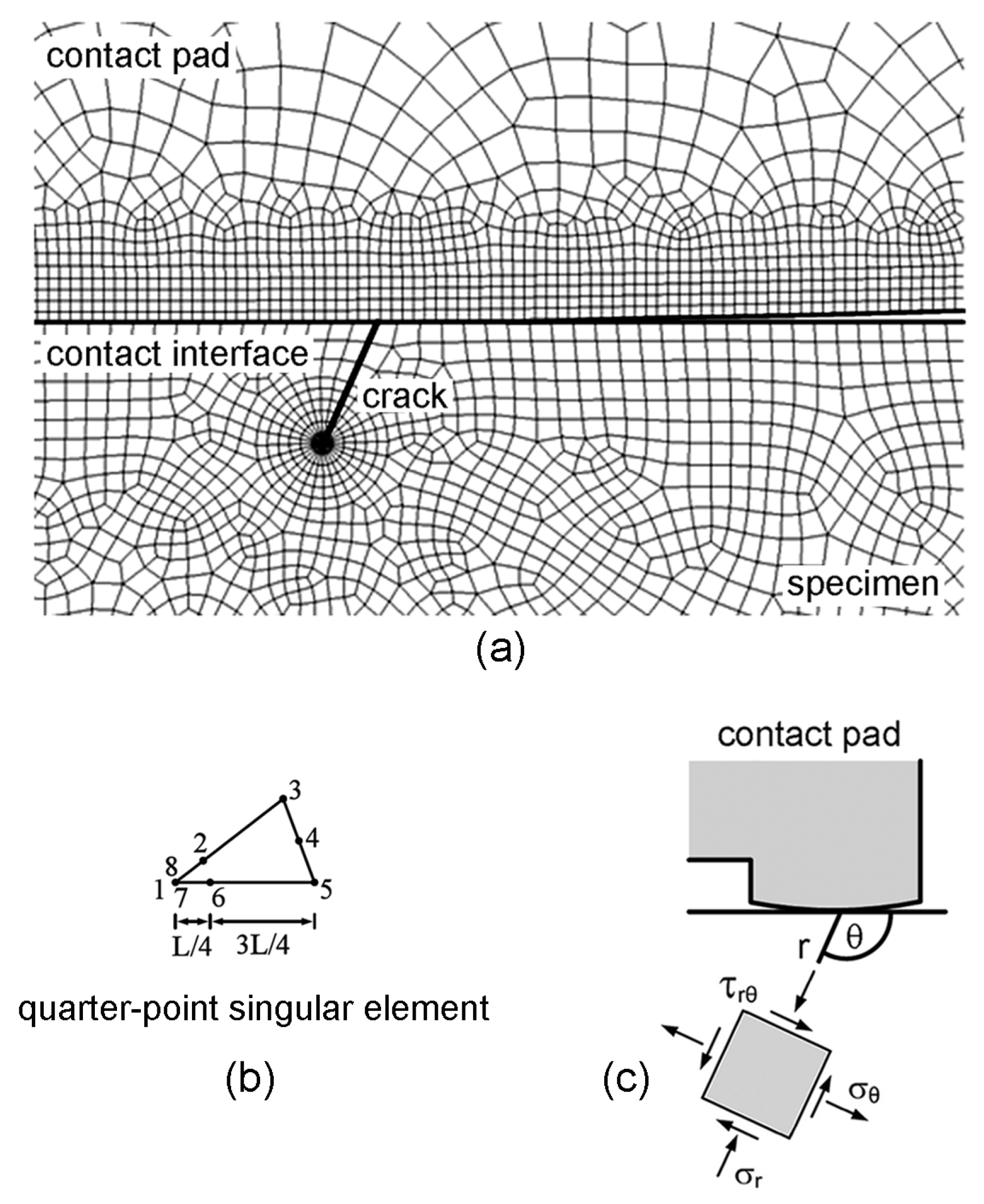
Figure 13a). To reduce the calculation process time, a half of the fretting fatigue specimen with a crack was used for FEA. Quarter-point singular elements were applied at crack tip (
Figure 13b), while the quadratic quadrilateral elements were used for the remaining elements. Polar coordinates were applied to numerically evaluate the inclined angle (θ) of an initial propagating crack, as shown in
Figure 13c.
According to the fracture mechanics approach for a small fretting fatigue crack [
4,
40], the length of an initial propagating crack could be assumed as the critical smallest crack length (
ao), i.e.,
where Δσ
e and Δ
Kth are the fatigue limit of plain fatigue and the threshold stress intensity factor range, respectively. For JIS S45C steel, Δσ
e and Δ
Kth were 250 MPa and 4 MPa·m
1/2, respectively. Thus,
ao was given as 80 μm. In the previous study [
6,
41], the sensitivities of path radius and length of propagating crack on fretting fatigue crack path were evaluated. The FEA result corresponded to the experimental result when
ao/2 was used as: (i) the path radius for calculating the crack orientation; and (ii) the length of propagating crack for every FEA step. Accordingly, a similar procedure of crack path prediction was applied here.
Size of elements was adjusted until the variation of stress intensity factor at crack tip was lower than 5%, i.e., the smallest size of element at crack tip was 1 μm. Based on path radius of
ao/2, the direction of Δσ
θmax was determined and the crack was extended by
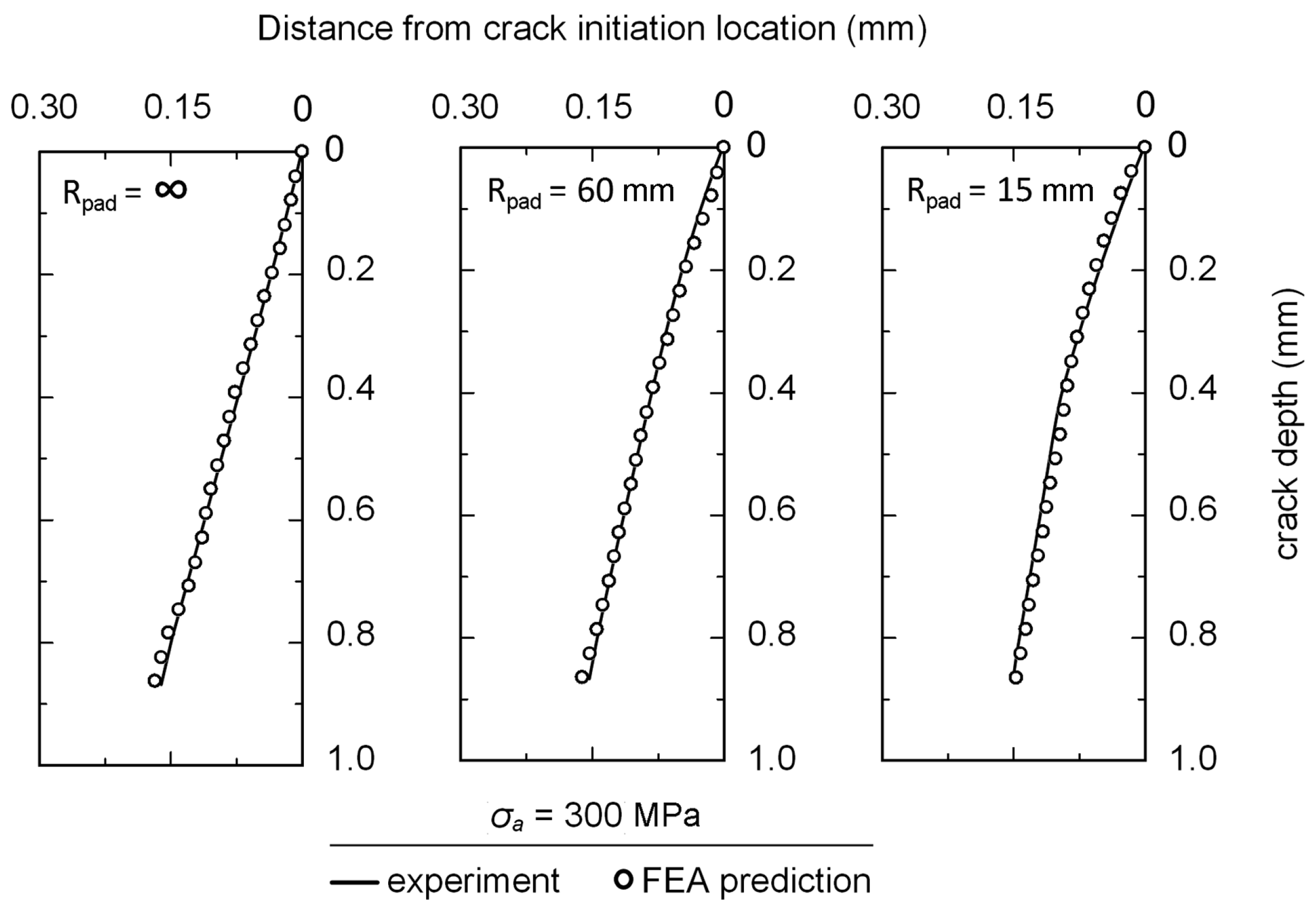
ao/2. This process was repeated for each FEA step to obtain a fretting fatigue crack path. Comparisons between the predicted crack paths and the experimental crack paths at a stress amplitude of 300 MPa are shown in
Figure 14. Predicted crack paths were in good agreement with the experimental results.
3.4. Fretting-Contact-Induced Crack Opening/Closure
It is known that the FCG behavior may be influenced by the crack opening/closure behavior, and the effective stress intensity factor range (Δ
Keff) should be applied as the driving force of FCG [
26]. In the previous study [
38], the crack opening under compressive bulk alternating stress was found from both FEA and experiment, i.e., an elastic compliance method was applied to measure the crack opening of bridge-type fretting fatigue experiment. The restraint of deformation of contact region side of crack surface, which was induced by the contact pressure and tangential stress, was the dominant cause of the crack opening under compressive bulk alternating stress, i.e., the fretting-contact-induced crack opening/closure.
Accordingly, the influence of geometry of contact pad on the fretting-contact-induced crack opening/closure was evaluated using FEA. Plane-strain linear-elastic FEA was performed using a half model of fretting fatigue specimen with a crack. Frictionless contact is assumed for the contact between crack surfaces. The stresses (σ
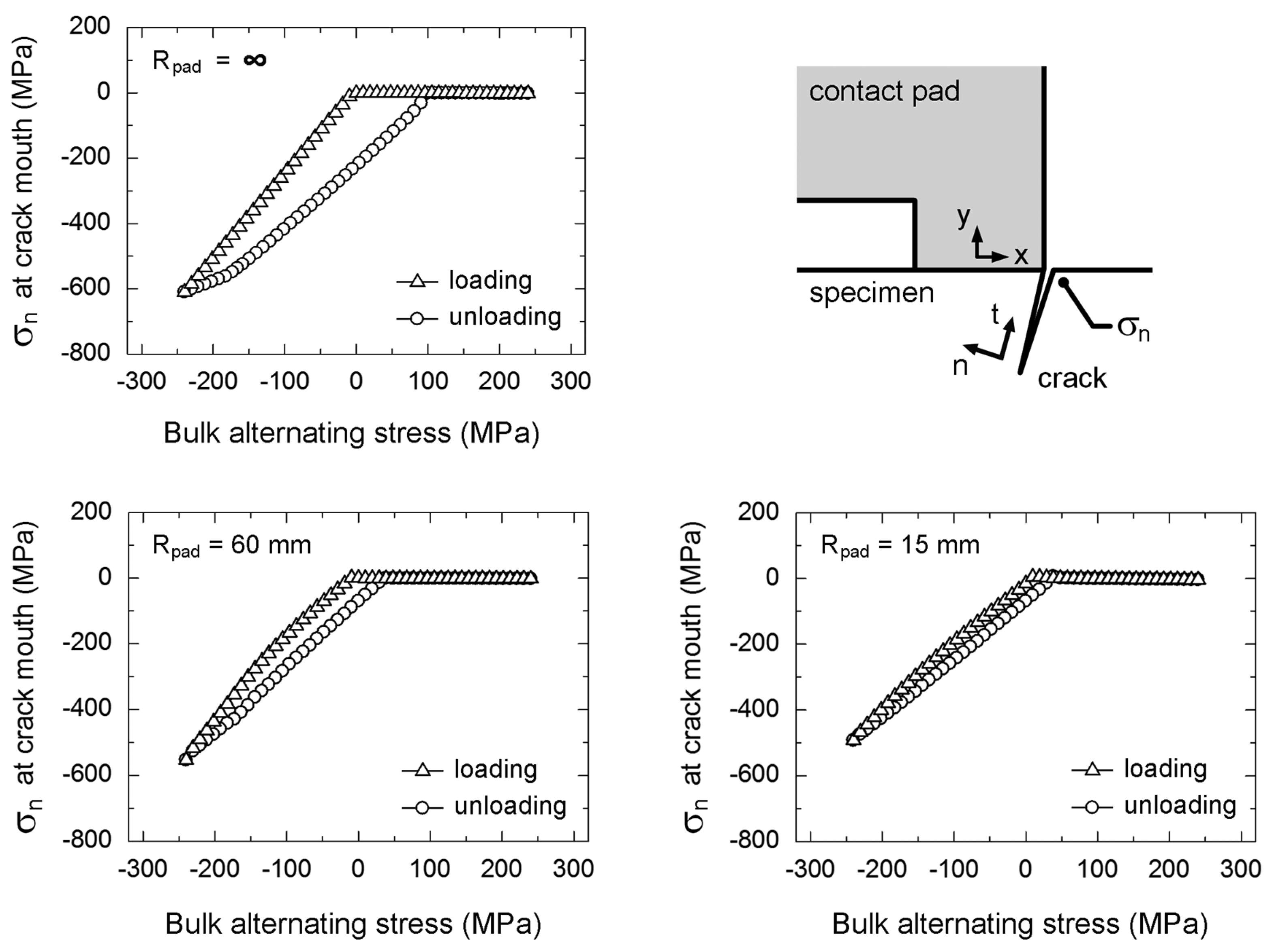
n) at 10 μm away from the crack mouth of fretting fatigue specimen with an 80-μm crack tested at a stress amplitude of 300 MPa are shown in
Figure 15. The opening of crack surfaces is the situation when the stress normal to crack surface (σ
n) at 10 μm away from the crack mouth becomes zero. The crack opening and closing at crack mouth of fretting fatigue specimen occurred at different bulk alternating stresses, i.e., crack closing is possible under a tensile bulk alternating stress, while crack opening is possible under a compressive bulk alternating stress. The opening stress was influenced by the radius of contact pad (
Rpad), i.e., the opening stress of specimen with
Rpad = ∞ (flat-on-flat contact) occurred at the lowest compressive bulk alternating stress following by those of specimens with
Rpad = 60 and 15 mm (cylindrical-on-flat contacts), respectively.
In the present study, the effective stress intensity factor range (Δ
Kθmax,eff) was used as a driving force for the FCG with the fretting-contact-induced crack opening/closure. The contour integral method [
34] was applied for FEA of the maximum tangential stress intensity factor (
Kθmax), which can be given as:
The effective stress intensity factor range (Δ
Kθmax,eff) can be determined as:
where
Kθmax,max is the maximum tangential stress intensity factor at the maximum bulk alternating stress, and
Kθmax,op is the maximum tangential stress intensity factor at crack opening stress, which can be determined from the change in slope during loading of
Figure 15.
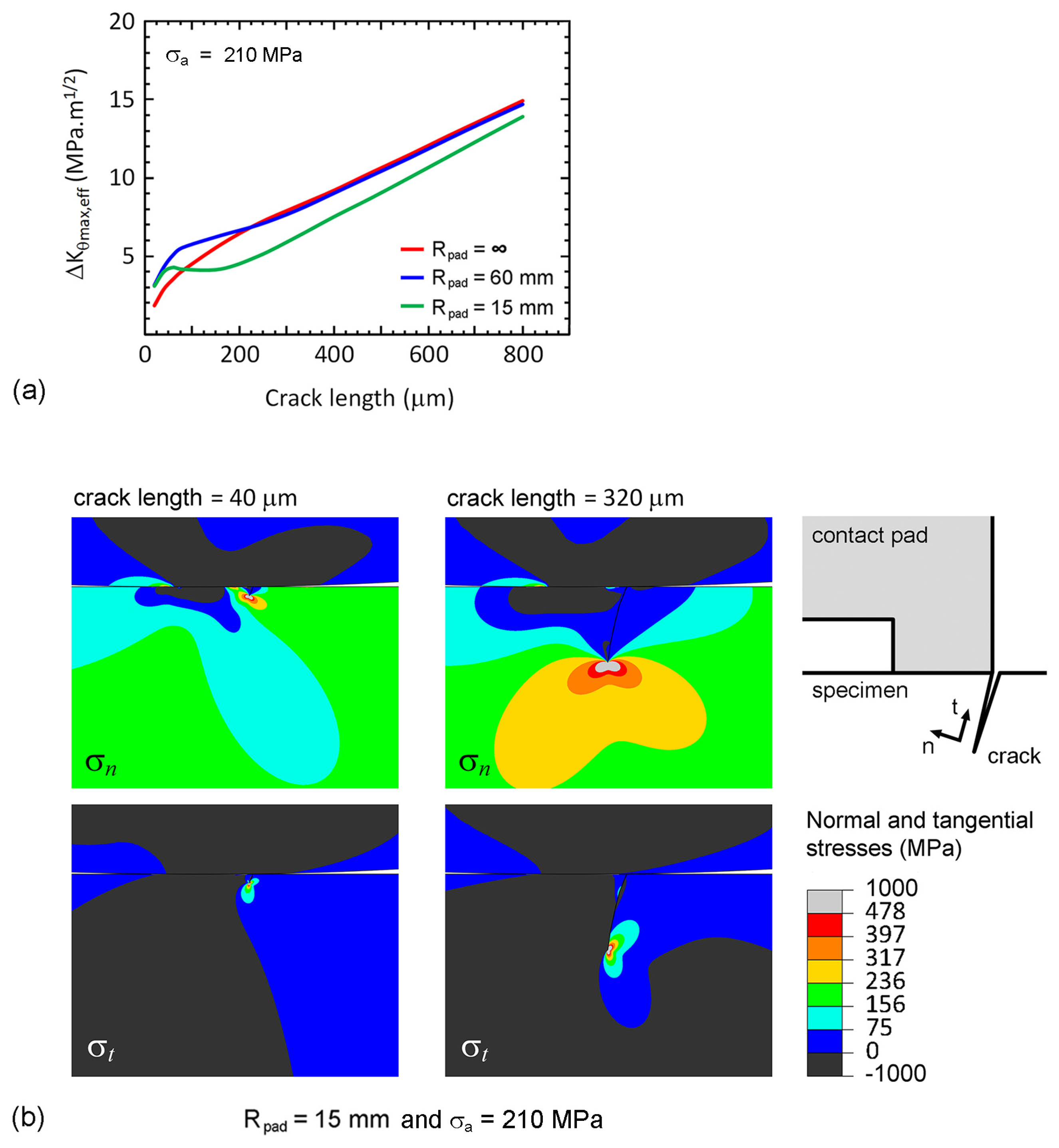
Relationships between the effective stress intensity factor range (Δ
Kθmax,eff) and crack length (
a) of fretting experiments at stress amplitude of 210 MPa are shown in
Figure 16a. At the beginning of crack propagation, i.e.,
a < 100 μm, the crack tips of cylindrical-on-flat contacts were outside the region of Hertzian contact stress, thus the Hertzian contact stress enhanced the crack propagation, i.e., Δ
Kθmax,eff of cylindrical-on-flat contacts were higher than that of flat-on-flat contact. As an example, the distributions of normal and tangential stresses on fretting fatigue specimen (
Rpad = 15 mm) with a 40-μm crack at the maximum σ
B are shown in
Figure 16b.
As crack propagated longer than 100 μm, the crack tip of cylindrical-on-flat contact was eventually surrounded by the Hertzian contact stress (
a = 320 μm in
Figure 16b). The Hertzian contact stress retarded the crack propagation, and the increasing rate of Δ
Kθmax,eff with crack length decreased. Since the number of cycles during the beginning of crack propagation (a < 100 μm) dominated the fatigue life, the fatigue resistance of flat-on-flat contact (low Δ
Kθmax,eff) became higher than those of cylindrical-on-flat contacts (high Δ
Kθmax,eff). When comparing between cylindrical-on-flat contacts with
Rpad = 60 and 15 mm, Δ
Kθmax,eff of specimen with
Rpad = 60 mm was higher than that of specimen with
Rpad = 15 mm (
Figure 16a). Therefore, the fatigue resistance of cylindrical-on-flat contact with
Rpad = 60 mm was slightly lower than that of cylindrical-on-flat contact with
Rpad = 15 mm. These findings corresponded to the fretting fatigue lives from experiments (
Figure 2).