Nanoscale Phase Evolution during Continuum Decomposition of Fe-Cr Alloys
Abstract
:1. Introduction
2. Phase-Field Model and Calculation Methods
2.1. Phase-Field Model
2.2. Numerical Calculation
3. Results and Discussion
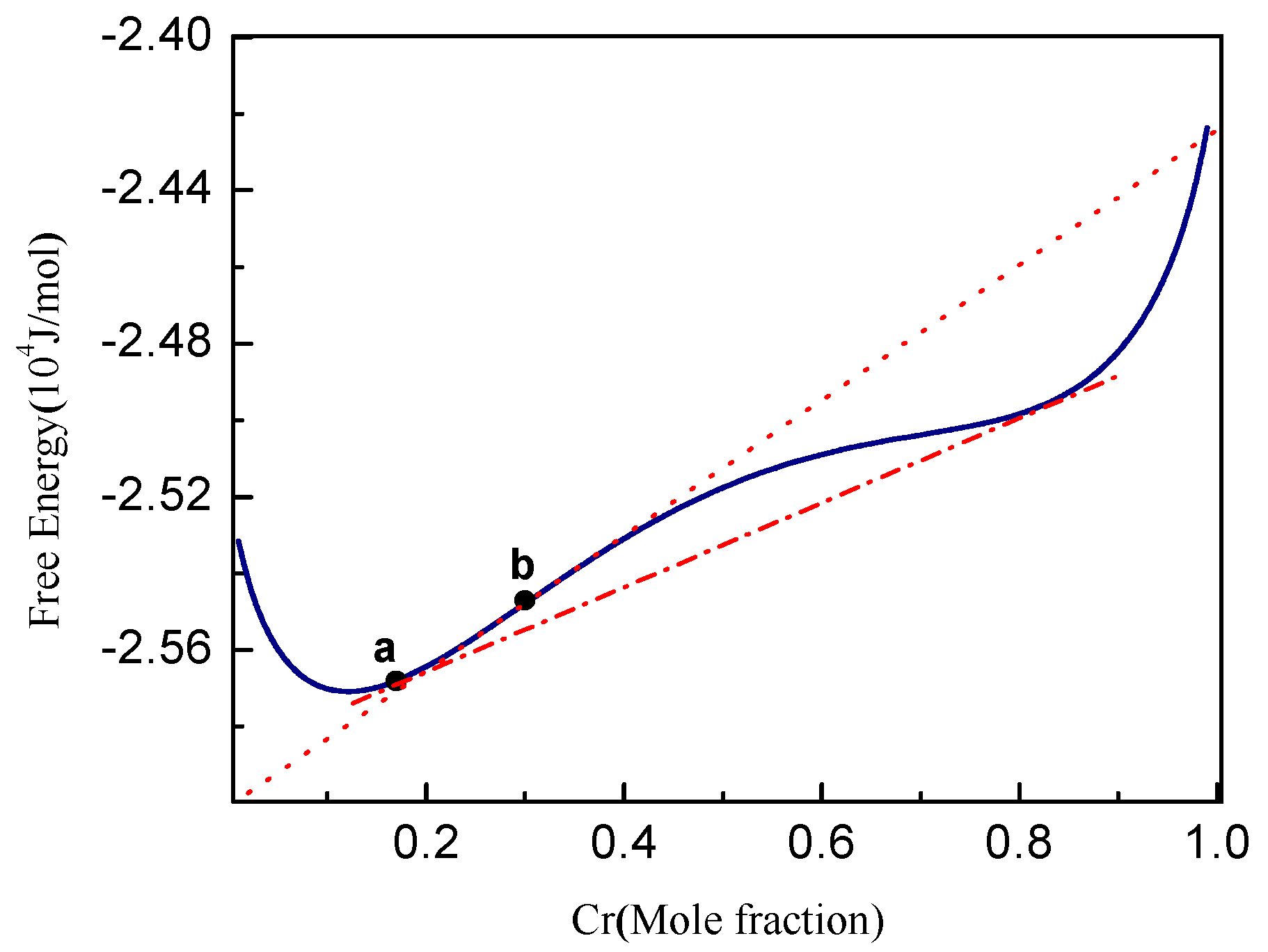
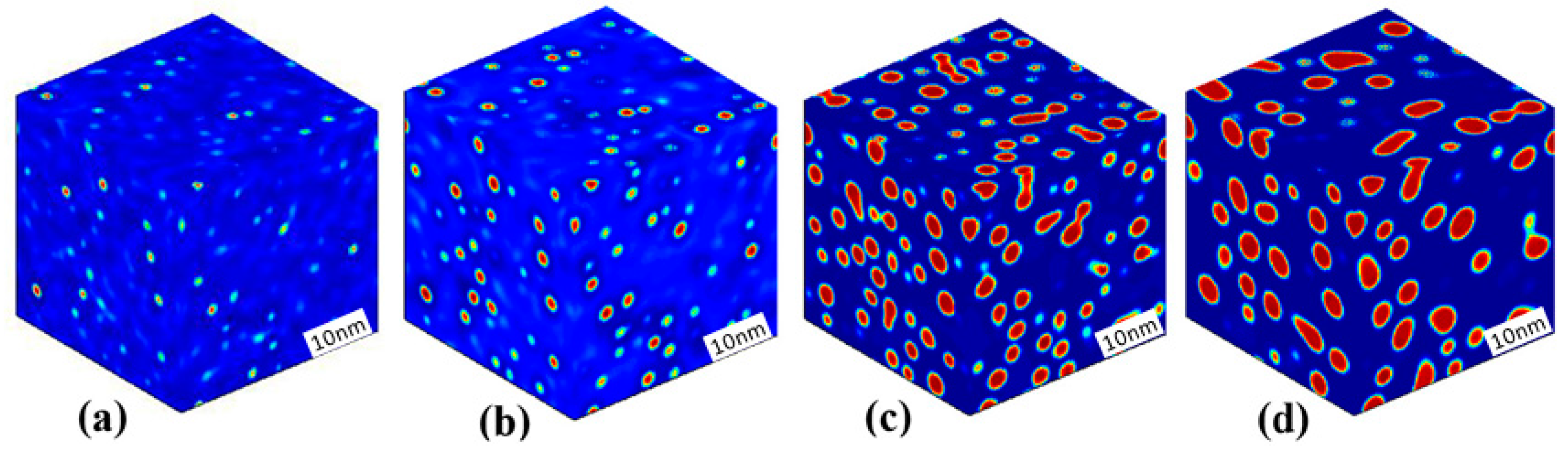
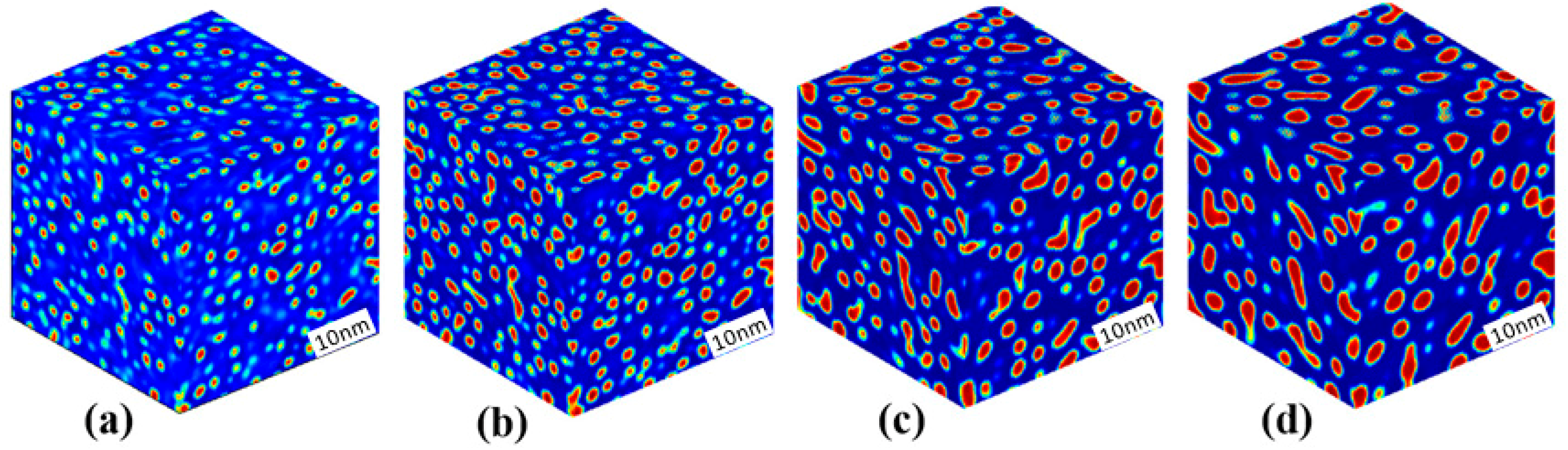
3.1. Phase Separation in Metastable Regions
3.2. Phase Separation Near the Spinodal Boundary
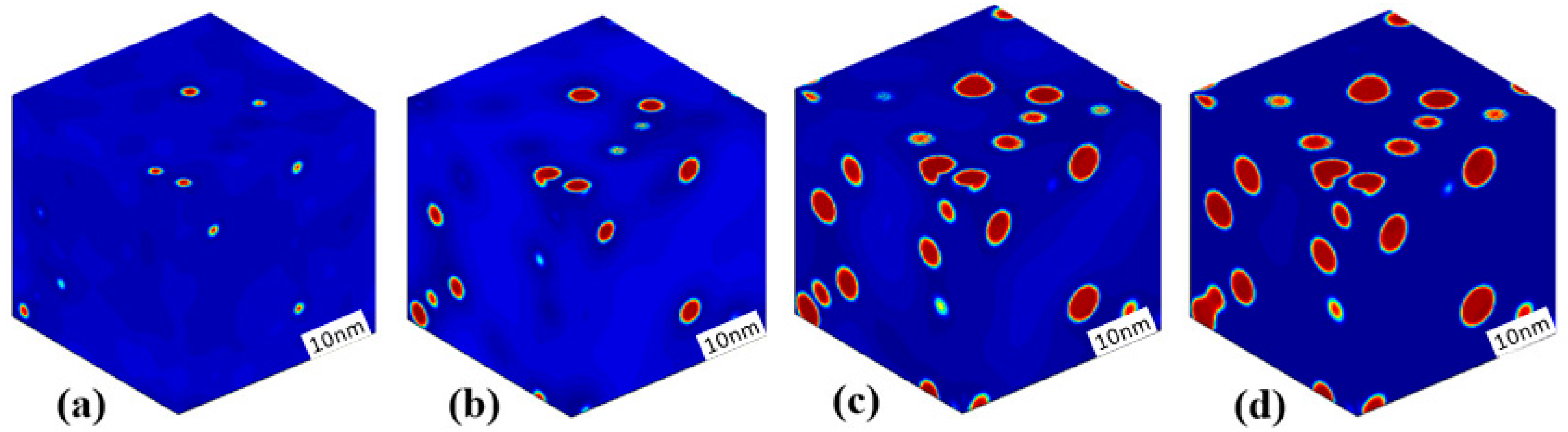
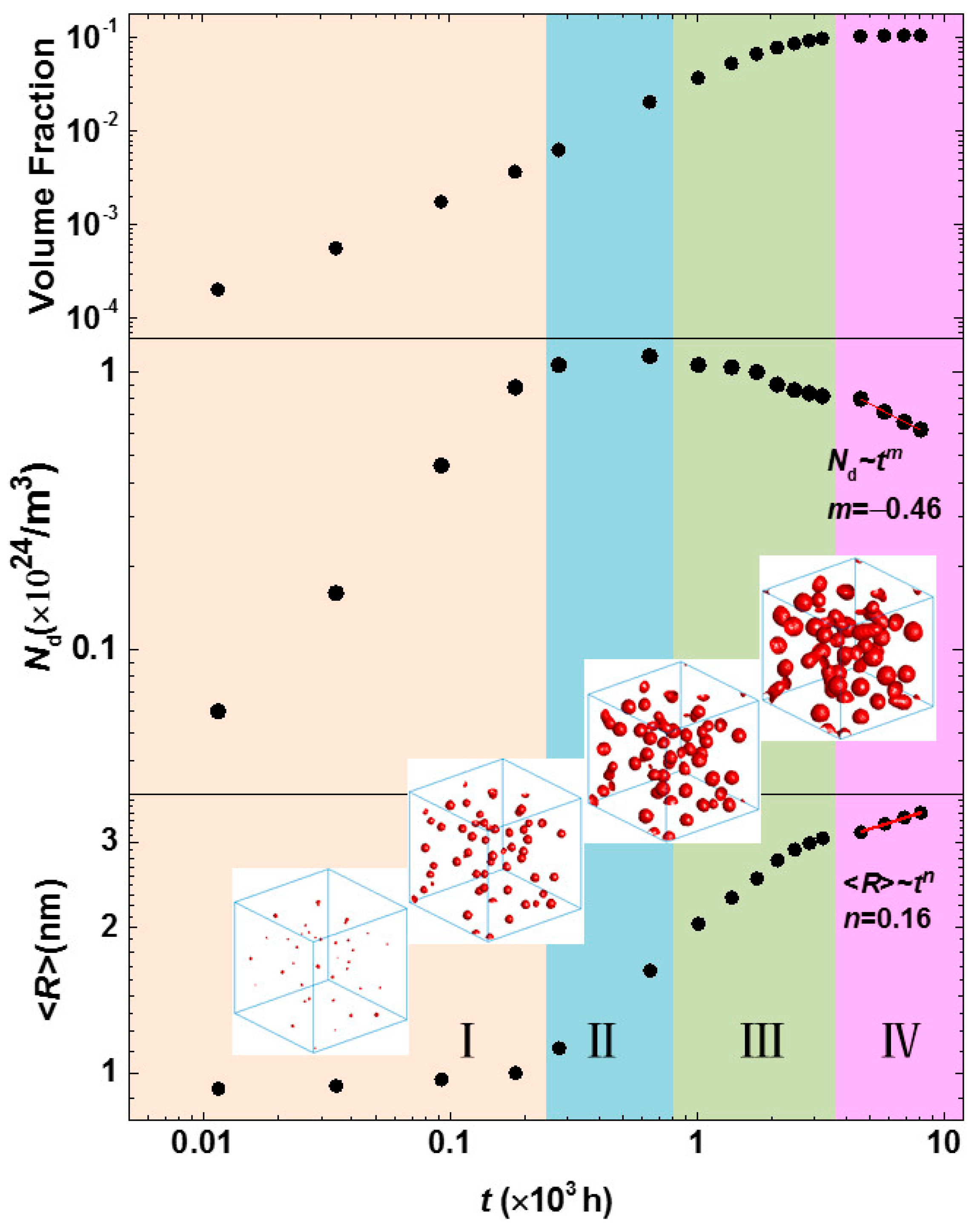
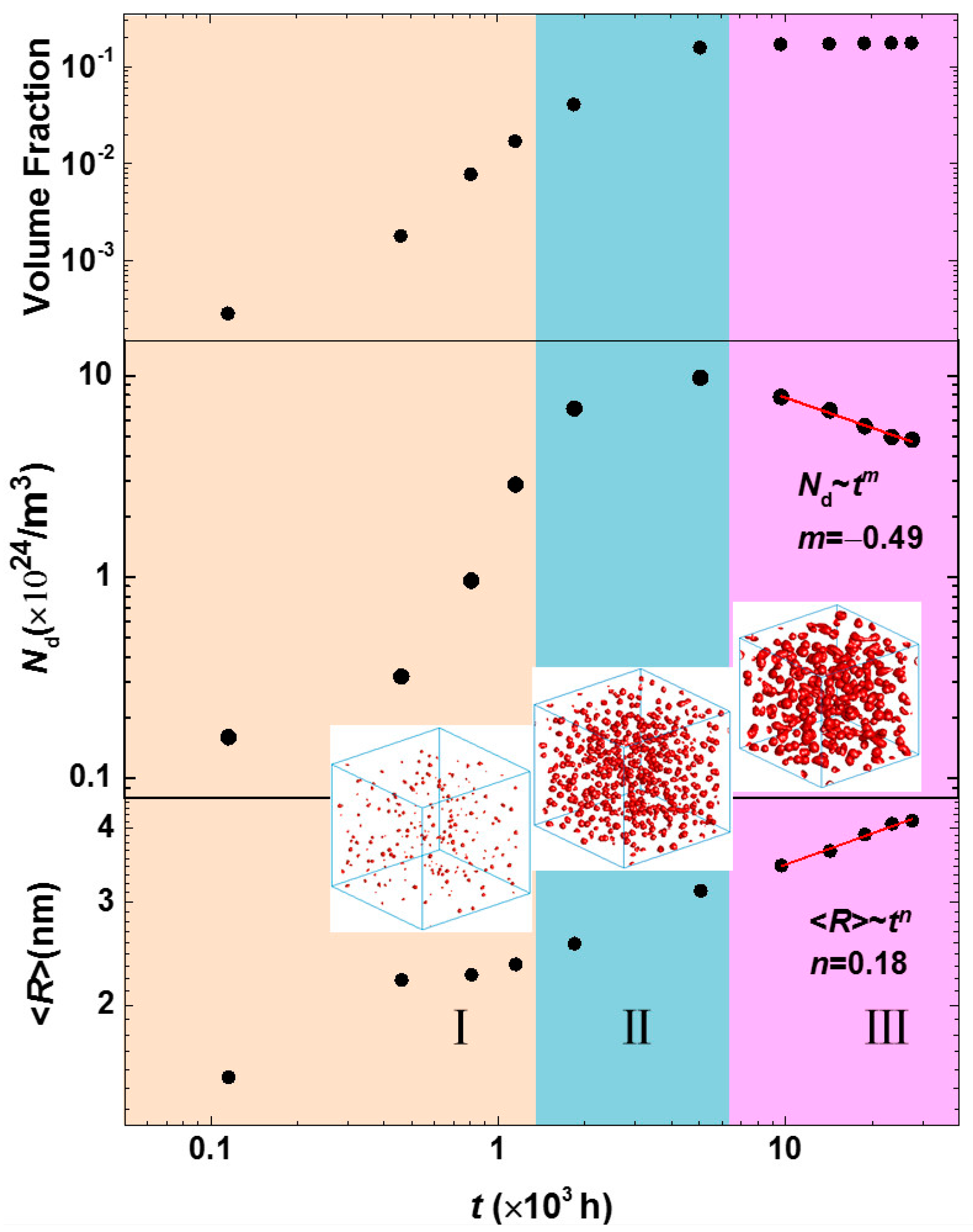
3.3. Phase Separation in Spinodal Decomposition Region
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Marshal, P. Austenitic Stainless Steels: Microstructure and Mechanical Properties; Elsevier Applied Science Publishers: Amsterdam, The Netherlands, 1984. [Google Scholar]
- Klueh, R.L.; Nelson, A.T. Ferritic/martensitic steels for next-generation reactors. J. Nucl. Mater. 2007, 37, 137–152. [Google Scholar] [CrossRef]
- Novy, S.; Pareige, P.; Pareige, C. Atomic scale analysis and phase separation understanding in a thermally aged Fe- 20 at.% Cr alloy. J. Nucl. Mater. 2009, 384, 96–102. [Google Scholar] [CrossRef]
- Sahu, J.K.; Krupp, U.; Ghosh, R.N.; Christ, H.J. Effect of 475 °C embrittlement on the mechanical properties of duplex stainless steel. Mater. Sci. Eng. A 2009, 508, 1–14. [Google Scholar] [CrossRef]
- Iacoviello, F.; Casari, F.; Gialanella, S. Effect of 475 °C embrittlement on duplex stainless steels localized corrosion resistance. Corros. Sci. 2005, 47, 909–922. [Google Scholar] [CrossRef]
- Pettersson, N.; Wessman, S.; Thuvander, M.; Hedström, P.; Odqvist, J.; Pettersson, R.F.A.; Hertzman, S. Nanostructure evolution and mechanical property changes during aging of a super duplex stainless steel at 300 °C. Mater. Sci. Eng. A 2015, 647, 241–248. [Google Scholar] [CrossRef]
- Senninger, O.; Soisson, F.; Martínez, E.; Nastar, M.; Fu, C.C.; Bréchet, Y. Modeling radiation induced segregation in iron-chromium alloys. Acta Mater. 2016, 103, 1–11. [Google Scholar] [CrossRef]
- Soriano-Vargas, O.; Avila-Davila, E.O.; Lopez-Hirata, V.M.; Cayetano-Castro, N.; Gonzalez-Velazquez, J.L. Effect of spinodal decomposition on the mechanical behavior of Fe-Cr alloys. Mater. Sci. Eng. A 2010, 527, 2910–2914. [Google Scholar] [CrossRef]
- Miller, M.K.; Russell, K.F. Comparison of the rate of decomposition in Fe-45% Cr, Fe-45% Cr-5% Ni and duplex stainless steels. Appl. Surf. Sci. 1996, 94–95, 398–402. [Google Scholar] [CrossRef]
- Westraadt, J.E.; Olivier, E.J.; Neethling, J.H.; Hedström, P.; Odqvist, J.; Xu, X.; Steuwer, A. A high-resolution analytical scanning transmission electron microscopy study of the early stages of spinodal decomposition in binary Fe-Cr. Mater. Charact. 2015, 109, 216–221. [Google Scholar] [CrossRef]
- Zhou, J.; Odqvist, J.; Ågren, J.; Ruban, A.; Thuvander, M.; Xiong, W.; Olson, G.B.; Hedström, P. Direct atom probe tomography observations of concentration fluctuations in Fe-Cr solid solution. Scr. Mater. 2015, 98, 13–15. [Google Scholar] [CrossRef]
- Suzudo, T.; Nagai, Y.; Schwenc, D.; Caro, A. Hardening in thermally-aged Fe-Cr binary alloys: Statistical parameters of atomistic configuration. Acta Mater. 2015, 89, 116–122. [Google Scholar] [CrossRef]
- Li, Y.S.; Zhu, H.; Zhang, L.; Cheng, X.L. Phase decomposition and morphology characteristic in thermal aging Fe-Cr alloys under applied strain: A phase-field simulation. J. Nucl. Mater. 2012, 429, 13–18. [Google Scholar] [CrossRef]
- Mukhamedov, B.O.; Ponomareva, A.V.; Abrikosov, I.A. Spinodal decomposition in ternary Fe-Cr-Co system. J. Alloys Compd. 2017, 695, 250–256. [Google Scholar] [CrossRef]
- Li, Y.S.; Li, S.X.; Zhang, T.Y. Effect of dislocations on spinodal decomposition in Fe-Cr alloys. J. Nucl. Mater. 2009, 395, 120–130. [Google Scholar] [CrossRef]
- Ustinovshikov, Y.; Shirobokova, M.; Pushkarev, B. A structural study of the Fe-Cr system alloys. Acta Mater. 1996, 44, 5021–5032. [Google Scholar] [CrossRef]
- Ustinovshikov, Y.; Pushkarev, B. Morphology of Fe-Cr alloys. Mater. Sci. Eng. A 1998, 241, 159–168. [Google Scholar] [CrossRef]
- Chandra, D.; Schwartz, L.H. Mössbauer effect study of the 475 °C decomposition of Fe-Cr. Metall. Trans. A 1971, 2, 2511–2519. [Google Scholar] [CrossRef]
- Fratzl, P.; Penrose, O.; Weinkamer, R.; Žižak, I. Coarsening in the Ising model with vacancy dynamics. Physica A 2000, 279, 100–109. [Google Scholar] [CrossRef]
- Cahn, J.W. The 1967 institute of metals lecture, spinodal decomposition. Trans. Met. Soc. AIME 1968, 242, 166–180. [Google Scholar]
- Xiong, W.; Selleby, M.; Chen, Q.; Odqvist, J.; Du, Y. Phase equilibria and thermodynamic properties in the Fe-Cr system. Crit. Rev. Solid State Mater. Sci. 2010, 35, 125–152. [Google Scholar] [CrossRef]
- Xiong, W.; Hedström, P.; Selleby, M. An improved thermodynamic modeling of the Fe-Cr system down to zero Kelvin coupled with key experiments. Calphad 2011, 35, 355–366. [Google Scholar] [CrossRef]
- Pareige, C.; Roussel, M.; Novy, S.; Kuksenko, V.; Olsson, P.; Domain, C.; Pareige, P. Kinetic study of phase transformation in a highly concentrated Fe-Cr alloy: Monte Carlo simulation versus experiments. Acta Mater. 2011, 59, 2404–2411. [Google Scholar] [CrossRef]
- Miller, M.K.; Hyde, J.M.; Hetherington, M.G.; Cerezo, A.; Smith, G.D.W.; Elliott, C.M. Spinodal decomposition in Fe-Cr alloys: Experimental study at the atomic level and comparison with computer models—I. introduction and methodology. Acta Metall. Mater. 1995, 43, 3385–3401. [Google Scholar] [CrossRef]
- Hyde, J.M.; Miller, M.K.; Hetherington, M.G.; Cerezo, A.; Smith, G.D.W.; Elliott, C.M. Spinodal decomposition in Fe-Cr Alloys: Experimental study at the atomic level and comparison with computer models—II. development of domain size and composition amplitude. Acta Metall. Mater. 1995, 43, 3403–3413. [Google Scholar] [CrossRef]
- Hyde, J.M.; Miller, M.K.; Hetherington, M.G.; Cerezo, A.; Smith, G.D.W.; Elliott, C.M. Spinodal decomposition in Fe-Cr alloys: Experimental study at the atomic level and comparison with computer models—III. development of morphology. Acta Metall. Mater. 1995, 43, 3415–3426. [Google Scholar] [CrossRef]
- Lifshitz, I.M.; Slyozov, V.V. The kinetics of precipitation from supersaturated solid solutions. J. Phys. Chem. Solids 1961, 19, 35–50. [Google Scholar] [CrossRef]
- Wagner, C. Theorie der alterung von niederschägen durch umlösen (Ostwald-Reifung). Z. Electrochem. 1961, 65, 581–591. [Google Scholar]
- Rogers, T.M.; Elder, K.R.; Desai, R.C. Numerical study of the late stages of spinodal decomposition. Phys. Rev. B 1988, 37, 9638. [Google Scholar] [CrossRef]
- Liu, W.; Li, Y.S.; Wu, X.C.; Hou, Z.Y.; Hu, K. Phase-field simulation of the separation kinetics of a nanoscale phase in a Fe-Cr alloy. J. Mater. Eng. Perform. 2016, 25, 1924–1930. [Google Scholar] [CrossRef]
- Steinbach, I. Phase-field models in materials science. Model. Simul. Mater. Sci. Eng. 2009, 17, 073001. [Google Scholar] [CrossRef]
- Yeddu, H.K.; Malik, A.; Ågren, J.; Amberg, G.; Borgenstam, A. Three-dimensional phase-field modeling of martensitic microstructure evolution in steels. Acta Mater. 2012, 60, 1538–1547. [Google Scholar] [CrossRef]
- Cahn, J.W. On spinodal decomposition. Acta Metall. 1961, 9, 795–801. [Google Scholar] [CrossRef]
- Mohanty, R.R.; Guyer, J.E.; Sohn, Y.H. Diffusion under temperature gradient: A phase-field model study. J. Appl. Phys. 2009, 6, 034912. [Google Scholar] [CrossRef]
- Andersson, J.O.; Ågren, J. Models for numerical treatment of multicomponent diffusion in simple phases. J. Appl. Phys. 1992, 72, 1350–1355. [Google Scholar] [CrossRef]
- Japan Institute of Metals. Metals Data Book; Maruzen: Tokyo, Japan, 1993. [Google Scholar]
- Koyama, T.; Onodera, H. Modeling of microstructure changes in Fe-Cr-Co magnetic alloy using the phase-field method. J. Phase Equilib. Diffus. 2006, 27, 22–29. [Google Scholar] [CrossRef]
- Moelans, N. A quantitative and thermodynamically consistent phase-field interpolation function for multi-phase systems. Acta Mater. 2011, 59, 1077–1086. [Google Scholar] [CrossRef]
- Cahn, J.W. Phase separation by spinodal decomposition in isotropic system. J. Chem. Phys. 1965, 42, 93–99. [Google Scholar] [CrossRef]
- Andersson, J.O.; Sundman, B. Thermodynamic properties of the Cr-Fe system. Calphad 1987, 11, 83–92. [Google Scholar] [CrossRef]
- Dinsdale, A.T. SGTE data for pure elements. Calphad 1991, 15, 317–425. [Google Scholar] [CrossRef]
- Miiller, F.; Kubaschewski, O. The thermodynamic properties and equilibrium diagram of the system Cr-Fe. High Temp. High Press. 1969, 1, 543–551. [Google Scholar]
- Cahn, J.W.; Hilliard, J.E. Free energy of a non-uniform system. 1. Interfacial free energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar] [CrossRef]
- Lass, E.A.; Johnson, W.C.; Shiflet, G.J. Correlation between CALPHAD data and the Cahn–Hilliard gradient energy coefficient k and exploration into its composition dependence. Calphad 2006, 30, 42–52. [Google Scholar] [CrossRef]
- Khachaturyan, A.G. Theory of Structure Transformation in Solids; John-Wiley and Sons: New York, NY, USA, 1983. [Google Scholar]
- Hu, S.Y.; Chen, L.Q. A phase-field model for evolving microstructures with strong elastic inhomogeneity. Acta Mater. 2001, 49, 1879–1890. [Google Scholar] [CrossRef]
- Zhu, J.Z.; Chen, L.Q. Coarsening kinetics from a variable-mobility Cahn-Hilliard equation: Application of a semi-implicit Fourier spectral method. Phys. Rev. E 1999, 60, 3564. [Google Scholar] [CrossRef]
- Zhu, J.Z. Phase-Field Modeling Microstructural Evolution and Properties. Ph.D. Thesis, Pennsylvania State University, State College, PA, USA, 2002. [Google Scholar]
- Brandes, E.A.; Brook, G.B. Smithells Metals Reference Book, 7th ed.; Butterworth-Heinemann: Oxford, UK, 1992. [Google Scholar]
- Dever, D.J. Temperature dependence of the elastic constants in α-iron single crystals: Relationship to spin order and diffusion anomalies. J. Appl. Phys. 1972, 43, 3293–3301. [Google Scholar] [CrossRef]
- Katahara, K.; Nimalendran, M.; Manghnani, M.H.; Fisher, E.S. Elastic moduli of paramagnetic chromium and Ti-V-Cr alloys. J. Phys. F 1979, 9, 2167–2176. [Google Scholar] [CrossRef]
- Li, Y.L.; Hu, S.Y.; Zhang, L.; Sun, X. Non-classical nuclei and growth kinetics of Cr precipitates in FeCr alloys during ageing. Model. Simul. Mater. Sci. Eng. 2014, 22, 025002. [Google Scholar] [CrossRef]
- Heo, T.W.; Zhang, L.; Du, Q.; Chen, L.Q. Incorporating diffuse-interface nuclei in phase-field simulations. Scr. Mater. 2010, 63, 8–11. [Google Scholar] [CrossRef]
- Zhang, L.; Ren, W.Q.; Samanta, A.; Du, Q. Recent developments in computational modelling of nucleation in phase transformations. NPJ Comput. Mater. 2016, 2, 16003. [Google Scholar] [CrossRef]
- Lopez-Hirata, V.M.; Soriano-Vargas, O.; Rosales-Dorantes, H.J.; Saucedo-Muñoz, M.L. Phase decomposition in an Fe-40 at.% Cr alloy after isothermal aging and its effect on hardening. Mater. Charact. 2011, 62, 789–792. [Google Scholar] [CrossRef]
- Mao, Z.G.; Sudbrack, C.K.; Yoon, K.E.; Martin, G.; Seidman, D.N. The mechanism of morphogenesis in a phase-separating concentrated multicomponent alloy. Nat. Mater. 2007, 6, 210–216. [Google Scholar] [CrossRef] [PubMed]
- Brenner, S.S.; Miller, M.K.; Sofia, W.A. Spinodal decomposition of iron-32 at.% chromium at 470 °C. Scr. Metall. 1982, 16, 831–836. [Google Scholar] [CrossRef]
- Bley, F. Neutron small-angle scattering study of unmixing in Fe-Cr alloys. Acta. Metall. Mater. 1992, 40, 1505–1517. [Google Scholar] [CrossRef]
- Lasalle, J.C.; Schwartz, L.H. Further studies of spinodal decomposition in Fe-Cr. Acta Metall. 1986, 34, 989–1000. [Google Scholar] [CrossRef]
- Yan, Z.L.; Li, Y.S.; Zhou, X.R.; Zhang, Y.D.; Hu, R. Evolution of nanoscale Cr-rich phase in a Fe-35 at.% Cr alloy during isothermal aging. J. Alloys Compd. 2017, 725, 1035–1043. [Google Scholar] [CrossRef]
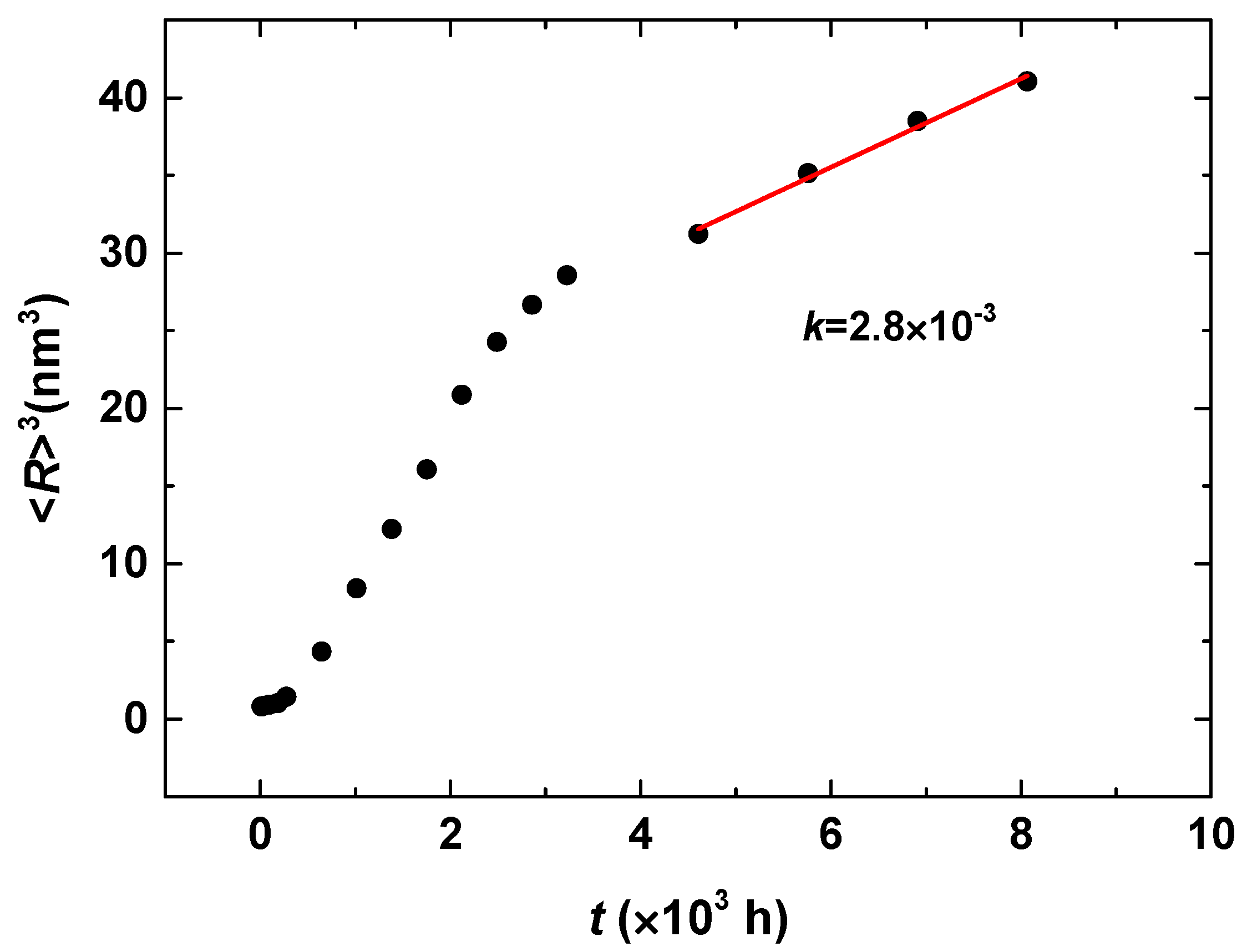
| Cr (at %) | 25 | 30 | 33 |
|---|---|---|---|
| k | 2.8 × 10−3 | 1.7 × 10−2 | 2.1 × 10−2 |
| n | 0.16 | 0.18 | 0.18 |
| m | −0.46 | −0.49 | −0.48 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Zhu, L.; Liu, C.; Shi, S. Nanoscale Phase Evolution during Continuum Decomposition of Fe-Cr Alloys. Materials 2017, 10, 1431. https://doi.org/10.3390/ma10121431
Li Y, Zhu L, Liu C, Shi S. Nanoscale Phase Evolution during Continuum Decomposition of Fe-Cr Alloys. Materials. 2017; 10(12):1431. https://doi.org/10.3390/ma10121431
Chicago/Turabian StyleLi, Yongsheng, Lihui Zhu, Chengwei Liu, and Shujing Shi. 2017. "Nanoscale Phase Evolution during Continuum Decomposition of Fe-Cr Alloys" Materials 10, no. 12: 1431. https://doi.org/10.3390/ma10121431
APA StyleLi, Y., Zhu, L., Liu, C., & Shi, S. (2017). Nanoscale Phase Evolution during Continuum Decomposition of Fe-Cr Alloys. Materials, 10(12), 1431. https://doi.org/10.3390/ma10121431





