Optically Controllable Linear-Polarization Rotator Using Chiral-Azobenzene-Doped Liquid Crystals
Abstract
1. Introduction
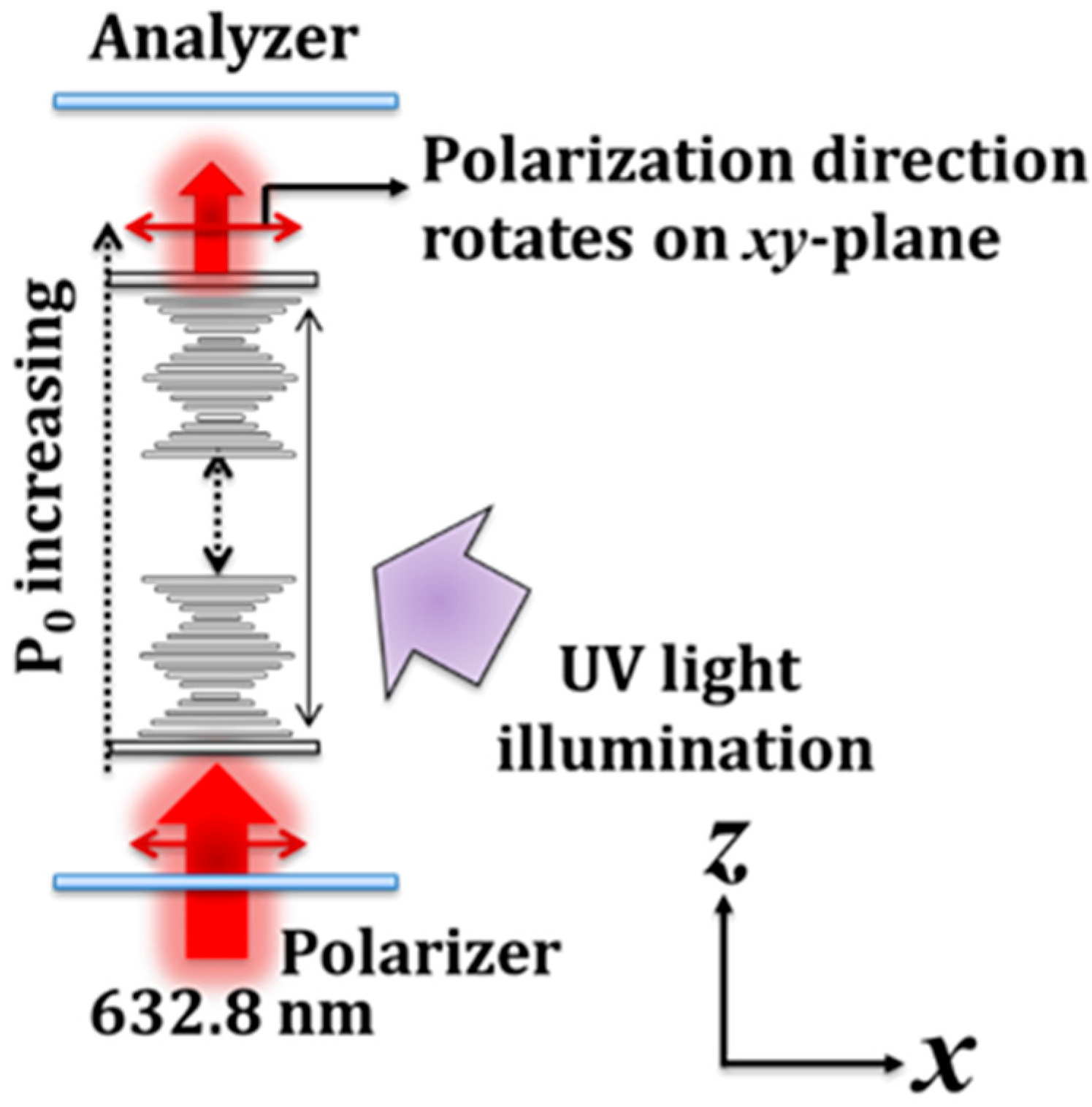
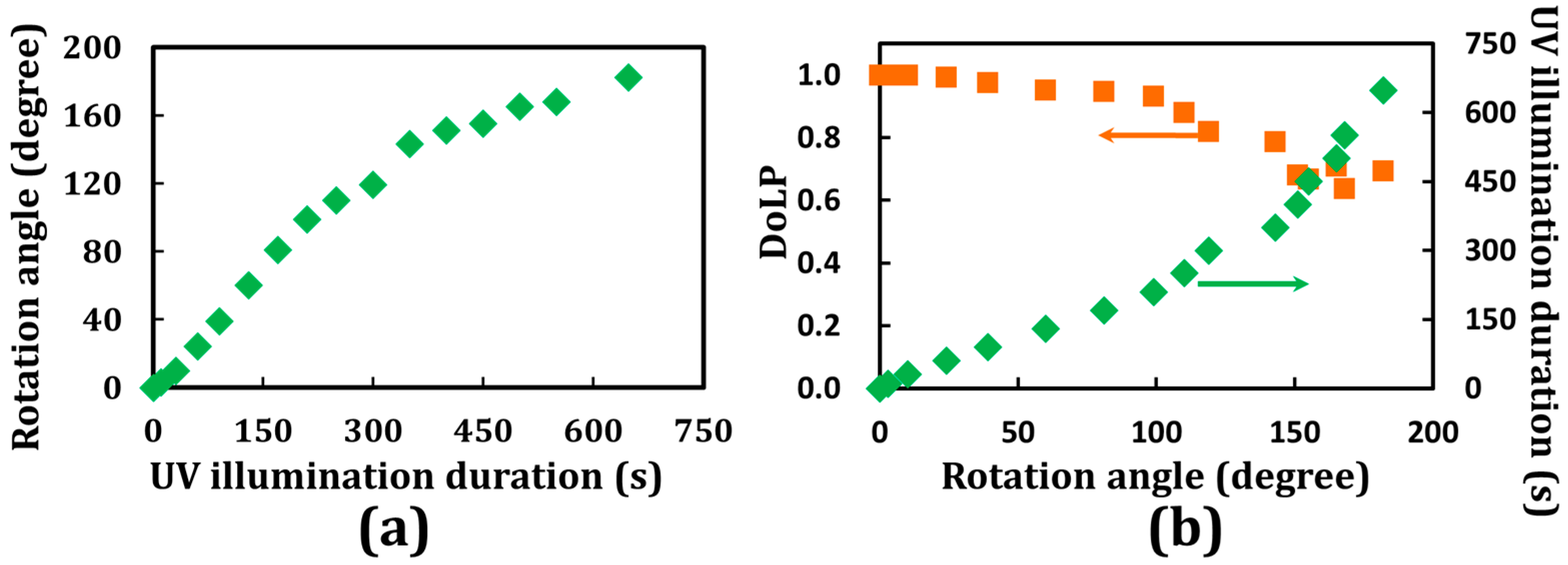
2. Materials and Methods
3. Discussions
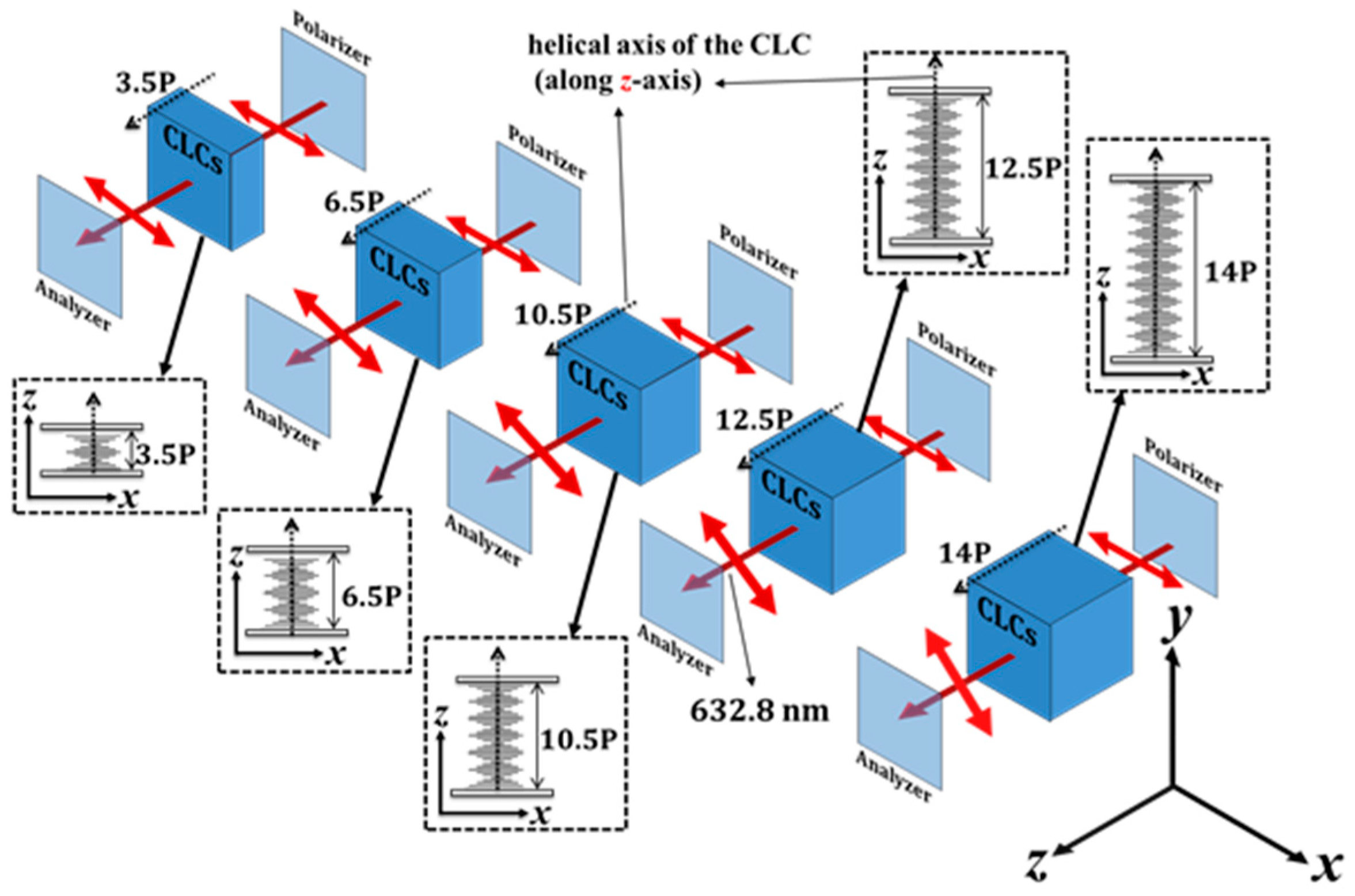
3.1. Effect of Changing the Number of Turns of the Helix on the Polarization Rotation Characteristics of CLCDs
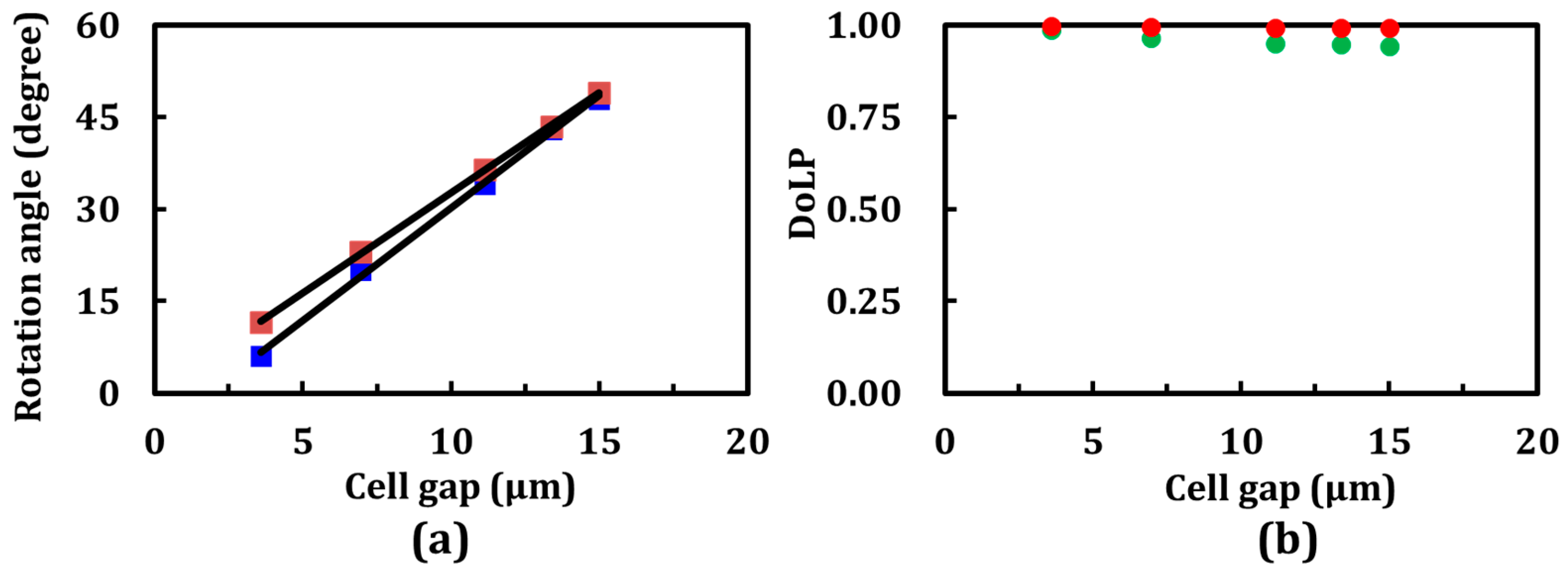
3.2. Effect of the Pitch on the Polarization Rotation Characteristics of CLCs
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wu, S.T.; Yang, D.K. Reflective Liquid Crystal Displays; Wiley: Chichester, UK, 2011. [Google Scholar]
- Coates, D. Development and applications of cholesteric liquid crystals. Liq. Cryst. 2015, 42, 653–665. [Google Scholar] [CrossRef]
- Podolskyy, D.; Banji, O.; Rudquist, P. Simple method for accurate measurements of the cholesteric pitch using a “stripe–wedge” Grandjean–Cano cell. Liq. Cryst. 2008, 7, 789–791. [Google Scholar] [CrossRef]
- Morris, S.M.; Ford, A.D.; Coles, H.J. Removing the discontinuous shift in emission wavelength of a chiral nematic liquid crystal laser. J. Appl. Phys. 2009, 106, 023112. [Google Scholar] [CrossRef]
- Funamoto, K.; Ozaki, M.; Yoshino, K. Discontinuous shift of lasing wavelength with temperature in cholesteric liquid crystal. Jpn. J. Appl. Phys. 2003, 42, L1523–L1525. [Google Scholar] [CrossRef]
- Coles, H.J.; Morris, S.M. Liquid-crystal lasers. Nat. Photonics 2010, 4, 676–685. [Google Scholar] [CrossRef]
- Zink, H.; Belyakov, V.A. Temperature hysteresis of the change in the cholesteric pitch and surface anchoring in thin planar layers. J. Exp. Theor. Phys. 1997, 85, 285–291. [Google Scholar] [CrossRef]
- Belyakov, V.A.; Kats, E.I. Surface anchoring and temperature variations of the pitch in thin cholesteric layers. J. Exp. Theor. Phys. 2000, 91, 488–496. [Google Scholar] [CrossRef]
- Belyakov, V.A.; Oswald, P.; Kats, E.I. Temperature pitch variations in planar cholesteric layers: The role of fluctuations and surface anchoring. J. Exp. Theor. Phys. 2003, 96, 915–921. [Google Scholar] [CrossRef]
- Belyakov, V.A.; Stewart, I.W.; Osipov, M.A. Dynamics of jump wise temperature pitch variations in planar cholesteric layers for a finite strength of surface anchoring. J. Exp. Theor. Phys. 2004, 99, 73–82. [Google Scholar] [CrossRef]
- Liu, C.K.; Huang, W.L.; Fuh, A.Y.G.; Cheng, K.T. Binary cholesteric/blue-phase liquid crystal textures fabricated using phototunable chirality in azo chiral-doped cholesteric liquid crystals. J. Appl. Phys. 2012, 111, 103114. [Google Scholar] [CrossRef]
- Liu, J.H.; Yang, P.C.; Hung, H.J.; Liaw, D.J. Photochemical tuning capability of cholesteric liquid crystal cells containing chiral dopants end capped with menthyl groups. Liq. Cryst. 2007, 34, 891–902. [Google Scholar] [CrossRef]
- Li, Q.; Green, L.; Venkataraman, N.; Shiyanovskaya, I.; Khan, A.; Urbas, A.; Doane, J.W. Reversible photoswitchable axially chiral dopants with high helical twisting power. J. Am. Chem. Soc. 2007, 129, 12908–12909. [Google Scholar] [CrossRef] [PubMed]
- White, T.J.; Bricker, R.L.; Natarajan, V.; Tabiryan, N.V.; Green, L.; Li, Q.; Bunning, T.J. Phototunable azobenzene cholesteric liquid crystals with 2000 nm range. Adv. Funct. Mater. 2009, 19, 3484–3488. [Google Scholar] [CrossRef]
- White, T.J.; Cazzell, S.A.; Freer, A.S.; Yang, D.K.; Sukhomlinova, L.; Su, L.L.; Kosa, T.; Taheri, B.; Bunning, T.J. Widely Tunable, Photoinvertible Cholesteric Liquid Crystals. Adv. Mater. 2011, 23, 1389–1392. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Luo, F.; Luo, Y.; Li, J.; Liu, C.; Liu, H.; Shen, Z.; Wang, W. Cholesteric liquid crystal depolarizer. Opt. Eng. 2007, 46, 070504. [Google Scholar] [CrossRef]
- Duarte, F.J. Tunable Laser Optics; CRC: Boca Raton, FL, USA, 2015. [Google Scholar]
- Hecht, E. Optics; Addison Wesley: San Francisco, CA, USA, 2002. [Google Scholar]
- Masson, J.B.; Gallot, G. Terahertz achromatic quarter-wave plate. Opt. Lett. 2006, 31, 265–267. [Google Scholar] [CrossRef] [PubMed]
- Gunyakov, V.A.; Timofeev, I.V.; Krakhalev, M.N.; Zyryanov, V.Y. Polarization exchange of optical eigenmode pair in twisted-nematic Fabry-Pérot resonator. Phys. Rev. E 2017, 96, 22711. [Google Scholar] [CrossRef] [PubMed]
- Ting, C.L.; Lin, T.H.; Liao, C.C.; Fuh, A.Y.G. Optical simulation of cholesteric liquid crystal displays using the finite-difference time-domain method. Opt. Express 2006, 14, 5594. [Google Scholar] [CrossRef] [PubMed]
- Yeh, P.; Gu, C. Optics of Liquid Crystals Displays; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Lin, J.D.; Hsieh, M.H.; Wei, G.J.; Mo, T.S.; Huang, S.Y.; Lee, C.R. Optically tunable/switchable omnidirectionally spherical microlaser based on a dye-doped cholesteric liquid crystal microdroplet with an azo-chiral dopant. Opt. Express 2013, 21, 15765–15776. [Google Scholar] [CrossRef] [PubMed]
- Fuh, A.Y.G.; Wu, Z.H.; Cheng, K.T.; Liu, C.K.; Chen, Y.D. Direct optical switching of bistable cholesteric textures in chiral azobenzene-doped liquid crystals. Opt. Express 2013, 21, 21840–21846. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.J.; Lin, J.D.; Lee, C.R. Optically stable and tunable quantum dot nanocrystals embedded cholesteric liquid crystal composite laser. J. Mater. Chem. C 2014, 2, 4388–4394. [Google Scholar] [CrossRef]
- Huang, T.C.; Chen, Y.Y.; Chu, C.C.; Hsiao, V.K.S. Optothermal Switching of Cholesteric Liquid Crystals: A Study of Azobenzene Derivatives and Laser Wavelengths. Materials 2015, 8, 6071–6084. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Yang, D.K. Dual frequency cholesteric light shutters. Appl. Phys. Lett. 1997, 70, 720–722. [Google Scholar] [CrossRef]
- Sutormin, V.S.; Timofeev, I.V.; Krakhalev, M.N.; Prishchepa, O.O.; Zyryanov, V.Y. Orientational transition in the cholesteric layer induced by electrically controlled ionic modification of the surface anchoring. Liq. Cryst. 2017, 44, 484–489. [Google Scholar] [CrossRef]
- Xiang, J.; Li, Y.; Li, Q.; Paterson, D.A.; Storey, J.M.D.; Imrie, C.T.; Lavrentovich, O.D. Electrically tunable selective reflection of light from ultraviolet to visible and infrared by heliconical cholesterics. Adv. Mater. 2015, 27, 3014–3018. [Google Scholar] [CrossRef] [PubMed]
- Xianyu, H.; Faris, S.; Crawford, G.P. In-plane switching of cholesteric liquid crystals for visible and near-infrared applications. Appl. Opt. 2004, 43, 5006–5015. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.K.; Chien, L.C.; Doane, J.W. Cholesteric liquid crystal/polymer dispersion for haze-free light shutter. Appl. Phys. Lett. 1992, 60, 3102–3104. [Google Scholar] [CrossRef]
- Liu, C.K.; Cheng, K.T.; Fuh, A.Y.G. Observation of anisotropically reflected colors in chiral monomer doped cholesteric liquid crystals. Appl. Phys. Lett. 2011, 98, 041106. [Google Scholar] [CrossRef]
- Lua, S.Y.; Chien, L.C. A polymer-stabilized single-layer color cholesteric liquid crystal display with anisotropic reflection. Appl. Phys. Lett. 2007, 91, 131119. [Google Scholar] [CrossRef]
- Cheng, K.T.; Liu, C.K.; Ting, C.L.; Fuh, A.Y.G. Optical Addressing in Dye-Doped Cholesteric Liquid Crystals. Opt. Commun. 2008, 281, 5133–5139. [Google Scholar] [CrossRef]
- Yang, D.K.; Mi, X.D. Modelling of the reflection of cholesteric liquid crystals using the Jones matrix. J. Phys. D Appl. Phys. 2000, 33, 672–676. [Google Scholar] [CrossRef]
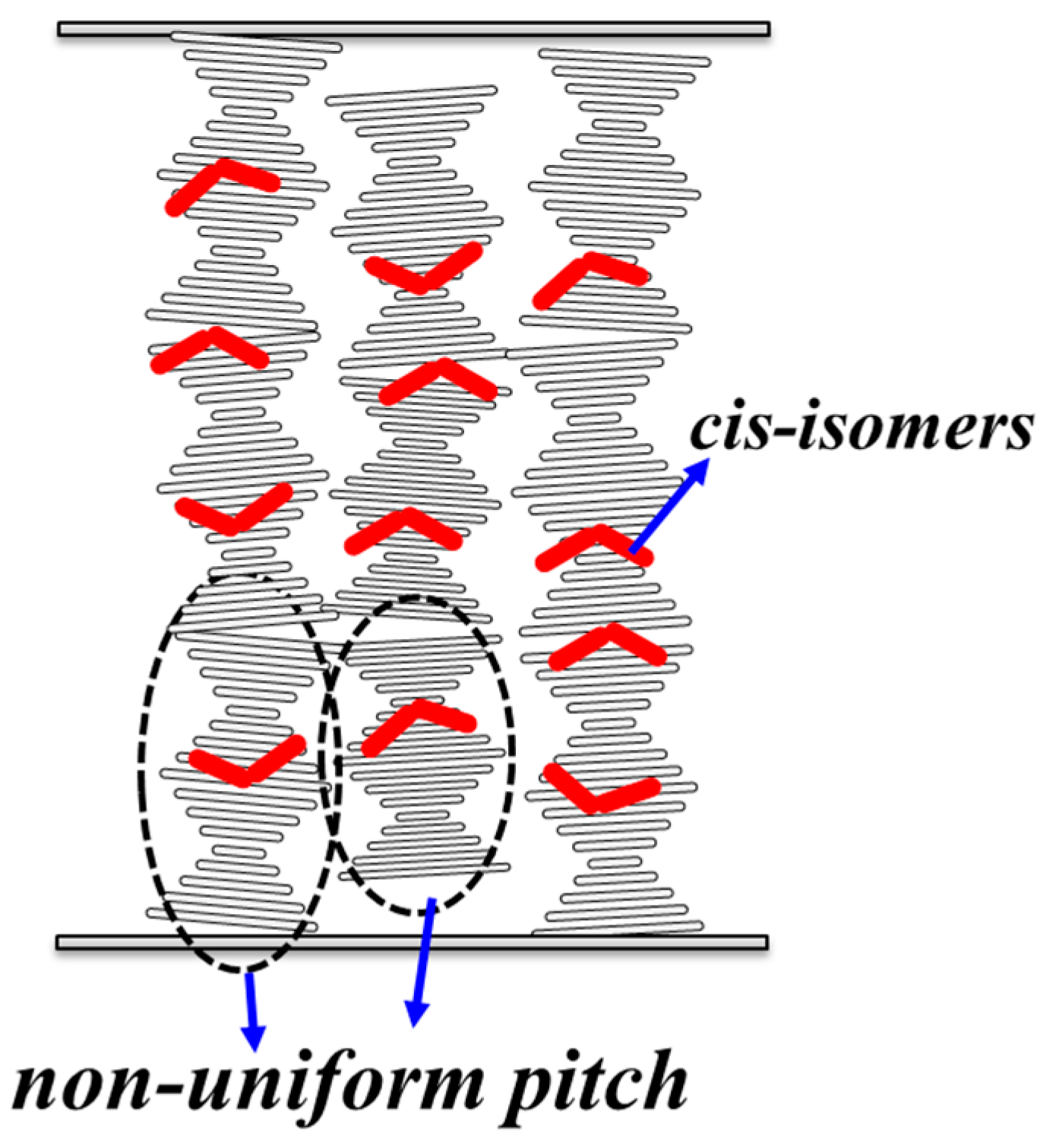
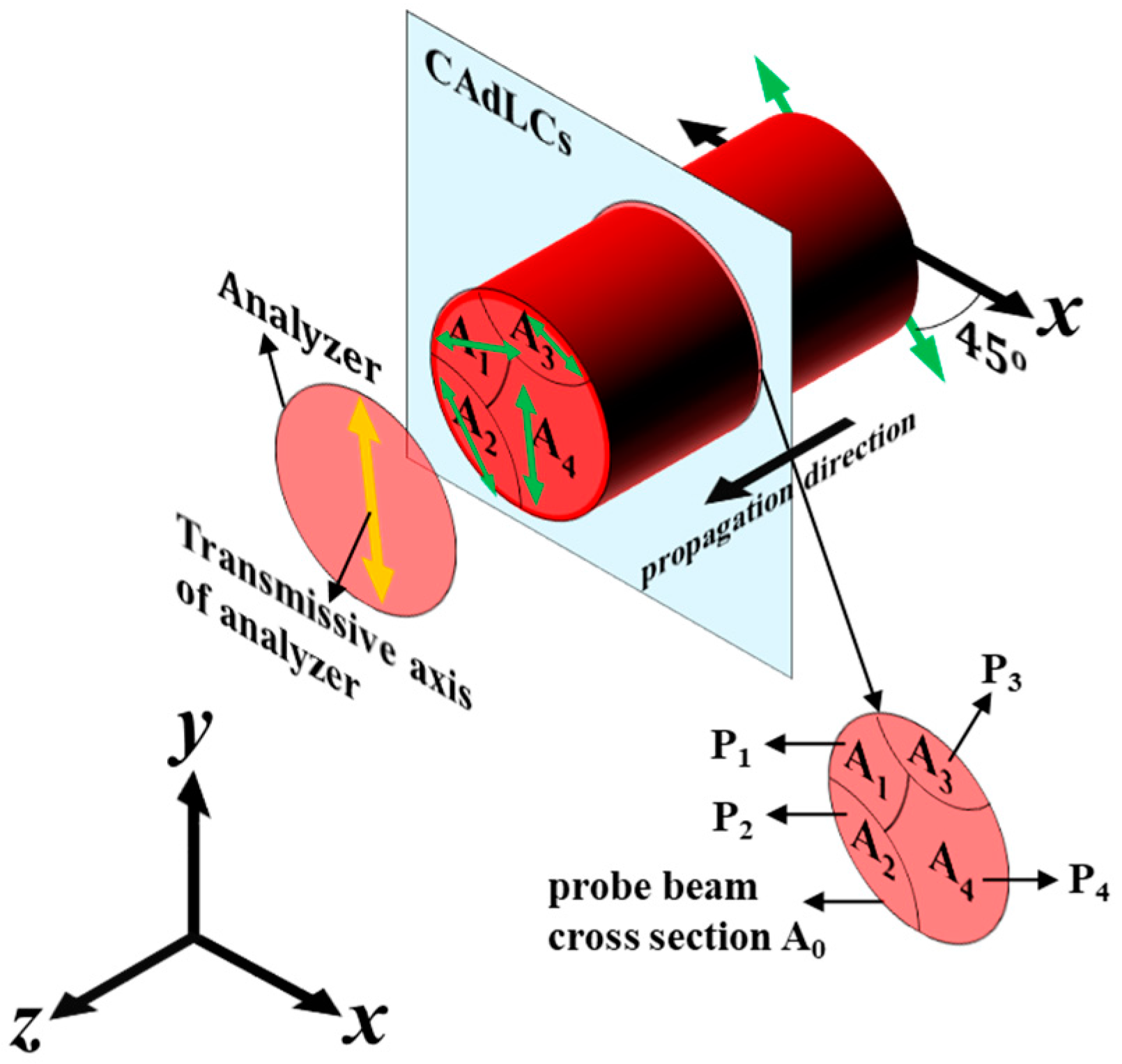

| UV Illumination Duration, t | Cell Gap Parameter, α |
|---|---|
| t = 2 (s) | α = k(2)[P(2) + β(2)] = 15 μm |
| t = 30 (s) | α = k(30)[P(30) + β(30)] = 15 μm |
| t = 60 (s) | α= k(60)[P(60) + β(60)] = 15 μm |
| UV Illumination Duration, t | Relationship of (t), k(t), and P(t) | Description |
|---|---|---|
| t = 2, 30, and 60 (s) | ϕ(60) > ϕ(30) > ϕ(2) | ϕ(t) increases with time, t |
| k(60) < k(30) < k(2) | k(t) decreases with time, t | |
| P(60) > P(30) > P(2) | P(t) increases with time, t |
| Pitch of 1 μm | ||||||||||
| Number of Turns of the Helix | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| DoLP | 0.999 | 0.997 | 0.995 | 0.993 | 0.990 | 0.988 | 0.987 | 0.987 | 0.987 | 0.988 |
| Pitch of 3 μm | ||||||||||
| Number of Turns of the Helix | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| DoLP | 0.883 | 0.997 | 0.904 | 0.989 | 0.908 | 0.975 | 0.923 | 0.968 | 0.925 | 0.949 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.-K.; Chiu, C.-Y.; Morris, S.M.; Tsai, M.-C.; Chen, C.-C.; Cheng, K.-T. Optically Controllable Linear-Polarization Rotator Using Chiral-Azobenzene-Doped Liquid Crystals. Materials 2017, 10, 1299. https://doi.org/10.3390/ma10111299
Liu C-K, Chiu C-Y, Morris SM, Tsai M-C, Chen C-C, Cheng K-T. Optically Controllable Linear-Polarization Rotator Using Chiral-Azobenzene-Doped Liquid Crystals. Materials. 2017; 10(11):1299. https://doi.org/10.3390/ma10111299
Chicago/Turabian StyleLiu, Cheng-Kai, Chian-Yu Chiu, Stephen M. Morris, Min-Cheng Tsai, Chii-Chang Chen, and Ko-Ting Cheng. 2017. "Optically Controllable Linear-Polarization Rotator Using Chiral-Azobenzene-Doped Liquid Crystals" Materials 10, no. 11: 1299. https://doi.org/10.3390/ma10111299
APA StyleLiu, C.-K., Chiu, C.-Y., Morris, S. M., Tsai, M.-C., Chen, C.-C., & Cheng, K.-T. (2017). Optically Controllable Linear-Polarization Rotator Using Chiral-Azobenzene-Doped Liquid Crystals. Materials, 10(11), 1299. https://doi.org/10.3390/ma10111299







