Dynamic Fracture Behavior of Steel Fiber Reinforced Self-Compacting Concretes (SFRSCCs)
Abstract
:1. Introduction
2. Experimental Procedure
2.1. Material Characterization
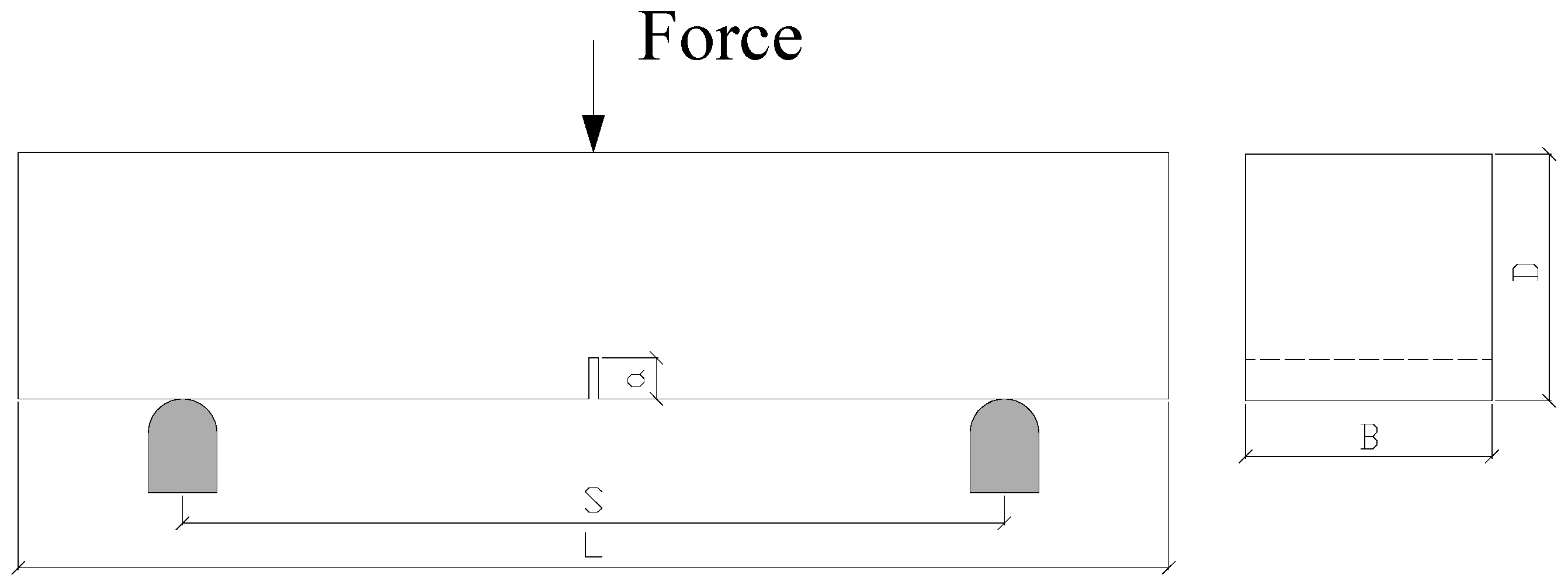
2.2. Three-Point Bending Tests
2.2.1. Tests under Low Loading Rates Ranging from 10−3 to 101 mm/s
2.2.2. Impact Tests at a Loading Rate of 103 mm/s
2.3. Determination of Elastic Modulus by Using a Three-Point Bending Test
3. Results and Discussion
3.1. Failure Pattern and Fracture Surfaces
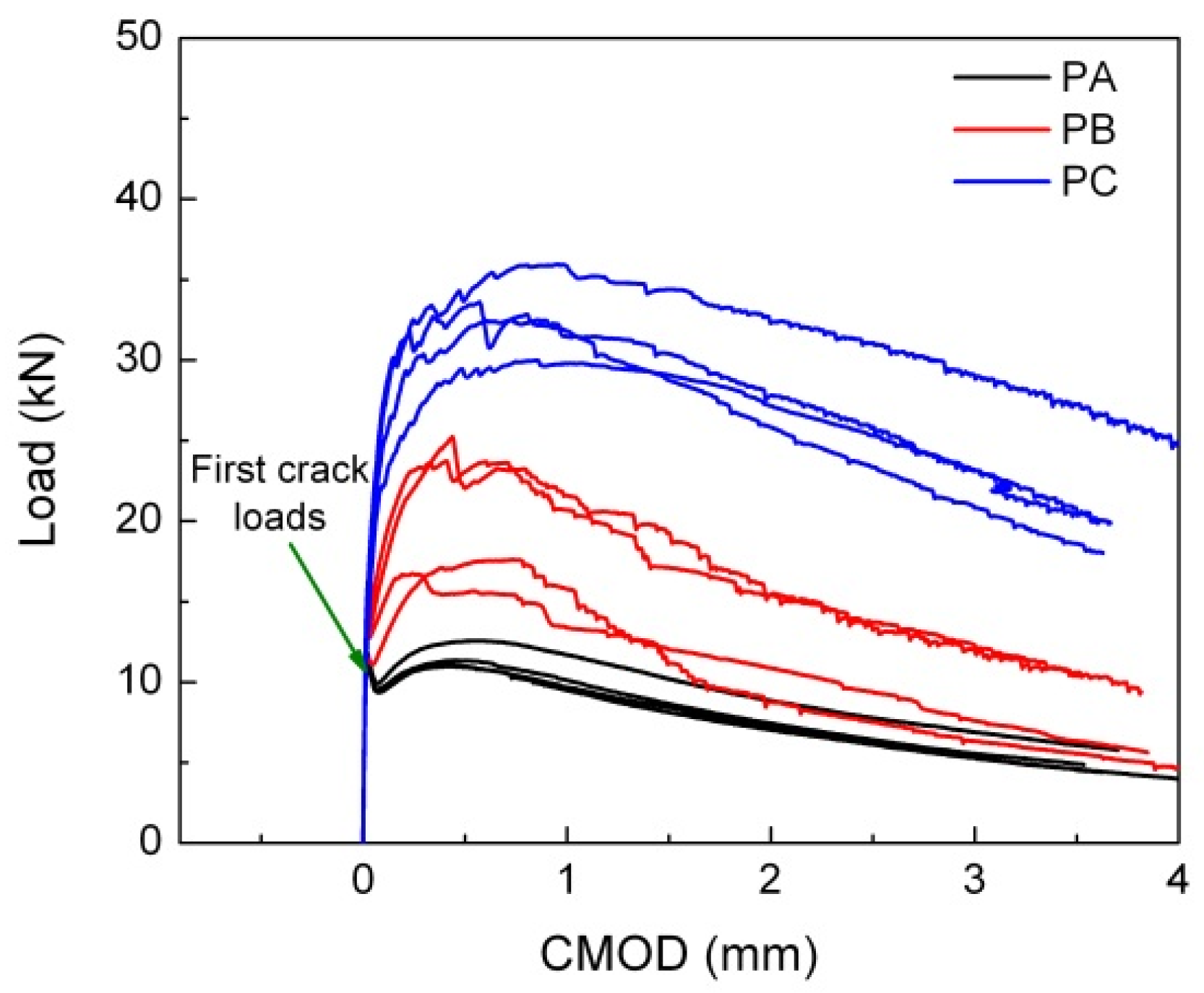
3.2. Quasi-Static Flexural Behavior
3.3. Dynamic Flexural Behavior
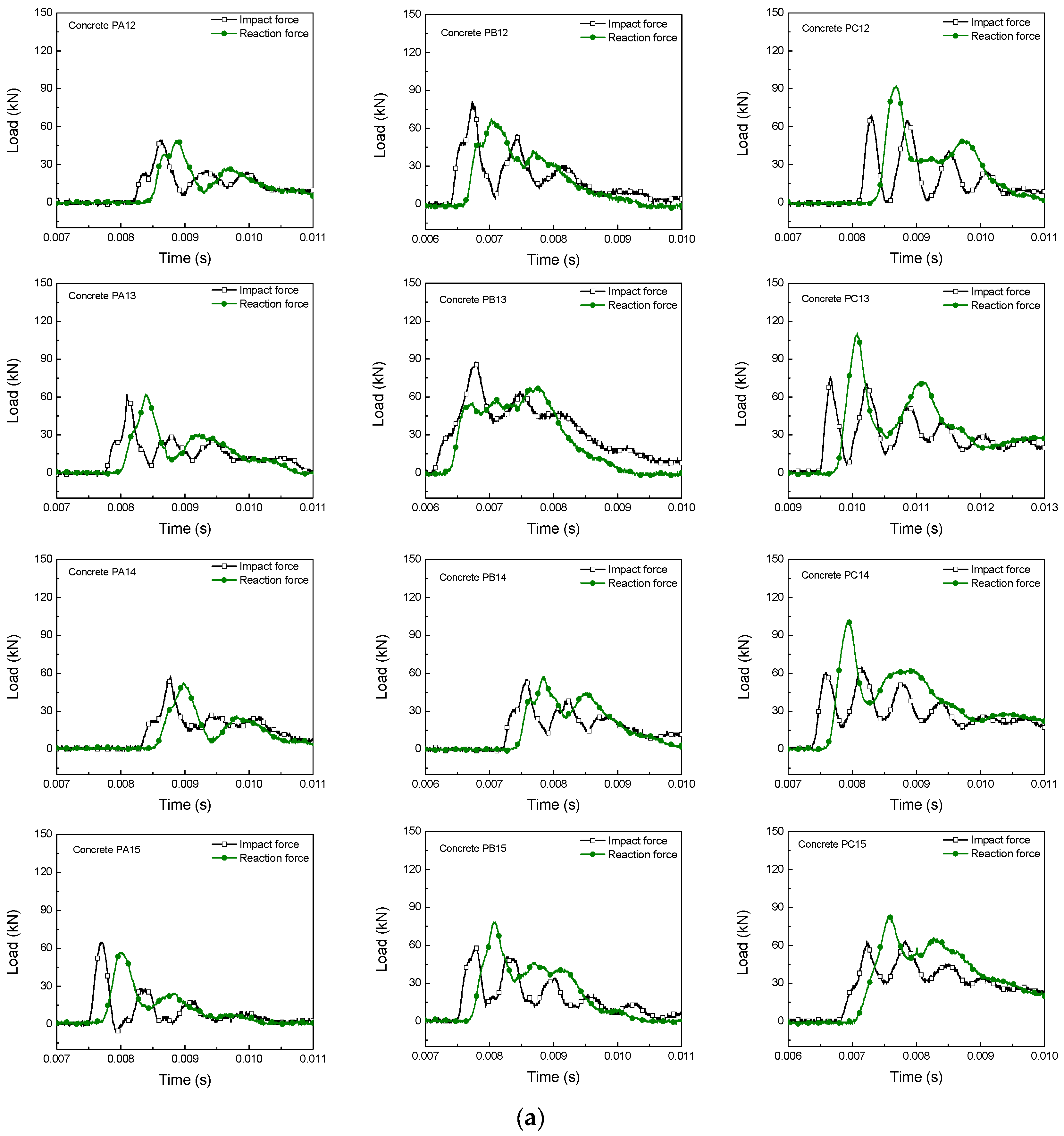
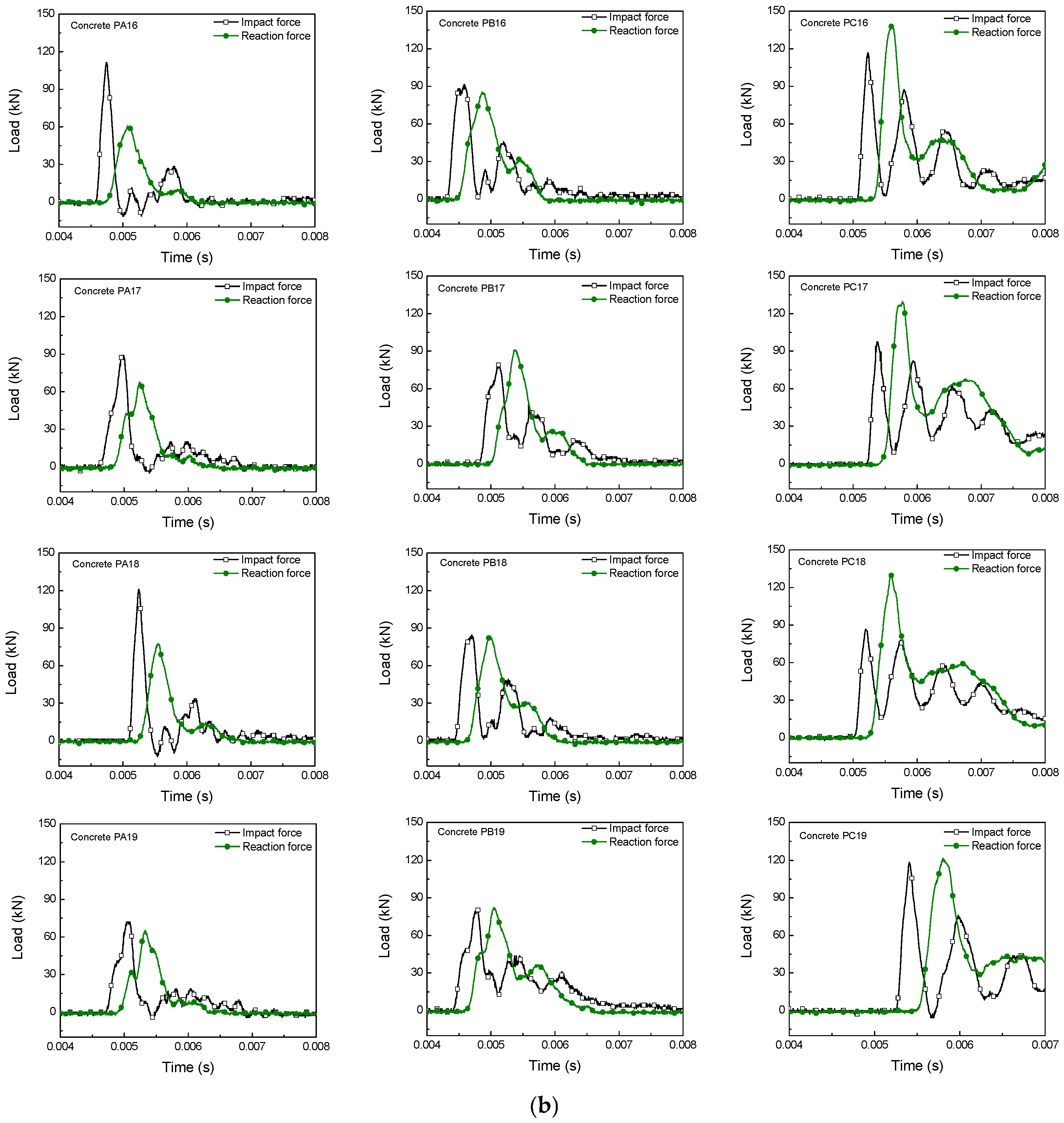
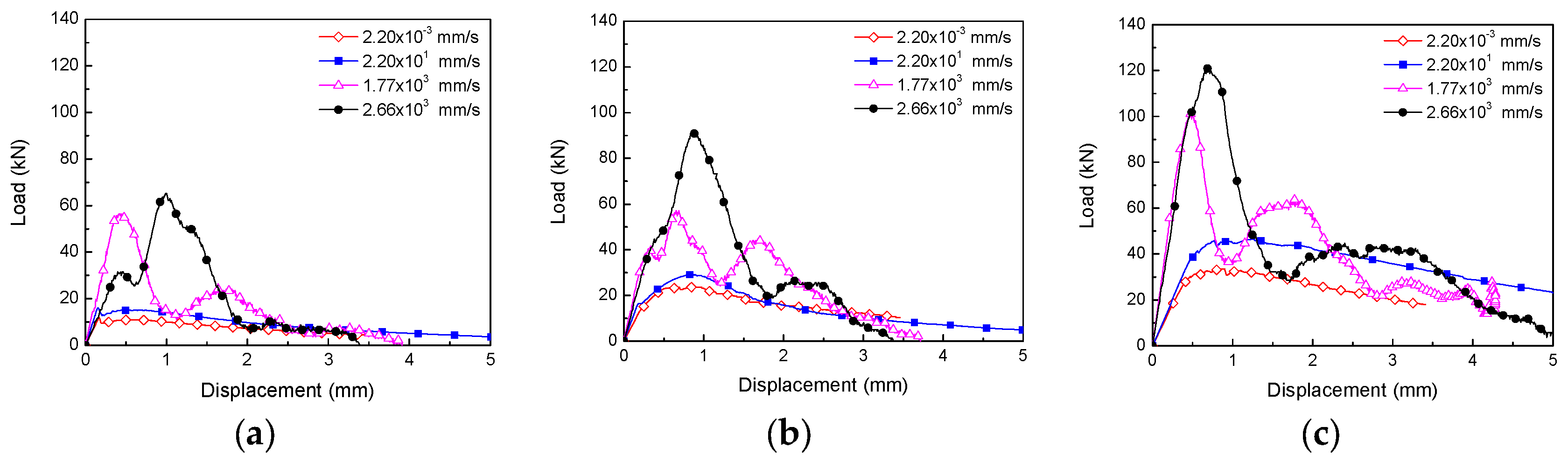
3.3.1. Load-Time and Load-Displacement Response
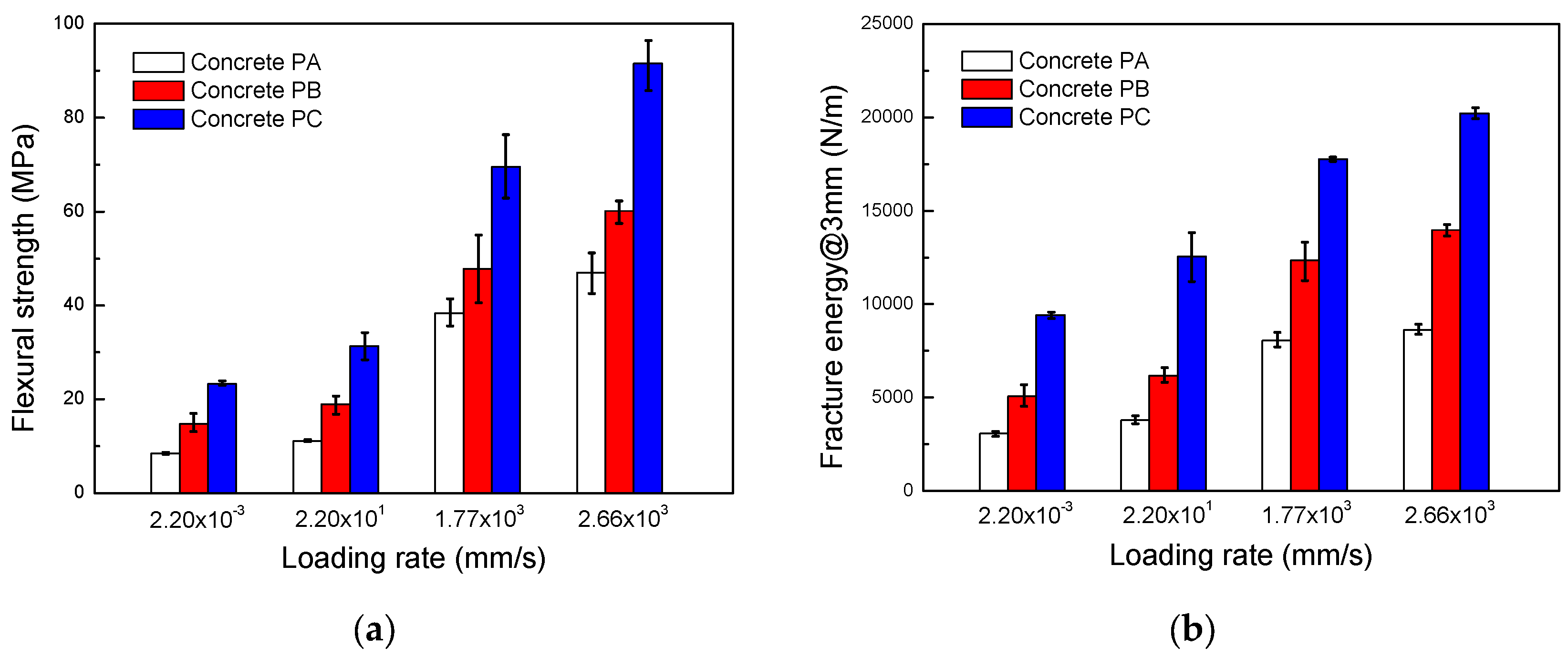
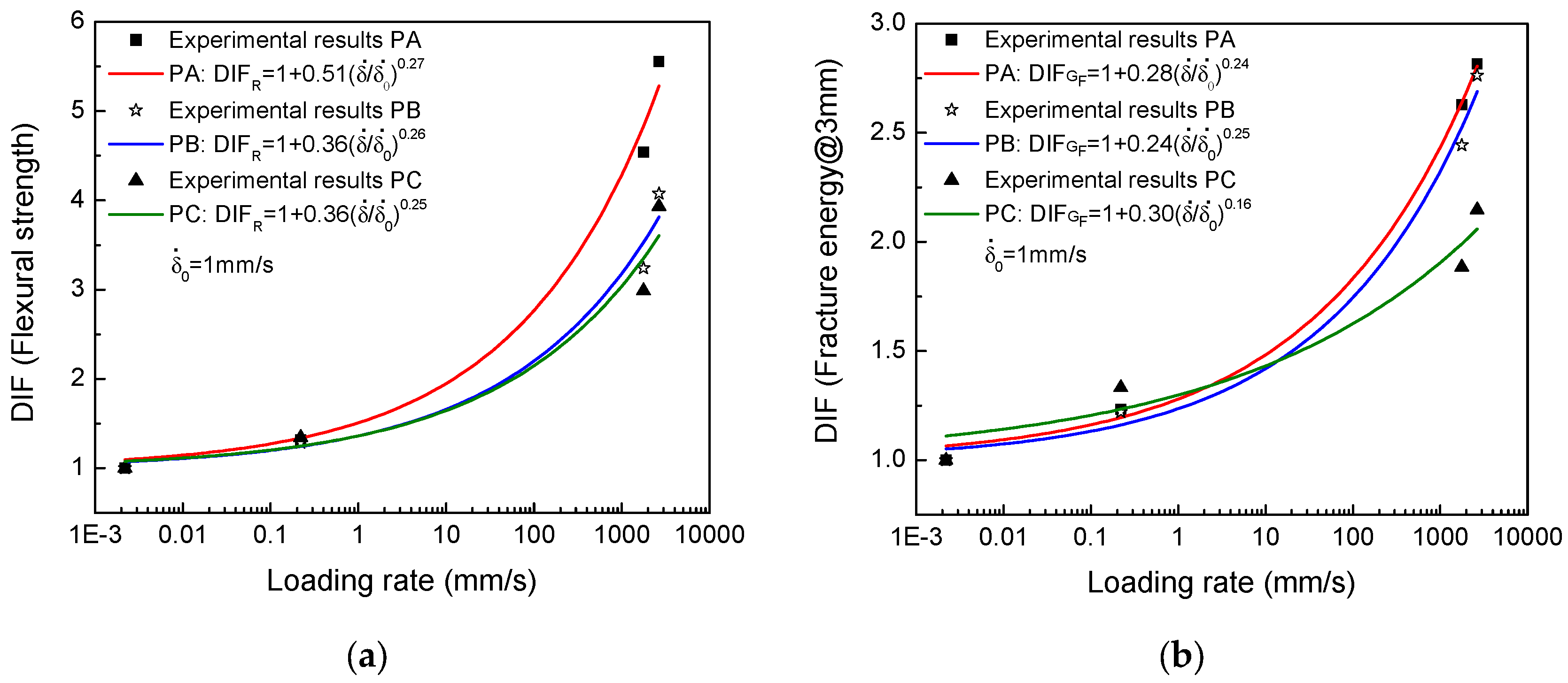
3.3.2. Loading Rate Effects on DIF
3.3.3. Equivalent Strain Rate for Various Loading Rates
3.4. Comparison with Conventional Vibrated Steel Fiber-Reinforced Concrete (CVSFRC)
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Okamura, H.; Ouchi, M. Self-compacting concrete. J. Adv. Concr. Technol. 2003, 1, 5–15. [Google Scholar] [CrossRef]
- Korte, S.; Boel, V.; De Corte, W.; De Schutter, G. Static and fatigue fracture mechanics properties of self-compacting concrete using three-point bending tests and wedge-splitting tests. Constr. Build. Mater. 2014, 57, 1–8. [Google Scholar] [CrossRef]
- Zhao, Y.; Ma, J.; Wu, Z.; Xu, S.; Gao, H. Study of fracture properties of self-compacting concrete using wedge splitting test. In Proceedings of the 1st International Symposium on Design, Performance and Use of Self-Consolidating Concrete, Changsha, China, 26–28 May 2005; Yu, Z., Shi, C., Henri, K.K., Xie, Y., Eds.; RILEM Publications SARL: Changsha, China, 2005; pp. 421–428. [Google Scholar]
- Cifuentes, H.; Karihaloo, B.L. Determination of size-independent specific fracture energy of normal- and high-strength self-compacting concrete from wedge splitting tests. Constr. Build. Mater. 2013, 48, 548–553. [Google Scholar] [CrossRef]
- Müller, H. Constitutive Modelling of High Strength/high Performance Concrete-State of the Art Report; FIB Bulletin 42: Lausanne, Switzerland, 2008. [Google Scholar]
- Ahmad, H.; Hashim, M.H.M.; Hamzah, S.H.; Bakar, A.A. Steel Fibre Reinforced Self-Compacting Concrete (SFRSC) performance in slab application: A review. In Proceedings of the 1st International Conference on Advanced Science, Engineering and Technology, Penang, Malaysia, 21–22 December 2015. [Google Scholar]
- Domone, P.L. A review of the hardened mechanical properties of self-compacting concrete. Cem. Concr. Compos. 2007, 29, 1–12. [Google Scholar] [CrossRef]
- ACI Committee. 237 ACI 237R-07: Self-Consolidating Concrete; American Concrete Institute: Farmington Hill, MI, USA, 2007; p. 34. [Google Scholar]
- Khaloo, A.; Raisi, E.M.; Hosseini, P.; Tahsiri, H. Mechanical performance of self-compacting concrete reinforced with steel fibers. Constr. Build. Mater. 2014, 51, 179–186. [Google Scholar] [CrossRef]
- Rambo, D.A.S.; Silva, F.A.; Filho, R.D.T. Flexural behavior of hybrid steel fiber reinforced self-consolidating concretes. Rev. Escola Minas 2014, 67, 27–32. [Google Scholar] [CrossRef]
- Svec, O. Flow Modelling of Steel Fibre Reinforced Self-Compacting Concrete. Ph.D. Thesis, Department of Civil Engineering, Technical University of Denmark, Lyngby, Denmark, 2014. [Google Scholar]
- Herrmann, H.; Lees, A. On the influence of the rheological boundary conditions on the fibre orientations in the production of steel fibre reinforced concrete elements. Proc. Est. Acad. Sci. 2016, 65, 408–413. [Google Scholar] [CrossRef]
- Johnston, C.D. Fiber-Reindorced Cements and Concretes (Advances in Concrete Technology), 1st ed.; Taylor & Francis: Abinggon, OX, USA, 2000; ISBN 978-9056996949. [Google Scholar]
- Tejchman, J.; Kozicki, J. Experimental and Theoretical Investigations of Steel-Fibrous Concrete; Springer: Berlin/Heidelberg, Germany, 2010; p. 280. ISBN 9783642146022. [Google Scholar]
- Eik, M.; Puttonen, J.; Herrmann, H. The effect of approximation accuracy of the orientation distribution function on the elastic properties of short fibre reinforced composites. Compos. Struct. 2016, 148, 12–18. [Google Scholar] [CrossRef]
- Barnett, S.J.; Lataste, J.F.; Parry, T.; Millard, S.G.; Soutsos, M.N. Assessment of fibre orientation in ultra high performance fibre reinforced concrete and its effect on flexural strength. Mater. Struct./Mater. Constr. 2010, 43, 1009–1023. [Google Scholar] [CrossRef]
- Herrmann, H.; Pastorelli, E.; Kallonen, A.; Suuronen, J.P. Methods for fibre orientation analysis of X-ray tomography images of steel fibre reinforced concrete (SFRC). J. Mater. Sci. 2016, 51, 3772–3783. [Google Scholar] [CrossRef]
- Laranjeira de Oliveira, F. Design-Oriented Constitutive Model for Steel Fiber Reinforced Concrete. Ph.D Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2010. [Google Scholar]
- Caverzan, A.; Cadoni, E.; Di Prisco, M. Dynamic tensile behaviour of high performance fibre reinforced cementitious composites after high temperature exposure. Mech. Mater. 2013, 59, 87–109. [Google Scholar] [CrossRef]
- Caverzan, A.; Cadoni, E.; Di Prisco, M. Dynamic tensile behaviour of self compacting steel fibre reinforced concrete. Appl. Mech. Mater. 2011, 82, 220–225. [Google Scholar] [CrossRef]
- Ding, Y.; Li, D.; Zhang, Y.; Azevedo, C. Experimental investigation on the composite effect of steel rebars and macro fibers on the impact behavior of high performance self-compacting concrete. Constr. Build. Mater. 2017, 136, 495–505. [Google Scholar] [CrossRef]
- Parant, E.; Rossi, P.; Jacquelin, E.; Boulay, C. Strain rate effect on bending behavior of new ultra-high-performance cement-based composite. ACI Mater. J. 2007, 104, 458–463. [Google Scholar]
- Soufeiani, L.; Raman, S.N.; Jumaat, M.Z.B.; Alengaram, U.J.; Ghadyani, G.; Mendis, P. Influences of the volume fraction and shape of steel fibers on fiber-reinforced concrete subjected to dynamic loading—A review. Eng. Struct. 2016, 124, 405–417. [Google Scholar] [CrossRef]
- Yoo, D.Y.; Yoon, Y.S.; Banthia, N. Flexural response of steel-fiber-reinforced concrete beams: Effects of strength, fiber content, and strain-rate. Cem. Concr. Compos. 2015, 64, 84–92. [Google Scholar] [CrossRef]
- Zhang, X.X.; Abd Elazim, A.M.; Ruiz, G.; Yu, R.C. Fracture behaviour of steel fibre-reinforced concrete at a wide range of loading rates. Int. J. Impact Eng. 2014, 71, 89–96. [Google Scholar] [CrossRef]
- Millard, S.G.; Molyneaux, T.C.K.; Barnett, S.J.; Gao, X. Dynamic enhancement of blast-resistant ultra high performance fibre-reinforced concrete under flexural and shear loading. Int. J. Impact Eng. 2010, 37, 405–413. [Google Scholar] [CrossRef]
- Zhang, X.; Ruiz, G.; Abd Elazim, A.M. Loading rate effect on crack velocities in steel fiber-reinforced concrete. Int. J. Impact Eng. 2015, 76, 60–66. [Google Scholar] [CrossRef]
- Naaman, A.E.; Gopalaratnamt, V.S. Impact properties of steel fibre reinforced concrete in bending. Int. J. Cem. Compos. Lightweight Concr. 1983, 5, 225–233. [Google Scholar] [CrossRef]
- Gopalaratnam, V.S.; Shah, S.P. Properties of steel fiber reinforced concrete subjected to impact loading. J. Am. Concr. Instit. 1986, 83, 117–126. [Google Scholar]
- Bentur, A.; Mindess, S. Fiber Reinforced Cementitious Composites, 2nd ed.; Taylor & Francis: London, UK; New York, NY, USA, 2007; p. 625. ISBN 9780415250481. [Google Scholar]
- Fakharifar, M.; Dalvand, A.; Arezoumandi, M.; Sharbatdar, M.K.; Chen, G.; Kheyroddin, A. Mechanical properties of high performance fiber reinforced cementitious composites. Constr. Build. Mater. 2014, 71, 510–520. [Google Scholar] [CrossRef]
- Caverzan, A.; Prisco, M.D.; Cadoni, E. Dynamic behaviour of HPFRCC: The influence of fibres dispersion. In Proceedings of the 11th International Conference on the Mechanical and Physical Behaviour of Materials Under Dynamic Loading, DYMAT 2015, Lugano, Switzerland, 7–11 September 2015. [Google Scholar]
- Habel, K.; Gauvreau, P. Response of ultra-high performance fiber reinforced concrete (UHPFRC) to impact and static loading. Cem. Concr. Compos. 2008, 30, 938–946. [Google Scholar] [CrossRef]
- Banthia, N. Impact resistance of HPFRCC. In Proceedings of the International RILEM Workshop on High Performance Fiber Reinforced Cementitious Composites in Structural Applications, Honolulu, HI, USA, 23–26 May 2005. [Google Scholar]
- ASTM International. C1611/C1611M, Standard Test Method for Slump Flow of Self-Consolidating Concrete; ASTM International: West Conshohocken, PA, USA, 2014; p. 6. [Google Scholar]
- Ferrara, L.; Park, Y.-D.; Shah, S.P. A method for mix-design of fiber-reinforced self-compacting concrete. Cem. Concr. Res. 2007, 37, 957–971. [Google Scholar] [CrossRef]
- ASTM International. C39/C39M, Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens; ASTM International: West Conshohocken, PA, USA, 2015; p. 7. [Google Scholar]
- ASTM International. C469/C469M, Standard Test Method for Static Modulus of Elasticity and Poisson’s Ratio of Concrete in Compression; ASTM international: West Conshohocken, PA, USA, 2014; p. 5. [Google Scholar]
- ACI Committee. 544 STATE-of-Art Report on Fiber Reinforced Concrete; Report 544.1 R-96 (Reapproved 2009); American Concrete Institute: Farmington Hills, MI, USA, 1996. [Google Scholar]
- Vandewalle, L. RILEM TC 162-TDF: Test and design methods for steel fibre reinforced concrete—Bending test. Mater. Struct./Mater. Constr. 2002, 35, 579–582. [Google Scholar] [CrossRef]
- BSI. BS EN 14651, Test Method for Metallic Fibre Concrete-Measuring the Flexural Tensile Strengh (Limit of Propportionally (LOP), Residual); BSI: London, UK, 2007; pp. 1–20. [Google Scholar]
- Zhang, X.X.; Ruiz, G.; Yu, R.C. A new drop-weight impact machine for studying fracture processes in structural concrete. Strain 2010, 46, 252–257. [Google Scholar] [CrossRef]
- Khalighi, Y.; Banthia, N. A study of FRP-concrete bond under impact. Appl. Mech. Mater. 2011, 82, 630–635. [Google Scholar] [CrossRef]
- Zhang, X.X.; Ruiz, G.; Yu, R.C.; Tarifa, M. Fracture behaviour of high-strength concrete at a wide range of loading rates. Int. J. Impact Eng. 2009, 36, 1204–1209. [Google Scholar] [CrossRef]
- Soleimani, S.M.; Banthia, N. A novel drop weight impact setup for testing reinforced concrete beams. Exp. Tech. 2014, 38, 72–79. [Google Scholar] [CrossRef]
- Sukontasukkul, P.; Nimityongskul, P.; Mindess, S. Effect of loading rate on damage of concrete. Cem. Concr. Res. 2004, 34, 2127–2134. [Google Scholar] [CrossRef]
- Tarifa, M.; Zhang, X.X.; Poveda, E.; Yu, R.C.; Ruiz, G. Contact analysis between the support and the specimen in a drop-weight impact test on concrete. An. Mec. Fract. 2012, 29, 101–106. [Google Scholar]
- RILEM TC 50-FMC Determination of the fracture energy of mortar and concrete by means of three-point bend tests on notched beams. Mater. Struct. 1985, 18, 99–101. [CrossRef]
- Guinea, G.V.; Pastor, J.Y.; Planas, J.; Elices, M. Stress intensity factor, compliance and CMOD for a general three-point-bend beam. Int. J. Fract. 1998, 89, 103–116. [Google Scholar] [CrossRef]
- Planas, J.; Guinea, G.V.; Elices, M. Stiffness associated with quasi-concentrated loads. Mater. Struct. 1994, 27, 311–318. [Google Scholar] [CrossRef]
- Ruiz, G.; Zhang, X.X.; Yu, R.C.; Porras, R.; Poveda, E.; Del Viso, J.R. Effect of loading rate on fracture energy of high-strength concrete. Strain 2011, 47, 518–524. [Google Scholar] [CrossRef]
- Kim, D.J.; El-Tawil, S.; Naaman, A.E. Loading rate effect on pullout behavior of deformed steel fibers. ACI Mater. J. 2008, 105, 576–584. [Google Scholar]
- Weerheijm, J.; Van Doormaal, J. Tensile failure of concrete at high loading rates: New test data on strength and fracture energy from instrumented spalling tests. Int. J. Impact Eng. 2007, 34, 609–626. [Google Scholar] [CrossRef]
- Vegt, I.; Breugel, V.K.; Weerheijm, J. Failure mechanisms of conrete under impact loading. In Proceedings of the Fracture Mechanics of Concrete and Concrete Structures, Catania, Italy, 17–22 June 2007; pp. 579–587. [Google Scholar]
- Weerheijm, J.; Vegt, I. How to determine the dynamic fracture energy of concrete. Theoretical considerations and experimental evidence. Appl. Mech. Mater. 2011, 82, 51–56. [Google Scholar] [CrossRef]
- Banthia, N.; Trottier, J.-F. Deformed steel fiber-cementitious matrix bond under impact. Cem. Concr. Res. 1991, 21, 158–168. [Google Scholar] [CrossRef]
- Zhang, X.X.; Ruiz, G.; Yu, R.C. Experimental study of combined size and strain rate effects on the fracture of reinforced concrete. J. Mater. Civ. Eng. 2008, 20, 544–551. [Google Scholar] [CrossRef]



| Concrete Type | Smooth Short Fibers Dramix OL 13/0.20 (kg/m3) | Hooked-End Long Fibers Dramix RC 80/30 BP (kg/m3) | Fiber Volume Ratio | Values of Slump Flow Tests (mm) |
|---|---|---|---|---|
| PA | 40 | - | 0.51% | 700 |
| PB | 40 | 20 | 0.77% | 665 |
| PC | 40 | 60 | 1.23% | 570 |
| Concrete Type | Compressive Strength | Elastic Modulus | Poisson’s Ratio | Density |
|---|---|---|---|---|
| fc | E | ν | ρ | |
| (MPa) | (GPa) | (kg/m3) | ||
| PA | 112 (1) | 46.4 (3) | 0.18 (0.01) | 2362 (3) |
| PB | 112 (6) | 45.2 (2) | 0.17 (0.01) | 2376 (32) |
| PC | 114 (3) | 45.9 (3) | 0.17 (0.01) | 2408 (11) |
| Concrete Type | Elastic Modulus (GPa) | Relative Error | |
|---|---|---|---|
| From Cylinder | From Beam | ||
| PA | 46.4 (3) | 44.8 (2) | 3.4% |
| PB | 45.2 (2) | 42.9 (3) | 5.1% |
| PC | 45.9 (3) | 44.0 (4) | 4.1% |
| Concrete Type | Testing Machine | H (mm) | (mm/s) | Pmax (kN) | R (MPa) | DIF for R | GF@3 mm (N/m) | DIF for GF@3 mm |
|---|---|---|---|---|---|---|---|---|
| PA Conventional SFRSCC | Servo-hydraulic testing machine | - | 2.20 × 10−3 | 11.96(0.5) | 8.46(0.3) | 1 | 3067(264) | 1 |
| - | 2.20 × 101 | 15.70(0.4) | 11.13(0.4) | 1.32 | 3784(420) | 1.23 | ||
| Drop-weight impact machine | 160 | 1.77 × 103 | 55.13(6) | 38.41(4) | 4.54 | 8060(774) | 2.63 | |
| 360 | 2.66 × 103 | 67.89(9) | 46.98(6) | 5.55 | 8635(547) | 2.82 | ||
| PB High-performance SFRSCC | Servo-hydraulic testing machine | - | 2.20 × 10−3 | 20.85(4) | 14.74(3) | 1 | 5056(1168) | 1 |
| - | 2.20 × 101 | 26.85(4) | 18.93(3) | 1.28 | 6171(789) | 1.22 | ||
| Drop-weight impact machine | 160 | 1.77 × 103 | 67.77(15) | 47.77(10) | 3.24 | 12347(2078) | 2.44 | |
| 360 | 2.66 × 103 | 85.47(5) | 60.07(5) | 4.07 | 13964(609) | 2.76 | ||
| PC High-performance SFRSCC | Servo-hydraulic testing machine | - | 2.20 × 10−3 | 33.06(0.8) | 23.28(0.05) | 1 | 9414(361) | 1 |
| - | 2.20 × 101 | 43.98(6) | 31.28(4) | 1.34 | 12552(2646) | 1.33 | ||
| Drop-weight impact machine | 160 | 1.77 × 103 | 98.41(14) | 69.53(11) | 2.98 | 17752(230) | 1.89 | |
| 360 | 2.66 × 103 | 129.67(11) | 91.50(6) | 3.93 | 20218(588) | 2.15 |
| Loading Rate (mm/s) | Strain Rate (s−1) |
|---|---|
| 2.20 × 10−3 | 1.0 × 10−5 |
| 2.20 × 101 | 9.9 × 10−2 |
| 1.77 × 103 | 8.1 × 100 |
| 2.66 × 103 | 1.2 × 101 |
| Dimensions, Compositions and Properties | Conventional Vibrated Steel Fiber Reinforced Concrete (CVSFRC) [25] | Steel Fiber Reinforced Self-Compacting Concrete (SFRSCC) |
|---|---|---|
| Beam size: B × D × S * (mm3) | 150 × 150 × 500 | 100 × 100 × 333 |
| Notch: a (mm) | 25 | 17 |
| Fiber content (volume ratio) | 0.83% | 0.77% |
| Mix proportions: C:S:A:W ** | 1:1.6:1.2:0.29 | 1:2.48:0:0.38 |
| Steel fiber shape | Hooked-end | Smooth + hooked-end |
| l/d *** | 50/0.75 | 13/0.20 + 30/0.38 |
| (Aspect ratio) | (67) | (65 and 80) |
| fc (MPa) | 92 | 112 |
| E (GPa) | 35 | 45 |
| Quasi-static load-deflection curve | High performance (deflection-hardening) | High performance (deflection-hardening) |
| DIF for R at 1.77 × 103 m/s | 2.71 | 3.24 |
| DIF for GF@3 mm at 1.77 × 103 m/s | 1.83 | 2.44 |
| DIF for R at 2.66 × 103 m/s | 3.48 | 4.07 |
| DIF for GF@2 mm at 2.66 × 103 m/s | 2.52 | 2.76 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Ruiz, G.; Tarifa, M.; Cendón, D.; Gálvez, F.; Alhazmi, W.H. Dynamic Fracture Behavior of Steel Fiber Reinforced Self-Compacting Concretes (SFRSCCs). Materials 2017, 10, 1270. https://doi.org/10.3390/ma10111270
Zhang X, Ruiz G, Tarifa M, Cendón D, Gálvez F, Alhazmi WH. Dynamic Fracture Behavior of Steel Fiber Reinforced Self-Compacting Concretes (SFRSCCs). Materials. 2017; 10(11):1270. https://doi.org/10.3390/ma10111270
Chicago/Turabian StyleZhang, Xiaoxin, Gonzalo Ruiz, Manuel Tarifa, David Cendón, Francisco Gálvez, and Waleed H. Alhazmi. 2017. "Dynamic Fracture Behavior of Steel Fiber Reinforced Self-Compacting Concretes (SFRSCCs)" Materials 10, no. 11: 1270. https://doi.org/10.3390/ma10111270
APA StyleZhang, X., Ruiz, G., Tarifa, M., Cendón, D., Gálvez, F., & Alhazmi, W. H. (2017). Dynamic Fracture Behavior of Steel Fiber Reinforced Self-Compacting Concretes (SFRSCCs). Materials, 10(11), 1270. https://doi.org/10.3390/ma10111270





