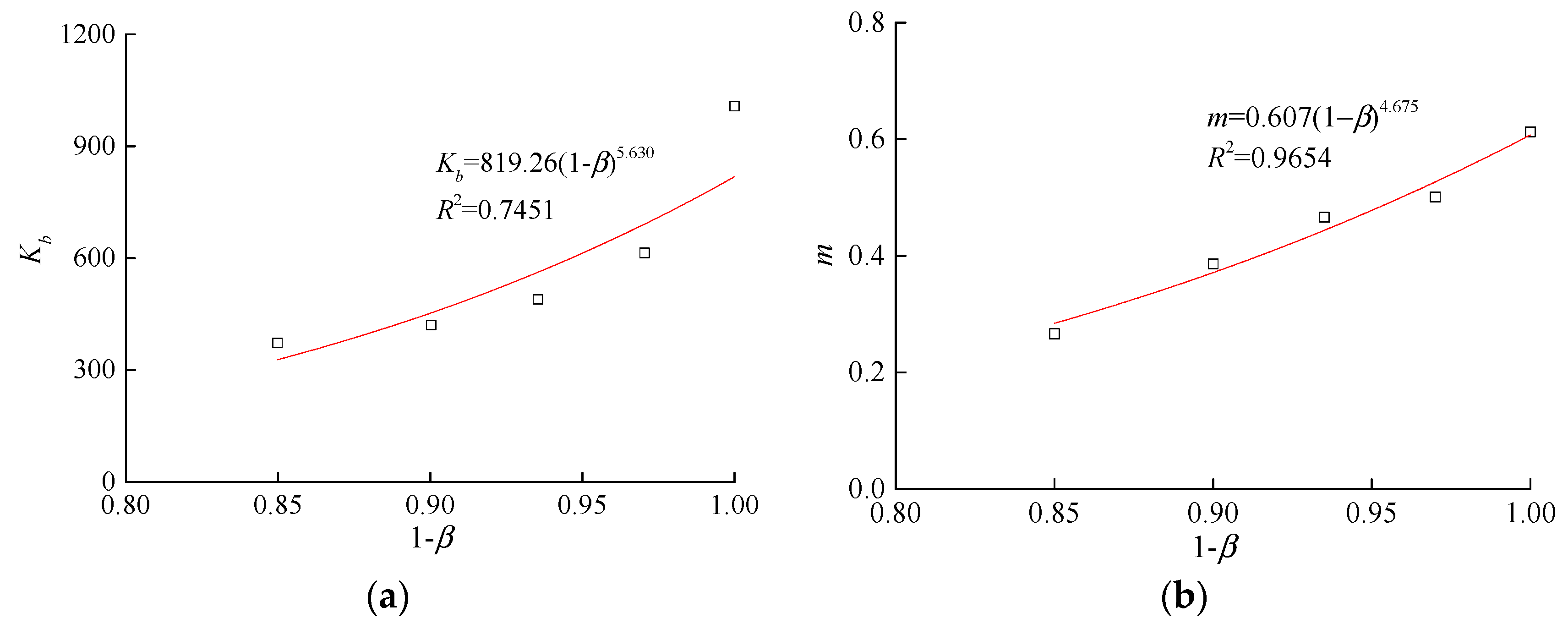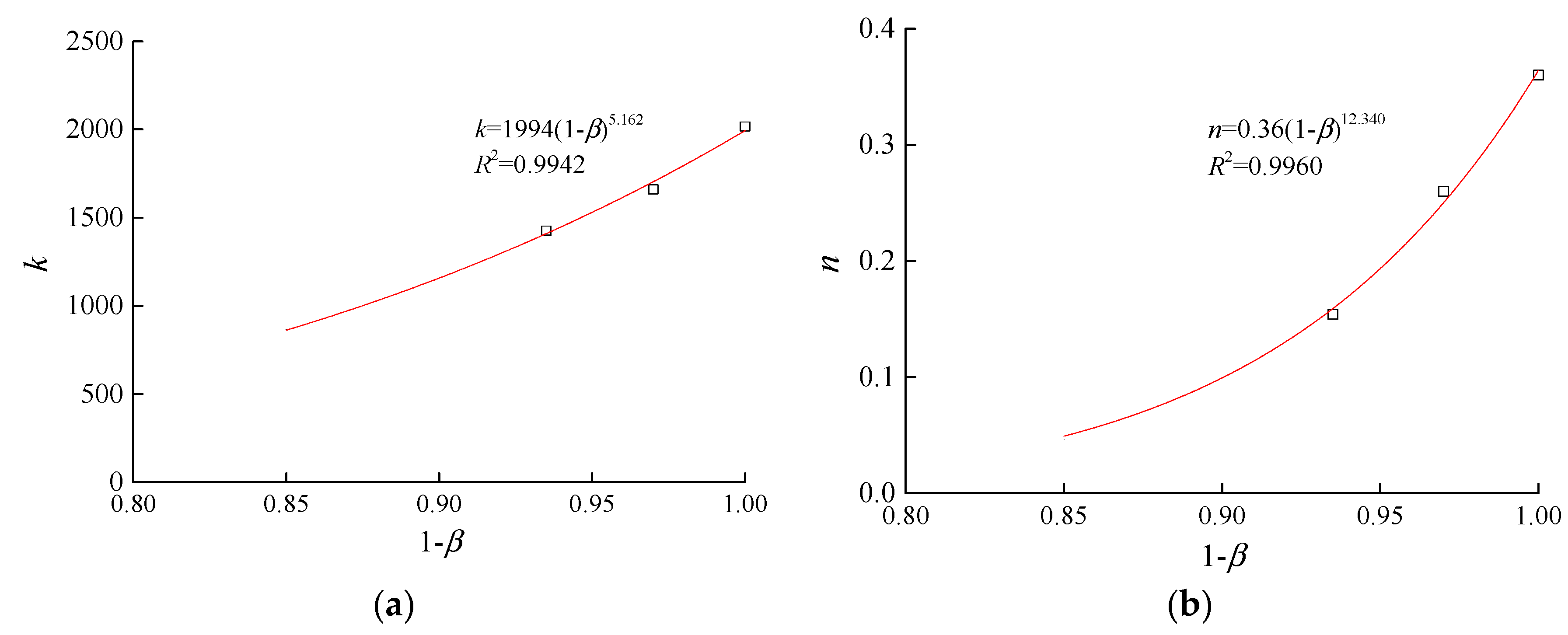In soils where suffusion erosion has occurred, the coarse particles of the soil form a skeletal frame. This allows for fine particles to traverse the pore channels formed by these coarse particles under the influence of seepage. Generally speaking, the loss of fine particles will not necessarily lead to the collapse of the skeletal frame. During suffusion erosion, if the erosion of fine particles by seepage is not coupled with soil deformation, the volumetric content of the coarse particles and their arrangement/contact relationships will remain unchanged, although the soil porosity and the pores and spaces between the skeletal particles will increase as the erosion increases. For soils composed of large homogeneous particles, if the particles are maximally packed and small quantities of extremely fine particles are present in the spaces between the large particles, and then fine particle losses will only affect the seepage characteristics of the soil while having a minimal impact on the deformation characteristics. This particular circumstance may be observed in artificial rockfills. In natural sandy gravels, fine particles fill the spaces between the coarse particles. Thus, reductions in the number of fine particles will reduce the number of force transfer pathways that are mediated by fine particles, and will thereby increase the compressibility of the soil. Since coarse particles form the skeletal frame of a soil, it may be hypothesized that piping suffusion will not significantly alter the stress-strain characteristics, but may have an effect on the deformation moduli. An experimental study is therefore necessary to quantify these effects. As the erosion of soil in dam foundations varies in space and time, studies of the effects of the erosion level on the strength and deformation moduli of soils will be useful when simulating the effects of piping erosion on the deformation of dam foundations and dam bodies.
2.1. Experimental Plan
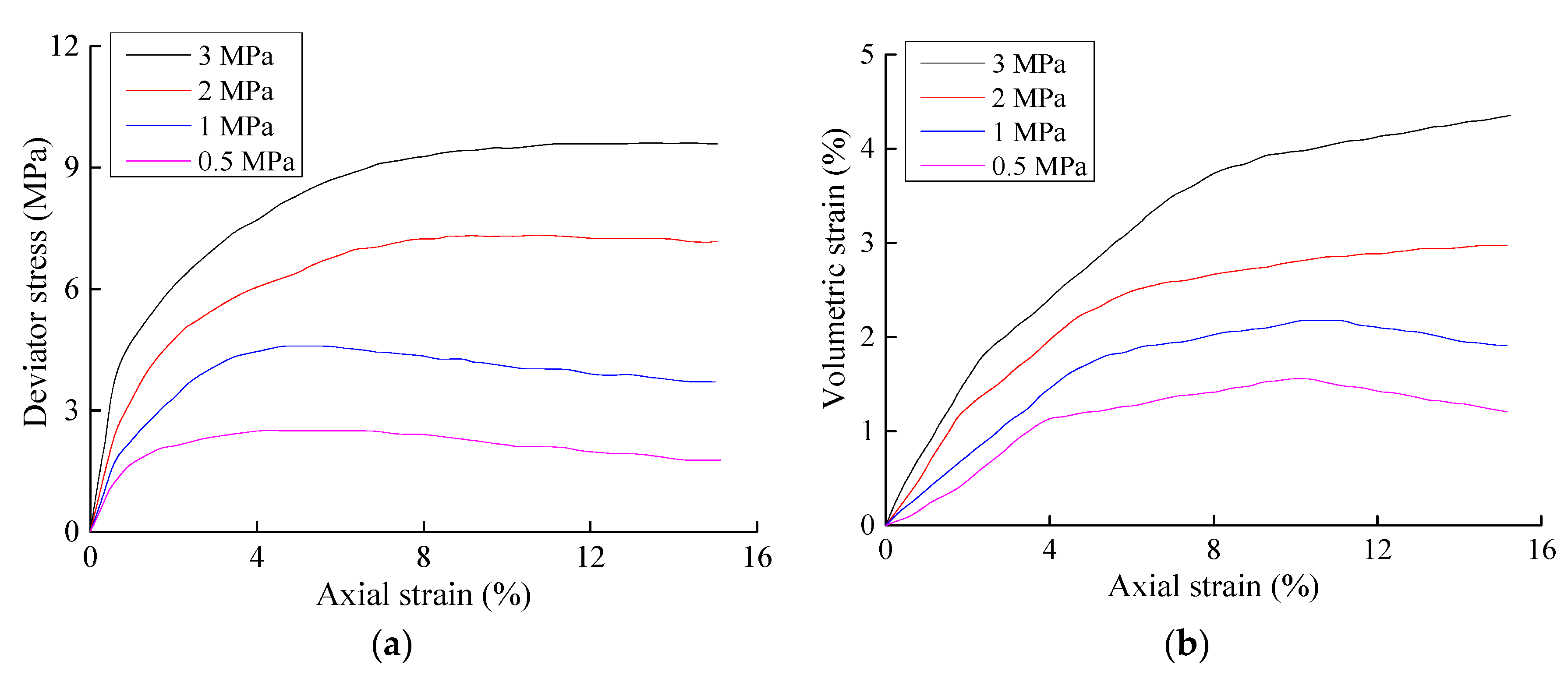
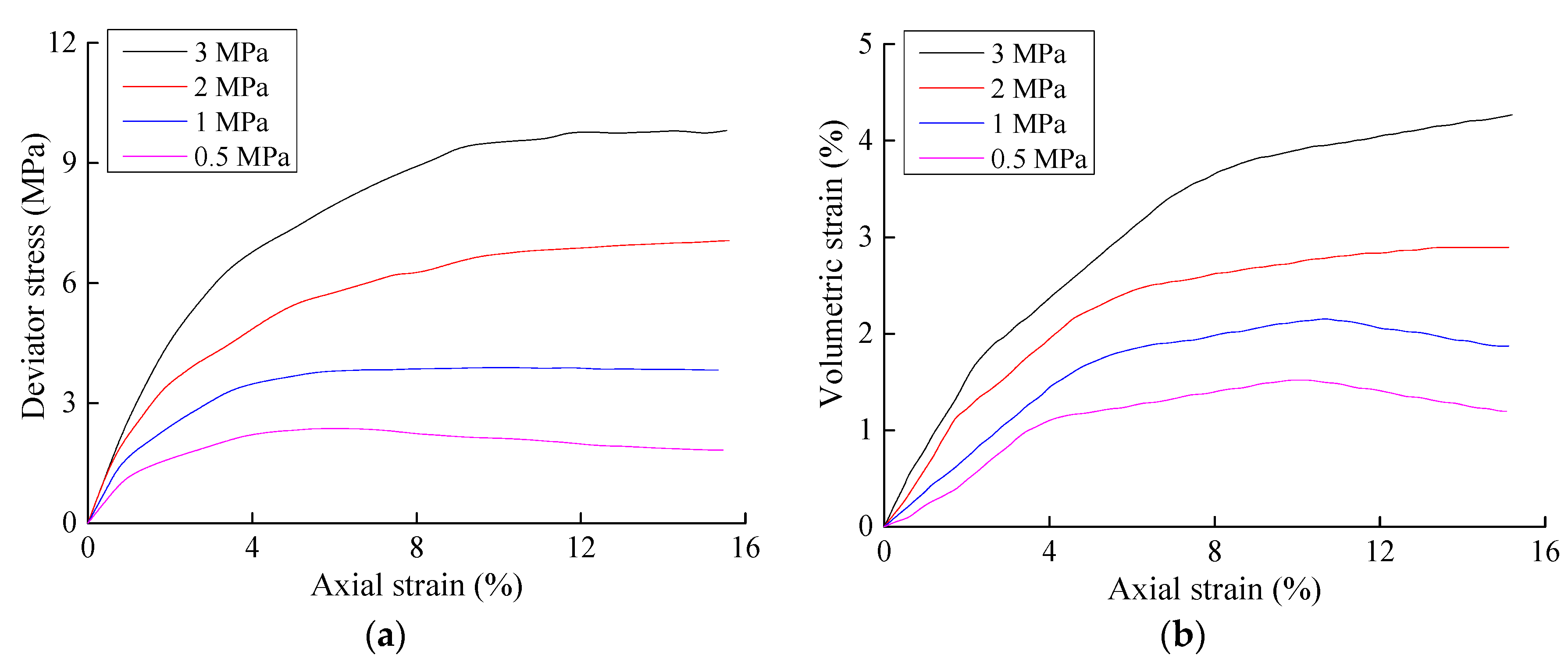
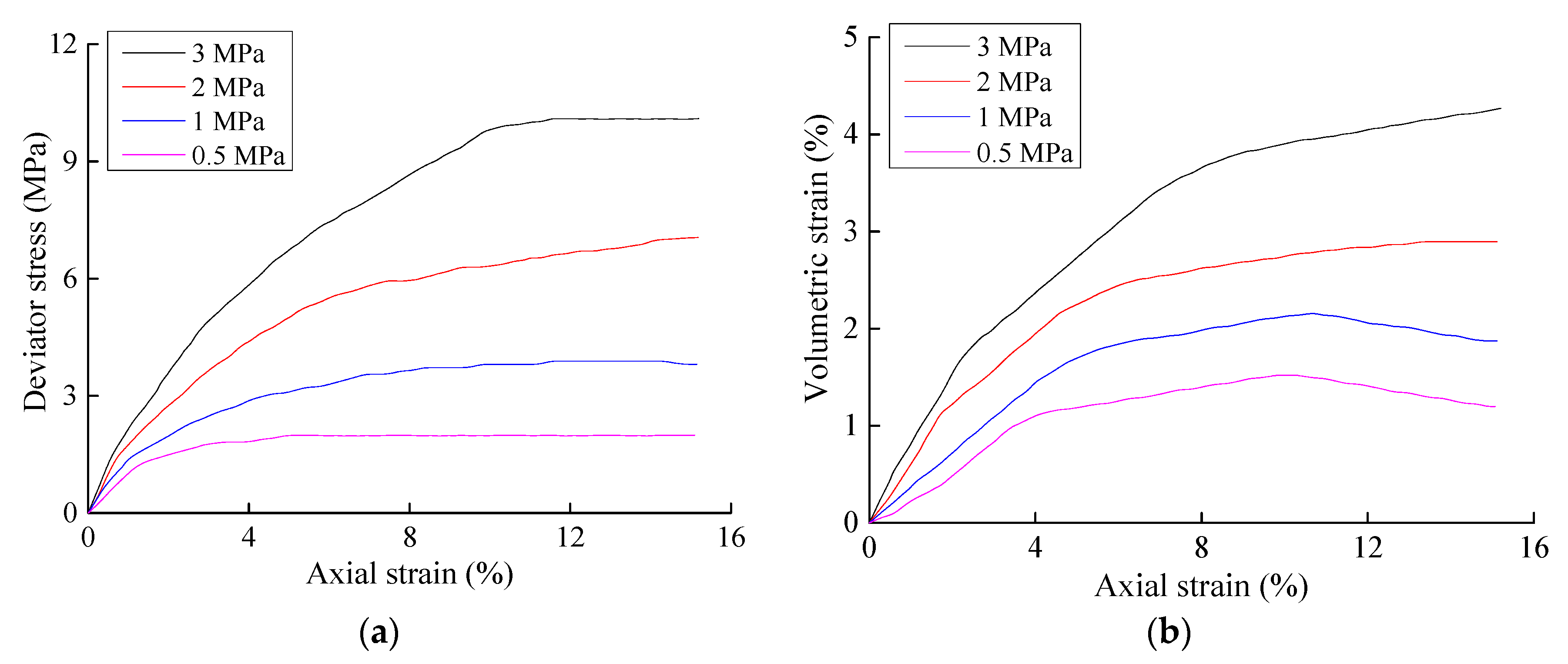
Triaxial and confined compression tests were performed on eroded and un-eroded sandy gravels to investigate the effects of particle losses on the strength and deformation characteristics/parameters of the soil. As it is difficult to obtain sandy gravelly samples that have been eroded by piping erosion with quantified levels of erosion, the samples used in this experiment were prepared with particle gradations and porosities equivalent to soils that have been eroded by piping erosion.
Based on the particle gradation and dry density of the natural samples, the characteristics of un-eroded samples were determined after similitude methods were used to remove the oversized particles. A list of ingredients for the un-eroded sample was thus obtained. To create samples that have been eroded by piping erosion, fine particles were removed from the list of ingredients used to prepare un-eroded samples, up to some weight corresponding to the desired quantity of fine particle loss. By creating samples in this manner, the volumetric content of the coarse particles was held constant, while the fine particle content was decreased in the eroded sample. This is generally consistent with the particle composition and porosity of soils that have been eroded by piping erosion. Triaxial tests and confined compression tests were then performed on samples with different levels of erosion, which revealed how the amount of erosion affected the stress-strain relationships of the soil.
In triaxial tests, when studying soil compressibility, it would be useful to record the deformation moduli during consolidation. However, due to the effects of membrane penetration, accurate measurements of volumetric deformation during isotropic consolidation are very difficult to perform. Since confined compression tests directly reflect the compressibility of the tested soil, they may be used to study the effects of fine particle losses on the volumetric deformation moduli of sandy gravels.
In this work, well-graded sandy gravels were used as the experimental material. The largest particles were 40 mm in diameter, and particles smaller than 5 mm accounted for 25.48% of the total weight of the natural soil. The specific gravity of particles larger than 5 mm was 2.83, while particles smaller than 5 mm had a specific gravity of 2.71. The eroded soil samples were prepared by removing fine particles (5 mm in diameter or smaller in accordance with the Standard [
11]) from the list of ingredients for un-eroded soil samples, according to the desired ratio of erosion. The samples that had the same particle gradation and porosity as actual eroded soils with the same erosion ratio were thus prepared. Three sets of triaxial tests were performed, with the first set being performed on un-eroded soils. The dry density of the un-eroded samples was 2.36 g/cm
3, while their porosity was 13.9%. In the second set of tests, the particles lost to erosion constituted 3% of the total mass, and the dry density and porosity of the resulting sample were 2.29 g/cm
3 and 16.5%, respectively. In the third set of tests, the particles lost to erosion accounted for 6.5% of the total mass, and the dry density of the resulting sample was 2.21 g/cm
3, while its porosity had increased to 19.5%. The triaxial test samples had a diameter of 150 mm and height of 300 mm, and saturated consolidated drained tests were performed. The samples for the confined compression tests had a height of 60 mm and a diameter of 100 mm. The confined compression tests were performed on un-eroded samples, and samples where fine particle erosion accounted for 3%, 6.5%, 10%, and 15%, respectively, of the total soil weight.
The moist tamping method was employed in this study. To avoid the fines migration during preparation of the sample, great care had to be taken to minimize disturbance. The automated experimental system used could conduct measurements and controls by computer through 16-bit A/D and D/A converters (AD1380KD, GEMAC, London, UK). The vertical load could be automatically applied by a motor-gear system at any rate. The cell pressure is applied by air pressure through an automatic air compressor (GA 5-11, Air Technologies, Columbus, OH, USA) regulated by E/P (Electronic to Pneumatic) transducers (550-AGD, Combine Co., Zhuhai, China). All of the pressure lines are connected to a draining system to remove any condensed water. The deviator load is measured by a submersible load cell (2022/2022-F, SENSY, Brussels, Belgium) mounted inside the cell. Axial displacement is measured externally by a Linear Variable Differential Transformer (LVDT) (GT2-P12, Keyence Corporation, Shanghai, China). Three pairs of clip gauges with the maximum capacity of ±0.002 m are employed to measure the radial strain.
The ratio between the amount of soil erosion and the total soil weight is henceforth defined as the erosion ratio. The erosion ratio differs from the volumetric erosion ratio, as the latter refers to the volume of the particles lost to erosion per unit volume. For soils with the same specific gravity in their soil particles, the volumetric erosion ratio = erosion ratio × (1 − initial porosity).
2.3. Results of the Confined Compression Tests
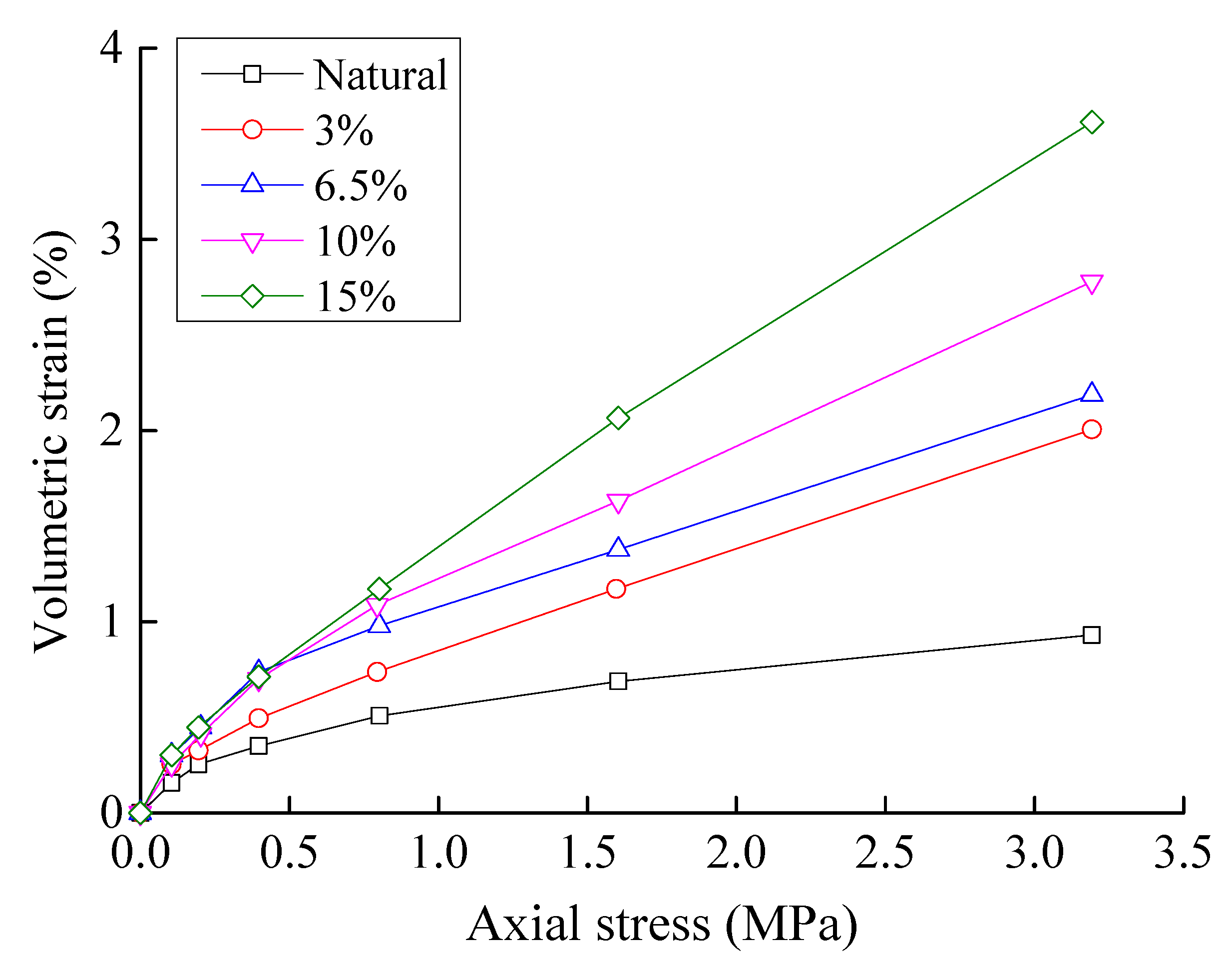
The sample preparation methods used for the confined compression tests were the same as those used for the triaxial tests, and all samples contained the same number of particles greater than 5 mm in size per unit volume. Samples with fine particle loss were obtained by reducing the content of particles smaller than 5 mm. The relationship between the axial pressure and volumetric strain is shown in
Figure 4. In this figure, the natural sample and the samples with 3%, 6.5%, 10%, and 15% particle loss had porosities of 13.9%, 16.5%, 19.5%, 22.6%, and 26.9%, respectively. The results of this test demonstrate that the pores and gaps within the coarse particle skeletal frame increase as the particle losses increase, and the quantity of confined compression will also increase for some given pressure.
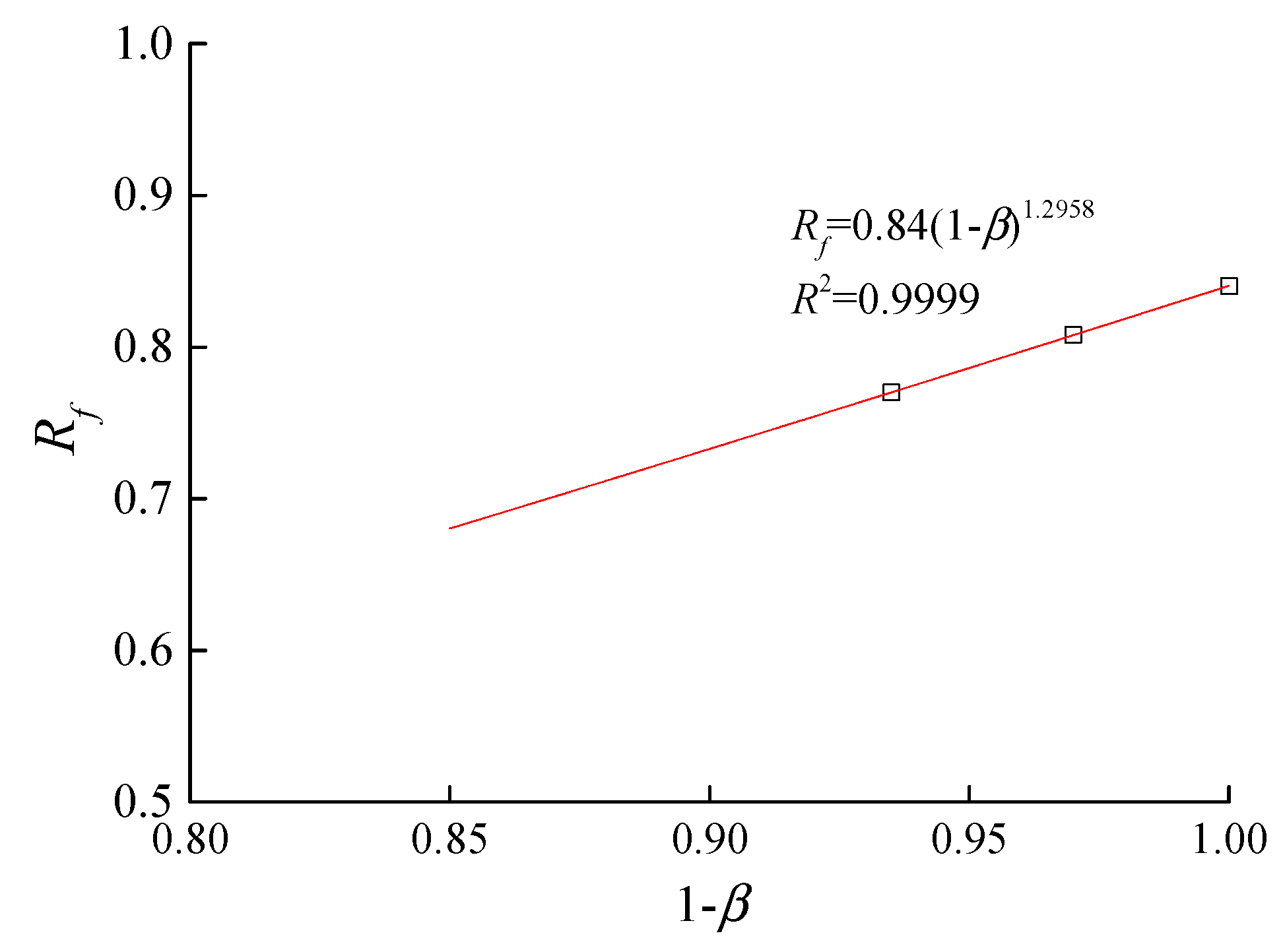
From the results above, the strength and deformation modulus of soil decrease as the particle losses increase. However, the stress-strain characteristics of the soil remain largely unchanged. Hence, the effects of the particle losses on the stress-strain relationships of soil can be described based on currently available models for describing the stress-strain relationships of sandy gravels in combination with currently available model parameters that are functions of the erosion ratio.