Time-Variant Reliability Analysis for Rubber O-Ring Seal Considering Both Material Degradation and Random Load
Abstract
:1. Introduction
2. Methods for Reliability Analysis
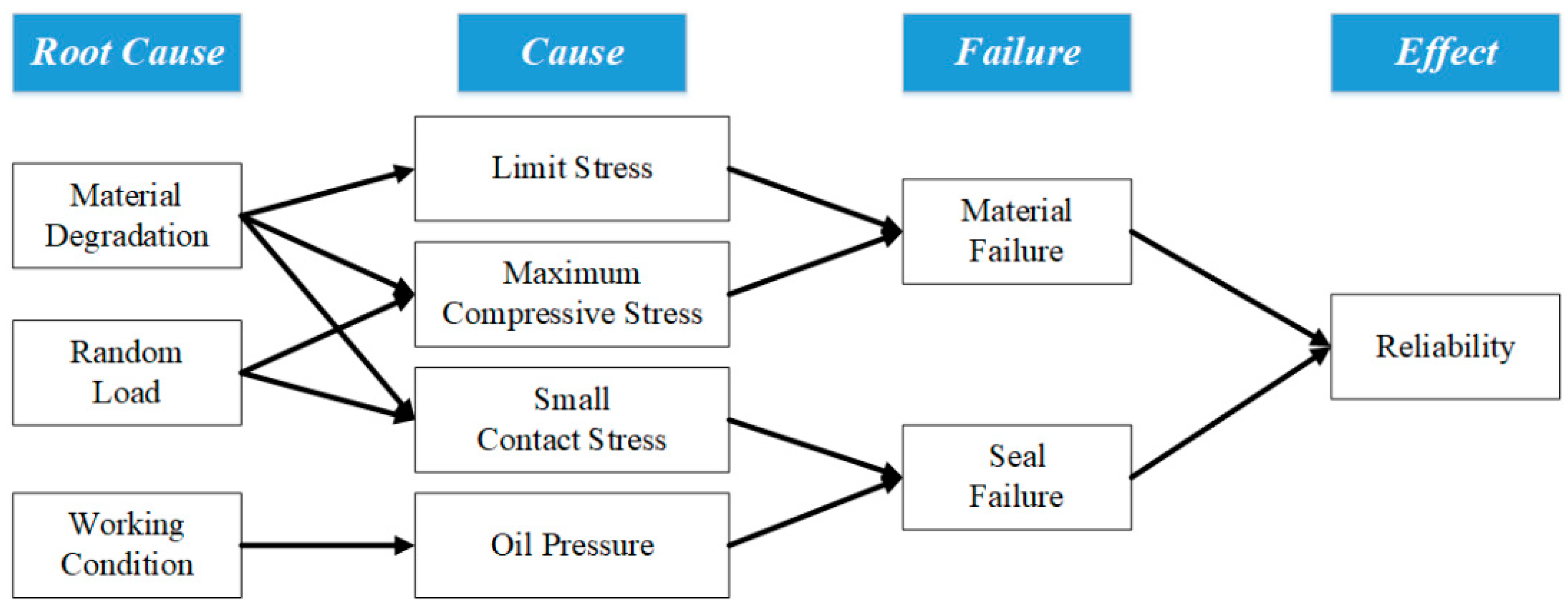
2.1. Failure Modes and Criterion
- (1).
- Rubber is the material used in O-rings, which is isotropic and incompressible. The volume of rubber remains the same during its deformation;
- (2).
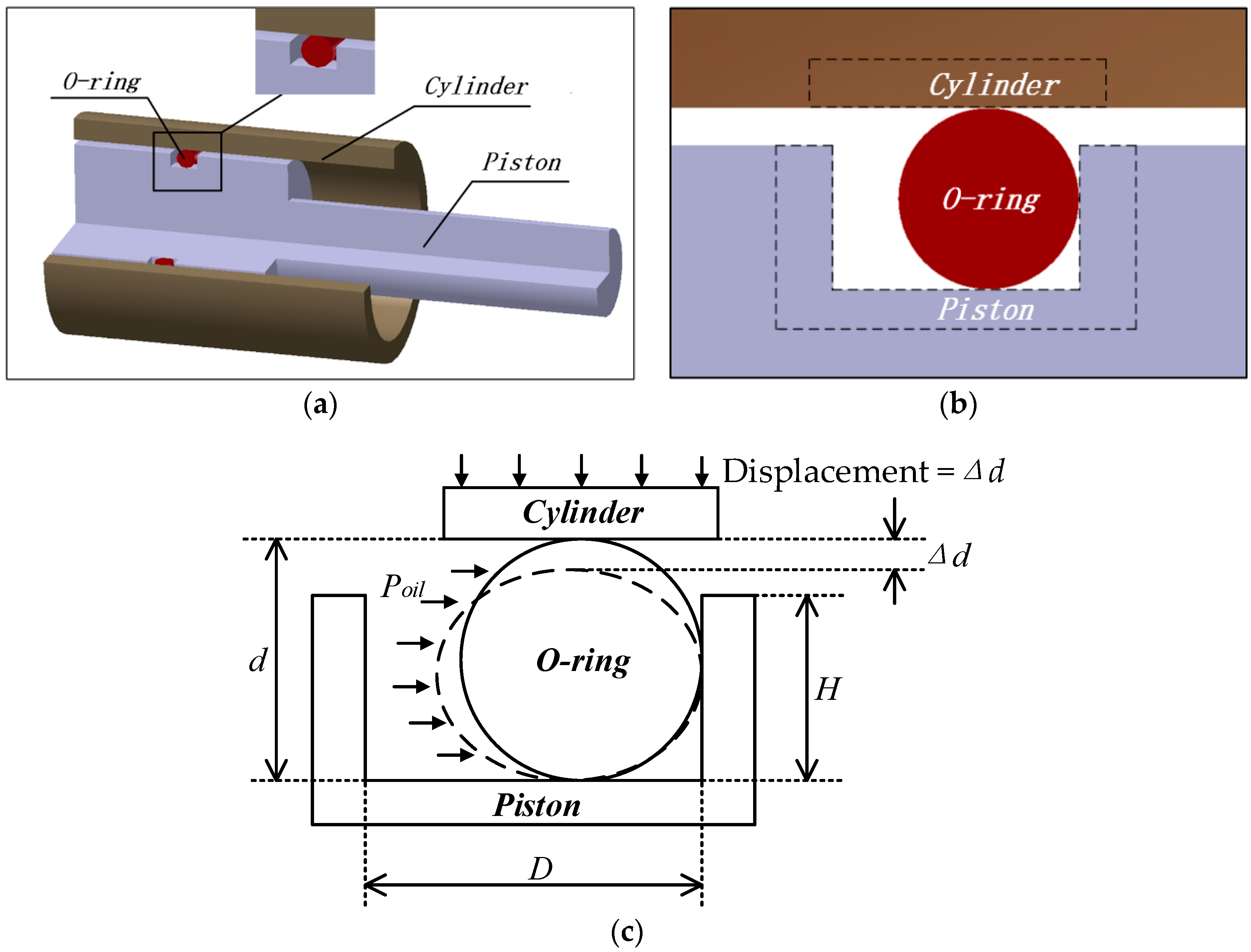
- As is shown in Figure 1a, the hydraulic system is completely axisymmetric, which means that all the cross profiles of the system bear the same stress. To reduce the computation and increase the accuracy of results, one cross profile (similar to Figure 1b) has been extracted, and the three-dimensional sealing device is changed into a planar question to make the analysis easier;
- (3).
- When constructing the geometric model of the sealing device, we regard the piston and cylinder as rigid bodies, which means when the model is compressed, only the O-ring will deform.
2.2. Materials
2.3. Reliability Modeling
3. Experiments and Simulations
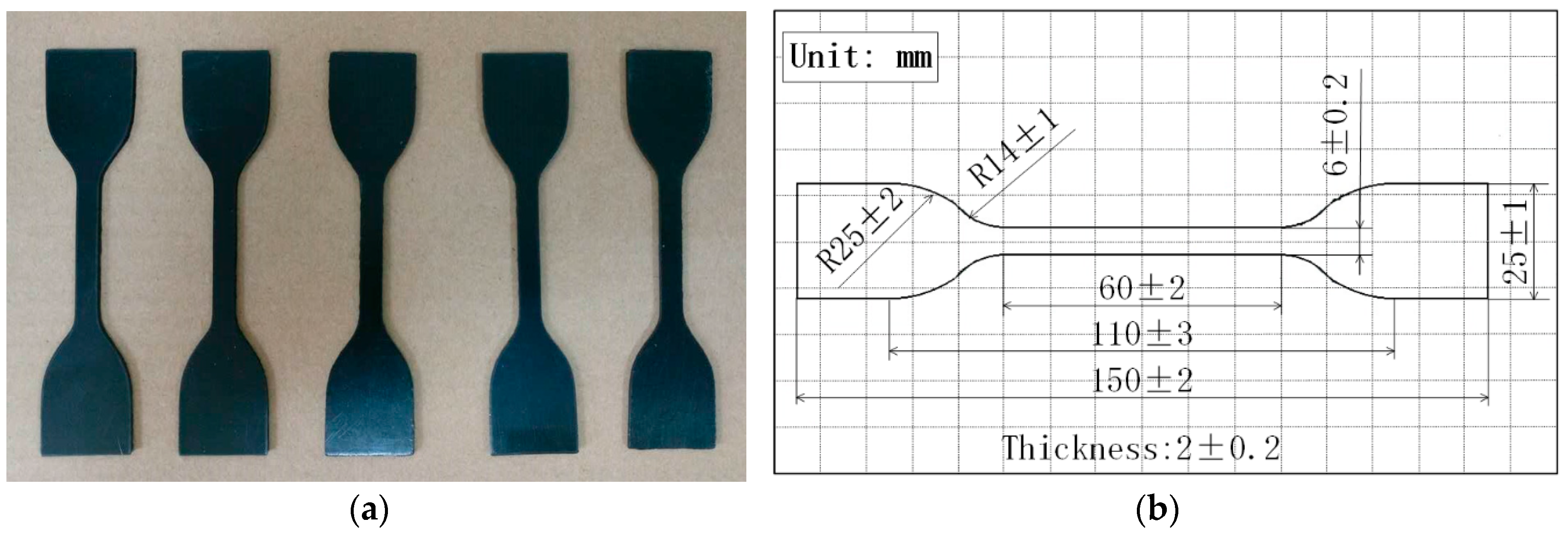
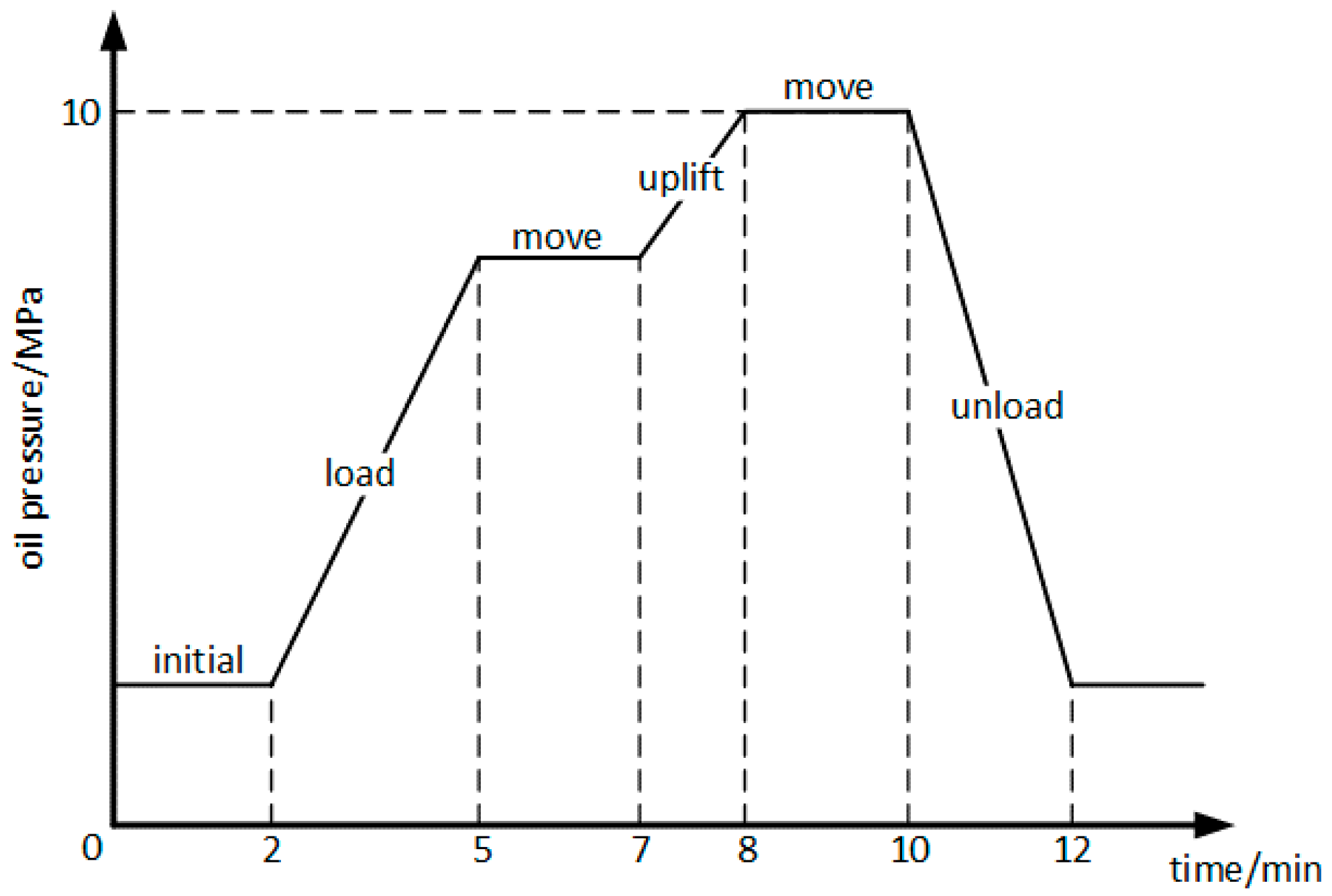
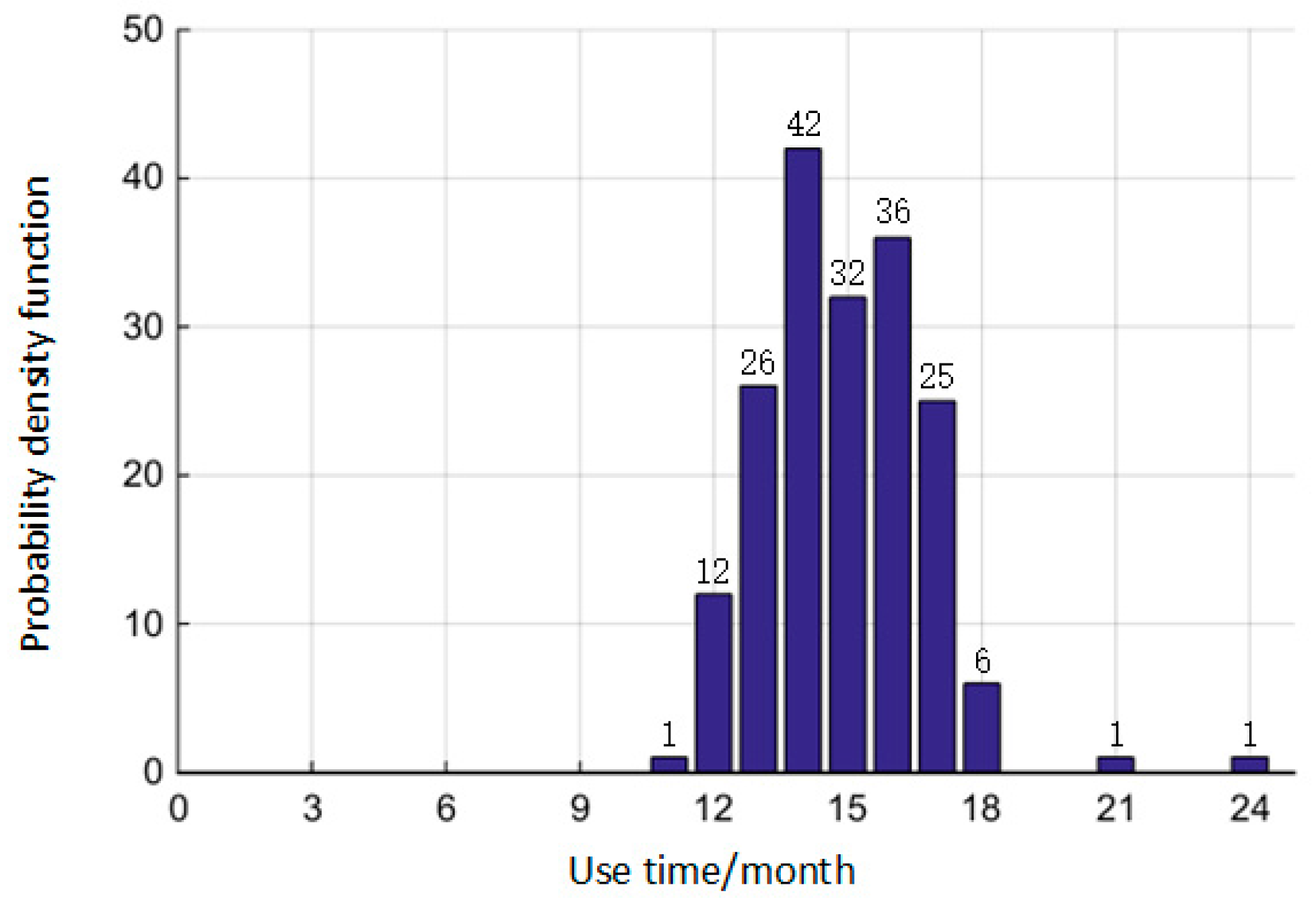
3.1. Experimental Design
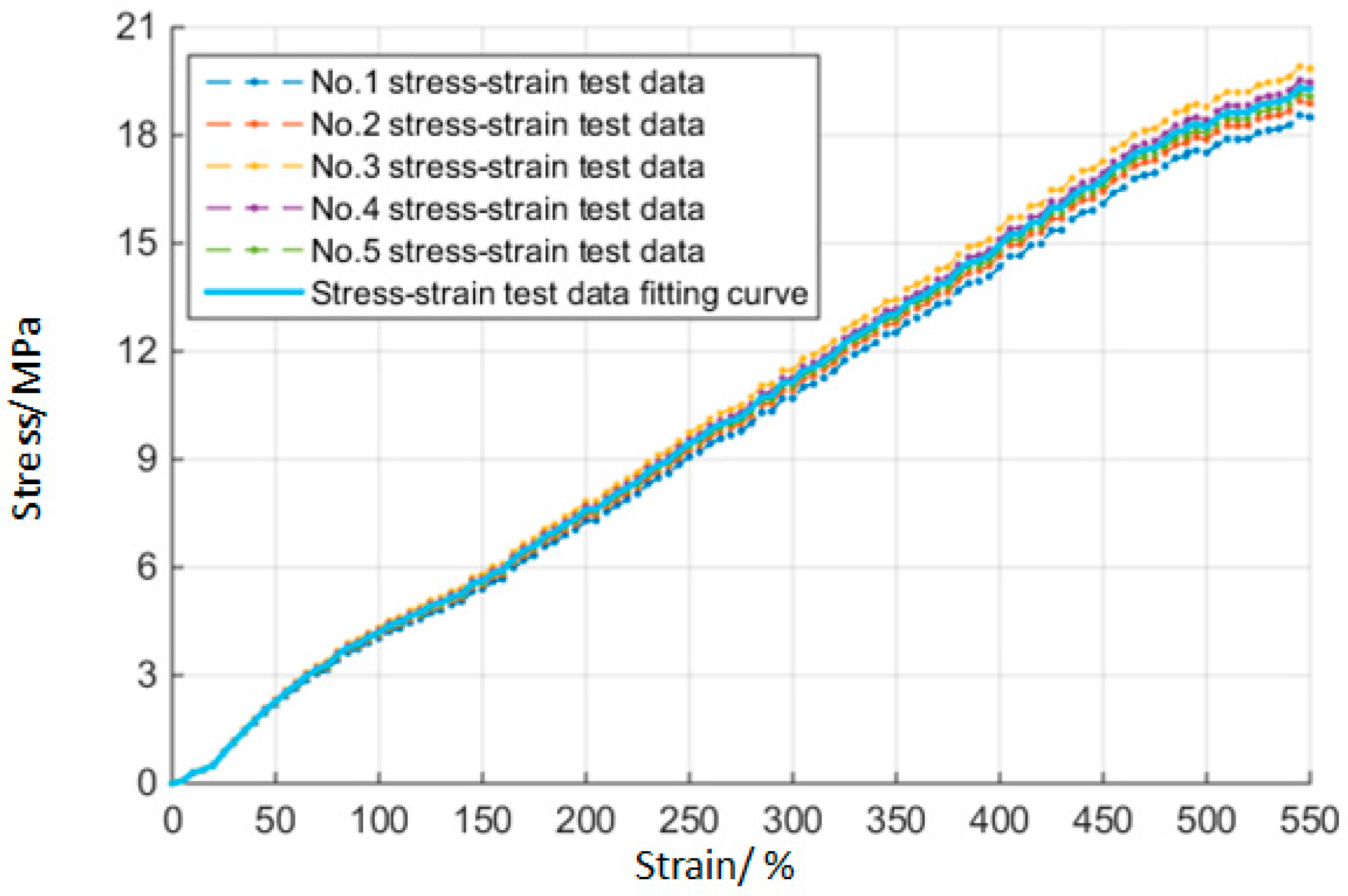
3.2. Experimental Results
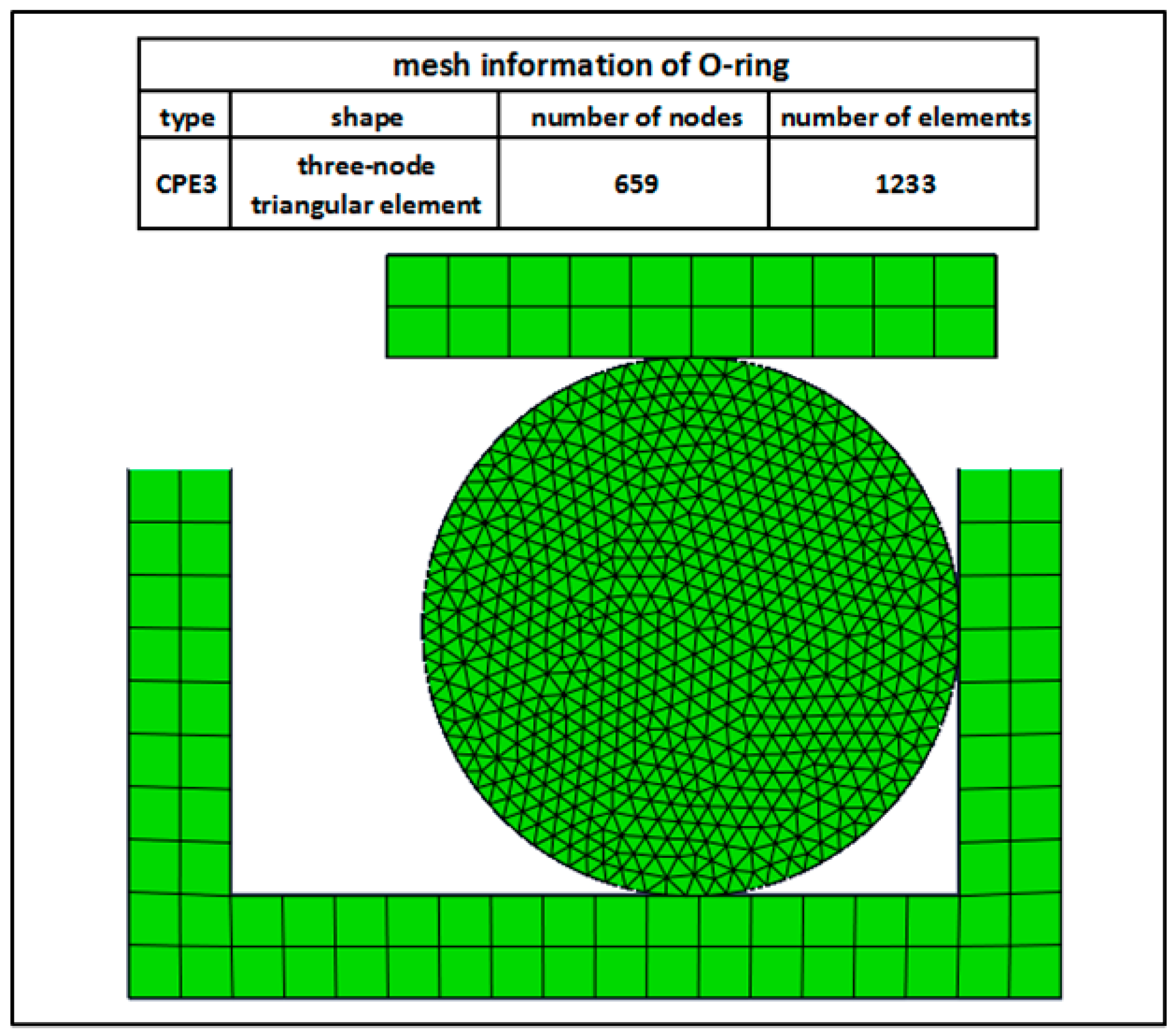
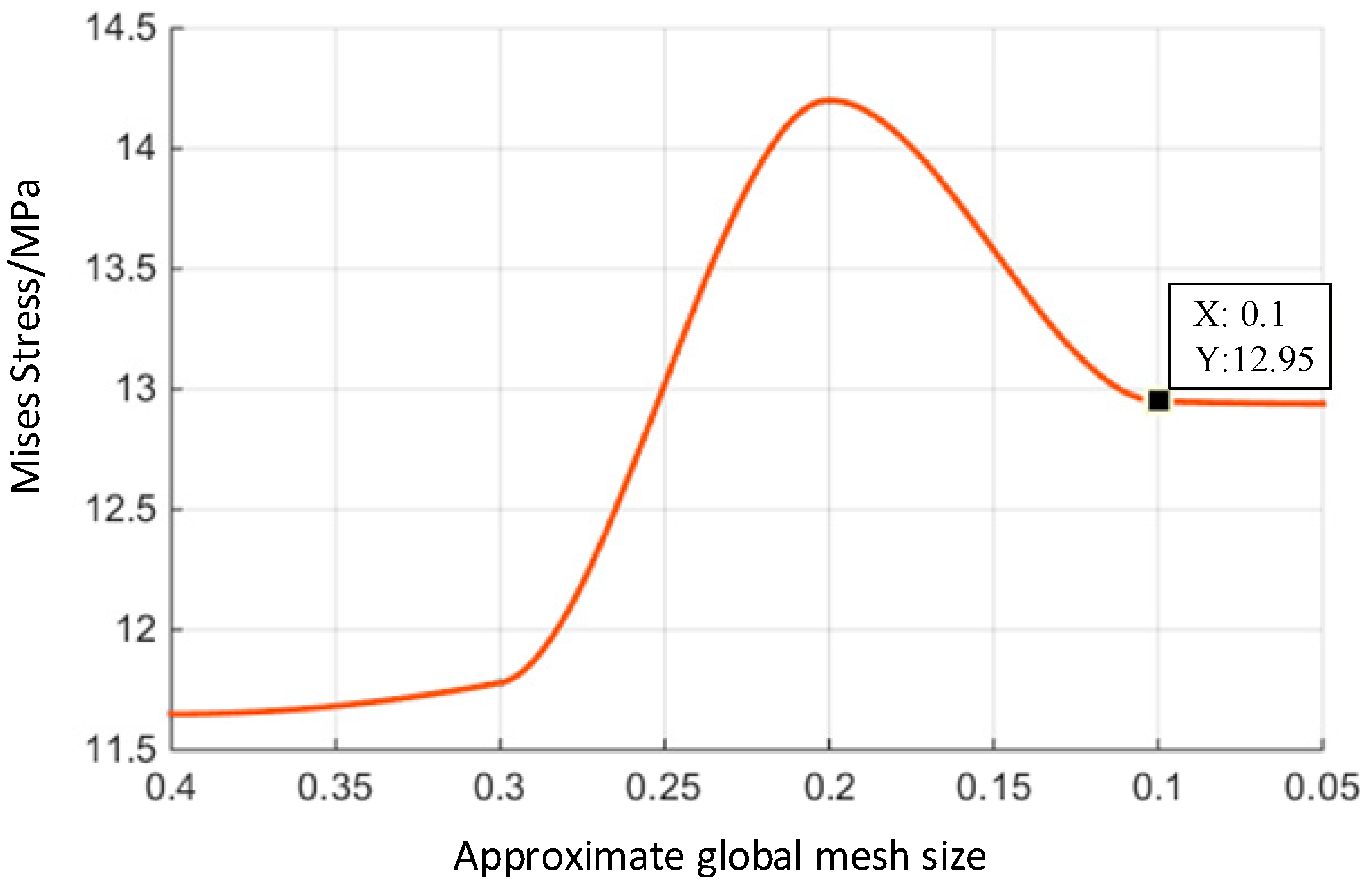
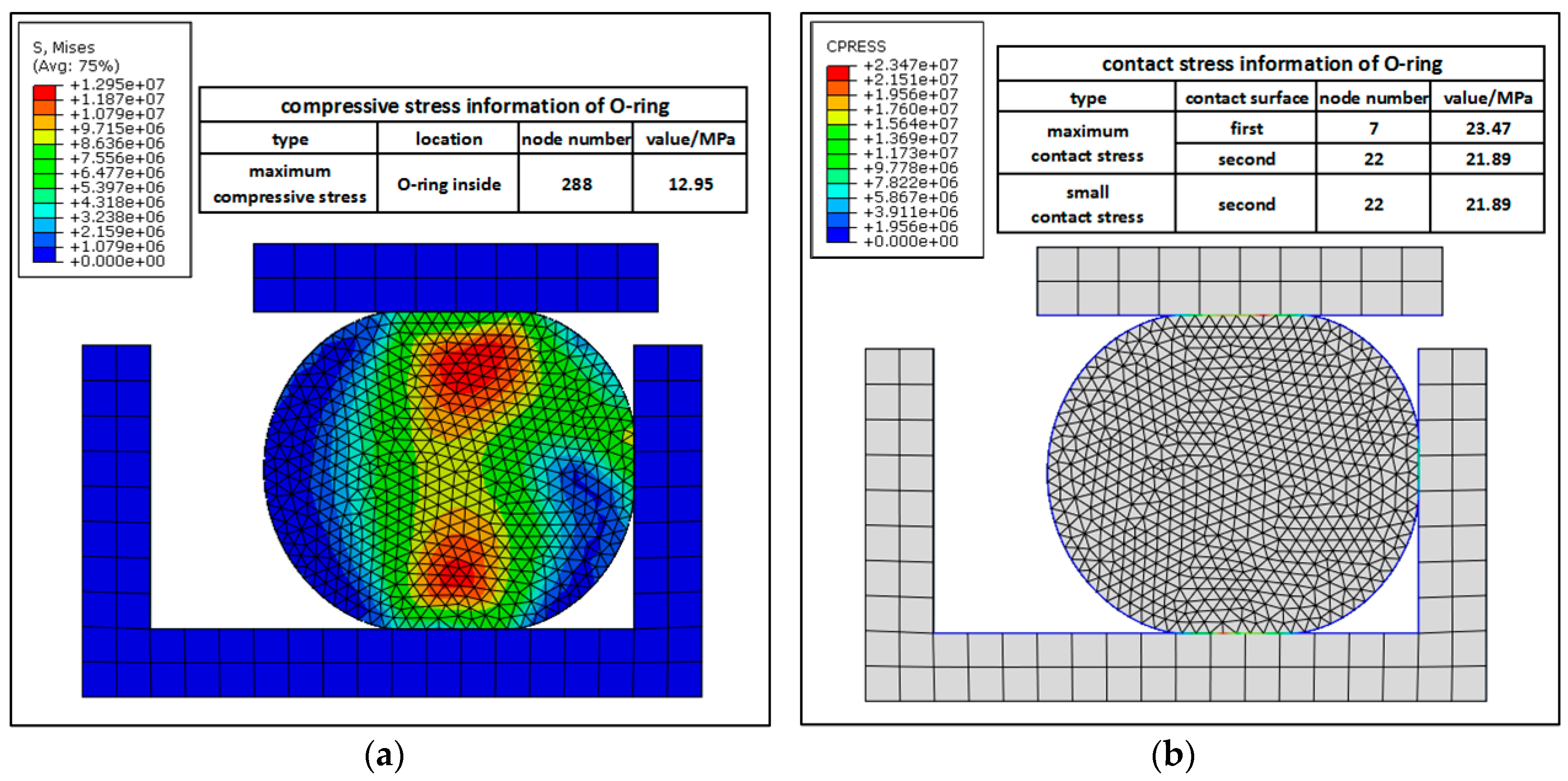
3.3. Simulations
4. Reliability Analysis under Multiple Conditions
4.1. Material Degradation and Random Load
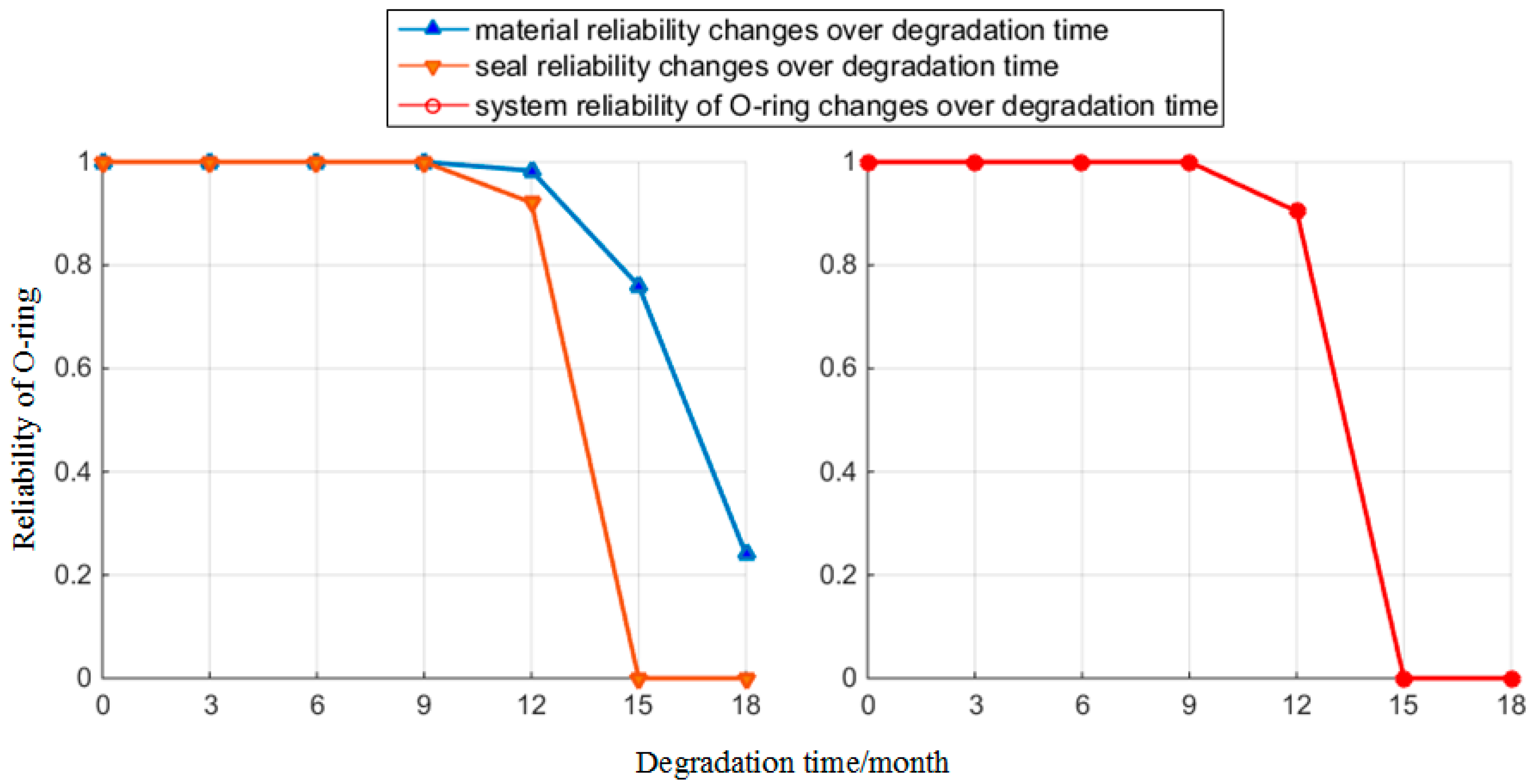
4.2. Result of Reliability Analysis
4.3. Discussion
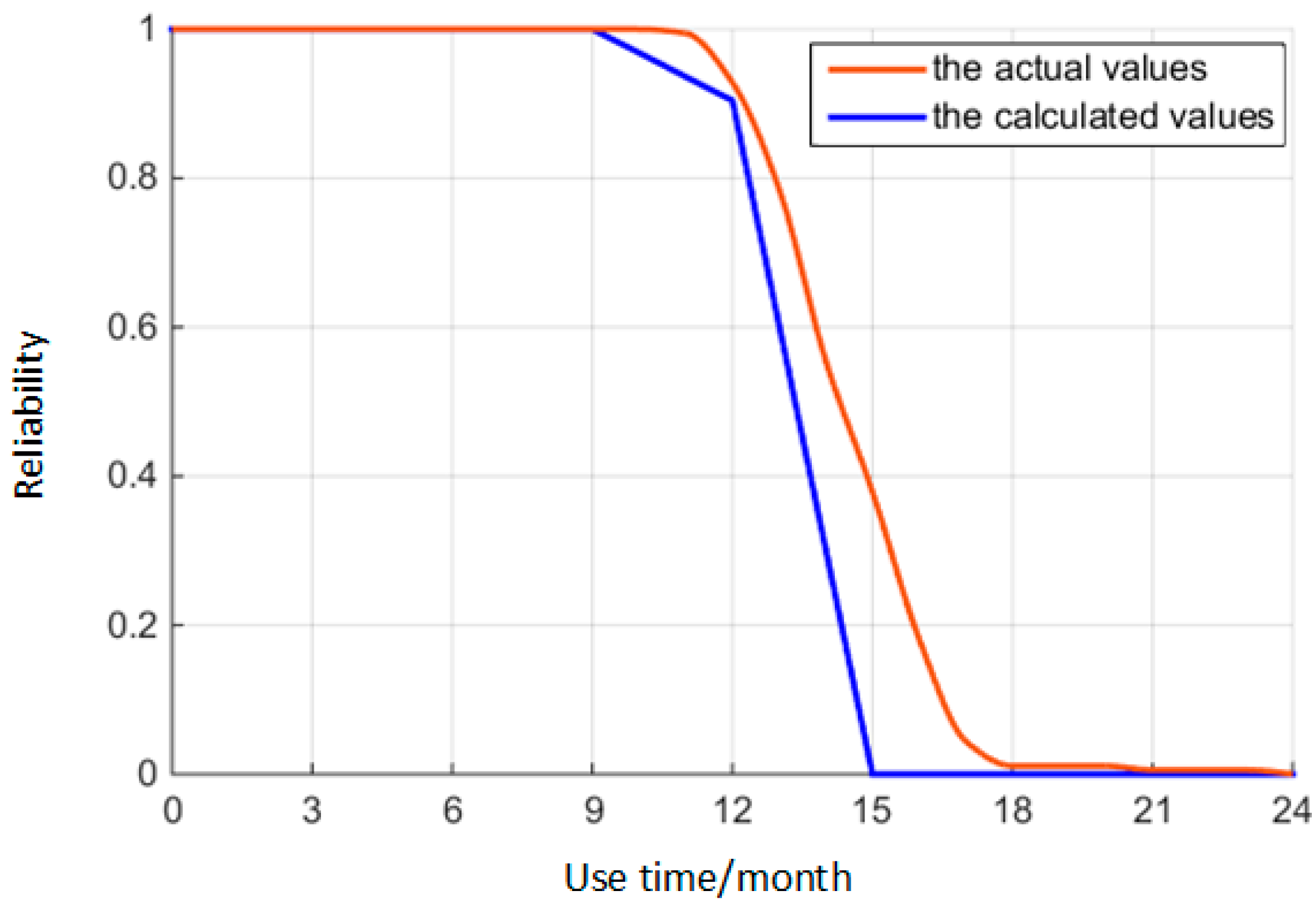
4.3.1. Life Prediction and Model Error Analysis
4.3.2. Effect of Oil Pressure
4.3.3. Comparison with the Actual Situation
5. Conclusions
- (1)
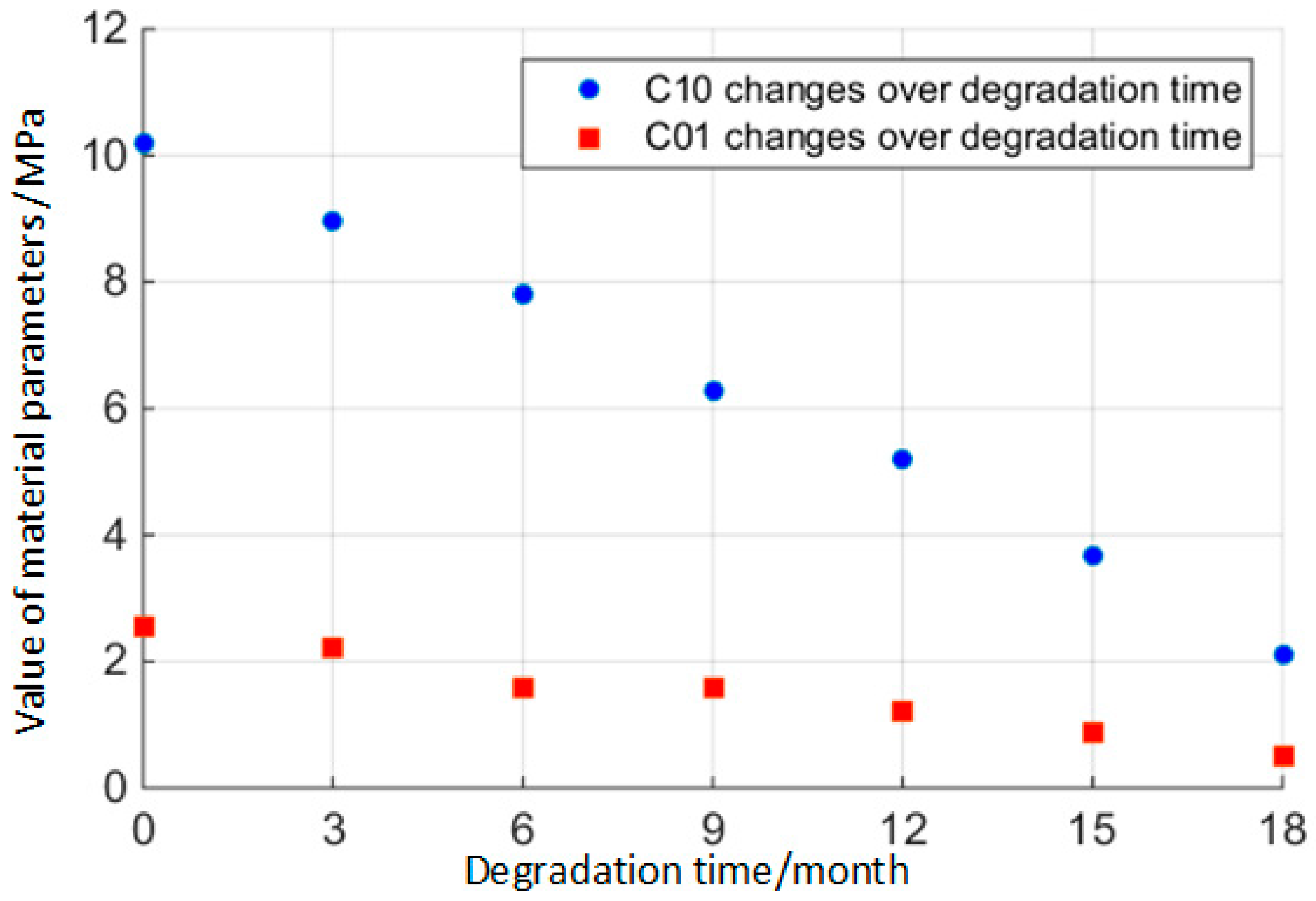
- In view of the time-variant degradation of rubber material parameters, its degradation rule can be obtained by using the experimental method in this paper. According to the experimental results, the performance of rubber material worsens with an increase in working hours.
- (2)
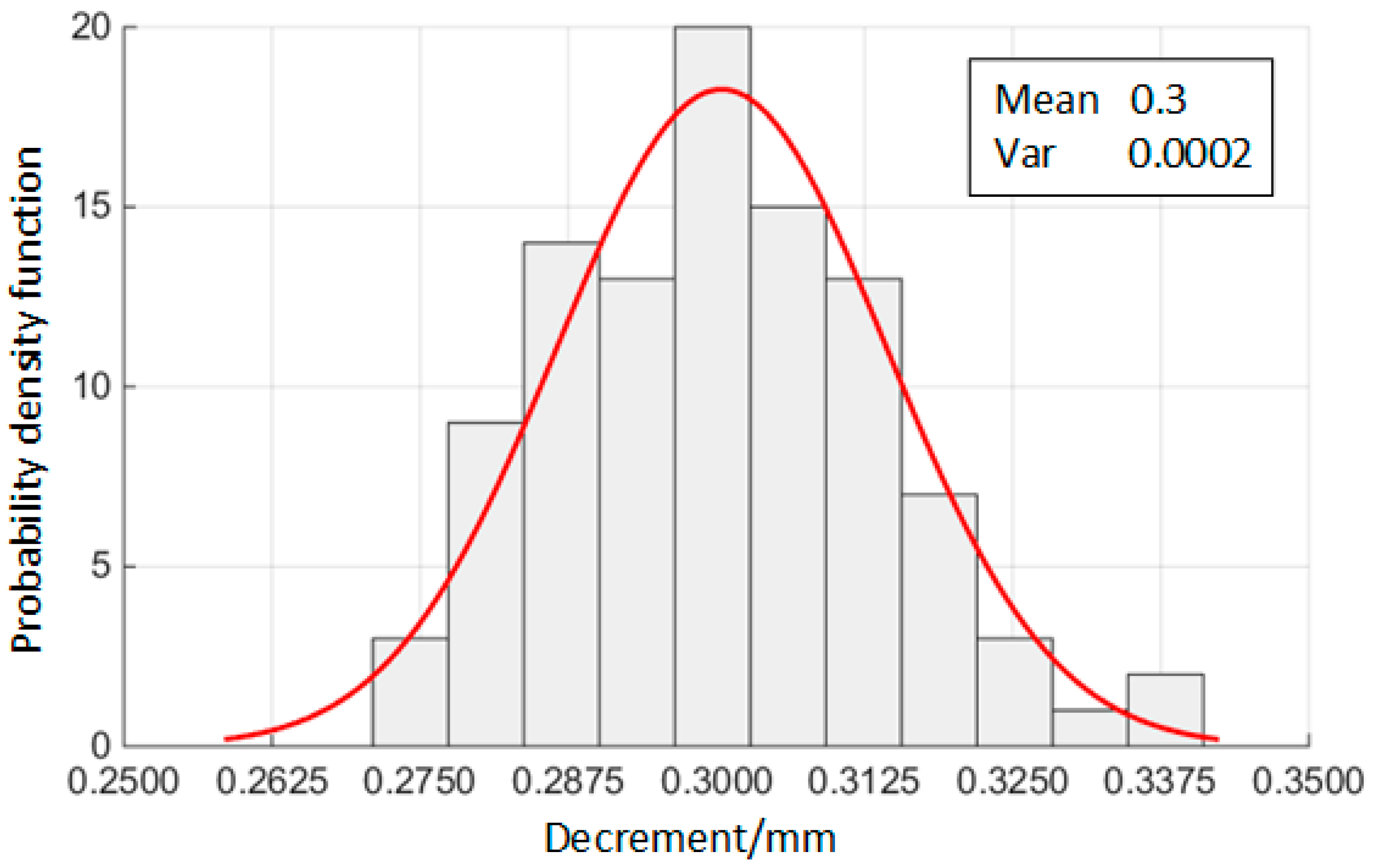
- The maintenance and replacement period of the O-ring predicted in this paper is 12 months, with the number of failures having increased sharply after the 12th month according to the actual situation. There is ample evidence to support why 12 months is used as the replacement cycle for the O-ring. Furthermore, the flaws in the processing technology would lead to varying decrements of the O-ring, despite the variations in decrement caused by the processing technology having little impact on the reliability.
- (3)
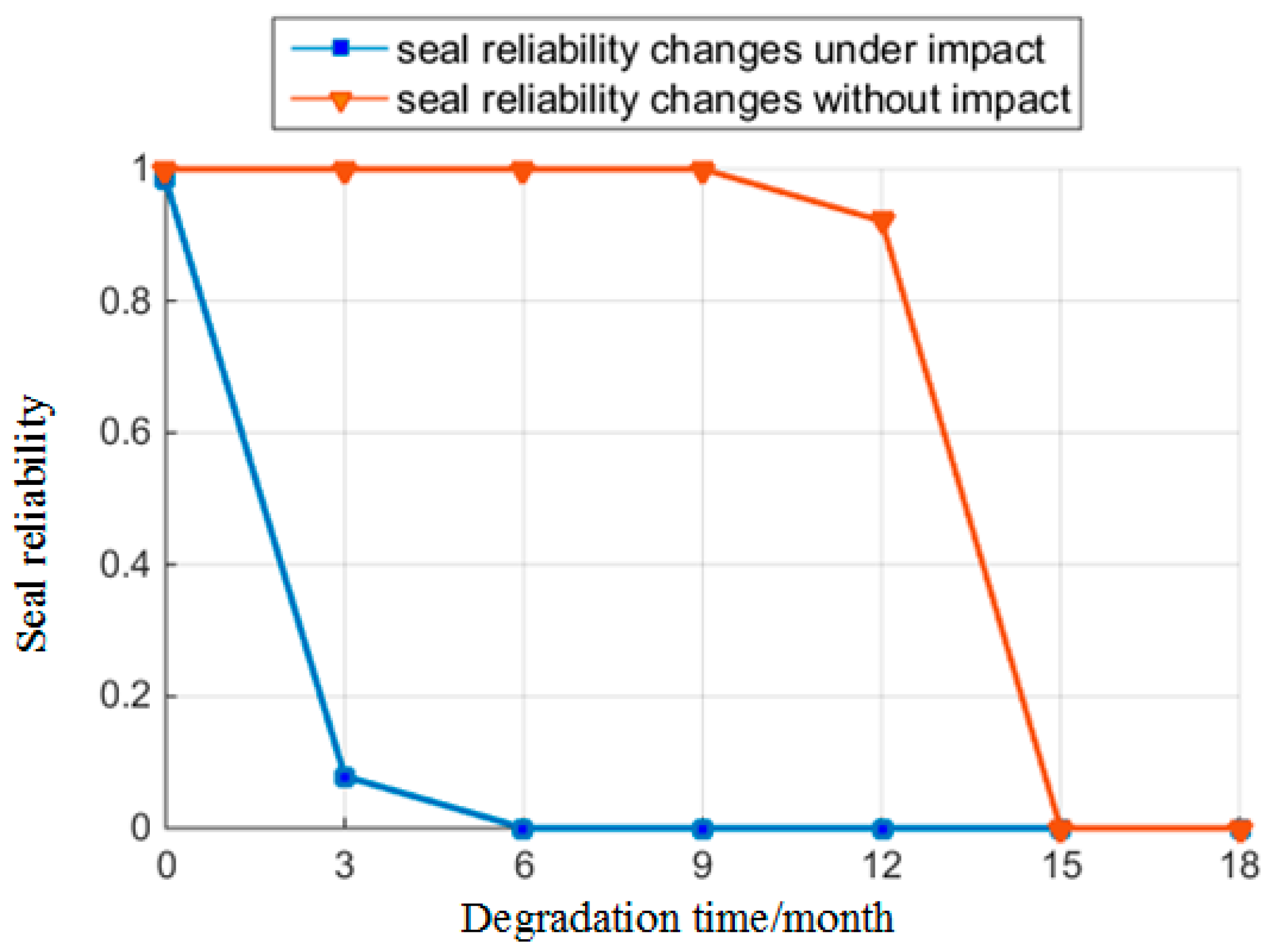
- The variation in working load would lead to a variation in oil pressure. Furthermore, the impact load creates considerable damage in the O-ring, which would trigger accidents. We optimized the input of the load and properly distributed the impact load to ensure the safe operation of this hydraulic system.
- (4)
- From the analysis results, the reliability model of the O-ring is obtained and calculated through the case analysis with consideration of both material reliability and seal reliability. In the case study, the reliability of the O-ring is high enough, as confirmed by the actual situation. The method in this paper can accurately and promptly calculate the reliability of the O-ring.
Author Contributions
Conflicts of Interest
List of Symbols/Nomenclature
| Symbols | Nomenclature | Definition | Unit |
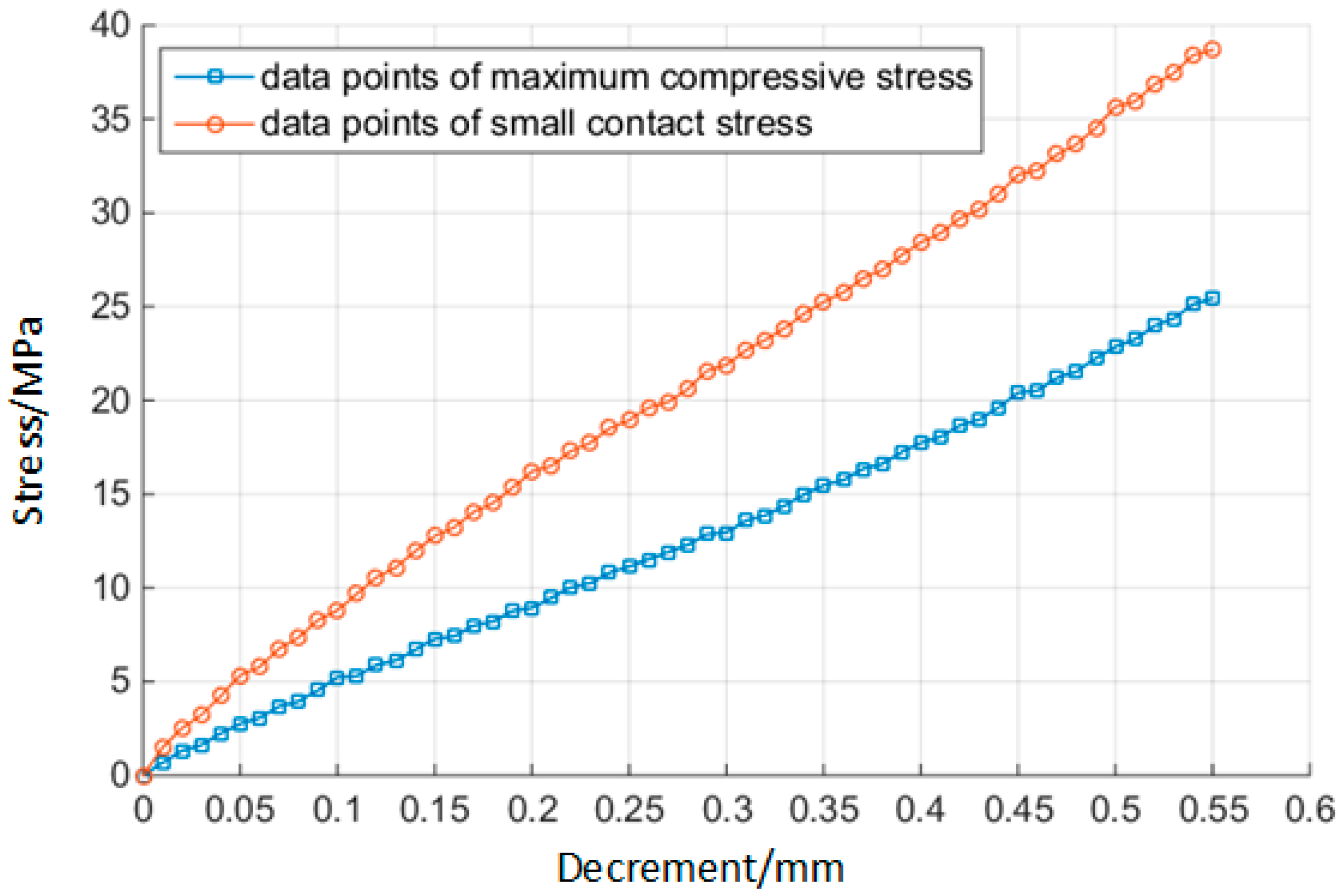
| The maximum compressive stress | The maximum value of the stress applied to the rubber during compression. | MPa | |
| and | The maximum contact stress | The maximum value of the stress generated by the contact surface when contacting each other. | MPa |
| The small contact stress | The minimum value between and . | MPa | |
| Limit stress | The stress value of the rubber in the compression process when the normal working capacity is lost. | MPa | |
| Oil pressure | The pressure of the hydraulic oil on O-ring during hydraulic system work. | MPa | |
| The maximum oil pressure | The maximum value of oil pressure. | MPa | |
| Decrement of O-ring | Decrement of O-ring during compression. | mm | |
| The mean of . | The mean of . | mm | |
| Material reliability | The probability that rubber material does not fail. | / | |
| Seal reliability | The probability of no leakage. | / | |
| System reliability | The probability of O-ring working properly. | / | |
| / | The upper limit of decrement | Decrement which satisfies with . | mm |
| / | The lower limit of decrement | Decrement which satisfies with . | mm |
| The limit of decrement | Decrement which satisfies with both and . | mm | |
| / | Contract properties | The properties of the two contact surface in ABAQUS. | / |
| / | Nephogram | A photograph of a cloud. | / |
| / | Deviation | The degree of deviation from the initial value. | % |
References
- Wang, C.J.; Lin, J.H. Seal Ring Structures with Reduced Moisture Induced Reliability Degradation a New Method. U.S. Patent 7,893,459, 10 April 2011. [Google Scholar]
- Chang, T.C.; Chen, S.B.; Cheng, T. Integrated Circuit Chip with Seal Ring Structure A New Method. U.S. Patent 8,242,586, 14 August 2012. [Google Scholar]
- ASME. Boiler and Pressure Vessel Code. 2017. Available online: http://go.asme.org/bpvc13 (accessed on 18 October 2017).
- ASTM. Standard Test Methods for Rubber O-Rings. 2015. Available online: https://www.astm.org/Standards/D1414.htm (accessed on 18 October 2017).
- Lee, J.Y.; Kumar, V.; Tang, X.W.; Lee, D.J. Mechanical and electrical behavior of rubber nanocomposites under static and cyclic strain. Compos. Sci. Technol. 2017, 142, 1–9. [Google Scholar] [CrossRef]
- Huang, R.H.; Zhang, X.; Tao, W. Study on aging of material for GIS sealing ring. In Proceedings of the TENCON 2015—2015 IEEE Region 10 Conference, Macao, China, 1–4 November 2015; IEEE Asia-Pacific Limited: Singapore, 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Shen, C.B.; Hai, Z.; Zhao, C.; Zhang, J.W.; John, L.E.; Michael, J.B.; Jeffrey, C.S. Packaging reliability effect of ENIG and ENEPIG surface finishes in board level thermal test under long-term aging and cycling. Materials 2017, 10, 451. [Google Scholar] [CrossRef] [PubMed]
- Marco, Y.; Huneau, B.; Masquelier, I.; Saux, V.L.; Charrier, P. Prediction of fatigue properties of natural rubber based on the descriptions of the cracks population and of the dissipated energy. Polym. Test. 2017, 59, 67–74. [Google Scholar] [CrossRef]
- Henning, S. Reliability of organic field-effect transistors. Adv. Mater. 2009, 21, 3859–3873. [Google Scholar] [CrossRef]
- Liu, L.; Li, X.Y.; Sun, F.Q.; Wang, N. A general accelerated degradation model based on the Wiener process. Materials 2016, 9, 981. [Google Scholar] [CrossRef] [PubMed]
- Okpin, N.; Cai, X.C.; Xi, Y.P. Corrosion prediction with parallel finite element modeling for coupled hygro-chemo transport into concrete under chloride-rich environment. Materials 2017, 10, 350. [Google Scholar] [CrossRef]
- Woo, C.S.; Kim, W.D.; Kim, J.D. A study on the material properties and fatigue life prediction of natural rubber component. Mater. Sci. Eng. 2008, 483, 376–381. [Google Scholar] [CrossRef]
- Fang, Y.F.; Xiong, J.B.; Tee, K.F. Time-variant structural fuzzy reliability analysis under stochastic loads applied several times. Struct. Eng. Mech. 2015, 3, 525–534. [Google Scholar] [CrossRef]
- Zuo, Z.G.; Liu, S.H.; Fan, Y.Z.; Wu, Y.L. Optimization of a centrifugal boiler circulating pump’s casing based on CFD and FEM analyses. Adv. Mech. Eng. 2014, 6, 1–10. [Google Scholar] [CrossRef]
- Li, Y.Q.; Hu, W.W.; Sun, Y.F.; Wang, Z.L.; Ali, M. A life prediction model of multilayered PTH based on fatigue mechanism. Materials 2017, 10, 382. [Google Scholar] [CrossRef] [PubMed]
- Wei, Z.L.; Wang, L.Q.; Guan, Y.; Yao, S.M.; Li, S.K. Static metal sealing mechanism of a subsea pipeline mechanical connector. Adv. Mech. Eng. 2016, 8, 1–16. [Google Scholar] [CrossRef]
- Gambino, P.J.; Graf, R.S.; Malinowski, J.C. Reliability of segmented edge seal ring for RF devices. In Proceedings of the IEEE International Interconnect Technology Conference, San Jose, CA, USA, 20–23 May 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 367–370. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, G.; Xia, P.; Li, H.P.; He, M. Finite element analysis and experimental study on contact pressure of hydraulic support bud-shaped composite sealing ring. Adv. Mech. Eng. 2016, 10, 1–9. [Google Scholar] [CrossRef]
- Mejri, M.; Cazuguel, M.; Cognard, J.Y. A time-variant reliability approach for ageing marine structures with non-linear behavior. Comput. Struct. 2011, 89, 1743–1753. [Google Scholar] [CrossRef]
- Jiang, C.; Ni, B.Y.; Han, X.; Tao, Y.R. Non-probabilistic convex model process: A new method of time-variant uncertainty analysis and its application to structural dynamic reliability problems. Comput. Methods Appl. Mech. Eng. 2014, 268, 656–676. [Google Scholar] [CrossRef]
- Mooney, R. A theory of large elastic deformation. J. Appl. Phys. 1940, 11, 582–592. [Google Scholar] [CrossRef]
- Rivlin, R.S. Large elastic deformation of isotropic material-IV: Further developments of the general theory. Philos. Trans. R. Soc. A 1948, 39, 761–767. [Google Scholar] [CrossRef]
- Tottn, G.E. Handbook of Hydraulic Fluid Technology, 2th ed.; Marcel Dekker: New York, NY, USA, 2011; pp. 62–69. ISBN 0824760220. [Google Scholar]
- Farsad, M.; Goch, G.; Evans, C. Application of correlation curve fitting to improve the absolute displacement measurement using speckle correlation. Precis. Eng. 2016, 46, 129–134. [Google Scholar] [CrossRef]
- Kamayaa, M.; Kitsunaib, Y.; Koshiishib, M. True stress-strain curve acquisition for irradiated stainless steel including the range exceeding necking strain. J. Nucl. Mater. 2015, 465, 316–325. [Google Scholar] [CrossRef]
- Lira, I. Monte Carlo evaluation of the uncertainty associated with the construction and use of a fitted curve. Measurement 2011, 44, 2156–2164. [Google Scholar] [CrossRef]
- Benjamin, S.B.; Wolter, J.F. Systems Engineering and Analysis, 5th ed.; Pearson Education: New York, NY, USA, 2010; pp. 149–173. ISBN 013221735X. [Google Scholar]
- Amlashi, H.; Moan, T. Ultimate strength analysis of a bulk carrier hull girder under alternate hold loading condition—A case study Part 1: Nonlinear finite element modeling and ultimate hull girder capacity. Mar. Struct. 2008, 21, 327–352. [Google Scholar] [CrossRef]
- Song, D.L.; Li, Y.; Zhang, K.F.; Liu, P.; Cheng, H.; Wu, T. Stress distribution modeling for interference-fit area of each individual layer around composite laminates joint. Compos. Part B 2015, 78, 469–479. [Google Scholar] [CrossRef]
- Care and Handing of Seals for Fluid Power Applications. Guide; BS 7714:2005; British Standards Institution: London, UK, 2005; ISBN 058044970X.
- Nogueira, I.; Fontes, C.; Sartori, I.; Pontes, K.; Embirucu, M. A model-based approach to quality monitoring of a polymerization process without online measurement of product specifications. Comput. Ind. Eng. 2017, 106, 123–136. [Google Scholar] [CrossRef]
| Parameters | Value |
|---|---|
| D (mm) | 3.60 |
| H (mm) | 2.10 |
| d (mm) | 2.65 |
| Input Parameters | Value |
|---|---|
| Time/Month | /MPa | /mm | /mm | |||
|---|---|---|---|---|---|---|
| 0 | 20.79 | 0.12 | 0.46 | 1 | 1 | 1 |
| 3 | 16.55 | 0.15 | 0.42 | 1 | 1 | 1 |
| 6 | 12.86 | 0.18 | 0.39 | 1 | 1 | 1 |
| 9 | 9.66 | 0.21 | 0.36 | 1 | 1 | 1 |
| 12 | 7.61 | 0.28 | 0.33 | 0.9831 | 0.9214 | 0.9044 |
| 15 | 5.06 | 0.42 | 0.31 | 0.7603 | 0 | 0 |
| 18 | 2.83 | out of range | 0.29 | 0.2398 | 0 | 0 |
| Time/Month | Deviation | Deviation | Deviation | |||
|---|---|---|---|---|---|---|
| 0 | 1 | 0.00% | 1 | 0.00% | 1 | 0.00% |
| 3 | 1 | 0.00% | 1 | 0.00% | 1 | 0.00% |
| 6 | 1 | 0.00% | 1 | 0.00% | 1 | 0.00% |
| 9 | 1 | 0.00% | 1 | 0.00% | 1 | 0.00% |
| 12 | 0.9835 | 0.04% | 0.9217 | 0.03% | 0.9048 | 0.04% |
| 15 | 0.7606 | 0.04% | 0 | 0.00% | 0 | 0.00% |
| 18 | 0.2399 | 0.04% | 0 | 0.00% | 0 | 0.00% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, B.; Sun, B.; Yan, M.; Ren, Y.; Zhang, W.; Zhou, K. Time-Variant Reliability Analysis for Rubber O-Ring Seal Considering Both Material Degradation and Random Load. Materials 2017, 10, 1211. https://doi.org/10.3390/ma10101211
Liao B, Sun B, Yan M, Ren Y, Zhang W, Zhou K. Time-Variant Reliability Analysis for Rubber O-Ring Seal Considering Both Material Degradation and Random Load. Materials. 2017; 10(10):1211. https://doi.org/10.3390/ma10101211
Chicago/Turabian StyleLiao, Baopeng, Bo Sun, Meichen Yan, Yi Ren, Weifang Zhang, and Kun Zhou. 2017. "Time-Variant Reliability Analysis for Rubber O-Ring Seal Considering Both Material Degradation and Random Load" Materials 10, no. 10: 1211. https://doi.org/10.3390/ma10101211






