L21 and XA Ordering Competition in Hafnium-Based Full-Heusler Alloys Hf2VZ (Z = Al, Ga, In, Tl, Si, Ge, Sn, Pb)
Abstract
:1. Introduction
2. Computational Details
3. Results and Discussion
3.1. Competition of L21 and XA Structure Ordering in Full-Heusler Hf2VZ Alloys
3.2. Structural and Mechanical Properties of Heusler-Based Hf2VZ with L21-Type Ordering
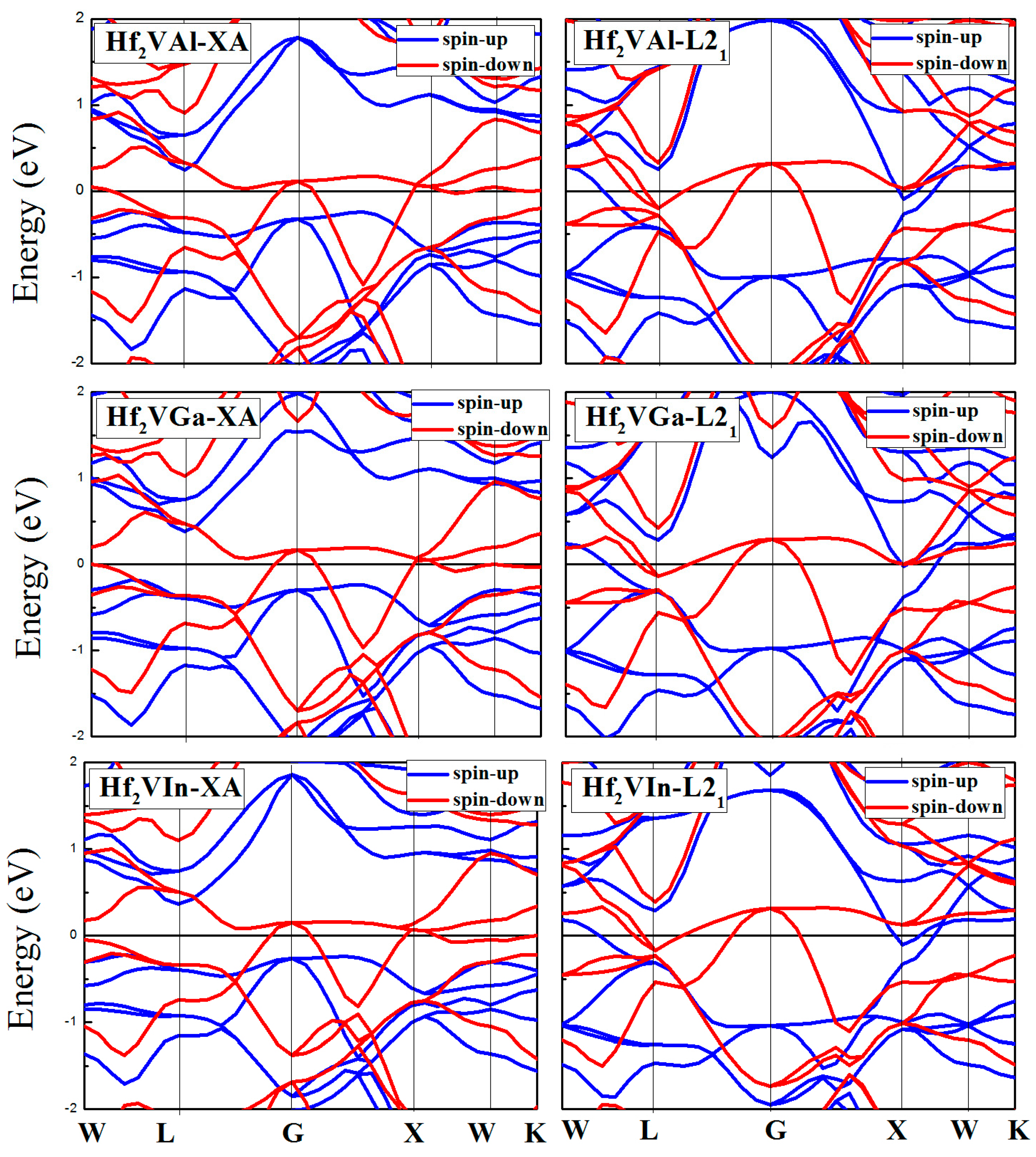
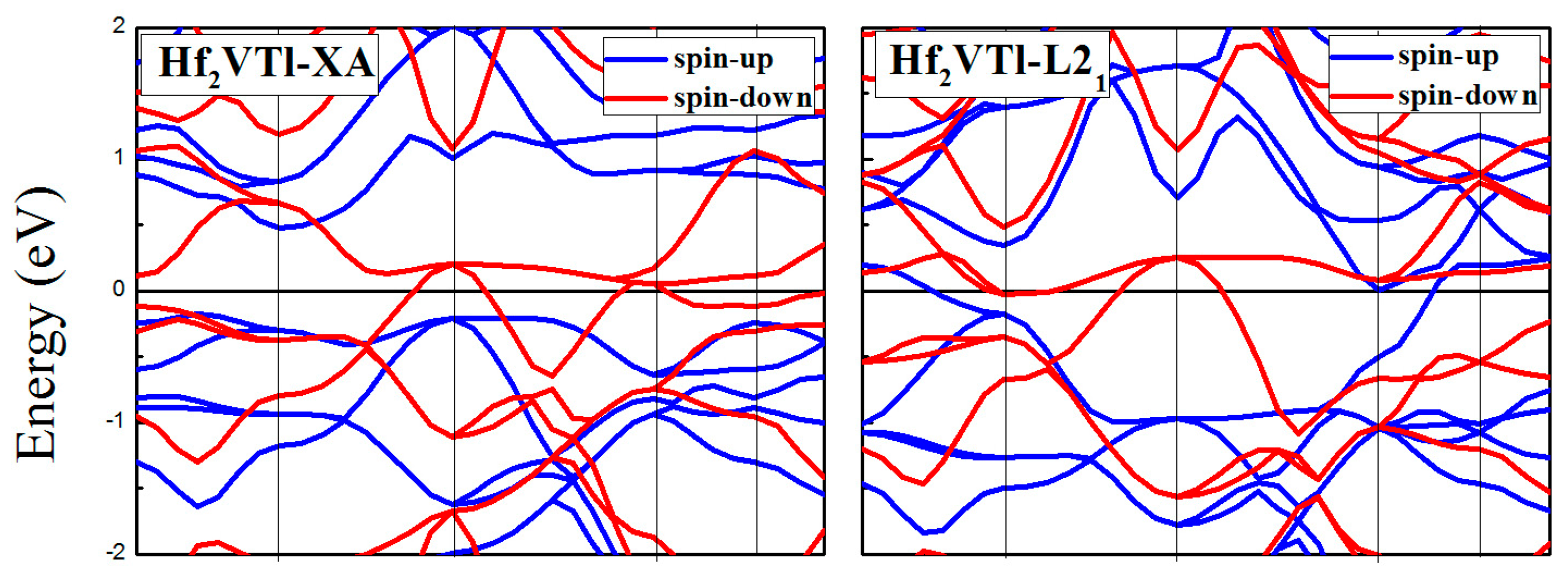
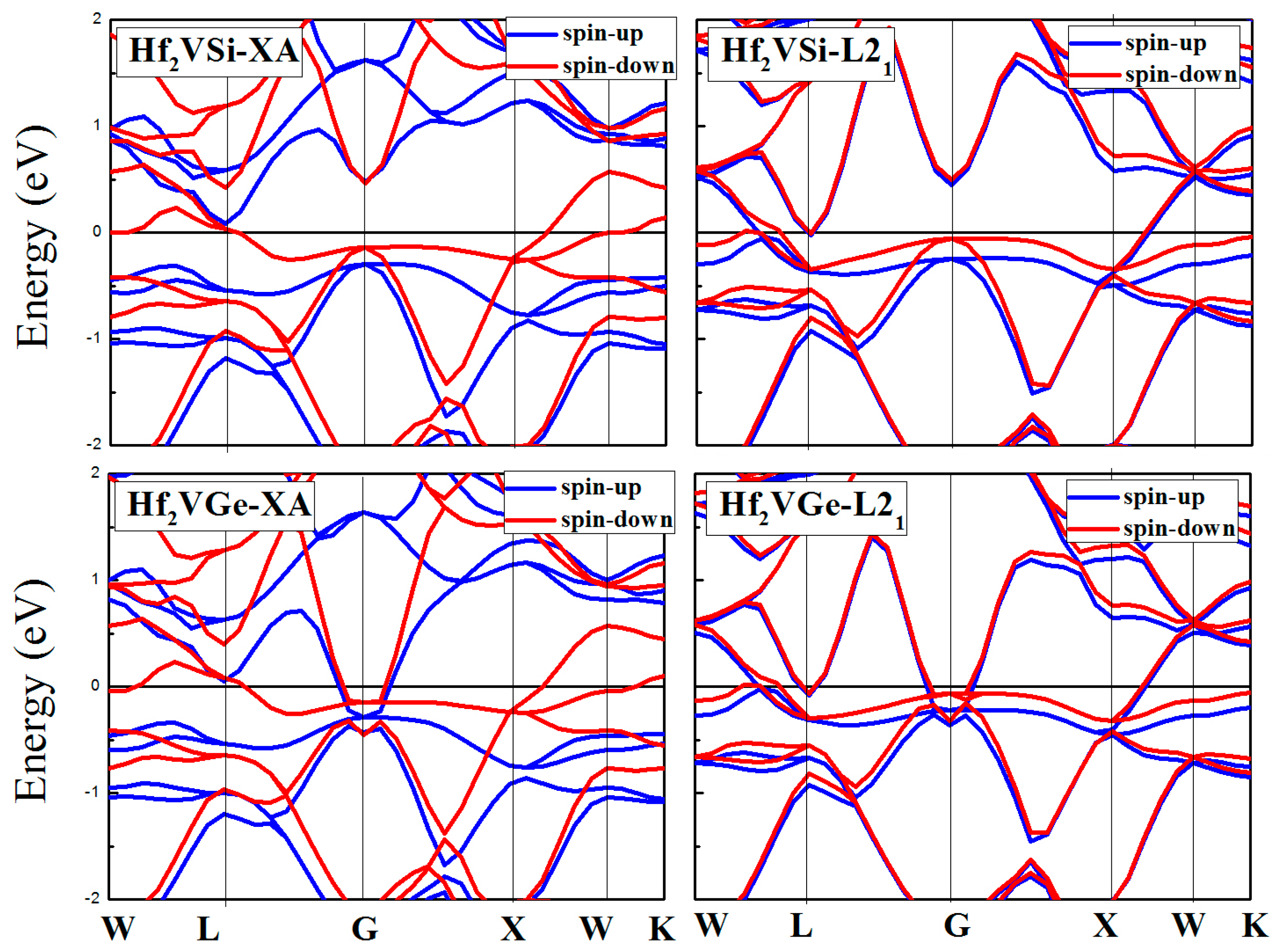
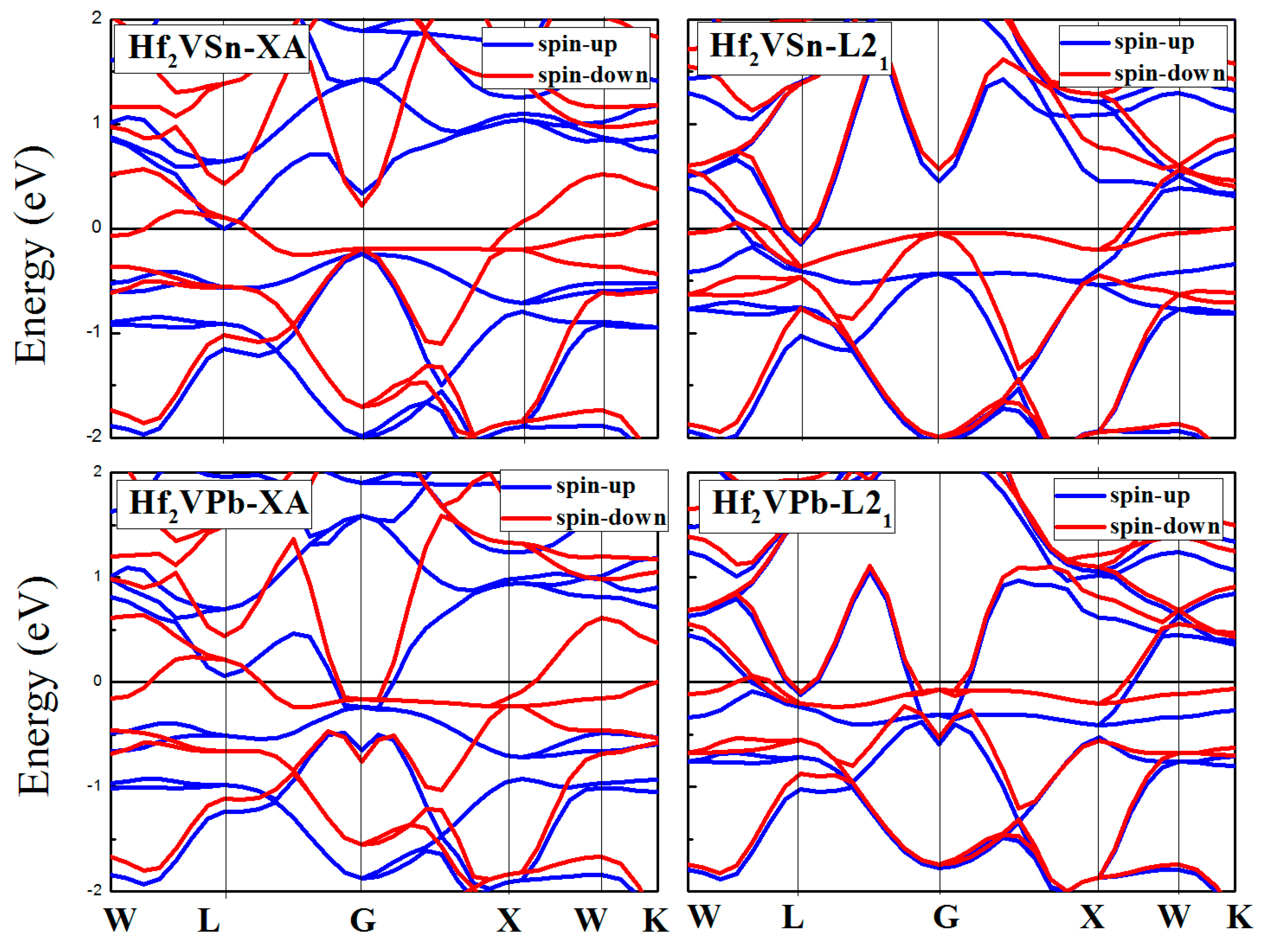
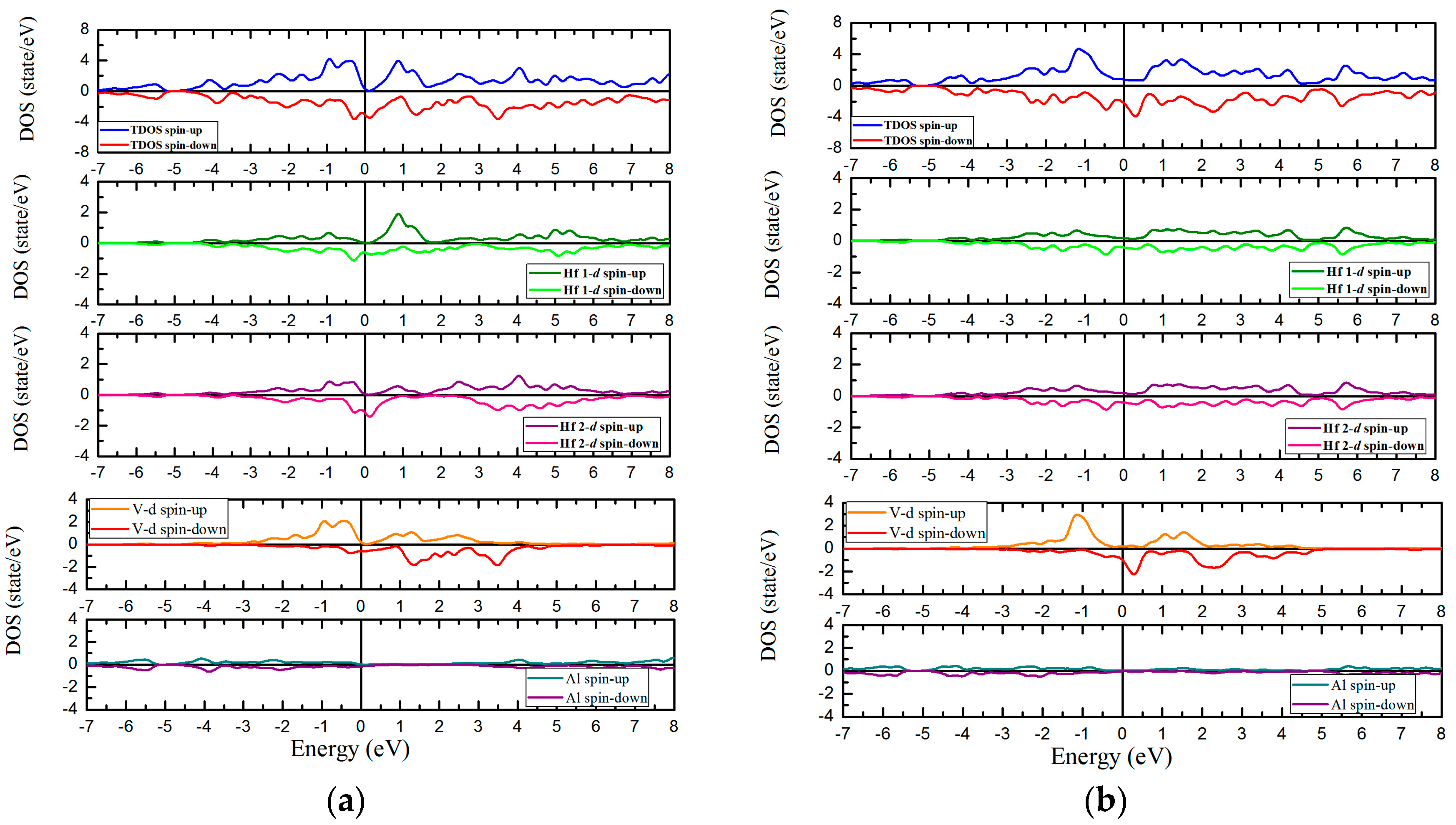
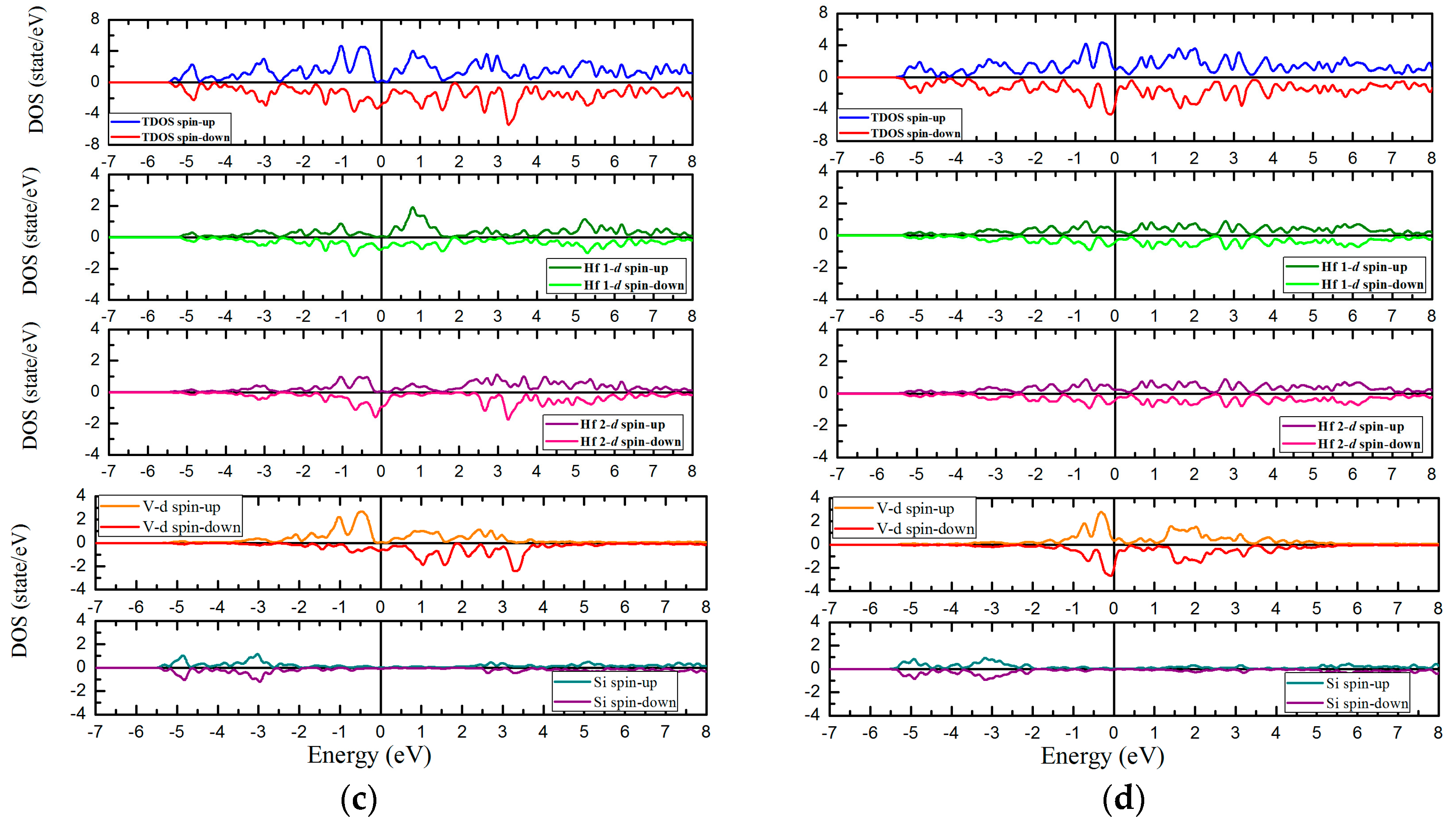
3.3. Calculated Electronic Behaviors of L21 and XA Types Hf2VZ
3.4. Magnetic and Slater-Pauling Properties of L21 and XA Types Hf2VZ
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hu, Y.; Zhang, J.M. The structural, electronic, magnetic, elastic properties of new Heusler alloys Hf2CrZ (Z = Al, Ga, In): A first-principles study. Solid State Commun. 2017, 259, 1–6. [Google Scholar] [CrossRef]
- Zhang, L.; Gao, Y.C. Electronic structures, magnetic properties and half-metallicity in the heusler alloy Hf2VAl. Chin. J. Phys. 2017, 55, 1466–1472. [Google Scholar] [CrossRef]
- Hu, Y.; Zhang, J.M. First-principles study of the Hf-based Heusler alloys: Hf2CoGa and Hf2CoIn. J. Magn. Magn. Mater. 2017, 421, 1–6. [Google Scholar] [CrossRef]
- Dahmane, F.; Mogulkoc, Y.; Doumi, B.; Tadjer, A.; Khenata, R.; Omran, S.B.; Rai, D.P.; Murtaza, G.; Varshney, D. Structural, electronic and magnetic properties of Fe2-based full Heusler alloys: A first principle study. J. Magn. Magn. Mater. 2016, 407, 167–174. [Google Scholar] [CrossRef]
- Bayar, E.; Kervan, N.; Kervan, S. Half-metallic ferrimagnetism in the Ti2CoAl Heusler compound. J. Magn. Magn. Mater. 2011, 323, 2945–2948. [Google Scholar] [CrossRef]
- Zhang, X.J.; Liu, Z.H.; Zhang, Y.J.; Liu, H.Y.; Liu, G.D.; Cui, Y.T.; Ma, X.Q. Theoretical and experimental study of the phase formation for Ti2YAl and Ti2Y’Ga (Y = Co, Fe; Y’ = Cr, Fe). Intermetallics 2016, 73, 26–30. [Google Scholar] [CrossRef]
- Wang, X.T.; Lin, T.T.; Rozale, H.; Dai, X.F.; Liu, G.D. Robust half-metallic properties in inverse heusler alloys composed of 4d transition metal elements: Zr2RhZ (Z = Al, Ga, In). J. Magn. Magn. Mater. 2016, 402, 190–195. [Google Scholar] [CrossRef]
- Deng, Z.Y.; Zhang, J.M. Half-metallic and magnetic properties of full-heusler alloys Zr2CrZ (Z = Ga, In) with Hg2CuTi-type structure: A first-principles study. J. Magn. Magn. Mater. 2016, 397, 120–124. [Google Scholar] [CrossRef]
- Fang, Q.L.; Zhang, J.M.; Xu, K.W. Magnetic properties and origin of the half-metallicity of Ti2MnZ (Z = Al, Ga, In, Si, Ge, Sn) Heusler alloys with the Hg2CuTi-type structure. J. Magn. Magn. Mater. 2014, 349, 104–108. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Z.; Lu, Z.; Xie, H.; Fang, W.; Li, S.; Liang, C.; Yin, F. The strain induced band gap modulation from narrow gap semiconductor to half-metal on Ti2CrGe: A first principles study. AIP Adv. 2015, 5, 156404. [Google Scholar] [CrossRef]
- Skaftouros, S.; Ozdogan, K.; Sasioglu, E.; Galanakis, I. Generalized Slater-Pauling rule for the inverse Heusler compounds. Phys. Rev. B 2013, 87, 4469–4487. [Google Scholar] [CrossRef]
- Skaftouros, S.; Ozdogan, K.; Sasıoglu, E.; Galanakis, I. Search for spin gapless semiconductors: The case of inverse Heusler compounds. Appl. Phys. Lett. 2013, 102, 022402. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.M.; Xu, G.Z.; Du, Y.; Liu, E.K.; Liu, Z.Y.; Liu, G.D.; Wang, W.H.; Wu, G.H. Phase stability, magnetism and generalized electron-filling rule of vanadium-based inverse Heusler compounds. EPL 2013, 104, 27012. [Google Scholar] [CrossRef]
- Jakobsson, A.; Mavropoulos, P.; Sasioglu, E.; Blugel, S.; Lezaic, M.; Sanyal, B.; Galanakis, I. First-principles calculations of exchange interactions, spin waves, and temperature dependence of magnetization in inverse-Heusler-based spin gapless semiconductors. Phys. Rev. B 2015, 91, 2445–2447. [Google Scholar] [CrossRef]
- Li, J.; Jin, Y. Half-metallicity of the inverse heusler alloy Mn2CoAl (001) surface: A first-principles study. Appl. Surf. Sci. 2013, 283, 876–880. [Google Scholar] [CrossRef]
- Wang, X.T.; Cheng, Z.X.; Liu, G.D. Largest magnetic moments in the half-Heusler alloys XCrZ (X = Li, K, Rb, Cs; Z = S, Se, Te): A first-principles study. Materials 2017, 10, 1078. [Google Scholar] [CrossRef] [PubMed]
- Galanakis, I.; Ozdogan, K.; Sasioglu, E.; Blugel, S. Conditions for spin-gapless semiconducting behavior in Mn2CoAl inverse heusler compound. J. Appl. Phys. 2014, 115, 668. [Google Scholar] [CrossRef]
- Feng, W.; Fu, X.; Wan, C.; Yuan, Z.; Han, X.; Quang, N.V.; Cho, S. Spin gapless semiconductor like Ti2MnAl film as a new candidate for spintronics application. Phys. Status Solidi RRL Rapid Res. Lett. 2016, 9, 641–645. [Google Scholar] [CrossRef]
- Birsan, A.; Palade, P.; Kuncser, V. Prediction of half metallic properties in Ti2CoSi Heusler alloy based on density functional theory. J. Magn. Magn. Mater. 2013, 331, 109–112. [Google Scholar] [CrossRef]
- Bainsla, L.; Mallick, A.I.; Raja, M.M.; Coelho, A.A.; Nigam, A.K.; Johnson, D.D.; Alam, A.; Suresh, K.G. Origin of spin gapless semiconductor behavior in CoFeCrGa: Theory and experiment. Phys. Rev. B Condens. Matter. 2015, 92, 45201. [Google Scholar] [CrossRef]
- Groot, R.A.D.; Mueller, F.M.; Engen, P.G.V.; Buschow, K.H.J. New class of materials: Half-metallic ferromagnets. Phys. Rev. Lett. 1983, 50, 2024–2027. [Google Scholar] [CrossRef]
- Luo, H.; Xin, Y.; Liu, B.; Meng, F.; Liu, H.; Liu, E.; Wu, G. Competition of L21, and XA structural ordering in heusler alloys X2CuAl (X = Sc, Ti, V, Cr, Mn, Fe, Co, Ni). J. Alloys Compd. 2016, 665, 180–185. [Google Scholar] [CrossRef]
- Payne, M.C.; Teter, M.P.; Allan, D.C.; Arias, T.A.; Joannopoulos, J.D. Iterative minimization techniques for ab initio total-energy calculations: Molecular dynamics and conjugate gradients. Rev. Mod. Phys. 1992, 64, 1045. [Google Scholar] [CrossRef]
- Segall, M.D.; Lindan, P.J.; Probert, M.A.; Pickard, C.J.; Hasnip, P.J.; Clark, S.J.; Payne, M.C. First-principles simulation: Ideas, illustrations and the CASTEP code. J. Phys. Condens. Matter 2002, 14, 2717–2744. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Qin, G.; Wu, W.; Hu, S.; Tao, Y.; Yan, X.; Jing, C.; Li, X.; Gu, H.; Cao, S.; Ren, W. Effect of swap disorder on the physical properties of the quaternary heusler alloy PdMnTiAl: A first-principles study. IUCrJ 2017, 4, 506–511. [Google Scholar] [CrossRef] [PubMed]
- Galehgirian, S.; Ahmadian, F. First principles study on half-metallic properties of heusler compounds Ti2VZ (Z = Al, Ga, and In). Solid State Commun. 2015, 202, 52–57. [Google Scholar] [CrossRef]
- Lukashev, P.; Kharel, P.; Gilbert, S.; Staten, B.; Hurley, N.; Fuglsby, R.; Huh, Y.; Valloppilly, S.; Zhang, W.; Yang, K.; et al. Investigation of spin-gapless semiconductivity and half-metallicity in Ti2MnAl-based compounds. Appl. Phys. Lett. 2016, 108, 156404. [Google Scholar] [CrossRef]
- Wang, X.; Cheng, Z.; Wang, J.; Liu, G. A full spectrum of spintronic properties demonstrated by a C1b-type Heusler compound Mn2Sn subjected to strain engineering. J. Mater. Chem. C 2016, 4, 8535–8544. [Google Scholar] [CrossRef]
- Benkaddour, K.; Chahed, A.; Amar, A.; Rozale, H.; Lakdja, A.; Benhelal, O.; Sayede, A. First-principles study of structural, elastic, thermodynamic, electronic and magnetic properties for the quaternary Heusler alloys CoRuFeZ (Z = Si, Ge, Sn). J. Alloys Compd. 2016, 687, 211–220. [Google Scholar] [CrossRef]
- Gooch, J.W. Elastic Constant; Springer: New York, NY, USA, 2011. [Google Scholar]
- Zhao, J.S.; Gao, Q.; Li, L.; Xie, H.H.; Hu, X.R.; Xu, C.L.; Deng, J.-B. First-principles study of the structure, electronic, magnetic and elastic properties of half-Heusler compounds LiXGe (X = Ca, Sr and Ba). Intermetallics 2017, 89, 65–73. [Google Scholar] [CrossRef]
- Born, M.; Huang, K. Dynamical Theory of Crystal Lattices; Clarendon Press: Oxford, UK, 1954. [Google Scholar]
- Wang, X.T.; Cheng, Z.X.; Wang, J.L.; Rozale, H.; Wang, L.Y.; Yu, Z.Y.; Liu, G.D. Strain-induced diverse transitions in physical nature in the newly designed inverse Heusler alloy Zr2MnAl. J. Alloys Compd. 2016, 686, 549–555. [Google Scholar] [CrossRef]
- Wang, X.; Cheng, Z.; Khenata, R.; Wu, Y.; Wang, L.; Liu, G. Lattice constant changes leading to significant changes of the spin-gapless features and physical nature in a inverse heusler compound Zr2MnGa. J. Magn. Magn. Mater. 2017, 444, 313–318. [Google Scholar] [CrossRef]
- Ahmadian, F. Half-metallic ferromagnetism in the Ti2FeGe Heusler compound: A first-principles study. J. Supercond. Nov. Magn. 2013, 26, 381–388. [Google Scholar] [CrossRef]
- Galanakis, I.; Dederichs, P.H.; Papanikolaou, N. Slater-Pauling behavior and origin of the half-metallicity of the full-Heusler alloys. Phys. Rev. B 2002, 66, 553–562. [Google Scholar] [CrossRef]
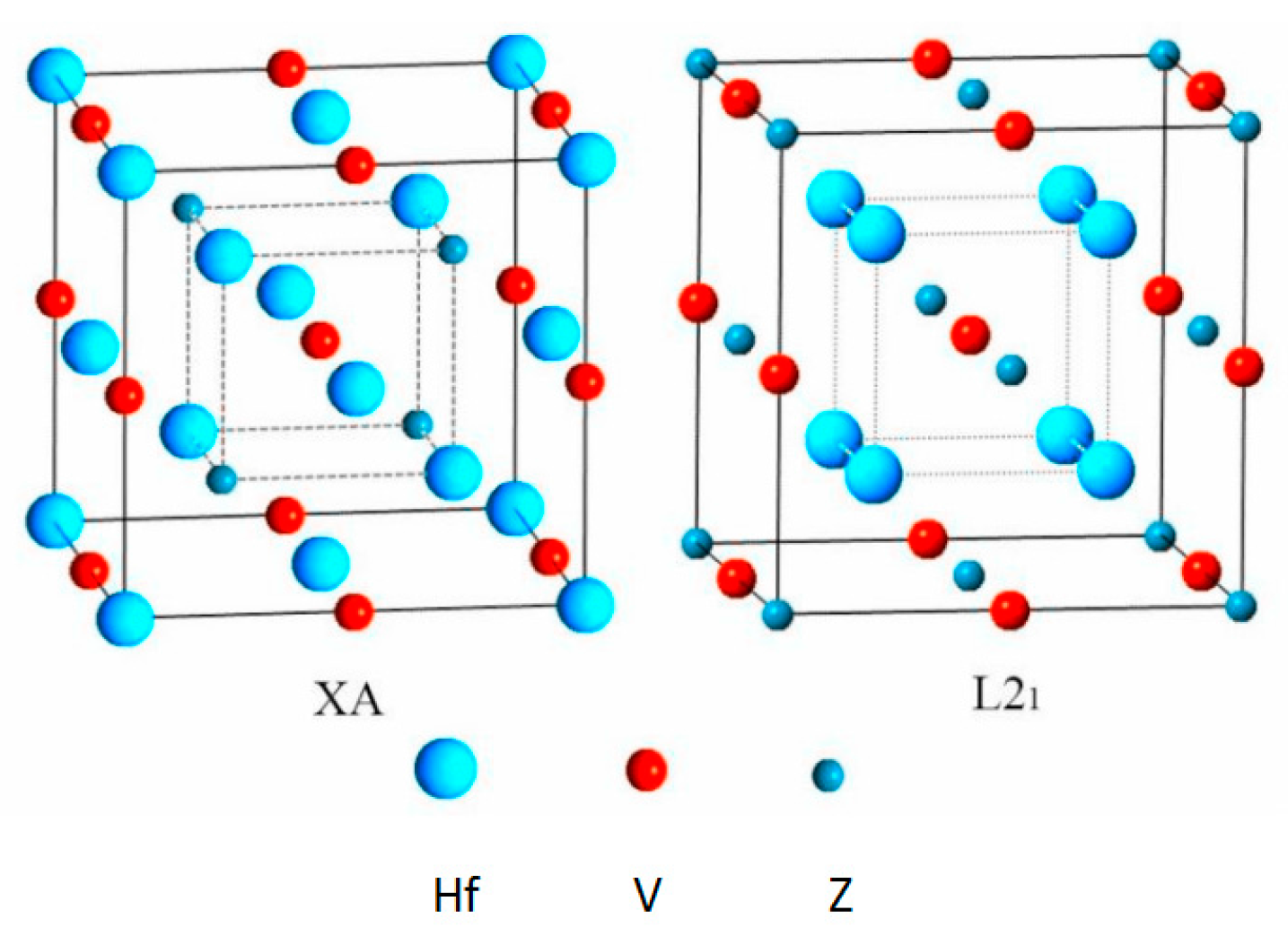
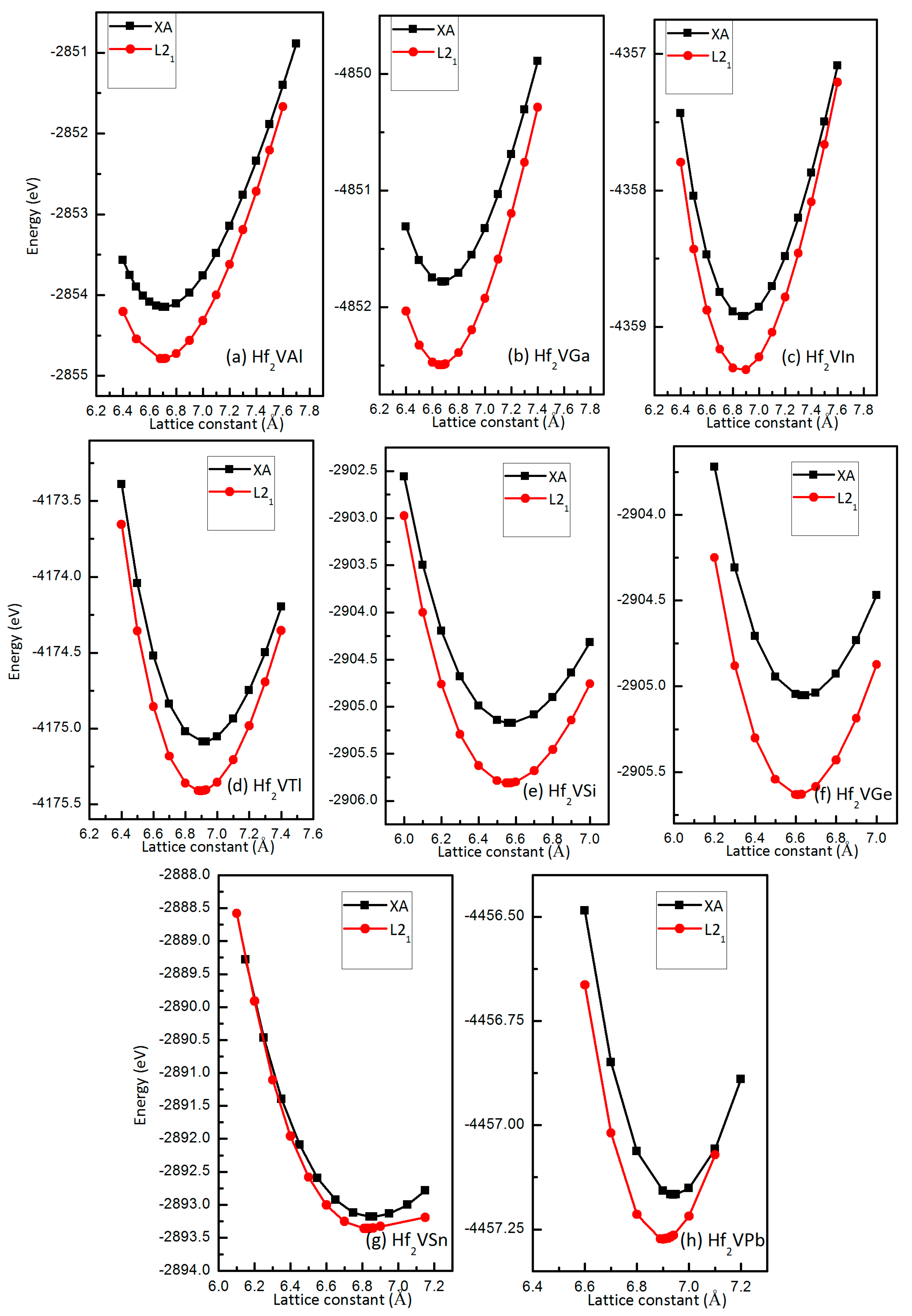
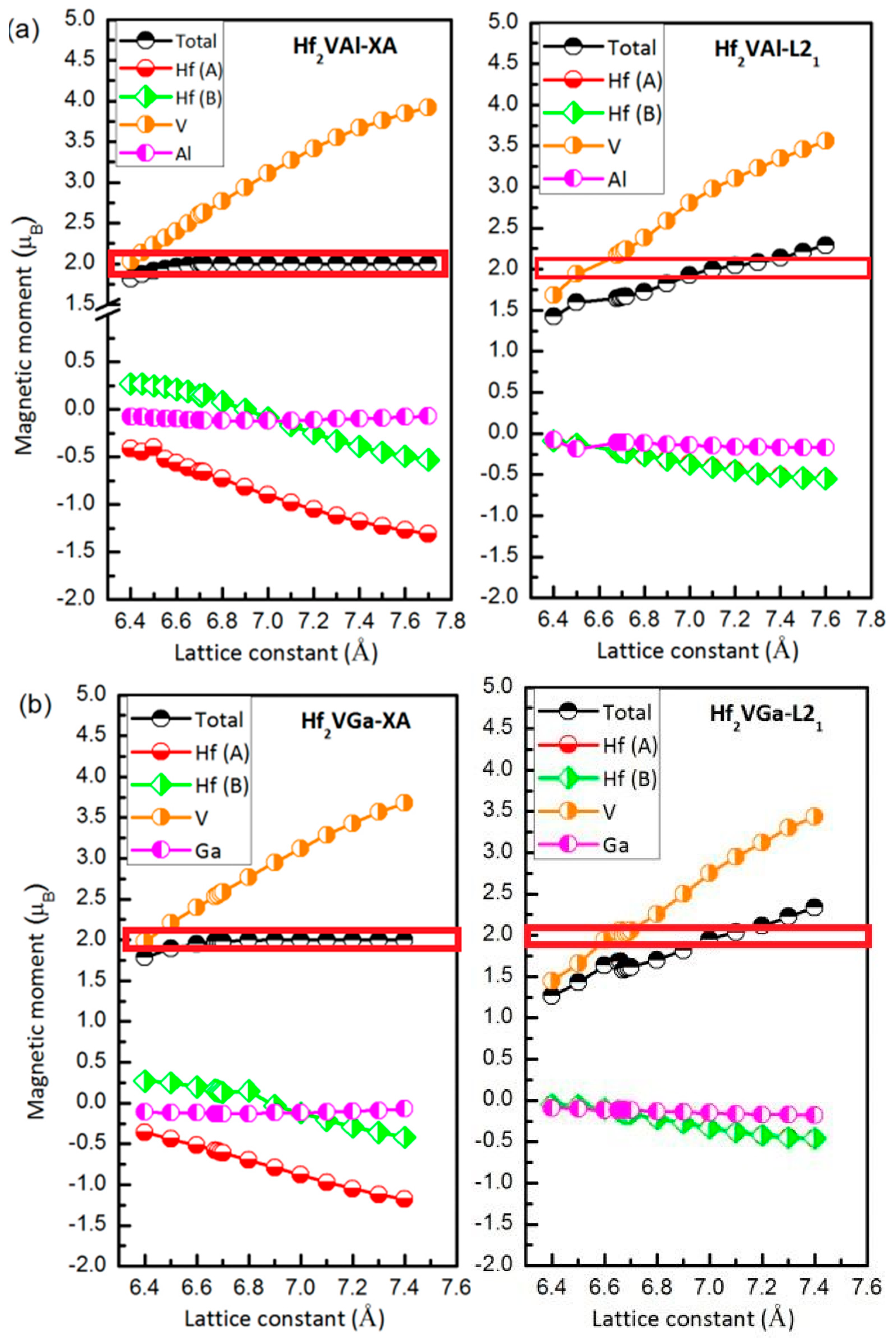
| Alloy | Structure | ΔE (eV/cell) | a (Å) | Mt (μB/f.u.) | MHf 1 (μB) | MHf 2 (μB) | MV (μB) | MZ (μB) | Stable Structure |
|---|---|---|---|---|---|---|---|---|---|
| Hf2VAl | XA | 0.64 | 6.71 | 2 | −0.65 | 0.14 | 2.62 | −0.12 | L21 |
| L21 | 6.69 | 1.65 | −0.21 | −0.21 | 2.19 | −0.11 | |||
| Hf2VGa | XA | 0.71 | 6.68 | 1.99 | −0.59 | 0.15 | 2.55 | −0.13 | L21 |
| L21 | 6.66 | 1.68 | −0.13 | −0.13 | 2.06 | −0.12 | |||
| Hf2VIn | XA | 0.39 | 6.88 | 2 | −0.75 | −0.01 | 2.88 | −0.12 | L21 |
| L21 | 6.90 | 1.70 | −0.24 | −0.24 | 2.31 | −0.13 | |||
| Hf2VTl | XA | 0.32 | 6.92 | 1.98 | −0.79 | −0.1 | 3.0 | −0.12 | L21 |
| L21 | 6.89 | 1.61 | −0.17 | −0.17 | 2.06 | −0.11 | |||
| Hf2VSi | XA | 0.63 | 6.57 | 1.02 | −0.74 | −0.25 | 2.08 | −0.06 | L21 |
| L21 | 6.56 | 0.24 | −0.03 | −0.03 | 0.31 | −0.01 | |||
| Hf2VGe | XA | 0.58 | 6.64 | 1.03 | −0.83 | −0.34 | 2.26 | −0.06 | L21 |
| L21 | 6.61 | 0.2 | −0.02 | −0.02 | 0.26 | −0.01 | |||
| Hf2VSn | XA | 0.18 | 6.85 | 1 | −1.07 | −0.51 | 2.64 | −0.05 | L21 |
| L21 | 6.82 | 0.49 | −0.06 | −0.06 | 0.63 | −0.03 | |||
| Hf2VPb | XA | 0.11 | 6.94 | 1 | −1.17 | −0.63 | 2.87 | −0.04 | L21 |
| L21 | 6.90 | 0.32 | −0.03 | −0.03 | 0.41 | −0.02 |
| Alloy | C11 | C12 | C44 | B | G | E | B/G | Formation Energy | Anisotropy Factor |
|---|---|---|---|---|---|---|---|---|---|
| Hf2VAl | 164.4 | 117.6 | 73.0 | 133.2 | 46.8 | 124.6 | 2.8 | −0.54 | 3.10 |
| Hf2VGa | 143 | 104.3 | 72.9 | 117.9 | 43.0 | 115.10 | 2.7 | −1.19 | 3.76 |
| Hf2VIn | 179.8 | 154.3 | 49.7 | 162.8 | 28.9 | 82.0 | 5.6 | −0.05 | 3.89 |
| Hf2VTl | 110.4 | 100.1 | 46.8 | 103.5 | 20.5 | 57.9 | 5.0 | −0.85 | 9.08 |
| Hf2VSi | 191 | 146.9 | 63.7 | 161.6 | 41.6 | 115.12 | 3.8 | −0.66 | 2.88 |
| Hf2VGe | 158.2 | 123.1 | 54.1 | 134.8 | 34.5 | 95.4 | 3.9 | −0.41 | 3.08 |
| Hf2VSn | 187.5 | 155.6 | 42.2 | 166.2 | 28.5 | 81.1 | 5.8 | −0.07 | 2.64 |
| Hf2VPb | 109.1 | 97.9 | 18.2 | 101.6 | 11.4 | 32.9 | 8.9 | −0.91 | 3.25 |
| Alloy | Structure | CBM | VBM | Band Gap | Half-Metallic Gap | p (%) |
|---|---|---|---|---|---|---|
| Hf2VAl | XA | 0.23 | −0.23 | 0.46 | 0.23 | 100 |
| L21 | - | - | - | - | 48 | |
| Hf2VGa | XA | 0.36 | −0.23 | 0.59 | 0.23 | 100 |
| L21 | - | - | - | - | 52 | |
| Hf2VIn | XA | 0.37 | −0.22 | 0.59 | 0.22 | 100 |
| L21 | - | - | - | - | 36 | |
| Hf2VTl | XA | 0.47 | −0.17 | 0.64 | 0.17 | 100 |
| L21 | - | - | - | - | 40 | |
| Hf2VSi | XA | 0.07 | −0.28 | 0.35 | 0.07 | 100 |
| L21 | - | - | - | - | 39 | |
| Hf2VGe | XA | - | - | - | - | 88 |
| L21 | - | - | - | - | 33 | |
| Hf2VSn | XA | 0.04 | −0.26 | 0.30 | 0.04 | 100 |
| L21 | - | - | - | - | 56 | |
| Hf2VPb | XA | - | - | - | - | 94 |
| L21 | - | - | - | - | 36 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Cheng, Z.; Wang, W. L21 and XA Ordering Competition in Hafnium-Based Full-Heusler Alloys Hf2VZ (Z = Al, Ga, In, Tl, Si, Ge, Sn, Pb). Materials 2017, 10, 1200. https://doi.org/10.3390/ma10101200
Wang X, Cheng Z, Wang W. L21 and XA Ordering Competition in Hafnium-Based Full-Heusler Alloys Hf2VZ (Z = Al, Ga, In, Tl, Si, Ge, Sn, Pb). Materials. 2017; 10(10):1200. https://doi.org/10.3390/ma10101200
Chicago/Turabian StyleWang, Xiaotian, Zhenxiang Cheng, and Wenhong Wang. 2017. "L21 and XA Ordering Competition in Hafnium-Based Full-Heusler Alloys Hf2VZ (Z = Al, Ga, In, Tl, Si, Ge, Sn, Pb)" Materials 10, no. 10: 1200. https://doi.org/10.3390/ma10101200







