Investigation of the Microstructure Evolution in a Fe-17Mn-1.5Al-0.3C Steel via In Situ Synchrotron X-ray Diffraction during a Tensile Test
Abstract
:1. Introduction
2. Material and Methods
2.1. Materials and Processing
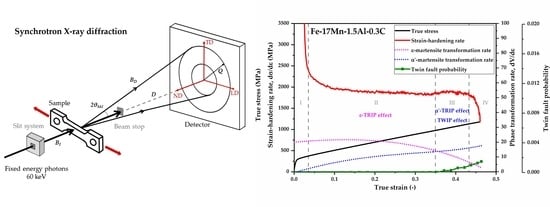
2.2. In Situ Tensile Test Tracked by Synchrotron X-ray Diffraction
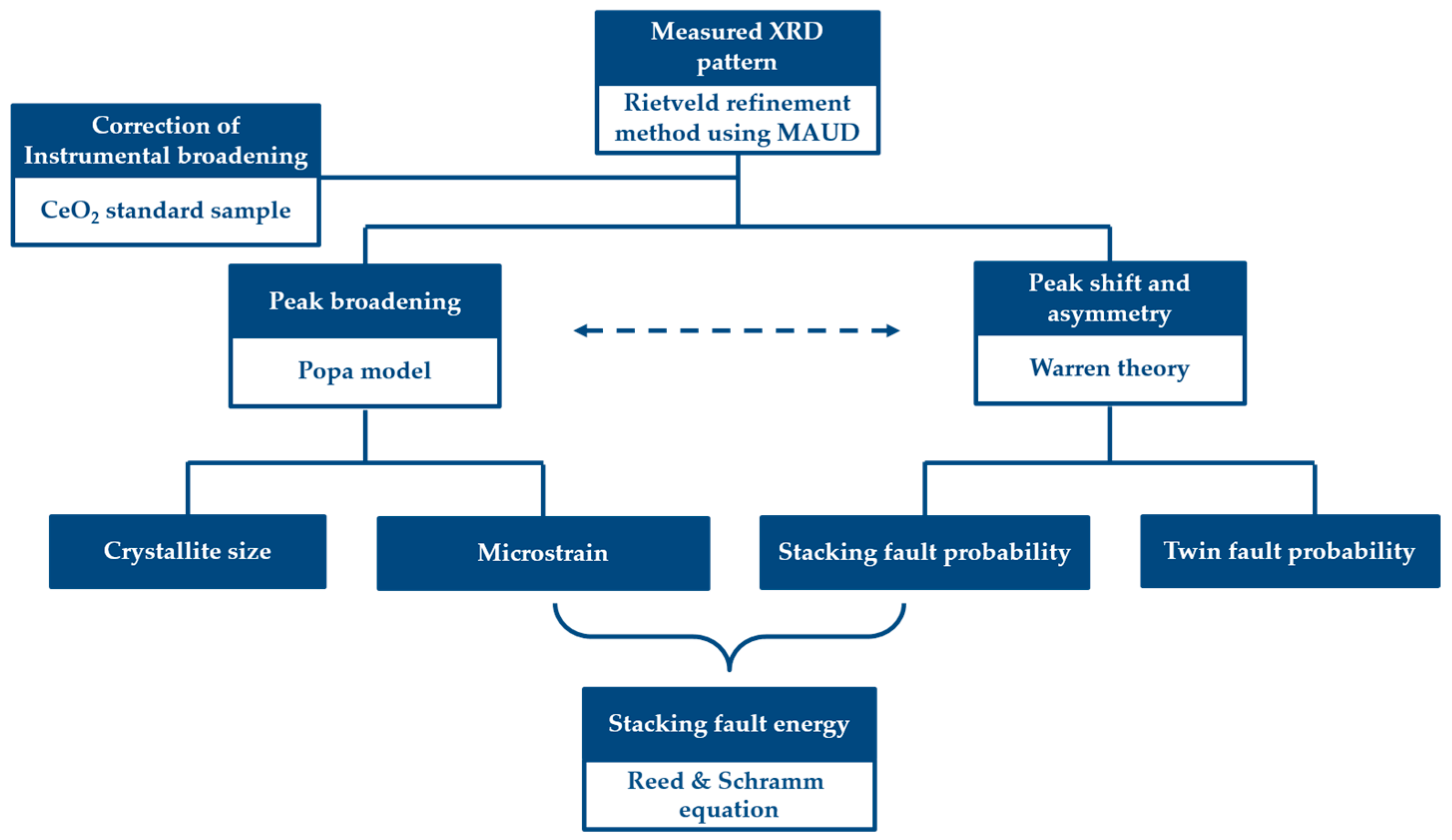
2.3. Quantitative Microstructure Analysis by the Rietveld Refinement Method
3. Results
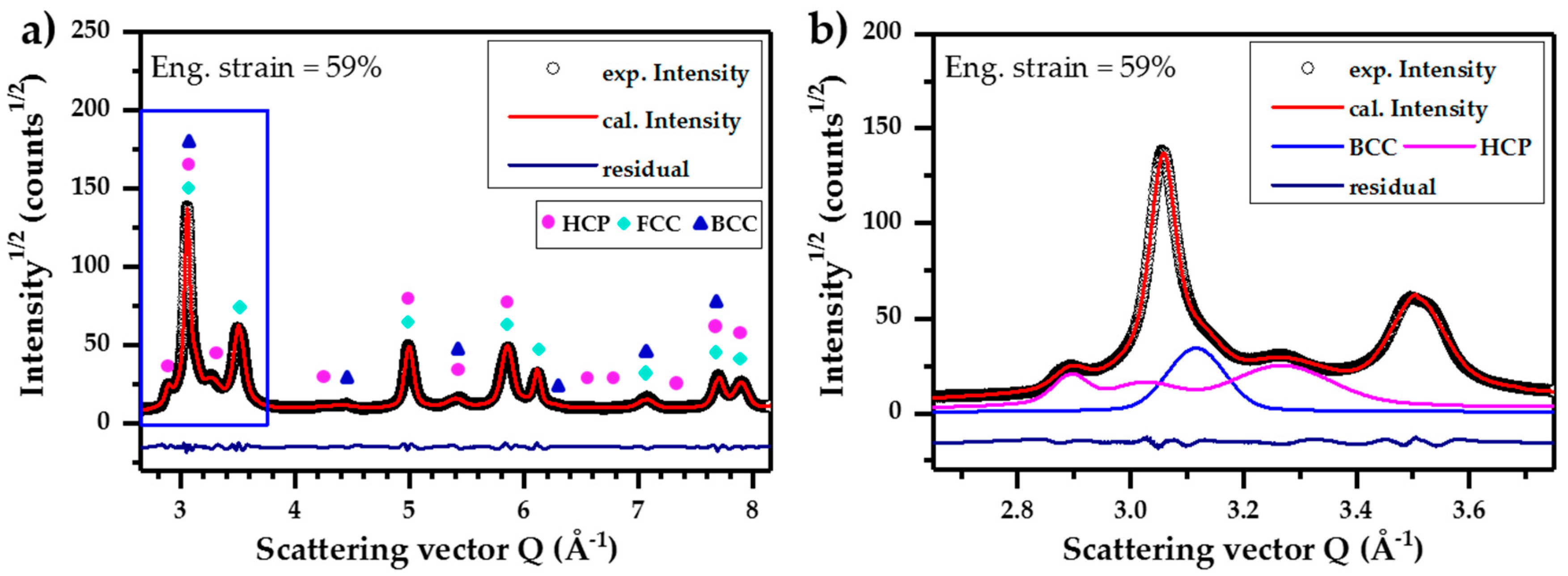
3.1. Microstructure Characterization
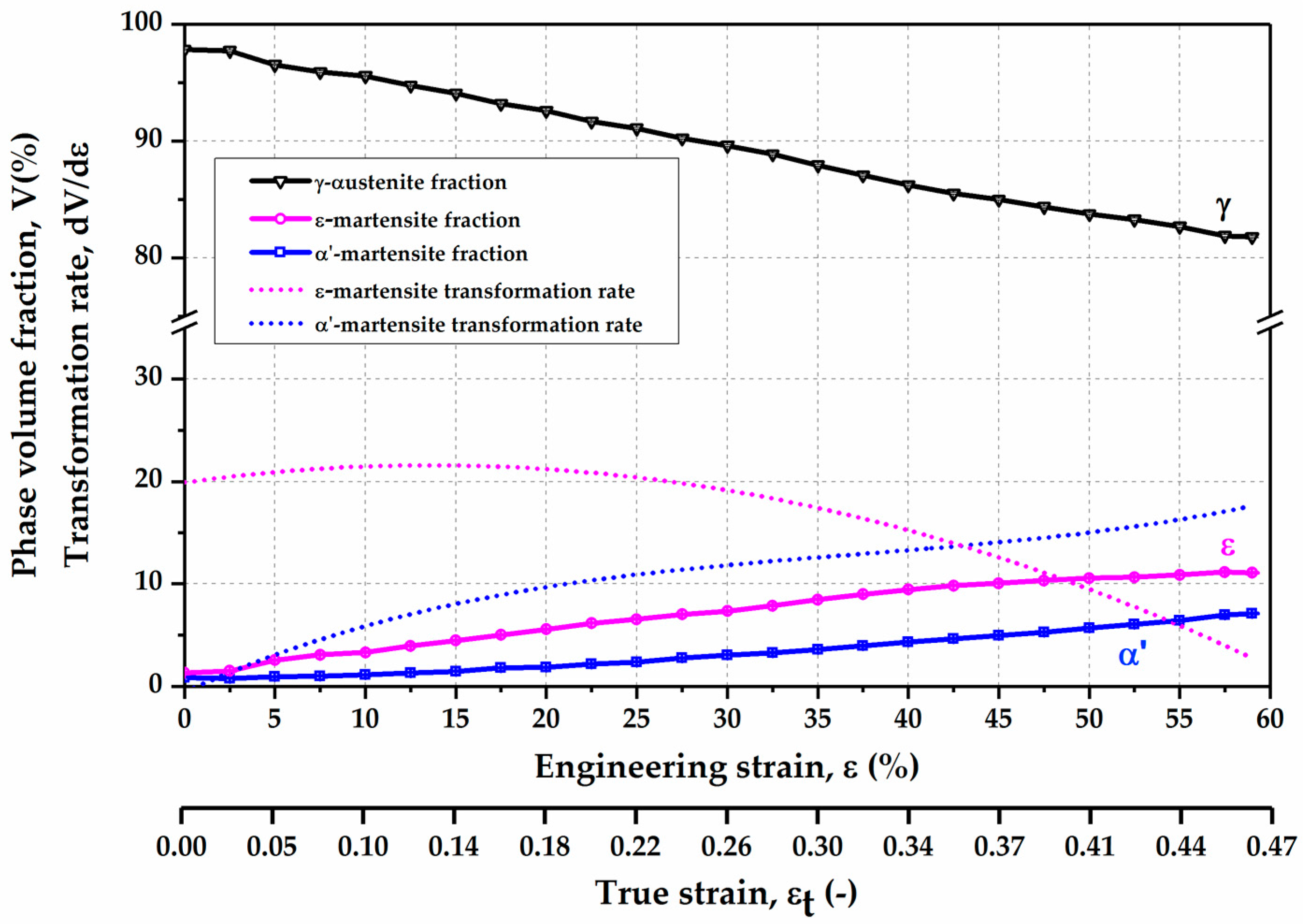
3.1.1. Phase Evolution
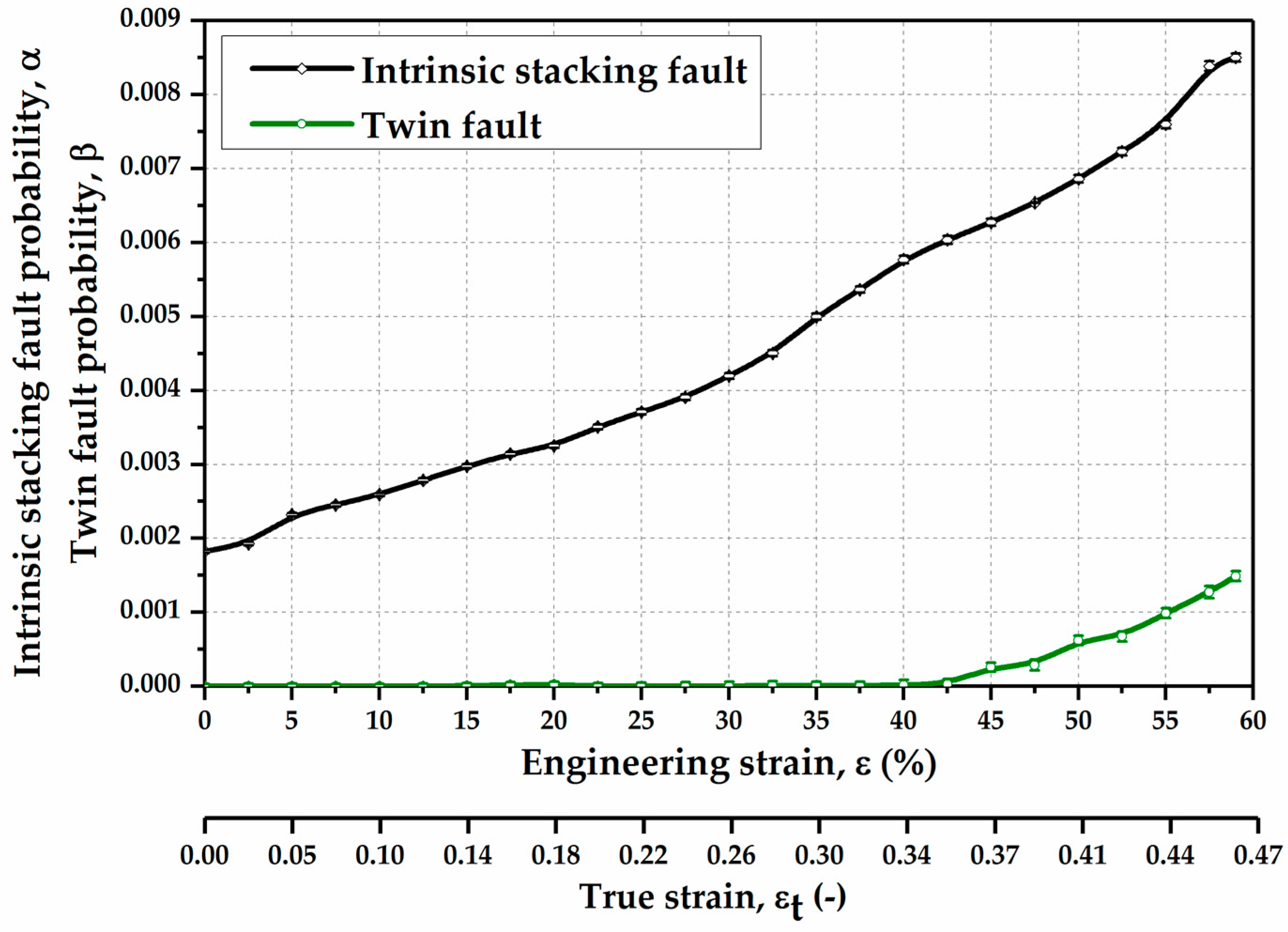
3.1.2. Planar Defects Evolution
3.2. SFE Evaluation
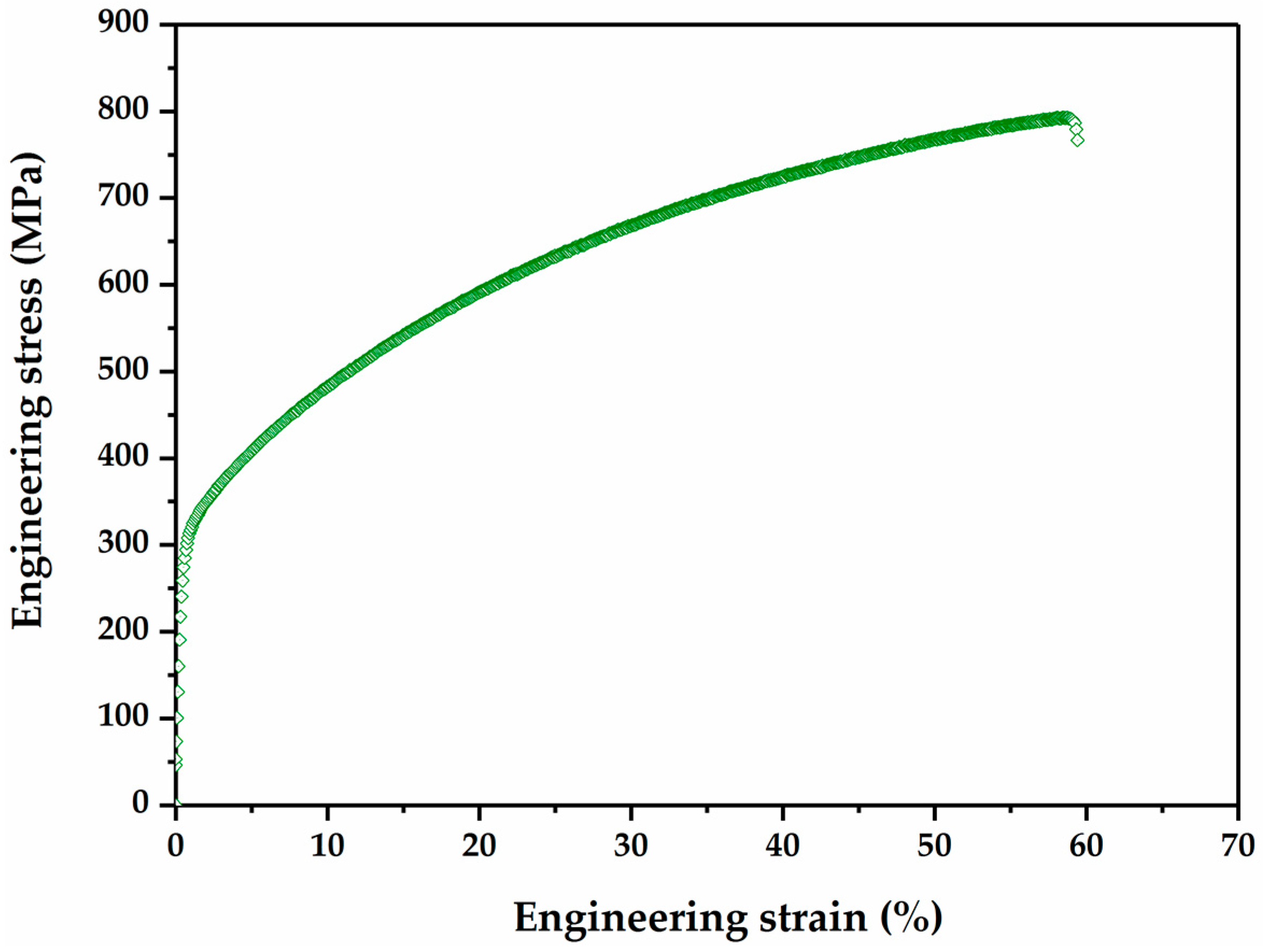
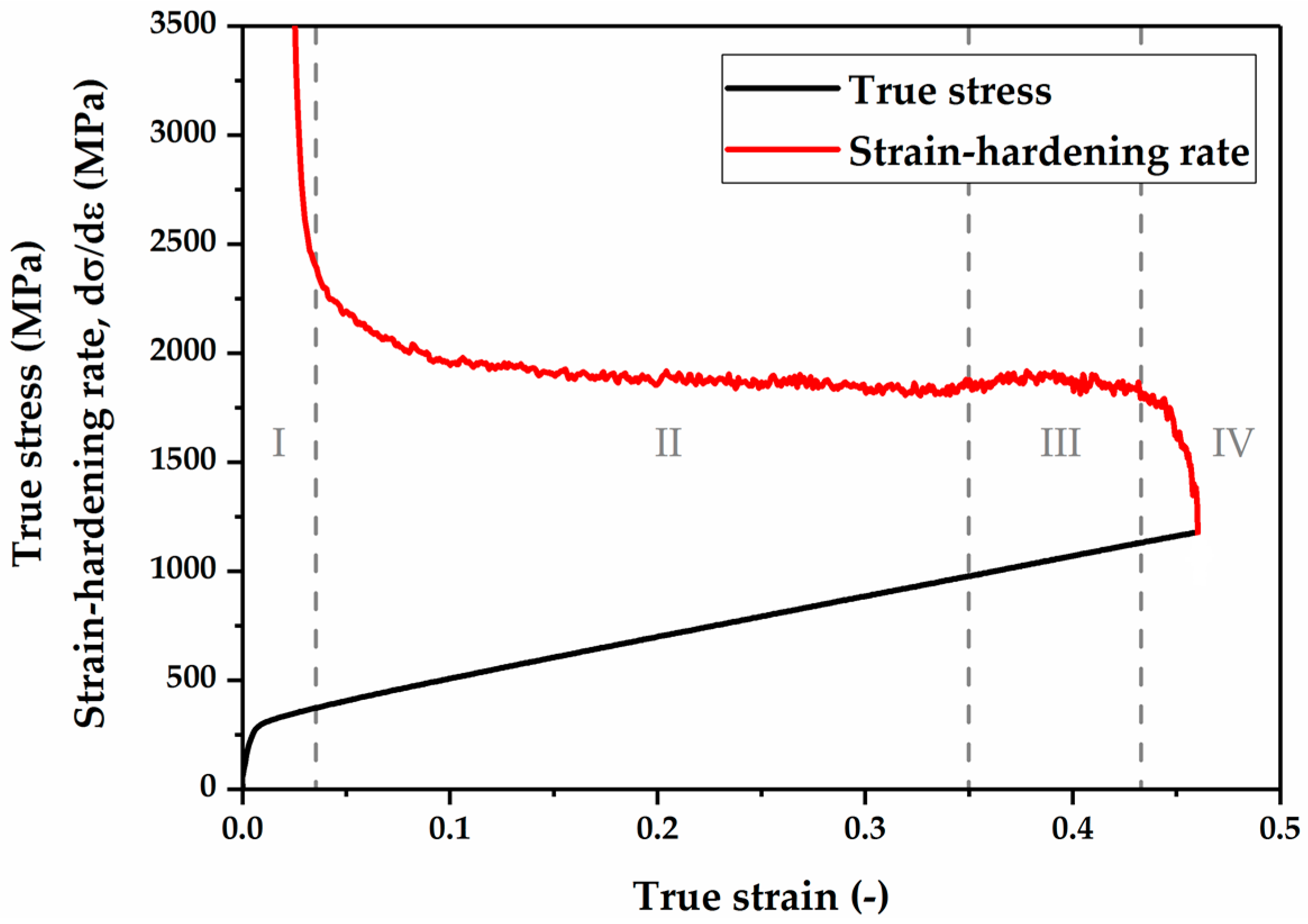
3.3. Tensile Properties
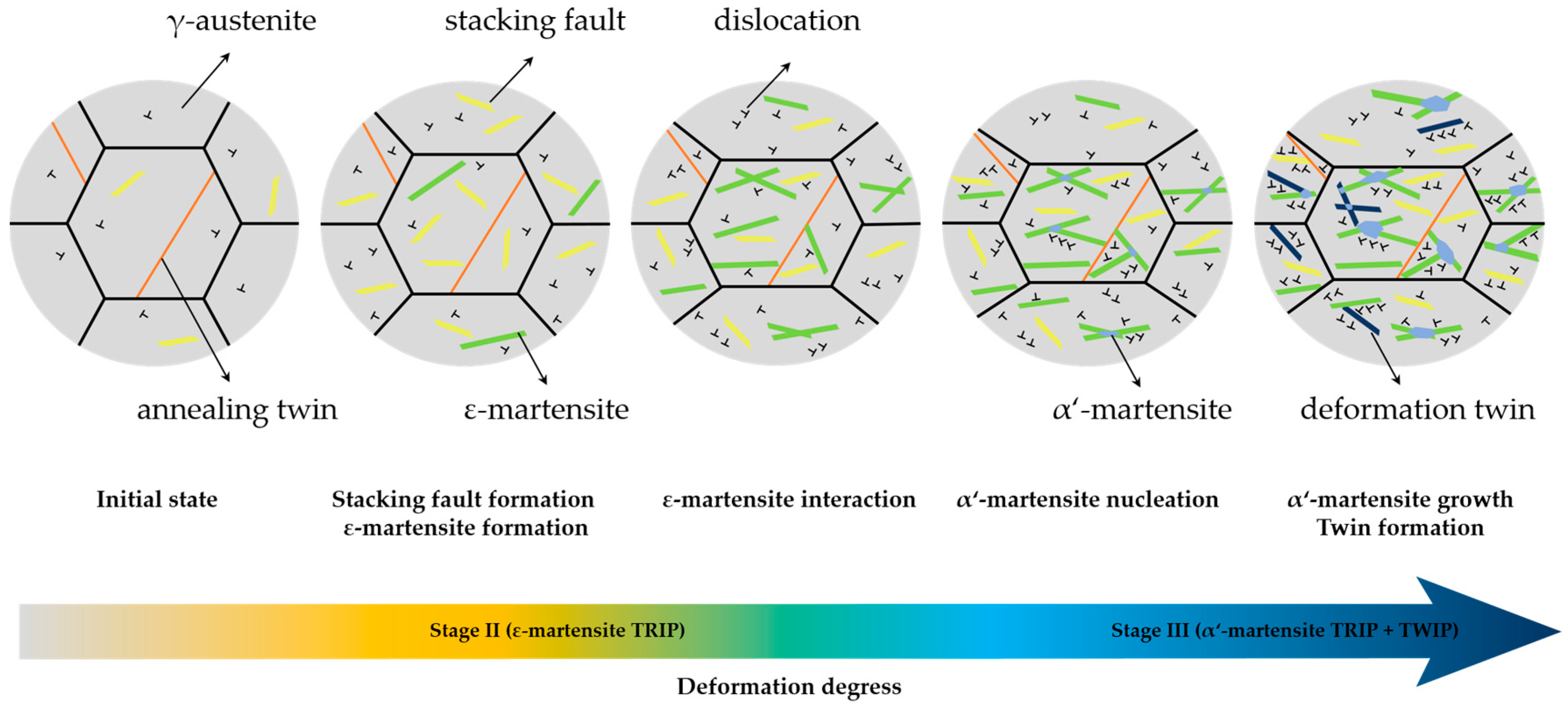
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fonstein, N. Advanced High Strength Sheet Steels: Physical Metallurgy, Design, Processing, and Properties; Springer International Publishing: New York, NY, USA, 2015. [Google Scholar]
- Brüx, U.; Frommeyer, G.; Grassel, O.; Meyer, L.W.; Weise, A. Development and characterization of high strength impact resistant Fe-Mn-(Al-, Si) TRIP/TWIP steels. Steel Res. Int. 2002, 73, 294–298. [Google Scholar] [CrossRef]
- Frommeyer, G.; Brüx, U.; Numann, P. Supra-Ductile and High-Strength Manganese-TRIP/TWIP Steels for High Energy Absorption Purposes. ISIJ Int. 2003, 43, 438–446. [Google Scholar] [CrossRef]
- Song, W.; Ingendahl, T.; Bleck, W. Control of Strain Hardening Behavior in High-Mn Austenitic Steels. Acta Metall. Sin. (Engl. Lett.) 2014, 27, 546–556. [Google Scholar] [CrossRef]
- Grässel, O.; Krüger, L.; Frommeyer, G.; Meyer, L. High strength Fe-Mn-(Al, Si) TRIP/TWIP steels development–Properties–Application. Int. J. Plast. 2000, 16, 1391–1409. [Google Scholar] [CrossRef]
- De Cooman, B.C.; Kwon, O.; Chin, K.-G. State-of-the-knowledge on TWIP steel. Mater. Sci. Technol. 2013, 28, 513–527. [Google Scholar] [CrossRef]
- Yoo, J.D.; Park, K.-T. Microband-induced plasticity in a high Mn-Al-C light steel. Mater. Sci. Eng. A 2008, 496, 417–424. [Google Scholar] [CrossRef]
- Song, W.; Zhang, W.; Appen, J.V.; Dronskowski, R.; Bleck, W. κ-Phase Formation in Fe-Mn-Al-C Austenitic Steels. Steel Res. Int. 2015, 86, 1161–1169. [Google Scholar] [CrossRef]
- Saeed-Akbari, A.; Imlau, J.; Prahl, U.; Bleck, W. Derivation and Variation in Composition-Dependent Stacking Fault Energy Maps Based on Subregular Solution Model in High-Manganese Steels. Metall. Mater. Trans. A 2009, 40, 3076–3090. [Google Scholar] [CrossRef]
- Saeed-Akbari, A.; Schwedt, A.; Bleck, W. Low stacking fault energy steels in the context of manganese-rich iron-based alloys. Scr. Mater. 2012, 66, 1024–1029. [Google Scholar] [CrossRef]
- Park, K.-T.; Kim, G.; Kim, S.K.; Lee, S.W.; Hwang, S.W.; Lee, C.S. On the transitions of deformation modes of fully austenitic steels at room temperature. Met. Mater. Int. 2010, 16, 1–6. [Google Scholar] [CrossRef]
- Gutierrez-Urrutia, I.; Raabe, D. Dislocation and twin substructure evolution during strain hardening of an Fe–22 wt. % Mn–0.6 wt. % C TWIP steel observed by electron channeling contrast imaging. Acta Mater. 2011, 59, 6449–6462. [Google Scholar] [CrossRef]
- Gutierrez-Urrutia, I.; Raabe, D. Multistage strain hardening through dislocation substructure and twinning in a high strength and ductile weight-reduced Fe-Mn-Al-C steel. Acta Mater. 2012, 60, 5791–5802. [Google Scholar] [CrossRef]
- Bouaziz, O.; Allain, S.; Scott, C. Effect of grain and twin boundaries on the hardening mechanisms of twinning-induced plasticity steels. Scr. Mater. 2008, 58, 484–487. [Google Scholar] [CrossRef]
- Bouaziz, O.; Scott, C.P.; Petitgand, G. Nanostructured steel with high work-hardening by the exploitation of the thermal stability of mechanically induced twins. Scr. Mater. 2009, 60, 714–716. [Google Scholar] [CrossRef]
- Kusakin, P.; Belyakov, A.; Haase, C.; Kaibyshev, R.; Molodov, D.A. Microstructure evolution and strengthening mechanisms of Fe-23Mn-0.3C-1.5Al TWIP steel during cold rolling. Mater. Sci. Eng. A 2014, 617, 52–60. [Google Scholar] [CrossRef]
- Tomota, Y.; Strum, M.; Morris, J.W. Microstructural dependence of Fe-high Mn tensile behavior. Metall. Trans. A 1986, 17, 537–547. [Google Scholar] [CrossRef]
- Ding, H.; Ding, H.; Song, D.; Tang, Z.; Yang, P. Strain hardening behavior of a TRIP/TWIP steel with 18.8% Mn. Mater. Sci. Eng. A 2011, 528, 868–873. [Google Scholar] [CrossRef]
- Grässel, O.; Frommeyer, G.; Derder, C.; Hofmann, H. Phase Transformations and Mechanical Properties of Fe-Mn-Si-Al TRIP-Steels. J. Phys. IV France 1997, 7, C5-383–C5-388. [Google Scholar]
- Liss, K.-D. Metals Challenged by Neutron and Synchrotron Radiation. Metals 2017, 7. [Google Scholar] [CrossRef]
- Liss, K.-D.; Chen, K. Frontiers of synchrotron research in materials science. MRS Bull. 2016, 41, 435–441. [Google Scholar] [CrossRef]
- Treusch, R. Production and Properties of Synchrotron Radiation. In Neutrons and Synchrotron Radiation in Engineering Materials Science: From Fundamentals to Material and Component Characterization; Reimers, W., Pyzalla, A.R., Schreyer, A., Clemens, H., Eds.; Wiley-VCH: Weinheim, Germany, 2008. [Google Scholar]
- Suwanpinij, P. The Synchrotron Radiation for Steel Research. Adv. Mater. Sci. Eng. 2016, 2016. [Google Scholar] [CrossRef]
- Carmele, D.; Rieger, T.; Herrmann, K.; Meyer, S.; Lippmann, T.; Stark, A.; Bleck, W.; Klemradt, U. Very Hard Synchrotron X-ray Radiation as an Advanced Characterization Method Applied to Advanced High-Strength Steels. Adv. Mater. Res. 2011, 409, 660–665. [Google Scholar] [CrossRef]
- Blondé, R.; Jimenez-Melero, E.; Zhao, L.; Wright, J.P.; Brück, E.; van der Zwaag, S.; van Dijk, N.H. High-energy X-ray diffraction study on the temperature-dependent mechanical stability of retained austenite in low-alloyed TRIP steels. Acta Mater. 2012, 60, 565–577. [Google Scholar] [CrossRef]
- Klemradt, U.; Rieger, T.; Herrmann, K.; Carmele, D.; Meyer, S.; Lippmann, T.; Stark, A.; Bleck, W. Monitoring of Heat Treatment Processes by High Energy Synchrotron Radiation. Acta Phys. Pol. A 2012, 121, 39–43. [Google Scholar] [CrossRef]
- Suwanpinij, P.; Stark, A.; Li, X.; Römer, F.; Herrmann, K.; Lippmann, T.; Bleck, W. In Situ High Energy X-Ray Diffraction for Investigating the Phase Transformation in Hot Rolled TRIP-Aided Steels. Adv. Eng. Mater. 2014, 16, 1044–1051. [Google Scholar] [CrossRef]
- Lejay, V.; Sidoroff, C.; Le Bourlot, C.; Perez, M.; Dierickx, P. Ageing of 100Cr6 steel: Synchrotron X-ray diffraction and dimensional analysis investigation. Mater. Sci. Technol. 2016, 32, 1106–1110. [Google Scholar] [CrossRef]
- Jiang, S.; Wang, H.; Wu, Y.; Liu, X.; Chen, H.; Yao, M.; Gault, B.; Ponge, D.; Raabe, D.; Hirata, A.; et al. Ultrastrong steel via minimal lattice misfit and high-density nanoprecipitation. Nature 2017, 544, 460–464. [Google Scholar] [CrossRef] [PubMed]
- Reimers, W.; Pyzalla, A.; Broda, M.; Brusch, G.; Dantz, D.; Schmackers, T.; Liss, K.-D.; Tschentscher, T. The Use of High-Energy Synchrotron Diffraction for Residual Stress Analyses. J. Mater. Sci. Lett. 1999, 18, 581–583. [Google Scholar] [CrossRef]
- Cakmak, E.; Choo, H.; An, K.; Ren, Y. A synchrotron X-ray diffraction study on the phase transformation kinetics and texture evolution of a TRIP steel subjected to torsional loading. Acta Mater. 2012, 60, 6703–6713. [Google Scholar] [CrossRef]
- Liss, K.-D. Quantum Beam Science—Applications to Probe or Influence Matter and Materials. Quantum Beam Sci. 2017, 1. [Google Scholar] [CrossRef]
- Dippel, A.-C.; Liermann, H.-P.; Delitz, J.T.; Walter, P.; Schulte-Schrepping, H.; Seeck, O.H.; Franz, H. Beamline P02.1 at PETRA III for high-resolution and high-energy powder diffraction. J. Synchrotron Rad. 2015, 22, 675–687. [Google Scholar] [CrossRef] [PubMed]
- Hammersley, A.P. FIT2D: An Introduction and Overview. Available online: http://www.esrf.eu/computing/scientific/FIT2D/FIT2D_INTRO/fit2d.html (accessed on 23 September 2017).
- Lutterotti, L. Total pattern fitting for the combined size-strain-stress-texture determination in thin film diffraction. Nucl. Instr. Meth. Phys. Res. B 2010, 268, 334–340. [Google Scholar] [CrossRef]
- Popa, N.C. The (hkl) Dependence of Diffraction-Line Broadening Caused by Strain and Size for all Laue Groups in Rietveld Refinement. J. Appl. Cryst. 1998, 31, 176–180. [Google Scholar] [CrossRef]
- Warren, B.E. X-ray studies of deformed metals. Prog. Met. Phys. 1959, 8, 147–202. [Google Scholar] [CrossRef]
- Warren, B.E. X-ray Diffraction; Dover Publications: New York, NY, USA, 1990; pp. 275–298. [Google Scholar]
- Yan, K.; Carr, D.G.; Callaghan, M.D.; Liss, K.-D.; Li, H. Deformation mechanisms of twinning-induced plasticity steels: In situ synchrotron characterization and modeling. Scr. Mater. 2010, 62, 246–249. [Google Scholar] [CrossRef]
- Reed, R.P.; Schramm, R.E. Relationship between stacking-fault energy and x-ray measurements of stacking-fault probability and microstrain. J. Appl. Phys. 1974, 45, 4705–4711. [Google Scholar] [CrossRef]
- Schramm, R.E.; Reed, R.P. Stacking fault energies of seven commercial austenitic stainless steels. Metall. Trans. A 1974, 6A, 1345–1351. [Google Scholar] [CrossRef]
- Lee, T.-H.; Shin, E.; Oh, C.-S.; Ha, H.-Y.; Kim, S.-J. Correlation between stacking fault energy and deformation microstructure in high-interstitial-alloyed austenitic steels. Acta Mater. 2010, 58, 3173–3186. [Google Scholar] [CrossRef]
- Ishida, K. Direct estimation of stacking fault energy by thermodynamic analysis. Phys. Stat. Solidi (A) 1976, 36, 717–728. [Google Scholar] [CrossRef]
- Jin, J.-E.; Lee, Y.-K. Effects of Al on microstructure and tensile properties of C-bearing high Mn TWIP steel. Acta Mater. 2012, 60, 1680–1688. [Google Scholar] [CrossRef]
- Asgari, S.; El-Danaf, E.; Kalidindi, S.R.; Doherty, R.D. Strain hardening regimes and microstructural evolution during large strain compression of low stacking fault energy fcc alloys that form deformation twins. Metall. Mater. Trans. A 1997, 28, 1781–1795. [Google Scholar] [CrossRef]
- Brooks, J.W.; Loretto, M.H.; Smallman, R.E. Direct observations of martensite nuclei in stainless steel. Acta Metall. 1979, 27, 1839–1847. [Google Scholar] [CrossRef]
- Kibey, S.; Liu, J.B.; Johnson, D.D.; Sehitoglu, H. Predicting twinning stress in fcc metals: Linking twin-energy pathways to twin nucleation. Acta Mater. 2007, 55, 6843–6851. [Google Scholar] [CrossRef]
- Galindo-Nava, E.I.; Rivera-Díaz-del-Castillo, P. Understanding martensite and twin formation in austenitic steels: A model describing TRIP and TWIP effects. Acta Mater. 2017, 128, 120–134. [Google Scholar] [CrossRef]
- Koyama, M.; Sawaguchi, T.; Lee, T.; Lee, C.S.; Tsuzaki, K. Work hardening associated with ε-martensitic transformation, deformation twinning and dynamic strain aging in Fe-17Mn-0.6C and Fe-17Mn-0.8C TWIP steels. Mater. Sci. Eng. A 2011, 528, 7310–7316. [Google Scholar] [CrossRef]
- Remy, L.; Pineau, A. Twinning and strain-induced F.C.C. → H.C.P. transformation in the Fe-Mn-Cr-C system. Mater. Sci. Eng. 1977, 28, 99–107. [Google Scholar] [CrossRef]
- Li, Z.; Pradeep, K.G.; Deng, Y.; Raabe, D.; Tasan, C.C. Metastable high-entropy dual-phase alloys overcome the strength-ductility trade-off. Nature 2016, 534, 227–230. [Google Scholar] [CrossRef] [PubMed]
- Murr, L.E.; Staudhammer, K.P.; Hecker, S.S. Effects of Strain State and Strain Rate on Deformation-Induced Transformation in 304 Stainless Steel: Part II. Microstructural Study. Metall. Trans. A 1982, 13, 627–635. [Google Scholar] [CrossRef]
- Tian, Y.; Gorbatov, O.I.; Borgenstam, A.; Ruban, A.V.; Hedström, P. Deformation Microstructure and Deformation-Induced Martensite in Austenitic Fe-Cr-Ni Alloys Depending on Stacking Fault Energy. Metall. Mater. Trans. A 2017, 48, 1–7. [Google Scholar] [CrossRef]




| Element | C | Si | Mn | P | S | Al | Fe |
|---|---|---|---|---|---|---|---|
| wt % | 0.32 | 0.03 | 17.24 | 0.009 | 0.008 | 1.75 | Bal. |
| hkl | 111 | 200 | 220 | 311 | 222 | 400 |
|---|---|---|---|---|---|---|
| Steel | (MPa) | (MPa) | (%) | (%) | Eco-Index (GPa %) |
|---|---|---|---|---|---|
| Fe-17Mn-1.5Al-0.3C | 288 | 743 | 58 | 59 | 43 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Song, W.; Bleck, W. Investigation of the Microstructure Evolution in a Fe-17Mn-1.5Al-0.3C Steel via In Situ Synchrotron X-ray Diffraction during a Tensile Test. Materials 2017, 10, 1129. https://doi.org/10.3390/ma10101129
Ma Y, Song W, Bleck W. Investigation of the Microstructure Evolution in a Fe-17Mn-1.5Al-0.3C Steel via In Situ Synchrotron X-ray Diffraction during a Tensile Test. Materials. 2017; 10(10):1129. https://doi.org/10.3390/ma10101129
Chicago/Turabian StyleMa, Yan, Wenwen Song, and Wolfgang Bleck. 2017. "Investigation of the Microstructure Evolution in a Fe-17Mn-1.5Al-0.3C Steel via In Situ Synchrotron X-ray Diffraction during a Tensile Test" Materials 10, no. 10: 1129. https://doi.org/10.3390/ma10101129