An Extended Damage Plasticity Model for Shotcrete: Formulation and Comparison with Other Shotcrete Models
Abstract
:1. Introduction
- Sezaki et al. [12] published test results on the evolution of Young’s modulus and uniaxial compressive strength up to the age of 28 days and stress–strain relations from short-term uniaxial and triaxial compression tests on specimens of different age.
- Huber [15] investigated the evolution of temperature due to hydration, of the Young’s modulus and of the uniaxial compressive strength up to the age of 7 days as well as the evolution of the total strain in shrinkage and creep tests.
- Fischnaller [16] presented test results on the evolution of Young’s modulus and uniaxial compressive strength and the results of relaxation and shrinkage tests up to the age of 7 days.
- Müller [17] published test results on the evolution of stiffness and strength, results of short-term uniaxial compression tests and the evolution of the total strain in shrinkage and creep tests.
2. An Extended Damage Plasticity Model for Shotcrete
2.1. Damage Plasticity Framework
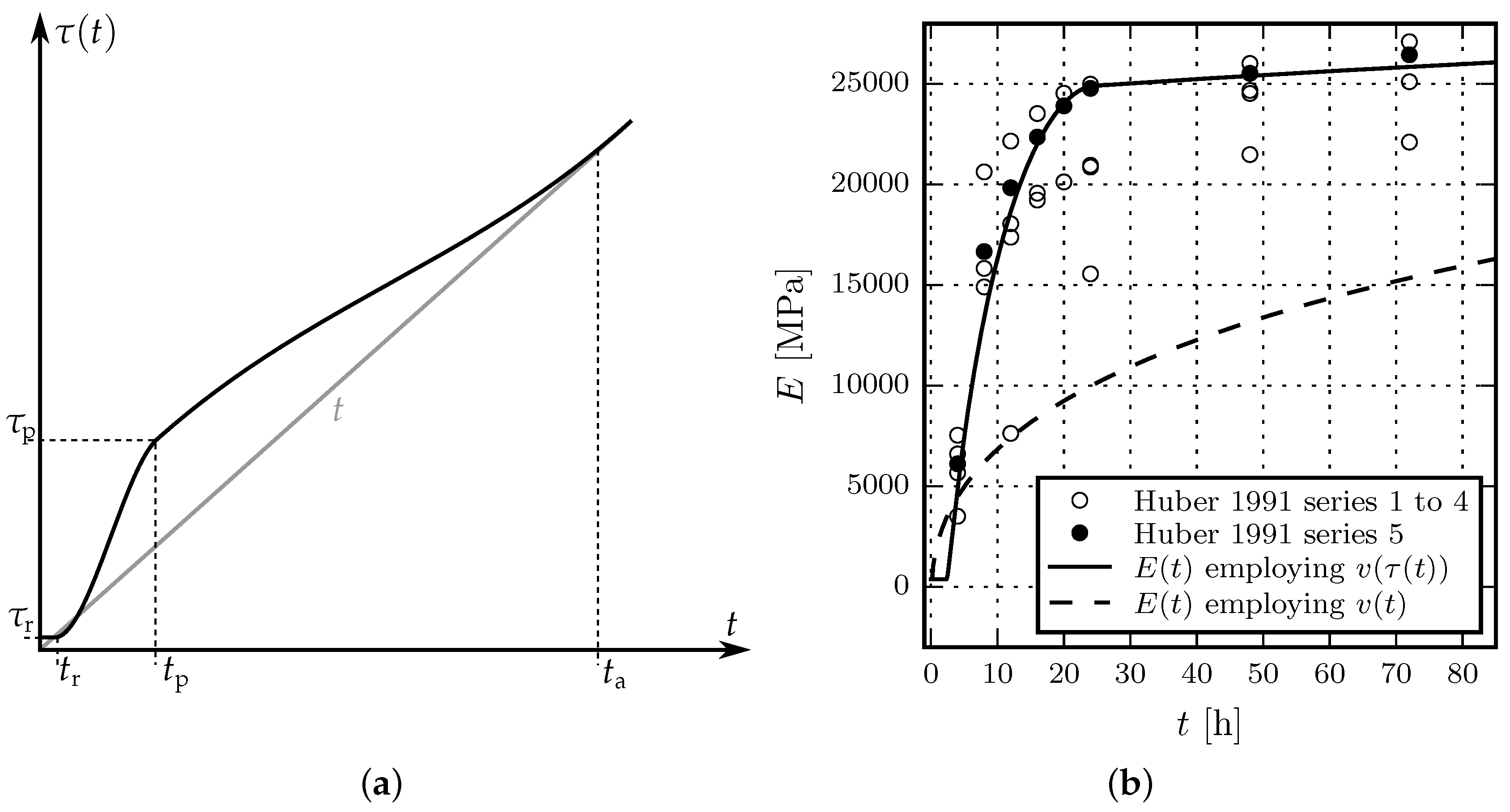
2.2. Evolution of Material Strength
2.3. Aging Material Behavior and Creep Strain
2.4. Shrinkage
3. Comparison of the New Shotcrete Model with Other Shotcrete Models
3.1. Brief Review of the Shotcrete Models Considered for the Comparison
3.1.1. Viscoplastic Shotcrete Model by Meschke
3.1.2. Shotcrete Model by Schädlich and Schweiger
3.1.3. Multi-field Shotcrete Model Based on the Hygro–Thermal–Chemo-Mechanical Concrete Model by Gawin et al.
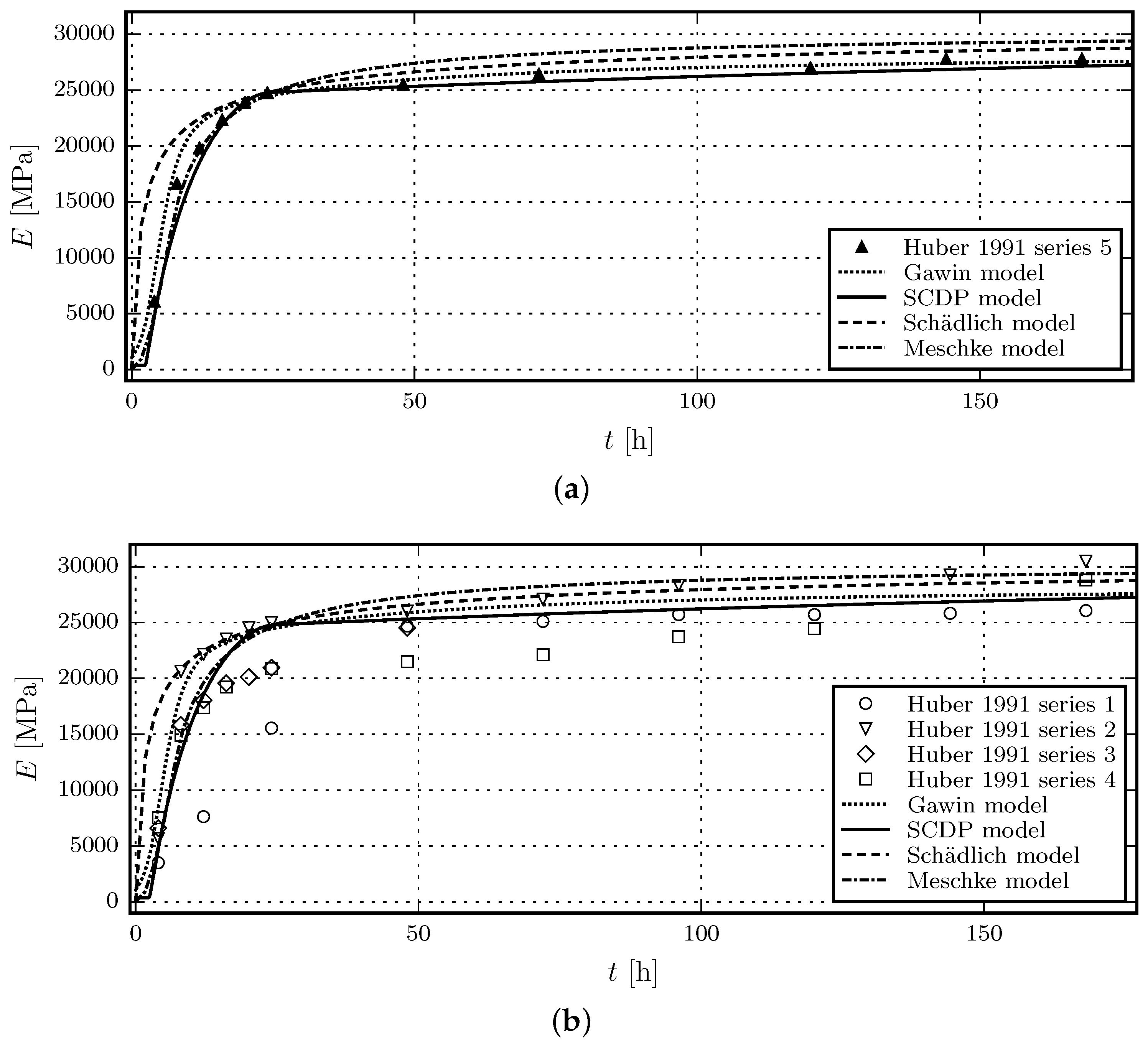
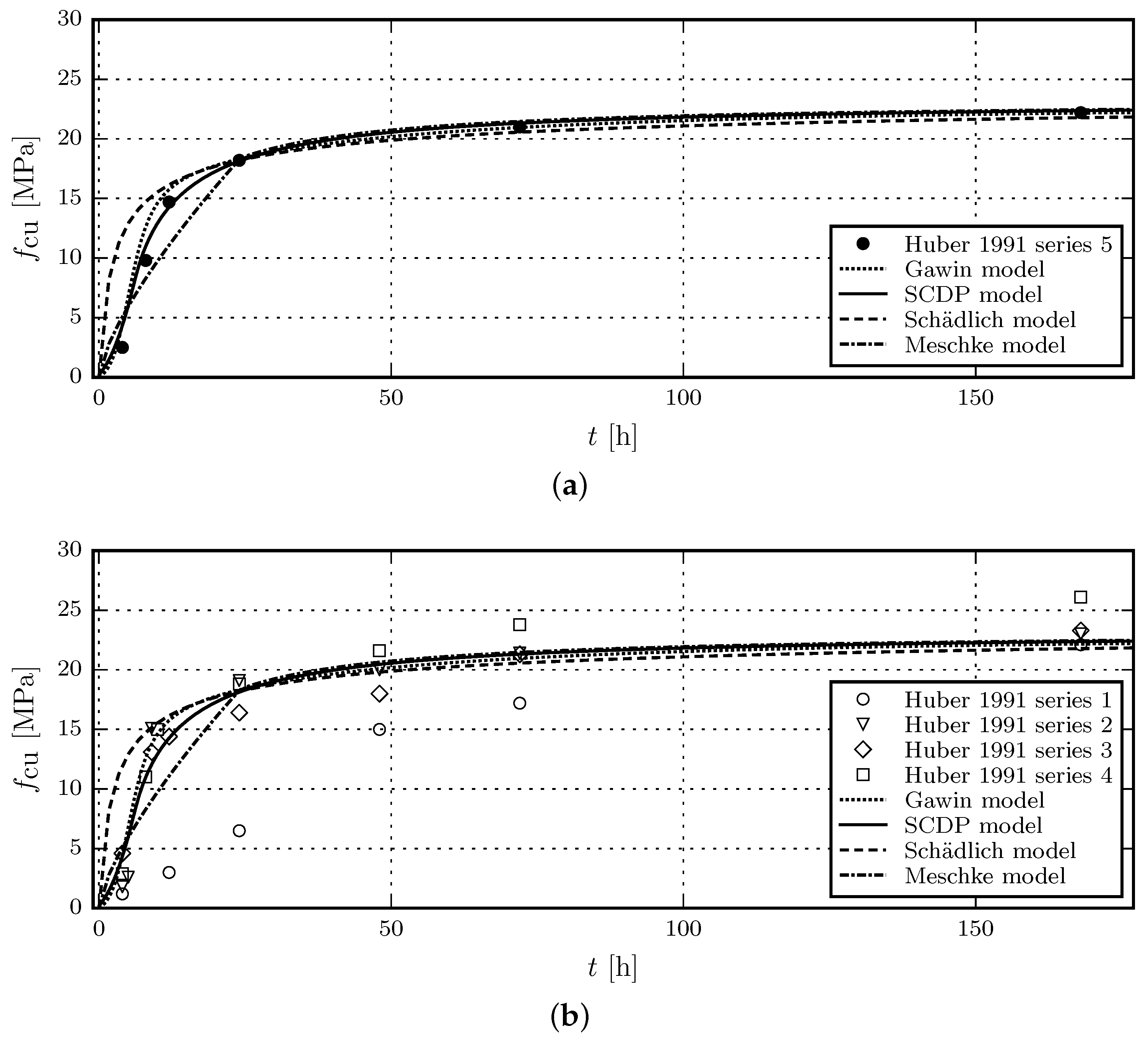
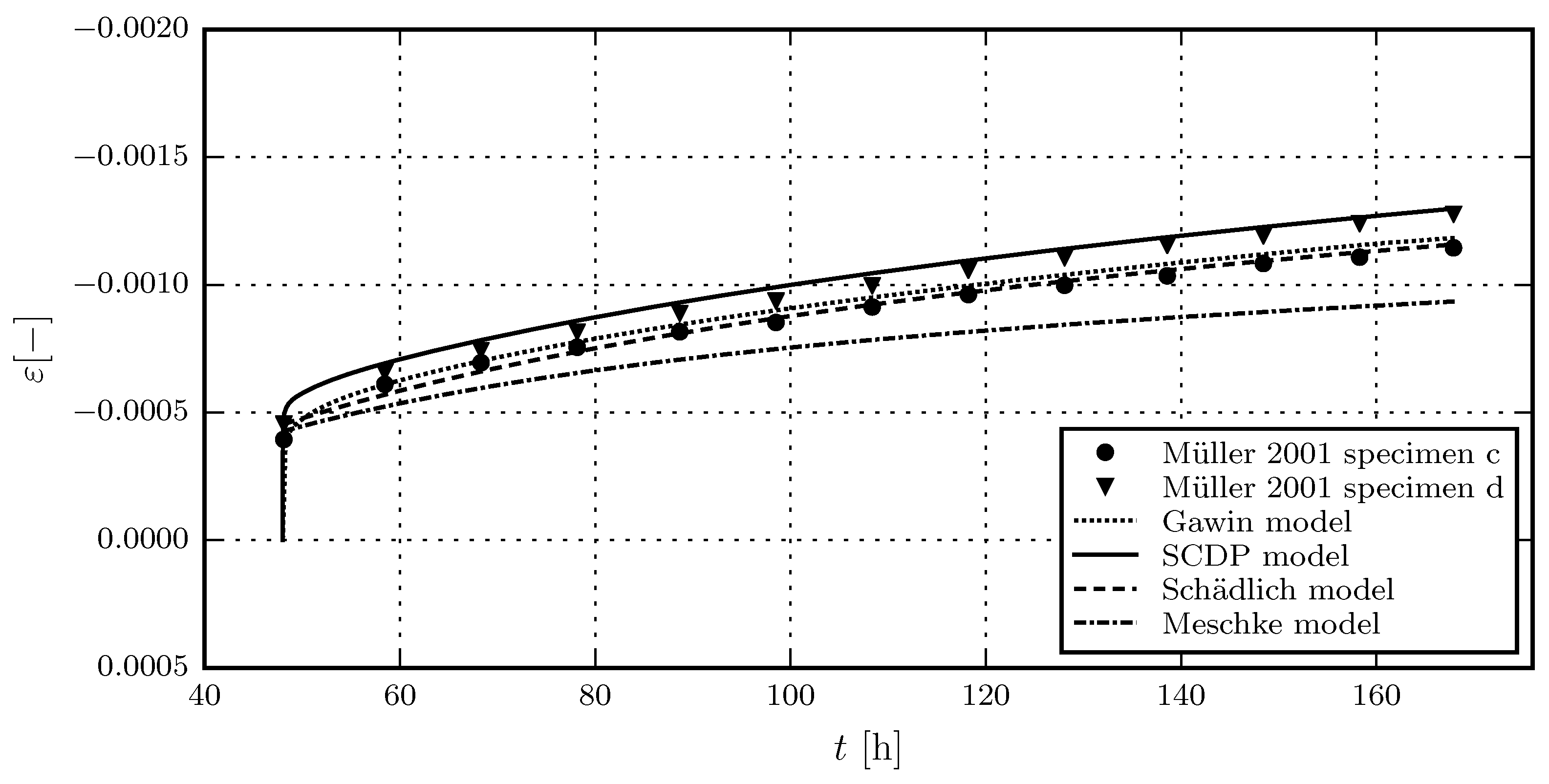
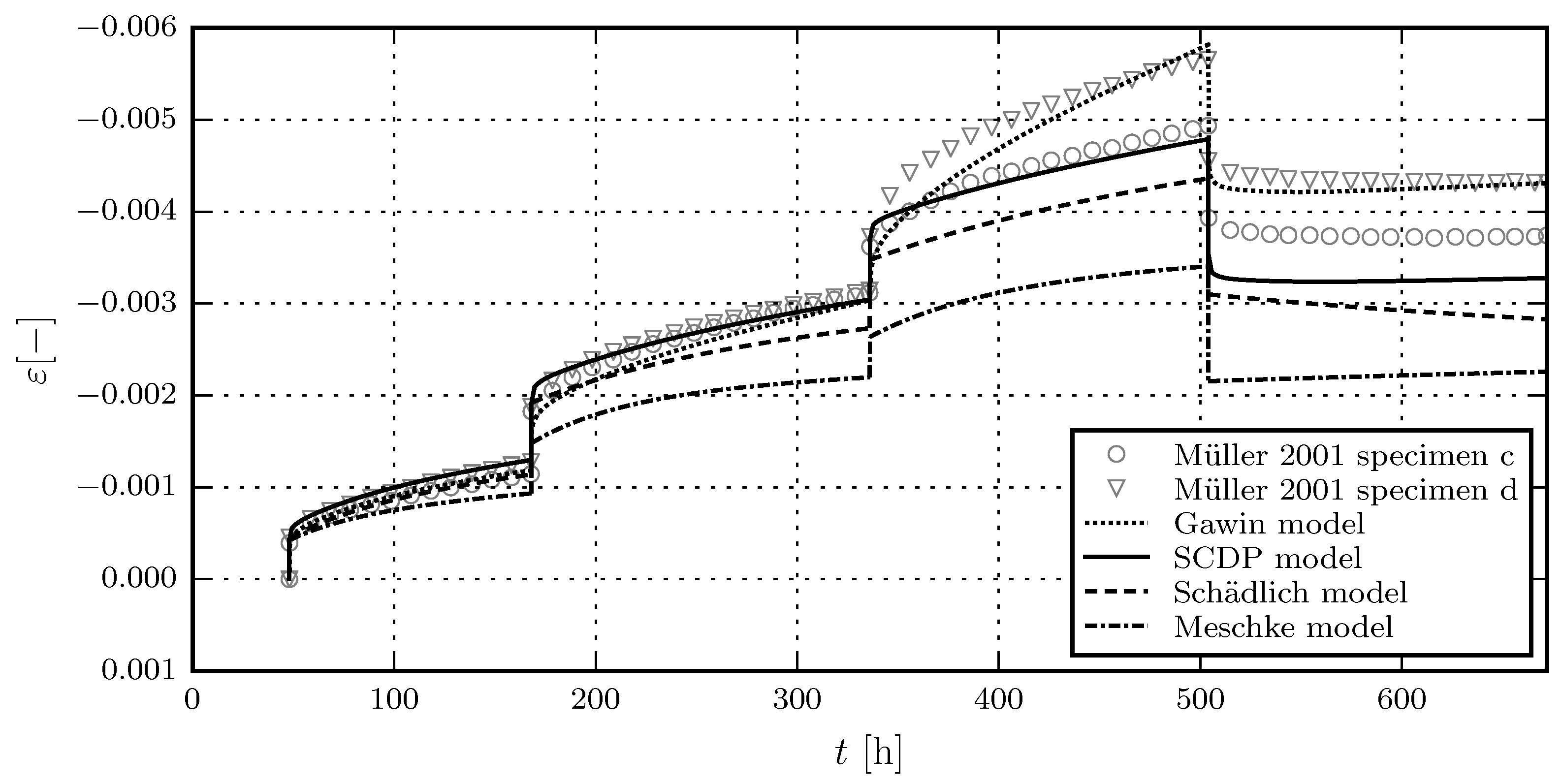
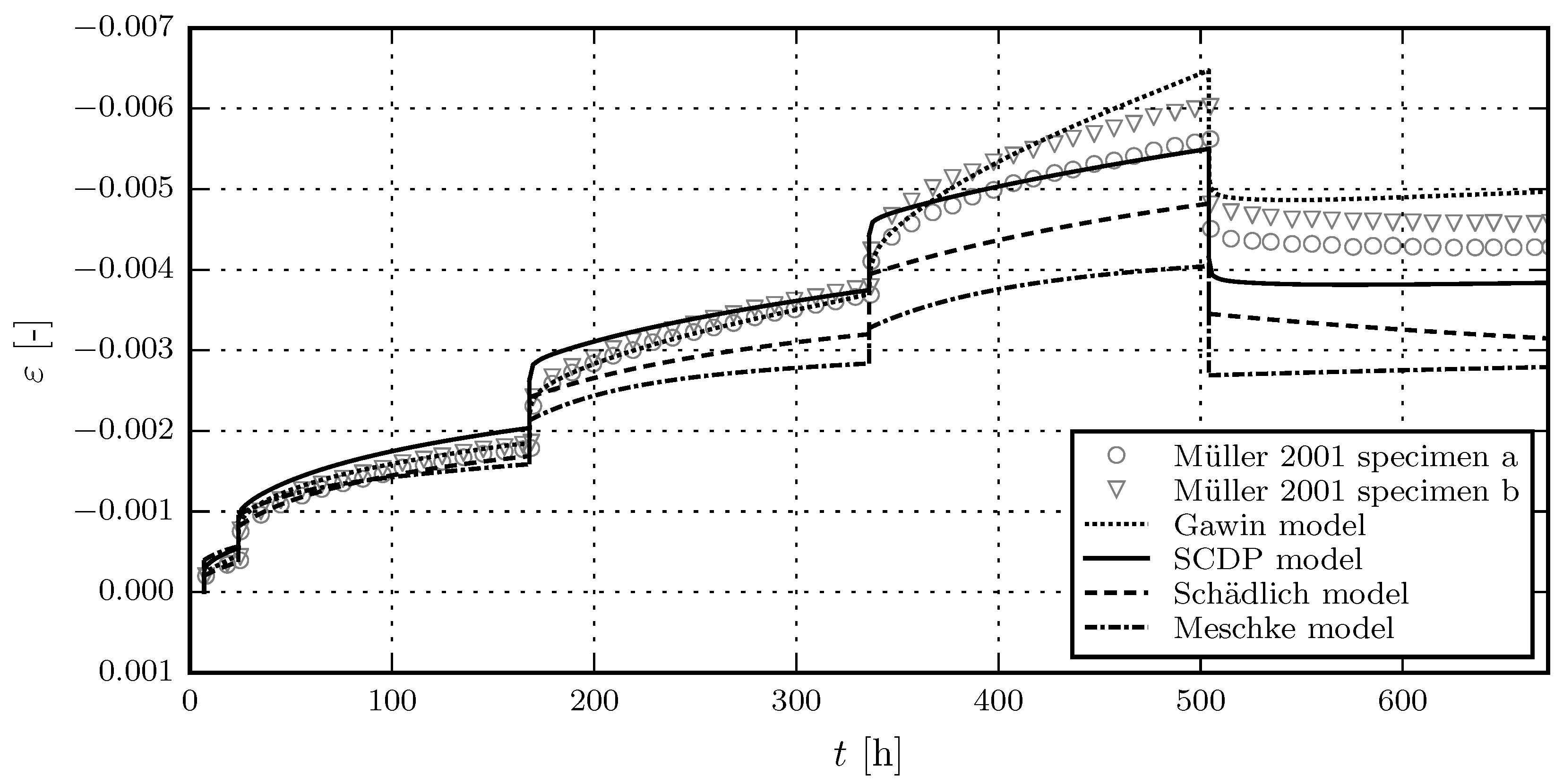
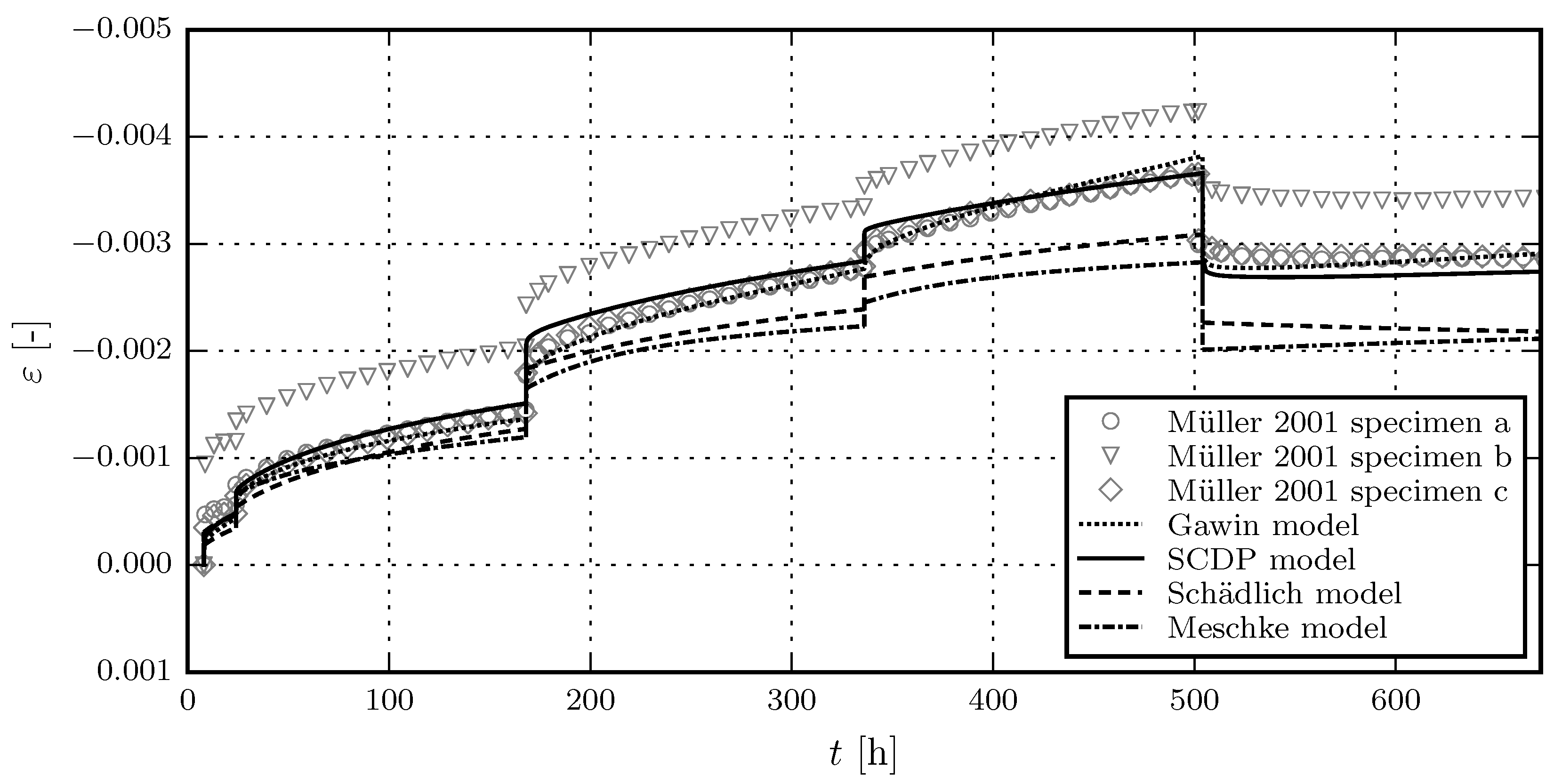
3.2. Evaluation of the Shotcrete Models on the Basis of Experimental Data
3.2.1. Comparison of Model Response with Experimental Results by Huber
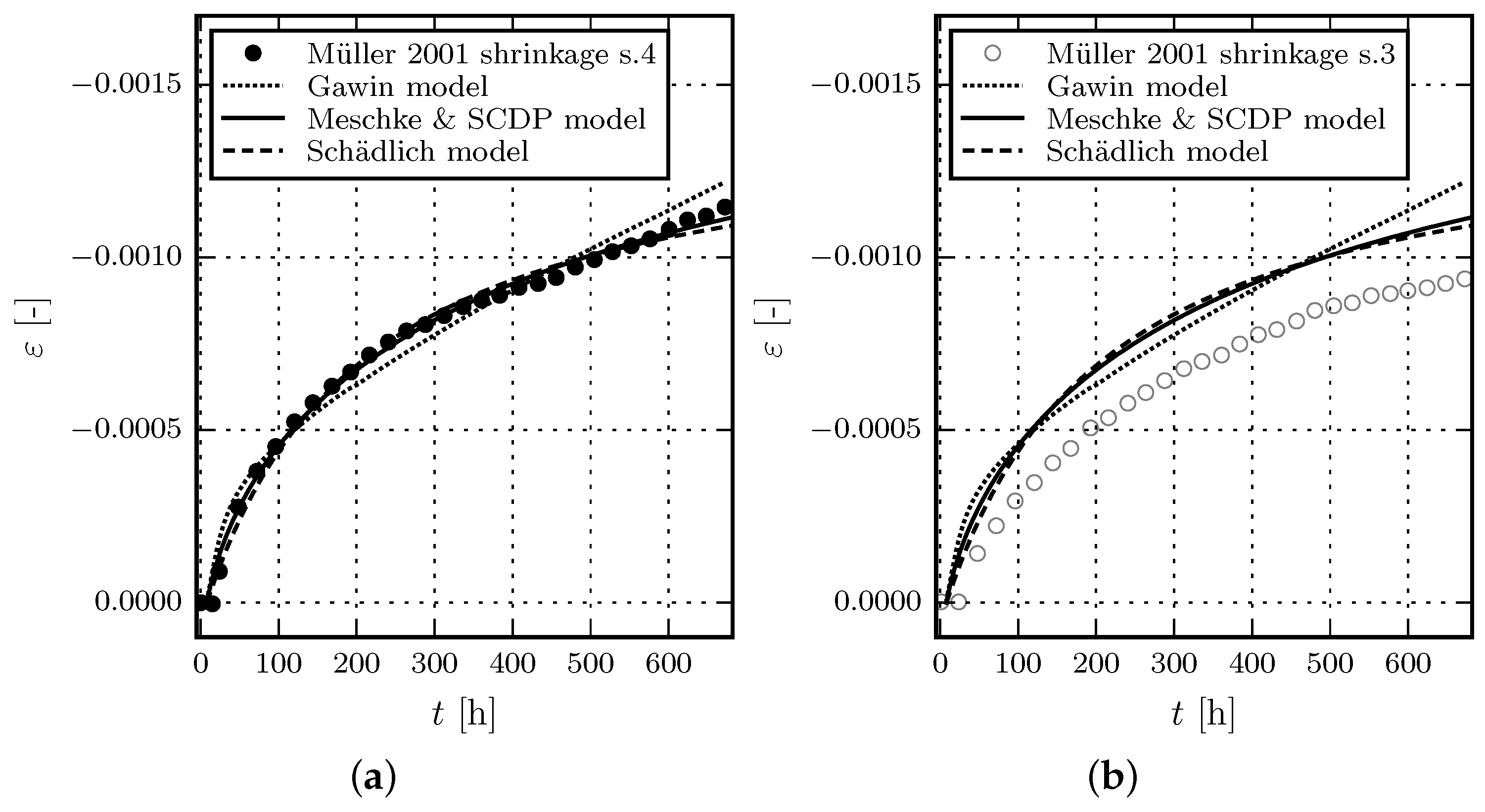
3.2.2. Comparison of Model Response with Experimental Results by Müller
4. Summary and Outlook
Author Contributions
Conflicts of Interest
References
- Pöttler, R. Time-dependent rock-shotcrete interaction—A numerical shortcut. Comp. Geotech. 1990, 9, 149–169. [Google Scholar] [CrossRef]
- Meschke, G. Consideration of aging of shotcrete in the context of a 3D-viscoplastic material model. Int. J. Numer. Meth. Eng. 1996, 39, 3145–3162. [Google Scholar] [CrossRef]
- Schütz, R.; Potts, D.M.; Zdravkovic, L. Advanced constitutive modelling of shotcrete: Model formulation and calibration. Comp. Geotech. 2011, 38, 834–845. [Google Scholar] [CrossRef]
- Schädlich, B.; Schweiger, H.F. A new constitutive model for shotcrete. In Proceedings of the 8th European Conference on Numerical Methods in Geotechnical Engineering, Delft, The Netherlands, 18–20 June 2014; CRC Press Taylor & Francis: Leiden, The Netherlands, 2014; pp. 103–108. [Google Scholar]
- Pickett, G. The effect of change in moisture content on the creep of concrete under a sustained load. J. Proc. 1942, 38, 333–356. [Google Scholar]
- Hellmich, C.; Ulm, F.J.; Mang, H.A. Multisurface chemoplasticity. I: Material model for shotcrete. J. Eng. Mech. 1999, 125, 692–701. [Google Scholar] [CrossRef]
- Ulm, F.J.; Coussy, O. Modeling of thermochemomechanical couplings of concrete at early ages. J. Eng. Mech. 1995, 121, 785–794. [Google Scholar] [CrossRef]
- Lackner, R.; Mang, H.A. Cracking in shotcrete tunnel shells. Eng. Fract. Mech. 2003, 70, 1047–1068. [Google Scholar] [CrossRef]
- Gawin, D.; Pesavento, F.; Schrefler, B.A. Hygro-thermo-chemo-mechanical modelling of concrete at early ages and beyond. Part I: Hydration and hygro-thermal phenomena. Int. J. Numer. Meth. Eng. 2006, 67, 299–331. [Google Scholar] [CrossRef]
- Gawin, D.; Pesavento, F.; Schrefler, B.A. Hygro-thermo-chemo-mechanical modelling of concrete at early ages and beyond. Part II: Shrinkage and creep of concrete. Int. J. Numer. Meth. Eng. 2006, 67, 332–363. [Google Scholar] [CrossRef]
- Sciume, G.; Benboudjema, F.; De Sa, C.; Pesavento, F.; Berthaud, Y.; Schrefler, B.A. A multiphysics model for concrete at early age applied to repairs. Eng. Struct. 2013, 57, 374–387. [Google Scholar] [CrossRef]
- Sezaki, M.; Kibe, T.; Ichikiwa, Y.; Kawamoto, T. An experimental study on the mechanical properties of shotcrete. J. Soc. Mater. Sci. 1989, 38, 106–110. [Google Scholar] [CrossRef]
- Aldrian, W. Beitrag zum Materialverhalten von Früh Belastetem Spritzbeton. Ph.D. Thesis, Montanuniversität Leoben, Leoben, Austria, 1991. [Google Scholar]
- Golser, J.; Rabensteiner, K.; Sigl, O.; Aldrian, W.; Wedenig, H.; Brandl, J.; Maier, C. Materialgesetz für Spritzbeton; Technischer Bericht, Straßenforschung FV 696; Federal Ministry for Buildings and Technology: Vienna, Austria, 1991. (In German) [Google Scholar]
- Huber, H.G. Untersuchungen zum Verformungsverhalten von Jungem Spritzbeton im Tunnelbau. Diploma Thesis, Innsbruck University, Innsbruck, Austria, 1991. [Google Scholar]
- Fischnaller, G. Untersuchungen zum Verformungsverhalten von Jungem Spritzbeton im Tunnelbau— Grundlagen und Versuche. Diploma Thesis, Innsbruck University, Innsbruck, Austria, 1992. [Google Scholar]
- Müller, M. Kriechversuche an Jungen Spritzbetonen zur Ermittlung der Parameter für Materialgesetze. Diploma Thesis, Montanuniversität Leoben, Leoben, Austria, 2001. [Google Scholar]
- Grassl, P.; Jirásek, M. Damage-plastic model for concrete failure. Int. J. Solids Struct. 2006, 43, 7166–7196. [Google Scholar] [CrossRef]
- Menétrey, P.; Willam, K.J. Triaxial failure criterion for concrete and its generalization. ACI Struct. J. 1995, 92, 311–318. [Google Scholar]
- Bažant, Z.; Prasannan, S. Solidification theory for concrete creep. I: Formulation. J. Eng. Mech. 1989, 115, 1691–1703. [Google Scholar] [CrossRef]
- Bažant, Z.; Panula, L. Practical prediction of time-dependent deformations of concrete. Mat. Struct. 1978, 11, 307–328. [Google Scholar]
- Unteregger, D.; Fuchs, B.; Hofstetter, G. A damage plasticity model for different types of intact rock. Int. J. Rock Mech. Min. Sci. 2015, 80, 402–411. [Google Scholar] [CrossRef]
- Meschke, G.; Kropik, C.; Mang, H. Numerical analysis of tunnel linings by means of a viscoplastic material model for shotcrete. Int. J. Meth. Eng. 1996, 39, 3145–3162. [Google Scholar] [CrossRef]
- Jirásek, M.; Bažant, Z. Inelastic Analysis of Structures; John Wiley & Sons, Ltd.: Chichester, West Sussex, UK, 2002. [Google Scholar]
- Bažant, Z.; Baweja, S. Creep and shrinkage prediction model for analysis and design of concrete structures—Model B3. Mater. Struct. 1995, 28, 357–365. [Google Scholar]
- TC-242-MDC RILEM Technical Committee. RILEM draft recommendation: TC-242-MDC multi-decade creep and shrinkage of concrete: Material model and structural analysis. Mater. Struct. 2015, 48, 753–770. [Google Scholar]
- Bažant, Z.; Cusatis, G.; Cedolin, L. Temperature effect on concrete creep modeled by microprestress-solidification theory. J. Eng. Mech. 2004, 130, 691–699. [Google Scholar] [CrossRef]
- CEB-FIP Model Code 1990; Comité Euro-International du Béton: Lausanne, Switzerland, 1991.
- Richtlinie Spritzbeton; Österreichische Vereinigung für Beton und Bautechnik (ÖVBB): Vienna, Austria, 1989 and 2009.
- Oluokon, F.A.; Burdette, E.G.; Deatherage, J.H. Splitting tensile strength and compressive strength relationship at early ages. ACI Mater. J. 1991, 88, 115–121. [Google Scholar]
- Sprayed Concrete—Part 1: Definitions, Specifications and Conformity; EN 14487-1; European Committee for Standardization: Brussels, Belgium, 2006.
- 209R-92: Prediction of Creep, Shrinkage, and Temperature Effects in Concrete Structures; ACI Committee 209; American Concrete Institute (ACI): Farmington Hills, MI, USA, 1992.
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Cervera, M.; Oliver, J.; Prato, T. Thermo-chemo-mechanical model for concrete I: Hydration and aging. J. Eng. Mech. 1999, 125, 1018–1027. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Hauggaard, A.B.; Baweja, S.; Ulm, F.J. Microprestress-solidification theory for concrete creep. I: Aging and drying effects. J. Eng. Mech. 1997, 123, 1188–1194. [Google Scholar] [CrossRef]
- Jirásek, M.; Havlásek, P. Microprestress–solidification theory of concrete creep: Reformulation and improvement. Cem. Concr. Res. 2014, 60, 51–62. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Hauggaard, A.B.; Baweja, S. Microprestress-solidification theory for concrete creep. II: Algorithm and Verification. J. Eng. Mech. 1997, 123, 1195–1201. [Google Scholar] [CrossRef]
- Kupfer, H.; Hilsdorf, H.K.; Rüsch, H. Behavior of concrete under biaxial stresses. J. Am. Concr. Inst. 1969, 66, 656–666. [Google Scholar]
- Bažant, Z.; Prasannan, S. Solidification theory for concrete creep. II: Verification and Application. J. Eng. Mech. 1989, 115, 1704–1725. [Google Scholar] [CrossRef]
- Jirásek, M.; Havlásek, P. Accurate approximations of concrete creep compliance functions based on continuous retardation spectra. Comput. Struct. 2014, 135, 155–168. [Google Scholar] [CrossRef]
- Schädlich, B.; Schweiger, H.; Marcher, T.; Saurer, E. Application of a novel constitutive shotcrete model to tunneling. In Rock Engineering and Rock Mechanics: Structures in and on Rock Masses: EUROCK 2014; CRC Press Taylor & Francis Group: Leiden, The Netherlands, 2014; pp. 799–804. [Google Scholar]
| Property | Quantity | Unit |
|---|---|---|
| aggregate content ( mm) | 1800 | |
| cement content | 350 | |
| water content | 160 | |
| accelerator | 57 | % |
| Property | Quantity | Unit |
|---|---|---|
| aggregate content (0/8 mm) | 1768 | |
| cement content SBM W&P | 340 | |
| water content | 150 |
| Step | Test Series 3 | Test Series 4/1 | Test Series 4/2 | |||
|---|---|---|---|---|---|---|
| Duration | Stress | Duration | Stress | Duration | Stress | |
| - | 8 | 0 | 7 | 0 | 48 | 0 |
| 1 | 16 | -1 | 17 | -1 | 120 | -4 |
| 2 | 144 | -2.5 | 144 | -4 | 168 | -10 |
| 3 | 168 | -7.5 | 168 | -10 | 168 | -15 |
| 4 | 168 | -10 | 168 | -15 | 168 | -0.6 |
| 5 | 168 | -0.6 | 168 | -0.6 | ||
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neuner, M.; Gamnitzer, P.; Hofstetter, G. An Extended Damage Plasticity Model for Shotcrete: Formulation and Comparison with Other Shotcrete Models. Materials 2017, 10, 82. https://doi.org/10.3390/ma10010082
Neuner M, Gamnitzer P, Hofstetter G. An Extended Damage Plasticity Model for Shotcrete: Formulation and Comparison with Other Shotcrete Models. Materials. 2017; 10(1):82. https://doi.org/10.3390/ma10010082
Chicago/Turabian StyleNeuner, Matthias, Peter Gamnitzer, and Günter Hofstetter. 2017. "An Extended Damage Plasticity Model for Shotcrete: Formulation and Comparison with Other Shotcrete Models" Materials 10, no. 1: 82. https://doi.org/10.3390/ma10010082
APA StyleNeuner, M., Gamnitzer, P., & Hofstetter, G. (2017). An Extended Damage Plasticity Model for Shotcrete: Formulation and Comparison with Other Shotcrete Models. Materials, 10(1), 82. https://doi.org/10.3390/ma10010082






