Diffusion Length Mapping for Dye-Sensitized Solar Cells
Abstract
:1. Introduction
2. Theoretical Basis
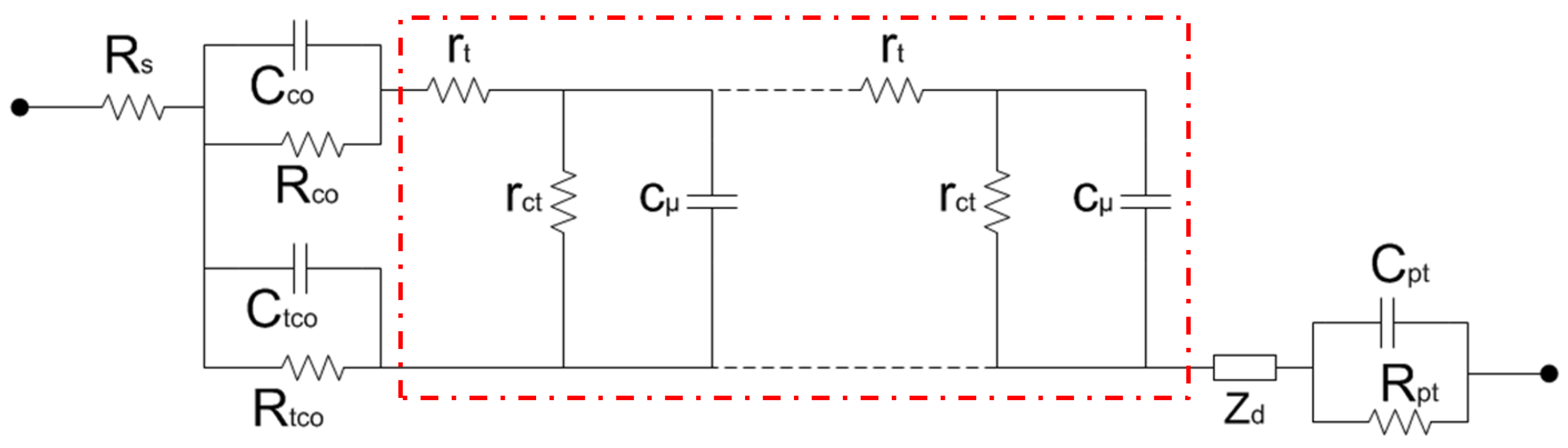
2.1. Estimation of L from Electrochemical Impedance Spectroscopy Measurements
2.2. Estimation of L from Incident Photon to Collected Electron Measurements
2.2.1. Linearization of the Free Electron Continuity Equation
2.2.2. Incident Photon to Collected Electron Ratio
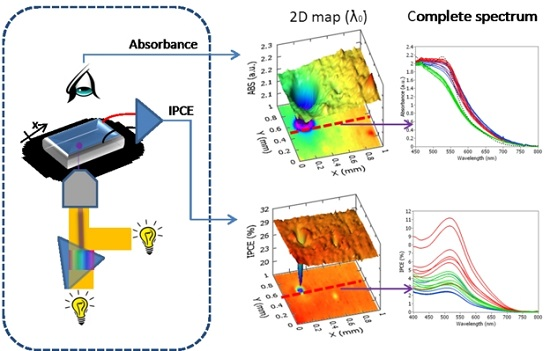
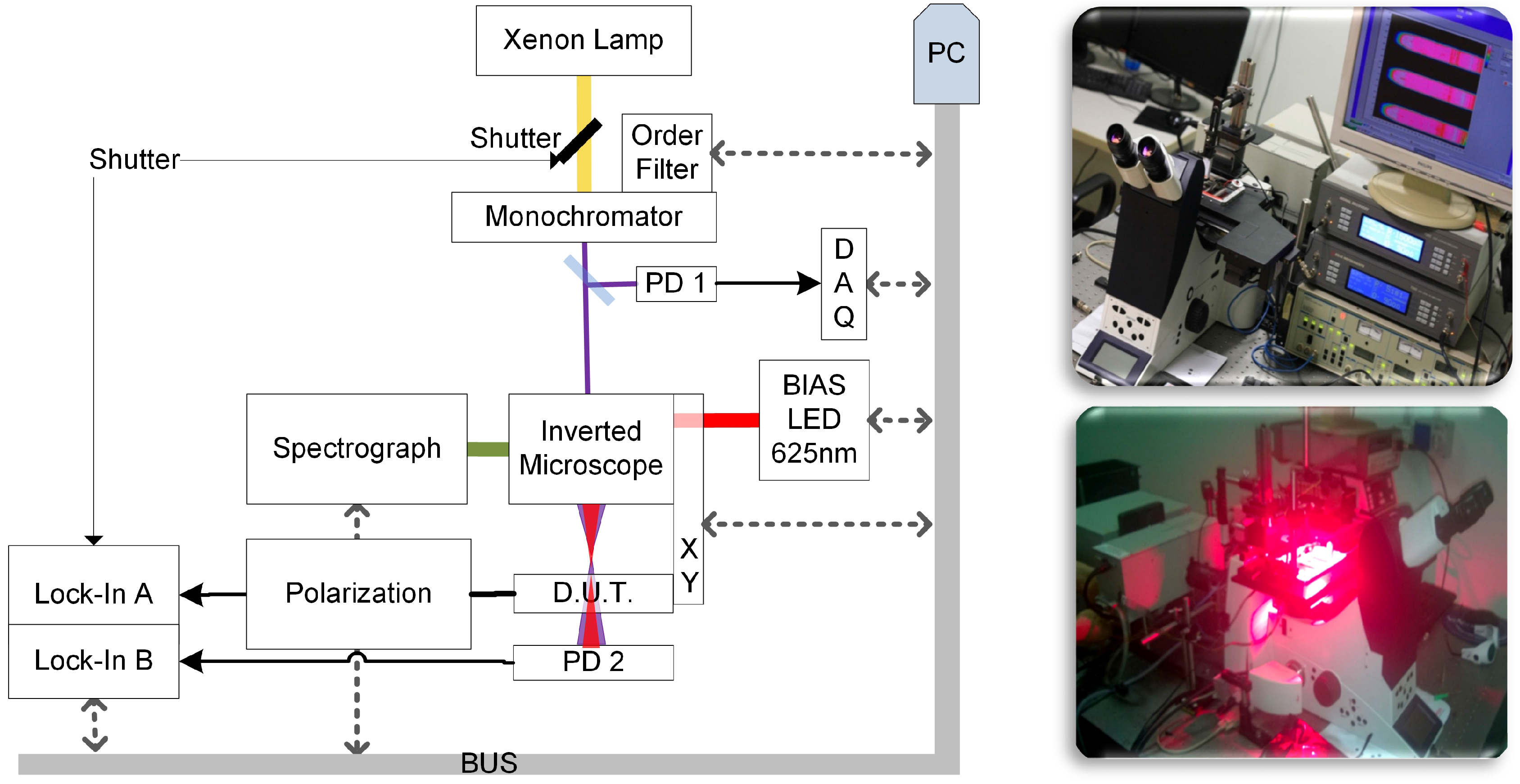
3. Scanning Apparatus (Spectrally-Resolved Analysis by Transmittance and Efficiency Mapping)
4. Results and Discussion
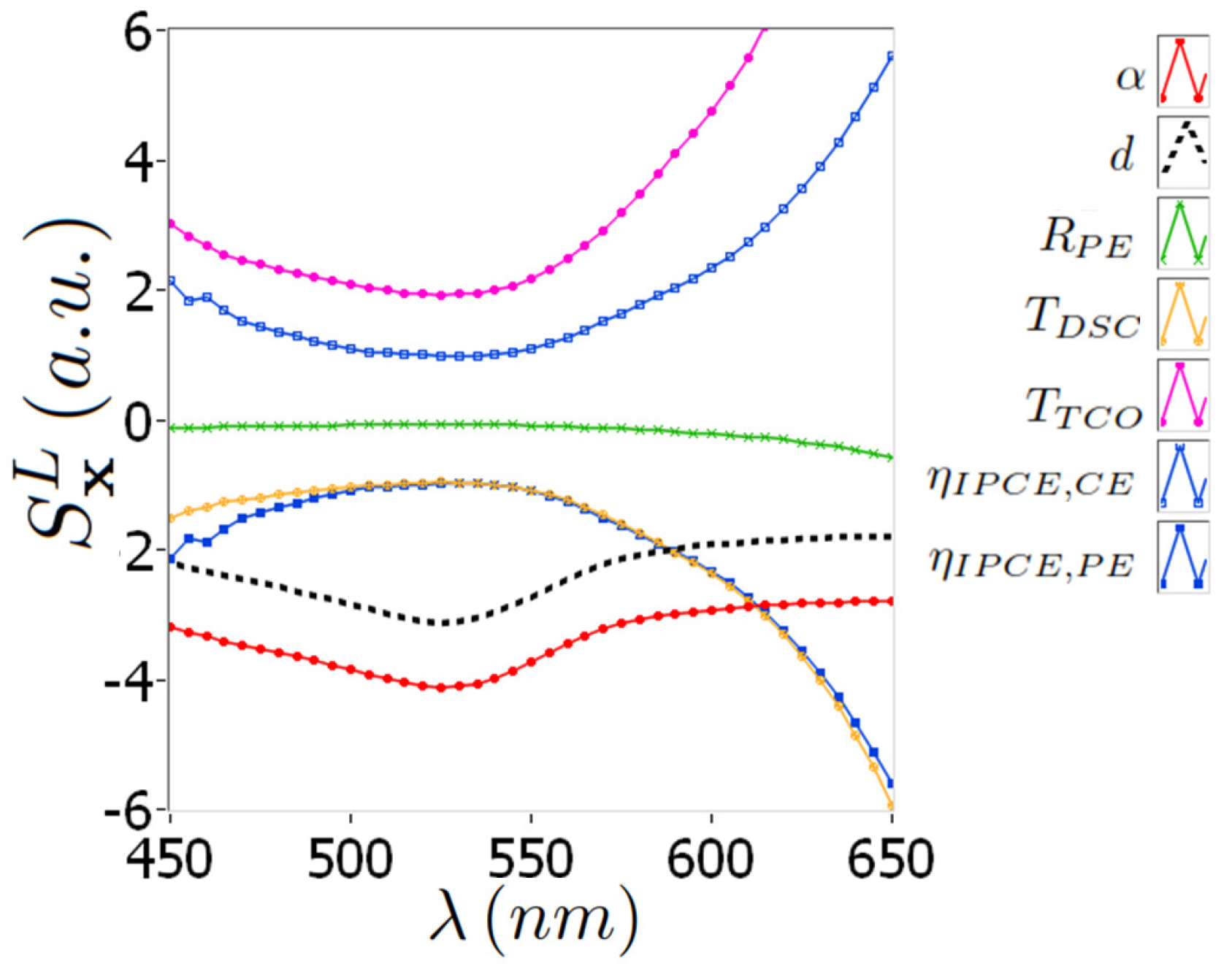
4.1. Sensitivity Analysis
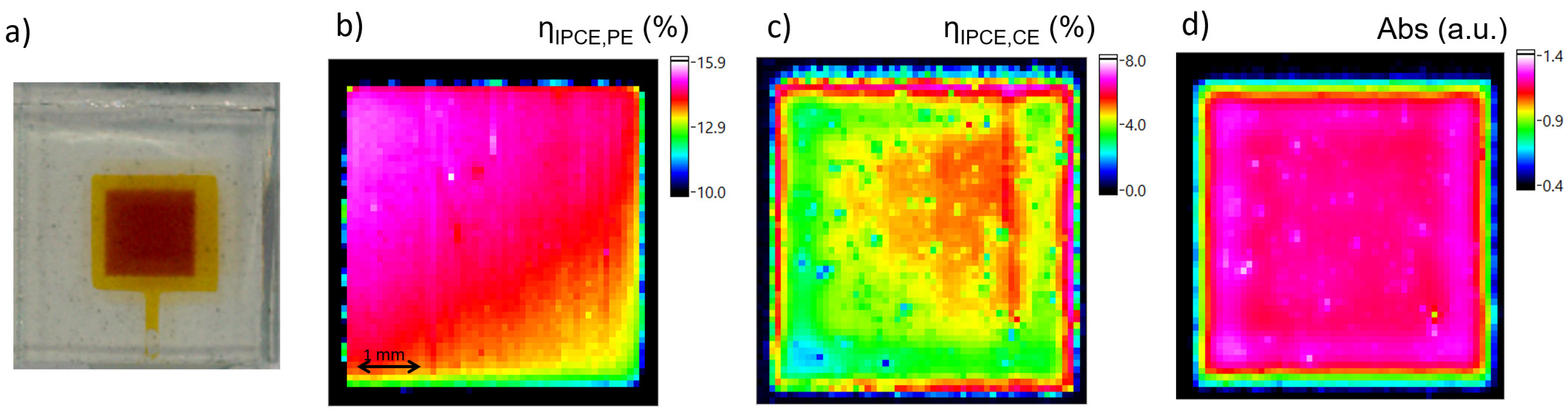
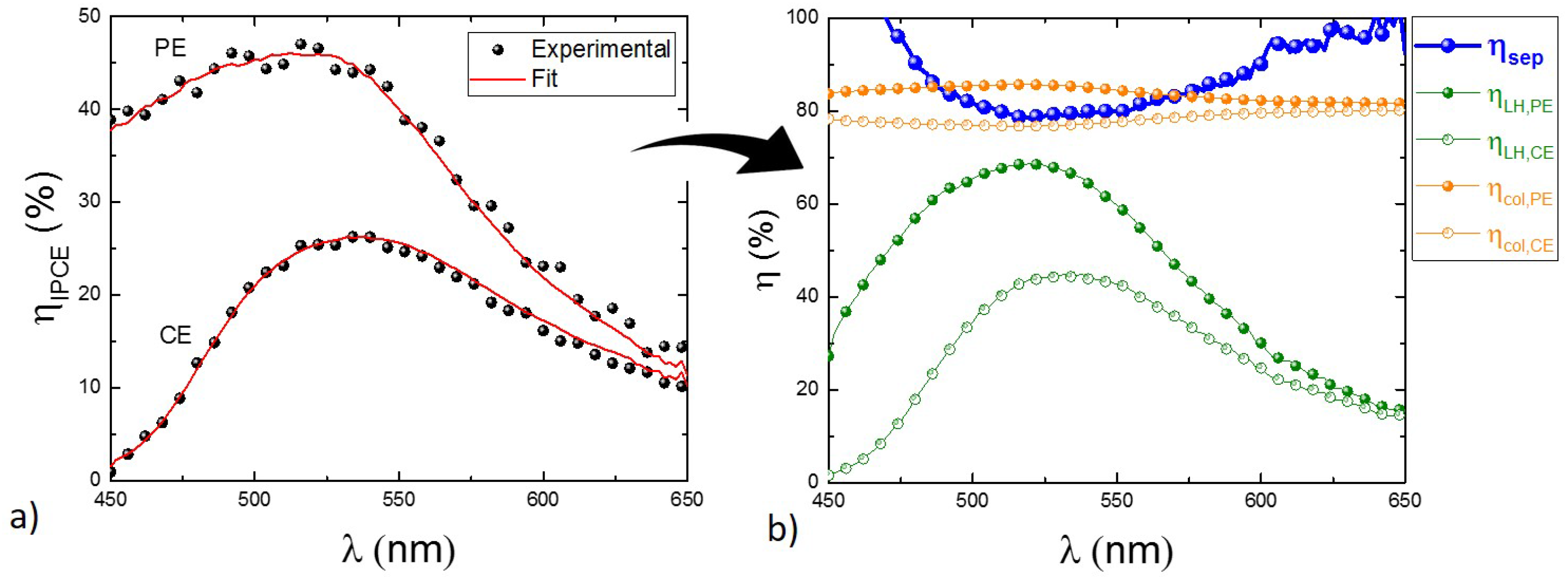
4.2. Estimation of L by Spectrally-Resolved Analysis by Transmittance and Efficiency Mapping
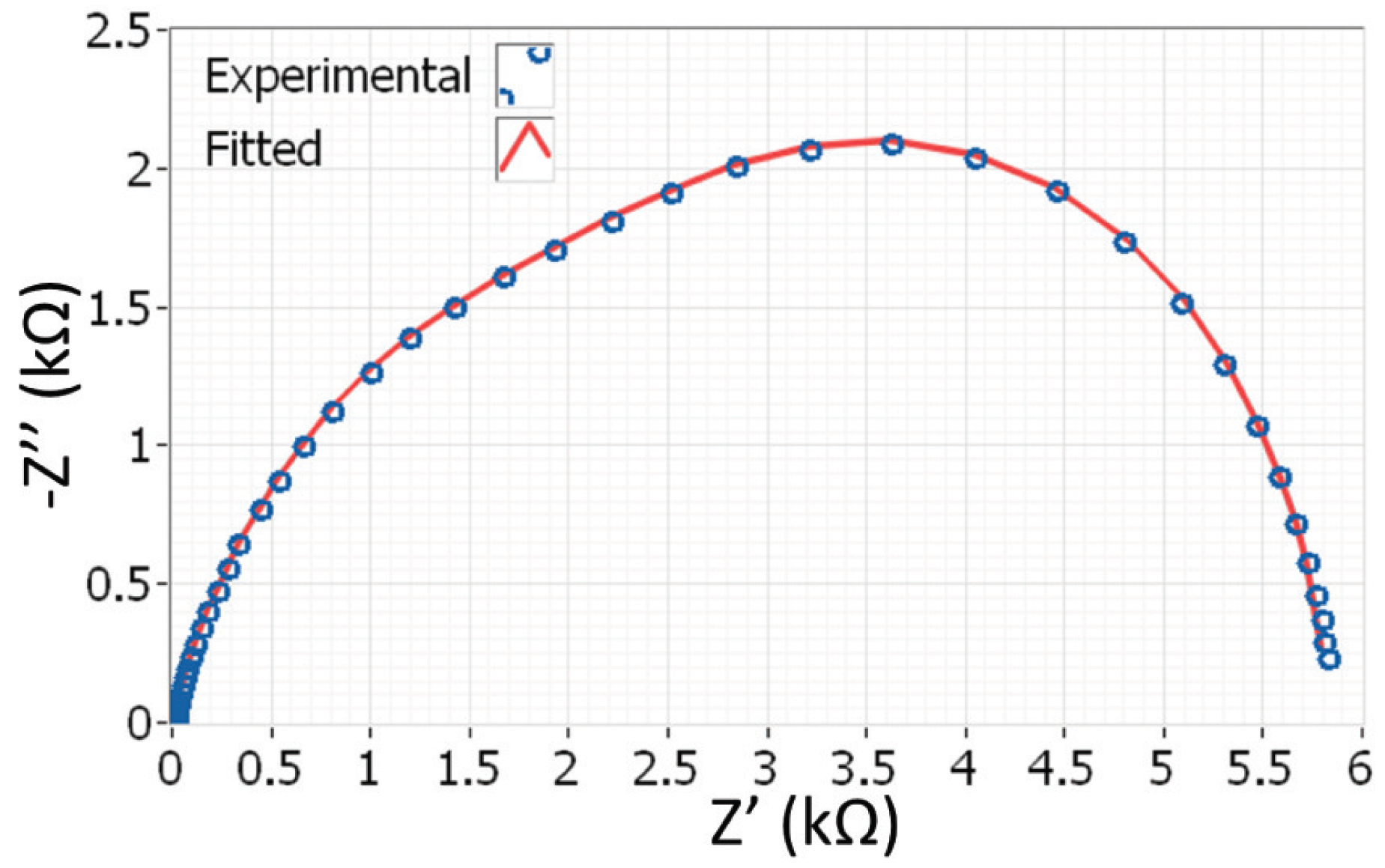
4.3. Estimation of L by Electrochemical Impedance Spectroscopy
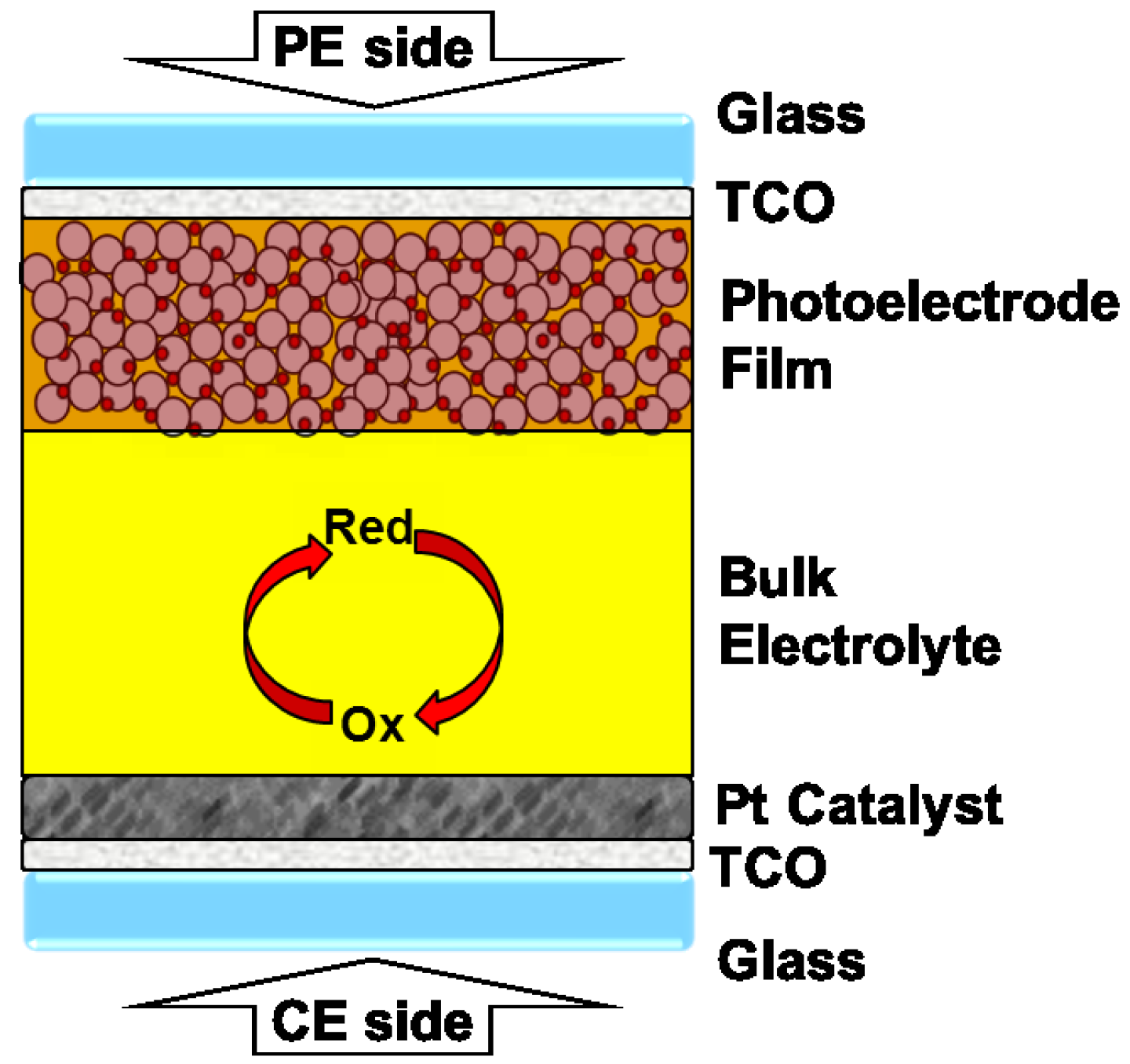
5. Materials and Methods
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chen, W.; Nikiforov, M.P.; Darling, S.B. Morphology characterization in organic and hybrid solar cells. Energy Environ. Sci. 2012, 5, 8045–8074. [Google Scholar] [CrossRef]
- Pfannmoller, M.; Kowalsky, W.; Schroder, R.R. Visualizing physical, electronic, and optical properties of organic photovoltaic cells. Energy Environ. Sci. 2013, 6, 2871–2891. [Google Scholar] [CrossRef]
- Fakharuddin, A.; Jose, R.; Brown, T.M.; Fabregat-Santiago, F.; Bisquert, J. A roadmap for dye-sensitized solar modules. Energy Environ. Sci. 2014, 7, 3952–3981. [Google Scholar] [CrossRef]
- Asghar, M.I.; Miettunen, K.; Halme, J.; Vahermaa, P.; Toivola, M.; Aitola, K.; Lund, P. Review of stability for advanced dye solar cells. Energy Environ. Sci. 2010, 3, 418–426. [Google Scholar] [CrossRef]
- Gao, Y.; Martin, T.P.; Thomas, A.K.; Grey, J.K. Resonance Raman spectroscopic- and photocurrent imaging of polythiophene/fullerene solar cells. J. Phys. Chem. Lett. 2010, 1, 178–182. [Google Scholar] [CrossRef]
- Gao, Y.; Martin, T.P.; Niles, E.T.; Wise, A.J.; Thomas, A.K.; Grey, J.K. Understanding morphology-dependent polymer aggregation properties and photocurrent generation in polythiophene/fullerene solar cells of variable compositions. J. Phys. Chem. C 2010, 114, 15121–15128. [Google Scholar] [CrossRef]
- Brenner, T.J.K.; McNeill, C.R. Spatially resolved spectroscopic mapping of photocurrent and photoluminescence in polymer blend photovoltaic devices. J. Phys. Chem. C 2011, 115, 19364–19370. [Google Scholar] [CrossRef]
- Bokalič, M.; Topič, M. Spatially Resolved Characterization in Thin-Film Photovoltaics; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Marek, J. Light-beam-induced current characterization of grain boundaries. J. Appl. Phys. 1984, 55, 318–326. [Google Scholar] [CrossRef]
- Carstensen, J.; Popkirov, G.; Bahr, J.; Föll, H. CELLO: An advanced LBIC measurement technique for solar cell local characterization. Sol. Energy Mater. Sol. Cells 2003, 76, 599–611. [Google Scholar] [CrossRef]
- Junghänel, M.; Tributsch, H. Monitoring the reactivity of oxide interfaces in dye solar cells with photocurrent imaging techniques. Comptes R. Chim. 2006, 9, 652–658. [Google Scholar] [CrossRef]
- Bokalič, M.; Krašovec, U.O.; Topič, M. Electroluminescence as a spatial characterisation technique for dye-sensitised solar cells. Prog. Photovolt. Res. Appl. 2013, 21, 1176–1180. [Google Scholar] [CrossRef]
- Raj, C.C.; Prasanth, R. A critical review of recent developments in nanomaterials for photoelectrodes in dye sensitized solar cells. J. Power Sources 2016, 317, 120–132. [Google Scholar] [CrossRef]
- Halme, J.; Vahermaa, P.; Miettunen, K.; Lund, P. Device physics of dye solar cells. Adv. Mater. 2010, 22, E210–E234. [Google Scholar] [CrossRef] [PubMed]
- Hagfeldt, A.; Boschloo, G.; Sun, L.; Kloo, L.; Pettersson, H. Dye-sensitized solar cells. Chem. Rev. 2010, 110, 6595–6663. [Google Scholar] [CrossRef] [PubMed]
- Ye, M.; Wen, X.; Wang, M.; Iocozzia, J.; Zhang, N.; Lin, C.; Lin, Z. Recent advances in dye-sensitized solar cells: From photoanodes, sensitizers and electrolytes to counter electrodes. Mater. Today 2015, 18, 155–162. [Google Scholar] [CrossRef]
- Fabregat-Santiago, F.; Bisquert, J.; Cevey, L.; Chen, P.; Wang, M.; Zakeeruddin, S.M.; Grätzel, M. Electron transport and recombination in solid-state dye solar cell with spiro-OMeTAD as hole conductor. J. Am. Chem. Soc. 2009, 131, 558–562. [Google Scholar] [CrossRef] [PubMed]
- Navas, J.; Guillen, E.; Alcantara, R.; Fernandez-Lorenzo, C.; Martin-Calleja, J.; Oskam, G.; Idigoras, J.; Berger, T.; Anta, J.A. Direct estimation of the electron diffusion length in dye-sensitized solar cells. J. Phys. Chem. Lett. 2011, 2, 1045–1050. [Google Scholar] [CrossRef]
- Park, J.K.; Kang, J.C.; Kim, S.Y.; Son, B.H.; Park, J.Y.; Lee, S.; Ahn, Y.H. Diffusion length in nanoporous photoelectrodes of dye-sensitized solar cells under operating conditions measured by photocurrent microscopy. J. Phys. Chem. Lett. 2012, 3, 3632–3638. [Google Scholar] [CrossRef] [PubMed]
- Dunn, H.K.; Westin, P.O.; Staff, D.R.; Peter, L.M.; Walker, A.B.; Boschloo, G.; Hagfeldt, A. Determination of the electron diffusion length in dye-sensitized solar cells by substrate contact patterning. J. Phys. Chem. C 2011, 115, 13932–13937. [Google Scholar] [CrossRef]
- Barnes, P.R.F.; Liu, L.; Li, X.; Anderson, A.Y.; Kisserwan, H.; Ghaddar, T.H.; Durrant, J.R.; O’Regan, B.C. Re-evaluation of recombination losses in dye-sensitized cells: The failure of dynamic relaxation methods to correctly predict diffusion length in nanoporous photoelectrodes. Nano Lett. 2009, 9, 3532–3538. [Google Scholar] [CrossRef] [PubMed]
- Barnes, P.R.; Anderson, A.Y.; Koops, S.E.; Durrant, J.R.; O’Regan, B.C. Electron injection efficiency and diffusion length in dye-sensitized solar cells derived from incident photon conversion efficiency measurements. J. Phys. Chem. C 2008, 113, 1126–1136. [Google Scholar] [CrossRef]
- Jennings, J.R.; Li, F.; Wang, Q. Reliable determination of electron diffusion length and charge separation efficiency in dye-sensitized solar cells. J. Phys. Chem. C 2010, 114, 14665–14674. [Google Scholar] [CrossRef]
- Agresti, A.; Cinà, L.; Pescetelli, S.; Taheri, B.; Di Carlo, A. Stability of dye-sensitized solar cell under reverse bias condition: Resonance Raman spectroscopy combined with spectrally resolved analysis by transmittance and efficiency mapping. Vib. Spectrosc. 2016, 84, 106–117. [Google Scholar] [CrossRef]
- Soedergren, S.; Hagfeldt, A.; Olsson, J.; Lindquist, S.E. Theoretical models for the action spectrum and the current-voltage characteristics of microporous semiconductor films in photoelectrochemical cells. J. Phys. Chem. 1994, 98, 5552–5556. [Google Scholar] [CrossRef]
- Wang, H.; Peter, L.M. A comparison of different methods to determine the electron diffusion length in dye-sensitized solar cells. J. Phys. Chem. C 2009, 113, 18125–18133. [Google Scholar] [CrossRef]
- Fabregat-Santiago, F.; Bisquert, J.; Garcia-Belmonte, G.; Boschloo, G.; Hagfeldt, A. Influence of electrolyte in transport and recombination in dye-sensitized solar cells studied by impedance spectroscopy. Sol. Energy Mater. Sol. Cells 2005, 87, 117–131. [Google Scholar] [CrossRef]
- Fabregat-Santiago, F.; Bisquert, J.; Palomares, E.; Otero, L.; Kuang, D.; Zakeeruddin, S.M.; Grätzel, M. Correlation between photovoltaic performance and impedance spectroscopy of dye-sensitized solar cells based on ionic liquids. J. Phys. Chem. C 2007, 111, 6550–6560. [Google Scholar] [CrossRef]
- Garland, J.; Crain, D.; Roy, D. Utilization of electrochemical impedance spectroscopy for experimental characterization of the diode features of charge recombination in a dye sensitized solar cell. Electrochim. Acta 2014, 148, 62–72. [Google Scholar] [CrossRef]
- Bisquert, J. Theory of the impedance of electron diffusion and recombination in a thin layer. J. Phys. Chem. B 2002, 106, 325–333. [Google Scholar] [CrossRef]
- Jennings, J.R.; Wang, Q. Impedance spectroscopy of dye-sensitized solar cells: Analysis of measurement and fitting errors. J. Electrochem. Soc. 2012, 159, F141–F149. [Google Scholar] [CrossRef]
- Bisquert, J.; Mora-Sero, I. Simulation of steady-state characteristics of dye-sensitized solar cells and the interpretation of the diffusion length. J. Phys. Chem. Lett. 2010, 1, 450–456. [Google Scholar] [CrossRef]
- Fabregat-Santiago, F.; Garcia-Belmonte, G.; Bisquert, J.; Zaban, A.; Salvador, P. Decoupling of transport, charge storage, and interfacial charge transfer in the nanocrystalline TiO2/electrolyte system by impedance methods. J. Phys. Chem. B 2002, 106, 334–339. [Google Scholar] [CrossRef]
- Halme, J.; Boschloo, G.; Hagfeldt, A.; Lund, P. Spectral characteristics of light harvesting, electron injection, and steady-state charge collection in pressed TiO2 dye solar cells. J. Phys. Chem. C 2008, 112, 5623–5637. [Google Scholar] [CrossRef]
- Ansari-Rad, M.; Abdi, Y.; Arzi, E. Reaction order and ideality factor in dye-sensitized nanocrystalline solar cells: A theoretical investigation. J. Phys. Chem. C 2012, 116, 10867–10872. [Google Scholar] [CrossRef]
- Villanueva-Cab, J.; Wang, H.; Oskam, G.; Peter, L.M. Electron diffusion and back reaction in dye-sensitized solar cells: The effect of nonlinear recombination kinetics. J. Phys. Chem. Lett. 2010, 1, 748–751. [Google Scholar] [CrossRef]
- Xue, G.; Guo, Y.; Yu, T.; Guan, J.; Yu, X.; Zhang, J.; Liu, J.; Zou, Z. Degradation mechanisms investigation for long-term thermal stability of dye-sensitized solar cells. Int. J. Electrochem. Sci. 2012, 7, 1496–1511. [Google Scholar]
- Fisher, A.; Peter, L.; Ponomarev, E.; Walker, A.; Wijayantha, K. Intensity dependence of the back reaction and transport of electrons in dye-sensitized nanocrystalline TiO2 solar cells. J. Phys. Chem. B 2000, 104, 949–958. [Google Scholar] [CrossRef]
- Trupke, T.; Würfel, P.; Uhlendorf, I. Dependence of the photocurrent conversion efficiency of dye-sensitized solar cells on the incident light intensity. J. Phys. Chem. B 2000, 104, 11484–11488. [Google Scholar] [CrossRef]
- Peter, L.; Wijayantha, K. Intensity dependence of the electron diffusion length in dye-sensitised nanocrystalline TiO2 photovoltaic cells. Electrochem. Commun. 1999, 1, 576–580. [Google Scholar] [CrossRef]
- Xue, G.; Yu, X.; Yu, T.; Bao, C.; Zhang, J.; Guan, J.; Huang, H.; Tang, Z.; Zou, Z. Understanding of the chopping frequency effect on IPCE measurements for dye-sensitized solar cells: From the viewpoint of electron transport and extinction spectrum. J. Phys. D Appl. Phys. 2012, 45. [Google Scholar] [CrossRef]
- Tian, H.; Liu, L.; Liu, B.; Yuan, S.; Wang, X.; Wang, Y.; Yu, T.; Zou, Z. Influence of capacitance characteristic on dye-sensitized solar cell’s IPCE measurement. J. Phys. D Appl. Phys. 2009, 42. [Google Scholar] [CrossRef]
- Hishikawa, Y.; Yanagida, M.; Koide, N. Performance Characterization of the Dye-Sensitized Solar Cells. In Proceedings of the Conference Record of the Thirty-First IEEE Photovoltaic Specialists Conference, Lake Buena Vista, FL, USA, 3–7 January 2005; pp. 67–70.
- Yang, X.; Yanagida, M.; Han, L. Reliable evaluation of dye-sensitized solar cells. Energy Environ. Sci. 2013, 6, 54–66. [Google Scholar] [CrossRef]
- Chen, C.Y.; Pootrakulchote, N.; Hung, T.H.; Tan, C.J.; Tsai, H.H.; Zakeeruddin, S.M.; Wu, C.G.; Grätzel, M. Ruthenium sensitizer with thienothiophene-linked Carbazole Antennas in conjunction with liquid electrolytes for dye-sensitized solar cells. J. Phys. Chem. C 2011, 115, 20043–20050. [Google Scholar] [CrossRef]
- Li, F.; Jennings, J.R.; Wang, Q. Determination of sensitizer regeneration efficiency in dye-sensitized solar cells. ACS Nano 2013, 7, 8233–8242. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Jennings, J.R.; Wang, X.; Fan, L.; Koh, Z.Y.; Yu, H.; Yan, L.; Wang, Q. Influence of ionic liquid on recombination and regeneration kinetics in dye-sensitized solar cells. J. Phys. Chem. C 2014, 118, 17153–17159. [Google Scholar] [CrossRef]
- Eperon, G.E.; Burlakov, V.M.; Goriely, A.; Snaith, H.J. Neutral color semitransparent microstructured perovskite solar cells. ACS Nano 2014, 8, 591–598. [Google Scholar] [CrossRef] [PubMed]
- Roldan-Carmona, C.; Malinkiewicz, O.; Betancur, R.; Longo, G.; Momblona, C.; Jaramillo, F.; Camacho, L.; Bolink, H.J. High efficiency single-junction semitransparent perovskite solar cells. Energy Environ. Sci. 2014, 7, 2968–2973. [Google Scholar] [CrossRef]
- Guo, F.; Azimi, H.; Hou, Y.; Przybilla, T.; Hu, M.; Bronnbauer, C.; Langner, S.; Spiecker, E.; Forberich, K.; Brabec, C.J. High-performance semitransparent perovskite solar cells with solution-processed silver nanowires as top electrodes. Nanoscale 2015, 7, 1642–1649. [Google Scholar] [CrossRef] [PubMed]
- Pastorelli, F.; Romero-Gomez, P.; Betancur, R.; Martinez-Otero, A.; Mantilla-Perez, P.; Bonod, N.; Martorell, J. Enhanced light harvesting in semitransparent organic solar cells using an optical metal cavity configuration. Adv. Energy Mater. 2015, 5. [Google Scholar] [CrossRef]
- Ren, X.; Li, X.; Choy, W.C. Optically enhanced semi-transparent organic solar cells through hybrid metal/nanoparticle/dielectric nanostructure. Nano Energy 2015, 17, 187–195. [Google Scholar] [CrossRef]
- Liu, Z.; You, P.; Liu, S.; Yan, F. Neutral-color semitransparent organic solar cells with all-graphene electrodes. ACS Nano 2015, 9, 12026–12034. [Google Scholar] [CrossRef] [PubMed]
- Pivrikas, A.; Sariciftci, N.S.; Juška, G.; Österbacka, R. A review of charge transport and recombination in polymer/fullerene organic solar cells. Prog. Photovolt. Res. Appl. 2007, 15, 677–696. [Google Scholar] [CrossRef]
- Tress, W.; Leo, K.; Riede, M. Optimum mobility, contact properties, and open-circuit voltage of organic solar cells: A drift-diffusion simulation study. Phys. Rev. B 2012, 85. [Google Scholar] [CrossRef]
- Hwang, I.; McNeill, C.R.; Greenham, N.C. Drift-diffusion modeling of photocurrent transients in bulk heterojunction solar cells. J. Appl. Phys. 2009, 106. [Google Scholar] [CrossRef]
- Bergmann, V.W.; Guo, Y.; Tanaka, H.; Hermes, I.M.; Li, D.; Klasen, A.; Bretschneider, S.A.; Nakamura, E.; Berger, R.; Weber, S.A.L. Local time-dependent charging in a perovskite solar cell. ACS Appl. Mater. Interfaces 2016, 8, 19402–19409. [Google Scholar]
- Guillen, E.; Ramos, F.J.; Anta, J.A.; Ahmad, S. Elucidating transport-recombination mechanisms in perovskite solar cells by small-perturbation techniques. J. Phys. Chem. C 2014, 118, 22913–22922. [Google Scholar] [CrossRef]
- Stranks, S.D.; Eperon, G.E.; Grancini, G.; Menelaou, C.; Alcocer, M.J.P.; Leijtens, T.; Herz, L.M.; Petrozza, A.; Snaith, H.J. Electron-hole diffusion lengths exceeding 1 micrometer in an organometal trihalide perovskite absorber. Science 2013, 342, 341–344. [Google Scholar] [PubMed]
- Minemoto, T.; Murata, M. Device modeling of perovskite solar cells based on structural similarity with thin film inorganic semiconductor solar cells. J. Appl. Phys. 2014, 116. [Google Scholar] [CrossRef]

© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cinà, L.; Taheri, B.; Reale, A.; Di Carlo, A. Diffusion Length Mapping for Dye-Sensitized Solar Cells. Energies 2016, 9, 686. https://doi.org/10.3390/en9090686
Cinà L, Taheri B, Reale A, Di Carlo A. Diffusion Length Mapping for Dye-Sensitized Solar Cells. Energies. 2016; 9(9):686. https://doi.org/10.3390/en9090686
Chicago/Turabian StyleCinà, Lucio, Babak Taheri, Andrea Reale, and Aldo Di Carlo. 2016. "Diffusion Length Mapping for Dye-Sensitized Solar Cells" Energies 9, no. 9: 686. https://doi.org/10.3390/en9090686
APA StyleCinà, L., Taheri, B., Reale, A., & Di Carlo, A. (2016). Diffusion Length Mapping for Dye-Sensitized Solar Cells. Energies, 9(9), 686. https://doi.org/10.3390/en9090686