Partial Discharge Measurement under an Oscillating Switching Impulse: A Potential Supplement to the Conventional Insulation Examination in the Field
Abstract
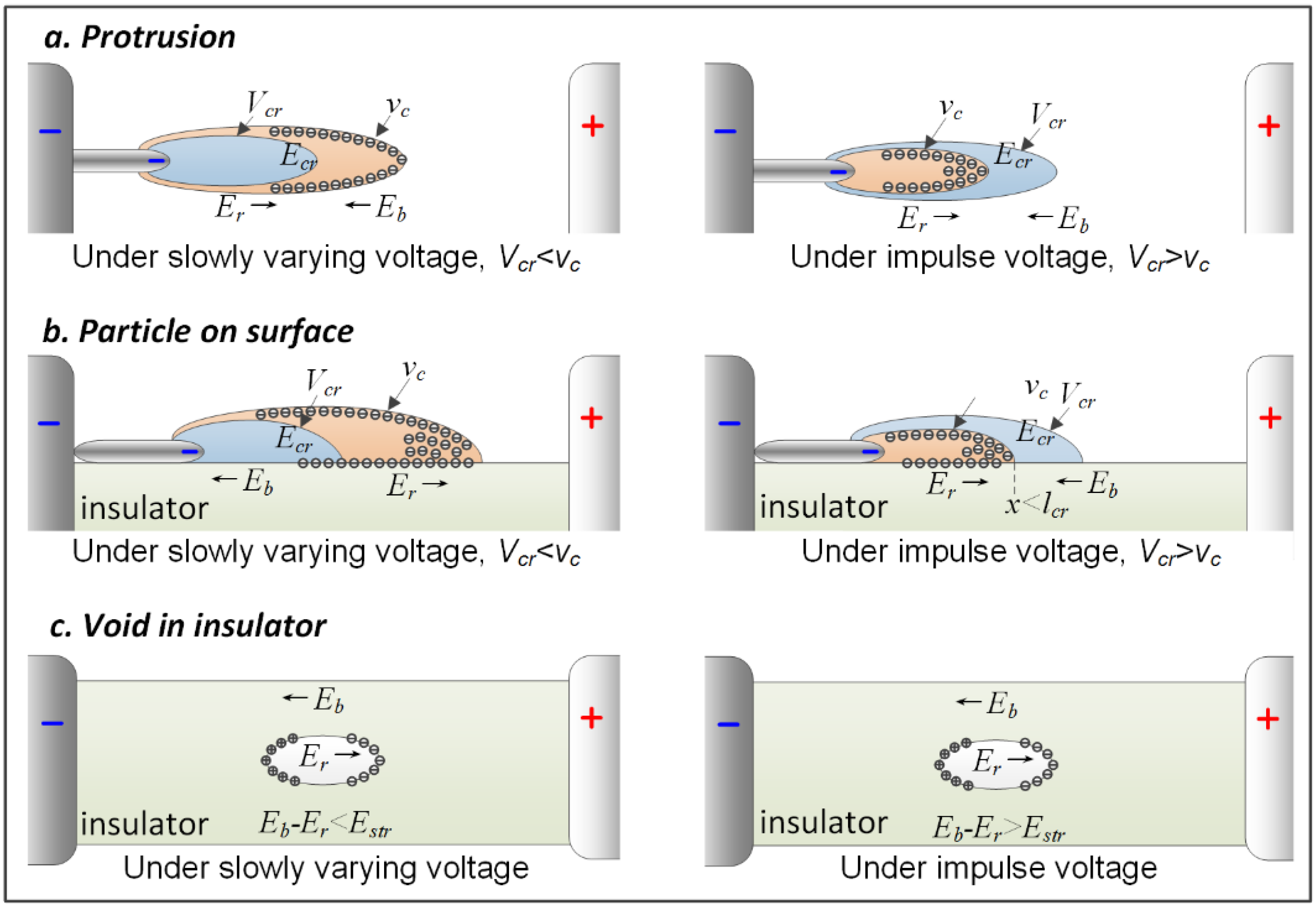
:1. Introduction
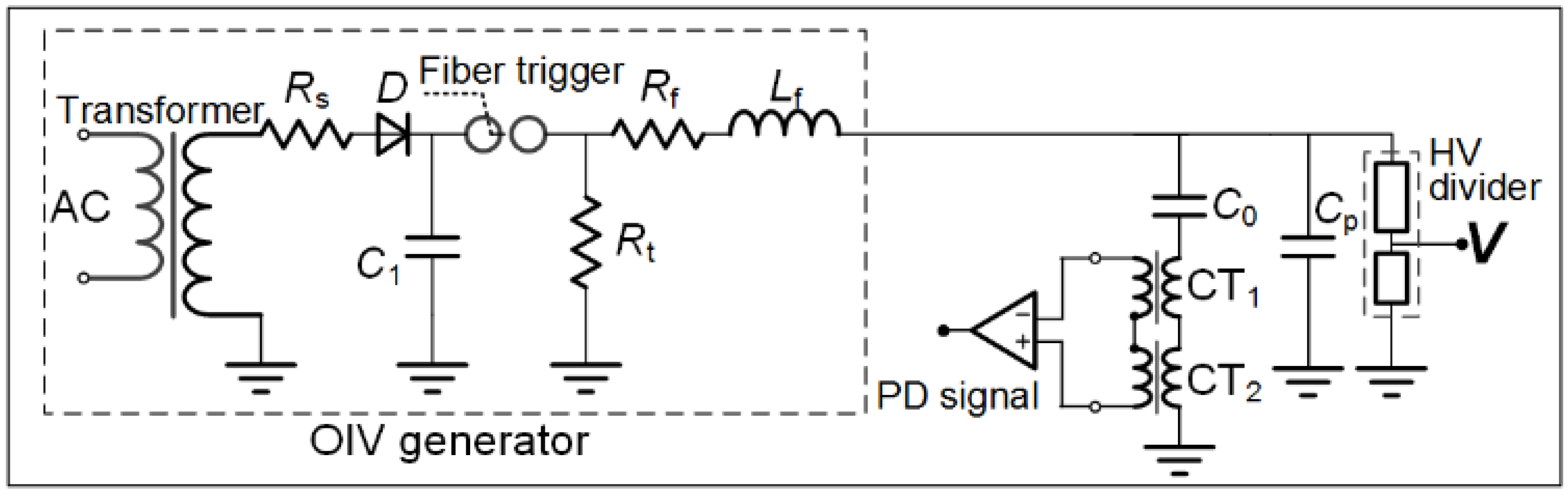
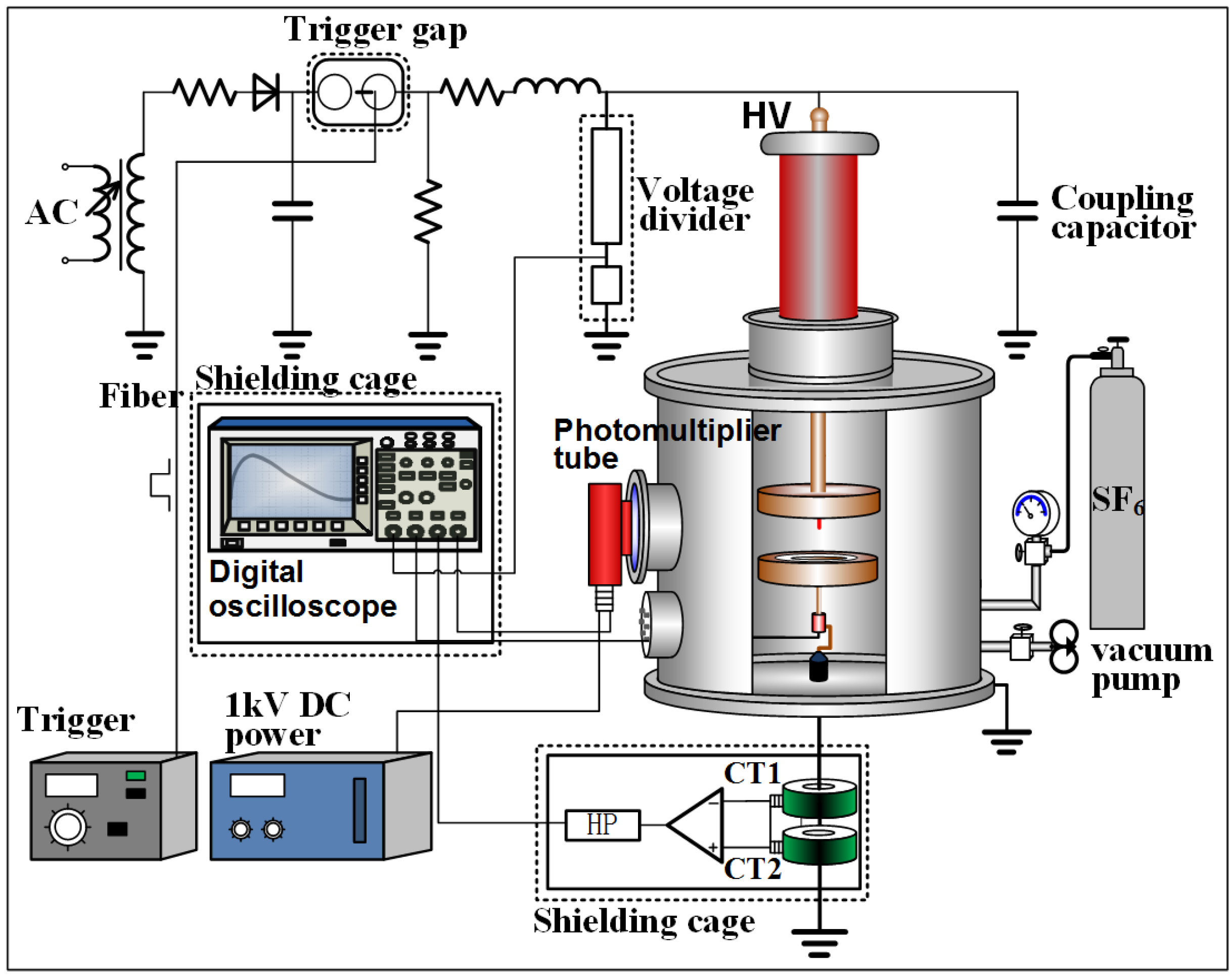
2. Experimental Setup
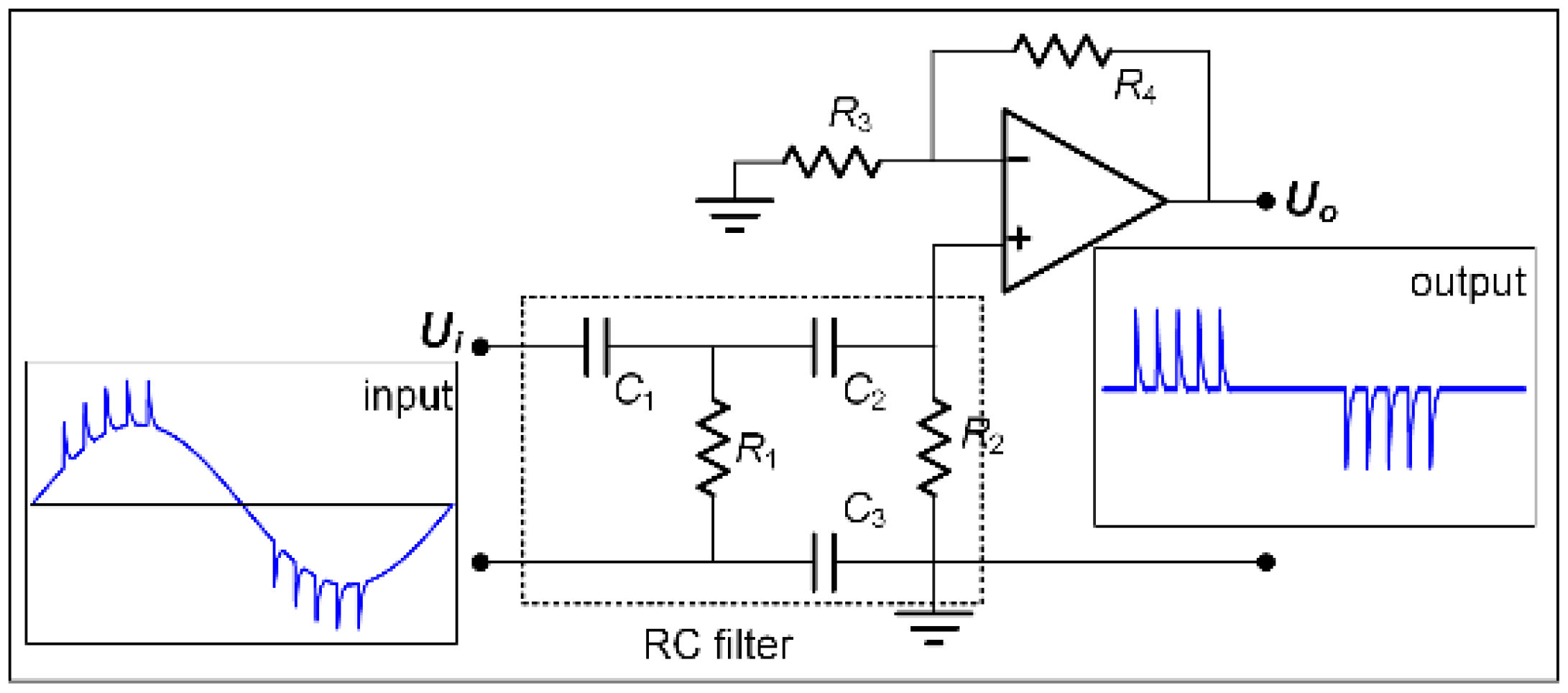
2.1. Partial Discharge (PD) Measurement under Impulse Conditions
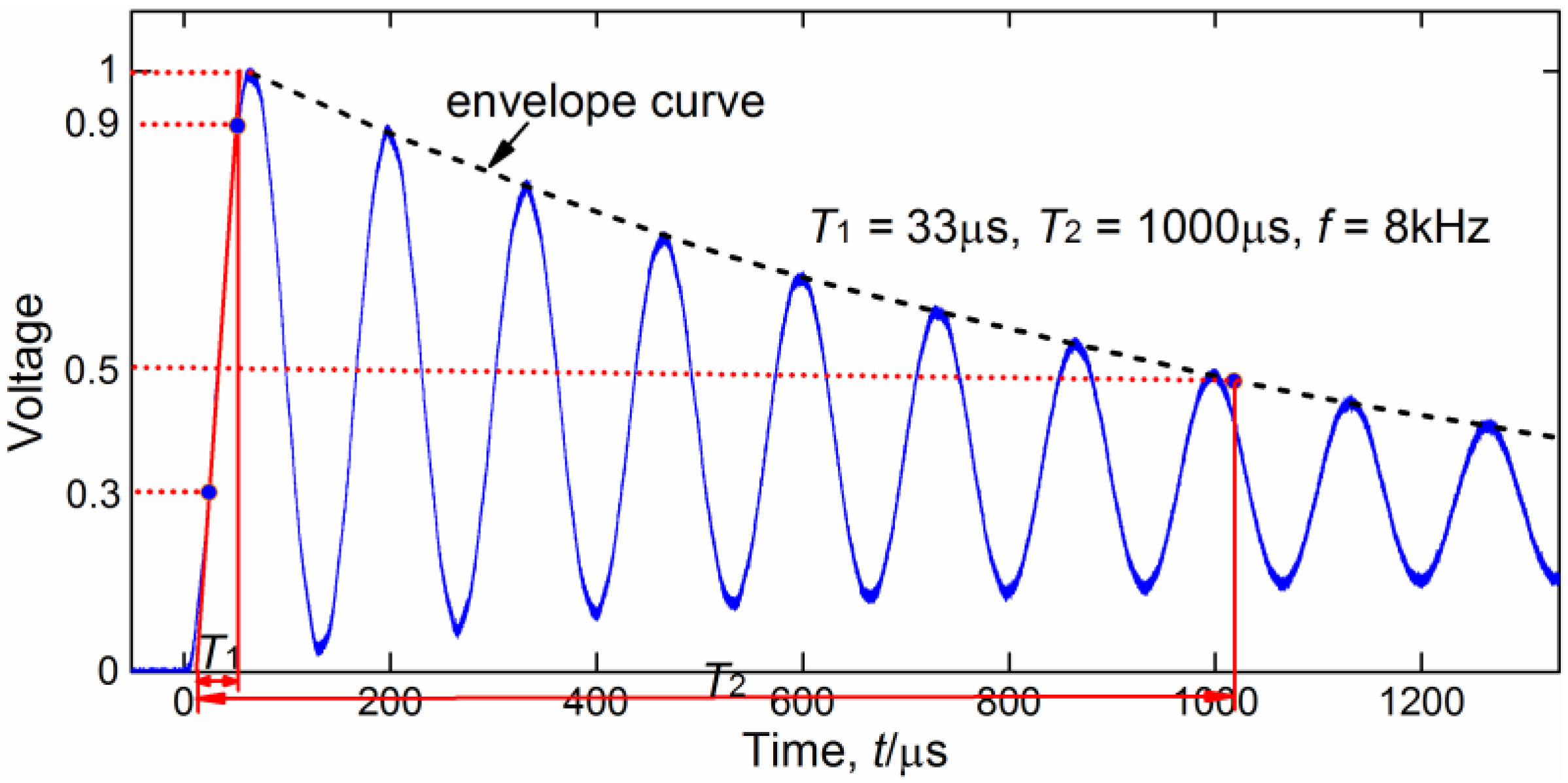
2.2. Artificial Defect Models and Experimental Setup
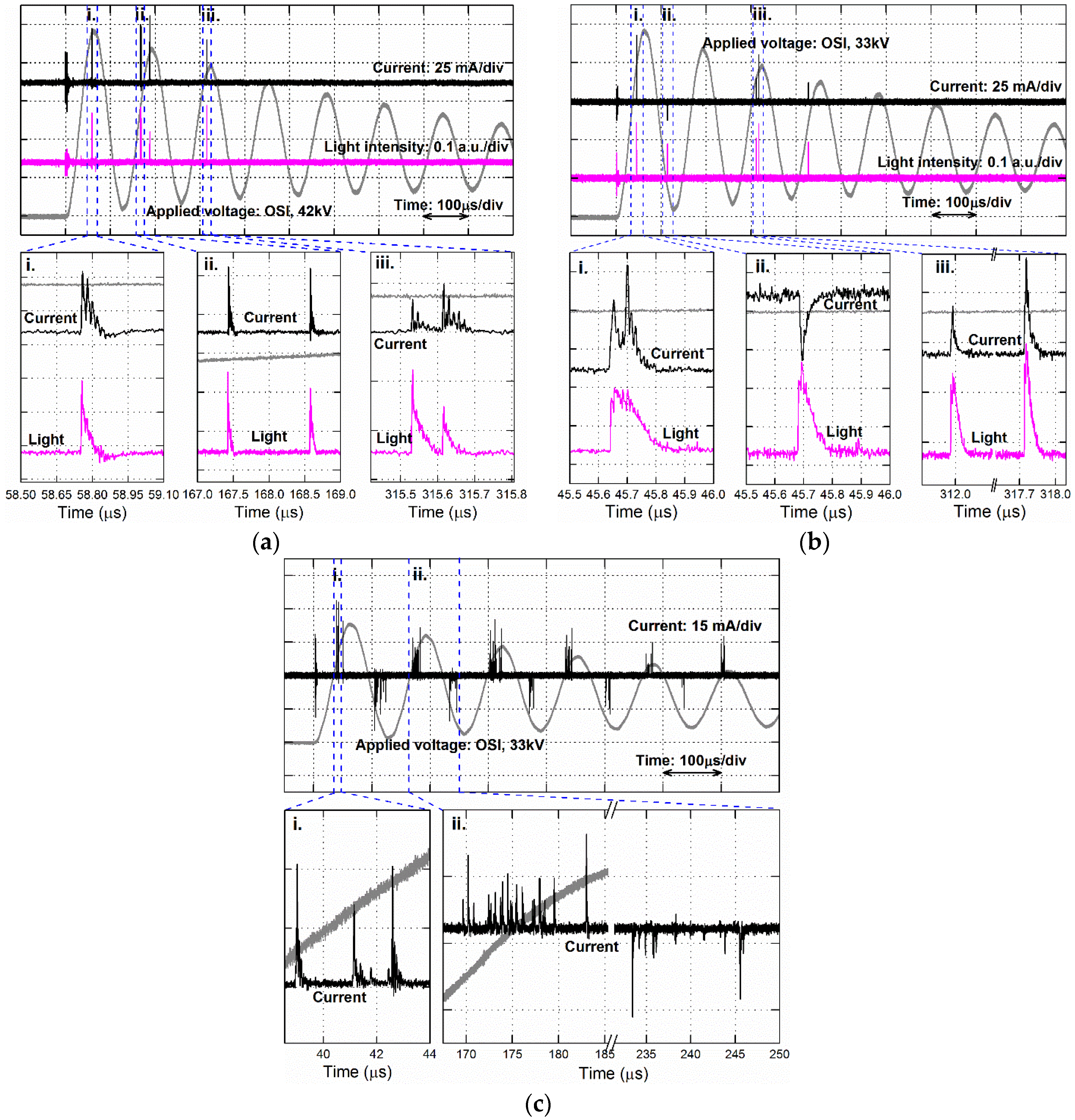
3. Results
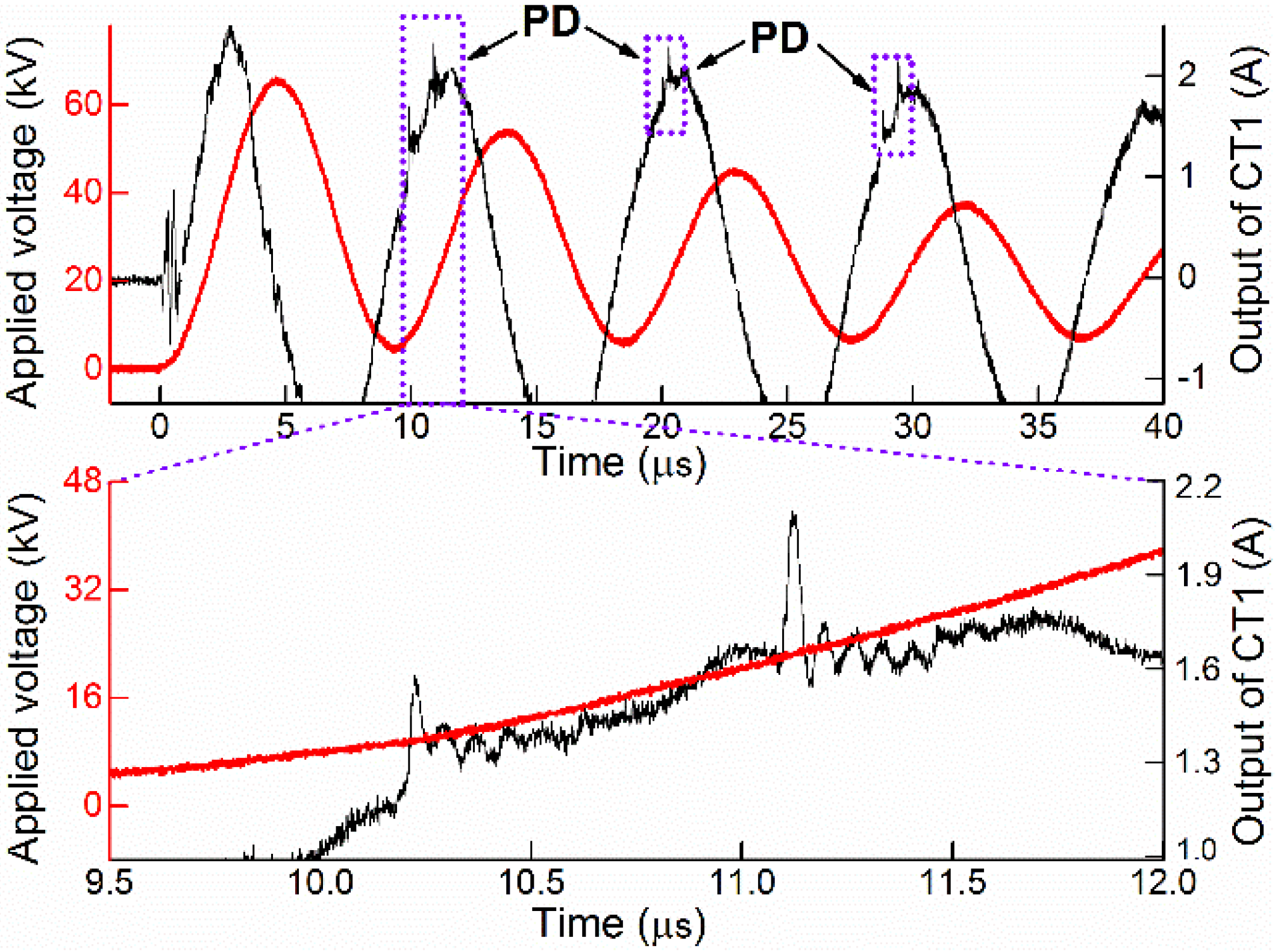
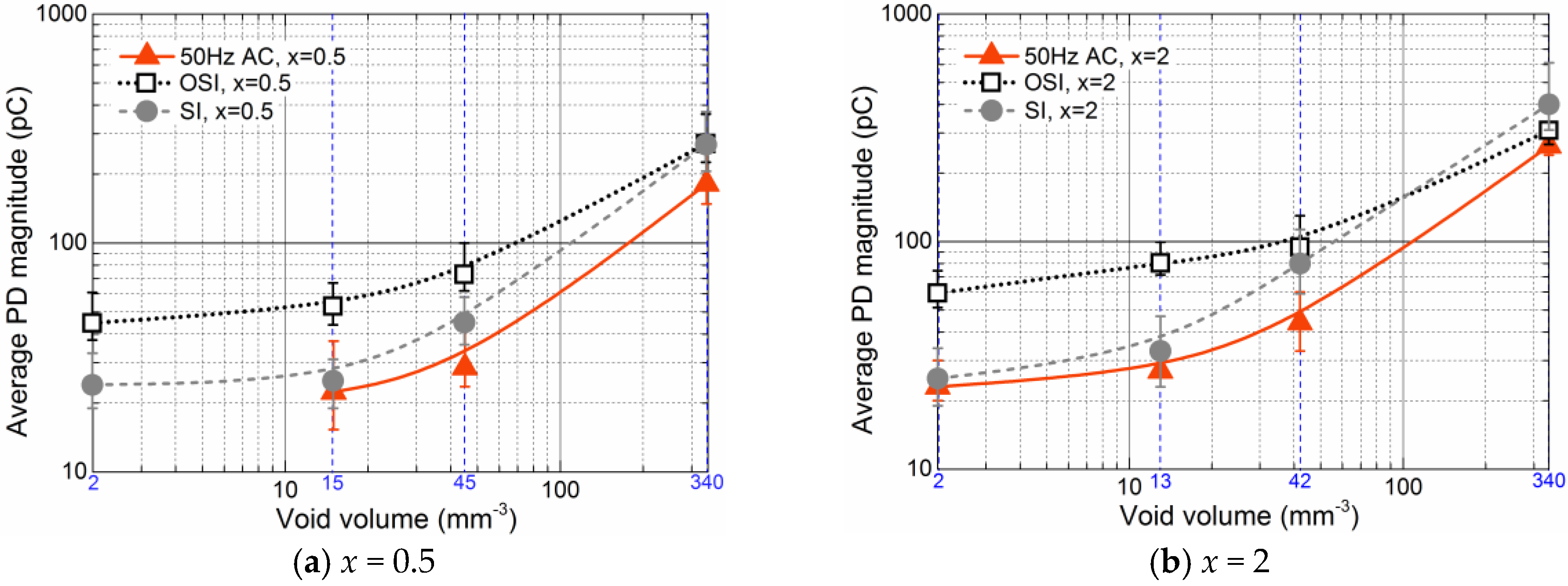
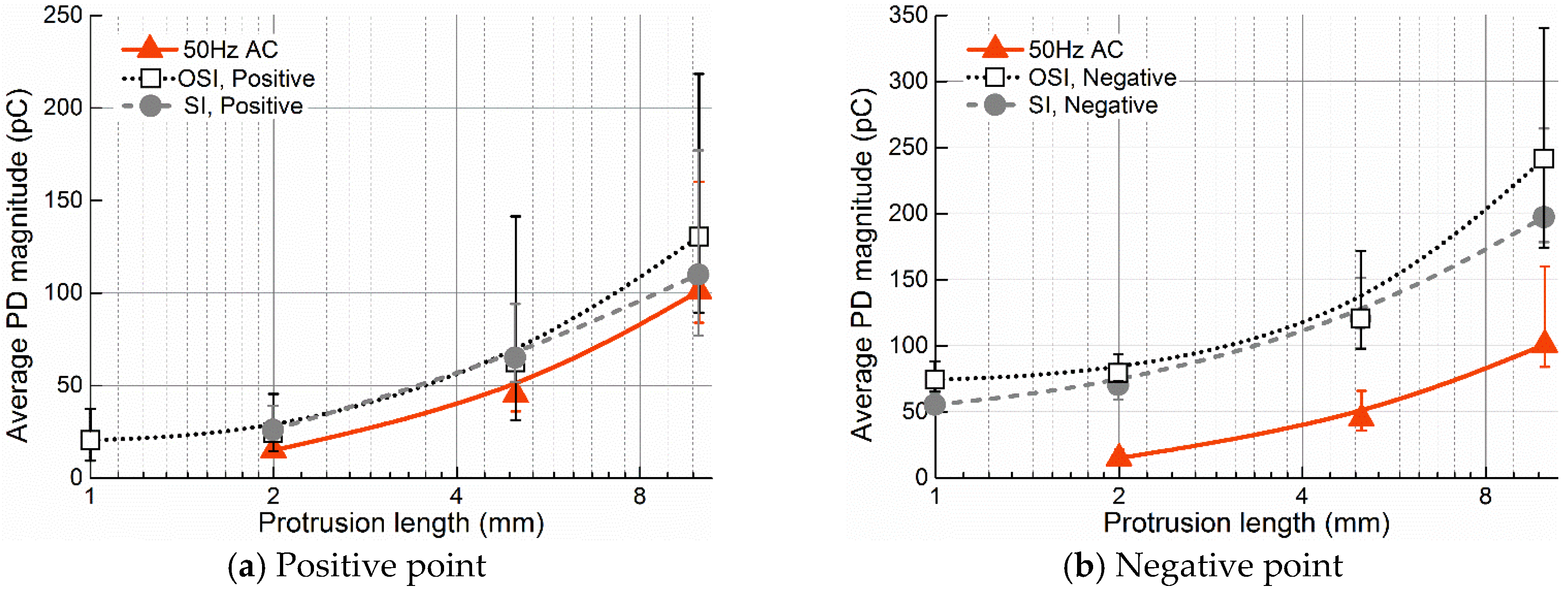
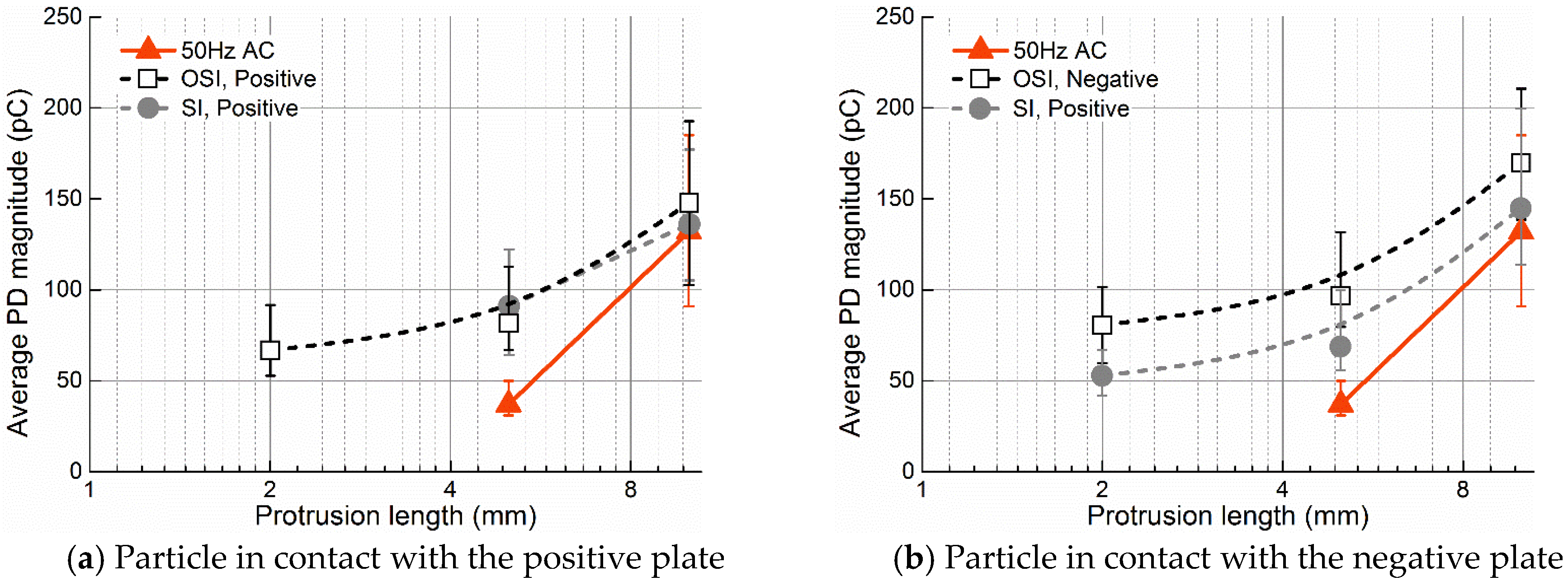
3.1. PDs under OSI Voltage
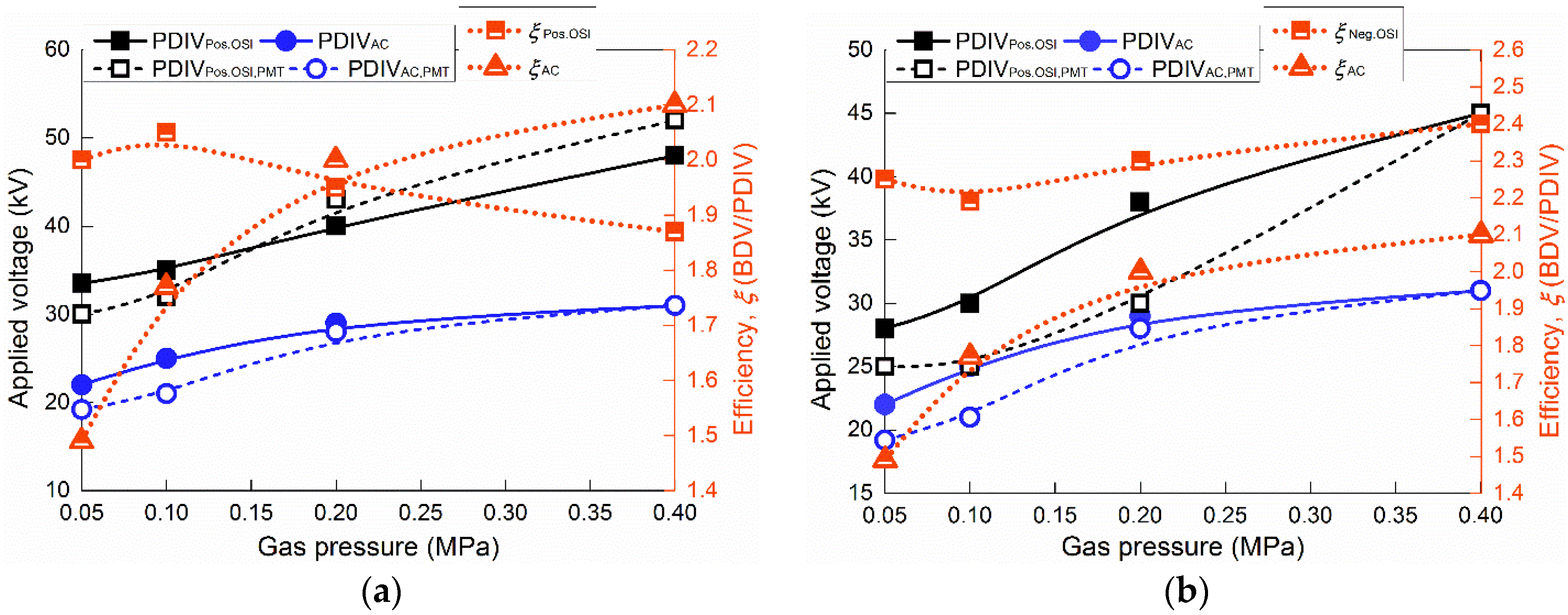
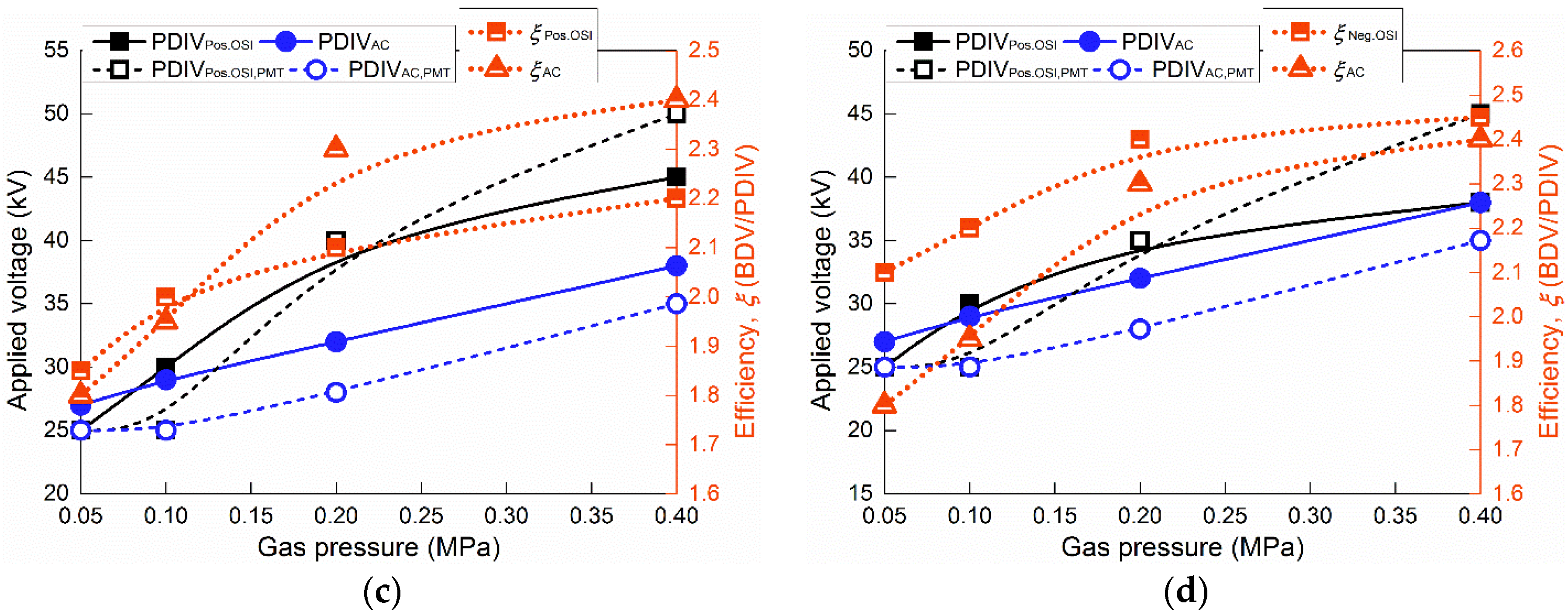
3.2. Efficiencies of the OSI, SI, and AC Voltages for Exciting PDs
3.2.1. PD Inception and Breakdown under Various Applied Voltages
3.2.2. Detectable Scales of the Three Defects under Various Applied Voltages
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- CIGRE Joint Task Force. Partial Discharge Detection System for GIS: Sensitivity Verification for the UHF Method and the Acoustic Method. Electra 1999, 183, 75–87. [Google Scholar]
- Takahashi, T.; Yamada, T.; Hayakawa, N.; Okubo, H. Space charge behavior in SF6 gas and sequential generation of PD pulses. IEEE Trans. Dielectr. Electr. Insul. 2000, 7, 141–145. [Google Scholar] [CrossRef]
- Hinterholzer, T.; Boeck, W. Breakdown in SF6 influenced by corona-stabilization. Electr. Insul. Dielectr. Phenom. 2000, 1, 413–416. [Google Scholar]
- High-Voltage Test Techniques-Part 3: Definitions and Requirements for On-site Testing; International Electrotechnical Commission (IEC): Geneva, Switzerland, 2006.
- Meijer, S.; Gulski, E.; Smit, J.J.; Kanters, A.J.L. Risk assessment of fixed defects in GIS under different voltage wave shapes. In Proceedings of 18th International Conference and Exhibition on Electricity Distribution, Turin, Italy, 6–9 June 2005.
- Okabe, S.; Yuasa, S.; Kaneko, S.; Ueta, G. Evaluation of breakdown characteristics of gas insulated switchgears for non-standard lightning impulse waveforms method-method for converting non-standard lightning impulses waveforms into standard impulse waveforms. IEEE Trans. Dielectr. Electr. Insul. 2009, 16, 42–51. [Google Scholar] [CrossRef]
- Anis, H.; Srivastava, K.D. Breakdown of rod-plane gaps in SF6 under positive switching impulses. IEEE Trans. Power App. Syst. 1982, 101, 537–546. [Google Scholar] [CrossRef]
- Niemeyer, L.; Ullrich, L.; Wiegart, N. The mechanism of leader breakdown in electronegative gases. IEEE Trans. Electr. Insul. 1989, 24, 309–324. [Google Scholar] [CrossRef]
- Hayakawa, N.; Yoshitake, Y.; Koshino, N.; Ueda, T.; Okubo, H. Impulse partial discharge characteristics and their mechanisms under non-uniform electric field in N2/SF6 gas mixture. IEEE Trans. Dielectr. Electr. Insul. 2005, 12, 1035–1042. [Google Scholar] [CrossRef]
- Wiegart, N.; Niemeyer, L.; Pinnekamp, F.; Boeck, W.; Kindersberger, J.; Morrow, R.; Zaengl, W.; Zwicky, M.; Gallimberti, I.; Boggs, S.A. Inhomogeneous field breakdown in GIS-the prediction of breakdown probabilities and voltages. III. Discharge development in SF6 and computer model of breakdown. IEEE Trans. Power Deliv. 1988, 3, 939–946. [Google Scholar] [CrossRef]
- Niemeyer, L. A generalized approach to partial discharge in modeling. IEEE Trans. Dielectr. Electr. Insul. 1995, 2, 510–528. [Google Scholar] [CrossRef]
- Ren, M.; Dong, M.; Xiao, Z.; Qiu, A. Partial discharge pulses at artificial protrusions in SF6 under negative IEC 60060-3 standard impulses. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 273–283. [Google Scholar] [CrossRef]
- Ren, M.; Dong, M.; Xiao, Z.; Qiu, A. Partial discharges in SF6 filled void under standard aperidic and oscillating switching impulses. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 262–272. [Google Scholar] [CrossRef]
- Densley, R.J.; Salvage, B. Partial Discharges in Gaseous Cavities in Solid Dielectrics under Impulse Voltage Conditions. IEEE Trans. Electr. Insul. 1971, EI-6, 54–62. [Google Scholar] [CrossRef]
- CIGRE Working Group. Insulation coordination of GIS: Return of experience, on site tests and diagnostic techniques. Electra 1998, 176, 67–95. [Google Scholar]
- Haller, R.; Hauschild, W.; Mosch, W. High-voltage field testing of GIS from a physical view-point. In Proceedings of the Second International Conference on Properties and Applications of Properties and Applications of Dielectric Materials, Beijing, China, 12–16 September 1988.
- Kornhuber, S.; Boltze, M.; Haller, R.; Mraz, P.; Pihera, J. PD behavior of basic test arrangements under different measurement conditions. In Proceedings of the International Conference on Condition Monitoring and Diagnosis (CMD), Bali, Indonesia, 23–27 September 2012.
- Crichton, G.C.; Karlsson, P.W.; Pedersen, A. Partial Discharges in Ellipsoidal and Spheroidal Voids. IEEE Trans. Electr. Insul. 1989, 24, 335–342. [Google Scholar] [CrossRef]
- Seeger, M.; Niemeyer, L.; Bujotzek, M. Partial discharges and breakdown at protrusions in uniform background fields in SF6. J. Phys. D: Appl. Phys. 2008, 41, 185204. [Google Scholar] [CrossRef]


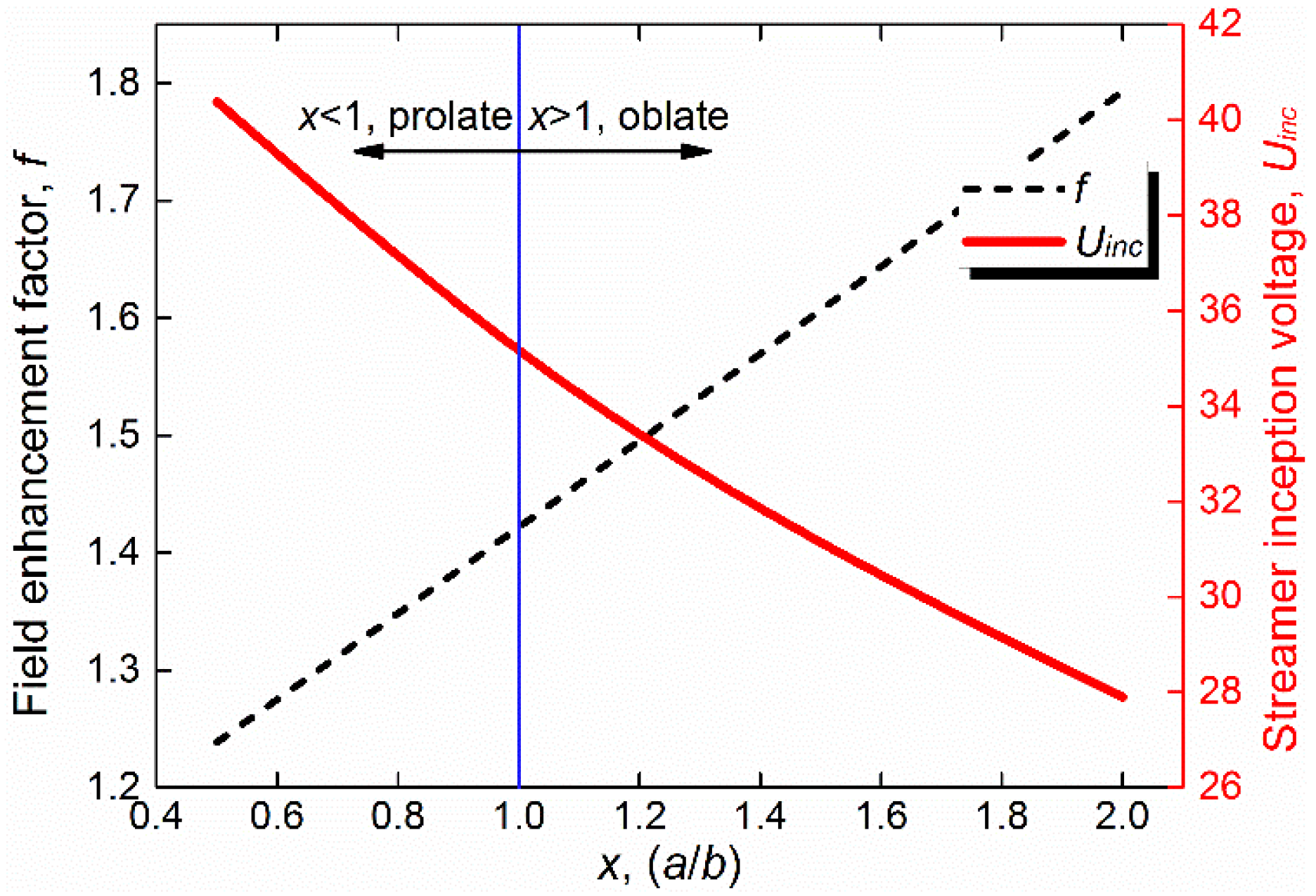
| Defects | Gap Between the Plate Electrodes (Background Field) | Defect Scale Parameters (Locally Enhanced Field) |
|---|---|---|
| Protrusion | D = 30 mm | r = 0.7 mm, L = 1, 2, 5 10 mm |
| Surface particle | D = 35 mm, θ = 60° | r = 0.7 mm, L = 1, 2, 5, 10 mm |
| Void | D = 20 mm | x{=a/b} = 0.5, 2 V{=πa2b} = 2, 15, 45, 340 mm3 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, M.; Dong, M.; Zhang, C.; Zhou, J. Partial Discharge Measurement under an Oscillating Switching Impulse: A Potential Supplement to the Conventional Insulation Examination in the Field. Energies 2016, 9, 623. https://doi.org/10.3390/en9080623
Ren M, Dong M, Zhang C, Zhou J. Partial Discharge Measurement under an Oscillating Switching Impulse: A Potential Supplement to the Conventional Insulation Examination in the Field. Energies. 2016; 9(8):623. https://doi.org/10.3390/en9080623
Chicago/Turabian StyleRen, Ming, Ming Dong, Chongxing Zhang, and Jierui Zhou. 2016. "Partial Discharge Measurement under an Oscillating Switching Impulse: A Potential Supplement to the Conventional Insulation Examination in the Field" Energies 9, no. 8: 623. https://doi.org/10.3390/en9080623
APA StyleRen, M., Dong, M., Zhang, C., & Zhou, J. (2016). Partial Discharge Measurement under an Oscillating Switching Impulse: A Potential Supplement to the Conventional Insulation Examination in the Field. Energies, 9(8), 623. https://doi.org/10.3390/en9080623







