Part-Load Performance Prediction and Operation Strategy Design of Organic Rankine Cycles with a Medium Cycle Used for Recovering Waste Heat from Gaseous Fuel Engines
Abstract
:1. Introduction
2. System Description
2.1. Gaseous Fuel Engine
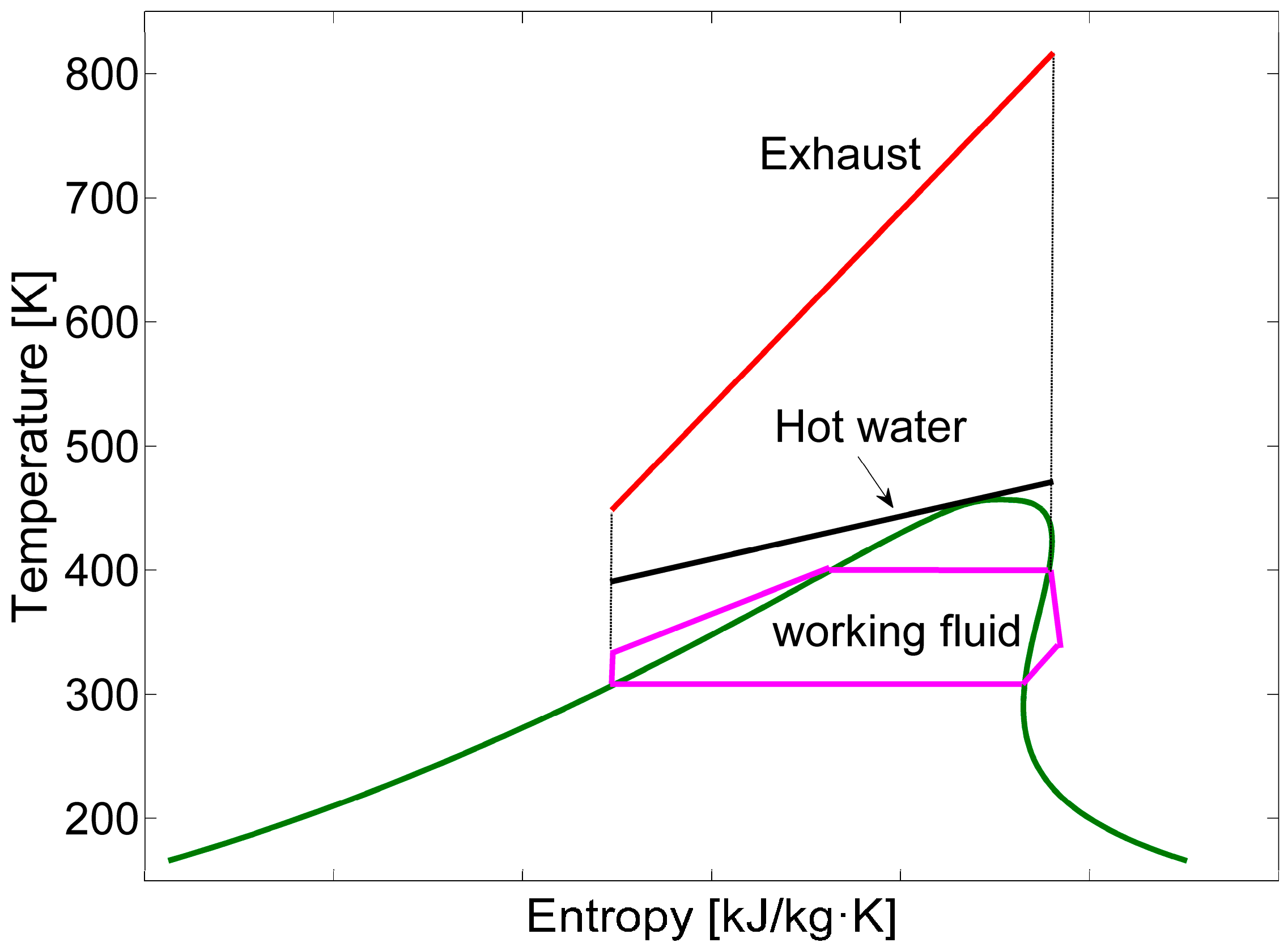
2.2. ORC-MC System
3. Mathematical Model
3.1. Sub-Models for the Main Components
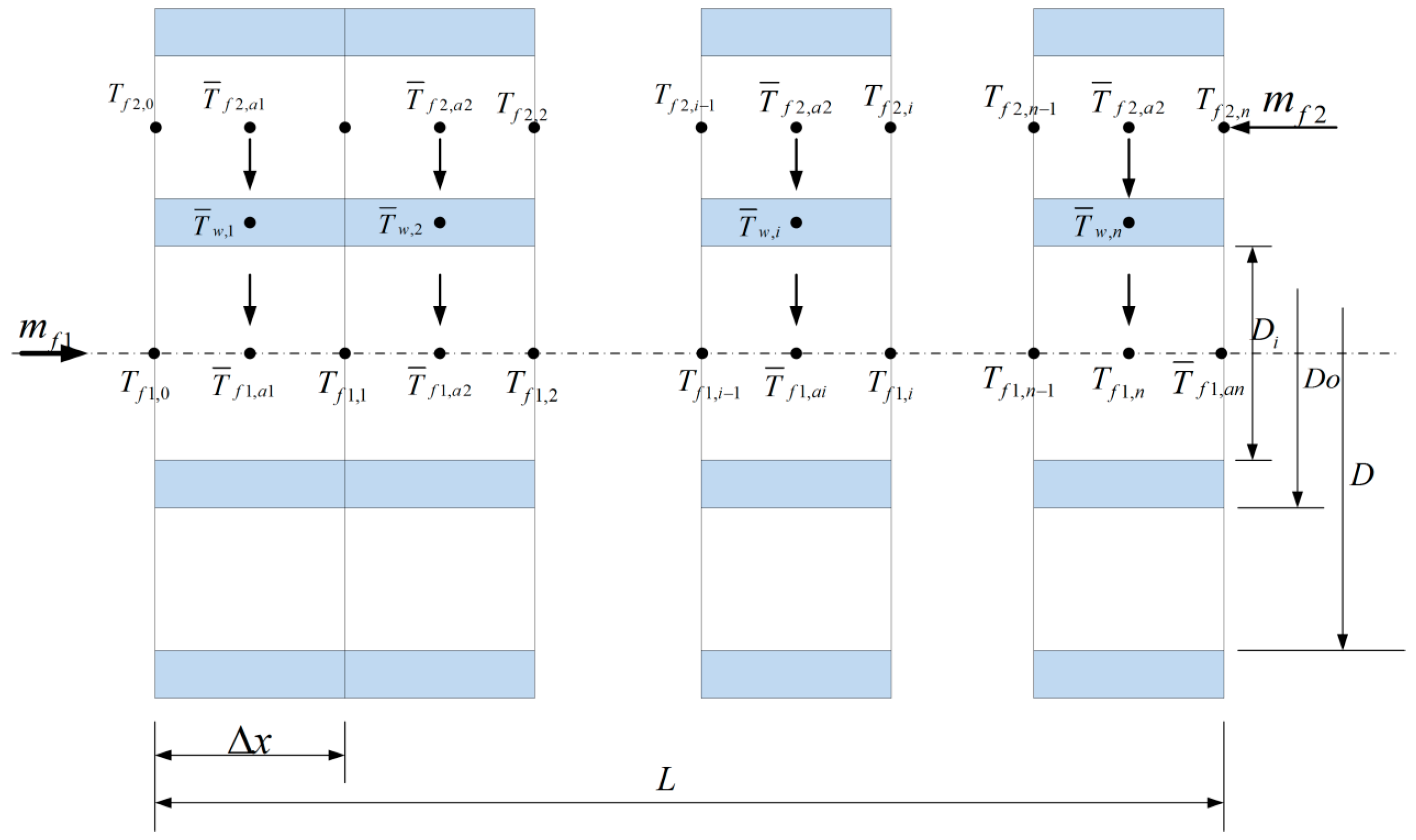
3.1.1. Hot Water Heat Exchanger
- The external pipe is assumed to be ideally insulated hence heat losses are neglected;
- The exhaust finally discharges to the environment and its pressure doesn’t change a lot, so the pressure is considered constant and the head losses of water in inner pipe is also neglected. Therefore, the momentum conservation equation is not applied to the cells of fluid.
- The hot water is considered to be incompressible and it is pressured into a constant value, while the exhaust is compressible;
- The axial conductive heat fluxes have been neglected for the fluids and pipe wall;
- No mass accumulation is considered for the fluids;
- Lumped thermal capacitance is assumed for both the metal pipe.
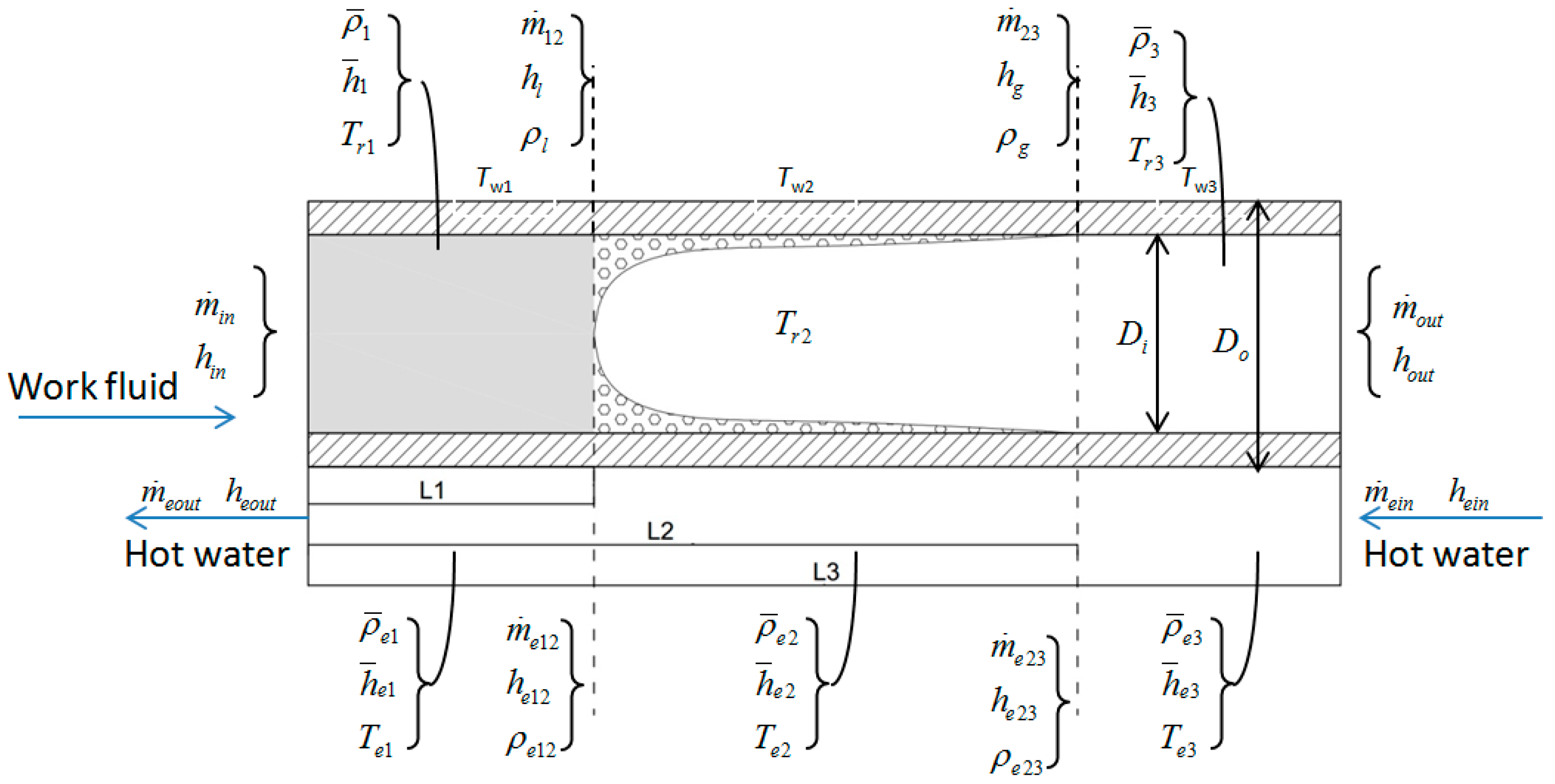
3.1.2. Evaporator
- The heat exchanger is a long, thin, horizontal tube.
- The working fluid and exhaust flowing through the heat exchanger tube can be modeled as a one-dimensional fluid flow.
- Axial conduction of working fluid and exhaust is negligible.
- Pressure drop along the heat exchanger tube due to momentum change in refrigerant and viscous friction are negligible. Thus the equation for conservation of momentum is not needed.
- The assumption of mean void fraction is used. Void fraction is defined as the ratio of vapor volume to total volume, and has long been used to describe certain characteristics of two-phase flows.
3.1.3. Pump and Turbine
3.1.4. System Performance Indicators
3.2. Model Validation
3.3. System Design
4. Results and Analysis
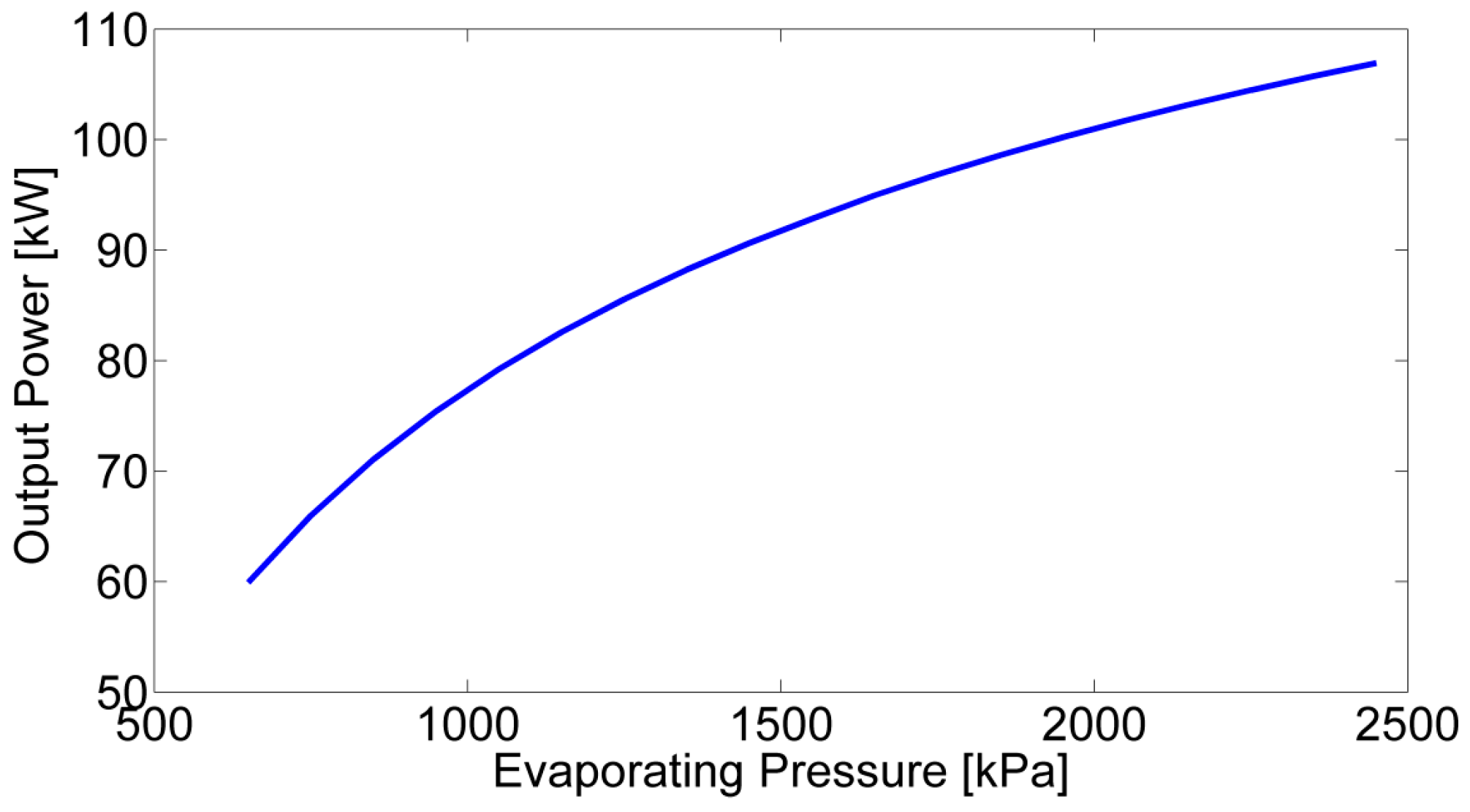
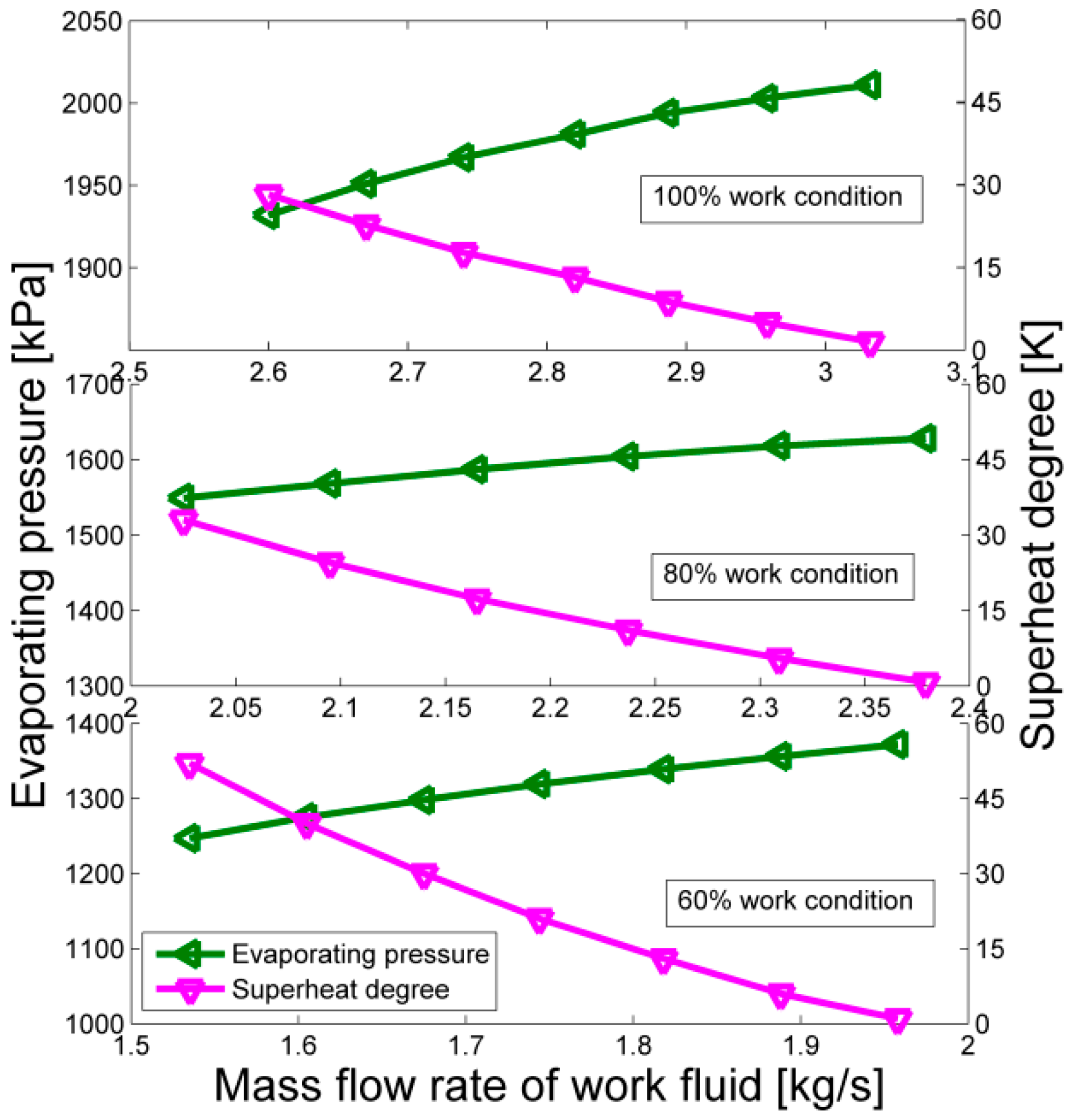
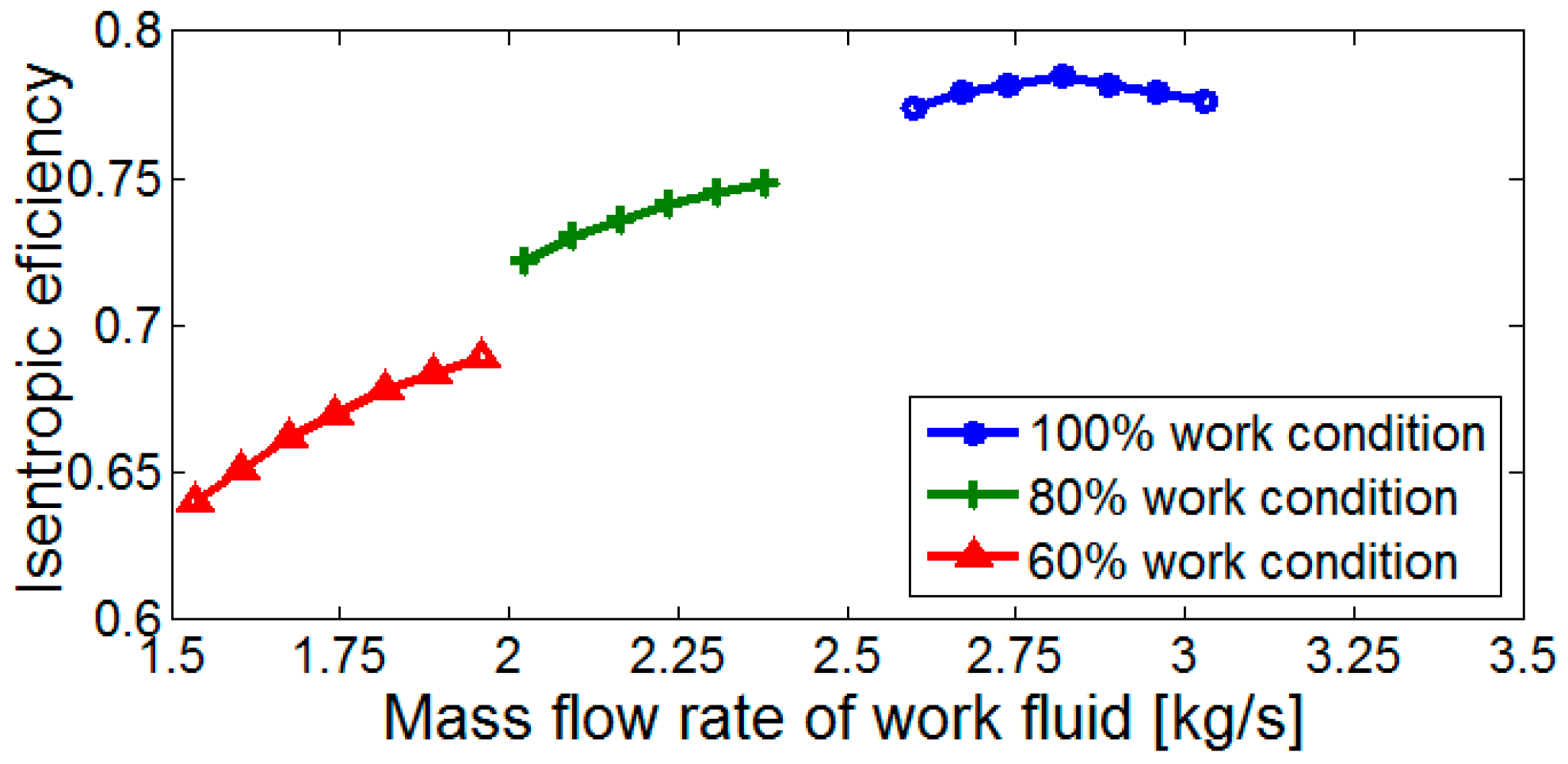
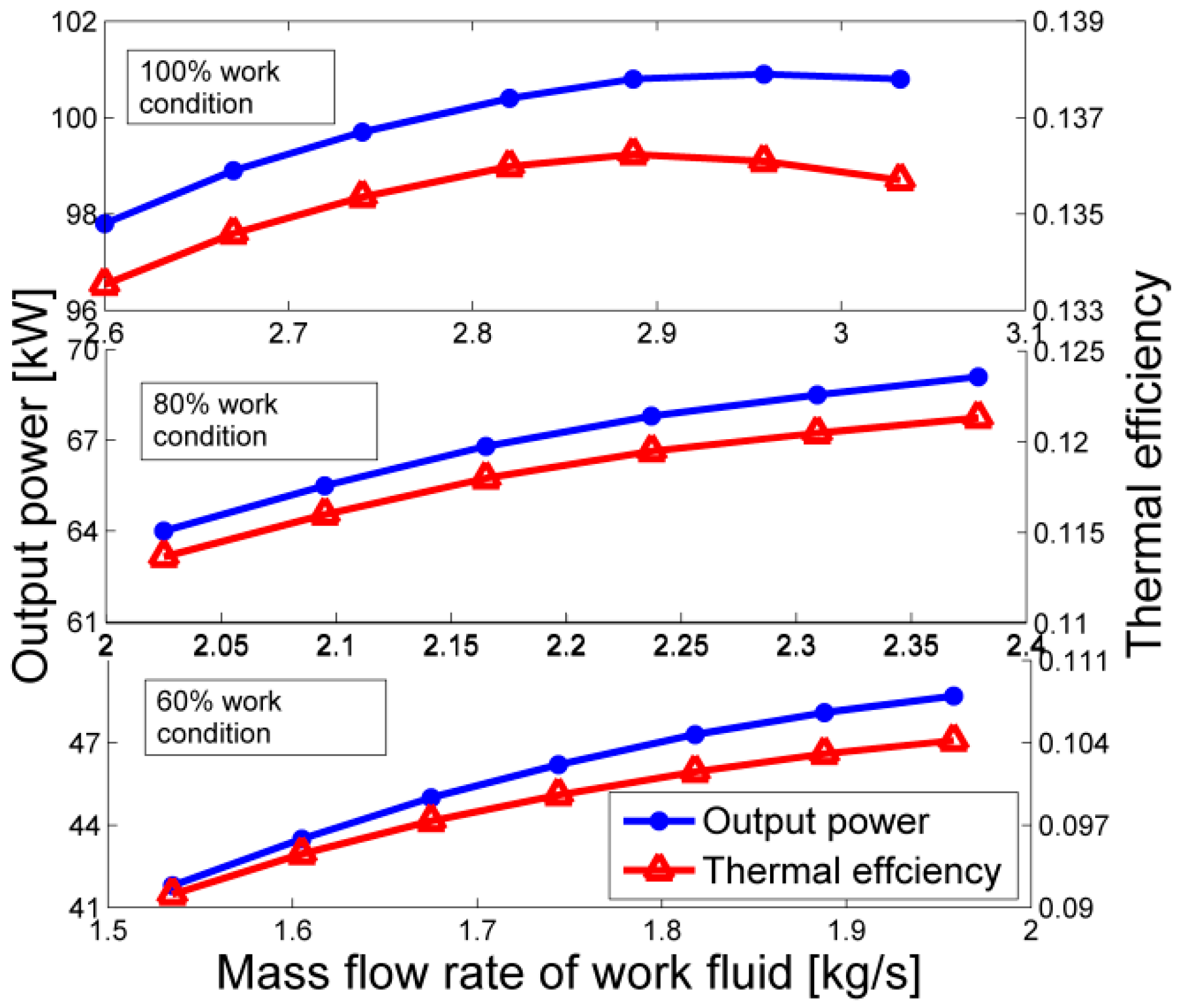
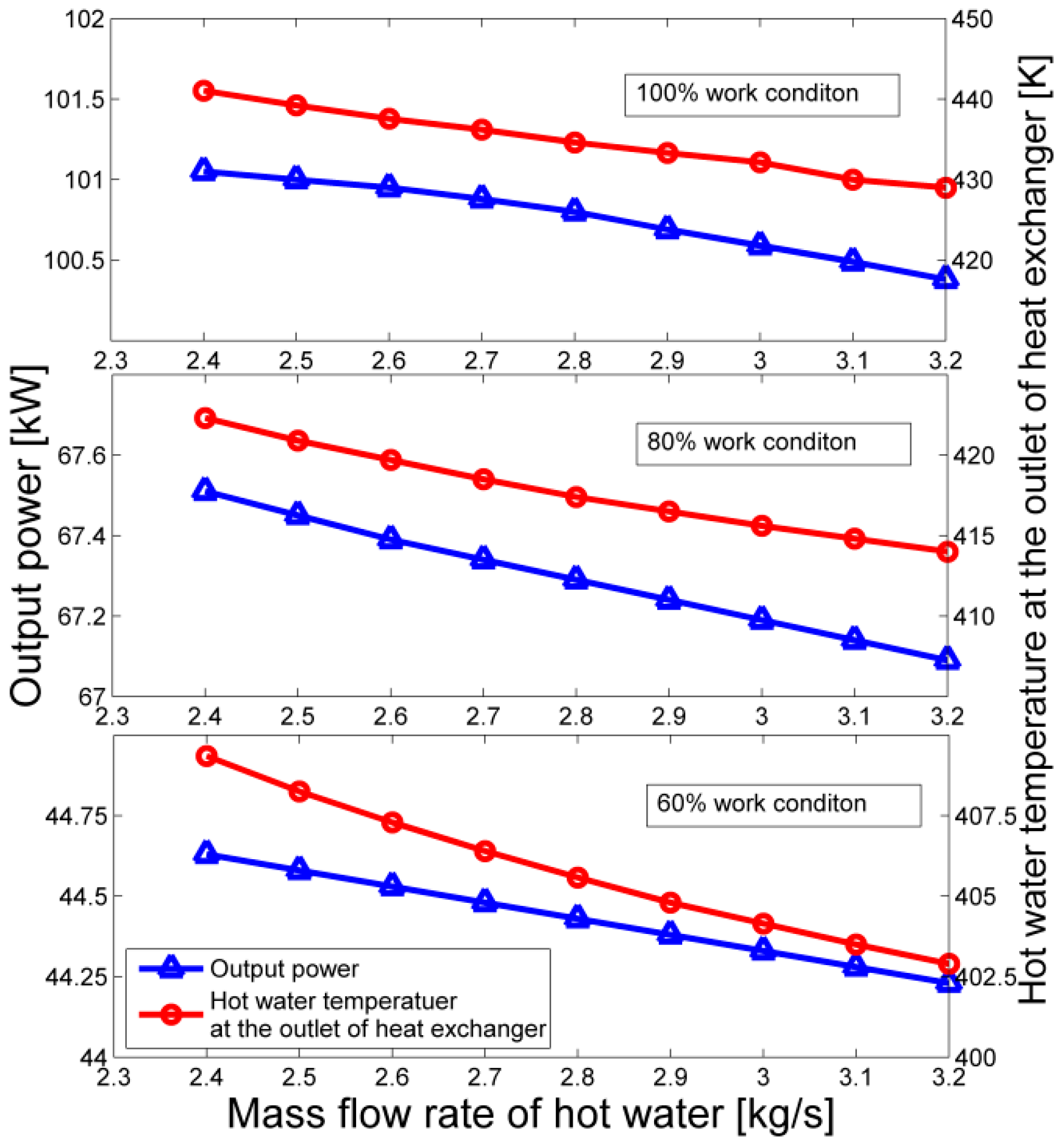
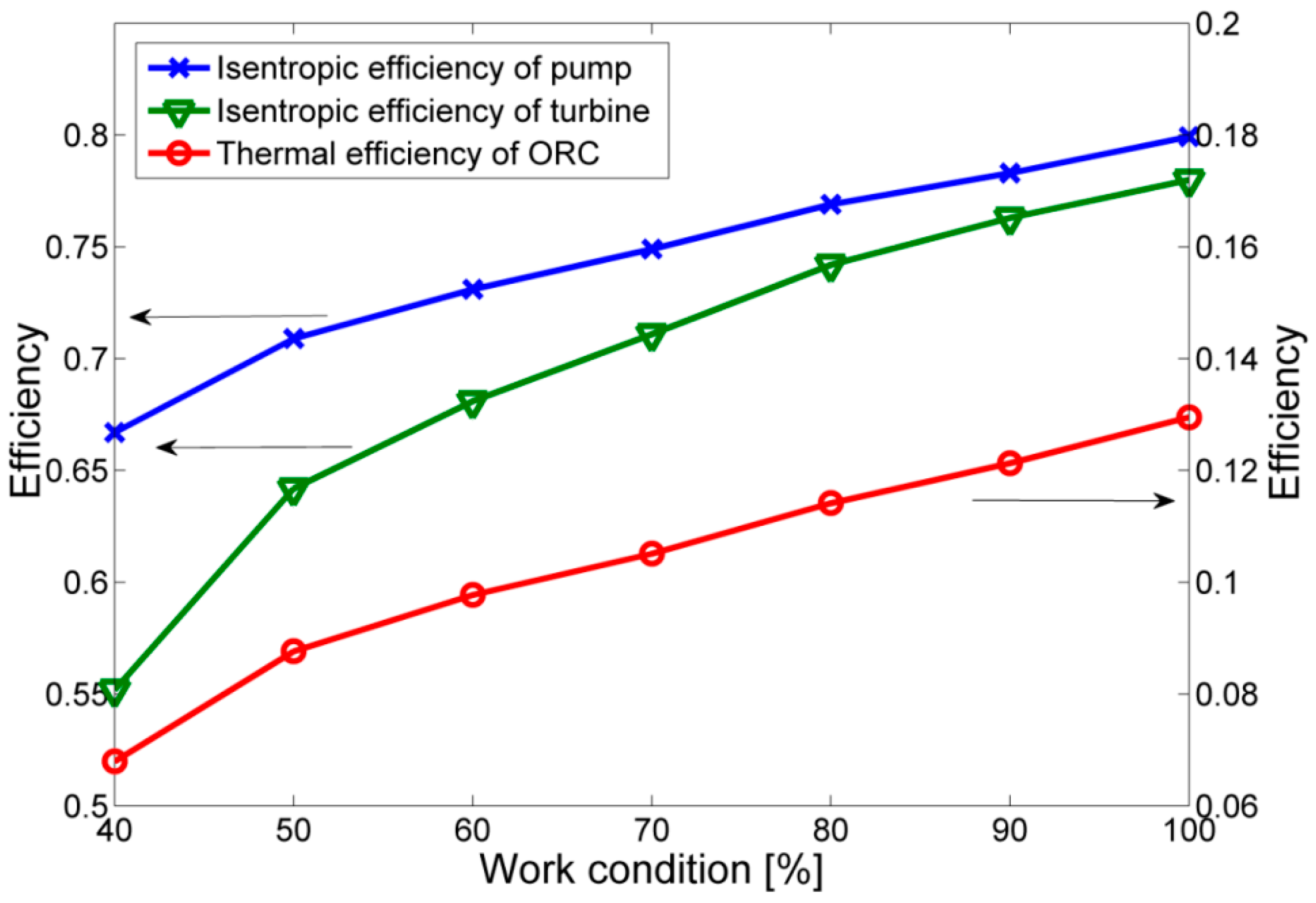
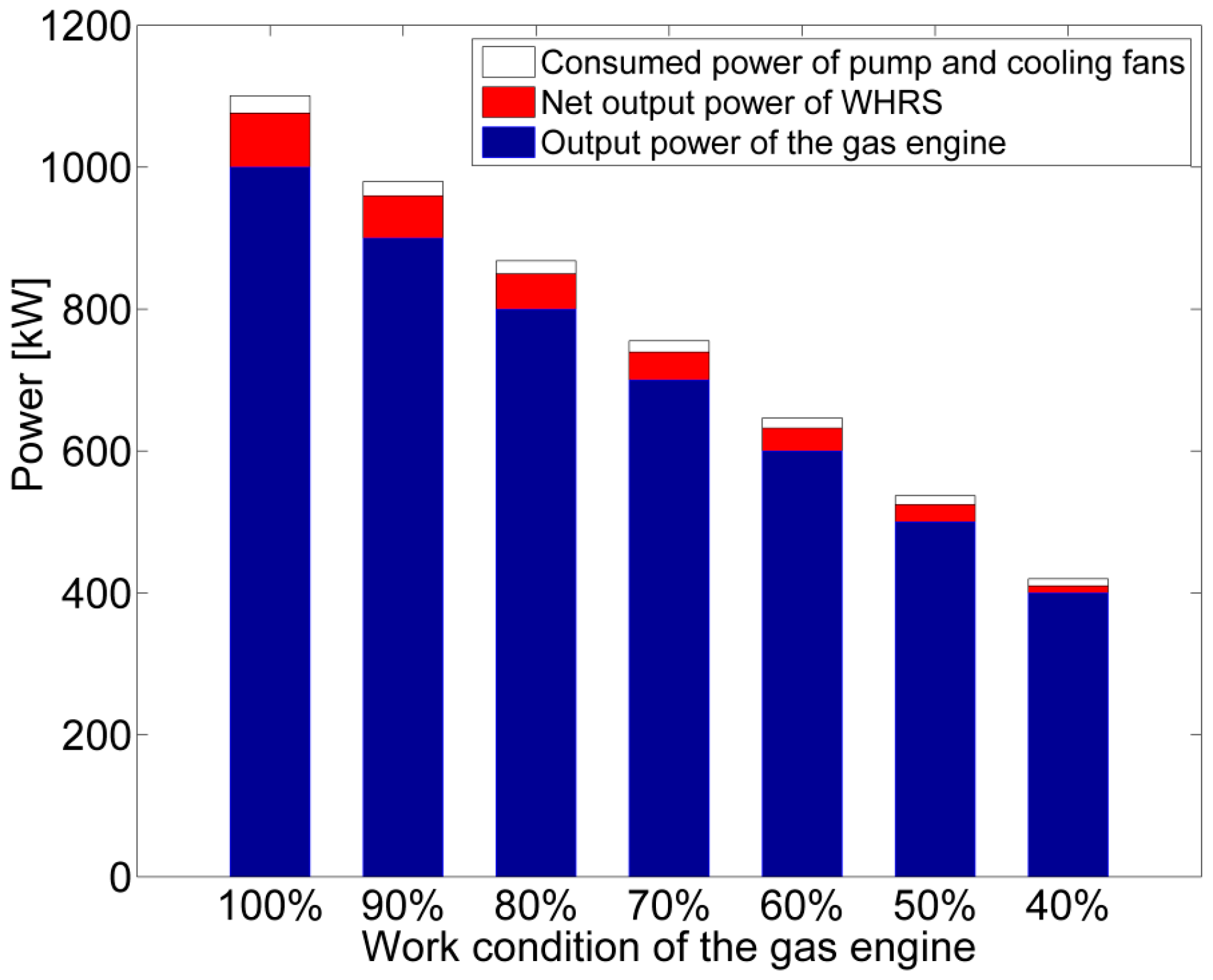
4.1. The Effects of Mass Flow Rate of Hot Water and Working Fluid at Different Working Conditions
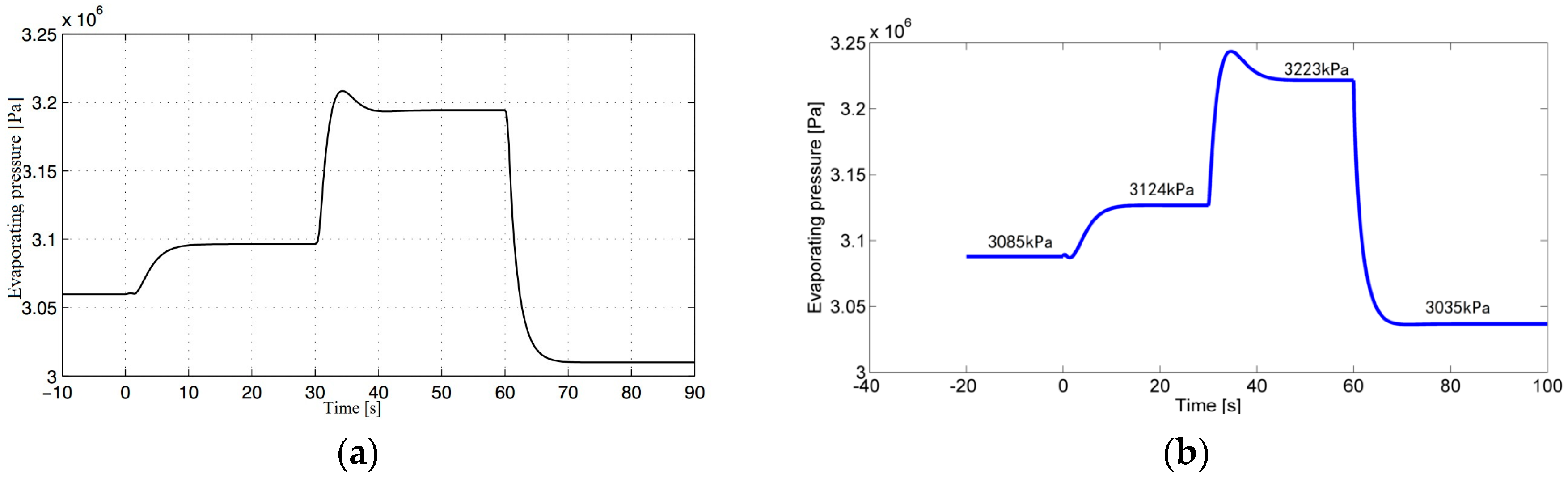
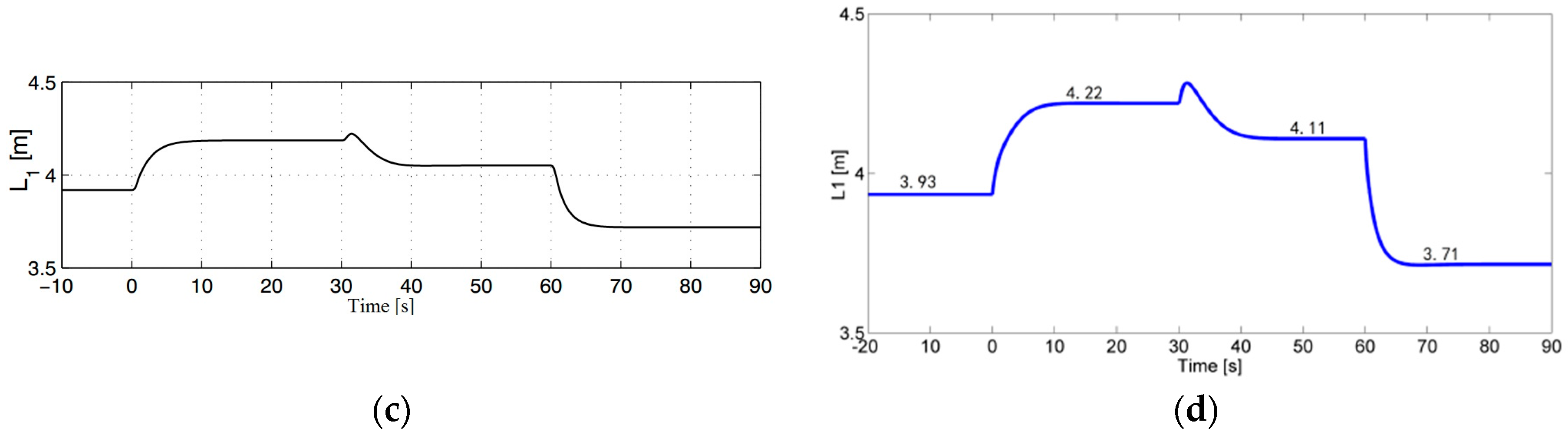
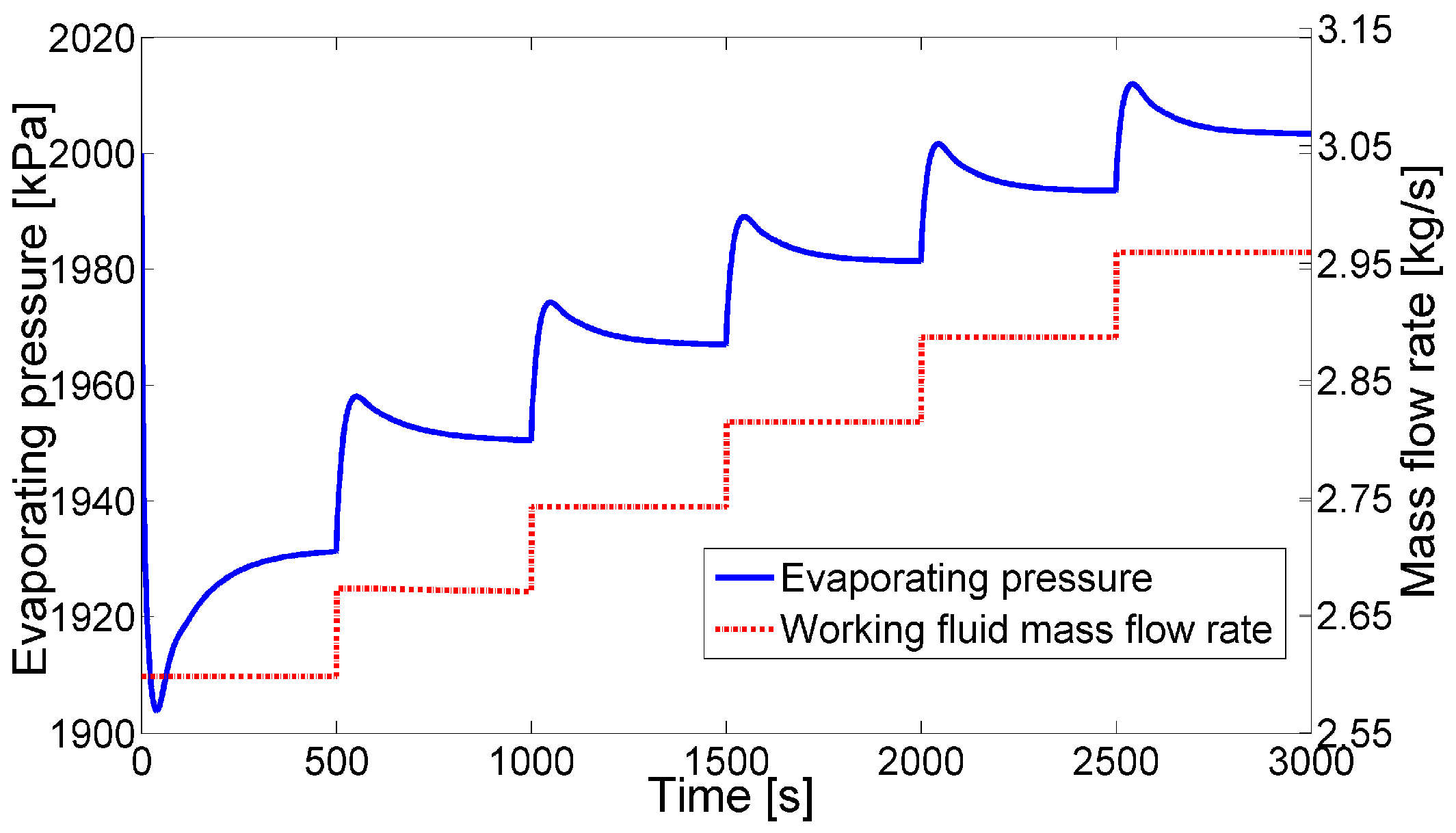
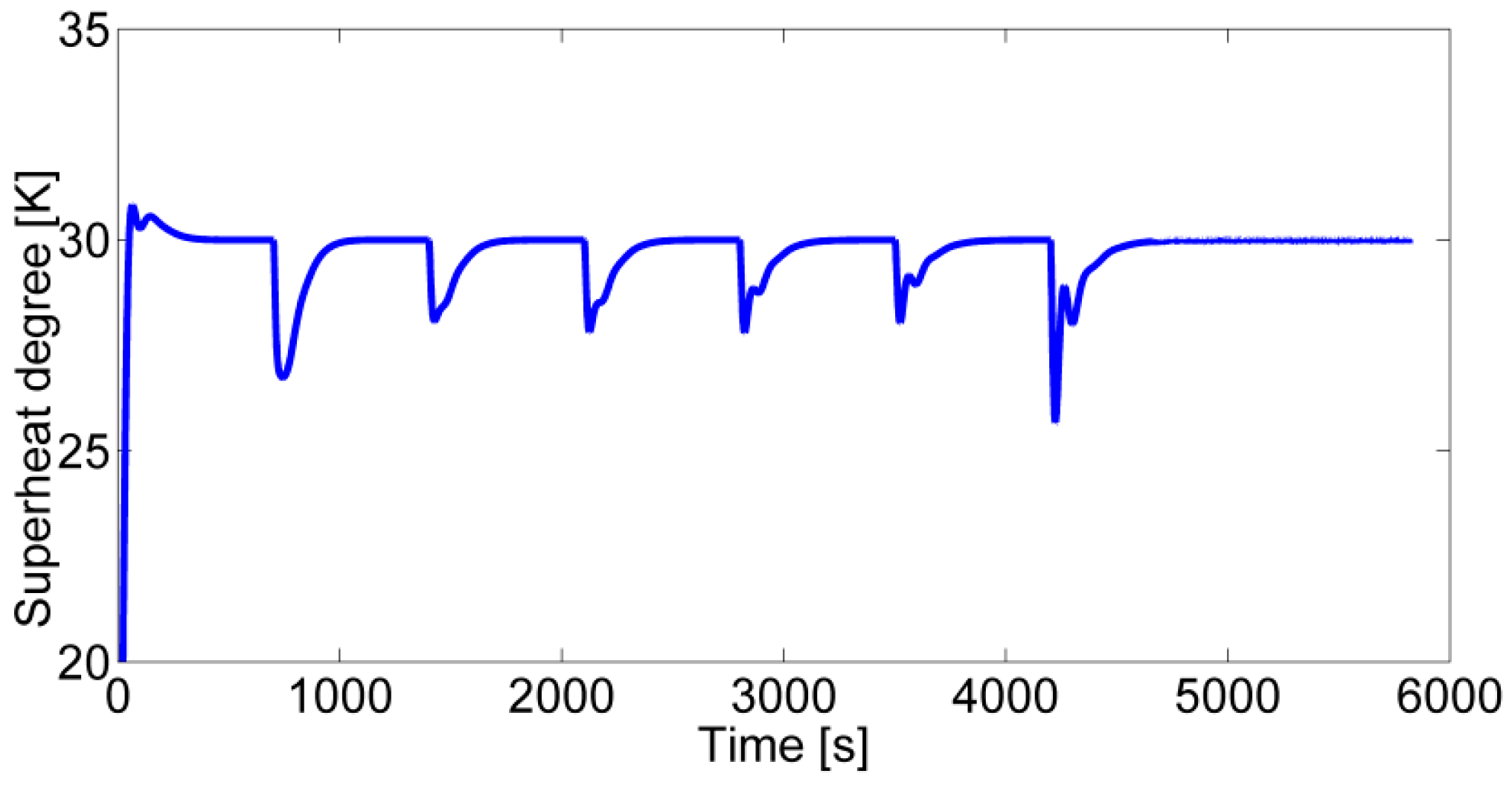
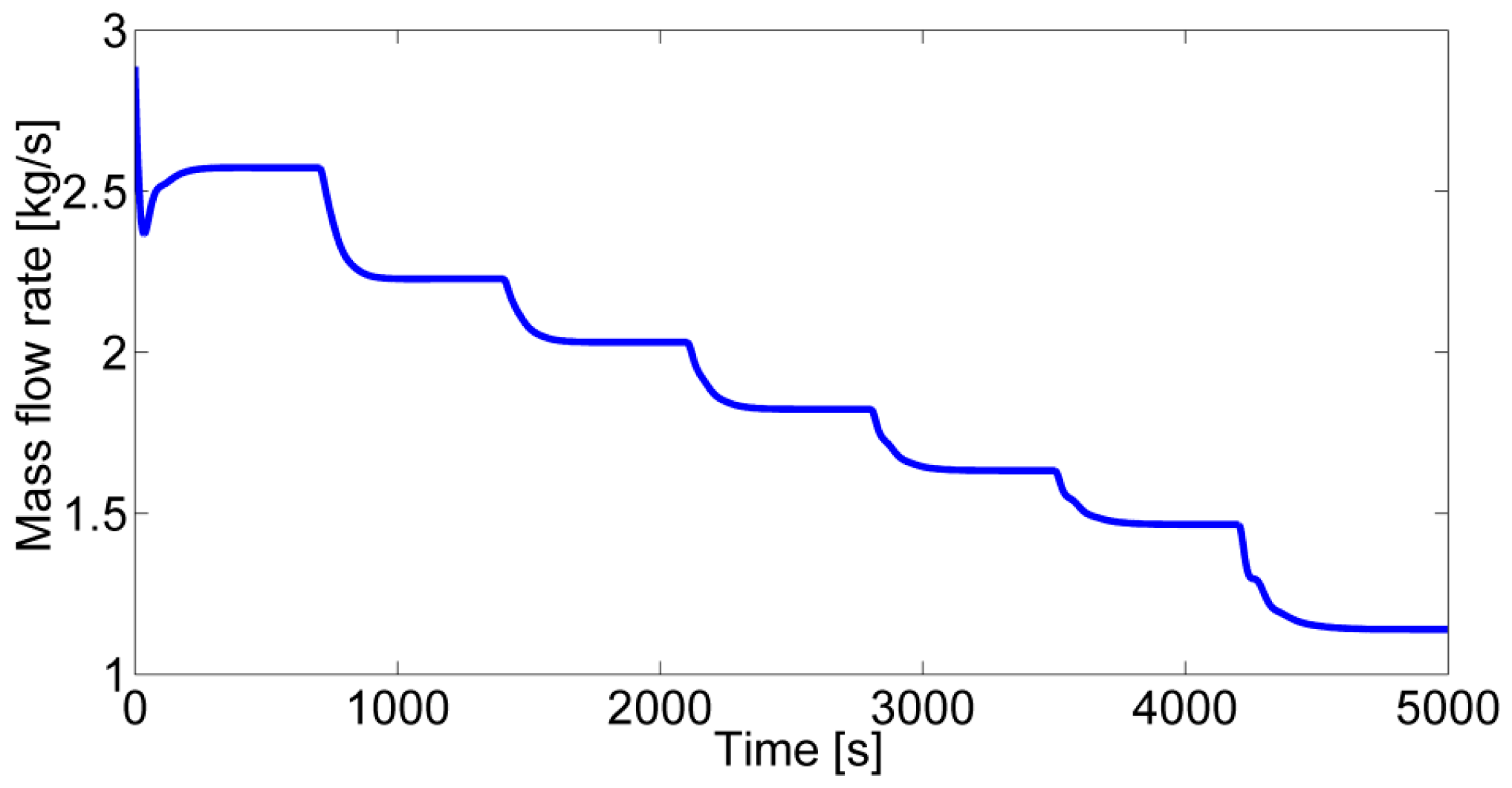
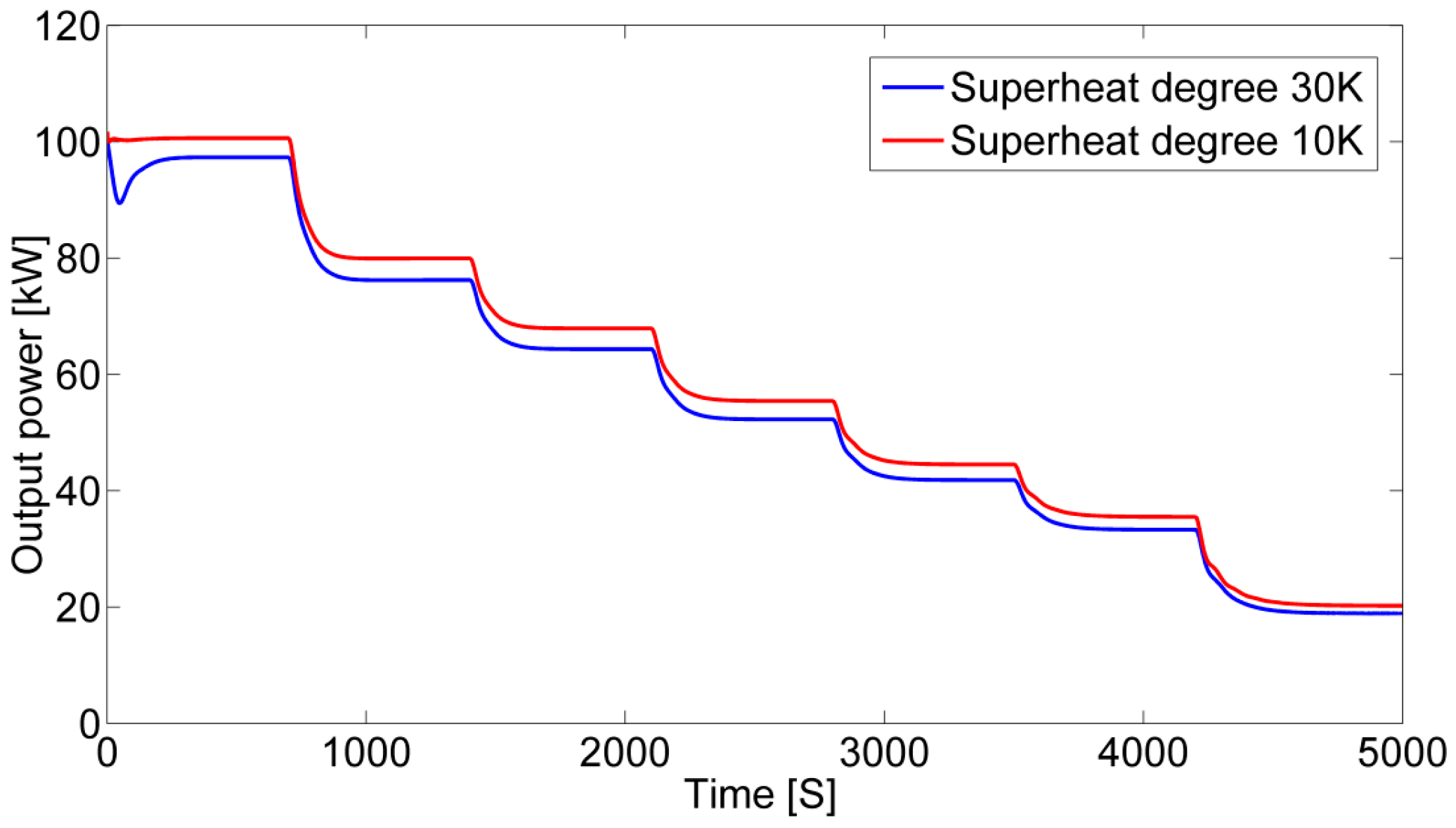
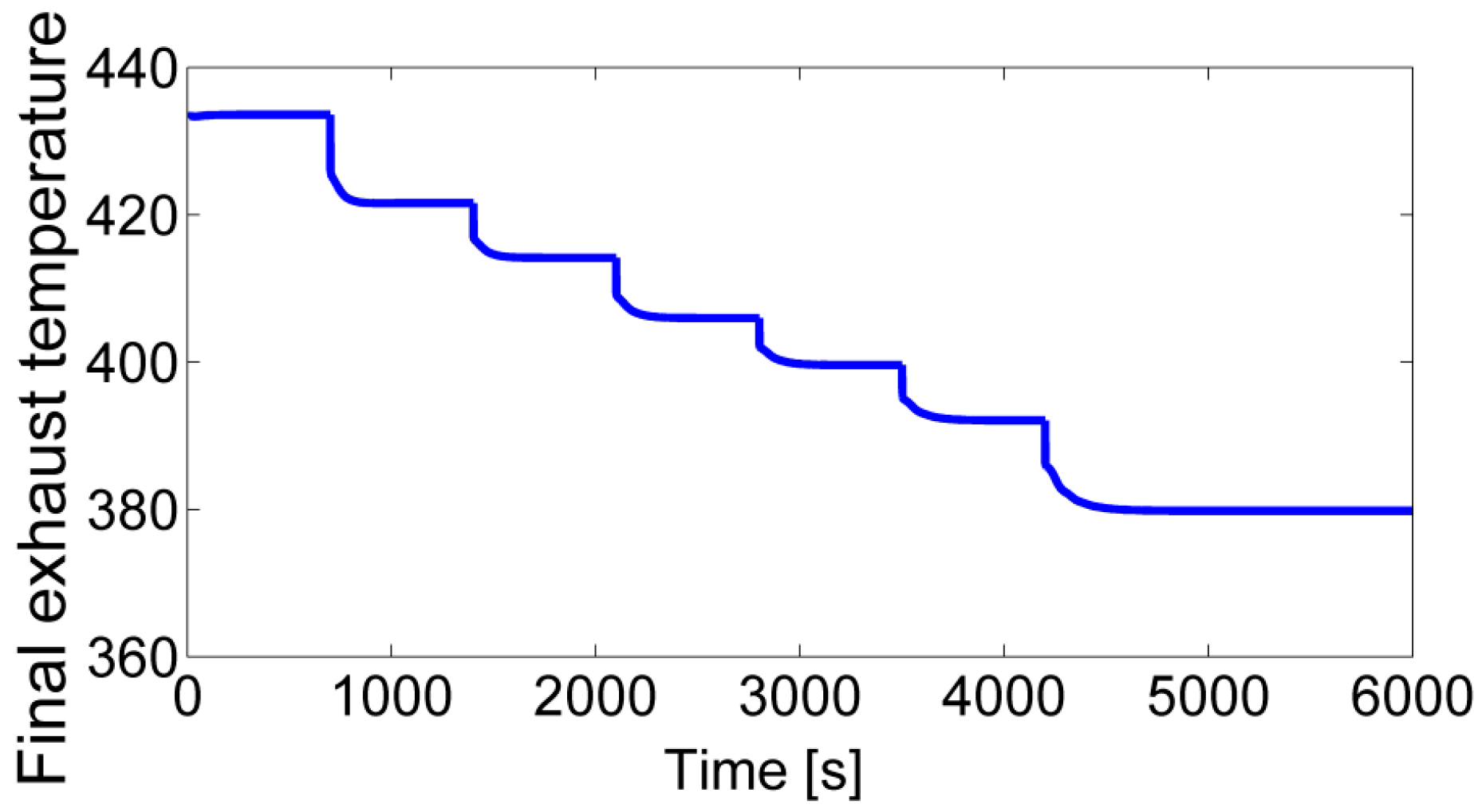
4.2. System Performance with Control
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| T | Temperature (K) |
| ρ | Density (kg/m3) |
| α | Heat transfer coefficient (W/m2·K) |
| Cp | Specific heat (J/kg·K) |
| m | Mass flow rate (kg/s) |
| A | Area (m2) |
| t | Time (s) |
| D | Diameter (m) |
| h | Specific enthalpy (J/kg) |
| Re | Reynolds number |
| Nu | Nusselt number |
| Pr | Prandtl number |
| γ | void fraction (m2/s) |
| S | Slip ratio |
| μ | Density ratio |
| u | Velocity (m/s) |
| L | Length (m) |
| p | Pressure (Pa) |
| x | Vapor quality |
| ω | Revolution speed (rpm) |
| ηv | Volumetric efficiency |
| Vcyl | Cylinder volume (m3) |
| Volume flow rate (m3/s) | |
| Cv | Turbine coefficient |
| W | Work (W) |
| ηst | Isentropic efficiency of expander |
| ηsp | Isentropic efficiency of pump |
| η | Dynamic viscosity (Pa·s) or liquid fraction or efficiency |
| cs | Isentropic gas speed(m/s) |
| l | Liquid |
| g | Gas or exhaust |
| e | Heat source (hot water) |
| c | Cold |
| f | Fluid |
| i | Inside |
| o | Outside |
| w | Wall |
| in | Inlet |
| out | Outlet |
| r | Working fluid |
| avg | Average |
| p | Pump |
| s | Isentropic |
| t | Turbine |
| ca | Cooling air |
| ORC | Organic Rankine Cycle |
| MB | Moving Boundary |
| WHR | Waste Heat Recovery |
| WHRS | Waste Heat Recovery System |
| MC | Medium Cycle |
| ICE | Internal Combustion Engine |
| ODP | Ozone Depression Potential |
| GWP | Global Warming Potential |
References
- Charles, S. Review of Organic Rankine cycles for internal combustion engine exhaust waste heat recovery. Appl. Therm. Eng. 2013, 51, 711–722. [Google Scholar]
- Aghaali, H.; Ångström, H. A review of turbo compounding as a waste heat recovery system for internal combustion engines. Renew. Sustain. Energy Rev. 2015, 49, 819–824. [Google Scholar] [CrossRef]
- Wang, T.Y.; Zhang, Y.J.; Peng, Z.J.; Shu, G.Q. A review of researches on thermal exhaust heat recovery with Rankine cycle. Renew. Sustain. Energy Rev. 2011, 15, 2862–2871. [Google Scholar] [CrossRef]
- Chammas, R.E.; Clodic, D. Combined cycle for hybrid vehicles. SAE Pap. 2005. [Google Scholar] [CrossRef]
- Ringler, J.; Seifert, M.; Guyotot, V.; Hübner, W. Rankine cycle for waste heat recovery of IC engines. SAE Pap. 2009. [Google Scholar] [CrossRef]
- Teng, H.; Regner, G.; Cowland, C. Waste heat recovery of heavy-duty diesel engines by Organic Rankine cycle Part I: hybrid energy system of diesel and Rankine engines. SAE Pap. 2007. [Google Scholar] [CrossRef]
- Battista, D.D.; Mauriello, M.; Cipollone, R. Waste heat recovery of an ORC-based power unit in a turbocharged diesel engine propelling a light duty vehicle. Appl. Energy 2015, 152, 109–120. [Google Scholar] [CrossRef]
- Quoilin, S.; Lemort, V.; Lebrun, J. Experimental study and modeling of an Organic Rankine Cycle using scroll expander. Appl. Energy 2010, 87, 1260–1268. [Google Scholar] [CrossRef]
- Yu, G.; Shu, G.; Tian, H.; Wei, H.; Liu, L. Simulation and thermodynamic analysis of a bottoming Organic Rankine Cycle (ORC) of diesel engine (DE). Energy 2013, 51, 281–290. [Google Scholar] [CrossRef]
- Manente, G.; Field, R.; DiPippo, R.; Tester, J.W.; Paci, M.; Rossi, N. Hybrid solar geothermal power generation to increase the energy production from a binary geothermal plant. In Proceedings of the ASME 2011 International Mechanical Engineering Congress and Exposition, Denver, CO, USA, 11–17 November 2011.
- Jensen, J.M.; Tummescheit, H. Moving boundary models for dynamic simulation of two-phase flows. In Proceedings of the Second International Modelica Conference, Oberpfaffenhofen, Germany, 18–19 March 2002.
- Manente, G.; Toffolo, A.; Lazzaretto, A. An Organic Rankine Cycle off-design model for the search of the optimal control strategy. Energy 2013, 58, 97–106. [Google Scholar] [CrossRef]
- Yousefzadeh, M.; Uzgoren, E. Mass-conserving dynamic Organic Rankine cycle model to investigate the link between mass distribution and system state. Energy 2015, 93, 1128–1139. [Google Scholar] [CrossRef]
- Wei, D.; Lu, X.; Lu, Z.; Gu, J. Dynamic modeling and simulation of an Organic Rankine Cycle (ORC) system for waste heat recovery. Appl. Therm. Eng. 2008, 28, 1216–1224. [Google Scholar] [CrossRef]
- Quoilin, S.; Aumann, R.; Grill, A.; Schuster, A.; Lemort, V.; Spliethoff, H. Dynamic modeling and optimal control strategy of waste heat recovery Organic Rankine Cycles. Appl. Energy 2011, 88, 2183–2190. [Google Scholar] [CrossRef]
- Mazzi, N.; Rech, S.; Lazzaretto, A. Off-design dynamic model of a real Organic Rankine Cycle system fuelled by exhaust gases from industrial processes. Energy 2015, 90, 537–551. [Google Scholar] [CrossRef]
- Rasmussen, B.P.; Shah, R.; Musser, A.B. Control-Oriented Modeling of Transcritical Vapor Compression Systems. Master’s Thesis, University of Illinois Urbana-Champaign, Champaign, IL, USA, 2002. [Google Scholar]
- Jensen, J.M. Dynamic Modeling of Thermo-Fluid Systems. Ph.D. Thesis, Technical University of Denmark, Copenhagen, Denmark, 2003. [Google Scholar]
- Milián, V.; Navarro-Esbrí, J.; Ginestar, D. Dynamic model of a shell-and-tube condenser. Analysis of the mean void fraction correlation influence on the model performance. Energy 2013, 59, 521–533. [Google Scholar] [CrossRef]
- Horst, T.A.; Rottengruber, H.-S.; Seifert, M.; Ringler, J. Dynamic heat exchanger model for performance prediction and control system design of automotive waste heat recovery systems. Appl. Energy 2013, 105, 293–303. [Google Scholar] [CrossRef]
- Hou, G.; Sun, R.; Hu, G.; Zhang, J. Supervisory predictive control of evaporator in Organic rankine cycle (ORC) system for waste heat recovery. In Proceedings of the International Conference on Advanced Mechatronic Systems, Zhengzhou, China, 11–13 August 2011.
- Zhang, J.; Zhang, W.; Hou, G.; Fang, F. Dynamic modeling and multivariable control of Organic Rankine Cycles in waste heat utilizing processes. Comput. Math. Appl. 2012, 64, 908–921. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, Y.; Gao, S.; Hou, G. Constrained predictive control based on state space model of Organic Rankine Cycle system for waste heat recovery. In Proceedings of the Chinese Control and Decision Conference (CCDC), Taiyuan, China, 23–25 May 2012.
- Benato, A.; Kærn, M.R.; Pierobon, L. Analysis of hot spots in boilers of Organic Rankine Cycle units during transient operation. Appl. Energy 2015, 151, 119–131. [Google Scholar] [CrossRef]
- Luong, D.; Tsao, T.-C. Linear quadratic integral control of an Organic Rankine Cycle for waste heat recovery in heavy-duty diesel powertrain. In Proceedings of the 2014 American Control Conference (ACC), Portland, OR, USA, 4–6 June 2014.
- Gewald, D.; Siokos, K.; Karellas, S. Waste heat recovery from a landfill gas-fired power plant. Renew. Sustain. Energy Rev. 2012, 16, 1779–1789. [Google Scholar] [CrossRef]
- Li, X. Research on Design and Performance Optimization of Diesel Engine Waste Heat Recovery Bottoming System and Key Component. Ph.D. Thesis, Tianjin University, Tianjin, China, 2014. [Google Scholar]
- Vaja, I. Definition of an Object Oriented Library for the Dynamic Simulation of Advanced Energy Systems: Methodologies, Tools and Application to Combined ICE-ORC Power Plants. Ph.D. Thesis, University of Parma, Parma, Italy, 2009. [Google Scholar]
- Sotirios, K.; Andreas, S. Supercritical fluid parameters in Organic Rankine Cycle applications. Int. J. Thermodyn. 2008, 11, 101–108. [Google Scholar]
- Schuster, A.; Karellas, S.; Aumann, R. Efficiency optimization potential in supercritical Organic Rankine Cycles. Energy 2010, 35, 1033–1039. [Google Scholar] [CrossRef]
- Meinel, D.; Wieland, C.; Spliethof, H. Effect and comparison of different working fluids on a two-stage Organic Rankine Cycle (ORC) concept. Appl. Therm. Eng. 2014, 63, 246–253. [Google Scholar] [CrossRef]
- Quoilin, S.; van Den Broek, M.; Declaye, S.; Dewallef, P.; Lemort, V. Techno-economic survey of Organic Rankine Cycle (ORC) systems. Renew. Sustain. Energy Rev. 2013, 22, 168–186. [Google Scholar] [CrossRef]
- Xie, H.; Yang, C. Dynamic behavior of Rankine cycle system for waste heat recovery of heavy duty diesel engines under driving cycle. Appl. Energy 2013, 112, 130–141. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, Y.; Wang, R.; Xu, J.; Fang, F. Modeling and constrained multivariable predictive control for ORC (Organic Rankine Cycle) based waste heat energy conversion systems. Energy 2014, 66, 128–138. [Google Scholar] [CrossRef]
- Bamgbopa, M.O.; Uzgoren, E. Quasi-dynamic model for an Organic Rankine Cycle. Energy Convers. Manag. 2013, 72, 117–124. [Google Scholar] [CrossRef]
- Shiming, Y. Heat Transfer, 4th ed.; Higher Education Press: Beijing, China, 1998; pp. 162–175. (In Chinese) [Google Scholar]
- Zivi, S.M. Estimation of steady-state steam void-fraction by means of the principle of minimum entropy production. J. Heat Trans. 1964, 86, 247–252. [Google Scholar] [CrossRef]
- Collier, J.G.; Thome, J.R. Convective Boiling and Condensation, 3rd ed.; Clarendon Press: Oxford, UK, 1994. [Google Scholar]
- Ahlgren, F.; Mondejar, M.E. Waste heat recovery in a cruise vessel in the Baltic Sea by using an Organic Rankine Cycle: A case study. J. Eng. Gas Turbines Power 2016, 138, 1–15. [Google Scholar]
- Peralez, J.; Dufour, P. Towards model-based control of a steam Rankine process for engine waste heat recovery. In Proceedings of the 2011 IEEE Vehicle Power and Propulsion Conference, Seoul, Korea, 9–12 October 2012.
- Li, Y.-R.; Wang, J.-N.; Du, M.-T. Influence of coupled pinch point temperature difference and evaporation temperature on performance of organic Ranking cycle. Energy 2012, 42, 503–509. [Google Scholar] [CrossRef]
- Shu, G.; Wang, X.; Tian, H. The performance of Rankine Cycle as waste heat recovery system for a natural gas engine at variable working conditions. SAE Pap. 2016. [Google Scholar] [CrossRef]

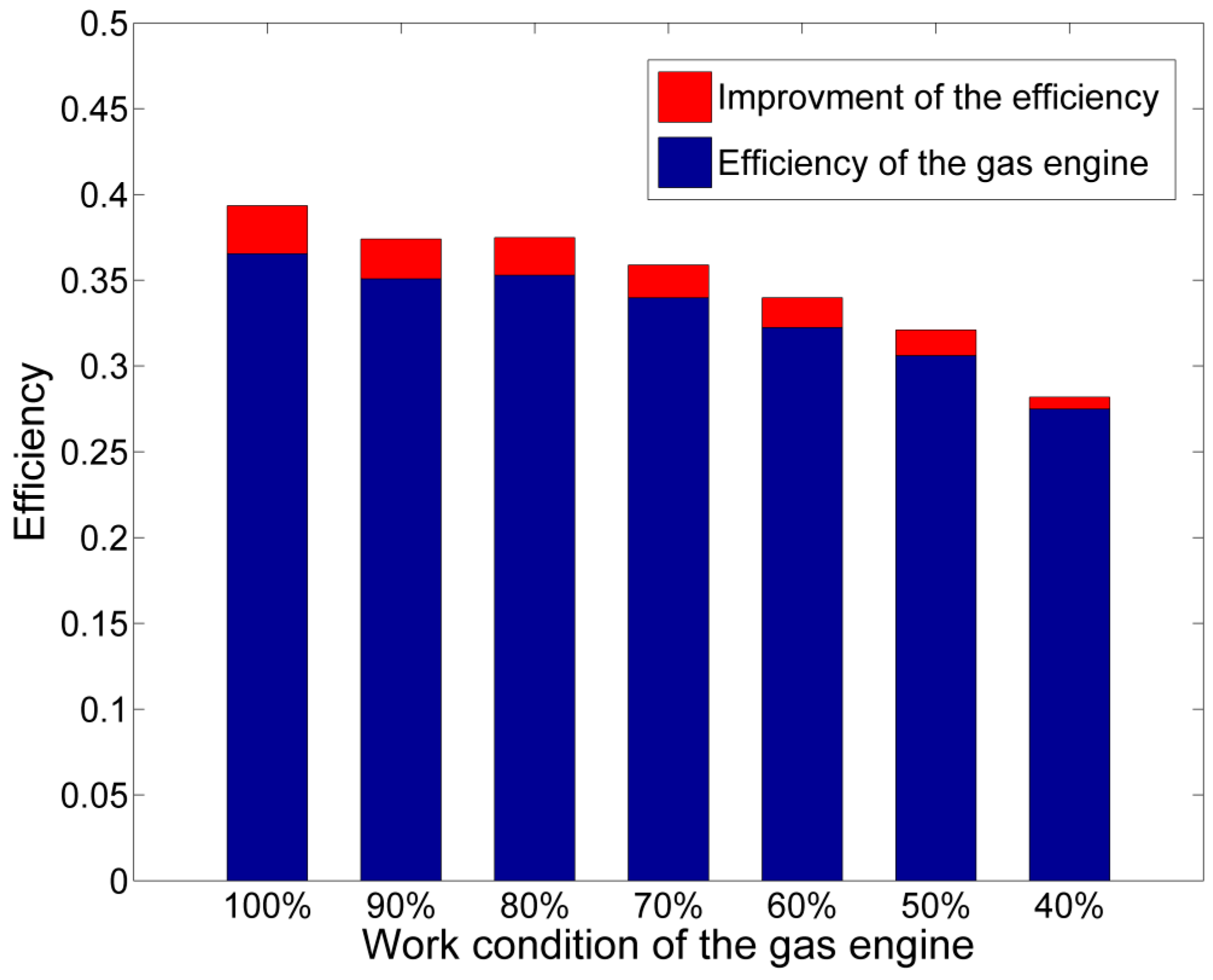
| Parameter | Unit | Value | ||||||
|---|---|---|---|---|---|---|---|---|
| Speed | r/min | 600 | 600 | 600 | 600 | 600 | 600 | 600 |
| Working condition load | - | 40% | 50% | 60% | 70% | 80% | 90% | 100% |
| Effective power | kW | 400 | 500 | 600 | 700 | 800 | 900 | 1000 |
| Exhaust temperature | °C | 470 | 515 | 525 | 527 | 530 | 532 | 540 |
| Heat consumption rate of gas | MJ/kWh | 13.09 | 11.76 | 11.08 | 10.59 | 10.20 | 10.26 | 9.85 |
| Intake air volume flow rate | m3/h | 1774 | 2145 | 2465 | 2748 | 3120 | 3510 | 4180 |
| Exhaust volume flow rate | m3/h | 1911 | 2310 | 2654 | 2959 | 3380 | 3800 | 4500 |
| Exhaust mass flow rate | kg/s | 0.69 | 0.834 | 0.958 | 1.069 | 1.221 | 1.372 | 1.625 |
| Thermal efficiency of engine | % | 27.5 | 30.61 | 32.25 | 33.98 | 35.29 | 35.08 | 36.55 |
| Pump and Turbine | |
| ηv = 0.8 | Vcyl = 2.7313 × 10−6 m3 |
| Cv = 0.0064 | ηs = 0.8 |
| ηsp = 0.8 | |
| Evaporator and Condenser Parameters | |
| Di = 0.02 m | Teout = 373 K |
| Do = 0.022 m | Cw = 385 J/kgK |
| L = 428.79 m | ρw = 8960 kg/m3 |
| L1 = 117.90 m | P = 2000 kPa |
| L2 = 75.89 m | Pc = 230 kPa |
| L3 = 13.01 m | delta Ts = 10 K |
| Tein = 433 K | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Tian, H.; Shu, G. Part-Load Performance Prediction and Operation Strategy Design of Organic Rankine Cycles with a Medium Cycle Used for Recovering Waste Heat from Gaseous Fuel Engines. Energies 2016, 9, 527. https://doi.org/10.3390/en9070527
Wang X, Tian H, Shu G. Part-Load Performance Prediction and Operation Strategy Design of Organic Rankine Cycles with a Medium Cycle Used for Recovering Waste Heat from Gaseous Fuel Engines. Energies. 2016; 9(7):527. https://doi.org/10.3390/en9070527
Chicago/Turabian StyleWang, Xuan, Hua Tian, and Gequn Shu. 2016. "Part-Load Performance Prediction and Operation Strategy Design of Organic Rankine Cycles with a Medium Cycle Used for Recovering Waste Heat from Gaseous Fuel Engines" Energies 9, no. 7: 527. https://doi.org/10.3390/en9070527
APA StyleWang, X., Tian, H., & Shu, G. (2016). Part-Load Performance Prediction and Operation Strategy Design of Organic Rankine Cycles with a Medium Cycle Used for Recovering Waste Heat from Gaseous Fuel Engines. Energies, 9(7), 527. https://doi.org/10.3390/en9070527






