Curtailment in a Highly Renewable Power System and Its Effect on Capacity Factors
Abstract
:1. Introduction
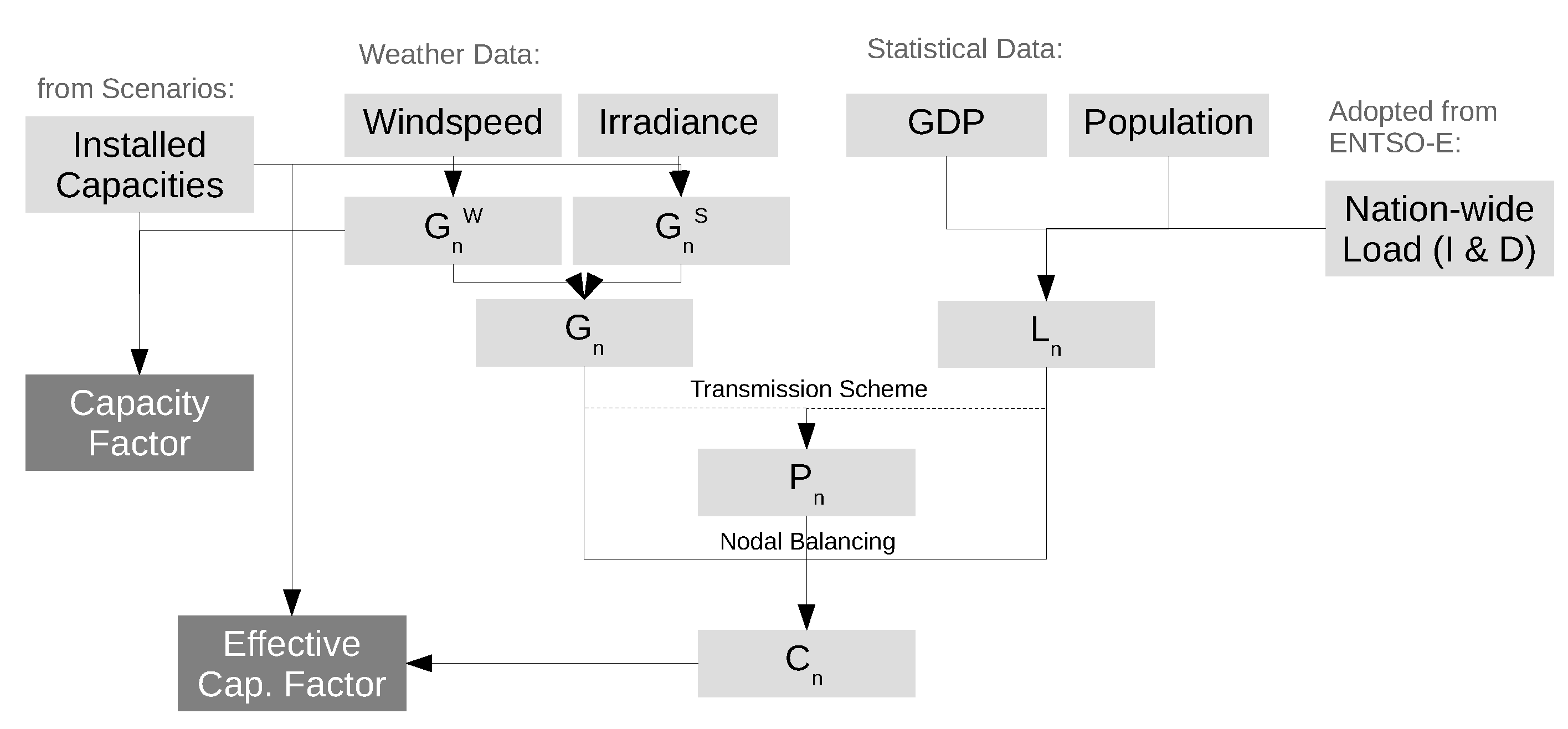
2. Methodology
2.1. Definitions
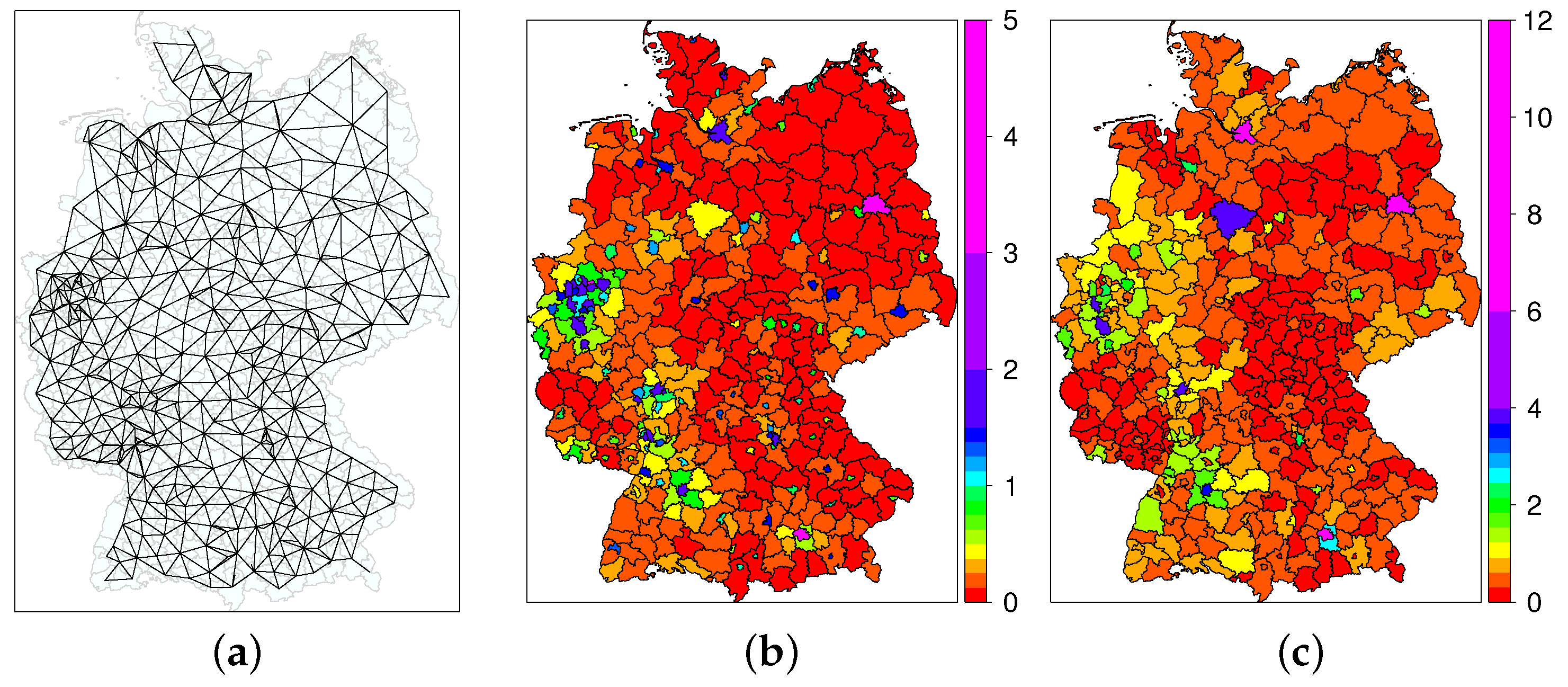
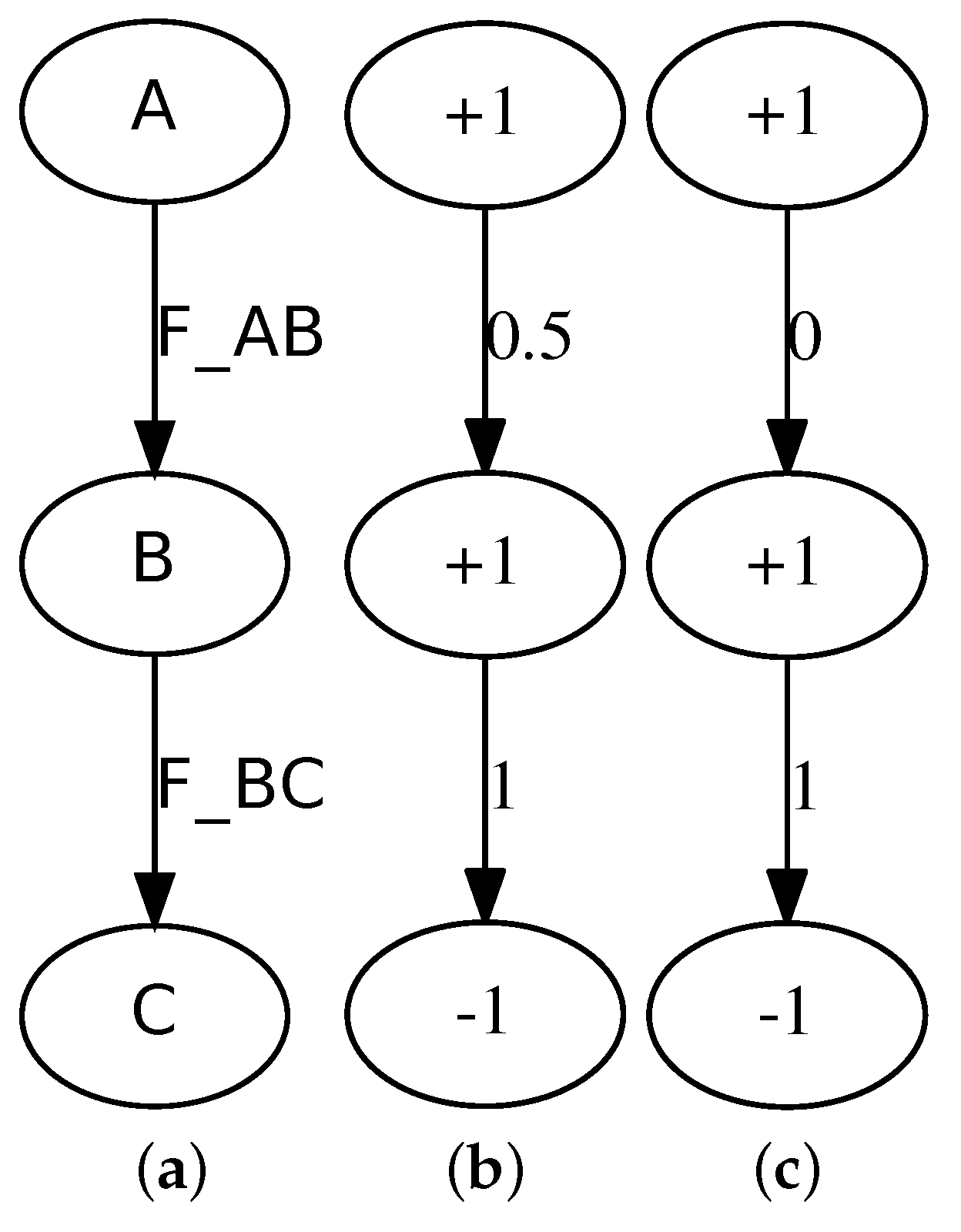
2.2. Transmission
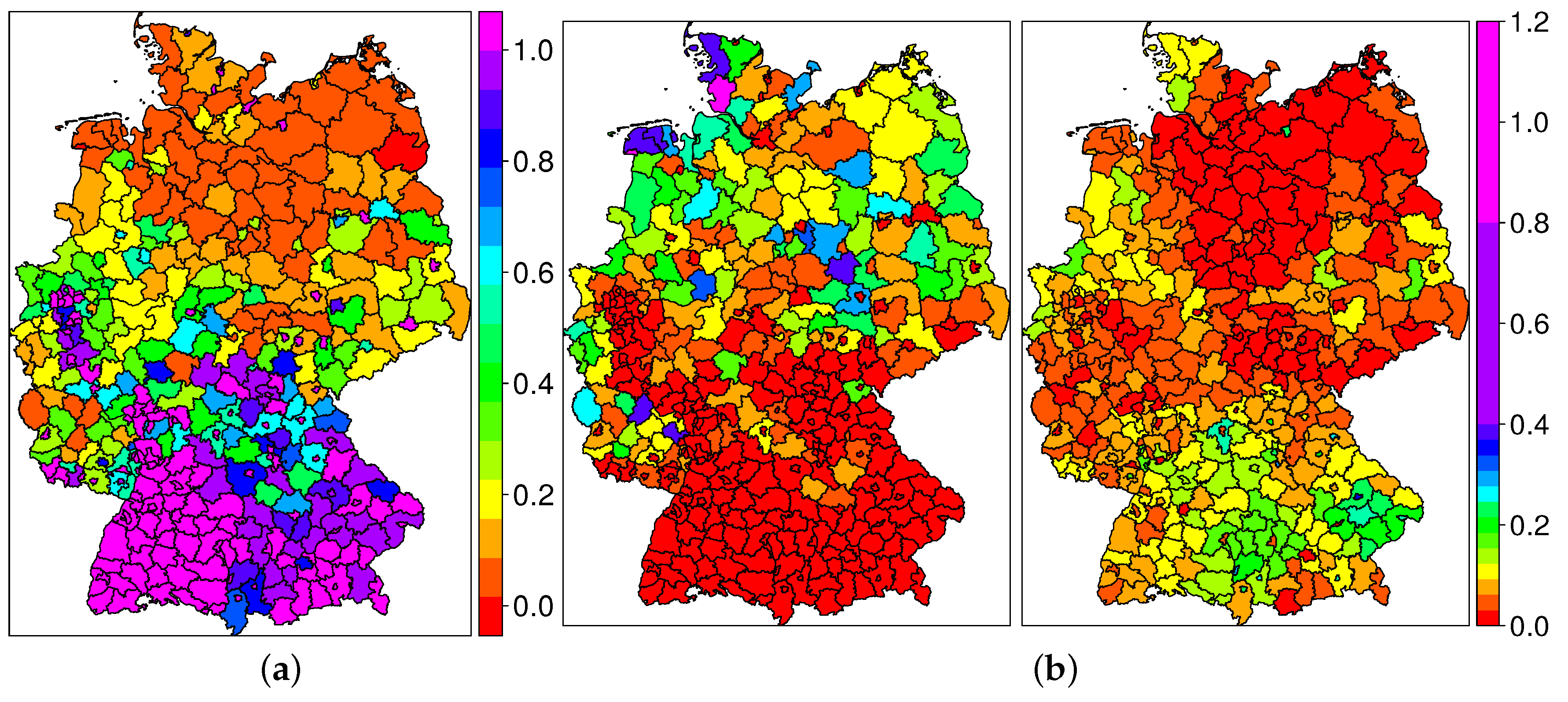
2.3. Scenario Definition
- Wind and PV capacities are distributed in such a way that . This means that every county produces on average as much renewable energy as it consumes.
- For every county, the currently-installed capacity of wind and PV (2013) is multiplied with the same factor. In this case, today’s spatial distribution of capacities is kept, but every installed wind turbine or PV module is upgraded by a certain factor. This process is usually referred to as repowering.
3. Data
3.1. Weather Data
- Wind speed data at hub height of 77 m and 2-m temperature data from the analysis product of the numerical weather prediction model (NWP) COSMO-DE [30], provided by the German Weather Service (Deutscher Wetterdienst, DWD) and
- Solar irradiation data from Meteosat Second Generation (MSG).
3.2. Generation Data
3.3. Load Data
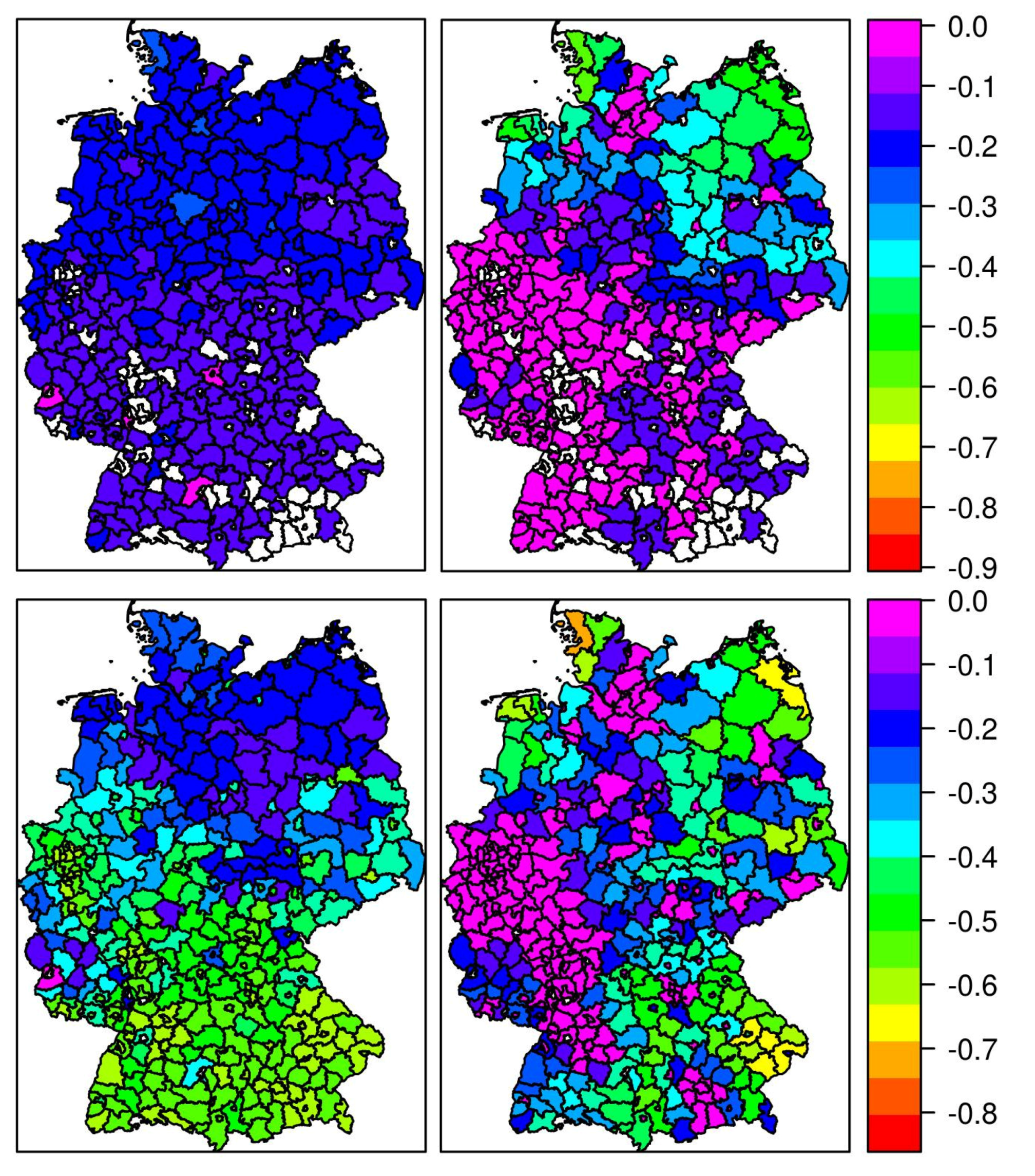
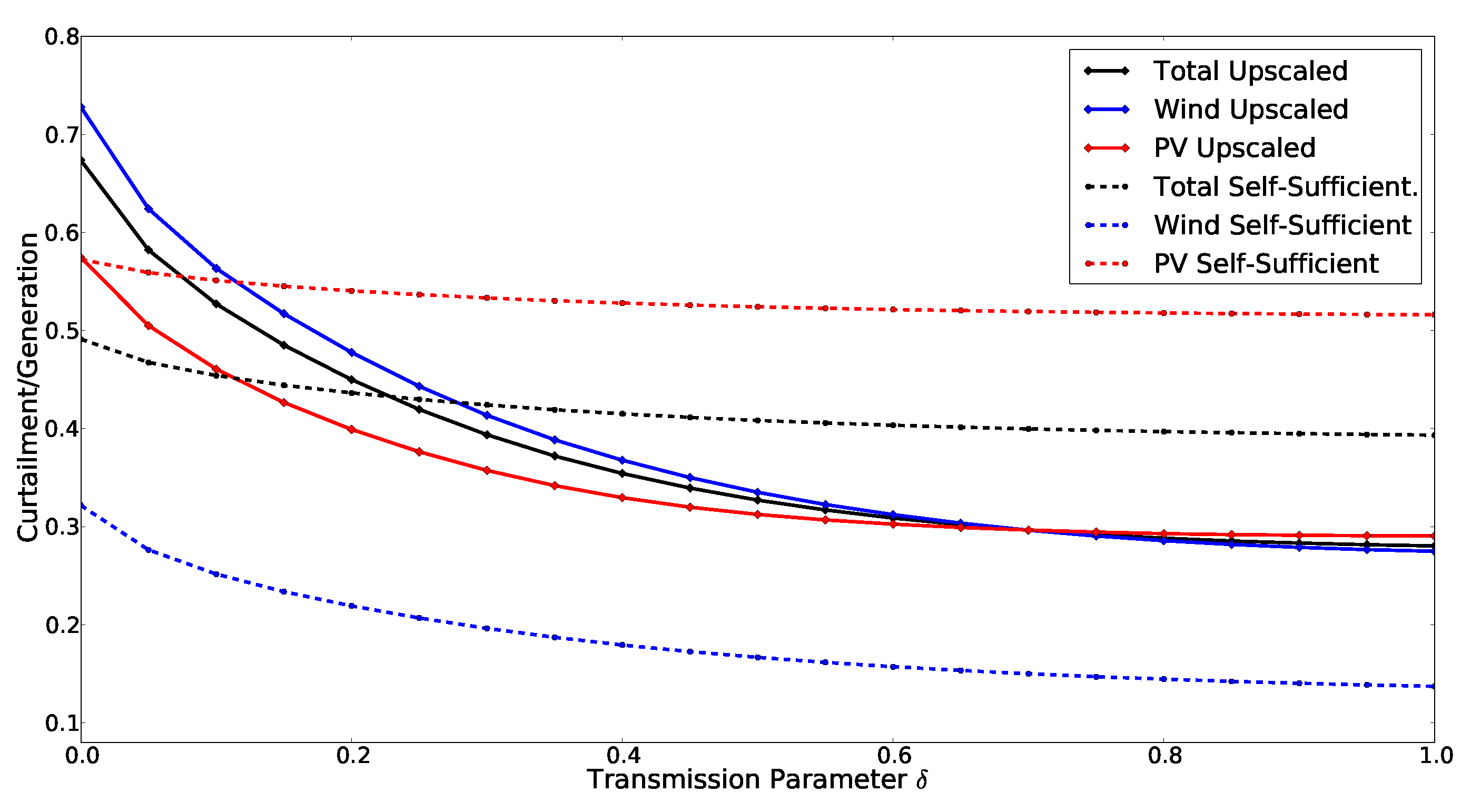
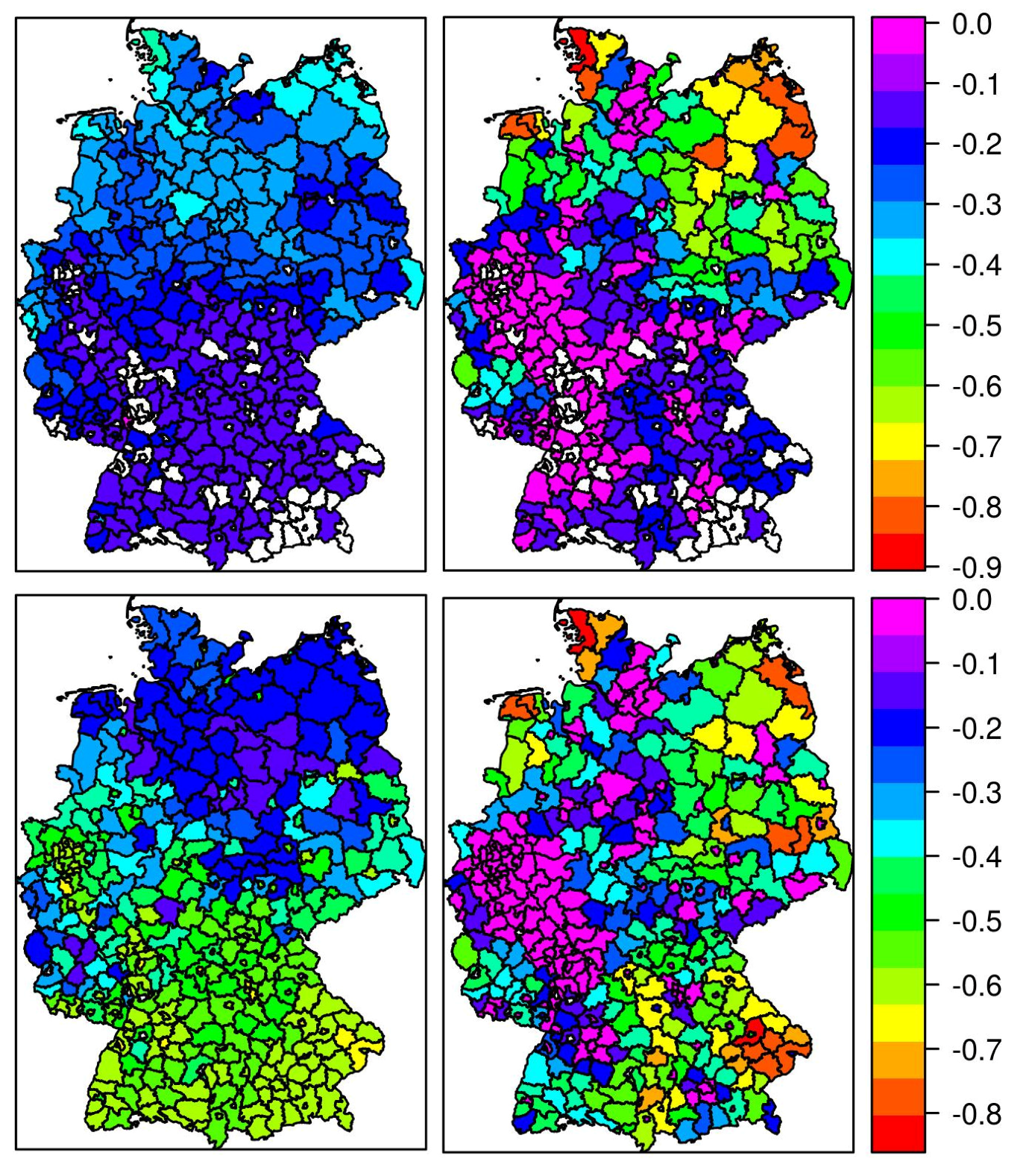
4. Results
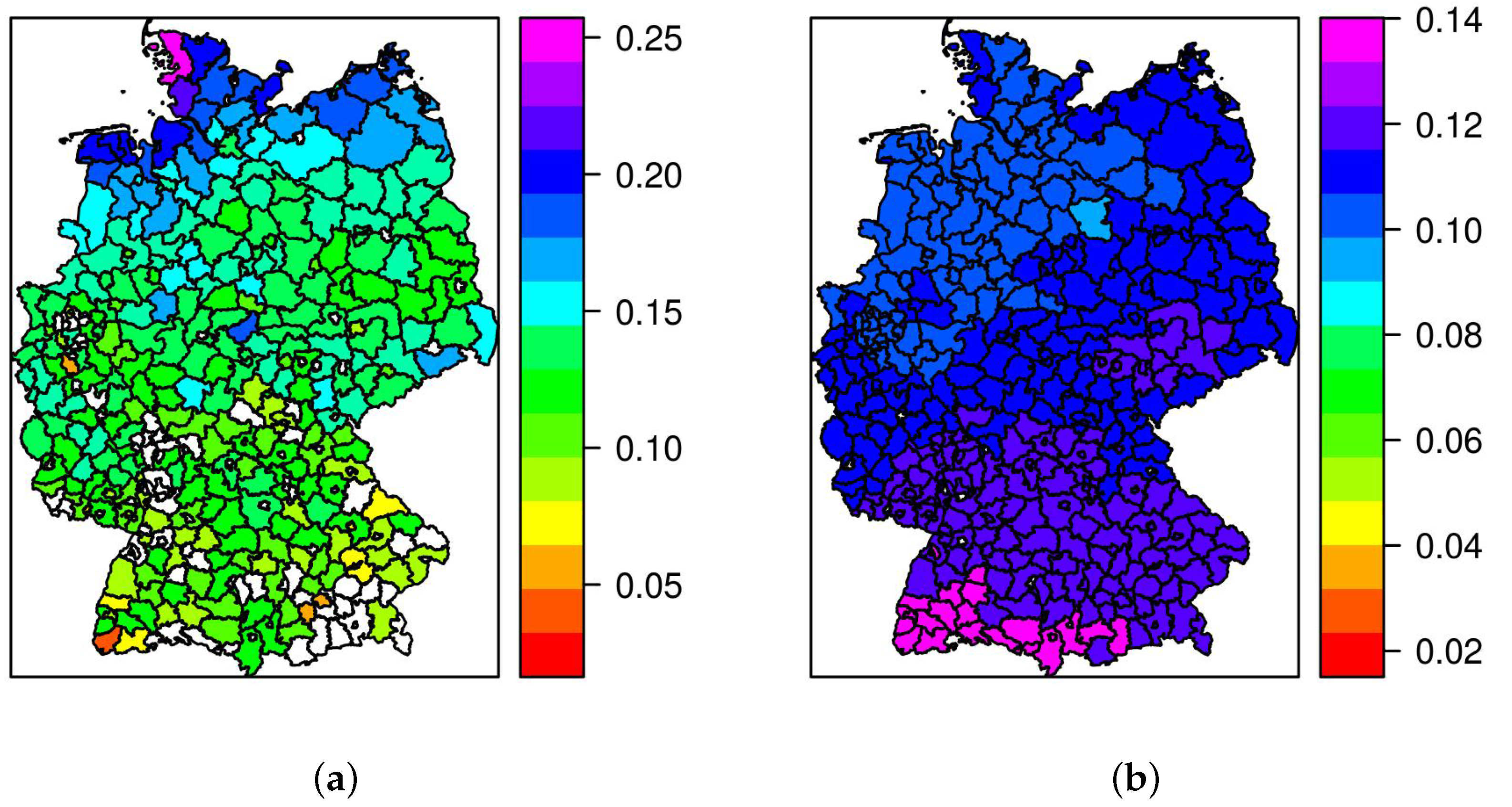
4.1. Meteorological Capacity Factors
4.2. Effective Capacity Factors
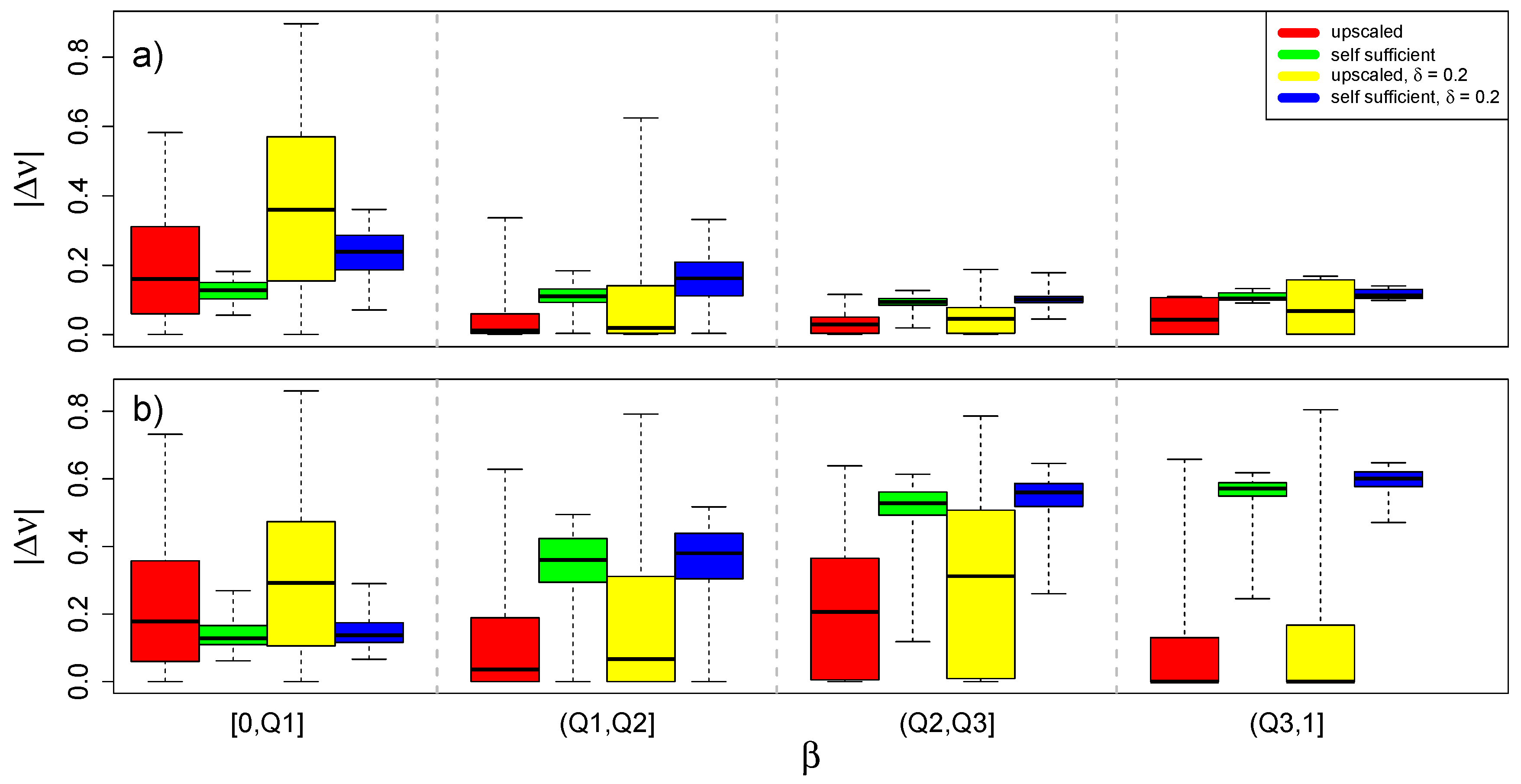
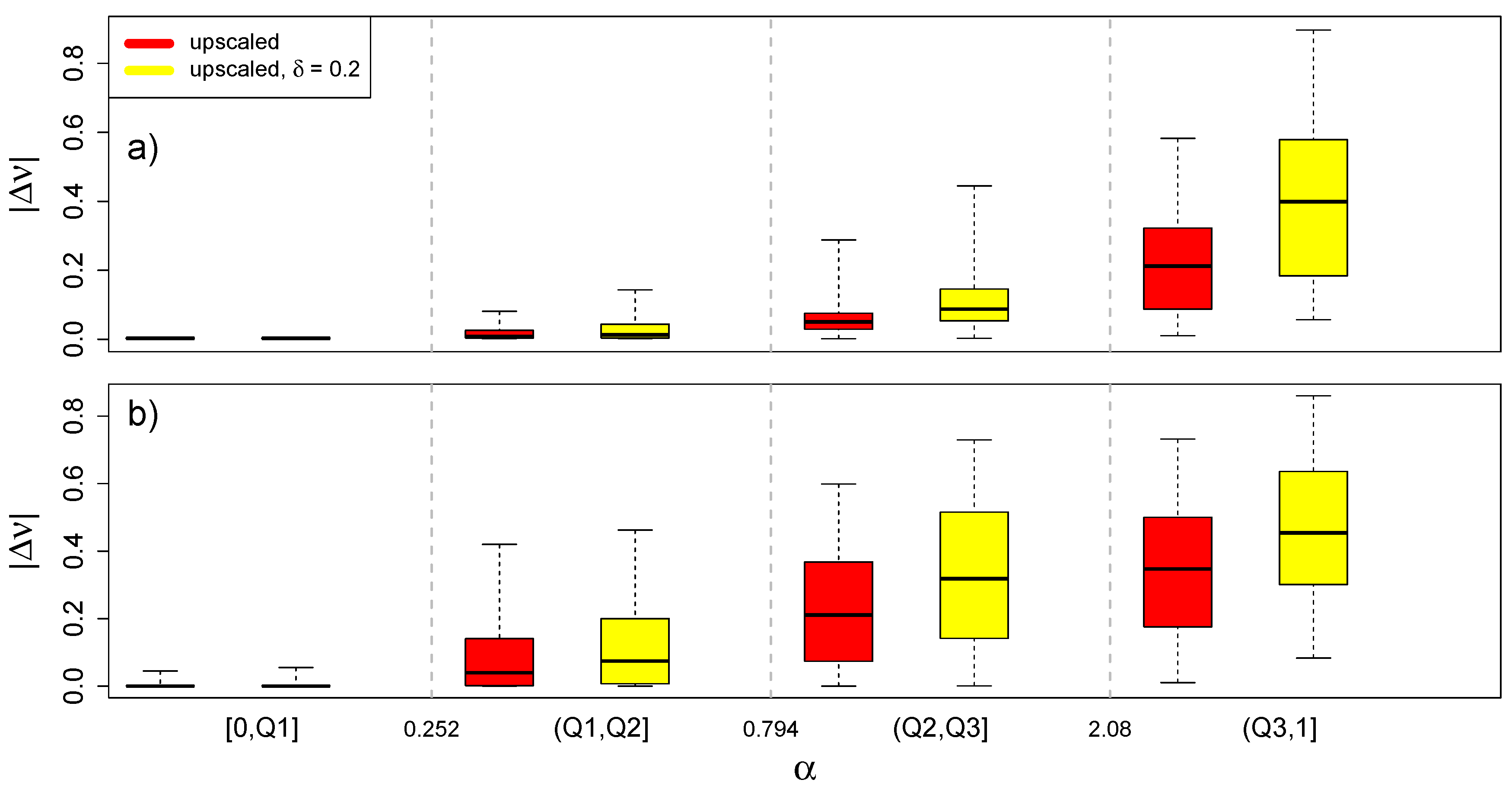
5. Discussion
5.1. Wind/PV Ratio
5.2. Share of Renewables
5.3. Limited Transmission
6. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Burger, B. Electricity Production from Solar and Wind in Germany in 2014; Fraunhofer ISE: Freiburg, Germany, 2013. [Google Scholar]
- Jacobson, M.Z.; Delucchi, M.A. Providing all global energy with wind, water, and solar power, Part I: Technologies, energy resources, quantities and areas of infrastructure, and materials. Energy Policy 2011, 3, 1154–1169. [Google Scholar] [CrossRef]
- De Vries, B.J.; van Vuuren, D.P.; Hoogwijk, M.M. Renewable energy sources: Their global potential for the first-half of the 21st century at a global level: An integrated approach. Energy Policy 2007, 35, 2590–2610. [Google Scholar] [CrossRef]
- Hasche, B. General statistics of geographically dispersed wind power. Wind Energy 2010, 13, 773–784. [Google Scholar] [CrossRef]
- Wiemken, E.; Beyer, H.; Heydenreich, W.; Kiefer, K. Power characteristics of PV ensembles: Experiences from the combined power production of 100 grid connected PV systems distributed over the area of Germany. Sol. Energy 2001, 70, 513–518. [Google Scholar] [CrossRef]
- Boccard, N. Capacity factor of wind power realized values vs. estimates. Energy Policy 2009, 37, 2679–2688. [Google Scholar] [CrossRef]
- Abed, K.A.; El-Mallah, A.A. Capacity factor of wind turbines. Energy 1997, 22, 487–491. [Google Scholar] [CrossRef]
- Justus, C.; Hargraves, W.; Yalcin, A. Nationwide assessment of potential output from wind-powered generators. J. Appl. Meteorol. 1976, 15, 673–678. [Google Scholar] [CrossRef]
- Diakov, V. Wind resource quality affected by high levels of renewables. Resources 2015, 4, 378–383. [Google Scholar] [CrossRef]
- Gu, Y.; Xie, L.; Rollow, B.; Hesselbaek, B. Congestion-induced wind curtailment: Sensitivity analysis and case studies. In Proceedings of the North American Power Symposium (NAPS), Boston, MA, USA, 4–6 August 2011; IEEE: Boston, MA, USA, 2011; pp. 1–7. [Google Scholar]
- Flora, R.; Marques, A.C.; Fuinhas, J.A. Wind power idle capacity in a panel of European countries. Energy 2014, 66, 823–830. [Google Scholar] [CrossRef]
- Faulstich, M.; Foth, H.; Calliess, C.; Hohmeyer, O.; Holm-Mueller, K.; Niekisch, M.; Schreurs, M. Climate-friendly, Reliable, Affordable: 100% Renewable Electricity Supply by 2050; Technical Report; German Advisory Council on the Environment (SRU): Berlin, Germany, 2010. [Google Scholar]
- Bundesnetzagentur. EEG in Zahlen. 2015. Available online: http://www.bundesnetzagentur.de/cln1422/DE/Sachgebiete/ElektrizitaetundGas/UnternehmenInstitutionen/ErneuerbareEnergien/ZahlenDatenInformationen/zahlenunddaten-node.html (accessed on 3 October 2015).
- Lew, D.; Bird, L.; Milligan, M.; Speer, B.; Wang, X.; Carlini, E.M.; Estanqueiro, A.; Flynn, D.; Gomez-Lazaro, E.; Menemenlis, N.; et al. Wind and solar curtailment. In Proceedings of the 12th International Workshop on Large-Scale Integration of Wind Power into Power Systems as well as on Transmission Networks for Offshore Wind Power Plants, London, UK, 22–24 October 2013.
- EirGrid; SONI. Delivering a Secure Sustainable Electricity System; Project Presentation; EirGrid: Dublin, Ireland, 2013. [Google Scholar]
- Bundesamt für Kartographie und Geodäsie. 2015. Available online: http://www.bkg.bund.de (accessed on 31 July 2015).
- Statistische Ämter des Bundes und der Länder. 2015. Available online: http://www.regionalstatistik.de (accessed on 31 July 2015).
- Negra, N.B.; Todorovic, J.; Ackermann, T. Loss evaluation of HVAC and HVDC transmission solutions for large offshore wind farms. Electr. Power Syst. Res. 2006, 76, 916–927. [Google Scholar] [CrossRef]
- Heide, D.; von Bremen, L.; Greiner, M.; Hoffmann, C.; Speckmann, M.; Bofinger, S. Seasonal optimal mix of wind and solar power in a future, highly renewable Europe. Renew. Energy 2010, 35, 2483–2489. [Google Scholar] [CrossRef]
- Kies, A.; Nag, K.; von Bremen, L.; Lorenz, E.; Heinemann, D. Investigation of balancing effects in long term renewable energy feed-in with respect to the transmission grid. Adv. Sci. Res. 2015, 12, 91–95. [Google Scholar] [CrossRef]
- Oswald, B.; Oeding, D. Elektrische Kraftwerke und Netze, 6th ed.; Springer-Verlag: Berlin/Heidelberg, Germany; New York, NY, USA, 2004. [Google Scholar]
- Heide, D. Statistical Physics of Power Flows on Networks with a High Share of Fluctuating Renewable Generation. Ph.D. Thesis, Johann Wolfgang Goethe-Universitaet Frankfurt am Main, Frankfurt, Germany, 2010. [Google Scholar]
- Rodriguez, R.A.; Dahl, M.; Becker, S.; Greiner, M. Localized vs. synchronized exports across a highly renewable pan-European transmission network. Energy Sustain. Soc. 2015, 5, 1–9. [Google Scholar] [CrossRef]
- Heide, D.; Greiner, M.; von Bremen, L.; Hoffmann, C. Reduced storage and balancing needs in a fully renewable European power system with excess wind and solar power generation. Renew. Energy 2011, 36, 2515–2523. [Google Scholar] [CrossRef]
- Rodriguez, R.A.; Becker, S.; Greiner, M. Cost-optimal design of a simplified, highly renewable pan-European electricity system. Energy 2015, 83, 658–668. [Google Scholar] [CrossRef]
- Kies, A.; von Bremen, L.; Chattopadhyay, K.; Lorenz, E.; Heinemann, D. Backup, storage and transmission estimates of a supra-European electricity grid with high shares of renewables. In Proceedings of the 14th Wind Integration Workshop, Brussels, Belgium, 20–22 October 2015.
- Becker, S.; Rodriguez, R.; Andresen, G.; Schramm, S.; Greiner, M. Transmission grid extensions during the build-up of a fully renewable pan-european electricity supply. Energy 2014, 64, 404–418. [Google Scholar] [CrossRef]
- Becker, S.; Frew, B.A.; Andresen, G.B.; Zeyer, T.; Schramm, S.; Greiner, M.; Jacobson, M.Z. Features of a fully renewable US electricity system: Optimized mixes of wind and solar PV and transmission grid extensions. Energy 2014, 72, 443–458. [Google Scholar] [CrossRef]
- Rodriguez, R.A.; Becker, S.; Andresen, G.B.; Heide, D.; Greiner, M. Transmission needs across a fully renewable European power system. Renew. Energy 2014, 63, 467–476. [Google Scholar] [CrossRef]
- Doms, G.; Schättler, U.; Baldauf, M. A Description of the Nonhydrostatic Regional COSMO Model, Part I: Dynamics and Numerics; Technical Report; Consortium for Small-Scale Modelling: Offenbach, Germany, 2011. [Google Scholar]
- Späth, S.; von Bremen, L.; Junk, C.; Heinemann, D. Time-consistent calibration of short-term regional wind power ensemble forecasts. Meteorol. Z. 2015, 24, 381–392. [Google Scholar]
- Klucher, T. Evaluation of models to predict insolation on tilted surfaces. Sol. Energy 1979, 23, 111–114. [Google Scholar] [CrossRef]
- SMA Solar Technology AG. Sunny Mini Central 6000TL/7000TL/8000TL; SMA Solar Technology AG: Niestetal, Germany, 2010. [Google Scholar]
- Bundesministerium für Wirtschaft und Energie. Erneuerbare Energien in Zahlen—Nationale und Internationale Entwicklung im Jahr 2013; Bundesministerium für Wirtschaft und Energie: Berlin, Germany, 2014. [Google Scholar]
- Grimm, V.; Martin, A.; Weibenzahl, M.; Zoettl, G. Transmission and generation investment in electricity markets: The effects of market splitting and network fee regimes. Eur. J. Oper. Res. 2016, 254, 493–509. [Google Scholar] [CrossRef]
- Kemfert, C.; Kunz, F.; Rosellón, J. A Welfare Analysis of the Electricity Transmission Regulatory Regime in Germany. DIW: Berlin, Germany, 2015. [Google Scholar]
- Baringo, L.; Conejo, A.J. Transmission and wind power investment. IEEE Trans. Power Syst. 2012, 27, 885–893. [Google Scholar] [CrossRef]
- Orfanos, G.A.; Georgilakis, P.S.; Hatziargyriou, N.D. Transmission expansion planning of systems with increasing wind power integration. IEEE Trans. Power Syst. 2013, 28, 1355–1362. [Google Scholar] [CrossRef]
- Erneuerbare-Energien-Gesetz, 2014. Available online: http://dejure.org/gesetze/EEG/12.html (accessed on 15 March 2016).
- Deutschlands Zukunft Gestalten—Koalitionsvertrag Zwischen CDU, CSU und SPD, 2013. Available online: http://www.bundesregierung.de/Content/DE/Anlagen/2013/2013-12-17-koalitionsvertrag.pdf (accessed on 18 March 2016).
- Betreiberdatenbasis: Betriebsdaten von Windanlagen. Available online: http://www.btrdb.de/ (accessed on 10 January 2015).
| Scenario | β | (GW) | (GW) | (GWkm) | |||
|---|---|---|---|---|---|---|---|
| Self-Sufficient | 0.68 | 0.14 | 0.52 | 0.39 | 160 | 389 | 13,800 |
| Upscaled | 0.35 | 0.27 | 0.29 | 0.28 | 289 | 206 | 27,065 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kies, A.; Schyska, B.U.; Von Bremen, L. Curtailment in a Highly Renewable Power System and Its Effect on Capacity Factors. Energies 2016, 9, 510. https://doi.org/10.3390/en9070510
Kies A, Schyska BU, Von Bremen L. Curtailment in a Highly Renewable Power System and Its Effect on Capacity Factors. Energies. 2016; 9(7):510. https://doi.org/10.3390/en9070510
Chicago/Turabian StyleKies, Alexander, Bruno U. Schyska, and Lueder Von Bremen. 2016. "Curtailment in a Highly Renewable Power System and Its Effect on Capacity Factors" Energies 9, no. 7: 510. https://doi.org/10.3390/en9070510
APA StyleKies, A., Schyska, B. U., & Von Bremen, L. (2016). Curtailment in a Highly Renewable Power System and Its Effect on Capacity Factors. Energies, 9(7), 510. https://doi.org/10.3390/en9070510





