Online Identification with Reliability Criterion and State of Charge Estimation Based on a Fuzzy Adaptive Extended Kalman Filter for Lithium-Ion Batteries
Abstract
:1. Introduction
- (1)
- The autoregressive moving average model with external input (ARMAX) of the battery is derived, which takes the OCV as a parameter needing identification. The zero-order hold discretization is implemented rather than the difference discretization to further improve the accuracy, and the RELS algorithm is used to realize the online identification.
- (2)
- The OCV error between the offline and online value serves as an assessment criterion to judge the reliability of the online parameters. Making use of the property that the OCV-SOC curves remain almost invariant at different aging levels [27,28], this method can apply to the whole life-cycle of the battery.
- (3)
- A fuzzy model is established to update R in real time to compensate the intrinsic model error, and the fuzzy rules are derived by using the verified prior knowledge.
- (4)
- The positive strategy based on an online identification strategy and the negative strategy using a fuzzy model to update R are combined to improve the SOC estimation accuracy.
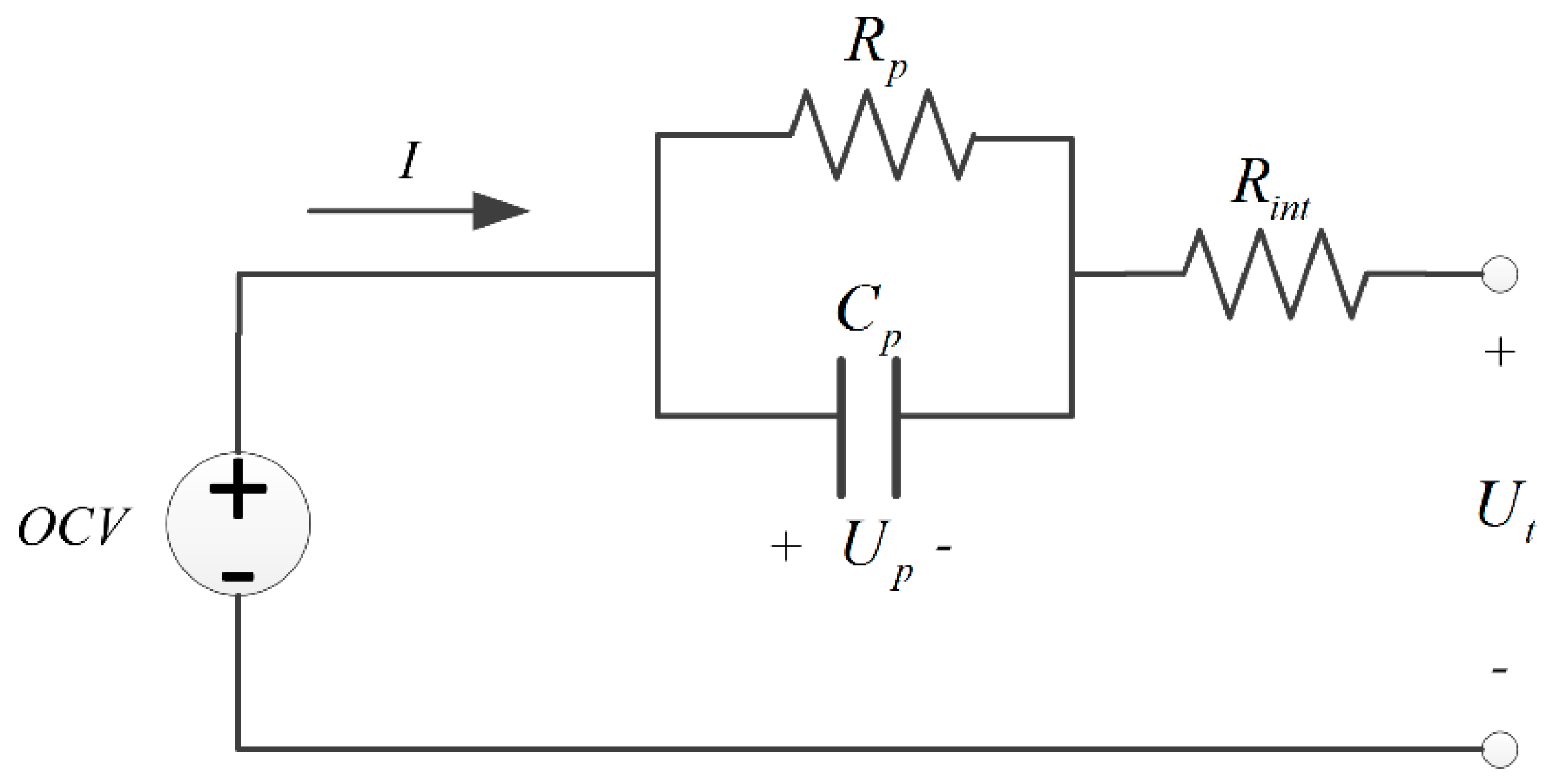
2. Equivalent Circuit Model
2.1. Thevenin Model
2.2. Model Error
3. Proposed Online Identification Strategy for ECM
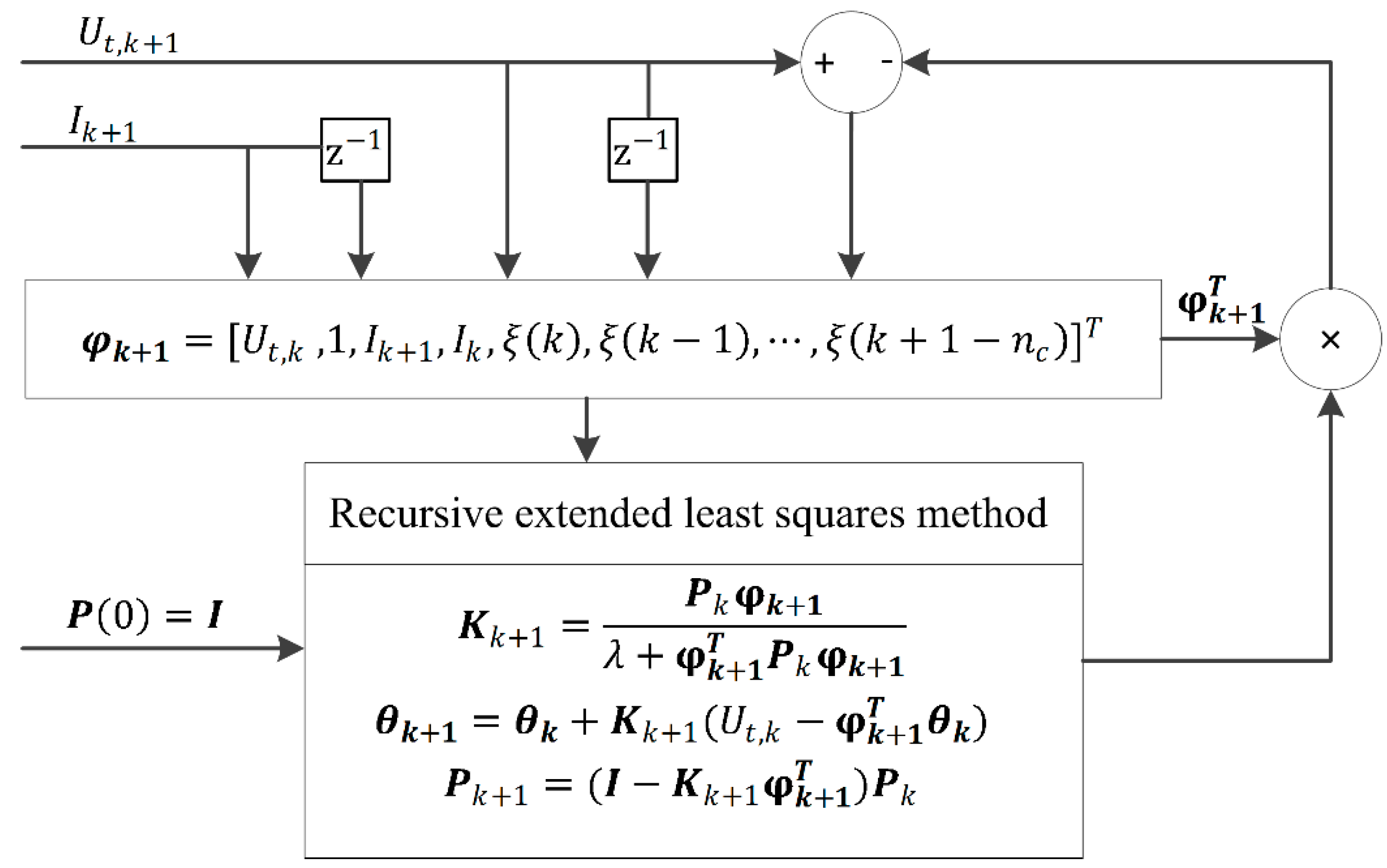
3.1. Online Identification Method
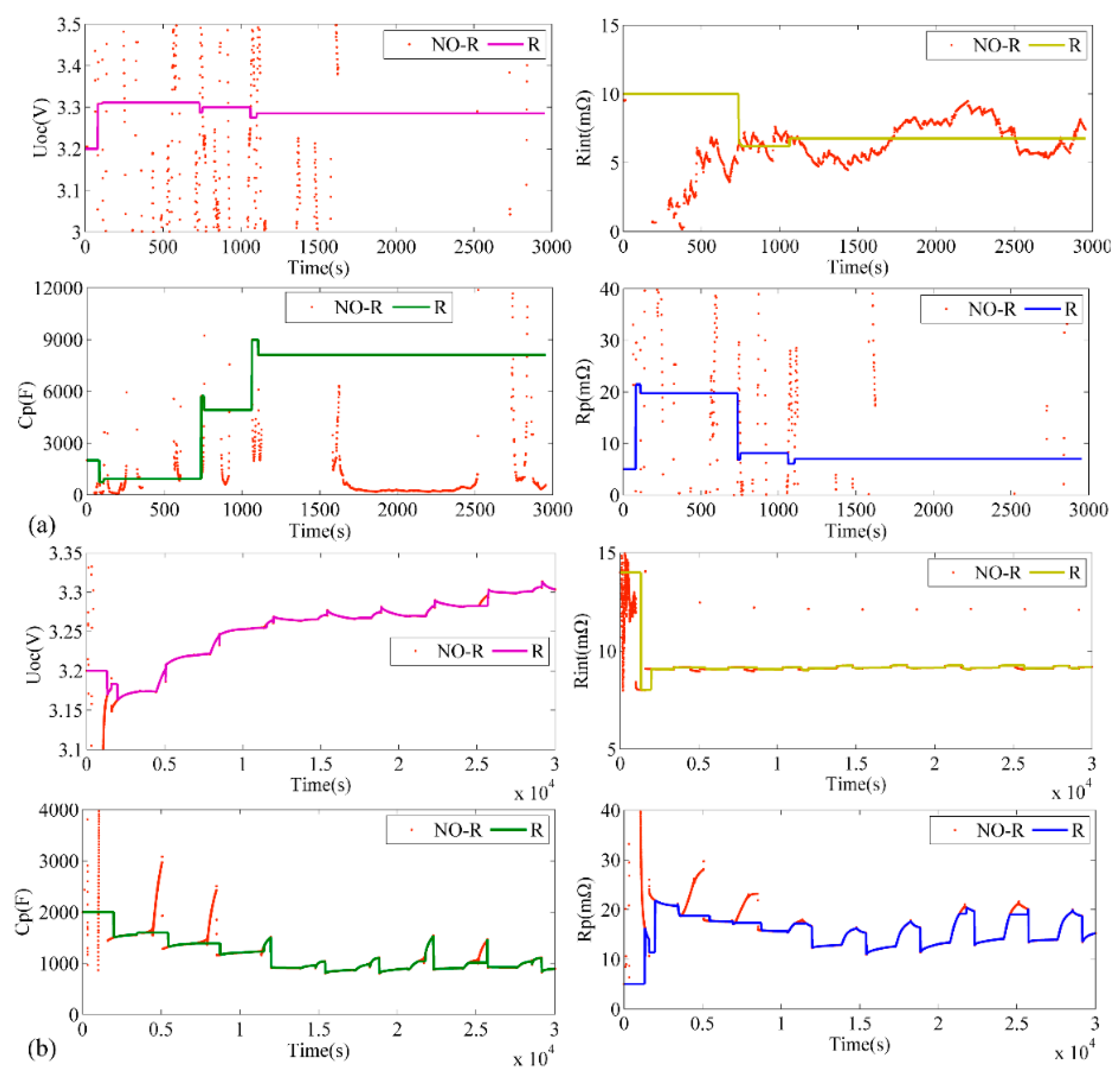
3.2. Parameters Reliability Criterion
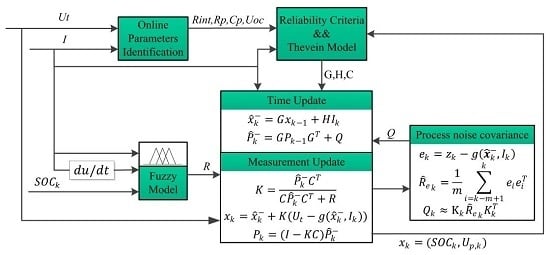
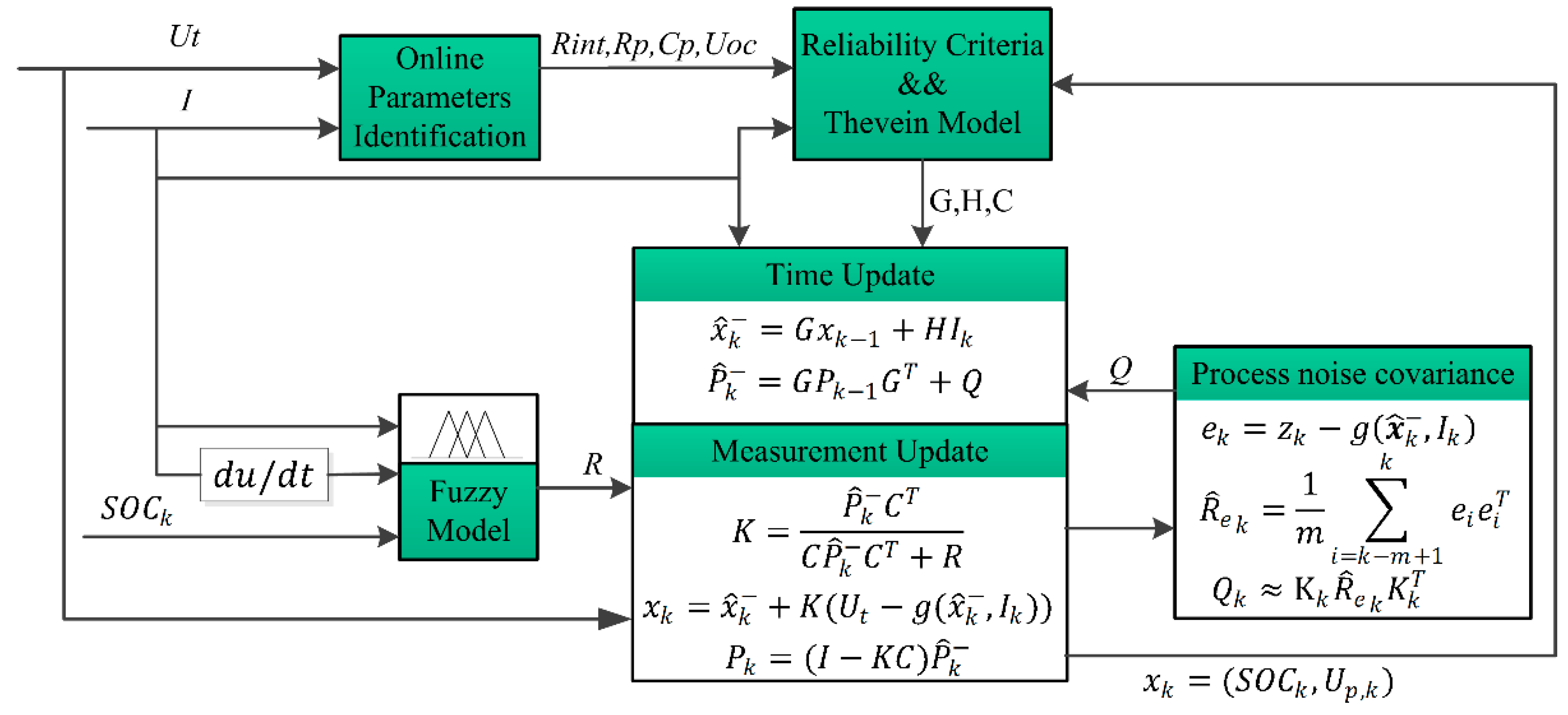
4. Fuzzy Adaptive Extended Kalman Filter for SOC Estimation
4.1. Adaptive Extended Kalman Filter
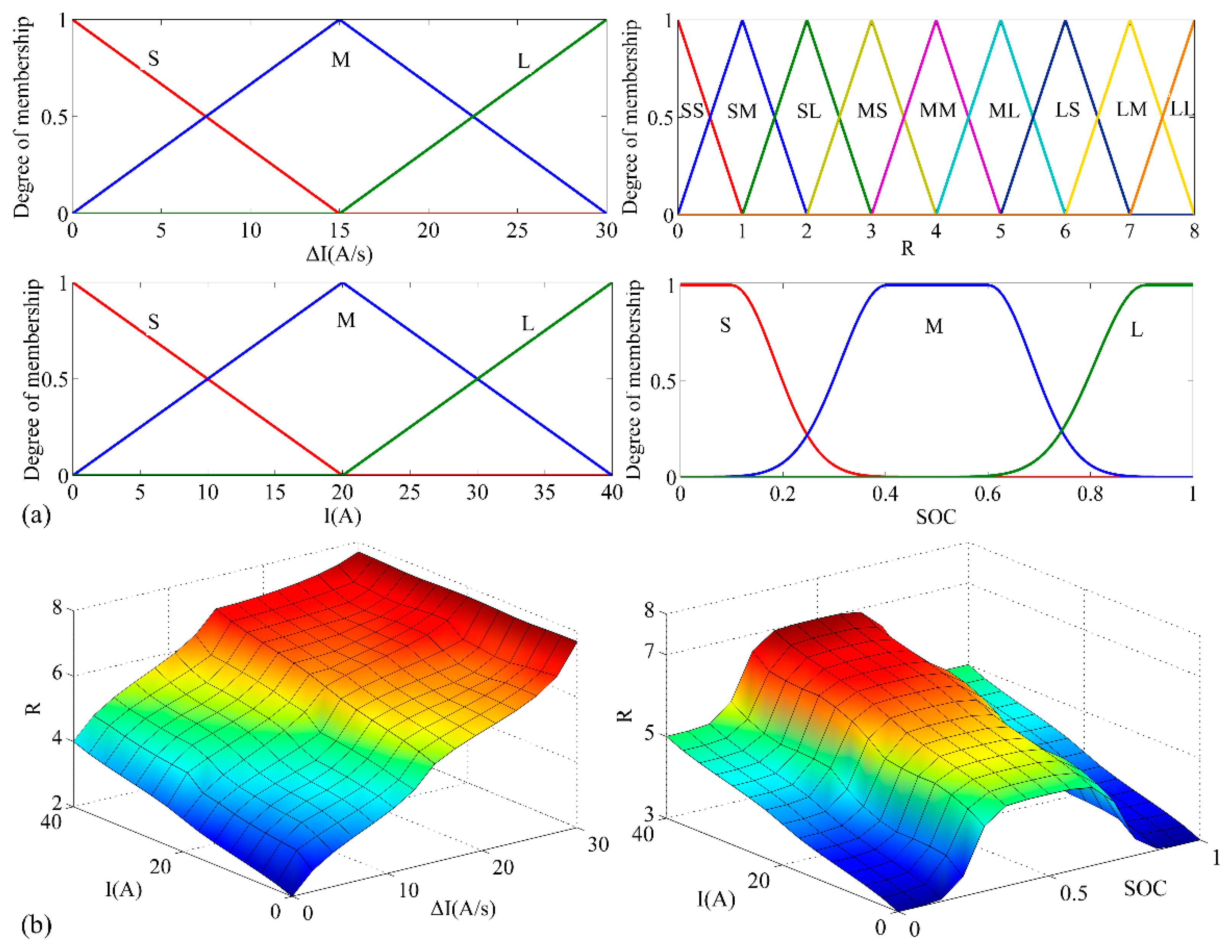
4.2. How to Establish the Fuzzy Model
5. Experiment Results and Discussion
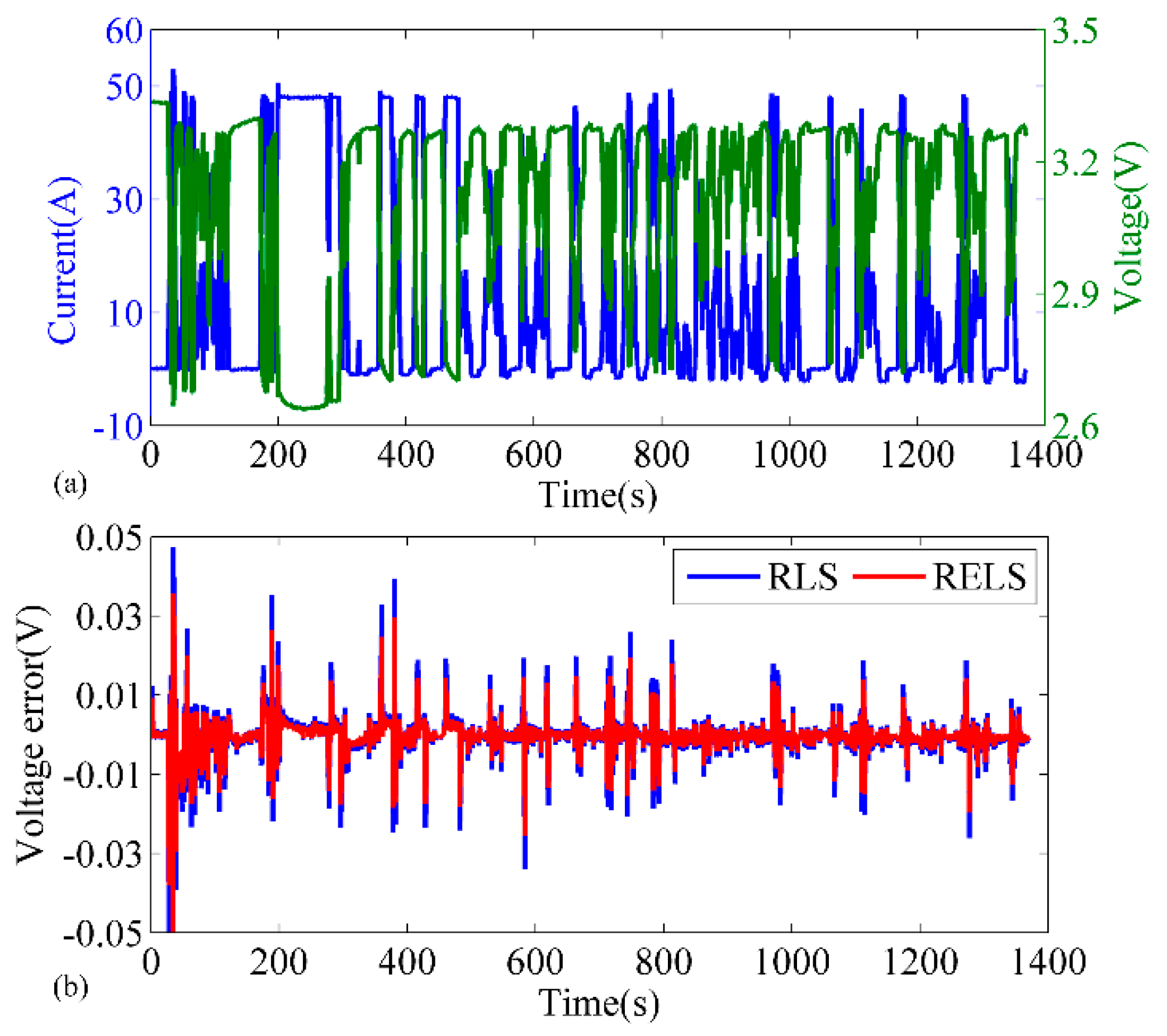
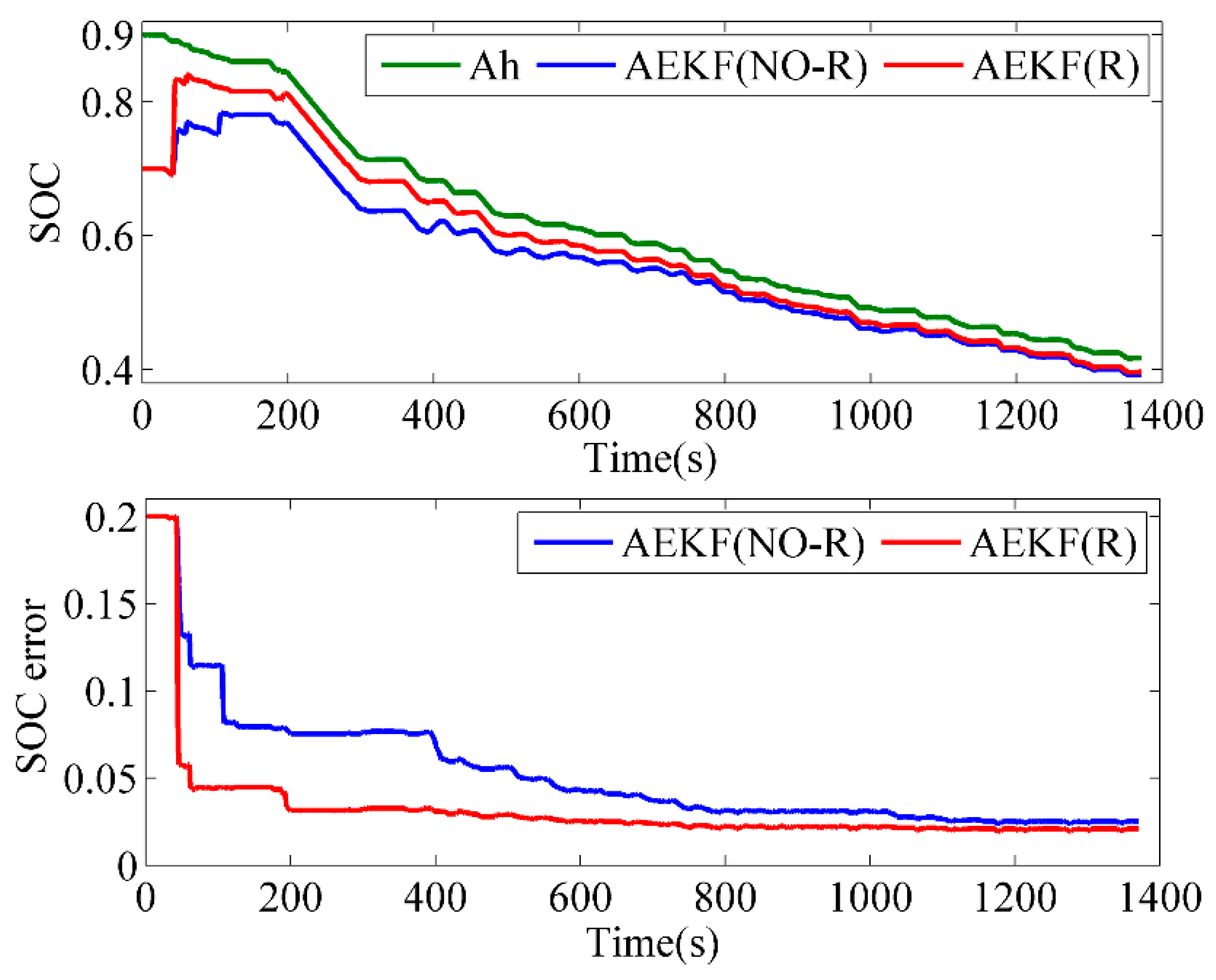
5.1. Verification of the Reliability Criterion
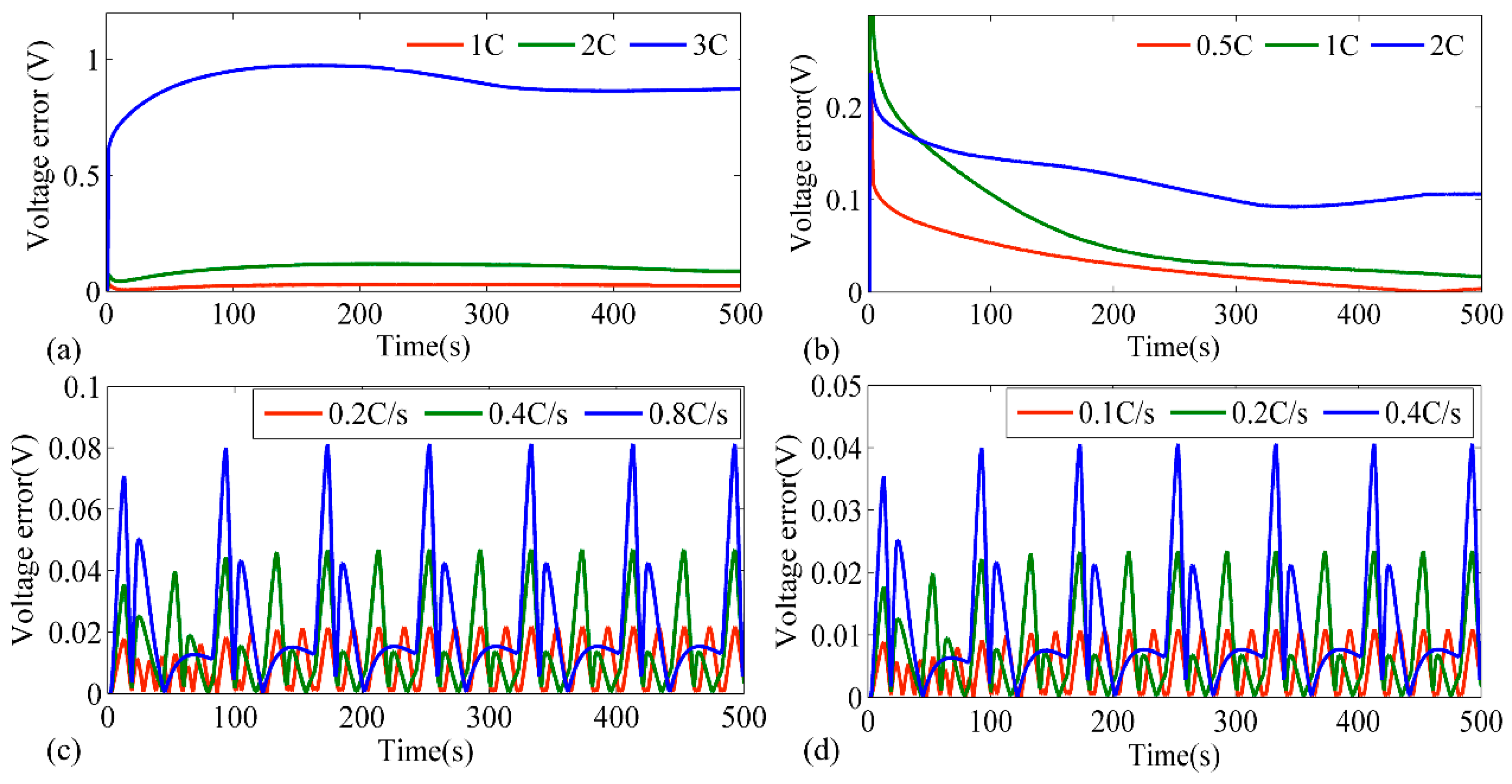
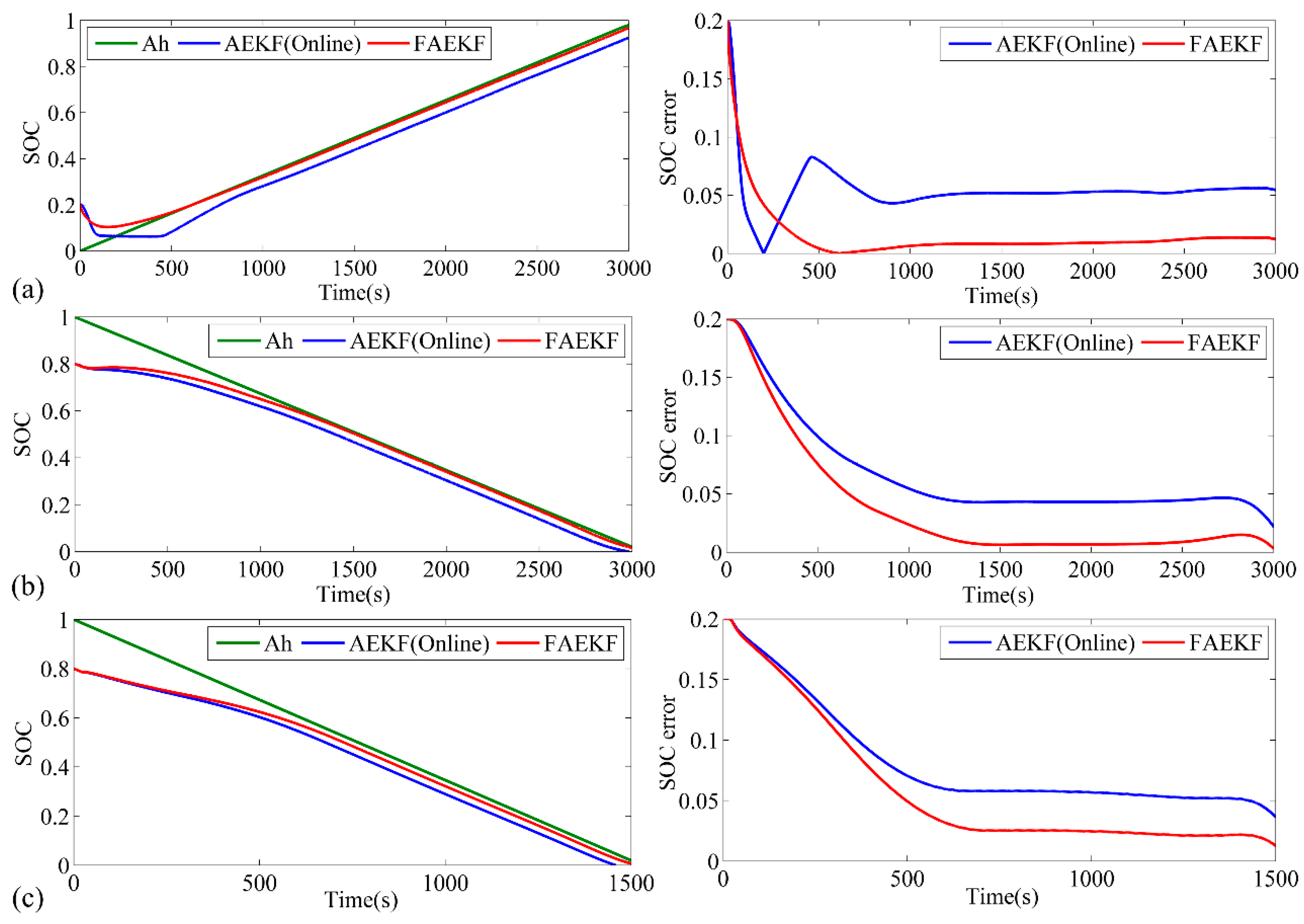
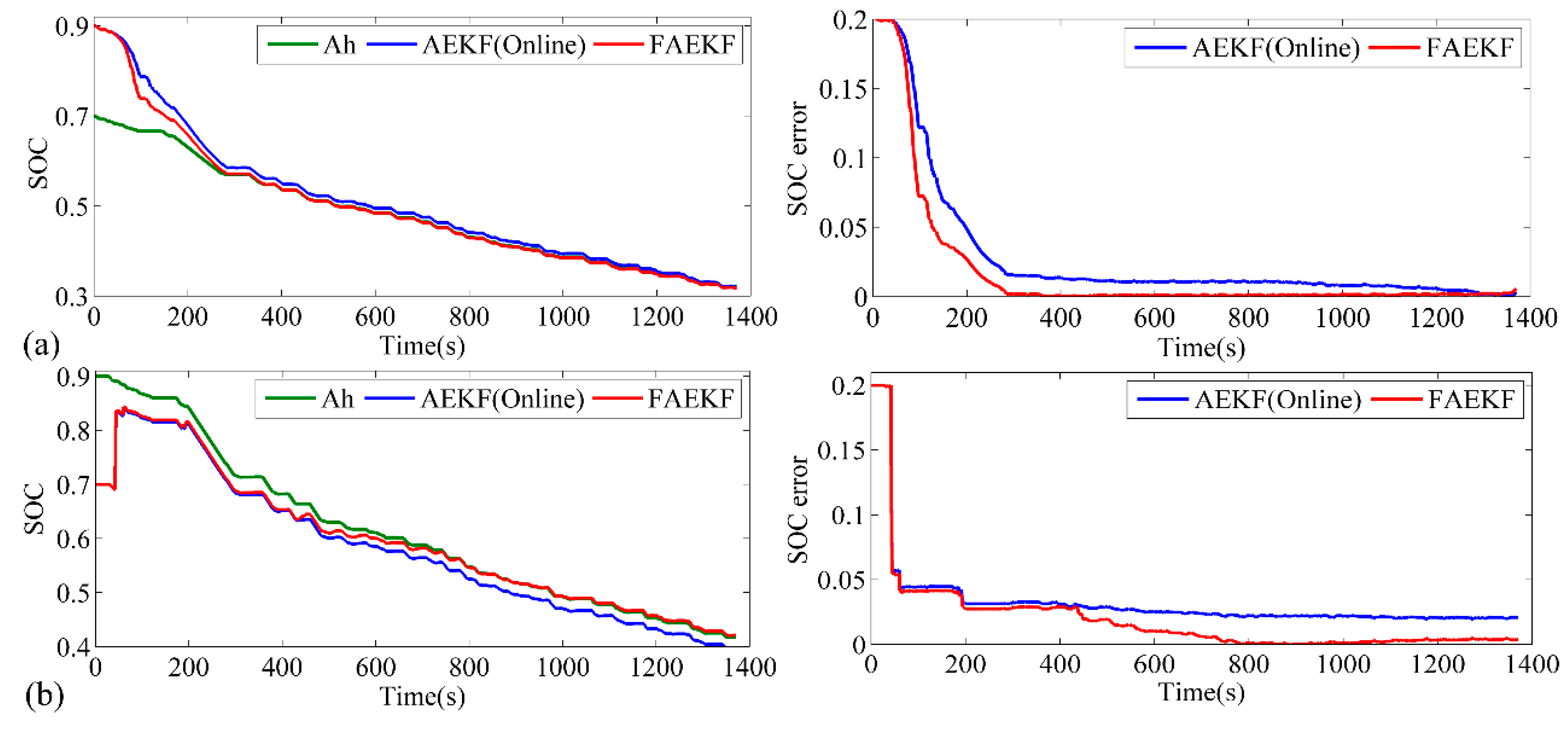
5.2. Verification of the FAEKF Algorithm
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Waag, W.; Fleischer, C.; Sauer, D.U. Critical review of the methods for monitoring of lithium-ion batteries in electric and hybrid vehicles. J. Power Sources 2014, 258, 321–339. [Google Scholar] [CrossRef]
- Lu, L.; Han, X.; Li, J.; Hua, J.; Ouyang, M. A review on the key issues for lithium-ion battery management in electric vehicles. J. Power Sources 2013, 226, 272–288. [Google Scholar] [CrossRef]
- He, W.; Williard, N.; Osterman, M.; Pecht, M. Prognostics of lithium-ion batteries based on Dempster–Shafer theory and the Bayesian Monte Carlo method. J. Power Sources 2011, 196, 10314–10321. [Google Scholar] [CrossRef]
- Wang, D.; Miao, Q.; Pecht, M. Prognostics of lithium-ion batteries based on relevance vectors and a conditional three-parameter capacity degradation model. J. Power Sources 2013, 239, 253–264. [Google Scholar] [CrossRef]
- Guo, X.; Kang, L.; Yao, Y.; Huang, Z.; Li, W. Joint Estimation of the Electric Vehicle Power Battery State of Charge Based on the Least Squares Method and the Kalman Filter Algorithm. Energies 2016, 9, 100. [Google Scholar] [CrossRef]
- Feng, F.; Lu, R.; Wei, G.; Zhu, C. Online estimation of model parameters and state of charge of LiFePO4 batteries using a novel open-circuit voltage at various ambient temperatures. Energies 2015, 8, 2950–2976. [Google Scholar] [CrossRef]
- Xing, Y.; He, W.; Pecht, M.; Tsui, K.L. State of charge estimation of lithium-ion batteries using the open-circuit voltage at various ambient temperatures. Appl. Energy 2014, 113, 106–115. [Google Scholar] [CrossRef]
- Charkhgard, M.; Farrokhi, M. State-of-charge estimation for lithium-ion batteries using neural networks and EKF. IEEE Trans. Ind. Electron. 2010, 57, 4178–4187. [Google Scholar] [CrossRef]
- Wang, J.; Chen, Q.; Cao, B. Support vector machine based battery model for electric vehicles. Energy Convers. Manage. 2006, 47, 858–864. [Google Scholar]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 2. Modeling and identification. J. Power Sources 2004, 134, 262–276. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Zhang, X.; Sun, F.; Fan, J. State-of-charge estimation of the lithium-ion battery using an adaptive extended Kalman filter based on an improved Thevenin model. IEEE Trans. Veh. Technol. 2011, 60, 1461–1469. [Google Scholar]
- He, W.; Williard, N.; Chen, C.; Pecht, M. State of charge estimation for electric vehicle batteries using unscented Kalman filtering. Microelectron. Reliab. 2013, 53, 840–847. [Google Scholar] [CrossRef]
- Yang, F.; Xing, Y.; Wang, D.; Tsui, K.L. A comparative study of three model-based algorithms for estimating state-of-charge of lithium-ion batteries under a new combined dynamic loading profile. Appl. Energies 2016, 164, 387–399. [Google Scholar] [CrossRef]
- Sun, F.; Hu, X.; Zou, Y.; Li, S. Adaptive unscented Kalman filtering for state of charge estimation of a lithium-ion battery for electric vehicles. Fuel Energy Abstr. 2011, 36, 3531–3540. [Google Scholar] [CrossRef]
- Schwunk, S.; Armbruster, N.; Straub, S.; Kehl, J.; Vetter, M. Particle filter for state of charge and state of health estimation for lithium–iron phosphate batteries. J. Power Sources 2013, 239, 705–710. [Google Scholar] [CrossRef]
- Lee, J.; Nam, O.; Cho, B.H. Li-ion battery SOC estimation method based on the reduced order extended Kalman filtering. J. Power Sources 2007, 174, 9–15. [Google Scholar] [CrossRef]
- Mohamed, A.H.; Schwarz, K.P. Adaptive Kalman filtering for INS/GPS. J. Geod. 1999, 73, 193–203. [Google Scholar] [CrossRef]
- Singh, P.; Vinjamuri, R.; Wang, X.; Reisner, D. Fuzzy logic modeling of EIS measurements on lithium-ion batteries. Electrochimica Acta 2006, 51, 1673–1679. [Google Scholar] [CrossRef]
- Singh, P.; Fennie, C.; Reisner, D. Fuzzy logic modelling of state-of-charge and available capacity of nickel/metal hydride batteries. J. Power Sources 2004, 136, 322–333. [Google Scholar] [CrossRef]
- Burgos, C.; Sáez, D.; Orchard, M.E.; Cárdenas, R. Fuzzy modelling for the state-of-charge estimation of lead-acid batteries. J. Power Sources 2015, 274, 355–366. [Google Scholar] [CrossRef]
- Loebis, D.; Sutton, R.; Chudley, J.; Naeem, W. Adaptive tuning of a Kalman filter via fuzzy logic for an intelligent AUV navigation system. Control Eng. Pract. 2004, 12, 1531–1539. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Fan, J. Evaluation of lithium-ion battery equivalent circuit models for state of charge estimation by an experimental approach. Energies 2011, 4, 582–598. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Xiong, R.; Sun, F.; Gong, X.; Gao, C. A data-driven based adaptive state of charge estimator of lithium-ion polymer battery used in electric vehicles. Appl. Energy 2014, 113, 1421–1433. [Google Scholar] [CrossRef]
- Feng, T.; Yang, L.; Zhao, X.; Zhang, H.; Qiang, J. Online identification of lithium-ion battery parameters based on an improved equivalent-circuit model and its implementation on battery state-of-power prediction. J. Power Sources 2015, 281, 192–203. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 3. State and parameter estimation. J. Power Sources 2004, 134, 277–292. [Google Scholar] [CrossRef]
- Bergveld, H.J.; Kruijt, W.S.; Notten, P.H. Battery Management Systems: Design by Modelling; Philips Research Book Series; Kluwer Academic Publishers: Boston, MA, USA, 2002. [Google Scholar]
- Snihir, I.; Rey, W.; Verbitskiy, E.; Belfadhel-Ayeb, A.; Notten, P.H. Battery open-circuit voltage estimation by a method of statistical analysis. J. Power Sources 2006, 159, 1484–1487. [Google Scholar] [CrossRef]
- Coleman, M.; Hurley, W.G.; Lee, C.K. An improved battery characterization method using a two-pulse load test. IEEE Trans. Energy Convers. 2008, 23, 708–713. [Google Scholar] [CrossRef]
- Han, J.; Kim, D.; Sunwoo, M. State-of-charge estimation of lead-acid batteries using an adaptive extended Kalman filter. J. Power Sources 2009, 188, 606–612. [Google Scholar] [CrossRef]
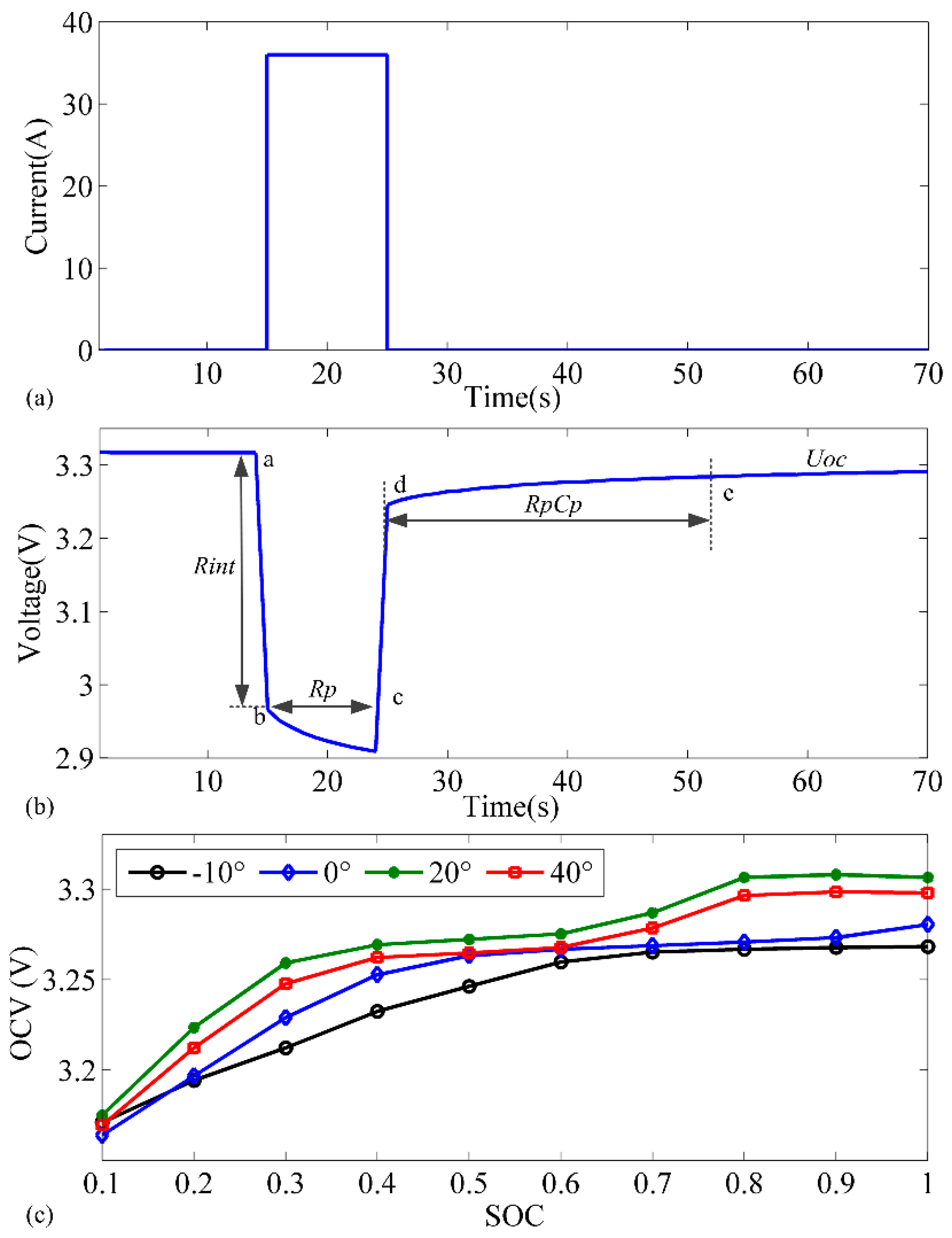

| SOC | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 |
| OCV (V) | 3.175 | 3.224 | 3.259 | 3.269 | 3.272 | 3.275 | 3.282 | 3.300 | 3.305 | 3.311 |
| Rint (mΩ) | 10.19 | 9.94 | 9.89 | 9.83 | 9.78 | 9.78 | 9.78 | 9.78 | 9.8 | 9.83 |
| Rp (mΩ) | 6.322 | 5.454 | 4.762 | 5.027 | 5.206 | 4.899 | 5.465 | 6.515 | 7.029 | 7.313 |
| Cp (F) | 6096 | 5715 | 5858 | 6628 | 6708 | 7077 | 6824 | 6190 | 6354 | 6487 |
| Condition | Constant Current | Mean Model Error | Current Change | Mean Model Error |
|---|---|---|---|---|
| Discharge | 1C | 0.0249 V | 0.2 C/s | 0.0096 V |
| 2C | 0.1007 V | 0.4 C/s | 0.0160 V | |
| 3C | 0.8978 V | 0.8 C/s | 0.0231 V | |
| Charge | 0.5C | 0.0303 V | 0.1 C/s | 0.0048 V |
| 1C | 0.0640 V | 0.2 C/s | 0.0080 V | |
| 2C | 0.1220 V | 0.4 C/s | 0.0114 V |
| Feature | Value |
|---|---|
| Maximum discharge current | 300 A |
| Maximum charge current | 300 A |
| Voltage range | 0–60 V |
| Current sampling error | ±50 mA |
| Voltage sampling error | ±5 mV |
| Temperature sampling error | ±0.1 K |
| Parameter | Value |
|---|---|
| Rated capacity | 10 Ah |
| Nominal voltage | 3.2 V |
| Maximum discharge current (continuous) | 36 A |
| Maximum charge current (continuous) | 24 A |
| Maximum discharge current (within 15 s) | 48 A |
| Cut-off voltage range | 2.5–3.6 V |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, Z.; Yang, L.; Cai, Y.; Deng, H. Online Identification with Reliability Criterion and State of Charge Estimation Based on a Fuzzy Adaptive Extended Kalman Filter for Lithium-Ion Batteries. Energies 2016, 9, 472. https://doi.org/10.3390/en9060472
Deng Z, Yang L, Cai Y, Deng H. Online Identification with Reliability Criterion and State of Charge Estimation Based on a Fuzzy Adaptive Extended Kalman Filter for Lithium-Ion Batteries. Energies. 2016; 9(6):472. https://doi.org/10.3390/en9060472
Chicago/Turabian StyleDeng, Zhongwei, Lin Yang, Yishan Cai, and Hao Deng. 2016. "Online Identification with Reliability Criterion and State of Charge Estimation Based on a Fuzzy Adaptive Extended Kalman Filter for Lithium-Ion Batteries" Energies 9, no. 6: 472. https://doi.org/10.3390/en9060472
APA StyleDeng, Z., Yang, L., Cai, Y., & Deng, H. (2016). Online Identification with Reliability Criterion and State of Charge Estimation Based on a Fuzzy Adaptive Extended Kalman Filter for Lithium-Ion Batteries. Energies, 9(6), 472. https://doi.org/10.3390/en9060472