Experiments on the Performance of Small Horizontal Axis Wind Turbine with Passive Pitch Control by Disk Pulley
Abstract
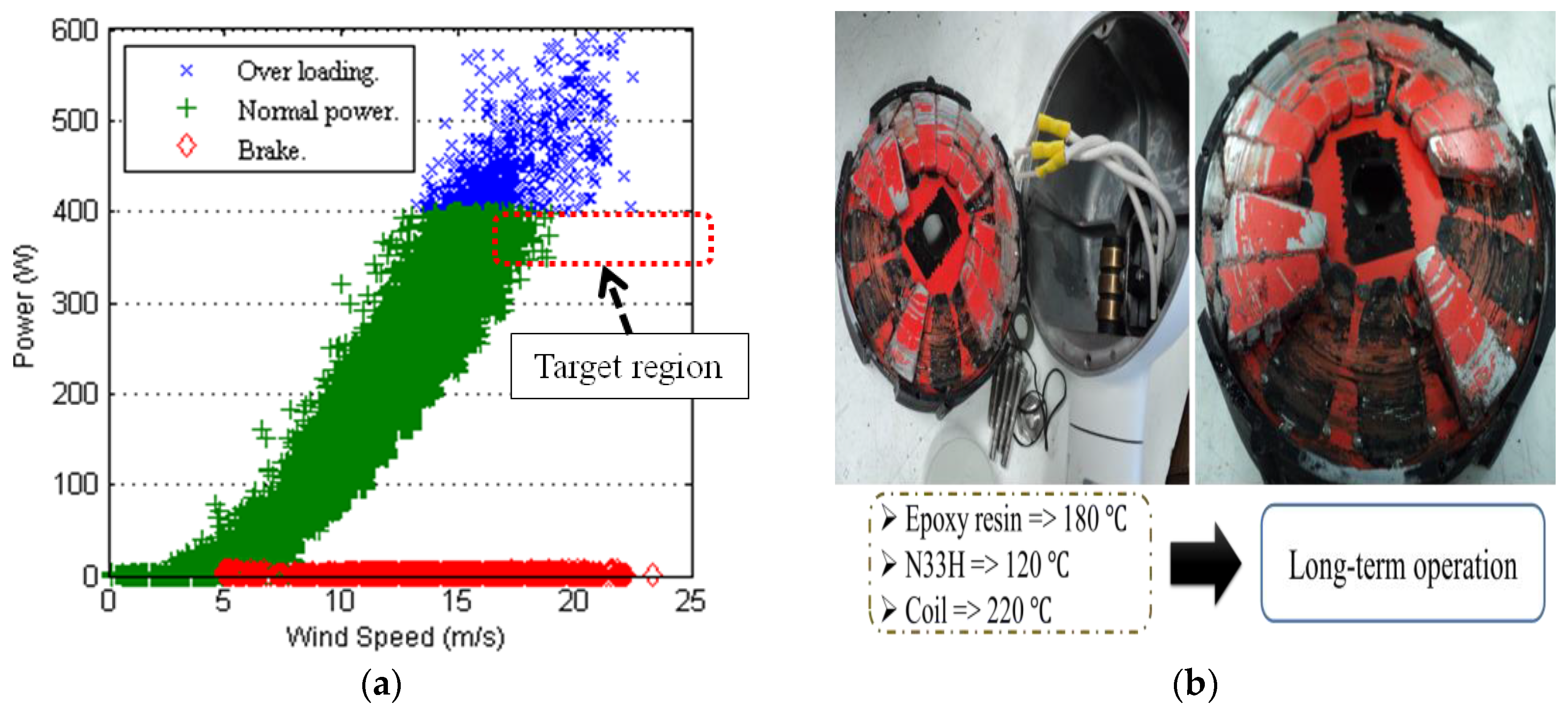
:1. Introduction
2. Blade Modeling by BEMT and Development of GUI Software
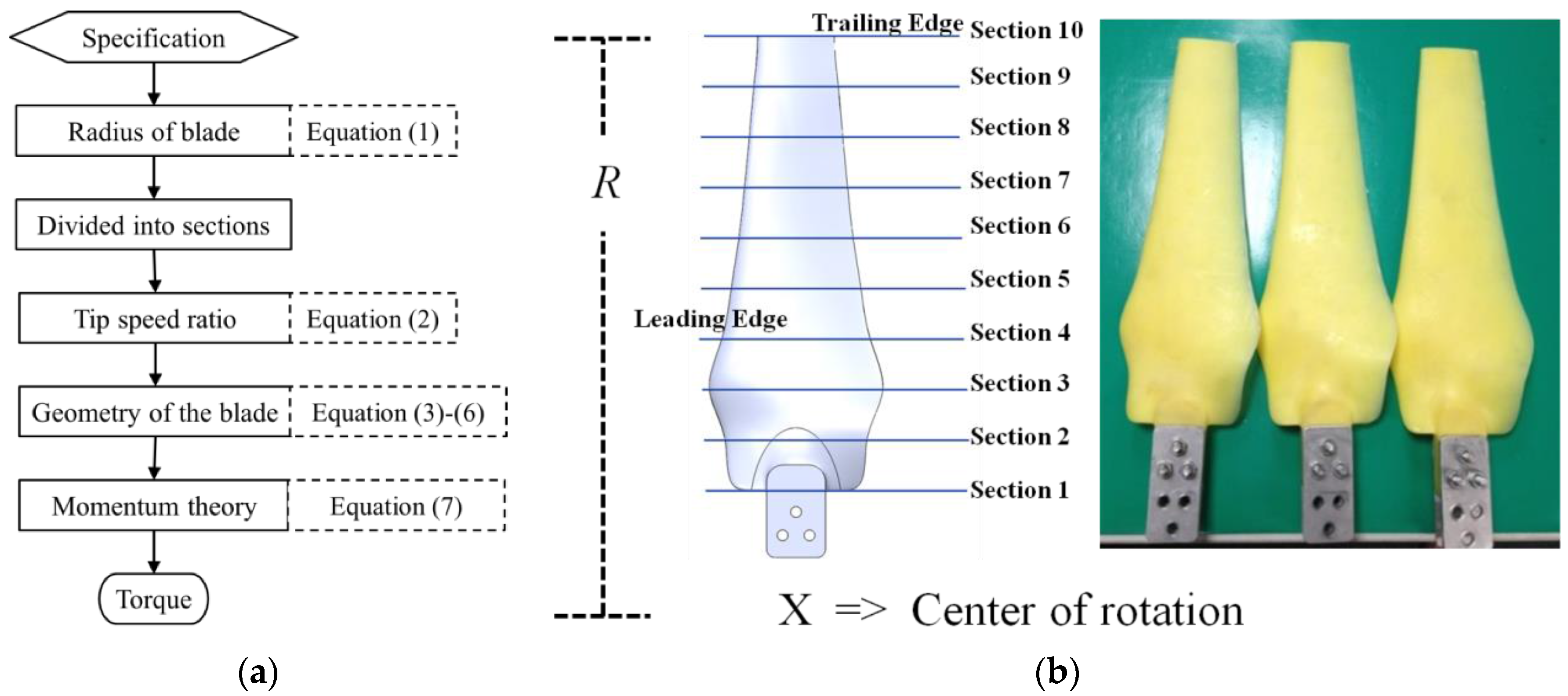
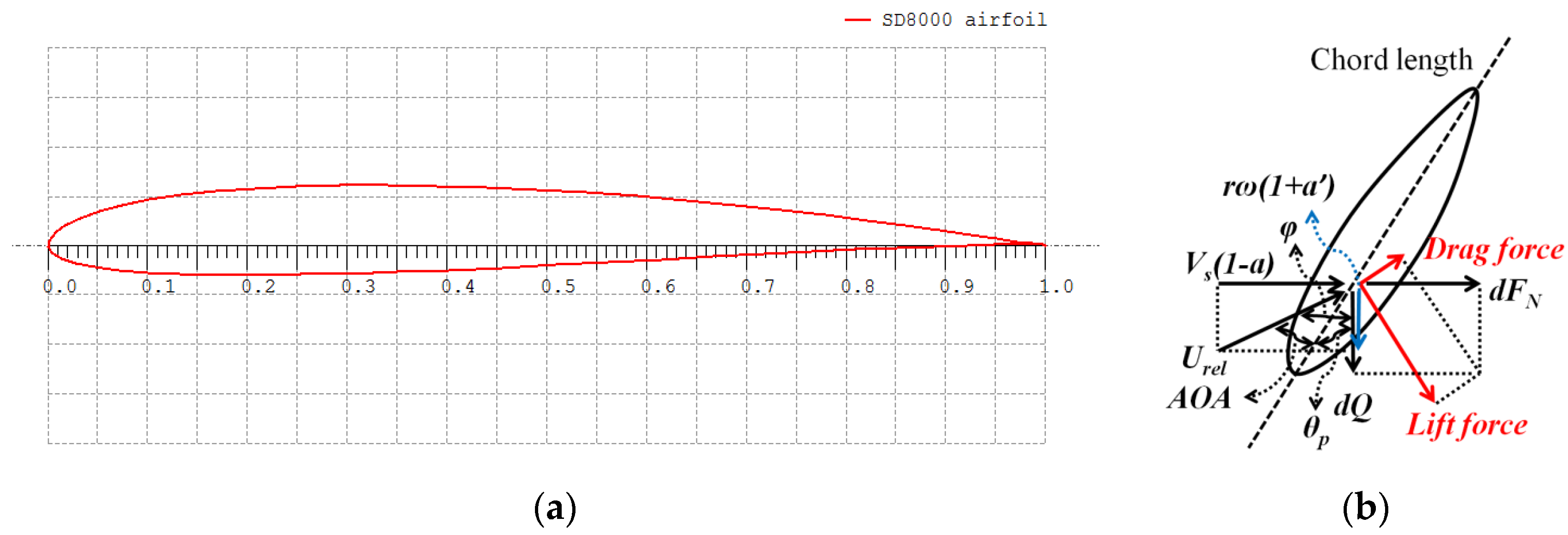
2.1. Theoretical Modeling of Blade Design
2.2. GUI of Blade Performance Development
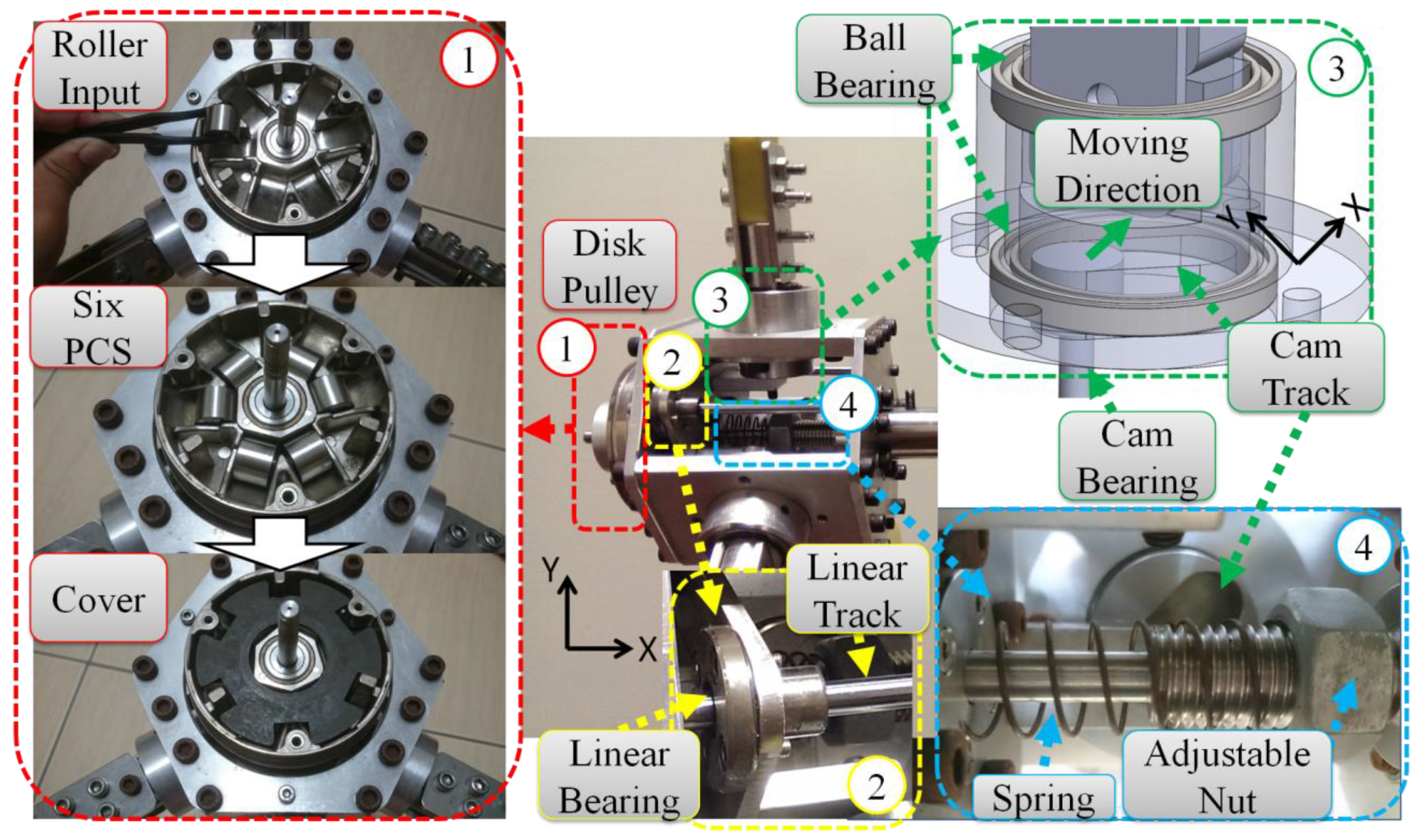
3. Mechanical Design of Pitch Control
3.1. Principle of Motion
3.2. Components Function
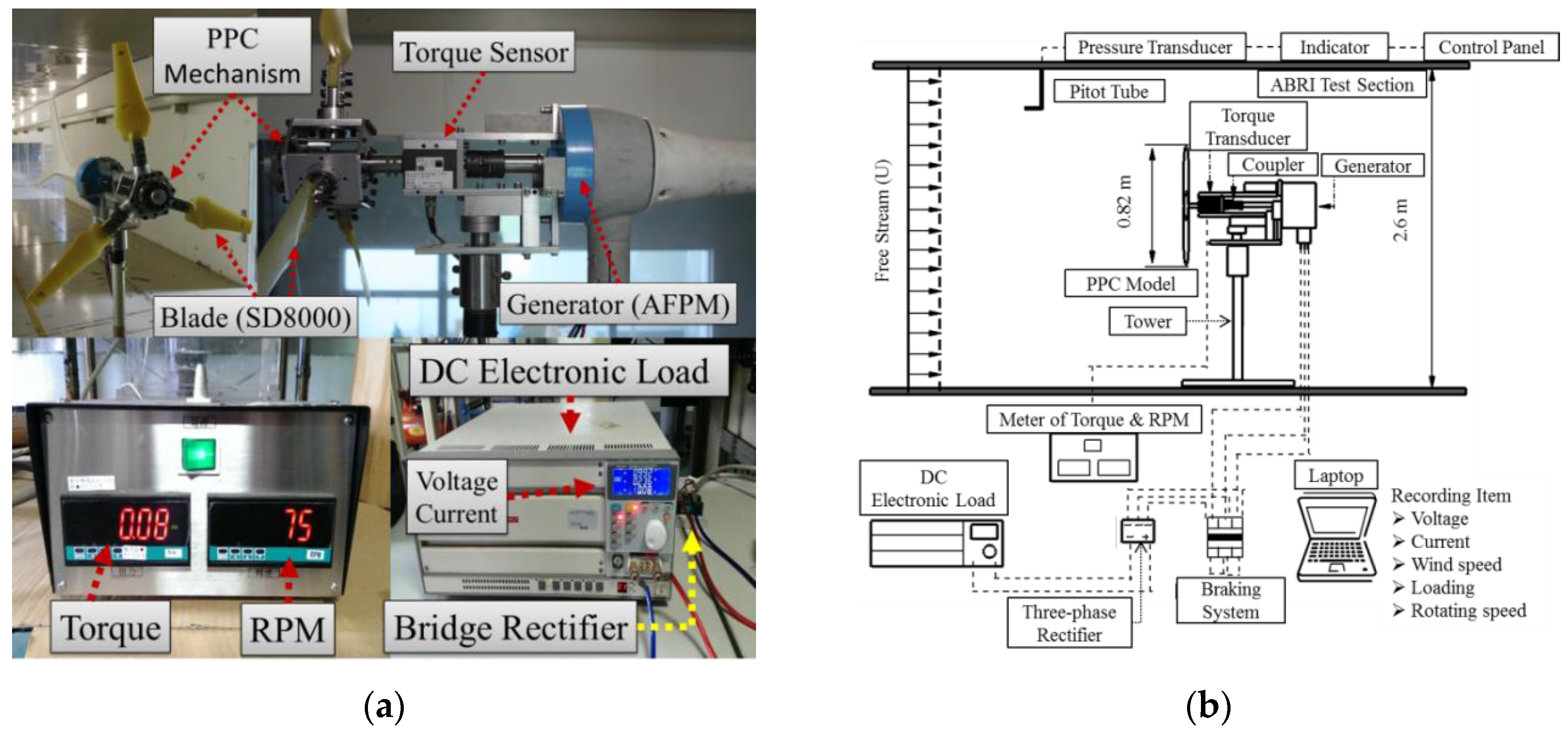
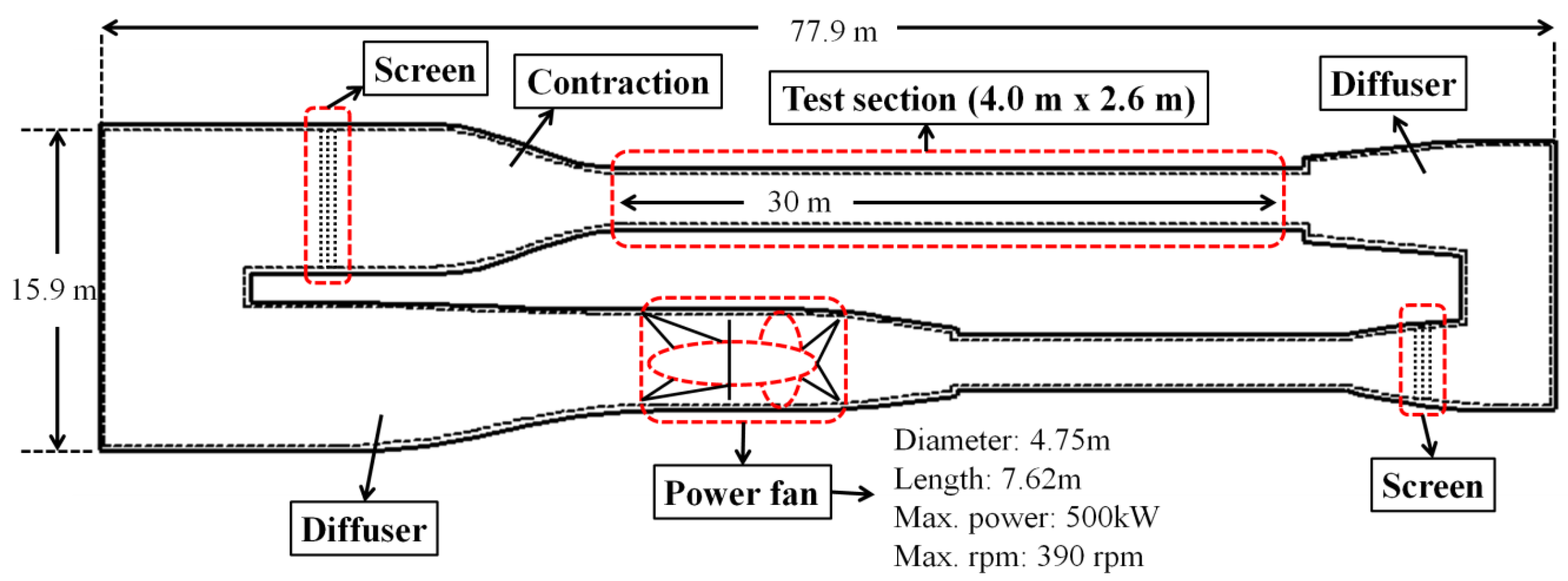
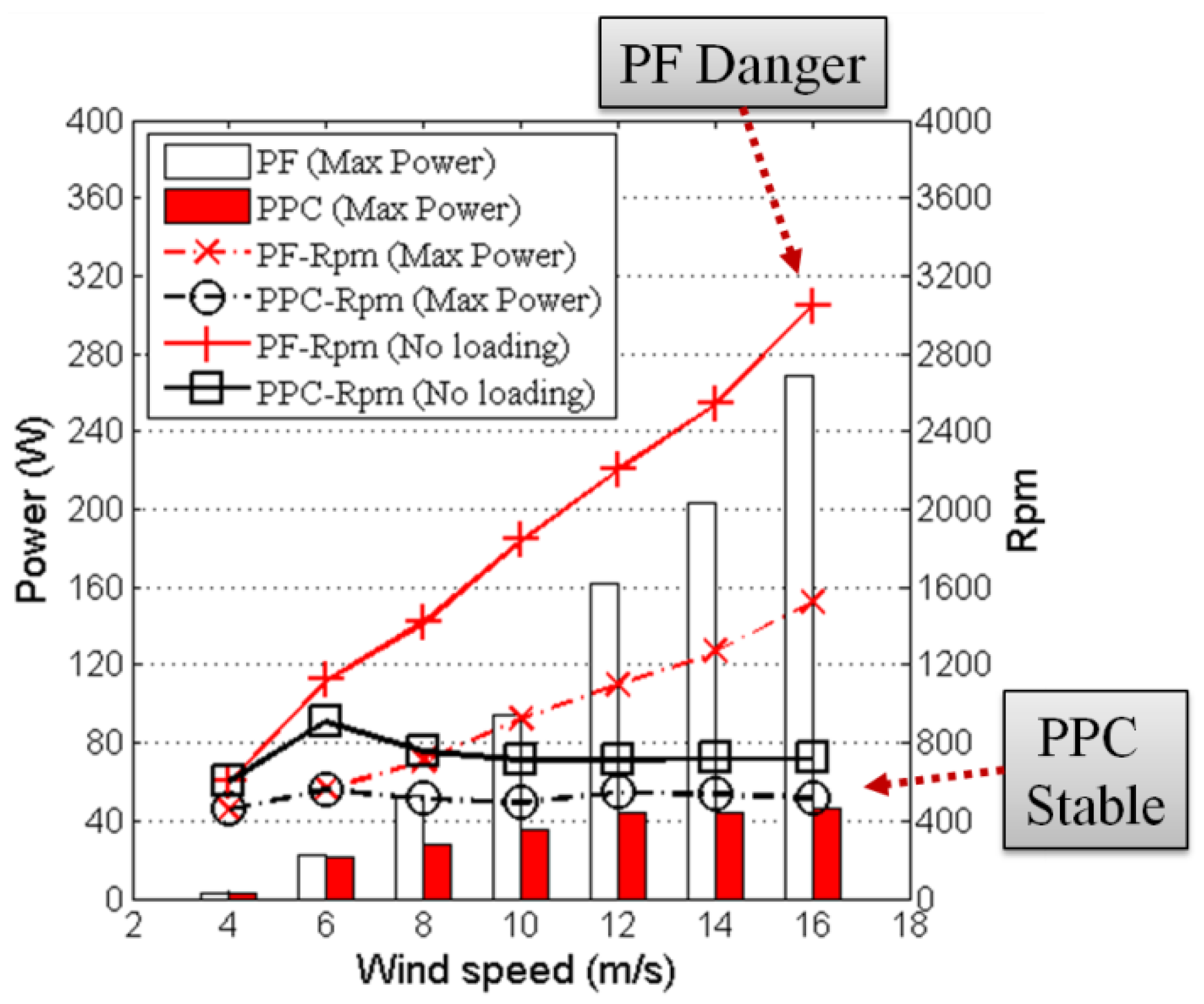
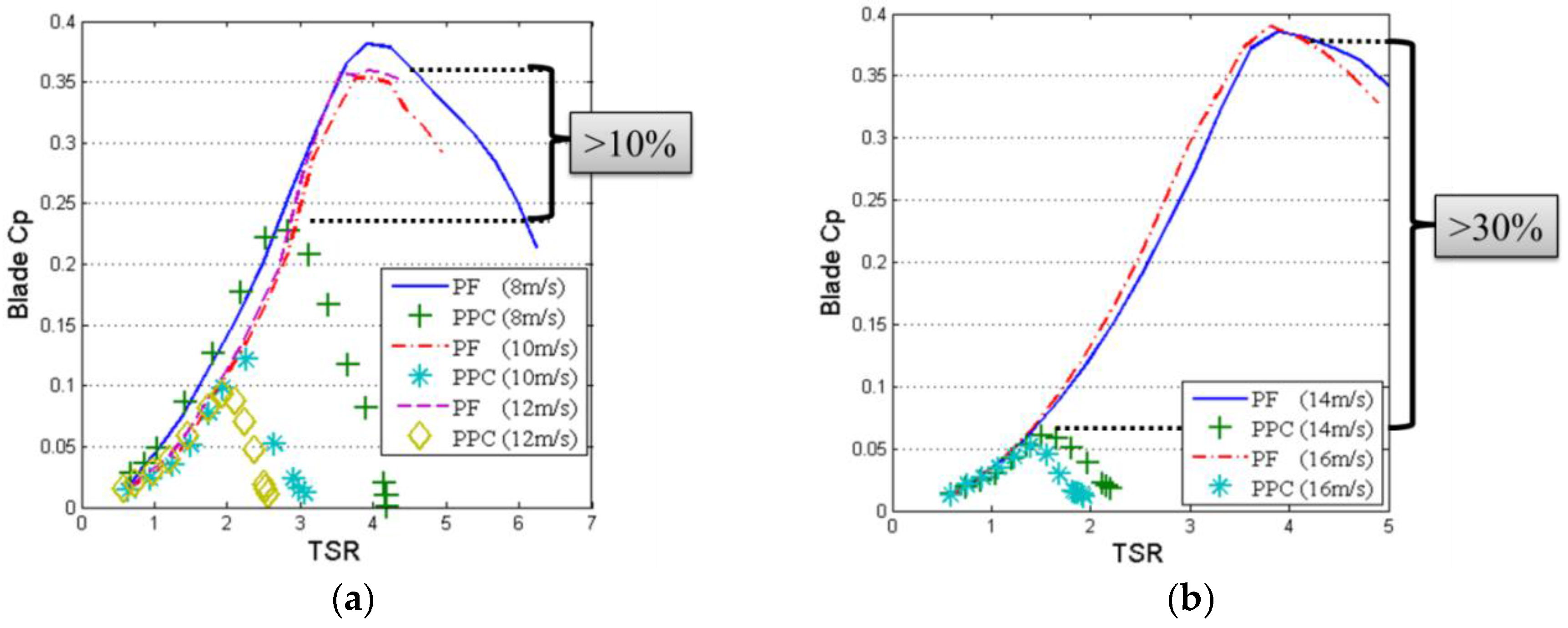
4. Experiment of ABRI Wind Tunnel
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| NCKU | National Cheng Kung University |
| PPC | Passive pitch control |
| PF | Pitch fixed |
References
- Mc Garrigle, E.V.; Leahy, P.G. Quantifying the value of improved wind energy forecasts in a pool-based electricity market. Renew. Energy 2015, 80, 517–524. [Google Scholar] [CrossRef]
- Browne, O.; Poletti, S.; Young, D. How does market power affect the impact of large scale wind investment in “energy only” wholesale electricity markets? Energy Policy 2015, 87, 17–27. [Google Scholar] [CrossRef]
- Gillenwater, M.; Lu, X.; Fischlein, M. Additionality of wind energy investments in the U.S. voluntary green power market. Renew. Energy 2014, 63, 452–457. [Google Scholar] [CrossRef]
- Choudhry, A.; Arjomandi, M.; Kelso, R. Methods to control dynamic stall for wind turbine applications. Renew. Energy 2016, 86, 26–37. [Google Scholar] [CrossRef]
- Choudhry, A.; Leknys, R.; Arjomandi, M.; Kelso, R. An insight into the dynamic stall lift characteristics. Exp. Thermal Fluid Sci. 2014, 58, 188–208. [Google Scholar] [CrossRef]
- Yen, J.; Ahmed, N.A. Enhancing vertical axis wind turbine by dynamic stall control using synthetic jets. J. Wind Eng. Ind. Aerodyn. 2013, 114, 12–17. [Google Scholar] [CrossRef]
- Xie, W.; Zeng, P.; Lei, L.P. A novel folding blade of wind turbine rotor for effective power control. Energy Convers. Manag. 2015, 101, 52–65. [Google Scholar] [CrossRef]
- Xie, W.; Zeng, P.; Lei, L.P. Wind tunnel experiments for innovative pitch regulated blade of horizontal axis wind turbine. Energy 2015, 91, 1070–1080. [Google Scholar] [CrossRef]
- Jauch, C.; Hippel, S. Hydraulic-pneumatic flywheel system in a wind turbine rotor for inertia control. IET Renew. Power Generat. 2016, 10, 33–41. [Google Scholar] [CrossRef]
- Barlas, T.K.; van Wingerden, W.; Hulskamp, A.W.; van Kuik, G.A.M.; Bersee, H.E.N. Smart dynamic rotor control using active flaps on a small-scale wind turbine: Aeroelastic modeling and comparison with wind tunnel measurements. Wind Energy 2013, 16, 1287–1301. [Google Scholar] [CrossRef]
- Kragh, K.A.; Fleming, P.A.; Scholbrock, A.K. Increased Power Capture by Rotor Speed-Dependent Yaw Control of Wind Turbines. J. Sol. Energy Eng. 2013, 135, 031018. [Google Scholar] [CrossRef]
- Ekelund, T. Yaw control for reduction of structural dynamic loads in wind turbines. J. Wind Eng. Ind. Aerodyn. 2000, 85, 241–262. [Google Scholar] [CrossRef]
- Shariatpanah, H.; Fadaeinedjad, R.; Rashidinejad, M. A New Model for PMSG-Based Wind Turbine with Yaw Control. IEEE Trans. Energy Convers. 2013, 28, 929–937. [Google Scholar] [CrossRef]
- Lesic, V.; Vasak, M.; Peric, N.; Wolbank, T.M.; Joksimovic, G. Fault-tolerant Control of a Wind Turbine with a Squirrel-cage Induction Generator and Rotor Bar Defects. Automatika 2013, 54, 316–328. [Google Scholar]
- Lee, J.; Kim, J.; Kim, Y.H.; Chun, Y.H.; Lee, S.H.; Seok, J.K.; Kang, Y.C. Rotor Speed-based Droop of a Wind Generator in a Wind Power Plant for the Virtual Inertial Control. J. Electr. Eng. Technol. 2013, 8, 1021–1028. [Google Scholar] [CrossRef]
- Simley, E.; Pao, L.Y.; Frehlich, R.; Jonkman, B.; Kelley, N. Analysis of light detection and ranging wind speed measurements for wind turbine control. Wind Energy 2014, 17, 413–433. [Google Scholar] [CrossRef]
- Chiang, M.H.; Wang, C.S.; Chen, C.S. Intelligent Pitch Control for a 2MW Wind Turbine. Int. J. Fuzzy Syst. 2012, 14, 89–96. [Google Scholar]
- Li, S.C. Self-powered passive adaptive control of pitch angle and Betz-shaped wind tunnel. In Proceedings of the International Conference on Renewable Energies and Power Quality, Madrid, Spain, 4–6 May 2010.
- Hertel, J.; Nygaard, T.; Duque, E. Passive pitch control of small horizontal axis wind turbines. In Proceedings of the 42nd AIAA Aerospace Sciences Meeting and Exhibit, Aerospace Sciences Meetings, Reno, NV, USA, 5–8 January 2004; pp. 2004–1369.
- Barlow, J.B.; Rae, W.H.; Pope, A. Low-Speed Wind Tunnel Testing, 3rd ed.; Wiley-Interscience: New York, NY, USA, 1999. [Google Scholar]
- Burton, T.; Jenkins, N.; Sharpe, D.; Bossanyi, E. Wind Energy Handbook; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2001. [Google Scholar]
- Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind Energy Explained—Theory, Design and Application; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2002. [Google Scholar]
- Lee, M.-H.; Shiah, Y.C.; Bai, C.-J. Experiments and numerical simulations of the rotor-blade performance for a small-scale horizontal axis wind turbine. J. Wind Eng. Ind. Aerodyn. 2016, 149, 17–29. [Google Scholar] [CrossRef]
- Hsiao, F.B.; Bai, C.J.; Chong, W.T. The Performance Test of Three Different Horizontal Axis Wind Turbine (HAWT) Blade Shapes Using Experimental and Numerical Methods. Energies 2013, 6, 2784–2803. [Google Scholar] [CrossRef]
- Bai, C.J.; Hsiao, F.B.; Li, M.H.; Huang, G.Y.; Chen, Y.J. Design of 10 kW Horizontal-Axis Wind Turbine (HAWT) Blade and Aerodynamic Investigation Using Numerical Simulation. Procedia Eng. 2013, 67, 279–287. [Google Scholar] [CrossRef]

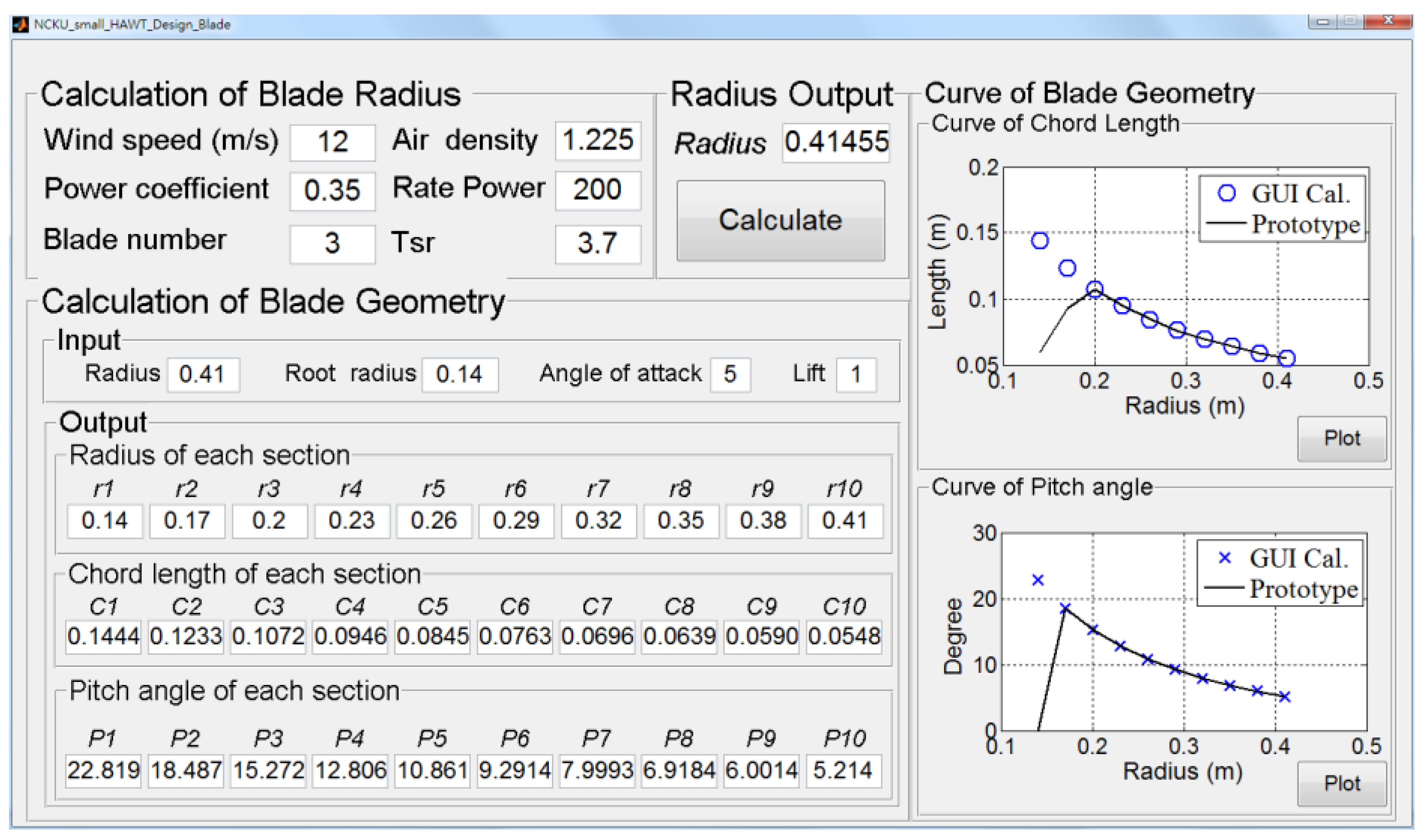
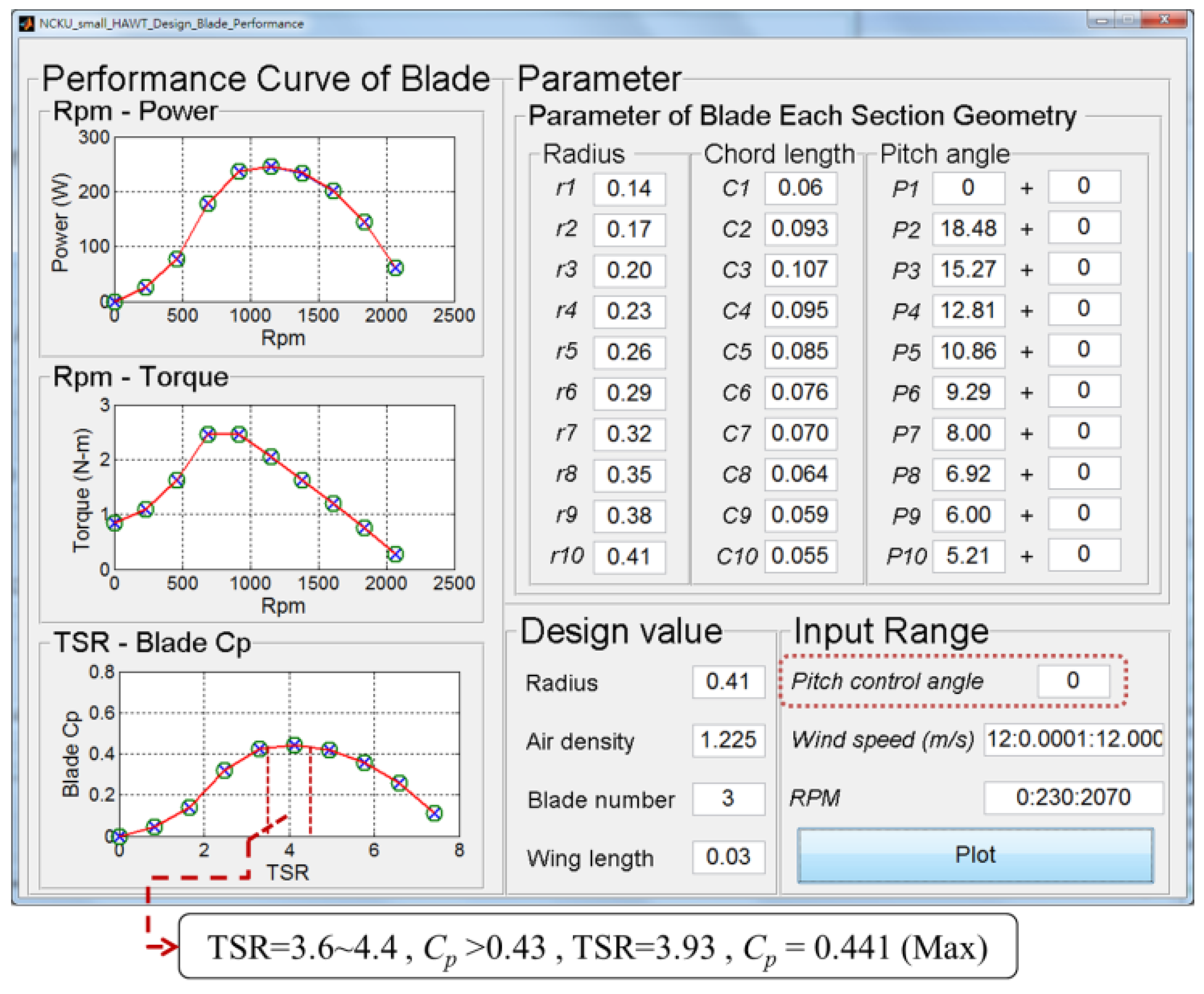
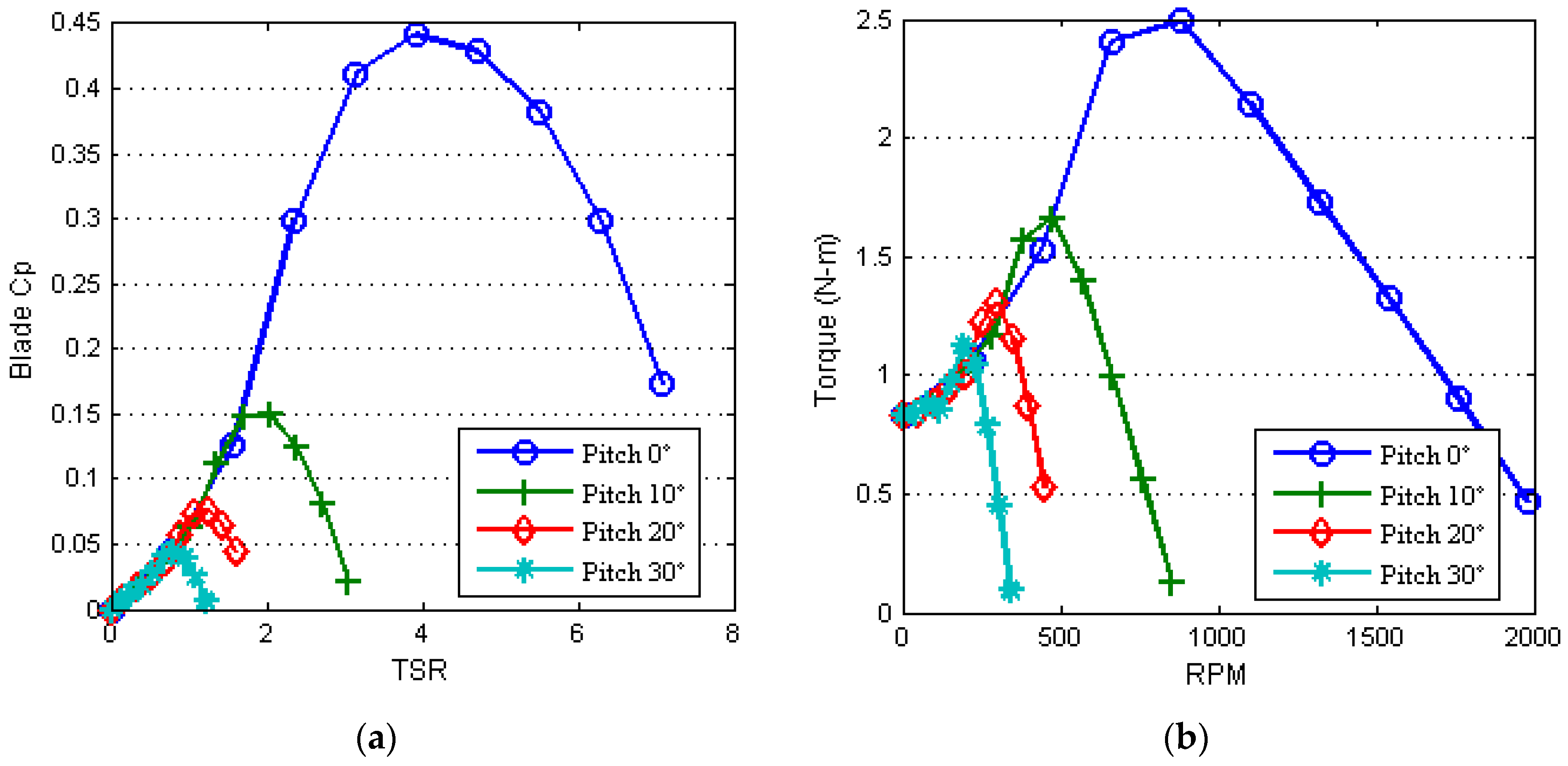
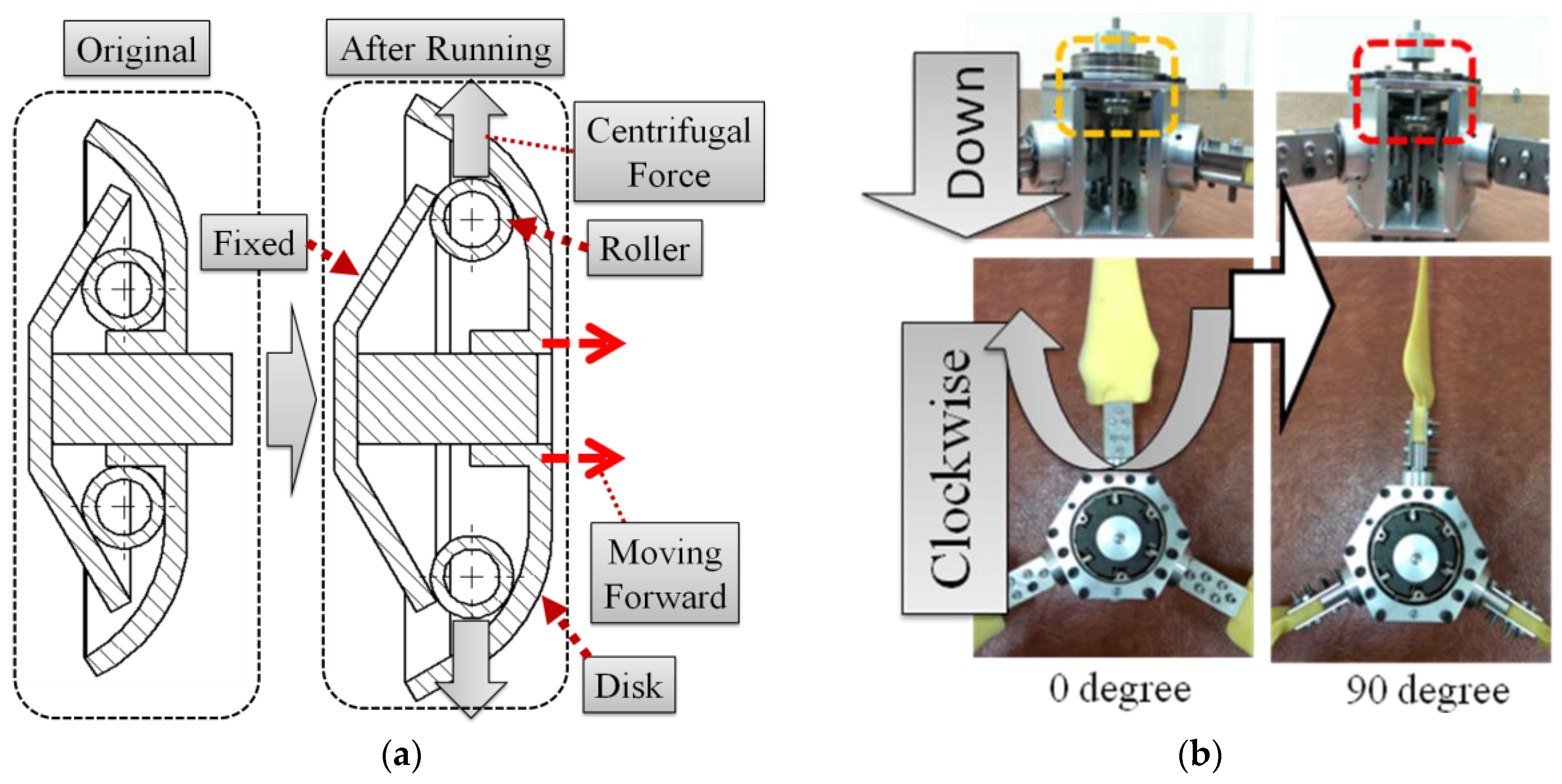
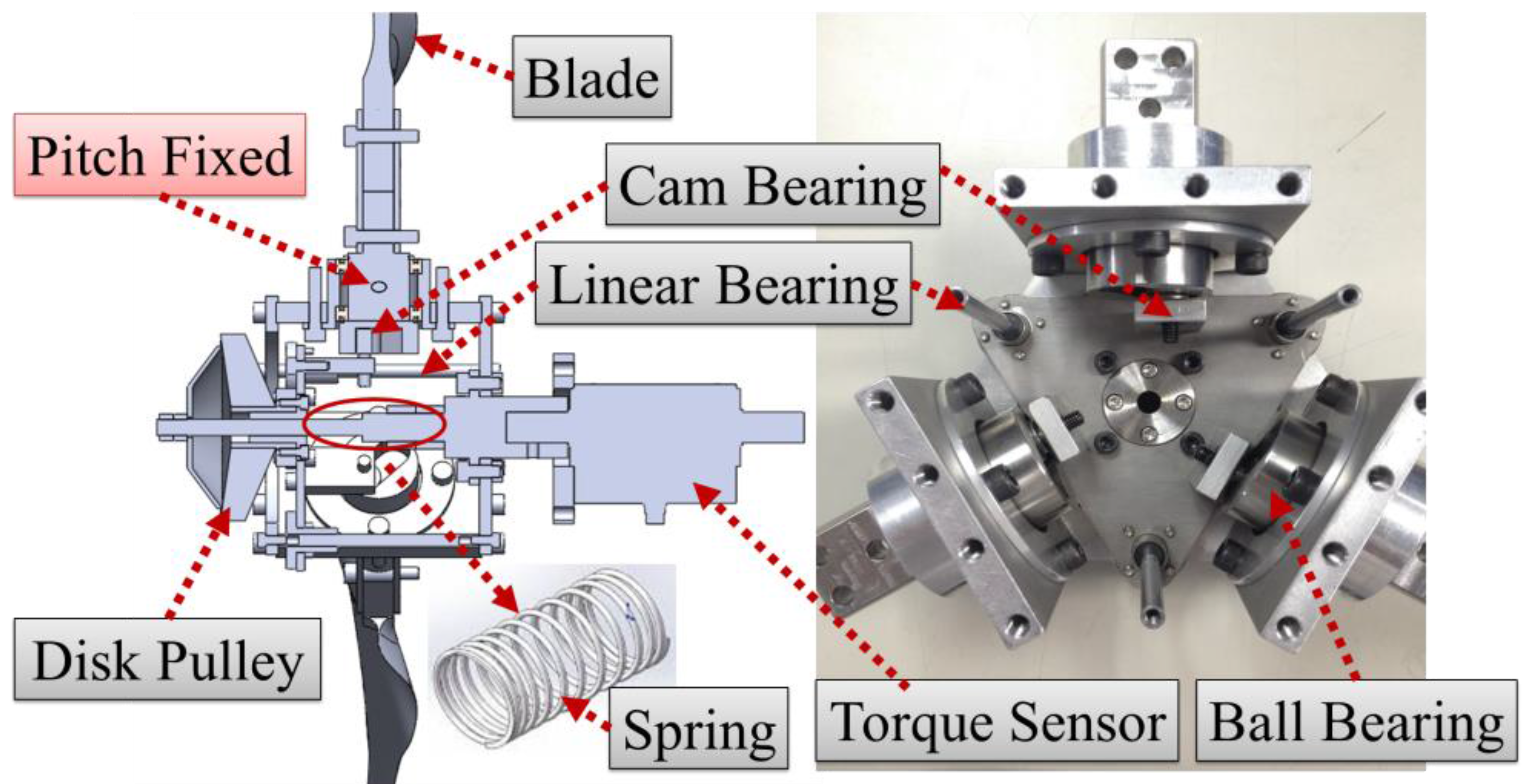
| Item | Parameter | Item | Parameter |
|---|---|---|---|
| ρ | 1.225 (kg·m−3) | R | 0.41 (m) |
| TSR | 3.7 | Root of blade | 0.14 (m) |
| α | 5° | B | 3 |
| Vs | 12 (m/s) | Rated Power | 200 (W) |
| Section | r/R | Chord Length (m) | Pitch Angle (deg) |
|---|---|---|---|
| 1 | 0.341 | 0.06 | 0 |
| 2 | 0.415 | 0.093 | 18.48 |
| 3 | 0.488 | 0.107 | 15.27 |
| 4 | 0.561 | 0.095 | 12.81 |
| 5 | 0.634 | 0.085 | 10.86 |
| 6 | 0.707 | 0.076 | 9.29 |
| 7 | 0.780 | 0.070 | 8.00 |
| 8 | 0.854 | 0.064 | 6.92 |
| 9 | 0.927 | 0.059 | 6.00 |
| 10 | 1.000 | 0.055 | 5.21 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.-J.; Shiah, Y.C. Experiments on the Performance of Small Horizontal Axis Wind Turbine with Passive Pitch Control by Disk Pulley. Energies 2016, 9, 353. https://doi.org/10.3390/en9050353
Chen Y-J, Shiah YC. Experiments on the Performance of Small Horizontal Axis Wind Turbine with Passive Pitch Control by Disk Pulley. Energies. 2016; 9(5):353. https://doi.org/10.3390/en9050353
Chicago/Turabian StyleChen, Yu-Jen, and Y. C. Shiah. 2016. "Experiments on the Performance of Small Horizontal Axis Wind Turbine with Passive Pitch Control by Disk Pulley" Energies 9, no. 5: 353. https://doi.org/10.3390/en9050353
APA StyleChen, Y.-J., & Shiah, Y. C. (2016). Experiments on the Performance of Small Horizontal Axis Wind Turbine with Passive Pitch Control by Disk Pulley. Energies, 9(5), 353. https://doi.org/10.3390/en9050353






