Multi-Objective Predictive Balancing Control of Battery Packs Based on Predictive Current
Abstract
:1. Introduction
2. Predictive Current Control
3. Balancing Control Strategy
3.1. The Analysis of Battery Pack Inconsistency
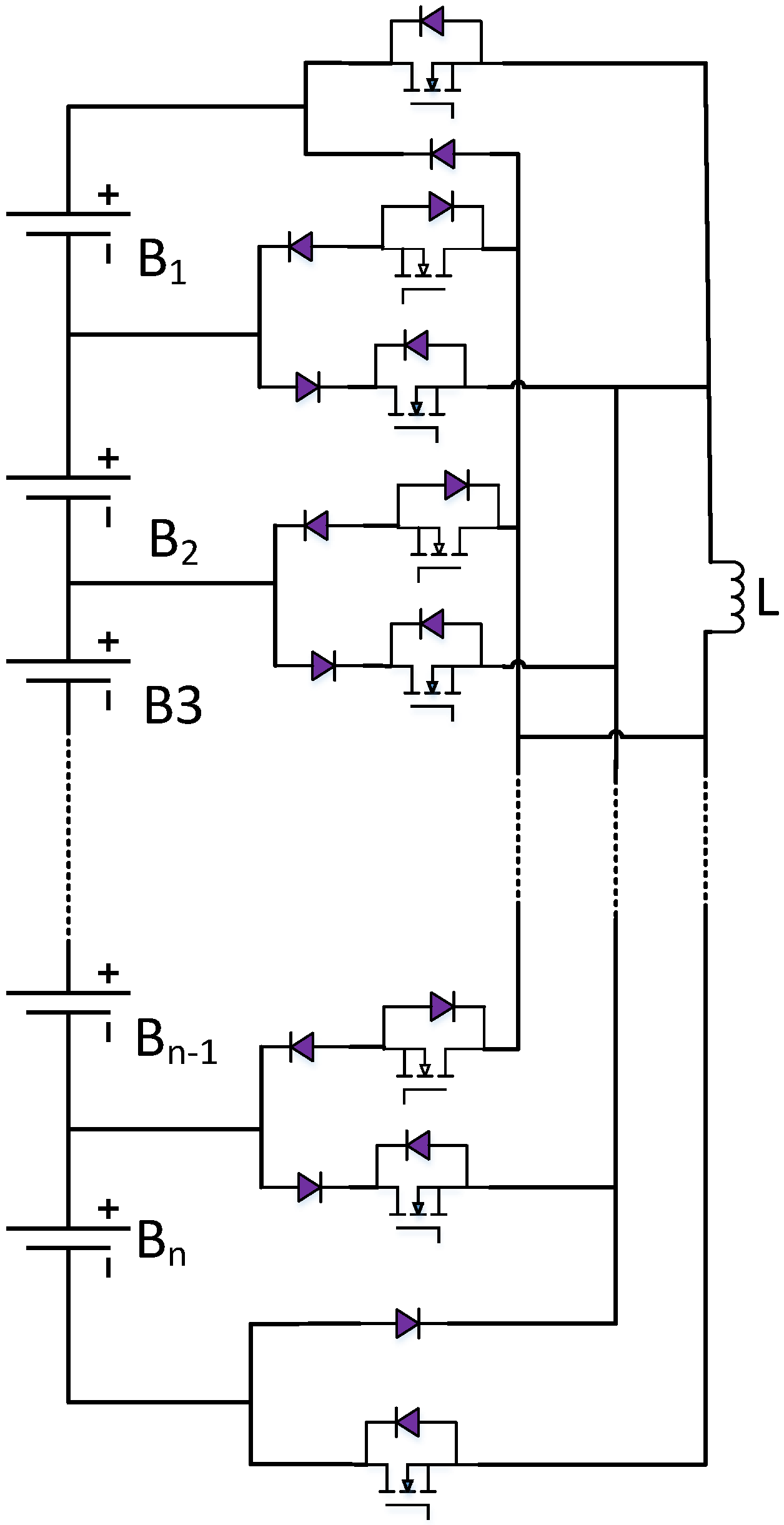
3.2. Battery Pack Balancing Method
3.2.1. Voltage Balancing
3.2.2. SOC Balancing
3.2.3. MOPBC
4. Battery Pack Balancing Control Modelling
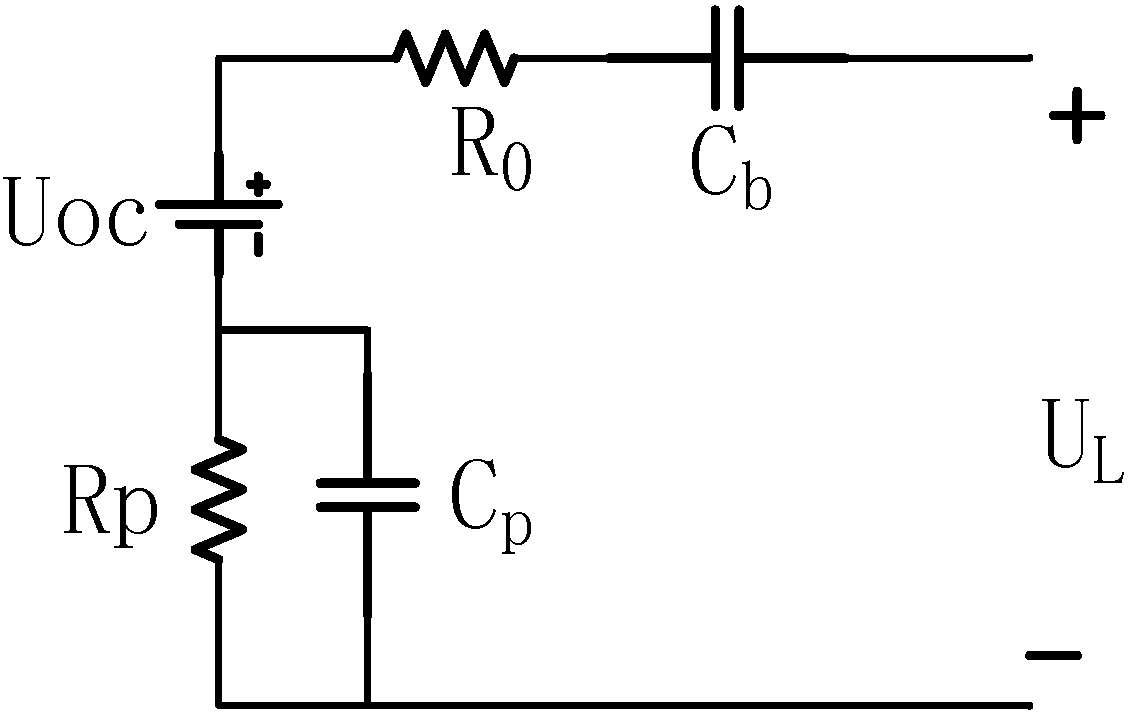
4.1. Battery Parameters Module
4.2. SOC Module
4.3. Temperature Module
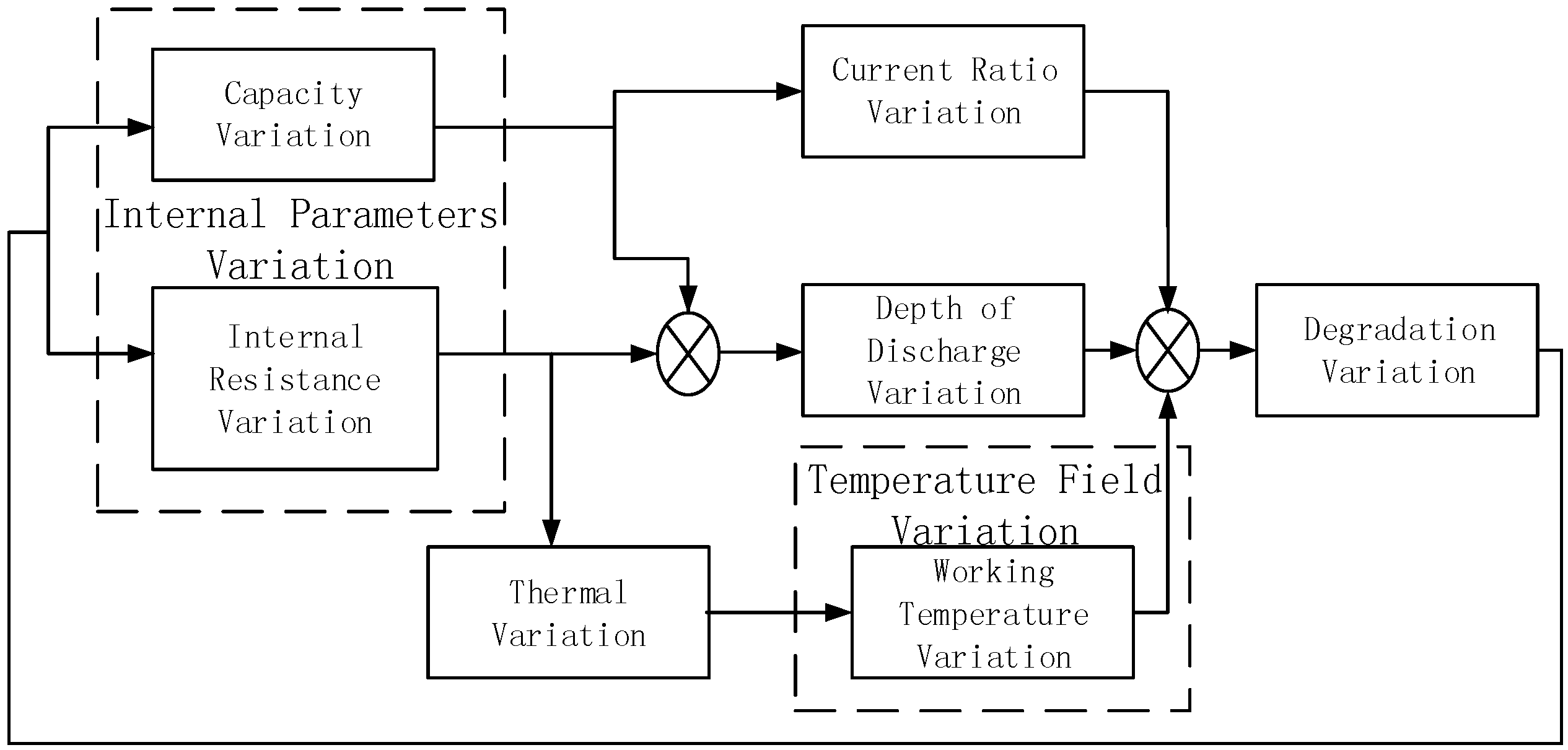
4.4. Degradation Module
4.5. MOPBC
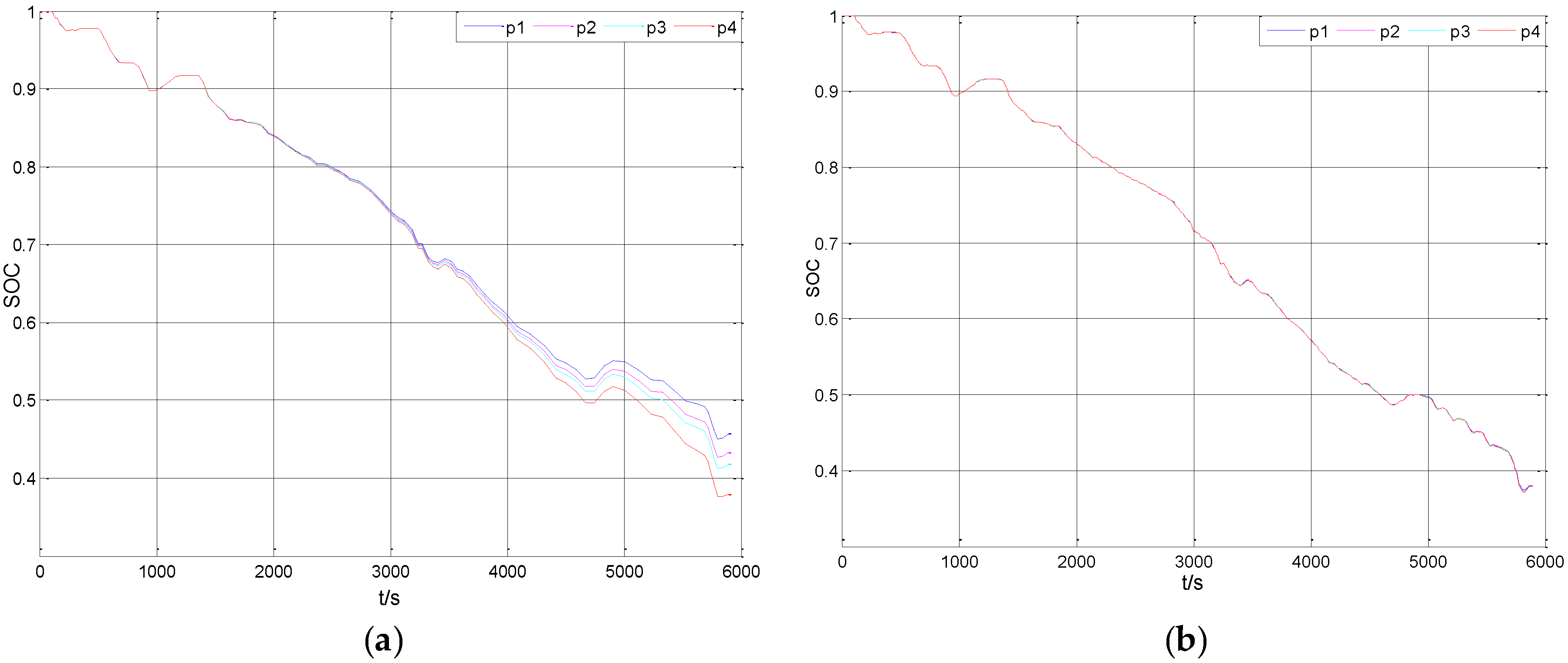
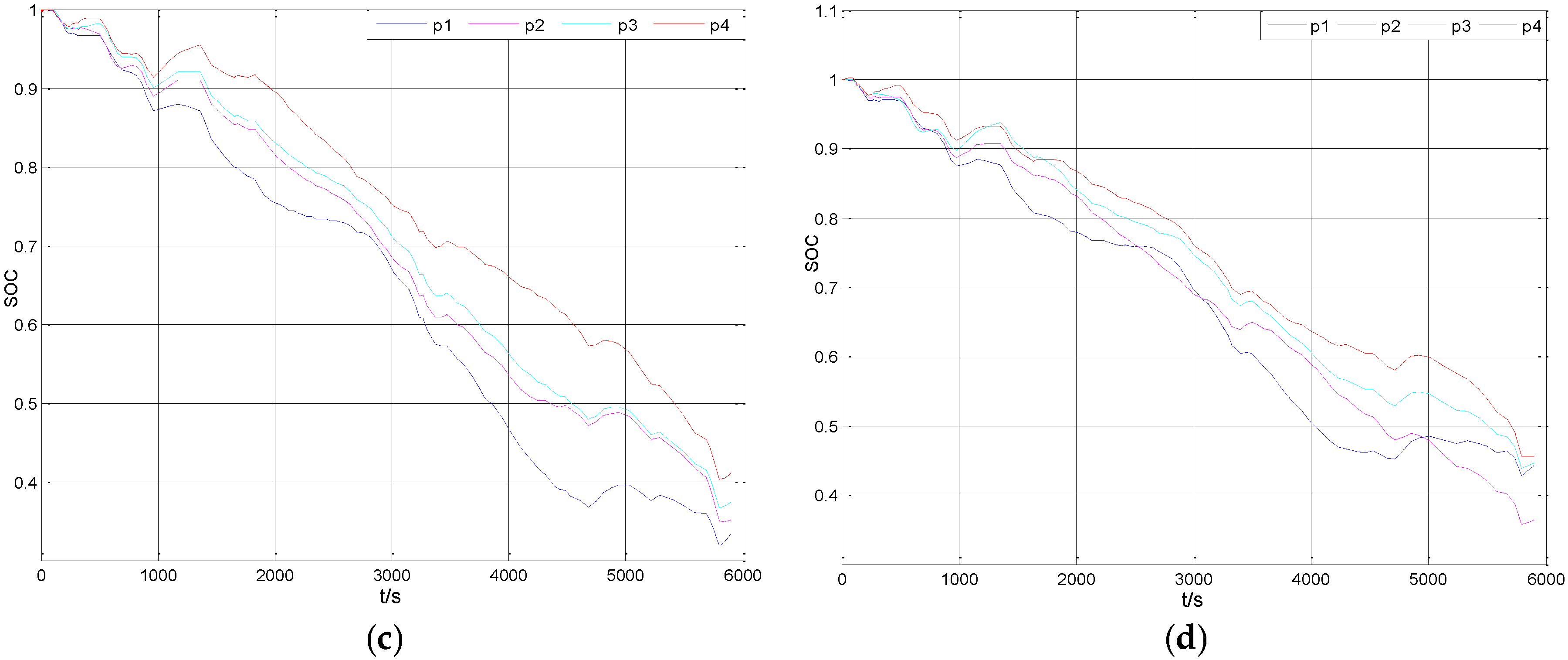
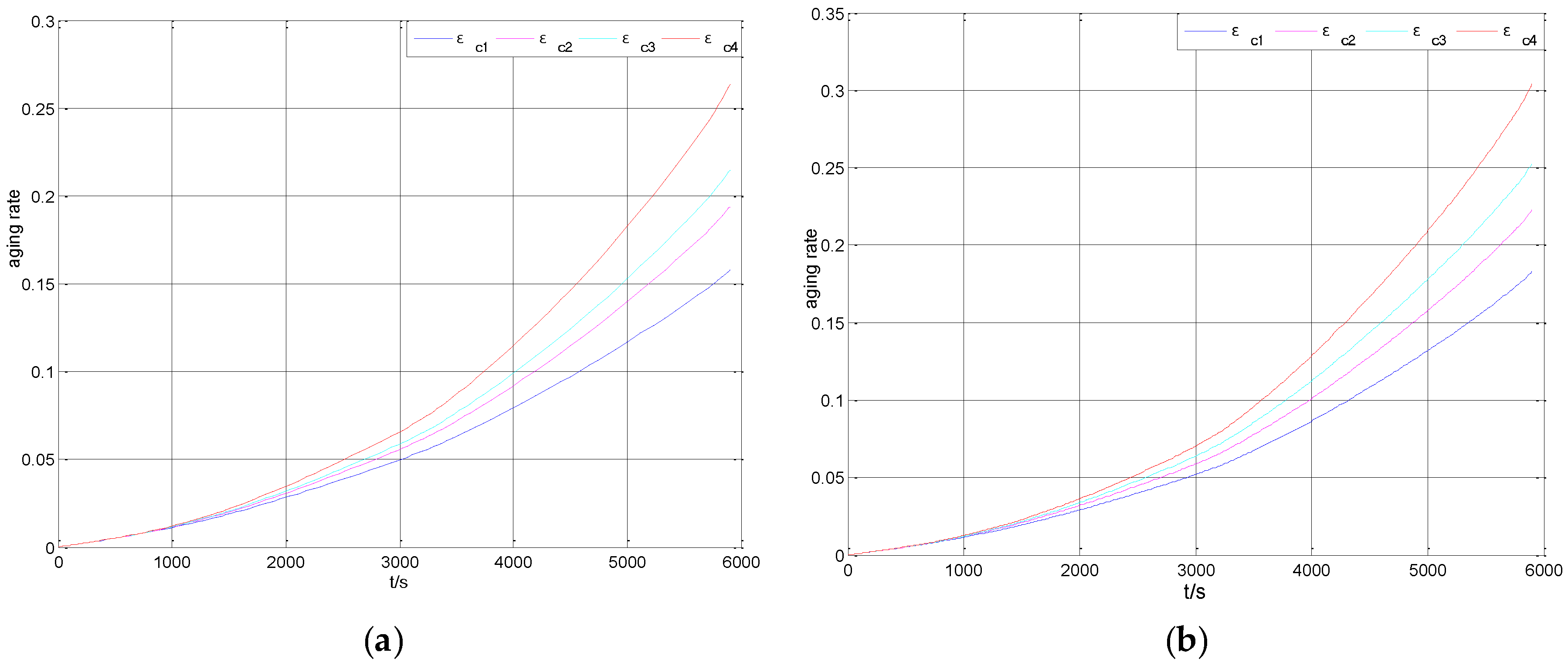
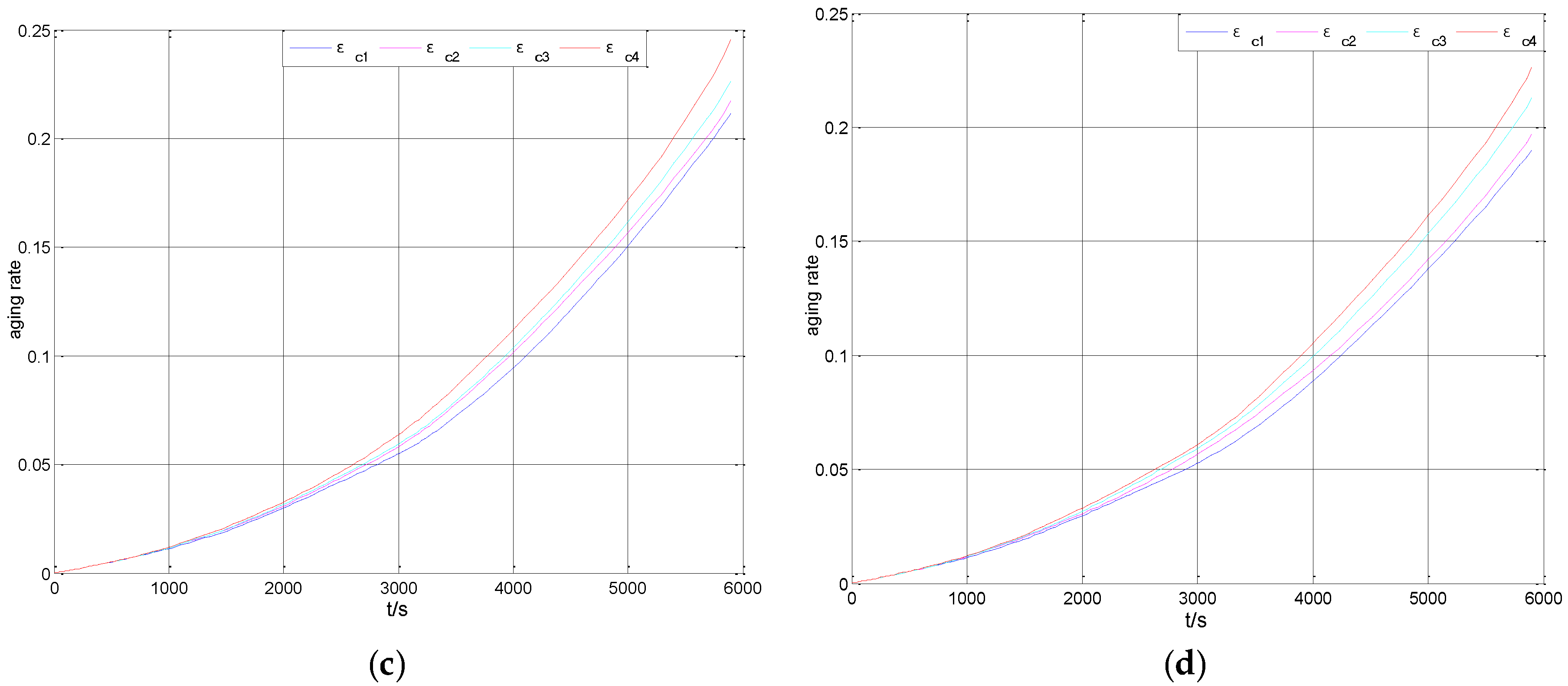
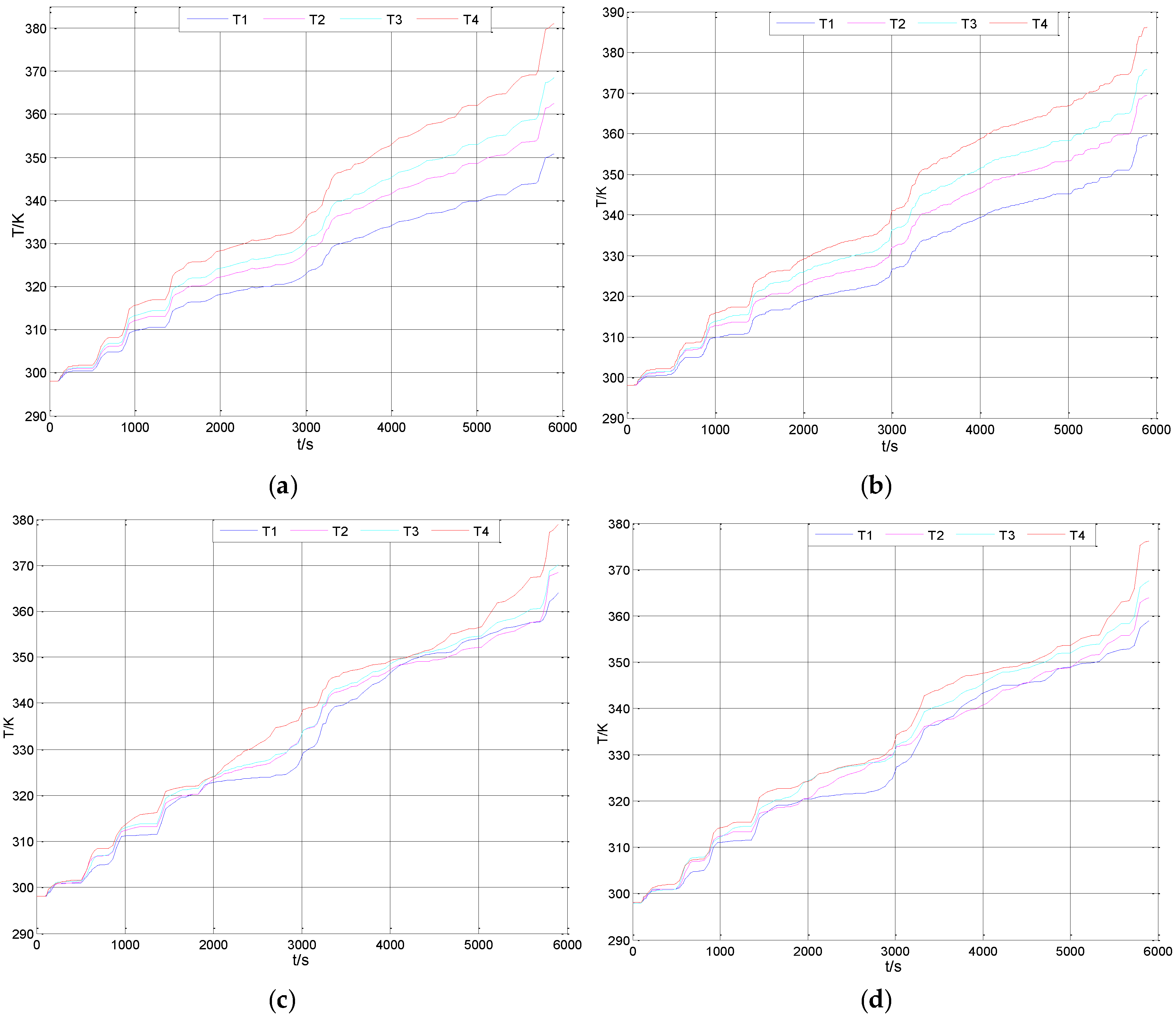
5. The Analysis of the Simulation Results
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Deng, Y.D.; Gao, H.O.; Wang, Z.F. Control strategies of parallel hybrid electric vehicle. J. Eng. J. Wuhan Univ. 2004, 37, 139–144. [Google Scholar]
- Cassani, P.A.; Williamson, S.S. Significance of Battery Cell Equalization and Monitoring for Practical Commercialization of Plug-In Hybrid Electric Vehicles. In Proceedings of the Applied Power Electronics Conference and Exposition, Washington, DC, USA, 15–19 February 2009; pp. 465–471.
- Daowd, M.; Omar, N.; Bossche, P.V.D.; Van Mierlo, J. A Review of Passive and Active Battery Balancing Based on MATLAB/Simulink. J. Int. Rev. Electr. Eng. 2011, 6, 2974–2989. [Google Scholar]
- Zhang, D.H.; Zhu, G.R.; He, S.J.; Qiu, S.; Ma, Y.; Wu, Q.-M.; Chen, W. Balancing Control Strategy for Li-Ion Batteries String Based on Dynamic Balanced Point. Energies 2013, 8, 1–5. [Google Scholar]
- Huang, W.; Abu, Q.J. Energy Sharing Control Scheme for State-of-Charge Balancing of Distributed Battery Energy Storage System. J. IEEE Trans. Ind. Electron. 2015, 62, 2764–2776. [Google Scholar] [CrossRef]
- Kandasamy, K.; Vilathgamuwa, D.M.; Tseng, K.J. Double star chopper cell converter for battery electric vehicles with inter-module SoC balancing and fault tolerant control. In Proceedings of the Industrial Electronics Society, Dallas, TX, USA, 29 October 2014–1 November 2014; pp. 2991–2996.
- Kim, J.H.; Shin, J.W.; Jeon, C.Y.; Cho, B.H. Screening process of Li-Ion series battery pack for improved voltage/SOC balancing. In Proceedings of the Power Electronics Conference (IPEC), Sapporo, Japan, 21–24 June 2010; pp. 1174–1179.
- Maharjan, L.; Inoue, S.; Akagi, H.; Asakura, J. State-of-Charge (SOC)-Balancing Control of a Battery Energy Storage System Based on a Cascade PWM Converter. J. IEEE Trans. Power Electron. 2009, 24, 1628–1636. [Google Scholar] [CrossRef]
- Bonfiglio, C.; Roessler, W. A Cost Optimized Battery Management System with Active Cell Balancing for Lithium Ion Battery Stacks. In Proceedings of Vehicle Power and Propulsion Conference, Dearborn, MI, USA, 7–10 September 2009; pp. 304–309.
- Danielson, C.; Borrelli, F.; Oliver, D.; Anderson, D.; Kuang, M.; Phillips, T. Balancing of battery networks via constrained optimal control. In Proceedings of the American Control Conference (ACC), Montreal, QC, Canada, 27–29 June 2012; pp. 4293–4298.
- Sun, C.; Moura, S.J.; Hu, X.; Hedrick, J.K.; Sun, F. Dynamic Traffic Feedback Data Enabled Energy Management in Plug-in Hybrid Electric Vehicles. J. Control Syst. Technol. 2015, 23, 1075–1086. [Google Scholar]
- He, Y.; Rios, J.; Chowdhury, M.; Bhavsar, P. Forward power-train energy management modeling for assessing benefits of integrating predictive traffic data into plug-in-hybrid electric vehicles. J. Transp. Res. D Trans. Environ. 2012, 17, 201–207. [Google Scholar] [CrossRef]
- Sun, C.; Hu, X.; Moura, S.J.; Sun, F. Velocity Predictors for Predictive Energy Management in Hybrid Electric Vehicles. J. IEEE Trans. Control Syst. Technol. 2015, 23, 1197–1204. [Google Scholar]
- Shu, H.; Gao, Y.P.; Yang, W.; Jiang, Y. Study on Predictive Control of Fuel Economy for Medium HEVs. J. Highw. Transp. Res. Dev. 2009, 26, 149–153. [Google Scholar]
- Li, N.; Bai, K.; Chen, H.; Liu, P.; Niu, H. Summary of Equalization for LiFePO4 Li-ion Batteries. J. North China Electr. Power 2012, 2, 60–65. [Google Scholar]
- Wang, Z.P.; Sun, F.C.; Lin, C. An Analysis on the Influence of Inconsistencies upon the Service Life of Power Battery Packs. J. Trans. Beijing Inst. Technol. 2006, 26, 577–580. [Google Scholar]
- Ma, Y.L.; Chen, Q.S. Research on the Inequality of Lead Acid Batteries and Equalizing Charge. J. Wuhan Unive. Sci. Technol. (Nat. Sci. Ed.). 2001, 24, 48–51. [Google Scholar]
- Gao, L.J.; Liu, S.Y.; Dougal, R.A. Dynamic Lithium-Ion Battery Model For System Simulation. IEEE Trans. J. Compon. Packag. Technol. 2002, 25, 495–505. [Google Scholar]
- Tian, H.L. Modeling of Capacity Decline and Research of Performance Prediction of Lithium-Ion Battery Pack. Master’s Thesis, Beijing Institute of Technology, Beijing, China, 2015. [Google Scholar]
| Variable | Symbol | Value | Unit |
|---|---|---|---|
| Rated voltage | Vb | 3.7 | V |
| Rated capacity | CE | 10 | Ah |
| Initial SOC | SOCinit | 1, 1, 1, 1 | - |
| Initial resistance | R | 1, 1.2, 1.3, 1.5 | m |
| The average balancing current | Iave | 1.8 | A |
| Switching frequency | fs | 10 | kHz |
| Battery mass | m | 1.2 | Kg |
| Specific heat | cp | 0.9 | J/(kg·K) |
| External surface area | S | 0.046 | m2 |
| Ambient temperature | Ta | 298 | K |
| Balancing weight | 0.8410, 0.0118, 0.1472 | - | |
| Coulombic efficiency | η | 1 | - |
| Compensation coefficient | 1 | - | |
| Forecast period | tf | 0.5 | s |
| Non-Balancing | B1 | B2 | B3 | B4 | ∆max | ∆ave |
|---|---|---|---|---|---|---|
| SOC | 0.4572 | 0.4329 | 0.4178 | 0.3794 | 0.0778 | 0.4218 |
| Temperature (K) | 350.790 | 362.427 | 368.469 | 381.101 | 30.311 | 365.697 |
| Degradation Rate | 0.1576 | 0.1937 | 0.2146 | 0.2633 | 0.1057 | 0.2037 |
| SOC Balancing | B1 | B2 | B3 | B4 | ∆max | ∆ave |
| SOC | 0.3798 | 0.3787 | 0.3790 | 0.3787 | 0.0011 | 0.3791 |
| Temperature (K) | 359.583 | 369.408 | 375.760 | 386.239 | 26.656 | 372.748 |
| Degradation Rate | 0.1831 | 0.2229 | 0.2527 | 0.3040 | 0.1209 | 0.2407 |
| Multi-Objective Balancing | B1 | B2 | B3 | B4 | ∆max | ∆ave |
| SOC | 0.3330 | 0.3510 | 0.3740 | 0.4097 | 0.0767 | 0.3669 |
| Temperature (K) | 363.989 | 368.350 | 370.136 | 378.822 | 14.833 | 370.324 |
| Degradation Rate | 0.2116 | 0.2172 | 0.2264 | 0.2454 | 0.0338 | 0.2252 |
| MOPBC | B1 | B2 | B3 | B4 | ∆max | ∆ave |
| SOC | 0.4430 | 0.3640 | 0.4463 | 0.4555 | 0.0915 | 0.4272 |
| Temperature (K) | 358.974 | 363.955 | 367.471 | 376.182 | 17.208 | 366.646 |
| Degradation Rate | 0.1901 | 0.1971 | 0.2127 | 0.2265 | 0.0364 | 0.2066 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Kang, L.; Guo, X.; Yao, Y. Multi-Objective Predictive Balancing Control of Battery Packs Based on Predictive Current. Energies 2016, 9, 298. https://doi.org/10.3390/en9040298
Li W, Kang L, Guo X, Yao Y. Multi-Objective Predictive Balancing Control of Battery Packs Based on Predictive Current. Energies. 2016; 9(4):298. https://doi.org/10.3390/en9040298
Chicago/Turabian StyleLi, Wenbiao, Longyun Kang, Xiangwei Guo, and Yuan Yao. 2016. "Multi-Objective Predictive Balancing Control of Battery Packs Based on Predictive Current" Energies 9, no. 4: 298. https://doi.org/10.3390/en9040298
APA StyleLi, W., Kang, L., Guo, X., & Yao, Y. (2016). Multi-Objective Predictive Balancing Control of Battery Packs Based on Predictive Current. Energies, 9(4), 298. https://doi.org/10.3390/en9040298





