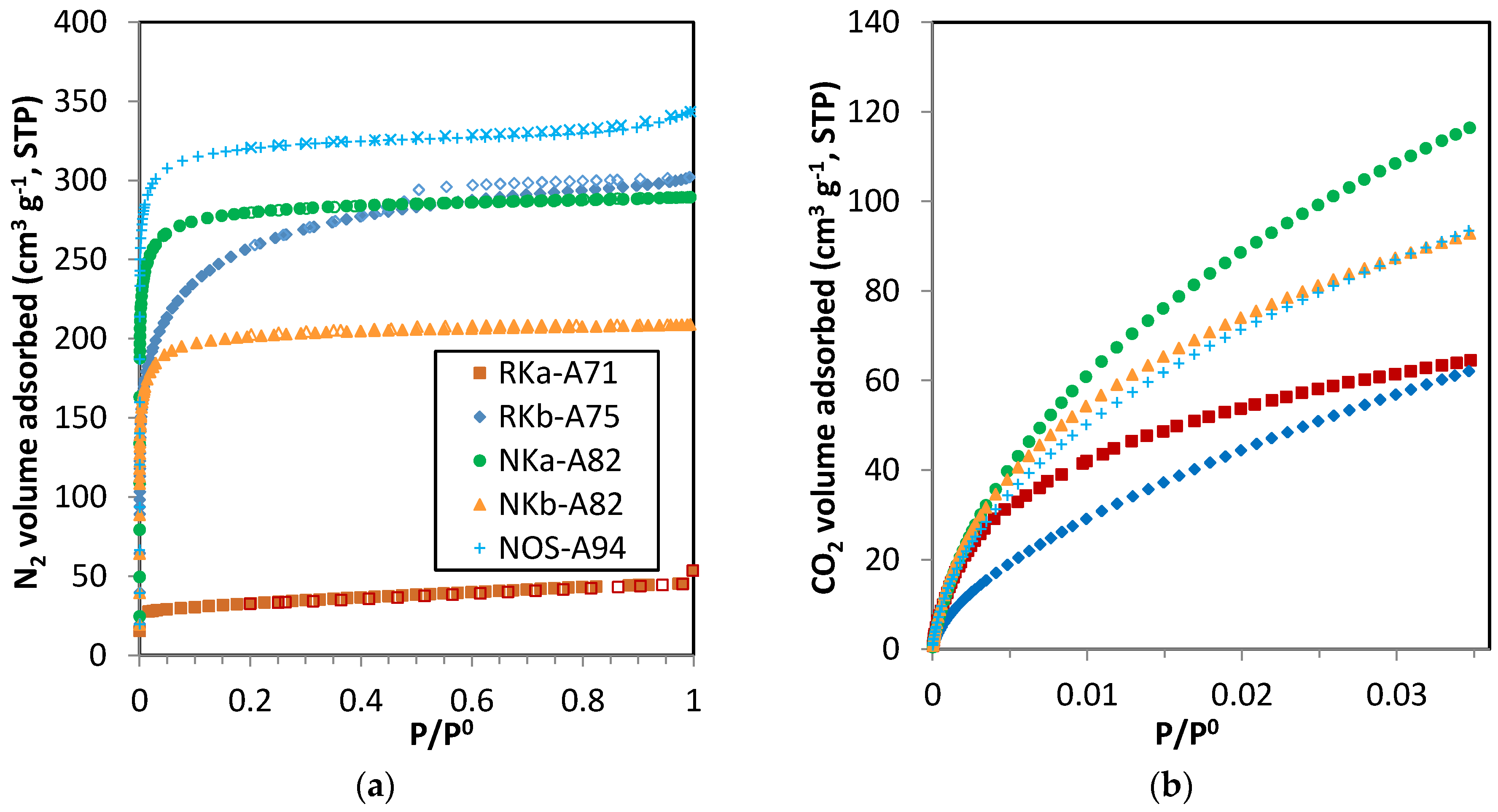
3.3.1. Single-Component Adsorption Isotherms
H
2, CH
4, and N
2 adsorption isotherms at 25 °C and sub-atmospheric pressures (up to 100.3 kPa) for the NK and NOS carbons were obtained using a Micromeritics TriStar 3000 volumetric equipment. BPL was also tested for comparison purposes. Detailed textural characteristics of this activated carbon can be found elsewhere [
27]. Prior to analysis the samples were outgassed overnight at 100 °C under vacuum.
Experimental data of the single component CO
2, H
2, CH
4, and N
2 adsorption isotherms were fitted to the Sips equation, as follows:
where
q represents the concentration of the adsorbed species,
qs the saturation capacity and
P the pressure of the adsorptive. The parameters
b,
n and
qs are temperature dependent;
b usually takes the form of the adsorption affinity. The parameter
n shows the heterogeneity of the system and its value is usually greater than unity; therefore, the larger the value of
n, the more heterogeneous the system is.
This empirical three-parameter equation has been widely used for fitting the isotherm data of different hydrocarbons on activated carbon. The Sips equation is believed to give a more accurate fit over a larger pressure regime than the standard Langmuir or Freundlich equations, and provides more accurate prediction of the quantity adsorbed at saturation than the Langmuir equation for heterogeneous adsorbents. However, it suffers from the same disadvantage as the Freundlich equation: it does not reduce to Henry’s Law at low surface coverage [
28].
Fitting of the model to the experimental data was conducted by means of the
Solver Excel tool (Microsoft Office Excel 2010) departing from values of
qs and
n of 1 and
b of 0. The goodness of the fit was evaluated on the basis of the minimum squared relative error (SRE) as given by the following expression:
where
qexp,i and
qmod,i are the experimental and Sips-predicted adsorbed amounts of component
i, respectively, and
N is the number of experimental data points. The optimal parameters and squared relative errors from fitting the Sips model to the single-component data of CO
2, H
2, CH
4, and N
2 at 25 °C are summarized in
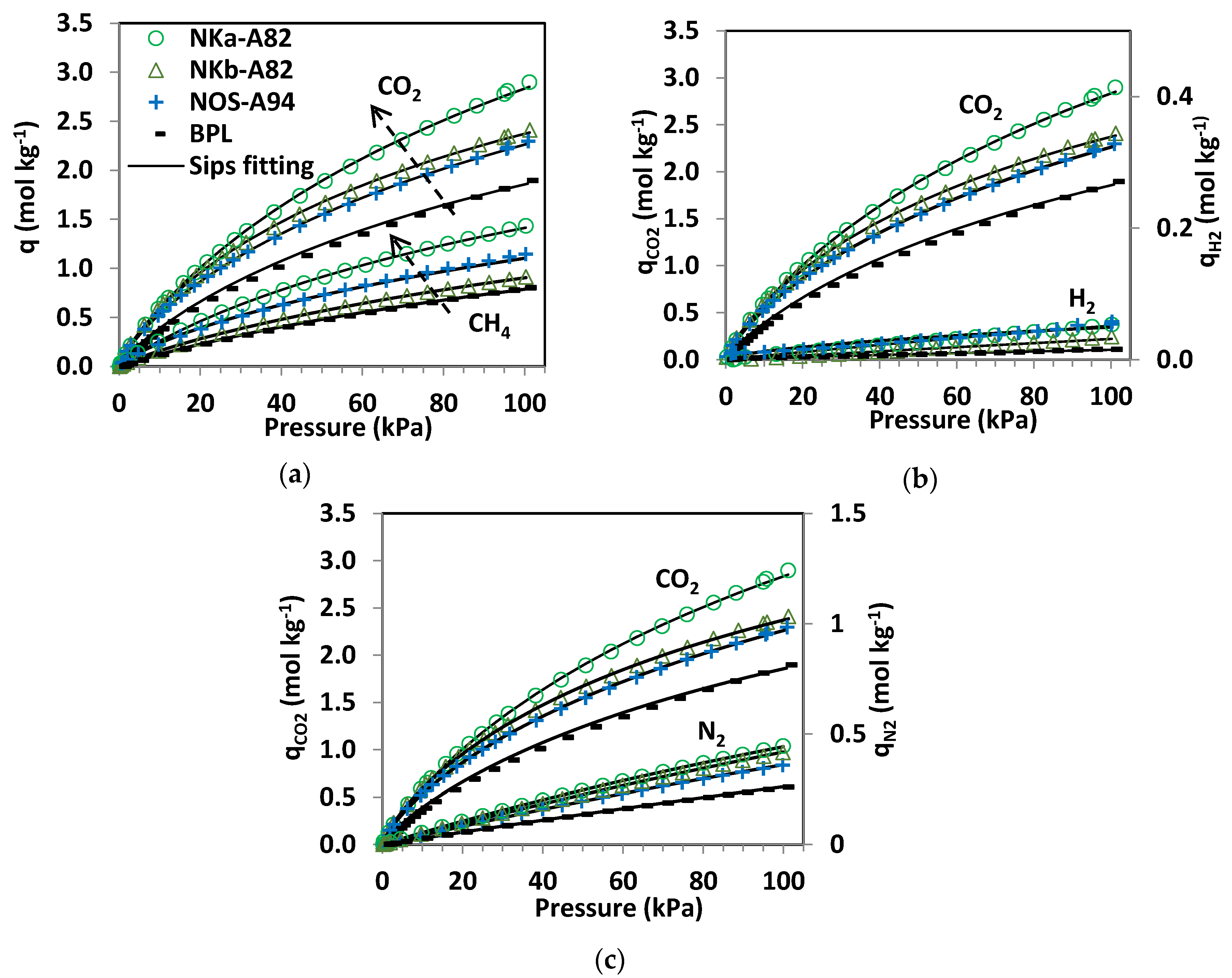
Table 5. Isotherm experimental data and fittings to the Sips model are shown in
Figure 4.
The experimental adsorption data show that much more CO
2 is adsorbed than CH
4 and more significantly than N
2 and H
2 on the tested carbons. The differences in CO
2, CH
4 and N
2 uptake may be explained by the larger quadrupole moment of CO
2 that produces a strong attraction towards the adsorbent surface resulting in a greater uptake. The high level of polarizability of CO
2 and CH
4 can create a momentary shift in its neutral electrostatic field but this attraction force is much weaker than the quadrupole moment [
29]. In contrast, N
2 molecules are nonpolar and smaller, compared with CH
4 molecules. For this reason, the differences in CO
2 and N
2 uptake are greater than the differences in CO
2 and CH
4 uptake. Since the narrow micropores allow the strongest interaction between the carbonaceous solid and the hydrogen molecule, it is to be expected that this fraction of the porous volume will make a major contribution to the hydrogen adsorption capacity of the materials. Although hydrogen should only interact through induced polarization, surface chemistry may influence hydrogen adsorption on carbonaceous surfaces, particularly at sub-atmospheric pressures [
30,
31].
By comparing the quantities adsorbed by the phenol-formaldehyde carbons in
Figure 4 it can be seen that NKa-A82 is the sample with the greatest CO
2, CH
4, N
2 and H
2 uptakes over the sub-atmospheric pressure range tested. Moreover, the adsorption capacities of the three PF carbons are greater than that of the reference carbon, BPL. In terms of CO
2 adsorption, the performance at pressures below 20 kPa is quite similar for the NK and NOS carbons and it is only at higher pressures where NKa-A82 stands out. CH
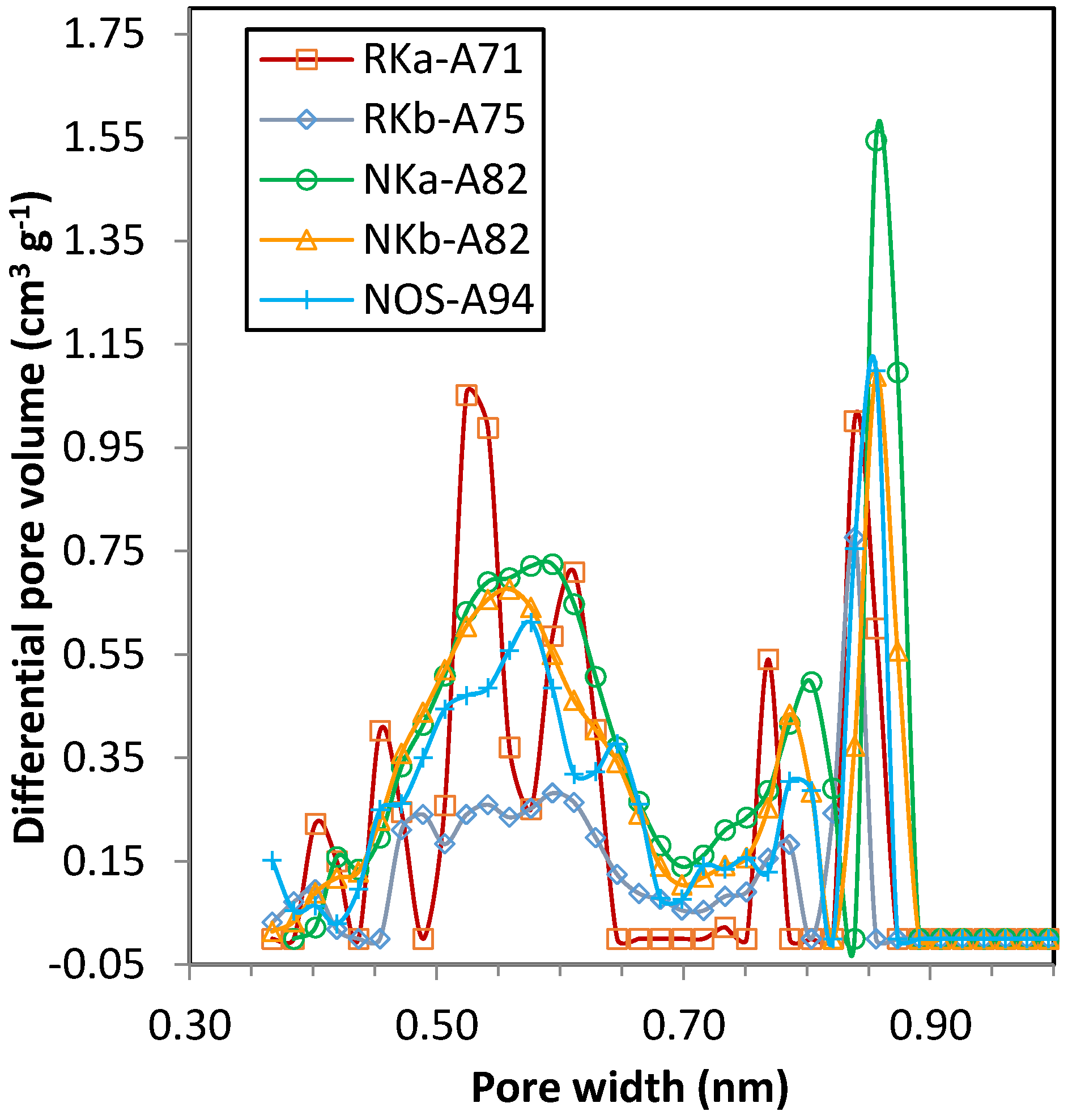
4 adsorption isotherms show differentiated uptakes for the three PF carbons that follow the order NKa > NOS > NKb. All three samples present relevant microporosity; in sample NKb narrow micropores (<1 nm) are mainly encountered, whereas for NKa and NOS microporosity >1 nm is also present, in agreement with the textural parameters estimated from the DR relation (see
Table 4). In this scenario selectivity effects related to the kinetic diameters of the two gas molecules (3.30 Å for CO
2 and 3.80 Å for CH
4) [
29] may play a role in the change in the CO
2 and CH
4 adsorption trends of the three PF carbons. N
2 and H
2 adsorption is characterised by linear isotherms that reveal the unspecific nature of the adsorbate-adsorbent interaction [
32].
The pure component CO
2, H
2, CH
4, and N
2 adsorption isotherms fitted to the Sips model (Equation (1)) are represented by the continuous lines in
Figure 4. The saturation capacities (
qs) and the parameter
n have been fitted to the adsorption data for the four gas species independently (
Table 5).
The Sips model reproduces the adsorption of CO2, CH4, and N2 with good accuracy, with substantial deviations for the adsorption of H2. It should be noted that the experimental H2 adsorption data at sub-atmospheric pressures and ambient temperature are subject to greater uncertainty due to the significantly lower uptakes of H2 under these conditions. The values of qs and b follow the trend CO2 > CH4 > N2 >> H2, as might be expected from the experimental data where the capacity and, consequently, the affinity of the carbons to adsorb CO2 and CH4 is one and two orders of magnitude greater than that of N2 and H2, respectively. The parameter n takes values close to unity for CO2 and CH4 while for N2 takes values of unity, suggesting that heterogeneity plays a minor role in these systems. The uneven fitting of the H2 isotherms for the studied carbons can be mainly ascribed to uncertainty of the experimental data. Sample NOS is where greatest deviation from unity in the values of n is found for the adsorption of CO2, CH4 and H2.
3.3.2. Multicomponent Adsorption Prediction
In order to predict multicomponent adsorption from binary CO
2-H
2, CO
2-CH
4, and CO
2-N
2 mixtures, the fitting of the single component adsorption data to the Sips model represented by Equation (1) was rerun to account for the interaction between components in each binary mixture. Given that CO
2 is the strongest adsorbate, the fitting was conducted keeping
qs constant (the value of
qs estimated from the fitting of single component CO
2 adsorption isotherm for each sample) and adjusting the
b and
n values to minimize the relative error for the pairs CO
2-H
2, CO
2-CH
4, and CO
2-N
2, respectively. The values of the parameters estimated from these fittings are collected in
Table 6.
The fitted parameters follow the same trend observed in the previous independent Sips fittings: the n values are close to unity and the b values follow the order CO2 > CH4 > N2 >> H2. When mixed the affinity, as represented by the parameter b, increases for the strong adsorbate (CO2) when compared to the pure component CO2 adsorption data independent fitting. Likewise, the weaker adsorbate shows a substantial decrease in affinity particularly in the CO2-H2 and CO2-N2 systems.
In this way, use of the parameters from the fitting of pure component data pairs guarantees the thermodynamic consistency of the resulting analytical expression of the multicomponent Sips model. Using the same analogy for extending the single-component Langmuir equation to that for multicomponent adsorption, the following equation is obtained for the multicomponent Sips model [
33]:
where
i and
j stand for the components in the binary mixture,
y is the mole fraction of the corresponding component in the gas phase, and
N is the number of components in the gas mixture,
i.e., 2. However, this equation only corresponds to a specific case of surface energetic heterogeneity. For normal activated carbons in which the energy sites are highly correlated, the Ideal Adsorbed Solution Theory (IAST) should be used. Application of the IAST with the concept of hypothetical pure-component pressure results in the following equation [
34]:
It can be seen that Equations (3) and (4) deliver different expressions to reproduce the multicomponent Sips model on the basis of different assumptions regarding the heterogeneity of the adsorbate-adsorbent system. Nevertheless, both equations were used in the present study to predict the binary adsorption equilibrium for CO
2-H
2, CO
2-CH
4, and CO
2-N
2 systems and the results are discussed and compared. The parameter values used for such multicomponent adsorption predictions were those previously obtained from the combined fitting of the pure component adsorption data of the pairs of gases in each mixture as shown in
Table 6.
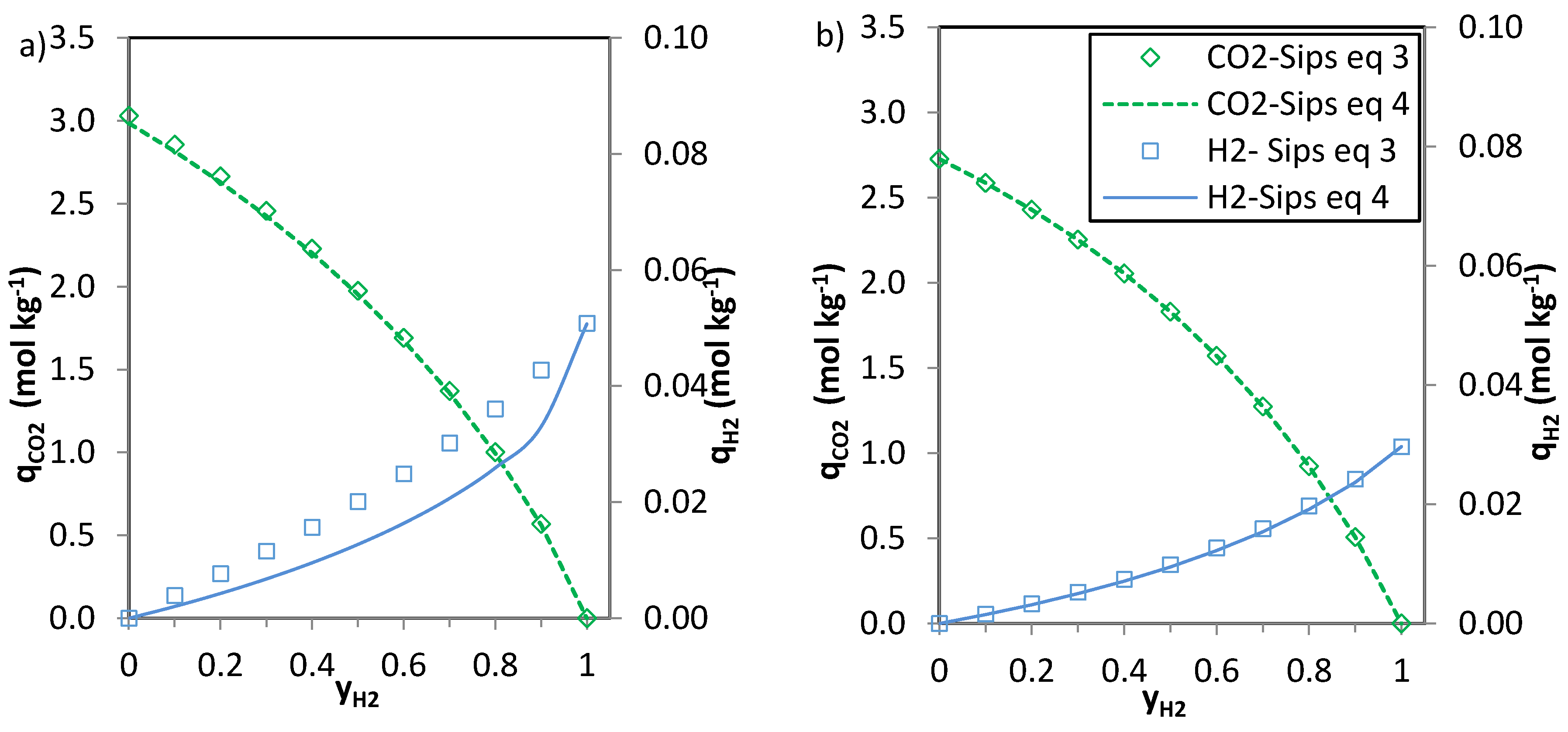
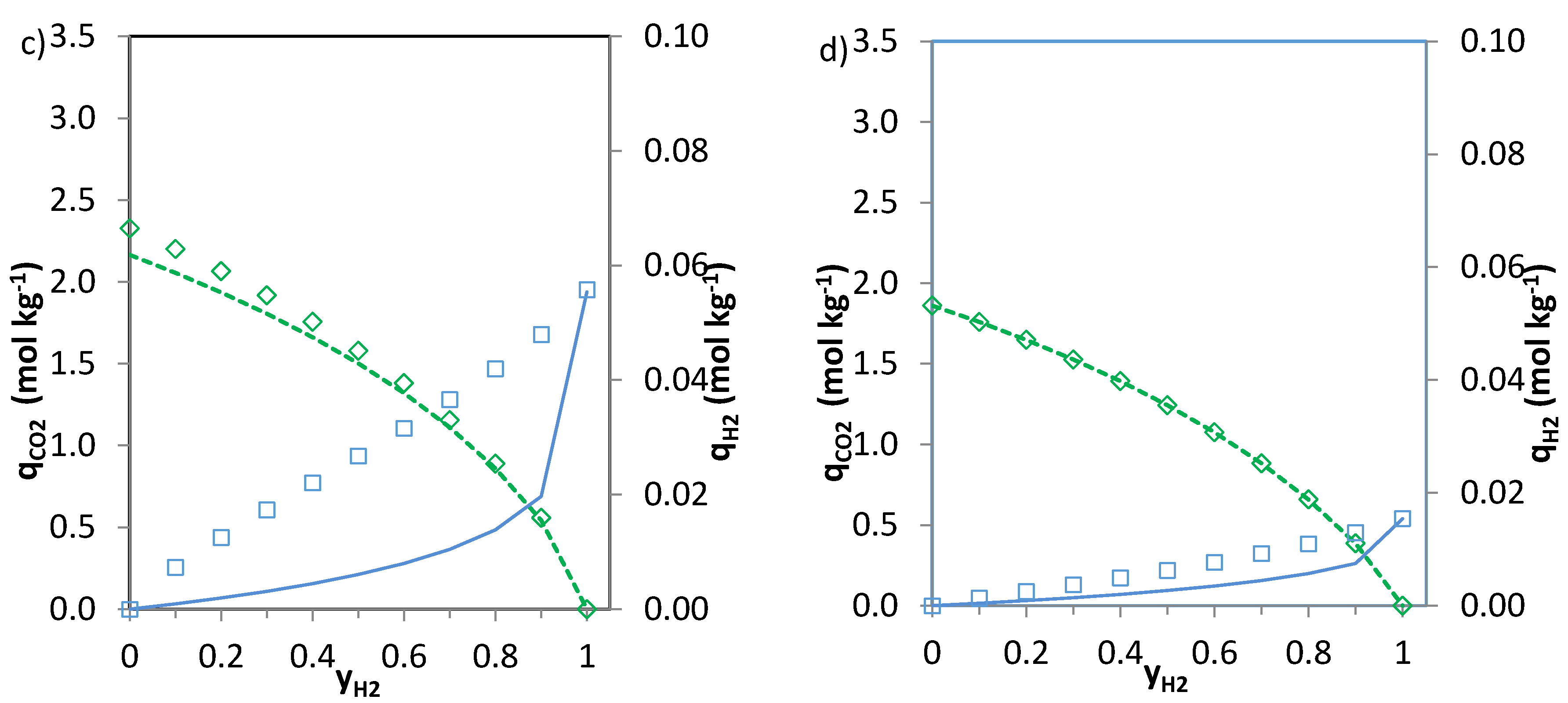
The predictions of the binary gas adsorption equilibria from the multicomponent Sips model represented by Equations (3) and (4) and from the parameters included in
Table 6 are depicted in
Figure 5,
Figure 6 and
Figure 7. Multicomponent predictions were assessed under the following temperature and pressure conditions: 25 °C and 100 kPa.
Globally, the predicted multicomponent adsorption isotherms show a reduction in the uptakes of the four components when mixed in binary CO2-H2, CO2-CH4 or CO2-N2 mixtures. However, while the CO2 uptake when mixed in a 1:1 molar ratio is reduced to 60%, 70% and 75% (average values for the four evaluated carbons in the CO2-CH4, CO2-N2 and CO2-H2 binary mixtures, respectively) of the pure gas CO2 adsorption at 25 °C and 100 kPa, the H2, N2 and CH4 uptakes drastically drop down to around 30–35% of those corresponding to pure gas adsorption. This suggests that the presence of another component in the mixture influences the adsorption of CO2 to a lesser extent.
It is apparent that when
n (
Table 6) approaches unity the values of the numerator and the denominator of Equations (3) and (4) tend to match each other and both Equations (3) and (4) give similar predictions. This suggests that there is little heterogeneity in the systems that could influence the adsorption of the binary mixtures onto the evaluated carbons. The CO
2-H
2 system is where greater deviations between the two predictions are observed, particularly for the H
2 uptake. It should be noted that at sub-atmospheric pressures and room temperature experimental H
2 adsorption is characterised by extremely low uptakes. In addition, the affinity of the carbons towards H
2 adsorption is significantly lower than that to CO
2. Consequently, binary adsorption prediction for the CO
2-H
2 system is subject to greater uncertainty. Moreover, predicted CO
2 adsorption in the CO
2-H
2 binary mixtures nearly matches pure component CO
2 adsorption at similar partial pressures suggesting that H
2 adsorption in these mixtures can be considered as negligible. This is in agreement with previous results from the research team [
6,
35].
The CO2 uptake at yj = 0 (where j stands for H2, N2 and CH4, respectively) is slightly overestimated for the CO2-H2 and CO2-N2 systems compared to the pure component CO2 adsorption data. This may be attributed to the different affinity of the adsorbent towards CO2 and H2 or N2.
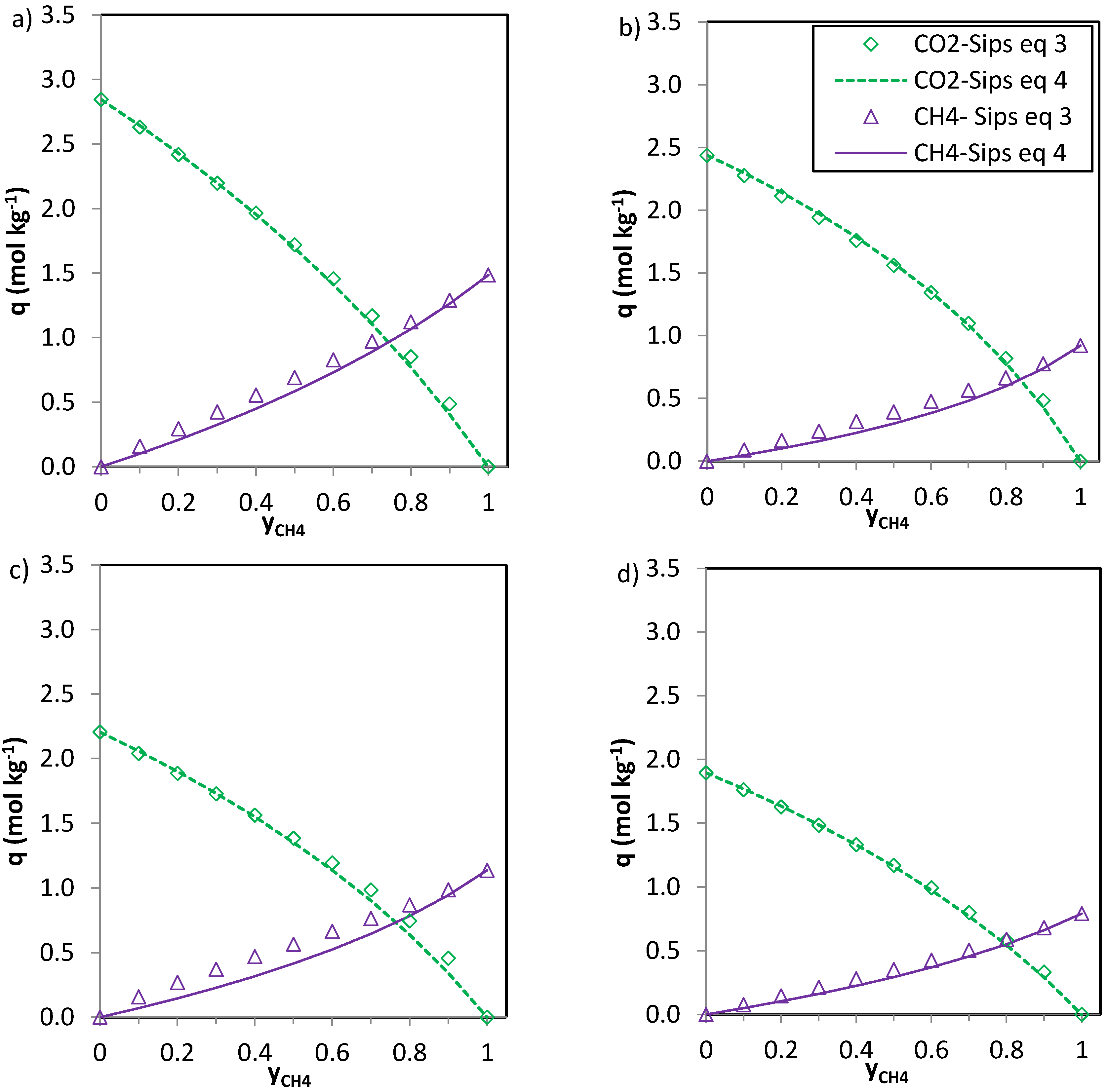
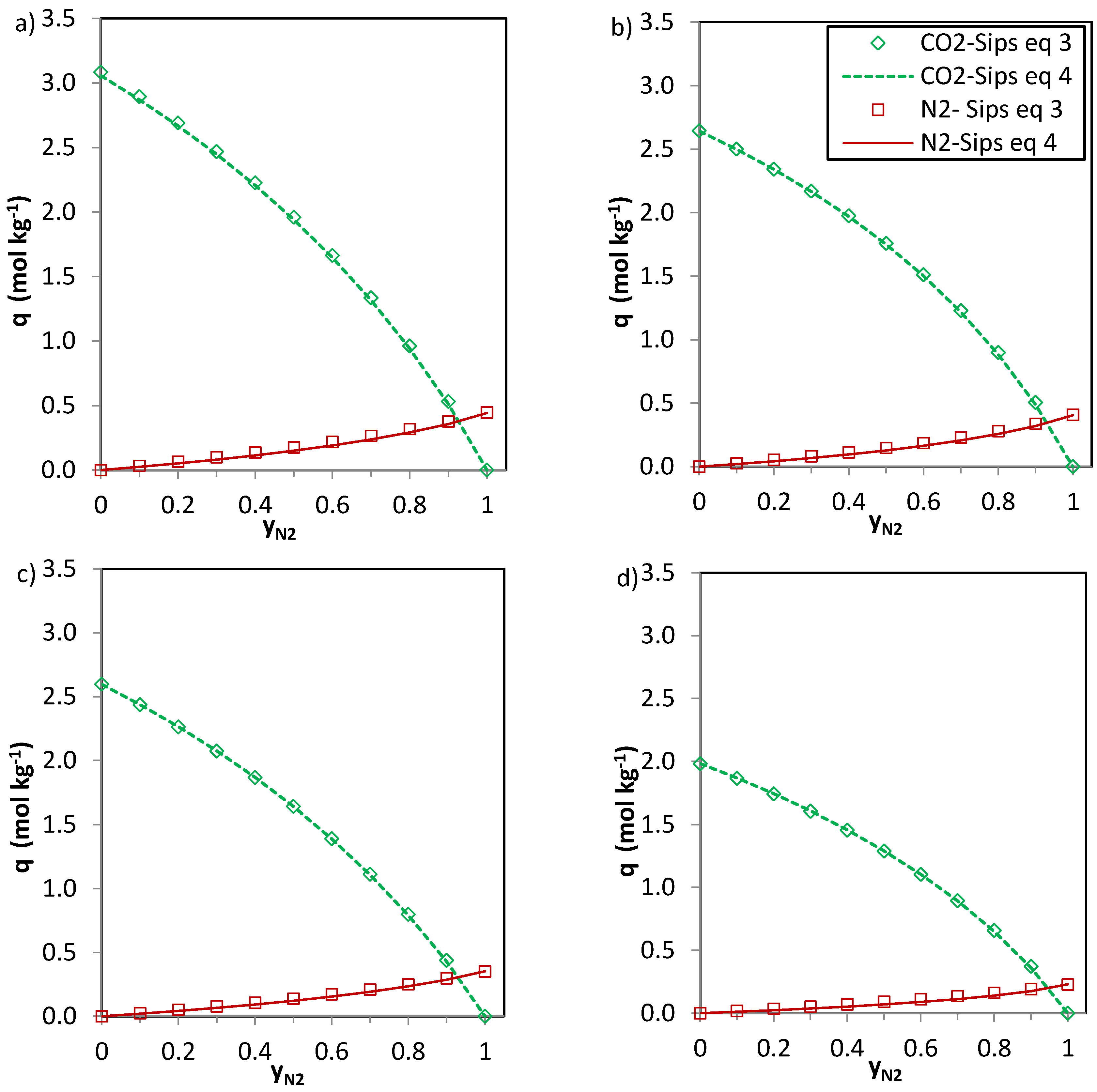
In the case of CO
2-CH
4 (
Figure 6) and CO
2-N
2 (
Figure 7) the predictions of the two Equations (3) and (4) seem consistent. The values of
n (
Table 6) are close to unity for the CO
2-N
2 system and thus Equations 3 and 4 deliver similar predictions. For the phenolic resin-biomass composite derived carbon, NOS-A94, Equation (3) predicts slightly greater CH
4 uptakes (+0.15 mol·kg
−1) than Equation (4) for molar fractions of methane (
yCH4) in the binary mixture between 0.3 and 0.6. Both CO
2 and CH
4 show specific interaction with the carbon surface, as reflected by the shape of the isotherms (type I, according to the IUPAC classification). However, despite the preferential adsorption of CO
2 over CH
4, competition between both adsorbates exists. The significantly higher critical temperature of CO
2 in comparison with CH
4 makes carbon dioxide more likely to behave as a condensable steam than as a supercritical gas, making it less volatile and increasing its chances of adsorption. Moreover, CO
2 presents a higher polarizability which may enhance attractive forces with the surface and a permanent quadrupole, leading to stronger interactions with any solid surface.
The simplified extended Sips model (Equation (3)) shows limitations bearing in mind the assumptions needed to extend the single component Sips equation to the multicomponent one. However, the observed deviations between the multicomponent predictions represented by Equations (3) and (4) are small and therefore, both could be applied to predict the adsorption of CO
2, CH
4, and N
2 on the evaluated carbons in binary CO
2-CH
4, and CO
2-N
2 mixtures. The H
2 uptakes predicted for the CO
2-H
2 systems should be handled with care given the uncertainty of the experimental H
2 adsorption data under sub-atmospheric pressures and room temperature. H
2 adsorption can be regarded as negligible in the CO
2-H
2 systems. Moreover, data on the performance of the phenolic resin-derived carbon for CO
2-CH
4 adsorption were also experimentally obtained in a lab scale fixed-bed adsorption unit. Details can be found elsewhere [
6]. The CO
2 and CH
4 uptakes assessed at 120 kPa and 25 °C for a 1:1 CO
2:CH
4 binary mixture are in good agreement with the multicomponent predictions at 100 kPa and 25 °C presented herein; for instance, the predicted CO
2 uptake on carbon NKa-A82 for a 1:1 CO
2:CH
4 mixture at 120 kPa is 1.90 mol·kg
−1 in agreement with 2.03 mol·kg
−1 estimated experimentally.