The Behaviour of Fracture Growth in Sedimentary Rocks: A Numerical Study Based on Hydraulic Fracturing Processes
Abstract
:1. Introduction
2. A Brief Introduction to the Numerical Code, RFPA
- The rock to be modelled is assumed to be composed of many mesoscopic elements. Here the mesoscopic elements that are used to represent the heterogeneity of rock are also utilized as the elements in the finite element analysis.
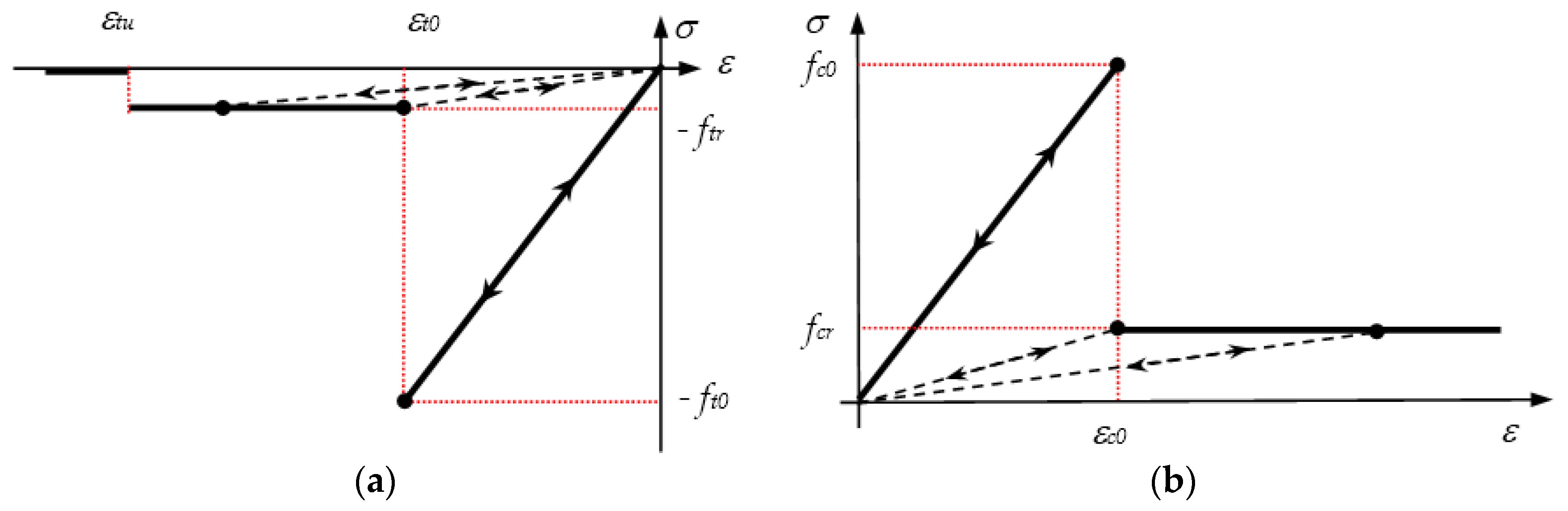
- The rock material at the elemental scale is assumed to be elasto-brittle with a residual strength. In the pre-peak region, the mesoscopic elements deform elastically, while in the post-peak region, the element will damage brittlely. The mechanical behaviour of rock is described by an elastic-damage constitutive law, and the residual strain/deformation upon unloading is not considered.
- An element is considered to fail in tensile mode when maximum tensile stress criterion is satisfied and fail in shear when the shear stress satisfies the Mohr-Coulomb failure criterion.
- The rock is assumed to be fully saturated with fluid flow governed by Darcy’s law. Additionally, the coupled process between stress/strain and fluid flow in the deforming rock mass is governed by Biot’s consolidation theory [22].
- The isotropic conditions are considered for the hydraulic behaviour at the elemental scale; the permeability of an element varies as a function of the stress state during elastic deformation, and increases dramatically when the element fails.
- The heterogeneity of rock materials is considered by assuming that the mechanical properties, such as Young’s modulus and the strength properties, conform to the Weibull distribution (specified by the Weibull distribution parameters).
2.1. Damage Evolution of the Element in Tensional State
2.2. Damage Evolution of the Element in Compressive State
- (1)
- initiate solution using a prescribed finite element mesh;
- (2)
- (3)
- conduct an effective stress analysis to solve for the mechanical displacements (Equations (2)–(4));
- (4)
- based on the strength criterions (Equations (8) and (12)), check the element state (damage or elasticity), those elements that are stressed beyond the pre-defined strength threshold levels are assumed to be brittlely damaged;
- (5)
- reconcile the coupling between the stress and flow (where D = 0);
- (6)
- update the mechanical and hydraulic properties for the evolution of damage (where D > 0).
- (7)
- the model, with its associated new parameters, is then reanalysed. The next load increment is added only when there are no more elements strained beyond the strength-threshold corresponding to the equilibrium stress field and a compatible strain field. The model iterates to follow the evolution of failure along a stress path in pseudo-time, until the next time step.
3. Numerical Simulation and Discussion
3.1. Hydraulic Fracturing Process in the Models without Interfaces
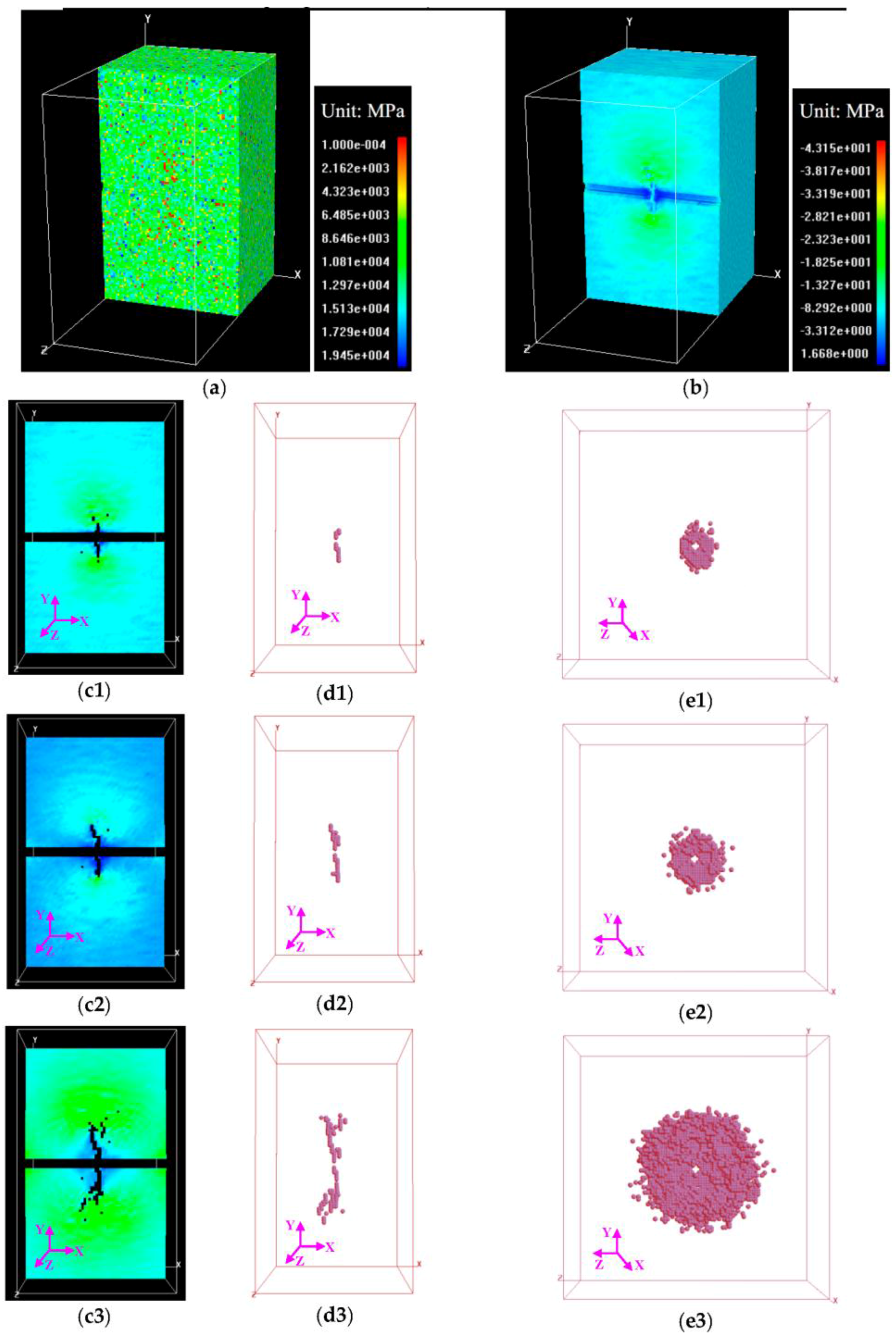
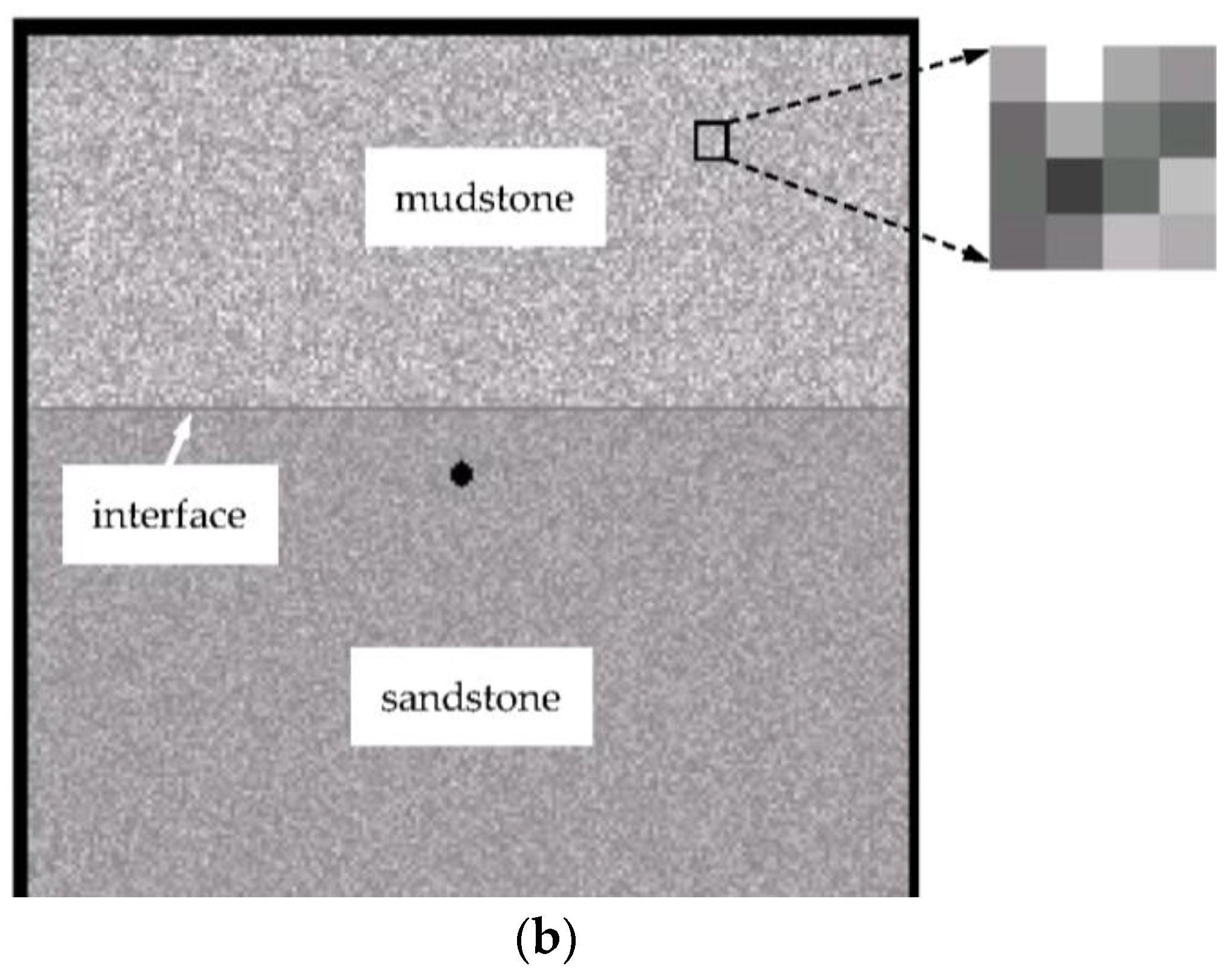
3.2. Hydraulic Fracturing Process in the Models with Interfaces
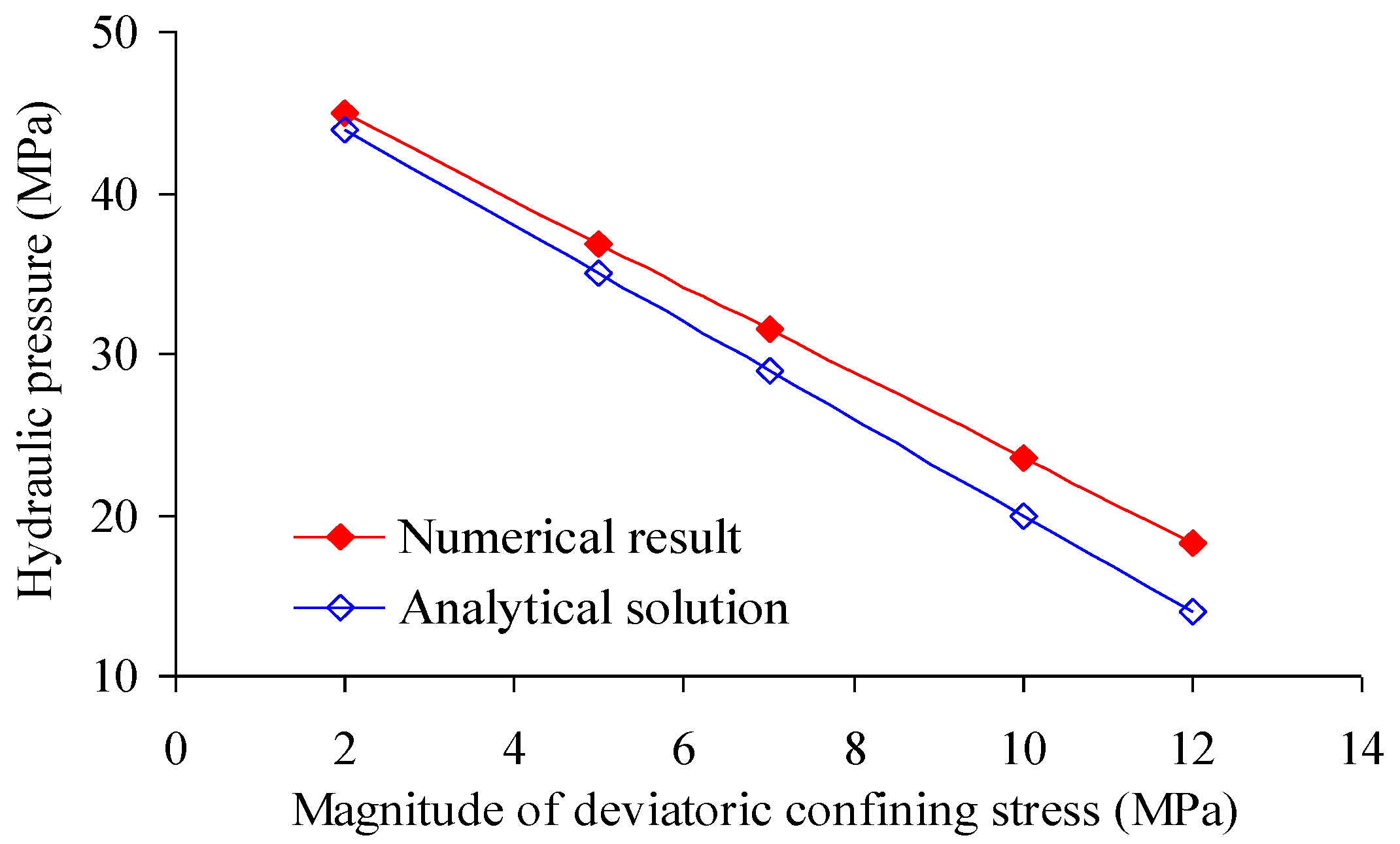
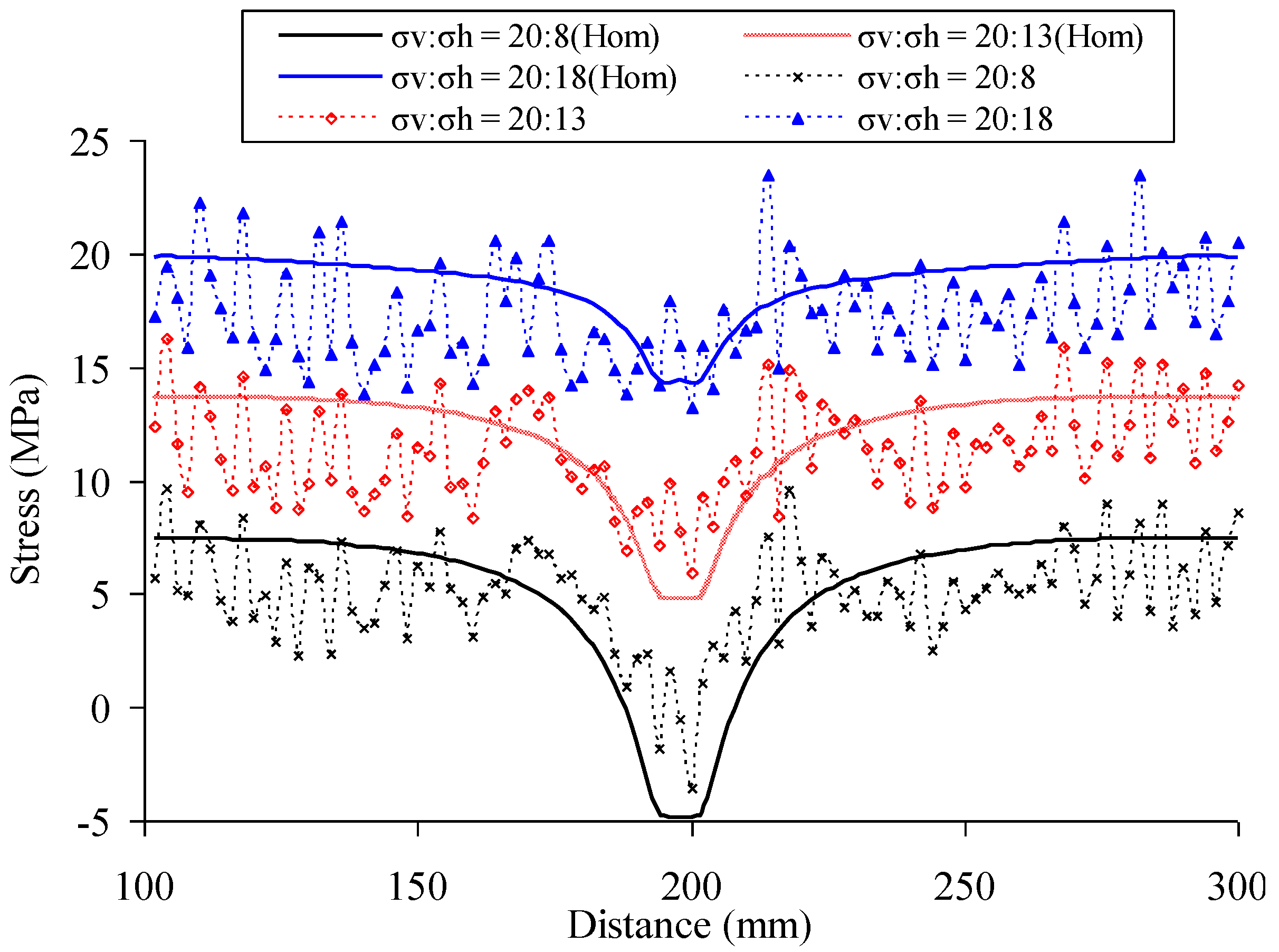
3.2.1. The Influence of Confining Stress on Hydro-Fracture Propagation
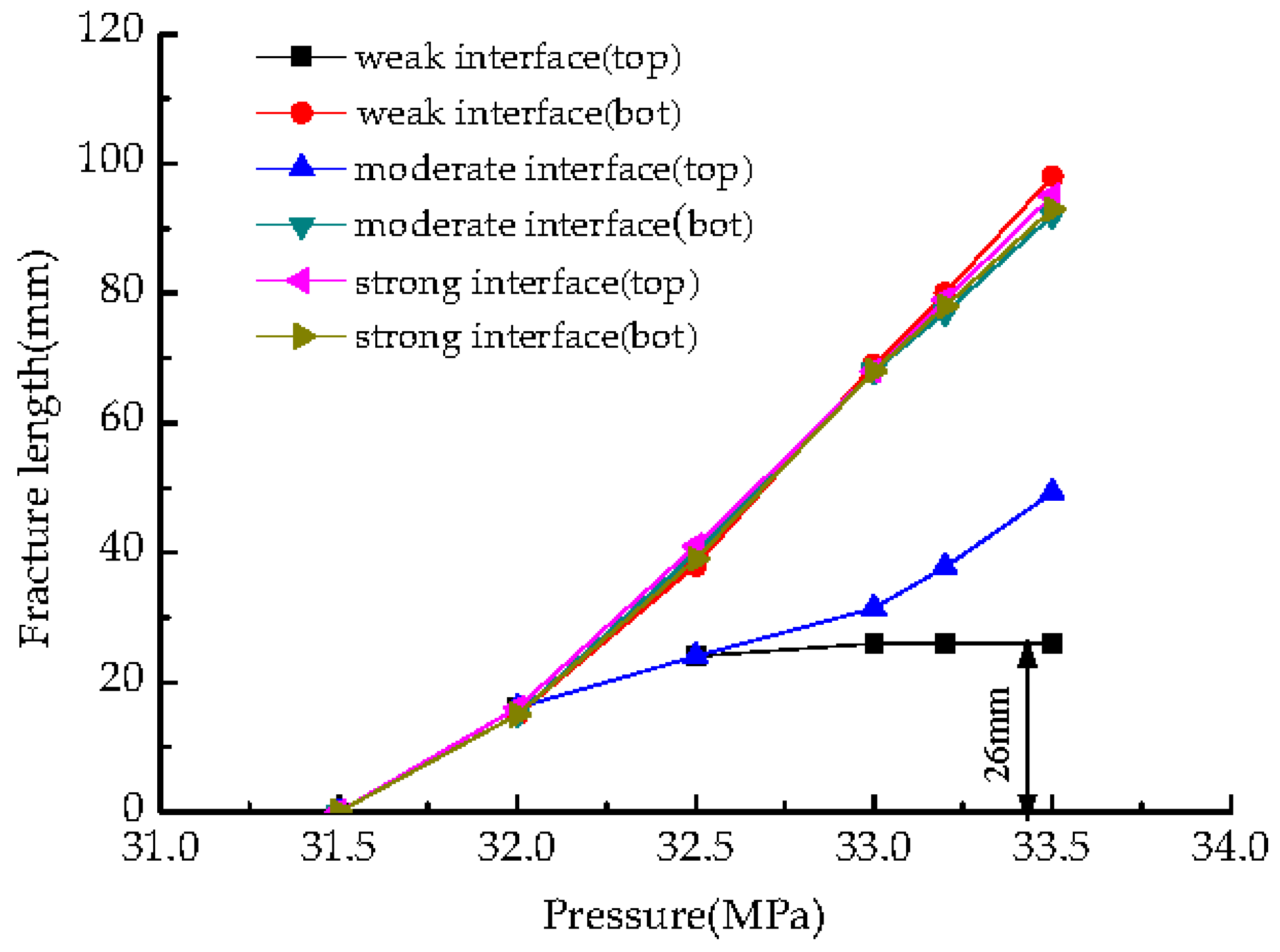
3.2.2. The Influence of Interface Strength on Hydro-Fracture Propagation
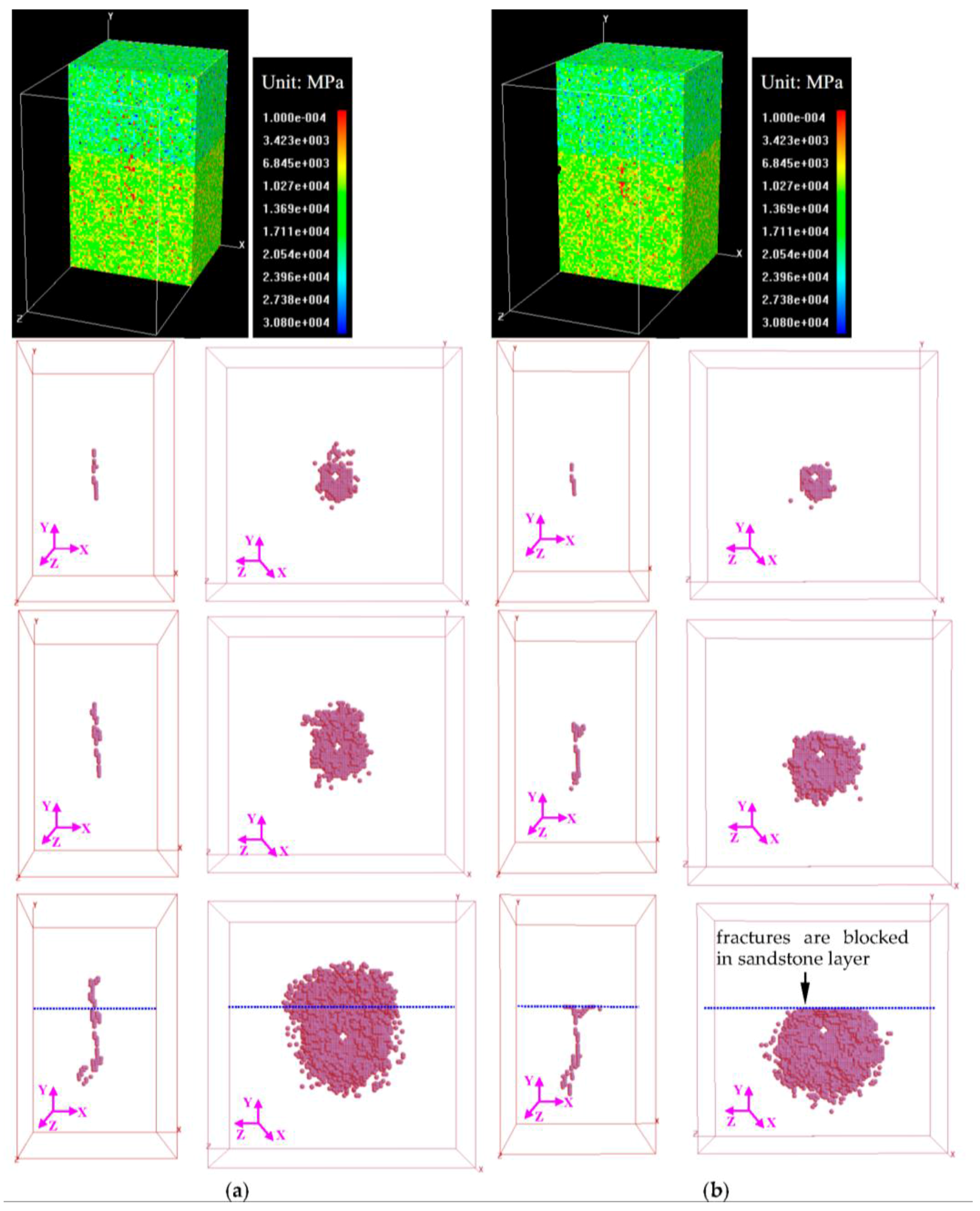
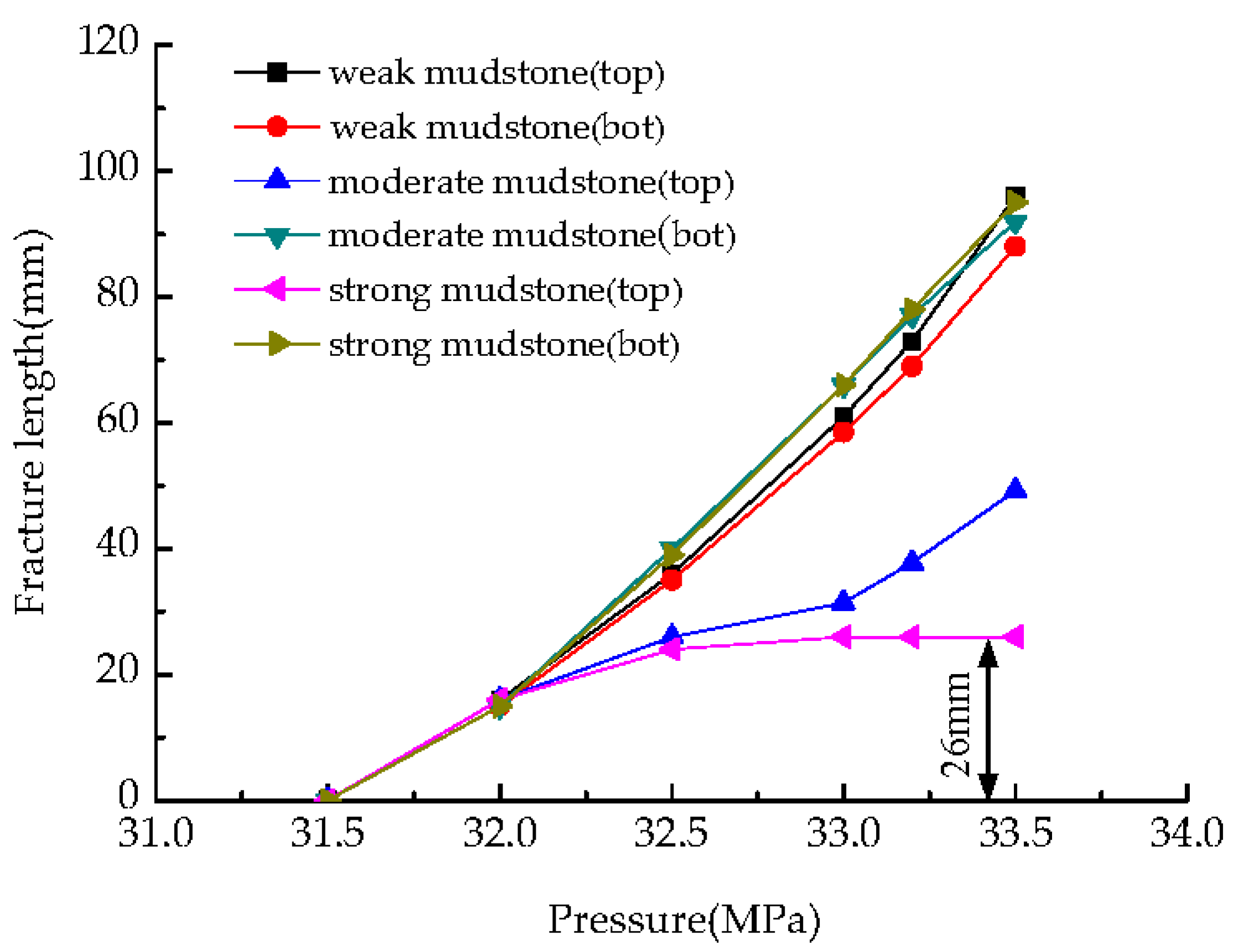
3.2.3. The Influence of Top Layer Strength on Hydro-Fracture Propagation
4. Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cooke, M.L.; Underwood, C.A. Fracture termination and step-over at bedding interfaces due to frictional slip and interface opening. J. Struct. Geol. 2001, 23, 223–238. [Google Scholar] [CrossRef]
- Clifton, H.E. Supply, segregation, successions, and significance of shallow marine conglomeratic deposits. Bull. Can. Pet. Geol. 2003, 51, 370–388. [Google Scholar] [CrossRef]
- Wang, Y.S.; Liu, H.M.; Gao, Y.J.; Tian, M.R.; Tang, D. Sandbody genesis and hydrocarbon accumulation mechanism of beach-bar reservoir in faulted-lacustrine-basins: A case study from the upper of the fourth member of Shahejie Formation, Dongying Sag. Front. Earth Sci. 2012, 19, 100–107. [Google Scholar]
- Li, L.C.; Wang, L.; Xia, Y.J.; Yang, T. The Feasibility of Developing Reserves in Beach-Bar Sandstone Reservoirs; Research Report of Oil Production Technology Research Institute, Shengli Oilfield Branch Company: Dongying, China, 2013. [Google Scholar]
- Warpinski, N.R.; Teufel, L.W. Influence of geologic discontinuities on hydraulic fracture propagation. J. Petrol. Technol. 1987, 39, 209–220. [Google Scholar] [CrossRef]
- Jeffrey, R.G. A symmetrically propped hydraulic fractures. SPE Prod. Facil. 1966, 11, 244–249. [Google Scholar]
- Zhang, X.; Jeffrey, R.G.; Thiercelin, M. Deflection and propagation of fluid-driven fractures at frictional bedding interfaces: A numerical investigation. J. Struct. Geol. 2007, 29, 396–410. [Google Scholar] [CrossRef]
- Han, G. Natural Fractures in Unconventional Reservoir Rocks: Identification, Characterization, and its Impact to Engineering Design. In Proceeding of the Conference on American Rock Mechanics, ARMA, San Francisco, CA, USA, 26–29 June 2011; pp. 11–509.
- Jeffrey, R.G.; Weber, C.R.; Vlahovic, W.; Enever, J.R. Hydraulic fracturing experiments in the great northern coal seam. In Proceedings of the 1994 SPE Asia Pacific Oil & Gas Conference, Melbourne, Austrila, 25–27 January 1994.
- Helgeson, D.E.; Aydin, A. Characteristics of joint propagation across layer interfaces in sedimentary rocks. J. Struct. Geol. 1991, 13, 897–911. [Google Scholar] [CrossRef]
- Gudmundsson, A.; Brenner, S.L. How hydro-fractures become arrested. Terra Nova 2001, 13, 456–462. [Google Scholar] [CrossRef]
- Gudmundsson, A.; Fjeldskaar, I.; Brenner, S.L. Propagation pathways and fluid transport of hydro-fractures in jointed and layered rocks in geothermal fields. J. Volcanol. Geotherm. Res. 2002, 116, 257–278. [Google Scholar] [CrossRef]
- Gudmundsson, A.; Simmenes, T.H.; Larsen, B.; Philipp, S.L. Effects of internal structure and local stresses on fracture propagation, deflection, and arrest in fault zones. J. Struct. Geol. 2010, 32, 1643–1655. [Google Scholar] [CrossRef]
- Adachi, J.; Siebrits, E.; Peirce, A.; Desroches, J. Computer simulation of hydraulic fractures. Int. J. Rock Mech. Min. Sci. 2007, 44, 739–757. [Google Scholar] [CrossRef]
- Zhang, X.; Jeffrey, R.G.; Thiercelin, M. Escape of fluid-driven fractures from frictional bedding interfaces: A numerical study. J. Struct. Geol. 2008, 30, 478–490. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, X.; He, J.; Wu, Y.; Zhang, B. Numerical analysis on the stability of hydraulic fracture propagation. Energies 2015, 8, 9860–9877. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, X.; Yuan, W.; He, J.; Li, G.; Wu, Y. Numerical Analysis on the Optimization of Hydraulic Fracture Networks. Energies 2015, 8, 12061–12079. [Google Scholar] [CrossRef]
- Ma, S.; Guo, J.C.; Li, L.L.; Xia, Y.J.; Yang, T. Experimental and numerical study on fracture propagation near open-hole horizontal well under hydraulic pressure. Eur. J. Environ. Civ. Eng. 2015. [Google Scholar] [CrossRef]
- Wen, X.L. Using horizontal well fracturing technology to improve reservoir reserve development ratio in the beach-bar sandstone reservoirs with low permeability. China Pet. Chem. Stand. Qual. 2012, 32, 1–2. [Google Scholar]
- Tang, C.A.; Tham, L.G.; Lee, P.K.K.; Yang, T.H.; Li, L.C. Coupled analysis of flow, stress and damage (FSD) in rock failure. Int. J. Rock. Mech. Min. Sci. 2002, 39, 477–489. [Google Scholar] [CrossRef]
- Li, L.C.; Tang, C.A.; Li, G.; Wang, S.Y.; Liang, Z.Z.; Zhang, Y.B. Numerical simulation of 3D hydraulic fracturing based on an improved flow-stress-damage model and a parallel FEM technique. Rock Mech. Rock Eng. 2012, 45, 801–818. [Google Scholar] [CrossRef]
- Biot, M.A. General theory of three-dimensional consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Weibull, W.A. A statistical distribution function of wide applicability. J. Appl. Mech. 1951, 18, 293–297. [Google Scholar]
- Tang, C.A.; Liu, H.; Lee, P.K.K.; Tsui, Y.; Tham, L.G. Numerical studies of the influence of microstructure on rock failure in uniaxial compression. Part I: Effect of heterogeneity. Int. J. Rock Mech. Min. Sci. 2000, 37, 555–569. [Google Scholar] [CrossRef]
- Wong, T.F.; Wong, R.H.C.; Chau, K.T.; Tang, C.A. Microcrack statistics, Weibull distribution and micromechanical modeling of compressive failure in rock. Mech. Mater. 2006, 38, 664–681. [Google Scholar] [CrossRef]
- Zhu, W.L.; Wong, T.F. Network modeling of the evolution of permeability and dilatancy in compact rock. J. Geophys. Res. 1999, 104, 2963–2971. [Google Scholar] [CrossRef]
- Yale, D.P.; Lyons, S.L.; Qin, G. Coupled geomechanics-fluid flow modeling in petroleum reservoirs: Coupled versus uncoupled response. In Pacific Rocks; Girard, J., Liebman, M., Breed, C., Doe, T., Eds.; Balkema: Rotterdam, The Netherlands, 2000; pp. 137–144. [Google Scholar]
- Lemaitre, J.; Desmorat, R. Engineering Damage Mechanics: Ductile, Creep, Fatigue and Brittle Failures; Springer-Verlag: Berlin, Germany, 2005. [Google Scholar]
- Murakami, S. Continuum Damage Mechanics—A Continuum Mechanics Approach to the Analysis of Damage and Fracture; Springer: New York, NY, USA, 2012. [Google Scholar]
- Mazars, J.; Pijaudier-Cabot, G. Continuum damage theory—Application to concrete. J. Eng. Mech. ASCE 1987, 115, 345–365. [Google Scholar] [CrossRef]
- Shimizu, H.; Murata, S.; Ishida, T. The distinct element analysis for hydraulic fracturing in hard rock considering fluid viscosity and particle size distribution. Int. J. Rock Mech. Min. Sci. 2011, 48, 712–727. [Google Scholar] [CrossRef]
- Petit, J.P.; Barquins, M. Can natural faults propagate under mode II conditions? Tectonics 1988, 7, 1243–1256. [Google Scholar] [CrossRef]
- Tang, C.A.; Kou, S.Q. Crack propagation and coalescence in brittle materials under compression. Eng. Fract. Mech. 1998, 61, 311–324. [Google Scholar] [CrossRef]
- Healy, D.; Jones, R.R.; Holdsworth, R.E. Three-dimensional brittle shear fracturing by tensile crack interaction. Nature 2006, 439. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Tang, C.A.; Li, L.C.; Li, H. An unconditionally stable explicit and precise multiple timescale finite element modeling scheme for the fully coupled hydro-mechanical analysis of saturated poroelastic media. Comput. Geotech. 2016, 71, 69–81. [Google Scholar] [CrossRef]
- Zhuang, X.; Huang, R.; Liang, C.; Rabczuk, T. A coupled thermo-hydro-mechanical model of jointed hard rock for compressed air energy storage. Math. Probl. Eng. 2014, 179169. [Google Scholar] [CrossRef]
- Lee, S.H.; Ghassemi, A. Three-dimensional thermo-poro-mechanical modeling of well stimulation and induced microseismicity. In Proceedings of the 45th US Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 26–29 June 2011.
- Rawal, C.; Ghassemi, A. Poroelastic rock failure analysis around multiple hydraulic fractures using a BEM/FEM model. In Proceedings of the 45th US Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 26–29 June 2011.
- Rabczuk, T.; Belytschko, T. A three dimensional large deformation meshfree method for arbitrary evolving cracks. Comput. Methods Appl. M 2007, 196, 2777–2799. [Google Scholar] [CrossRef]
- Rabczuk, T.; Zi, G.; Bordas, S.; Nguyen-Xuan, H. A simple and robust three-dimensional cracking-particle method without enrichment. Comput. Methods Appl. M 2010, 199, 2437–2455. [Google Scholar] [CrossRef]
- Rabczuk, T.; Bordas, S.; Zi, G. A three-dimensional meshfree method for continuous multiple crack initiation, nucleation and propagation in statics and dynamics. Comput. Mech. 2007, 40, 473–495. [Google Scholar] [CrossRef]
- Zhuang, X.; Augarde, C.; Mathisen, K. Fracture modelling using meshless methods and level sets in 3D: Framework and modelling. Int. J. Numer. Meth. Eng. 2012, 92, 969–998. [Google Scholar] [CrossRef]
- Budarapu, P.; Gracie, R.; Bordas, S.; Rabczuk, T. An adaptive multiscale method for quasi-static crack growth. Comput. Mech. 2014, 53, 1129–1148. [Google Scholar] [CrossRef]
- Yang, T.H.; Zhu, W.C.; Yu, Q.L.; Liu, H.L. The role of pore pressure during hydraulic fracturing and implications for groundwater outbursts in mining and tunnelling. Hydrogeol. J. 2011, 19, 995–1008. [Google Scholar] [CrossRef]
- Tang, C.A.; Tham, L.G.; Wang, S.H.; Liu, H.; Li, W.H. A numerical study of the influence of heterogeneity on the strength characterization of rock under uniaxial tension. Mech. Mater. 2007, 39, 326–339. [Google Scholar] [CrossRef]
- Cai, M.F.; He, M.C.; Liu, D.Y. Rock Mechanics and Engineering; Science Press: Beijing, China, 2002. [Google Scholar]
- Malvar, L.J.; Fourney, M.E. A three dimensional application of the smeared crack approach. Eng. Fract. Mech. 1990, 35, 251–260. [Google Scholar] [CrossRef]
- Pietruszczak, S.; Xu, G. Brittle response of concrete as a localization problem. Int. J. Solids Struct. 1995, 32, 1517–1533. [Google Scholar] [CrossRef]
- Pearce, C.J.; Thavalingam, A.; Liao, Z.; Bicanic, N. Computational aspects of the discontinuous deformation analysis framework for modeling concrete fracture. Eng. Fract. Mech. 2000, 65, 283–298. [Google Scholar] [CrossRef]
- Yuan, S.C.; Harrison, J.P. Development of a hydro-mechanical local degradation approach and its application to modelling fluid flow during progressive fracturing of heterogeneous rocks. Int. J. Rock Mech. Min. Sci. 2005, 42, 961–984. [Google Scholar] [CrossRef]
- Ma, G.W.; Wang, X.J.; Ren, F. Numerical simulation of compressive failure of heterogeneous rock-like materials using SPH method. Int. J. Rock Mech. Min. Sci. 2011, 48, 353–363. [Google Scholar] [CrossRef]
- Hubbert, M.K.; Willis, D.G. Mechanics of hydraulic fracturing. Trans AIME 1957, 210, 153–166. [Google Scholar]
- Haimson, B.C.; Fairhurst, C. Initiation and extension of hydraulic fractures in rock. Soc. Pet. Eng. J. 1967, 7, 310–318. [Google Scholar] [CrossRef]
- Medlin, W.L.; Fitch, J.L. Abnormal treating pressures in MHF treatments. In Proceedings of the 58th SPE Annual Technical Conference and Exhibition, San Francisco, CA, USA, 5–8 October 1983. SPE 12108.
- Hossain, M.M.; Rahman, M.K. Numerical simulation of complex fracture growth during tight reservoir stimulation by hydraulic fracturing. J. Pet. Sci. Eng. 2008, 60, 86–104. [Google Scholar] [CrossRef]
- Erdogan, F.; Biricikoglu, V. Two bonded half planes with a crack going through the interface. Int. J. Eng. Sci. 1973, 11, 745–766. [Google Scholar] [CrossRef]
- Pollard, D.D.; Aydin, A. Progress in understanding joints over the last century. Geol. Soc. Am. Bull. 1988, 100, 1181–1204. [Google Scholar] [CrossRef]
- Zhu, W.C.; Tang, C.A.; Wang, S.Y. Numerical study on the influence of mesomechanical properties on macroscopic fracture of concrete. Struct. Eng. Mech. 2005, 19, 519–533. [Google Scholar] [CrossRef]
- Li, L.C.; Yang, T.H.; Liang, Z.Z.; Zhu, W.C.; Tang, C.A. Numerical investigation of groundwater outbursts near faults in underground coal mines. Int. J. Coal Geol. 2011, 85, 276–288. [Google Scholar]
- Goodman, R.E. Introduction to Rock Mechanics; John Wiley: New York, NY, USA, 1989. [Google Scholar]
- Li, L.C.; Meng, Q.M.; Li, G.; Wang, S.Y. A numerical investigation of the hydraulic fracturing behavior of conglomerate in Glutenite formation. Acta Geotech. 2013. [Google Scholar] [CrossRef]
- Bonafede, M.; Rivalta, E. The tensile dislocation problem in a layered elastic medium. Geophys. J. Int. 1999, 136, 341–356. [Google Scholar] [CrossRef]
- Fairhurst, C. On the validity of the Brazilian test for brittle materials. Int. J. Rock Mech. Min. Sci. 1964, 1, 535–546. [Google Scholar] [CrossRef]
- Gross, M.R. The origin and spacing of cross-joints: Examples from the Monterey Formation, Santa Barbara, California. J. Struct. Geol. 1993, 15, 737–751. [Google Scholar] [CrossRef]
- Teufel, L.W.; Clark, J.C. Hydraulic fracture propagation in layered rocks: Experimental studies of fracture containment. Soc. Pet. Eng. J. 1984, 24, 19–34. [Google Scholar] [CrossRef]
- Renshaw, C.E.; Pollard, D.D. An experimentally verified criterion for propagation across unbonded frictional interfaces in brittle, linear elastic materials. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1995, 32, 237–249. [Google Scholar] [CrossRef]
- Zhao, S.X.; Yu, H.J. Economical production technologies research and application of ultra low permeability beach-bar sand reservoirs. Pet. Geol. Recovery Effic. 2009, 16, 96–98. [Google Scholar]
- Wang, F.Y.; Wu, X.D. Technology of water injection for beach-bar sand reservoirs with low permeability in Block Fan 151. Fault-Block Oil Gas Field 2010, 17, 596–598. [Google Scholar]
- Chawla, K.K. Composite Materials: Science and Engineering; Springer: New York, NY, USA, 1998. [Google Scholar]
- Larsen, B.; Grunnaleite, I.; Gudmundsson, A. How fracture systems affect permeability development in shallow-water carbonate rocks: An example from the Gargano Peninsula, Italy. J. Struct. Geol. 2010, 32, 1212–1230. [Google Scholar] [CrossRef]
- Charlez, P.A. Rock Mechanics: Petroleum Applications; Editions Technip: Paris, France, 1997; Volume 2. [Google Scholar]
- Thiercelin, M.; Roegiers, J.C.; Boone, T.J.; Ingraffea, A.R. An investigation of the material parameters that govern the behavior of fractures approaching rock interfaces. In Proceedings of the LSRM Sixth International Congress of Rock Mechanics, Montreal, QC, Canada, 30 August–3 September 1987; pp. 263–269.
- Li, C.Q. Investigation on the New Technology of Developing Reserves in Beach-Bar Sandstone Reservoirs; Research Report of Oil Production Technology Research Institute, Shengli Oilfield Branch Company: Dongying, China, 2009. [Google Scholar]
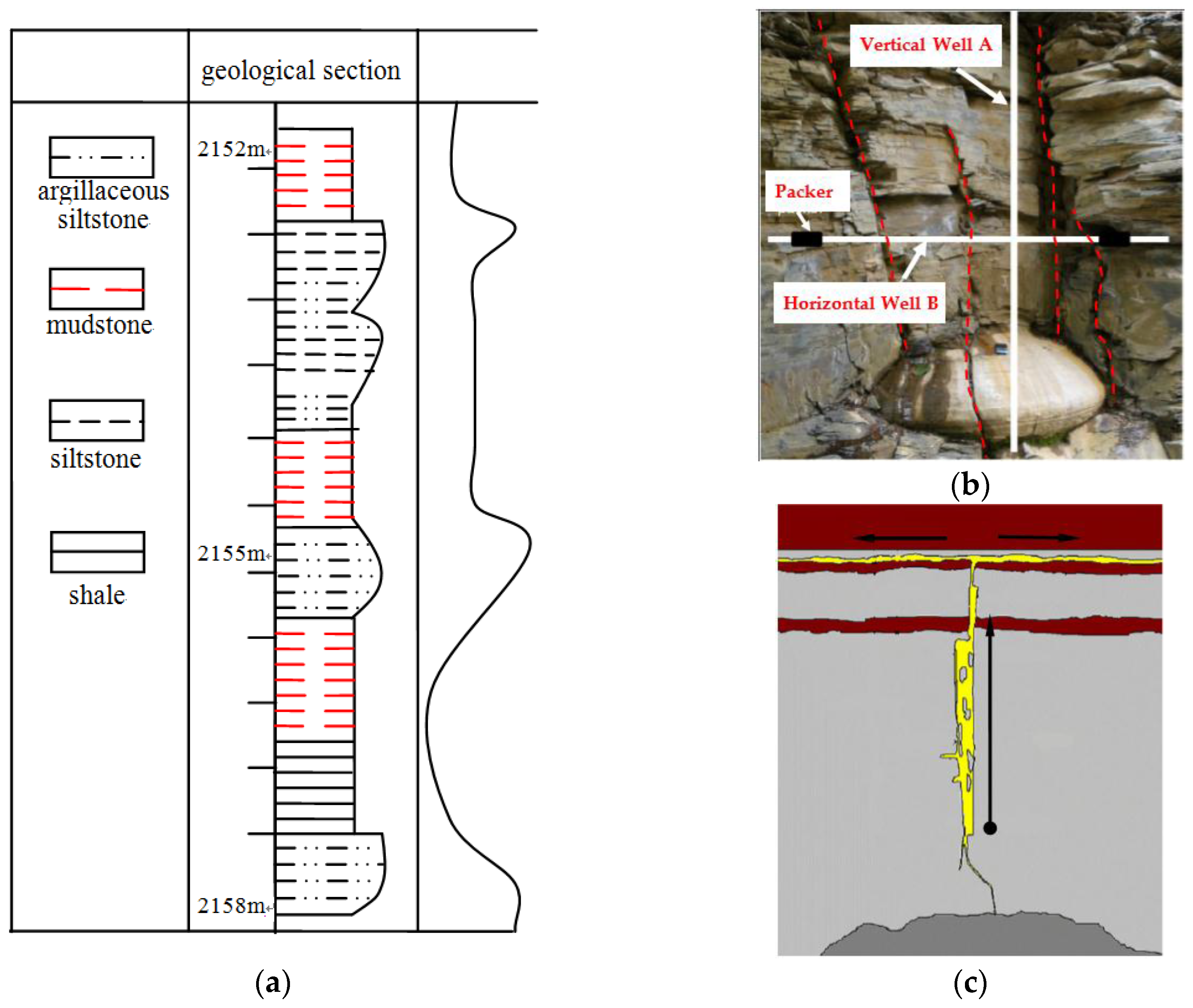

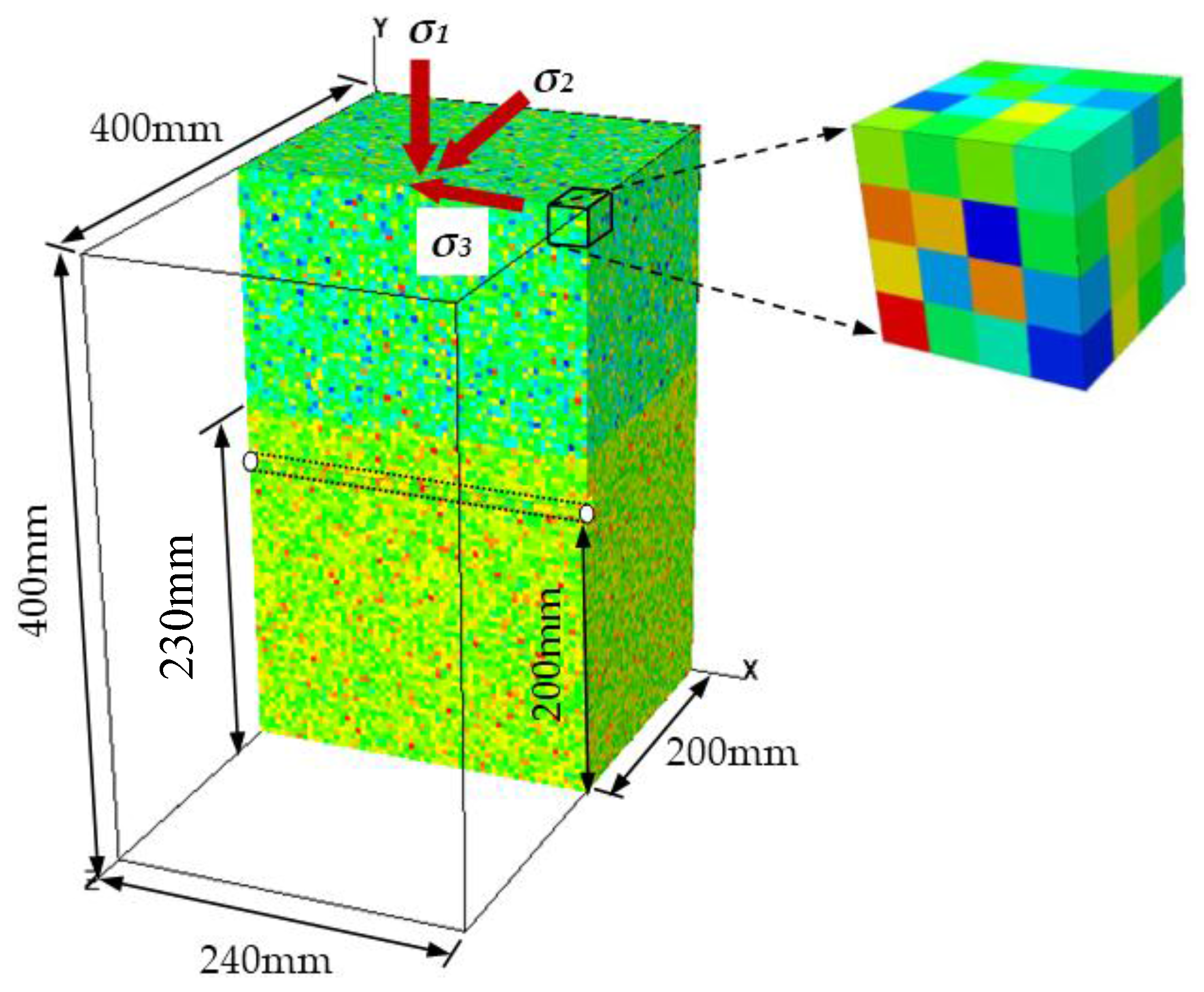
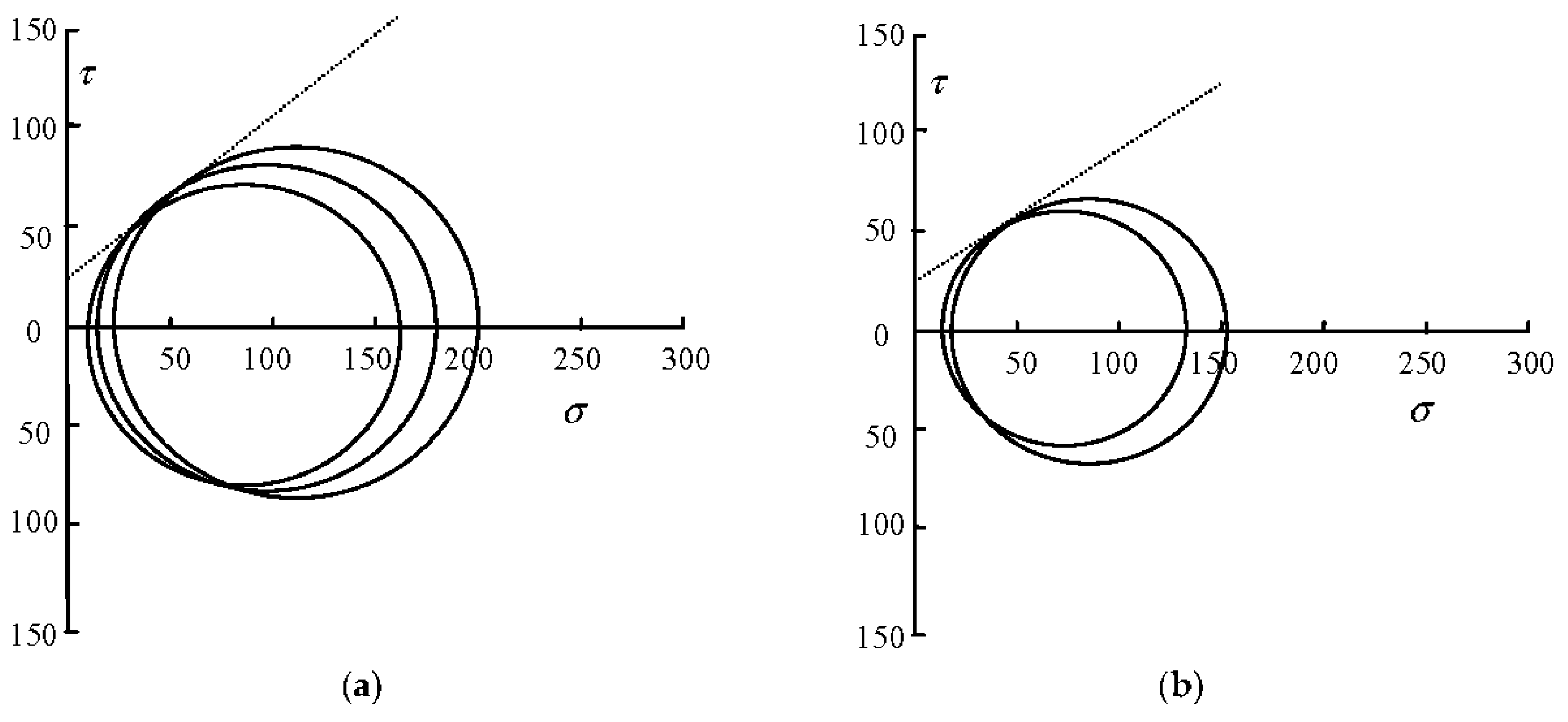

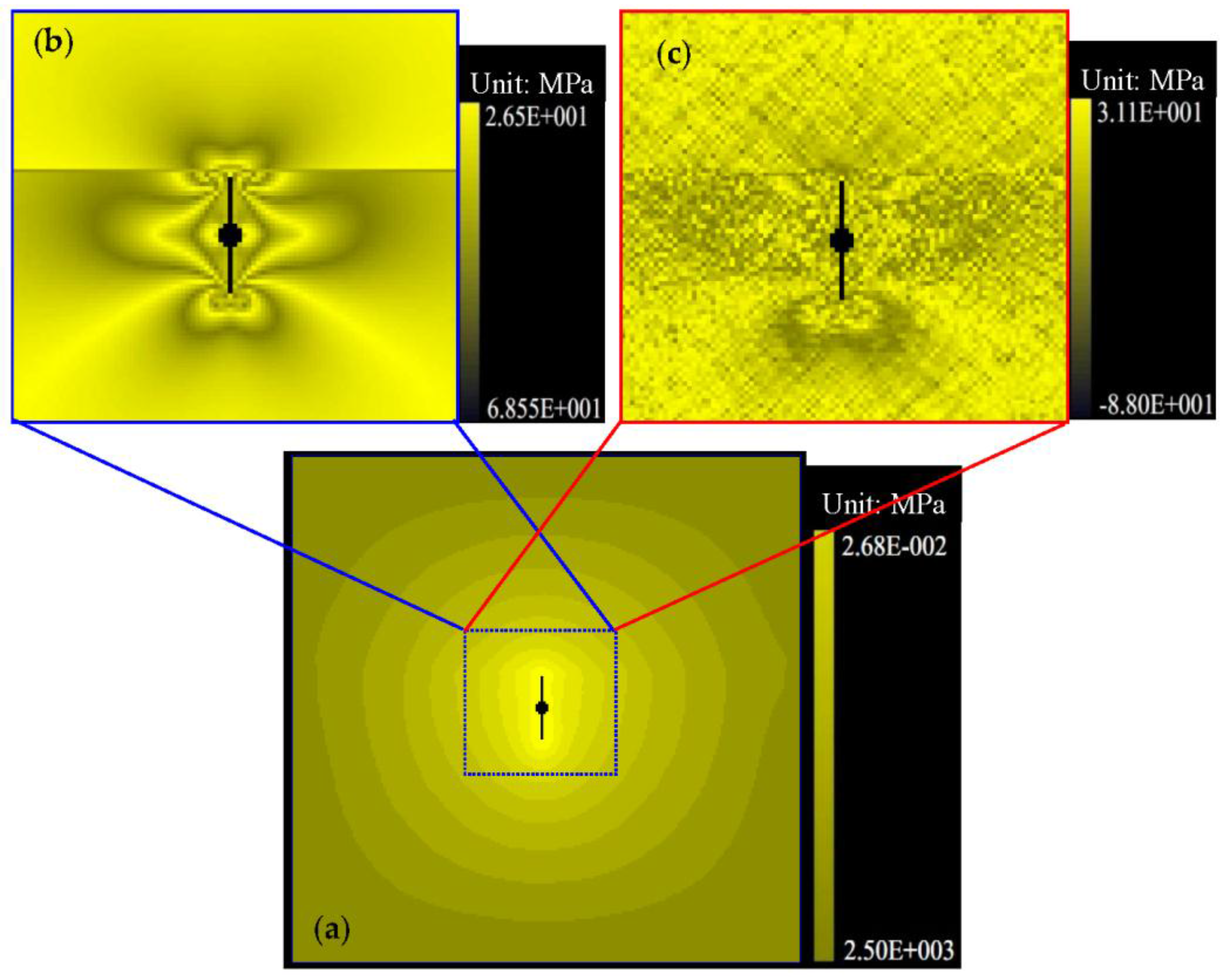







| Confining stress | Case I | Case II | Case III | Case IV | Case V |
|---|---|---|---|---|---|
| (MPa) | 20.0 | 20.0 | 20.0 | 20.0 | 20.0 |
| (MPa) | 8.0 | 10.0 | 13.0 | 15.0 | 18.0 |
| (MPa) | 5.0 | 5.0 | 5.0 | 5.0 | 5.0 |
| Well No. | Rock Formations | No. of Rock Core | Confining Stress (MPa) | Peak Strength (MPa) | Elastic Modulus (GPa) | Poisson’s Ratio |
|---|---|---|---|---|---|---|
| Bin-438A | mudstone | 0-1 | 10 | 160.53 | 19.56 | 0.162 |
| 0-2 | 15 | 179.36 | 21.58 | 0.174 | ||
| 0-3 | 20 | 197.65 | 26.72 | 0.204 | ||
| sandstone | 90-1 | 15 | 140.77 | 11.08 | 0.236 | |
| 90-2 | 20 | 154.20 | 11.53 | 0.287 |
| Parameters and Unit | Sandstone | Mudstone |
|---|---|---|
| Heterogeneity index (m) | 2.5 | 2.5 |
| Young’s modulus (E0), GPa | 9 | 15 |
| Uniaxial compressive strength (), MPa | 100 | 120 |
| Poisson’s ratio (v) | 0.25 | 0.2 |
| Internal friction angle (), ° | 30 | 35 |
| Uniaxial tensional strength (), MPa | 10 | 12 |
| Permeability coefficient (k0), cm/s | 1.0 × 10−7 | 1.0 × 10−8 |
| Coefficient of the pore water pressure (unfractured) (α) | 0.0001 | 0.0001 |
| Coefficient of the pore water pressure (fractured) (α) | 1.0 | 1.0 |
| Coupling coefficient (β) | 0.01 | 0.01 |
| Case | (MPa) | (MPa) |
|---|---|---|
| I | 20.0 | 8.0 |
| II | 20.0 | 13.0 |
| III | 20.0 | 18.0 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Xia, Y.; Huang, B.; Zhang, L.; Li, M.; Li, A. The Behaviour of Fracture Growth in Sedimentary Rocks: A Numerical Study Based on Hydraulic Fracturing Processes. Energies 2016, 9, 169. https://doi.org/10.3390/en9030169
Li L, Xia Y, Huang B, Zhang L, Li M, Li A. The Behaviour of Fracture Growth in Sedimentary Rocks: A Numerical Study Based on Hydraulic Fracturing Processes. Energies. 2016; 9(3):169. https://doi.org/10.3390/en9030169
Chicago/Turabian StyleLi, Lianchong, Yingjie Xia, Bo Huang, Liaoyuan Zhang, Ming Li, and Aishan Li. 2016. "The Behaviour of Fracture Growth in Sedimentary Rocks: A Numerical Study Based on Hydraulic Fracturing Processes" Energies 9, no. 3: 169. https://doi.org/10.3390/en9030169
APA StyleLi, L., Xia, Y., Huang, B., Zhang, L., Li, M., & Li, A. (2016). The Behaviour of Fracture Growth in Sedimentary Rocks: A Numerical Study Based on Hydraulic Fracturing Processes. Energies, 9(3), 169. https://doi.org/10.3390/en9030169





